Abstract
The nonlinear Schrödinger equation (NLS) is a canonical evolution equation, which describes the dynamics of weakly nonlinear wave packets in time and space in a wide range of physical media, such as nonlinear optics, cold gases, plasmas and hydrodynamics. Due to its integrability, the NLS provides families of exact solutions describing the dynamics of localised structures which can be observed experimentally in applicable nonlinear and dispersive media of interest. Depending on the co-ordinate of wave propagation, it is known that the NLS can be either expressed as a space- or time-evolution equation. Here, we discuss and examine in detail the limitation of the first-order asymptotic equivalence between these forms of the water wave NLS. In particular, we show that the the equivalence fails for specific periodic solutions. We will also emphasise the impact of the studies on application in geophysics and ocean engineering. We expect the results to stimulate similar studies for higher-order weakly nonlinear evolution equations and motivate numerical as well as experimental studies in nonlinear dispersive media.
1. Introduction
The theory of weakly nonlinear water waves has been found to be very useful for the modelling of ocean waves [1,2,3]. In finite and infinite water depth, the nonlinear Schrödinger equation (NLS) is the simplest evolution equation of this kind that takes into account dispersion and nonlinearity. Being an integrable equation, the NLS provides exact analytical solutions that describe the evolution of localised structures on the water surface in time and space, thus allowing subsequently the study and understanding of the dynamics of fundamental localised structures. The validity of the NLS has been experimentally confirmed even in the modelling of extreme localisations, beyond its well-known asymptotic limitations [4,5,6,7,8], and due to its interdisciplinary character analogies being able to be built into other nonlinear dispersive media, such as in optics [9], a research field in which several NLS applications have found strong interest [9,10,11,12,13,14]. Furthermore, the NLS admits basic models for the description of oceanic extreme events known as breathers [15,16,17]. Indeed, the family of Akhmediev breathers (ABs) [18] and Peregrine breathers [18,19] are strongly connected to the modulation instability (MI), also known as Benjamin–Feir instability [20], of Stokes waves [21]. In fact, the experimental investigation of exact solutions of the NLS, either numerically or in water wave facilities, has increased the degree of understanding of nonlinear and unstable water waves, as well as allowing the characterisation of the limitations of weakly nonlinear hydrodynamic models [8]. The choice of choosing the NLS representation of wave evolution in either time or space depends on the type of investigation, that is, depending on the space or time evolution coordinate of interest. Here, we investigate the asymptotic equivalence of both possible evolution expressions of the NLS within the context of exact solutions, ranging from stationary localised to pulsating and unstable envelopes. We show that, for a particular family of periodic solutions, such as it is the case for ABs, the latter equivalence is not valid. A detailed analysis of this feature, and its consequences and potential applications, will be discussed.
2. Analysis
We will first discuss the general propagation of wave packets with respect to either the space- or time-NLS, describing the asymptotic equivalence or otherwise, illustrating the mismatch of the localised wave propagation of exact NLS solutions, dimensionalized to satisfy both forms of the NLS in the spatio-temporal physical plane.
2.1. The Propagation of Wave Packets in Time and Space
In deep water, the spatio-temporal surface elevation is given by, at leading order, as one of the two expressions,
Here, denotes the complex conjugate, and are complex wave amplitudes of that are slowly varying relative to the phase . The omitted terms are , and the derivatives of are also . Later, we shall insert the small parameter α explicitly. The wave frequency ω and wavenumber k are related through the linear dispersion relation , where g denotes the gravitational acceleration. At the leading order in a weakly nonlinear asymptotic expansion, A satisfies the “space-NLS” equation [22]:
appropriate for an initial-value problem, which is set to be
For a hydrodynamic wavemaker problem, B satisfies the “time-NLS” equation [2]:
At the wavemaker, we impose the boundary condition
The “space-NLS” Equation (3) and the “time-NLS” Equation (6) are asymptotically equivalent up to , but importantly are not identical. In each of the Equations (1) and (2), the first two terms are , the remaining terms are , and the omitted terms are . At the leading linear non-dispersive order, , the solution of Equations (3) and (5) is , and the solution of Equations (6) and (8) is , since these must agree at this leading order,
Each of these distinct NLS equations can be cast into the same canonical form. Thus, in case A, we set
where denotes the complex conjugate. Then, Equation (3) takes the canonical form, in non-dimensional variables,
On the other hand, in case B, we set
It is useful to note that . The outcome is again the canonical NLS Equation (12). The transformations are identical, except that, in case A, T transforms to t but in case B, T transforms to x. This difference may be significant as we now show.
Each solution of the canonical Equation (12) generates a corresponding solution of either Equation (3) through the transformation Equation (10), or Equation (6) through the transformation Equation (13). The corresponding initial-value problem Equation (9) or wavemaker condition Equation (8) is obtained by putting in each case. Although the outcome is different, one might expect that, nevertheless, the solutions in each case will be asymptotically equivalent.
This is the issue that we will now explore. It is important to note that for any solution of Equation (12), then is also a solution for any real parameter . We shall take solutions of Equation (12) in this form so that the small parameter α is explicitly displayed. Then, asymptotic equivalence is expected in the limit when the amplitude parameter . Thus, each solution of Equation (12) generates a solution of the “space-NLS” Equation (3) or the “time-NLS” Equation (6),
where α is the wave steepness. These clearly agree at the leading order, being identical in the dependence on the dominant phase variable . However, they differ in the slow t and x dependence, and are in general only asymptotically equivalent when . That is apparently only when the solutions are localised around the phase line . In practice, solutions are used for small, but finite non-zero α and an asymptotic equivalence in the two types of NLS dynamics is expected. Next, we will discuss analytically the significant differences that will arise due to the two different dimensional transformations, especially for solutions which have a particular localisation. A detailed description of this latter fact will be discussed and illustrated in the next section with several specific examples.
2.2. The Evolution of Specific NLS Solutions
We will now discuss this equivalence or otherwise within the framework of some exact NLS solutions [15]. First, we consider the fundamental and stationary envelope soliton solution [23]:
This is a family of solutions with the single parameter being the amplitude α. Using the transformations Equations (14) or (15), respectively, we obtain the following two possible dimensional forms of this localised structure:
Note again that α is the wave steepness and that . These solutions differ only in the chirp factor, which, in case A, is a nonlinear frequency correction to the linear frequency ω, and, in case B, is a nonlinear wavenumber correction to the linear wavenumber k. However, these are asymptotically equivalent as from the linear dispersion relation . The spatio-temporal dynamics of the respective solutions from Equations (17) and (18) are plotted in Figure 1.
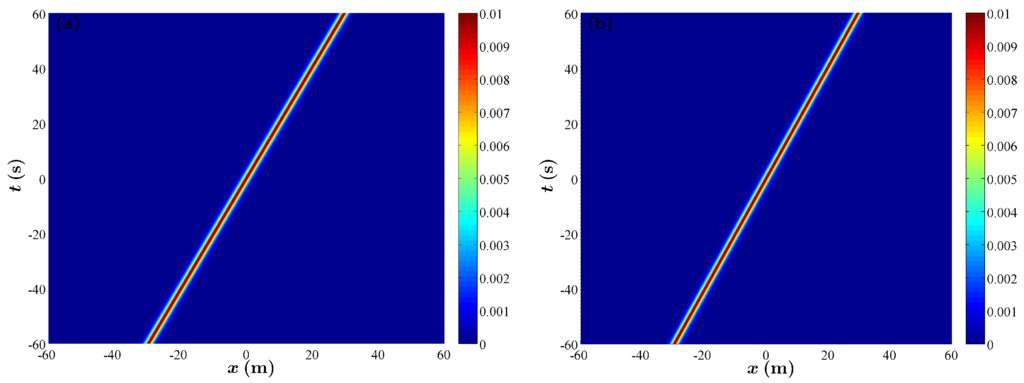
Figure 1.
(a) spatiotemporal evolution of the modulus of the soliton for the carrier parameters and m; (b) spatiotemporal evolution of the modulus of the soliton for the carrier parameters and m.
Second, we consider the doubly-localised Peregrine breather [19]:
Again, using the transformations (14) or (15), respectively, we obtain
Although these solutions are different both in the amplitude and in the chirp factor, they are asymptotically equivalent in the limit , as when , they are almost identical, and agree completely to within terms of . Importantly, the solutions are localised along . The respective solutions from Equations (20) and (21) are depicted in Figure 2.
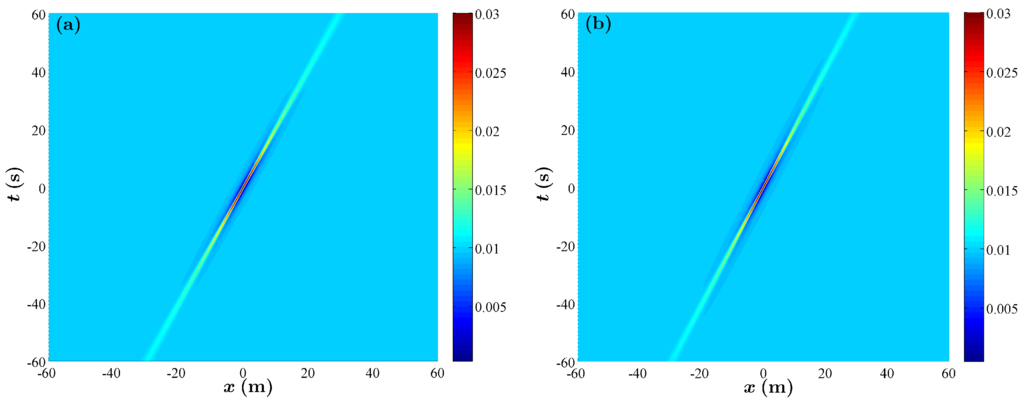
Figure 2.
(a) spatiotemporal evolution of the modulus of the Peregrine breather for the carrier parameters and m; (b) spatiotemporal evolution of the modulus of the Peregrine breather for the carrier parameters and m.
Next, we consider the periodic Kuznetsov–Ma breather [24,25]
where , and is a real-valued parameter. This is localised in X and periodic in T. After applying the transformations Equations (14) or (15), respectively, it becomes
Although formally different, each is localized in and periodic in , respectively. They are then asymptotically equivalent in the limit , as when , they are almost identical, and also agree completely to within terms of . The respective forms of the solutions from Equations (26) and (27) are plotted in Figure 3.
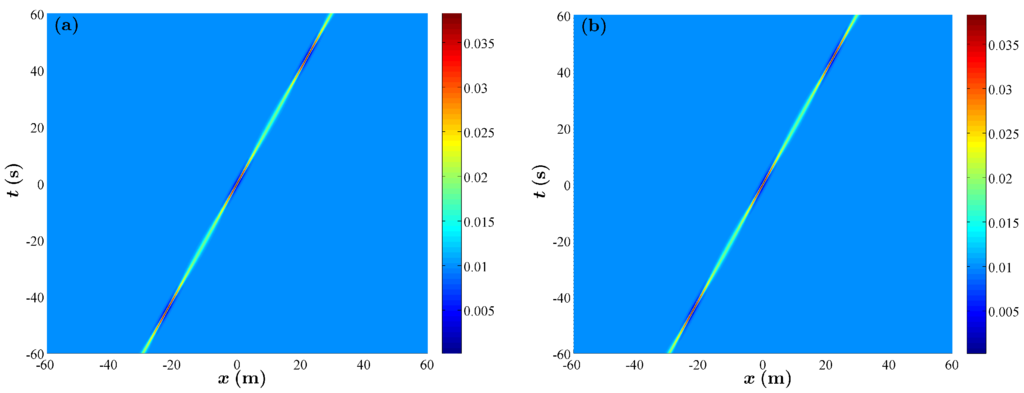
Figure 3.
(a) spatiotemporal evolution of the modulus of an Kuznetsov–Ma breather for and the carrier parameters and m; (b) spatiotemporal evolution of the modulus of an Kuznetsov breather for and the carrier parameters and m.
Finally, we consider the family of Akhmediev breathers (ABs) [18,26]
where , and is a real-valued parameter. This is periodic in X and localized in T. After transformation, as above, it becomes
Now, the case A and case B solutions are quite different. The respective solutions from Equations (26) and (27) are plotted in Figure 4.
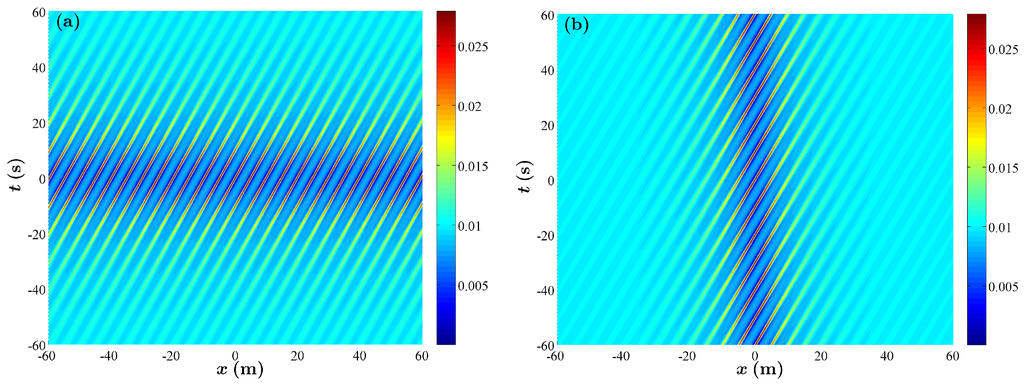
Figure 4.
(a) spatiotemporal evolution of the modulus of an AB for and the carrier parameters and m; (b) spatiotemporal evolution of the modulus of an AB for and the carrier parameters and m.
The explanation is that while both the breathers are periodic in , the A-breather is localized in t and the B-breather is localized in x. Hence, it is no longer possible to follow the solutions along the path where , and, therefore, establish asymptotic equivalence. Although, formally, the two solutions agree when , there is a persistent difference for small but finite α. We conclude that these two breathers are two distinct solutions in the physical space. This is reinforced by noting that to observe an A-breather in a wave tank, one should record a time series at a fixed location, but to observe a B-breather, this will not reveal the breather motion at the wavemaker , and, instead, one should take a snapshot at a fixed time and vice versa [27]. This fact is illustrated at the expected maximal breather focusing at in Figure 5.
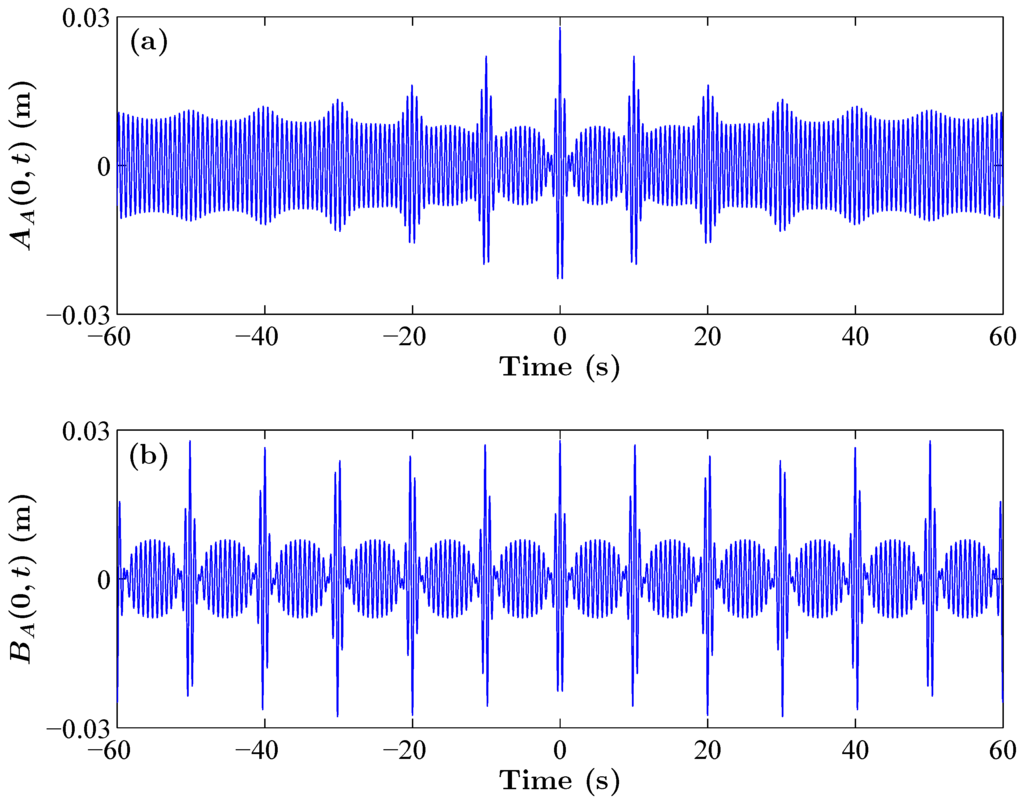
Figure 5.
(a) temporal surface variation of an AB for and background parameters and m; (b) temporal water surface variation of an AB for and background parameters and m.
Note that the evolution of the ABs for the A case have been reported in [28]. In the latter work, the boundary conditions, applied to the wave maker, define a gradual amplification of the periodic AB-type wave field. The boundary conditions, with respect to the case B, correspond to a slight homogeneous periodic perturbation of the constant background. The case B has been measured in [29,30]. We also would like to point out that the classical MI problem [20,31], starting from a three wave system, can be only described by ABs of case B. The temporal spectra of the case A when very large positive and negative time scales are considered would almost remain stationary, when the wave train is evolving in space.
3. Discussion and Conclusions
To conclude, we have discussed the asymptotic equivalence of localised structures within the framework of either the space- or the time-NLS. The choice of one of these two configurations of the NLS depends on whether one is interested in integrating the evolution of wave packets in time (as for numerical simulations), or in space (as for experimental purposes by tracking the evolution of waves along a water wave facility). We have the validity of this equivalence or otherwise by means of some exact solutions of the NLS. When the solutions exhibit a symmetry in the space coordinate with respect to Equation (12), as it is the case for Akhmediev breathers (ABs), the equivalence fails. Thus, it is physically possible to generate two types of AB solutions. This may be significant for applications. Indeed, breathers are nowadays used for several types of ocean engineering applications [32,33]. Generating ABs in a wave flume with respect to the space NLS allows for successive but progressive rogue waves gaining in amplitude with each impact at a fixed position, whereas with respect to the time-NLS, the solution would generate several extreme waves with similar envelope amplitudes in time, having different wave phases (and, therefore, different velocity fields), at the same position. When placing a model ship or offshore structure at the position of expected maximal AB compression, one could either study the wave impact related to progressive extreme events in the first case or to several rogue waves with similar significant heights in the second case. Indeed, it is known that deviations with respect to NLS dynamics are expected in an experiment, when the steepness of the carrier and the breather amplitude amplification are significant [8,34,35]. In fact, higher-order evolution equations such as the modified NLS [36,37,38], also known as Dysthe equations, or others [39,40,41] provide an accurate correction and a better prediction of the amplified wave field. These discrepancies with respect to NLS dynamics have an influence in the decay dynamics of the breathers after reaching the saturation point and a recurrence, referred to as Fermi–Pasta Ulam recurrence, is expected to occur [10,31,42,43,44]. We have also discussed the fact that, when considering the limiting case of infinite modulation period, which corresponds to the case of a Peregrine breather, both evolution dynamical forms become identical again in the dimensional spatio-temporal plane. We also expect these results to stimulate studies and applications in other nonlinear media such as in optics, Bose–Einstein Condensates, plasma and solids.
Acknowledgments
Amin Chabchoub is thankful to Odin Gramstad, Miguel Onorato and Nail Akhmediev for enlightening discussions. Amin Chabchoub acknowledges support from the Burgundy Region, the Association of German Engineers (VDI) and the Japan Society for the Promotion of Science (JSPS).
Author Contributions
Amin Chabchoub and Roger H. J. Grimshaw conducted the theoretical analysis, interpretation of the results and the writing of the manuscript equally.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| NLS | Nonlinear Schrödinger equation |
| MI | Modulation instability |
| AB | Akhmediev breather |
References
- Kharif, C.; Pelinovsky, E.; Slunyaev, A. Rogue Waves in the Ocean; Springer: Berlin, Germany, 2009. [Google Scholar]
- Osborne, A. Nonlinear Ocean Waves & the Inverse Scattering Transform; Academic Press: Amsterdam, The Netherlands, 2010; Volume 97. [Google Scholar]
- Babanin, A. Breaking and Dissipation of Ocean Surface Waves; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Yuen, H.C.; Lake, B.M. Nonlinear deep water waves: Theory and experiment. Phys. Fluids (1958–1988) 1975, 18, 956–960. [Google Scholar] [CrossRef]
- Chabchoub, A.; Hoffmann, N.; Akhmediev, N. Rogue wave observation in a water wave tank. Phys. Rev. Lett. 2011, 106, 204502. [Google Scholar] [CrossRef] [PubMed]
- Toffoli, A.; Waseda, T.; Houtani, H.; Kinoshita, T.; Collins, K.; Proment, D.; Onorato, M. Excitation of rogue waves in a variable medium: An experimental study on the interaction of water waves and currents. Phys. Rev. E 2013, 87, 051201. [Google Scholar] [CrossRef] [PubMed]
- Slunyaev, A.; Clauss, G.F.; Klein, M.; Onorato, M. Simulations and experiments of short intense envelope solitons of surface water waves. Phys. Fluids (1994–present) 2013, 25, 067105. [Google Scholar] [CrossRef]
- Chabchoub, A.; Onorato, M.; Akhmediev, N. Hydrodynamic solitons and breathers. In Rogue and Shock Waves; Onorato, M., Residori, S., Baronio, F., Eds.; Lecture Notes in Physics; Springer: Berlin, Germany, 2016. [Google Scholar]
- Chabchoub, A.; Kibler, B.; Finot, C.; Millot, G.; Onorato, M.; Dudley, J.M.; Babanin, A.V. The nonlinear Schrödinger equation and the propagation of weakly nonlinear waves in optical fibers and on the water surface. Ann. Phys. 2015, 361, 490–500. [Google Scholar] [CrossRef]
- Dudley, J.M.; Genty, G.; Dias, F.; Kibler, B.; Akhmediev, N. Modulation instability, akhmediev breathers and continuous wave supercontinuum generation. Opt. Express 2009, 17, 21497–21508. [Google Scholar] [CrossRef] [PubMed]
- Kibler, B.; Fatome, J.; Finot, C.; Millot, G.; Dias, F.; Genty, G.; Akhmediev, N.; Dudley, J.M. The Peregrine soliton in nonlinear fibre optics. Nat. Phys. 2010, 6, 790–795. [Google Scholar] [CrossRef]
- Onorato, M.; Residori, S.; Bortolozzo, U.; Montina, A.; Arecchi, F.T. Rogue waves and their generating mechanisms in different physical contexts. Phys. Rep. 2013, 528, 47–89. [Google Scholar] [CrossRef]
- Dudley, J.M.; Dias, F.; Erkintalo, M.; Genty, G. Instabilities, breathers and rogue waves in optics. Nat. Photonics 2014, 8, 755–764. [Google Scholar] [CrossRef]
- Tlidi, M.; Gandica, Y.; Sonnino, G.; Averlant, E.; Panajotov, K. Self-Replicating spots in the brusselator model and extreme events in the one-dimensional case with delay. Entropy 2016, 18, 64. [Google Scholar] [CrossRef]
- Dysthe, K.B.; Trulsen, K. Note on breather type solutions of the NLS as models for freak-waves. Phys. Scr. 1999, T82, 48–52. [Google Scholar] [CrossRef]
- Shrira, V.I.; Geogjaev, V.V. What makes the Peregrine soliton so special as a prototype of freak waves? J. Eng. Math. 2010, 67, 11–22. [Google Scholar] [CrossRef]
- Grimshaw, R.; Tovbis, A. Rogue waves: Analytical predictions. Proc. R. Soc. A 2013, 469, 20130094. [Google Scholar] [CrossRef]
- Akhmediev, N.; Eleonskii, V.M.; Kulagin, N.E. Generation of periodic trains of picosecond pulses in an optical fiber: Exact solutions. Sov. Phys. JETP 1985, 62, 894–899. [Google Scholar]
- Peregrine, D.H. Water waves, nonlinear Schrödinger equations and their solutions. J. Aust. Math. Soc. Series B. Appl. Math. 1983, 25, 16–43. [Google Scholar] [CrossRef]
- Benjamin, T.B.; Feir, J. The disintegration of wave trains on deep water Part 1. Theory. J. Fluid Mech. 1967, 27, 417–430. [Google Scholar] [CrossRef]
- Stokes, G.G. On the theory of oscillatory waves. Trans. Camb. Philos. Soc. 1847, 8, 441–473. [Google Scholar]
- Zakharov, V.E. Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Techn. Phys. 1968, 9, 190–194. [Google Scholar] [CrossRef]
- Shabat, A.; Zakharov, V. Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Sov. Phys. JETP 1972, 34, 62. [Google Scholar]
- Kuznetsov, E. Solitons in a parametrically unstable plasma. Akademiia Nauk SSSR Doklady 1977, 236, 575–577. [Google Scholar]
- Ma, Y.C. The perturbed plane-wave solutions of the cubic Schrödinger equation. Stud. Appl. Math. 1979, 60, 43–58. [Google Scholar] [CrossRef]
- Akhmediev, N.; Eleonskii, V.M.; Kulagin, N.E. Exact solutions of the first order of nonlinear Schrödinger equation. Theor. Math. Phys. (USSR) 1987, 72, 809–818. [Google Scholar] [CrossRef]
- Andonwati; Karjanto, N.; Van Groesen, E. Extreme wave phenomena in down-stream running modulated waves. Appl. Math. Model. 2007, 31, 1425–1443. [Google Scholar]
- Chabchoub, A.; Kibler, B.; Dudley, J.; Akhmediev, N. Hydrodynamics of periodic breathers. Philos. Trans. A Math. Phys. Eng. Sci. 2014, 372, 20140005. [Google Scholar] [CrossRef] [PubMed]
- Karjanto, N.; Van Groesen, E. Qualitative comparisons of experimental results on deterministic freak wave generation based on modulational instability. J. Hydro-Environ. Res. 2010, 3, 186–192. [Google Scholar] [CrossRef]
- Chabchoub, A.; Waseda, T. Hydrodynamic breathers modeling rogue waves. Proc. Violent Flows 2016, in press. [Google Scholar]
- Tulin, M.P.; Waseda, T. Laboratory observations of wave group evolution, including breaking effects. J. Fluid Mech. 1999, 378, 197–232. [Google Scholar] [CrossRef]
- Onorato, M.; Proment, D.; Clauss, G.; Klein, M. Rogue waves: From nonlinear Schrödinger breather solutions to sea-keeping test. PLoS ONE 2013, 8, e54629. [Google Scholar] [CrossRef] [PubMed]
- Alberello, A.; Chabchoub, A.; Babanin, A.V.; Monty, J.M.; Elsnab, J.; Lee, J.H.; Bitner-Gregersen, E.M.; Toffoli, A. The veolicty field underneath linear and nonlinear breaking waves. In Proceedings of the ASME 2016 30th International Conference on Ocean, Offshore and Arctic Engineering, Busan, Korea, 19–24 June 2016; p. 54481.
- Trulsen, K.; Dysthe, K.B. A modified nonlinear Schrödinger equation for broader bandwidth gravity waves on deep water. Wave Motion 1996, 24, 281–289. [Google Scholar] [CrossRef]
- Slunyaev, A.V.; Shrira, V.I. On the highest non-breaking wave in a group: Fully nonlinear water wave breathers versus weakly nonlinear theory. J. Fluid Mech. 2013, 735, 203–248. [Google Scholar] [CrossRef]
- Dysthe, K.B. Note on a modification to the nonlinear Schrödinger equation for application to deep water waves. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1979, 369, 105–114. [Google Scholar] [CrossRef]
- Trulsen, K.; Stansberg, C.T. Spatial evolution of water surface waves: Numerical simulation and experiment of bichromatic waves. In Proceedings of the Eleventh International Offshore and Polar Engineering Conference, Stavanger, Norway, 17–22 June 2001; International Society of Offshore and Polar Engineers: Mountain View, CA, USA, 2001. [Google Scholar]
- Chabchoub, A.; Hoffmann, N.; Onorato, M.; Genty, G.; Dudley, J.M.; Akhmediev, N. Hydrodynamic supercontinuum. Phys. Rev. Lett. 2013, 111, 054104. [Google Scholar] [CrossRef] [PubMed]
- Slunyaev, A. A high-order nonlinear envelope equation for gravity waves in finite-depth water. J. Exp. Theor. Phys. 2005, 101, 926–941. [Google Scholar] [CrossRef]
- Gramstad, O.; Trulsen, K. Hamiltonian form of the modified nonlinear Schrödinger equation for gravity waves on arbitrary depth. J. Fluid Mech. 2011, 670, 404–426. [Google Scholar] [CrossRef]
- Craig, W.; Guyenne, P.; Sulem, C. A Hamiltonian approach to nonlinear modulation of surface water waves. Wave Motion 2010, 47, 552–563. [Google Scholar] [CrossRef]
- Fermi, E.; Pasta, J.; Ulam, S. Studies of the Nonlinear Problems; Los Alamos Report LA-1940; Los Alamos Laboratory of the University of California: Los Alamos, NM, USA, 1955. [Google Scholar]
- Onorato, M.; Vozella, L.; Proment, D.; Lvov, Y.V. Route to thermalization in the α-Fermi–Pasta–Ulam system. Proc. Natl. Acad. Sci. USA 2015, 112, 4208–4213. [Google Scholar] [CrossRef] [PubMed]
- Kimmoun, O.; Hsu, H.C.; Branger, B.; Li, M.S.; Chen, Y.Y.; Kharif, C.; Onorato, M.; Kelleher, E.J.R.; Kibler, B.; Akhmediev, N.; et al. Modulation instability and phase-shifted Fermi-Pasta-Ulam recurrence. 2016; arXiv:1602.01604 [nlin.PS]. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).