A Time-Dependent Hierarchical Model for Elastic and Inelastic Scattering Data Analysis of Aerogels and Similar Soft Materials
Abstract
:1. Introduction
2. Results and Discussion
2.1. General Formalism of Stochastic Structural Models, and Its Relation to Scattering
2.2. The Hierarchical Model
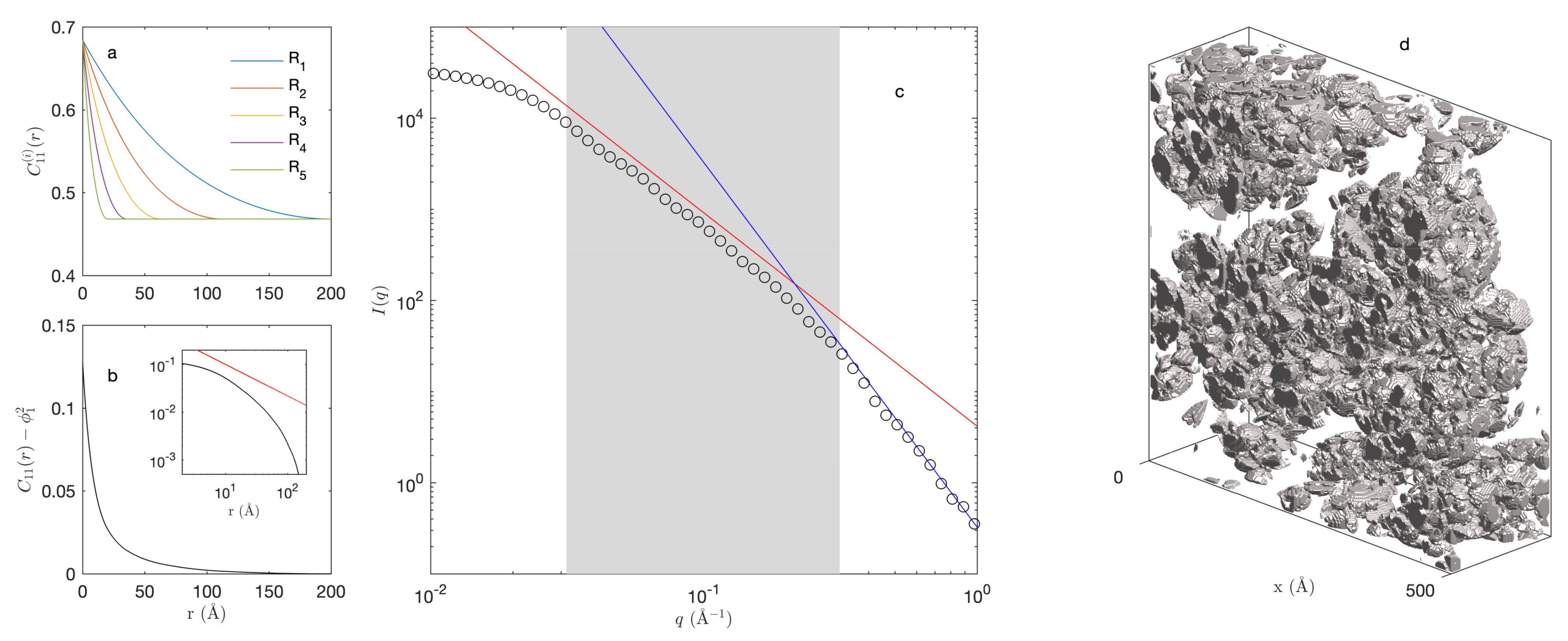
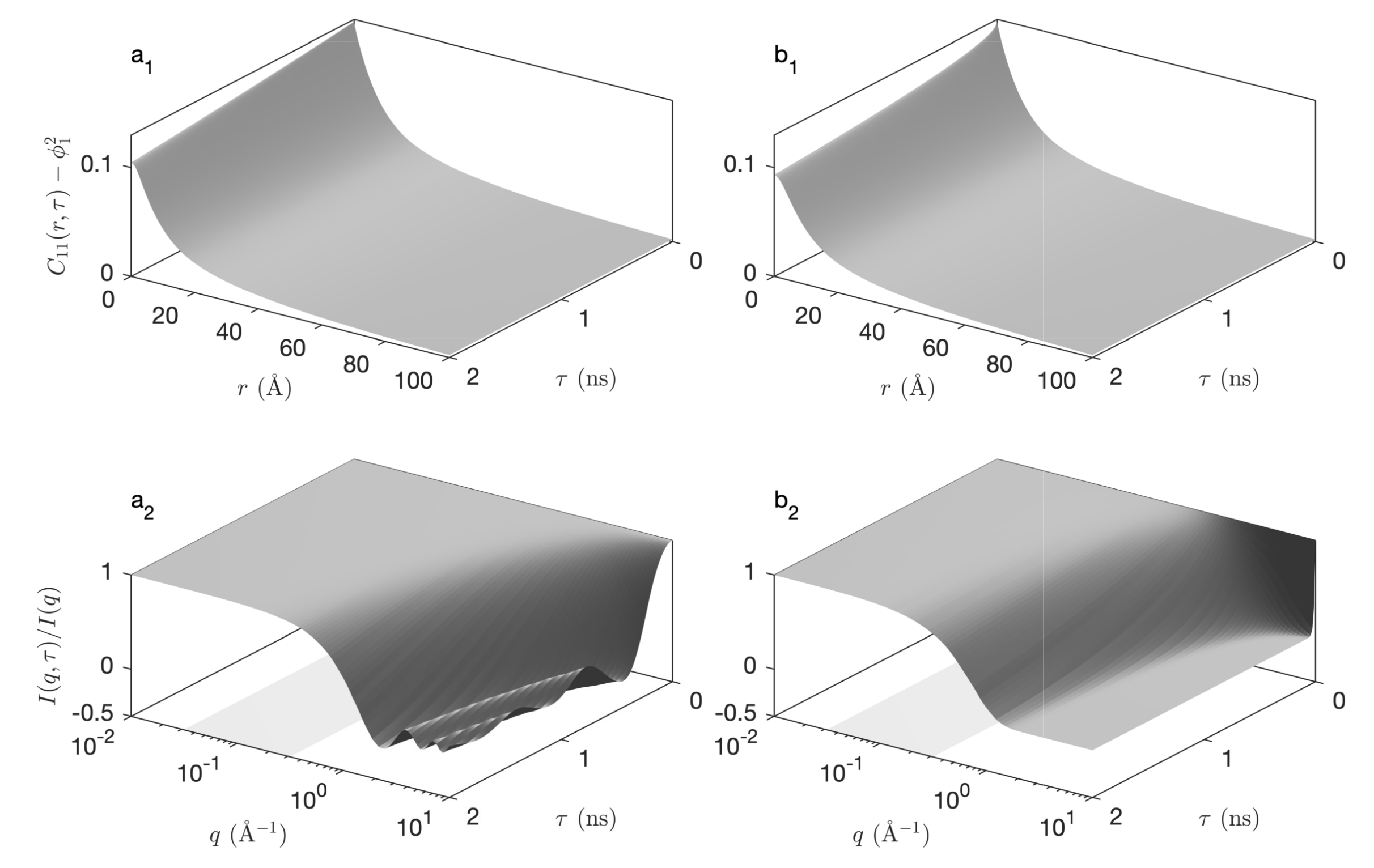
2.2.1. Static Properties: Elastic Scattering
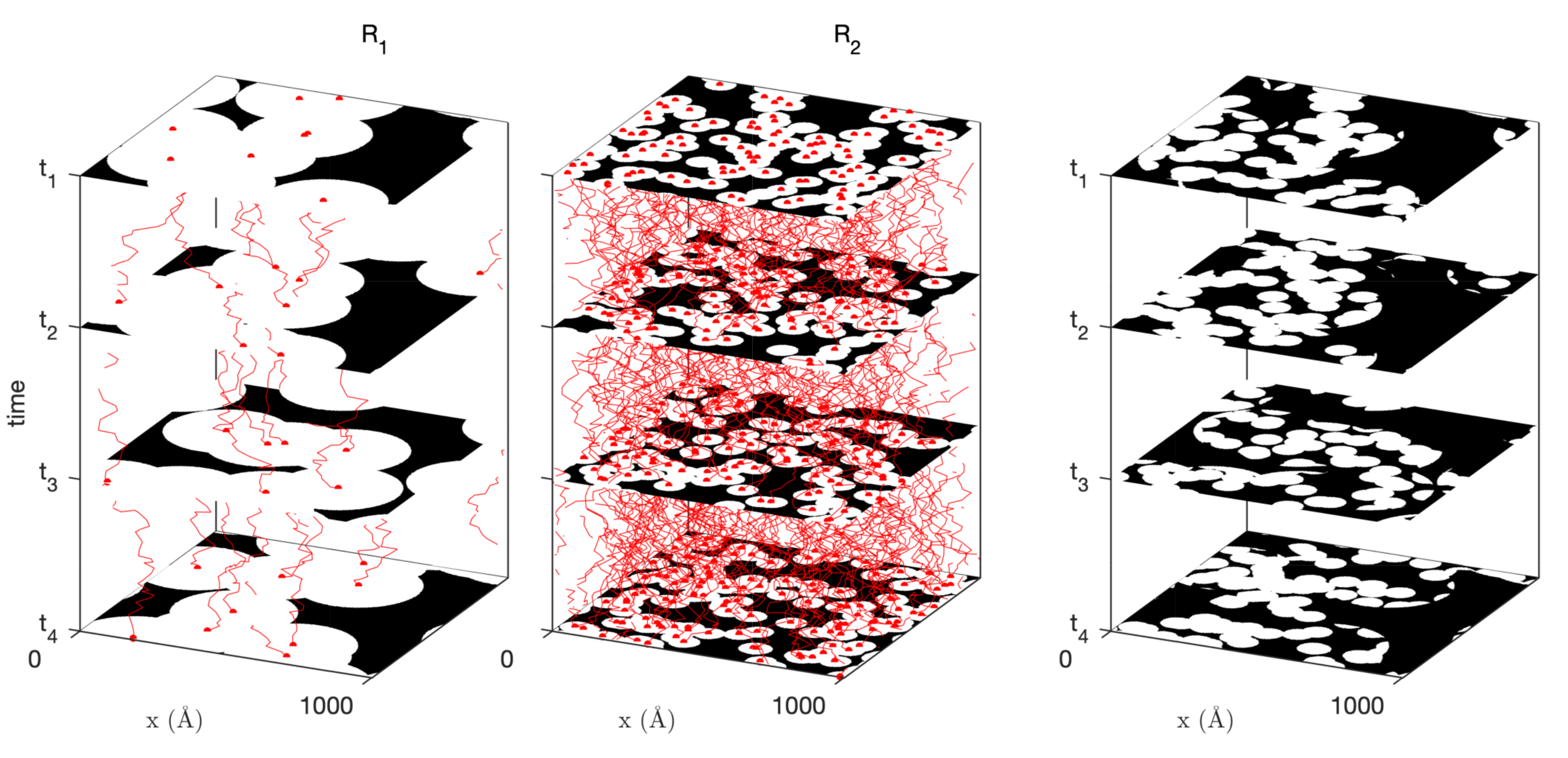
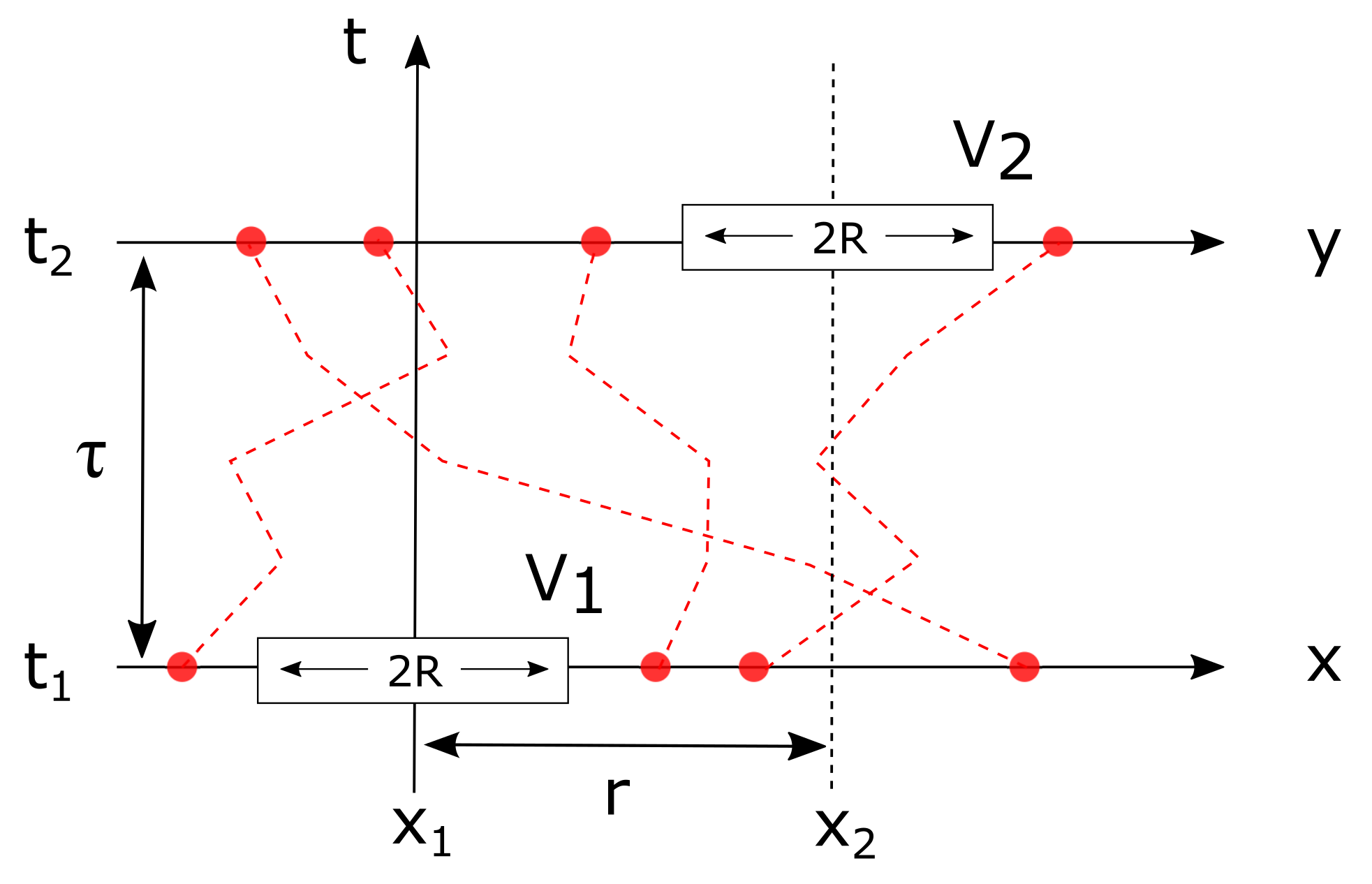
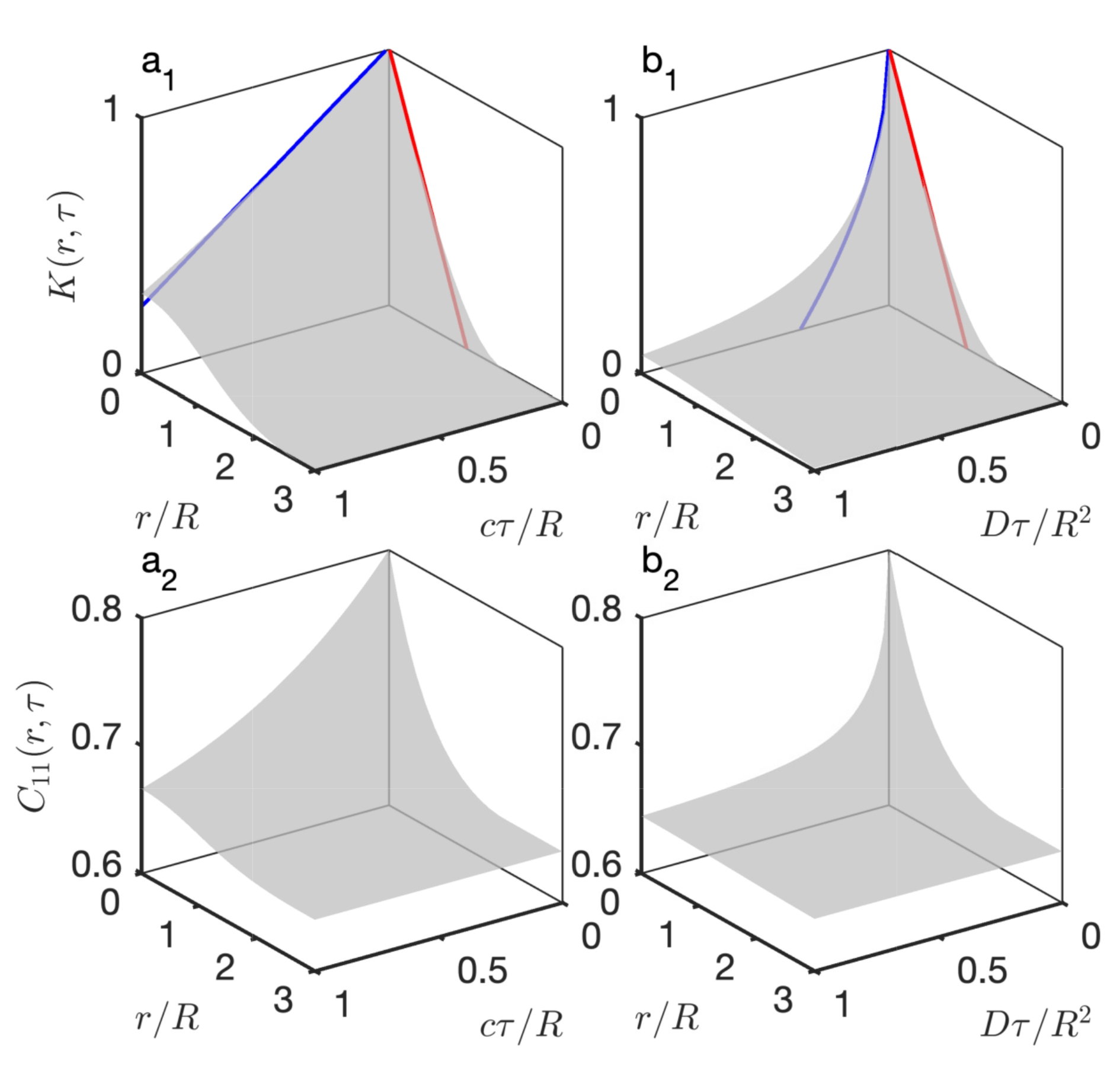
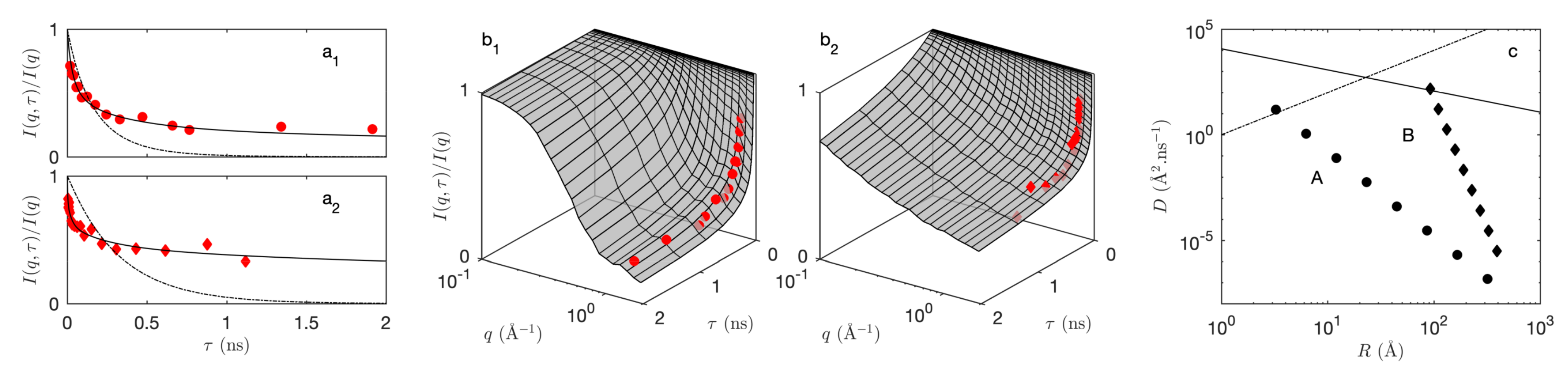
2.2.2. Dynamic Properties: Inelastic Scattering
2.3. Discussion
3. Conclusions
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
References
- Narayanan, T.; Wacklin, H.; Konovalov, O.; Lund, R. Recent applications of synchrotron radiation and neutrons in the study of soft matter. Crystallogr. Rev. 2017, 23, 160–226. [Google Scholar] [CrossRef]
- Glatter, O.; Kratky, O. Small Angle X-ray Scattering; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Sivia, D.S. Elementary Scattering Theory; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Holderer, O.; Zolnierczuk, P.; Pasini, S.; Stingaciu, L.; Monkenbusch, M. A better view through new glasses: Developments at the Jülich neutron spin echo spectrometers. Phys. B Condens. Matter 2019, 562, 9–12. [Google Scholar] [CrossRef]
- Squires, G.L. Introduction to the Theory of Thermal Neutron Scattering, 3rd ed.; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Gommes, C.J.; Jiao, Y.; Torquato, S. Microstructural degeneracy associated with a two-point correlation function and its information content. Phys. Rev. E 2012, 85, 051140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Matheron, G. Éléments pour une Théorie des Milieux Poreux; Masson: Paris, France, 1967. [Google Scholar]
- Torquato, S. Random Heterogeneous Materials; Springer: New York, NY, USA, 2002. [Google Scholar]
- Lantuéjoul, C. Geostatistical Simulations; Springer: Berlin, Germany, 2002. [Google Scholar]
- Jeulin, D. Morphological Models of Random Structures; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Sonntag, U.; Stoyan, D.; Hermann, H. Random set models in the interpretation of small-angle scattering data. Phys. Status Solidi 1981, 68, 281–288. [Google Scholar] [CrossRef]
- Berk, N. Scattering properties of a model bicontinuous structure with a well defined length scale. Phys. Rev. Lett. 1987, 58, 2718–2721. [Google Scholar] [CrossRef]
- Teubner, M. Level Surfaces of Gaussian Random Fields and Microemulsions. Europhys. Lett. 1991, 14, 403. [Google Scholar] [CrossRef]
- Chen, S.; Lee, D.; Kimishima, K.; Jinnai, H.; Hashimoto, T. Measurement of the Gaussian curvature of the surfactant film in an isometric bicontinuous one-phase microemulsion. Phys. Rev. E 1996, 54, 6526–6531. [Google Scholar] [CrossRef]
- Roberts, A.P. Morphology and thermal conductivity of model organic aerogels. Phys. Rev. E 1997, 55, R1286–R1289. [Google Scholar] [CrossRef] [Green Version]
- Gommes, C.J.; Roberts, A.P. Structure development of resorcinol-formaldehyde gels: Microphase separation or colloid aggregation. Phys. Rev. E 2008, 77, 041409. [Google Scholar] [CrossRef] [Green Version]
- Gille, W. Scattering properties and structure functions of Boolean models. Comput. Struct. 2011, 89, 2309–2315. [Google Scholar] [CrossRef]
- Gommes, C.J. Stochastic models of disordered mesoporous materials for small-angle scattering analysis and more. Microporous Mesoporous Mater. 2018, 257, 62–78. [Google Scholar] [CrossRef]
- Gommes, C.J.; Zorn, R.; Jaksch, S.; Frielinghaus, H.; Holderer, O. Inelastic neutron scattering analysis with time-dependent Gaussian-field models. J. Chem. Phys. 2021, 155, 024121. [Google Scholar] [CrossRef] [PubMed]
- Soler-Illia, G.; Sanchez, C.; Lebeau, B.; Patarin, J. Chemical strategies to design textured materials: From microporous and mesoporous oxides to nanonetworks and hierarchical structures. Chem. Rev. 2002, 102, 4093–4138. [Google Scholar] [CrossRef] [PubMed]
- Fratzl, P.; Weinkamer, R. Nature’s hierarchical materials. Prog. Mater. Sci. 2007, 52, 1263–1334. [Google Scholar] [CrossRef] [Green Version]
- Woignier, T.; Primera, J.; Alaoui, A.; Dieudonne, P.; Duffours, L.; Beurroies, I.; Calas-Etienne, S.; Despestis, F.; Faivre, A.; Etienne, P. Fractal Structure in Silica and Composites Aerogels. Gels 2021, 7, 1. [Google Scholar] [CrossRef]
- Schaefer, D.W.; Brinker, C.J.; Richter, D.; Farago, B.; Frick, B. Dynamics of weakly connected solids: Silica aerogels. Phys. Rev. Lett. 1990, 64, 2316–2319. [Google Scholar] [CrossRef]
- Lantuejoul, C. Ergodicity and integral range. J. Microsc. 1991, 161, 387–403. [Google Scholar] [CrossRef]
- Van Hove, L. Correlations in Space and Time and Born Approximation Scattering in Systems of Interacting Particles. Phys. Rev. 1954, 95, 249–262. [Google Scholar] [CrossRef] [Green Version]
- Guinier, A.; Fournet, G. Small-Angle Scattering of X-rays; Wiley: New York, NY, USA, 1955. [Google Scholar]
- Debye, P.; Anderson, H., Jr.; Brumberger, H. Scattering by an inhomogeneous solid. II. the correlation function and its application. J. Appl. Phys. 1957, 28, 679–683. [Google Scholar] [CrossRef]
- Ciccariello, S.; Goodisman, J.; Brumberger, H. On the Porod law. J. Appl. Crystallogr. 1988, 21, 117–128. [Google Scholar] [CrossRef]
- Jeulin, D. Morphology and effective properties of multi-scale random sets: A review. C. R. Méc. 2012, 340, 219–229. [Google Scholar] [CrossRef]
- Gommes, C.J.; Prieto, G.; Zecevic, J.; Vanhalle, M.; Goderis, B.; DeJong, K.P.; DeJongh, P.E. Mesoscale Characterization of Nanoparticles Distribution Using X-ray Scattering. Angew. Chem.-Int. Ed. 2015, 54, 11804–11808. [Google Scholar] [CrossRef]
- Gommes, C.J.; Prieto, G.; De Jongh, P.E. Small-angle scattering analysis of empty or loaded hierarchical porous materials. J. Phys. Chem. C 2016, 120, 1488–1506. [Google Scholar] [CrossRef]
- Serra, J. Image Analysis and Mathematical Morphology; Academic Press: London, UK, 1982; Volume 1. [Google Scholar]
- Savary, L.; Jeulin, D.; Thorel, A. Morphological analysis of carbon-polymer composite materials from thick sections. Acta Stereol. 1999, 18, 297–303. [Google Scholar]
- Schaefer, D.W.; Keefer, K.D. Fractal geometry of silica condensation polymers. Phys. Rev. Lett. 1984, 53, 1383–1386. [Google Scholar] [CrossRef]
- Vacher, R.; Woignier, T.; Pelous, J.; Courtens, E. Structure and self-similarity of silica aerogels. Phys. Rev. B 1988, 37, 6500–6503. [Google Scholar] [CrossRef] [PubMed]
- Brinker, C.J.; Scherer, G.W. Sol-Gel Science, the Physics and Chemistry of Sol-Gel Processing; Academic Press: New York, NY, USA, 1990. [Google Scholar]
- Vicsek, T. Fractal Growth Phenomena; World Scientific Publishing: Singapore, 1992. [Google Scholar]
- Gouyet, J.F. Phyisc and Fractal Structures; Springer: New York, NY, USA, 1996. [Google Scholar]
- Malcai, O.; Lidar, D.A.; Biham, O.; Avnir, D. Scaling range and cutoffs in empirical fractals. Phys. Rev. E 1997, 56, 2817–2828. [Google Scholar] [CrossRef] [Green Version]
- Berg, H. Random Walks in Biology, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 1993. [Google Scholar]
- Vacher, R.; Courtens, E.; Coddens, G.; Heidemann, A.; Tsujimi, Y.; Pelous, J.; Foret, M. Crossovers in the density of states of fractal silica aerogels. Phy. Rev. Lett. 1990, 65, 1008–1011. [Google Scholar] [CrossRef]
- Alexander, S.; Orbach, R. Density fo states of fractals: Fractons. J. Phys. Lett. 1982, 43, 625–631. [Google Scholar] [CrossRef] [Green Version]
- Amir, A.; Krich, J.J.; Vitelli, V.; Oreg, Y.; Imry, Y. Emergent Percolation Length and Localization in Random Elastic Networks. Phys. Rev. X 2013, 3, 021017. [Google Scholar] [CrossRef] [Green Version]
- Ma, H.; Jullien, R.; Scherer, G.W. Dangling bond deflection model: Growth of gel network with loop structure. Phys. Rev. E 2002, 65, 041403. [Google Scholar] [CrossRef] [PubMed]
- Danielsen, S.P.O.; Beech, H.K.; Wang, S.; El-Zaatari, B.M.; Wang, X.; Sapir, L.; Ouchi, T.; Wang, Z.; Johnson, P.N.; Hu, Y.; et al. Molecular Characterization of Polymer Networks. Chem. Rev. 2021, 121, 5042–5092. [Google Scholar] [CrossRef] [PubMed]
- Daughton, D.R.; MacDonald, J.; Mulders, N. Acoustic properties of silica aerogels from 400 mK to 400 K. Phys. B Condens. Matter 2003, 329–333, 1233–1234. [Google Scholar] [CrossRef]
- Grosberg, A.Y.; Joanny, J.; Srinin, W.; Rabin, Y. Scale-Dependent Viscosity in Polymer Fluids. J. Phys. Chem. B 2016, 120, 6383–6390. [Google Scholar] [CrossRef] [PubMed]
- Anglaret, E.; Pelous, J.; Hrubesh, L.H. Structural changes and elastic properties in aerogels investigated by Brillouin scattering. J. Non-Cryst. Solids 1995, 186, 137–141. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gommes, C.J. A Time-Dependent Hierarchical Model for Elastic and Inelastic Scattering Data Analysis of Aerogels and Similar Soft Materials. Gels 2022, 8, 236. https://doi.org/10.3390/gels8040236
Gommes CJ. A Time-Dependent Hierarchical Model for Elastic and Inelastic Scattering Data Analysis of Aerogels and Similar Soft Materials. Gels. 2022; 8(4):236. https://doi.org/10.3390/gels8040236
Chicago/Turabian StyleGommes, Cedric J. 2022. "A Time-Dependent Hierarchical Model for Elastic and Inelastic Scattering Data Analysis of Aerogels and Similar Soft Materials" Gels 8, no. 4: 236. https://doi.org/10.3390/gels8040236
APA StyleGommes, C. J. (2022). A Time-Dependent Hierarchical Model for Elastic and Inelastic Scattering Data Analysis of Aerogels and Similar Soft Materials. Gels, 8(4), 236. https://doi.org/10.3390/gels8040236





