Microscopic Insight into Knudsen and Electromagnetic Effects on Thermal Conductivity of Closed Mesoporous Metal Gels
Abstract
1. Introduction
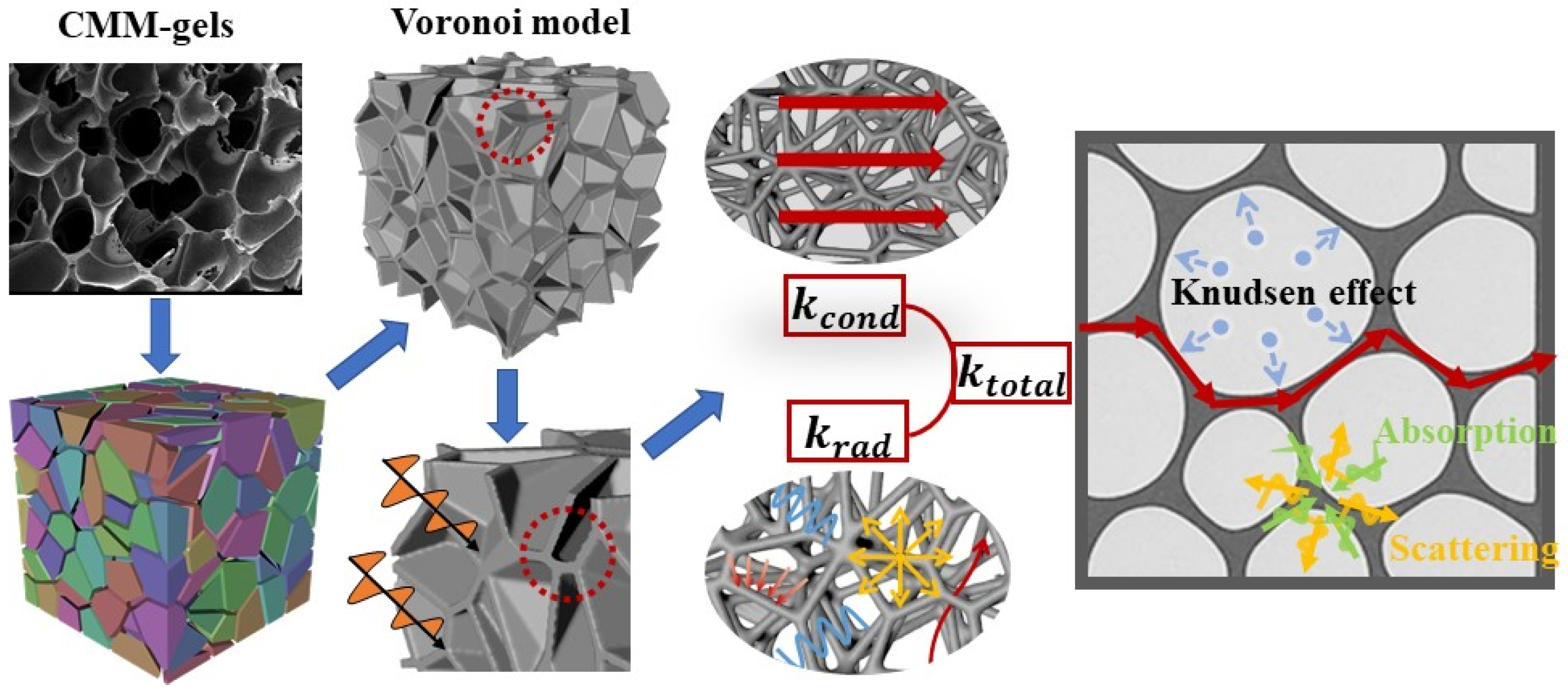
2. Models
2.1. Geometric Model
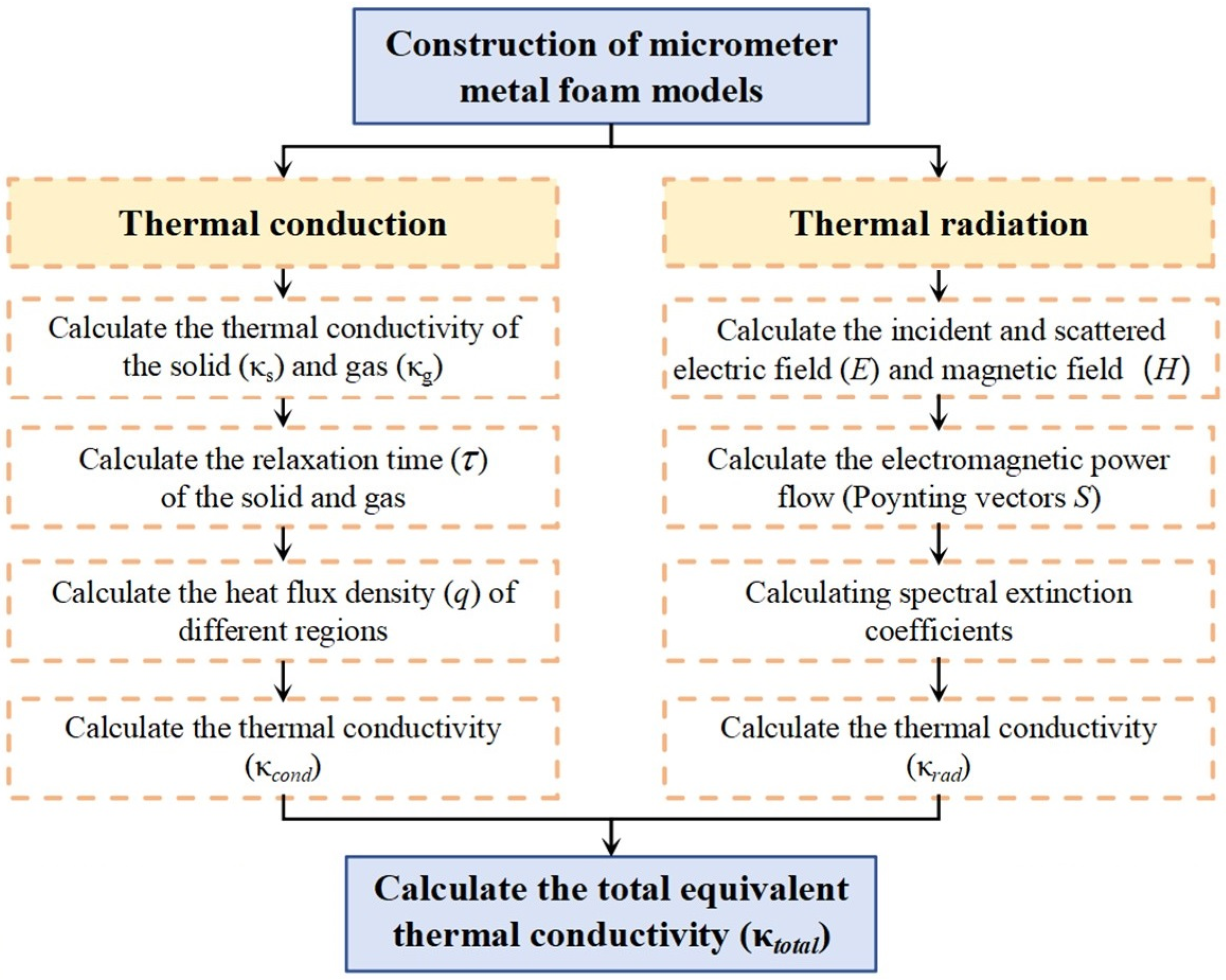
2.2. Calculation Methods
3. Results and Discussion
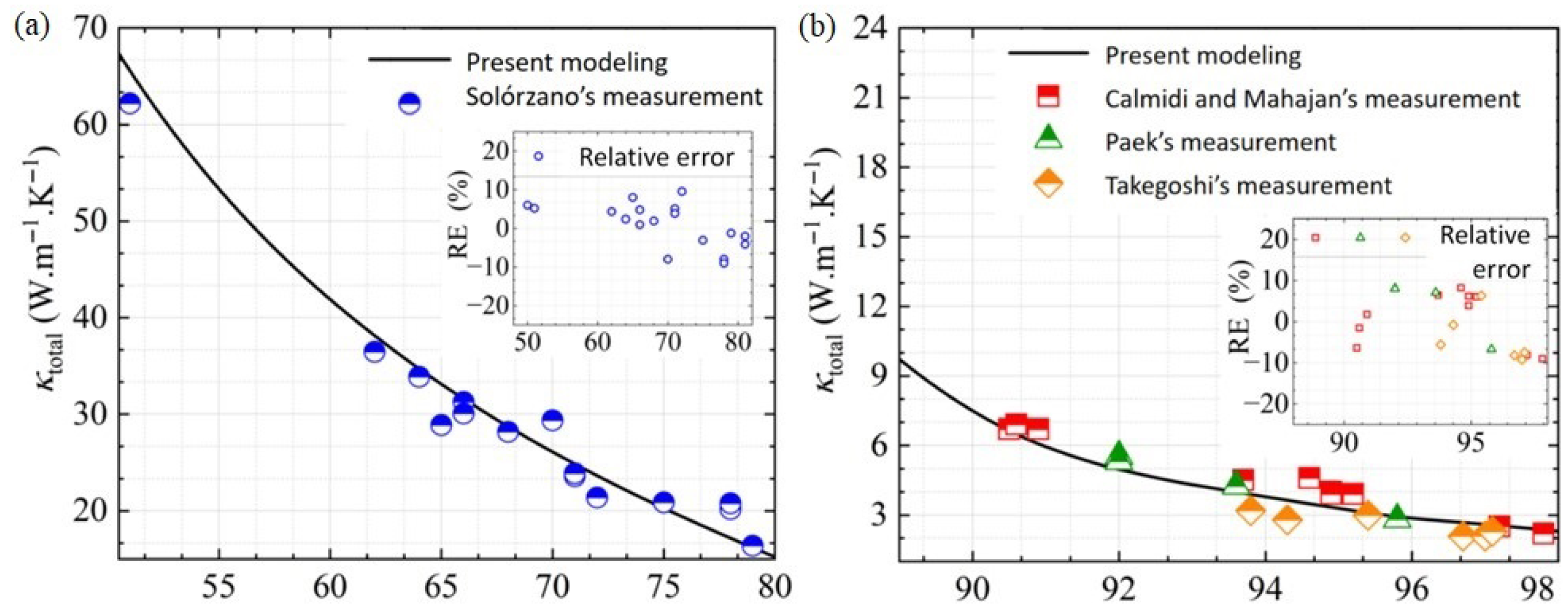
3.1. Model Verification
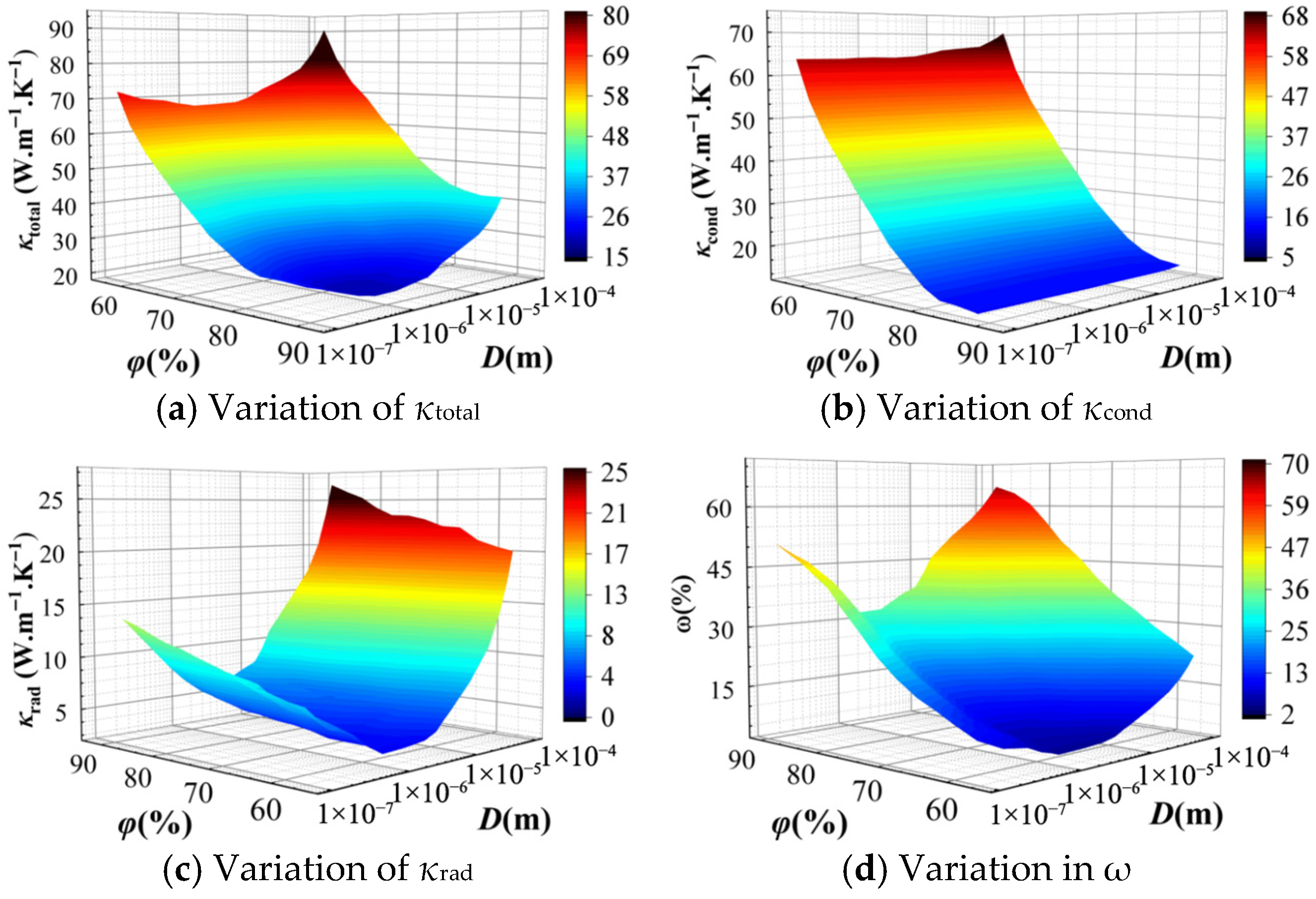
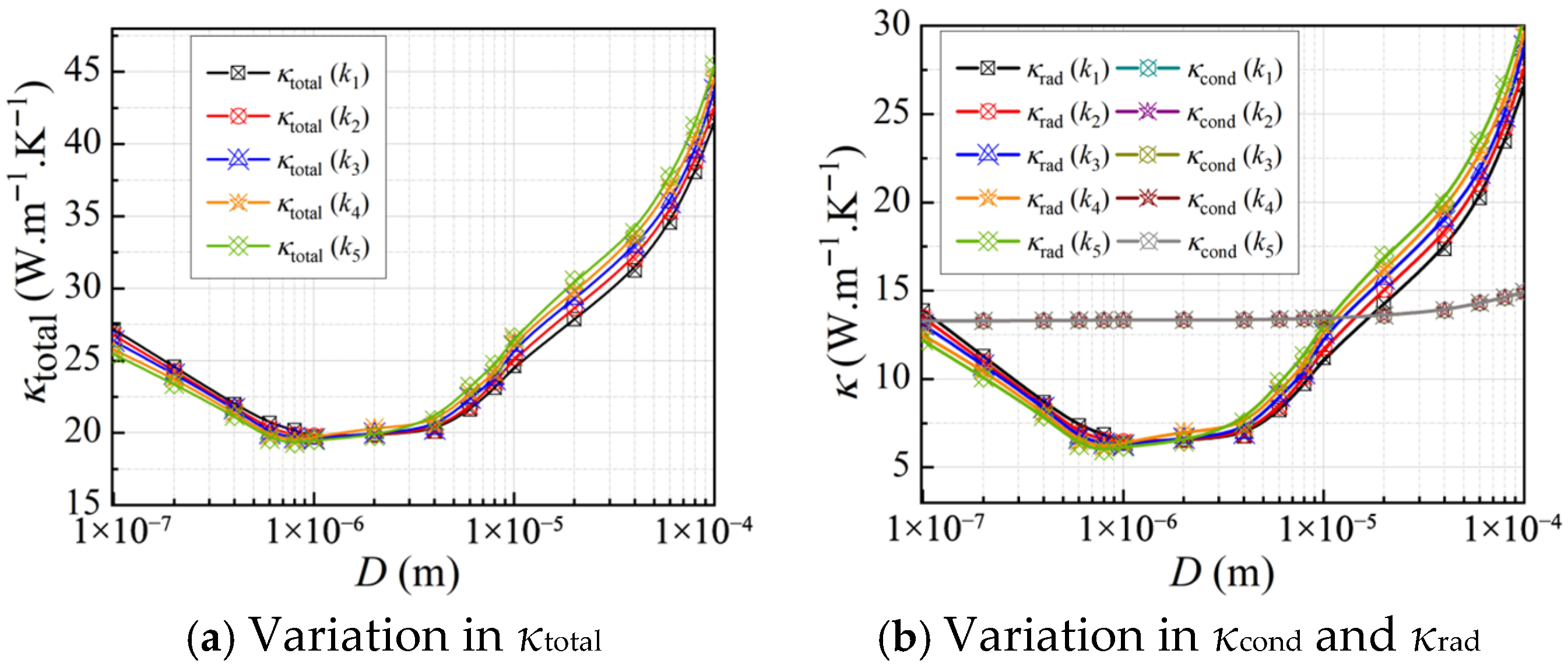
3.2. Factors Influencing the Equivalent Thermal Conductivity
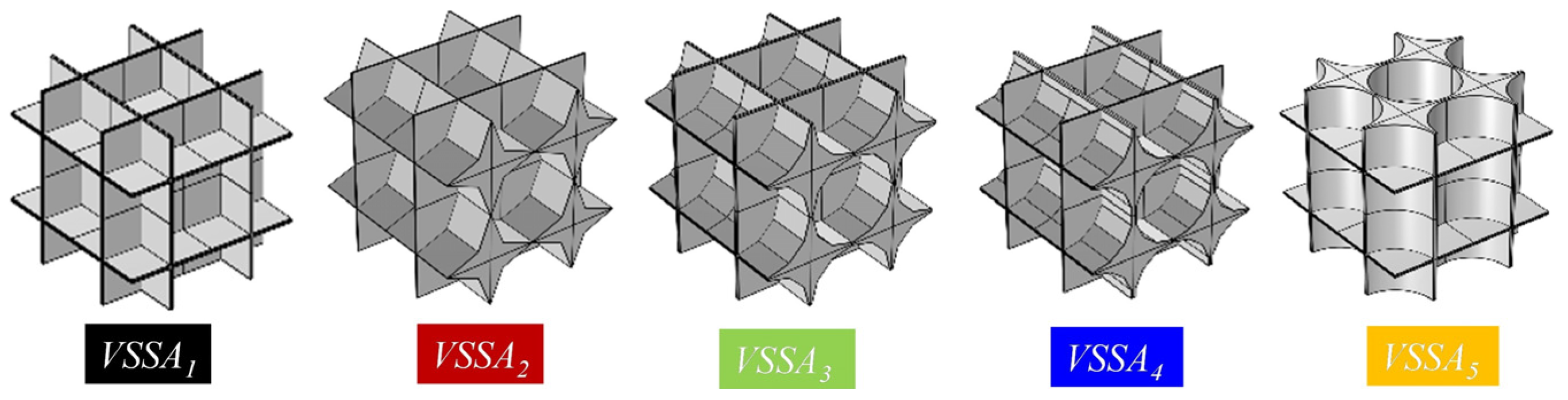
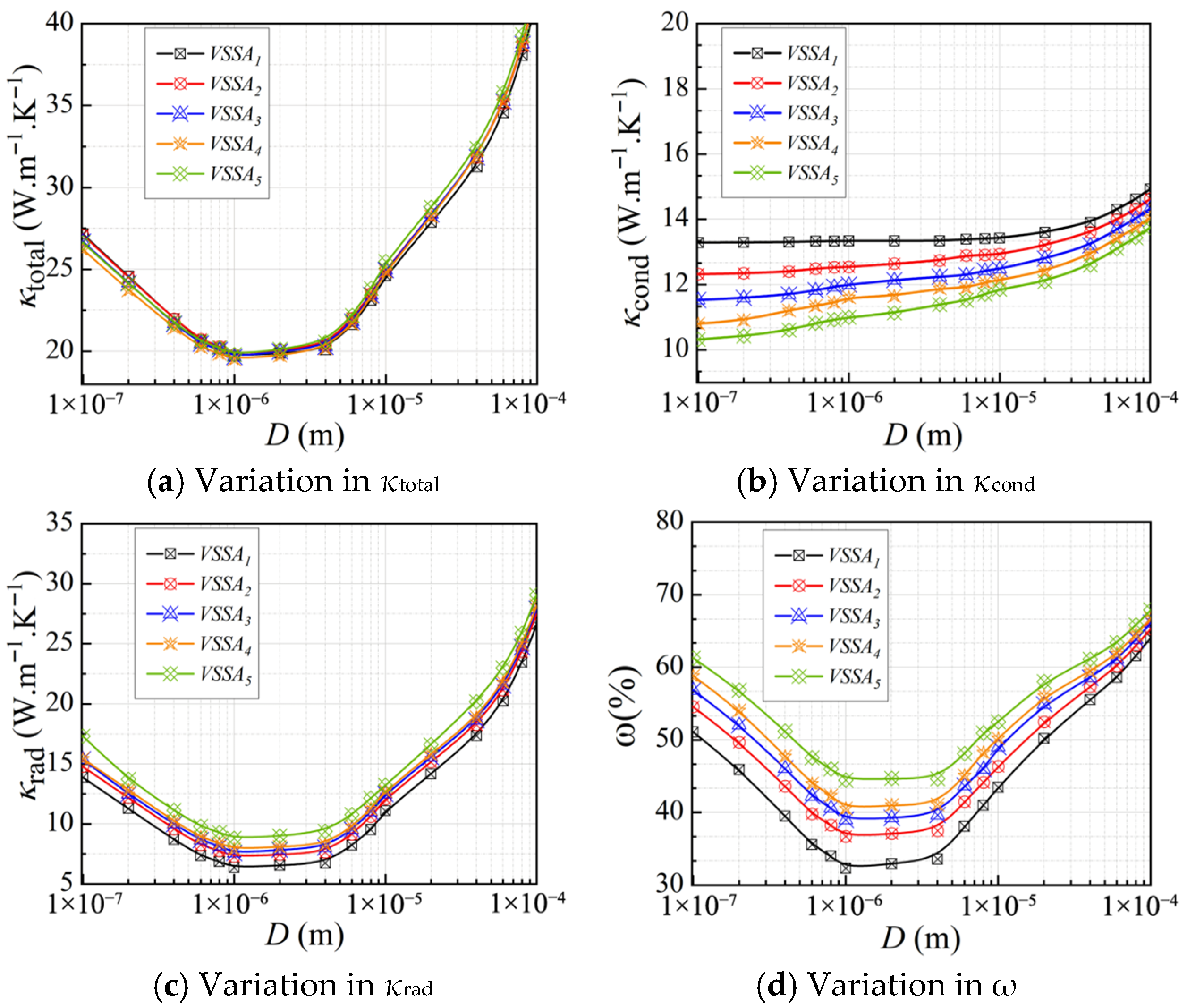
3.2.1. Effect of the Cellular Structure
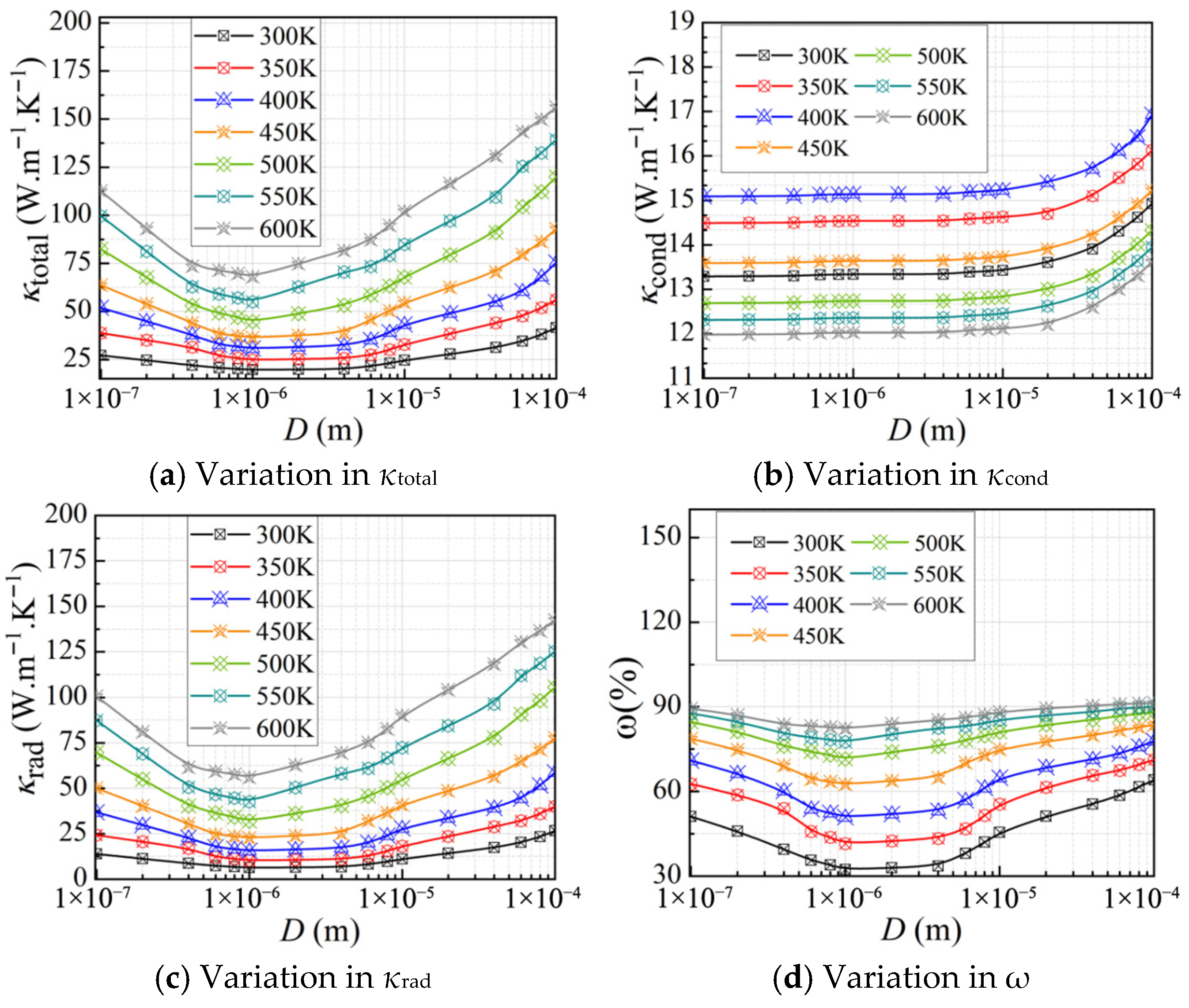
3.2.2. Effect of Temperature
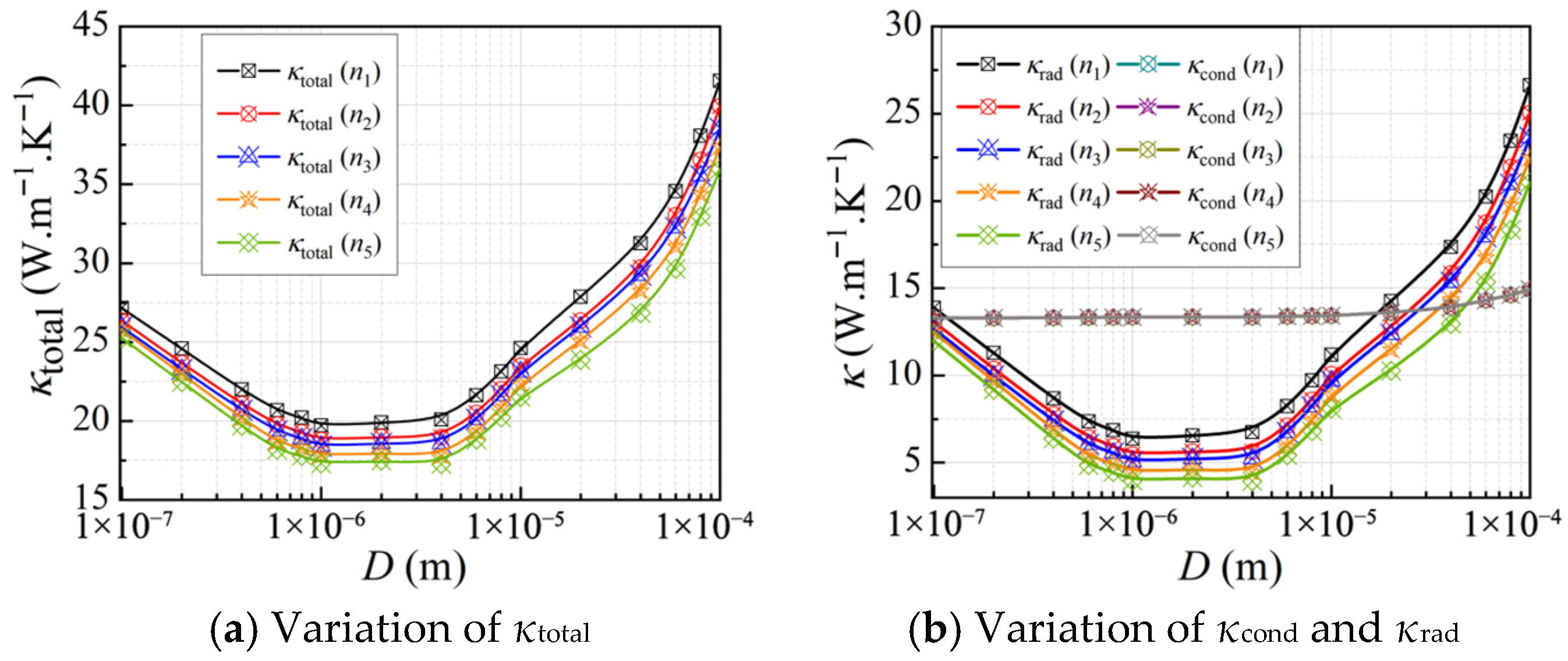
3.2.3. Effect of Volumetric Specific Surface Area
3.2.4. Effect of Material Properties
3.3. Spectral Radiative Properties
4. Conclusions
- The developed numerical model predicts the effective thermal conductivity, within 8.6% error compared with experimental measurements.
- Effective thermal conductivity decreases with increasing porosity, increases with temperature, and reaches a stable minimum at a pore size of about 1 μm. The effects of refractive index, extinction coefficient, and surface area are comparatively minor.
- Electromagnetic resonance phenomena, including surface plasmon and magnetic resonance at the gas–solid interface, significantly enhance internal radiative dissipation and further reduce thermal conductivity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lei, S.; Hu, C.; Li, Z.; Tan, S.; Wang, C.; Wu, Y. Boiling heat transfer enhancement on heterogeneous copper foams in the presence of transverse flow. Appl. Therm. Eng. 2025, 260, 124990. [Google Scholar]
- Palombo, M.; Barbetta, A.; Cametti, C.; Favero, G.; Capuani, S. Transient Anomalous Diffusion MRI Measurement Discriminates Porous Polymeric Matrices Characterized by Different Sub-Microstructures and Fractal Dimension. Gels 2022, 8, 95. [Google Scholar] [CrossRef]
- Chai, J.; Wang, G.; Wang, G.; Shao, R.; Zhao, J.; Zhao, G.; Park, C.B. Porous and Conductive Fiber Woven Textile for Multi-Functional Protection, Personal Warmth, and Intelligent Motion/Temperature Perception. Adv. Funct. Mater. 2025, 35, 2416428. [Google Scholar]
- Singh, A.; Rangarajan, S.; Sammakia, B. Utilizing Ragone framework for optimized phase change material-based heat sink design in electronic cooling applications. Int. J. Heat Mass Transf. 2024, 227, 125518. [Google Scholar] [CrossRef]
- Aichmayer, L.; Garrido, J.; Wang, W.; Berg, J.; Vlaskin, A.; Guo, Z.; Tallaire, A.; Stöhr, R.; Rüde, U. Experimental evaluation of a novel solar receiver for a micro gas-turbine based solar dish system in the KTH high-flux solar simulator. Energy 2018, 159, 184–195. [Google Scholar]
- Yu, H.; Zhang, H.; Zhao, J.; Liu, J.; Xia, X.; Wu, X. Thermal conductivity of micro/nano-porous polymers: Prediction models and applications. Front. Phys. 2022, 17, 1–19. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, H.; Buahom, P.; Liu, J.; Xia, X.; Park, C.B. Prediction of thermal conductivity of micro/nano porous dielectric materials: Theoretical model and impact factors. Energy 2021, 233, 121140. [Google Scholar] [CrossRef]
- Gong, P.; Wang, G.; Tran, M.P.; Buahom, P.; Zhai, S.; Li, G.; Park, C.B. Advanced bimodal polystyrene/multi-walled carbon nanotube nanocomposite foams for thermal insulation. Carbon 2017, 120, 1–10. [Google Scholar]
- Wang, G.; Wang, C.; Zhao, J.; Wang, G.; Park, C.B.; Zhao, G.; Janssen, H. Correction: Modelling of thermal transport through a nanocellular polymer foam: Toward the generation of a new superinsulating material. Nanoscale 2018, 10, 20469–20473. [Google Scholar] [CrossRef]
- Buahom, P.; Wang, C.; Alshrah, M.; Wang, G.; Gong, P.; Tran, M.P.; Park, C.B. Wrong expectation of superinsulation behavior from largely-expanded nanocellular foams. Nanoscale 2020, 12, 13064–13085. [Google Scholar] [CrossRef]
- Notario, B.; Pinto, J.; Solorzano, E.; de Saja, J.A.; Dumon, M.; Rodríguez-Pérez, M.A. Experimental validation of the Knudsen effect in nanocellular polymeric foams. Polymer 2015, 56, 57–67. [Google Scholar] [CrossRef]
- Bernardo, V.; Martin-de Leon, J.; Pinto, J.; Verdejo, R.; Rodriguez-Perez, M.A. Modeling the heat transfer by conduction of nanocellular polymers with bimodal cellular structures. Polymer 2019, 160, 126–137. [Google Scholar] [CrossRef]
- Chaichi, M.; Bahramian, A.R. Theoretical relation of the structure and thermal properties of gradient thermal insulator aerogels using fractal geometry. Microporous Mesoporous Mater. 2022, 333, 111722. [Google Scholar] [CrossRef]
- Yu, H.; Li, M.; Guo, N.; Chen, A.; Zhang, H.; Du, M. Fractal-Based Thermal Conductivity Prediction Modeling for Closed Mesoporous Polymer Gels. Gels 2025, 11, 391. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, H.; Xia, X. A fractal-skeleton model of high porosity macroporous aluminum and its heat transfer characterizes. J. Therm. Anal. Calorim. 2020, 141, 351–360. [Google Scholar] [CrossRef]
- Han, Y.F.; Xia, X.L.; Tan, H.P.; Liu, H.D. Modeling of phonon heat transfer in spherical segment of silica aerogel grains. Phys. B Condens. Matter 2013, 420, 58–63. [Google Scholar] [CrossRef]
- Zeng, T.; Liu, W. Phonon heat conduction in micro-and nano-core-shell structures with cylindrical and spherical geometries. J. Appl. Phys. 2003, 93, 4163–4168. [Google Scholar] [CrossRef]
- Xie, T.; He, Y.L. Heat transfer characteristics of silica aerogel composite materials: Structure reconstruction and numerical modeling. Int. J. Heat Mass Transf. 2016, 95, 621–635. [Google Scholar] [CrossRef]
- Sean, D.; Landsgesell, J.; Holm, C. Computer simulations of static and dynamical properties of weak polyelectrolyte nanogels in salty solutions. Gels 2017, 4, 2. [Google Scholar] [CrossRef]
- El Hajj, S.; Ntaté, M.B.; Breton, C.; Siadous, R.; Aid, R.; Dupuy, M.; David, B. Bone Spheroid Development Under Flow Conditions with Mesenchymal Stem Cells and Human Umbilical Vein Endothelial Cells in a 3D Porous Hydrogel Supplemented with Hydroxyapatite. Gels 2024, 10, 666. [Google Scholar] [CrossRef]
- Zhang, Z.M. Nano/Microscale Heat Transfer; Springer International Publishing: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Shen, S.; Narayanaswamy, A.; Chen, G. Surface phonon polaritons mediated energy transfer between nanoscale gaps. Nano Lett. 2009, 9, 2909–2915. [Google Scholar] [CrossRef]
- Howell, J.R.; Siegel, R.; Mengüç, M.P. Thermal Radiation Heat Transfer, 5th ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2010. [Google Scholar]
- Pozar, D.M. Microwave Engineering; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Tan, H.; Liu, L.; Yi, H.; Zhao, J.; Qi, H.; Tan, J. Recent progress in computational thermal radiative transfer. Chin. Sci. Bull. 2009, 54, 4135–4147. [Google Scholar] [CrossRef]
- Jin, Y.; Wu, Y.; Li, H.; Zhao, M.; Pan, J. Definition of fractal topography to essential understanding of scale-invariance. Sci. Rep. 2017, 7, 46672. [Google Scholar] [CrossRef] [PubMed]
- Vacher, R.; Woignier, T.; Pelous, J.; Courtens, E. Structure and self-similarity of silica aerogels. Phys. Rev. B 1988, 37, 6500. [Google Scholar] [CrossRef] [PubMed]
- Paun, M.A.; Paun, V.A.; Paun, V.P. Acoustic fractional propagation in terms of porous xerogel and fractal parameters. Gels 2024, 10, 83. [Google Scholar] [CrossRef] [PubMed]
- Hayase, Y.; Ohta, T. Sierpinski gasket in a reaction-diffusion system. Phys. Rev. Lett. 1998, 81, 1726. [Google Scholar] [CrossRef]
- Ma, Y.; Yu, B.; Zhang, D.; Zou, M. A self-similarity model for effective thermal conductivity of porous media. J. Phys. D Appl. Phys. 2003, 36, 2157. [Google Scholar] [CrossRef]
- Liu, H.; Liu, J.A.; Tian, Y.; Jiao, J.; Wu, X. Thermal insulation performance of silica aerogel composites doped with hollow opacifiers: Theoretical approach. Gels 2022, 8, 295. [Google Scholar] [CrossRef]
- Okabe, A.; Boots, B.; Sugihara, K.; Chiu, S.N. Spatial Tessellations: Concepts and Applications of Voronoi Diagrams; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Notario, B.; Pinto, J.; Rodriguez-Perez, M.A. Nanoporous polymeric materials: A new class of materials with enhanced properties. Prog. Mater. Sci. 2016, 78, 93–139. [Google Scholar] [CrossRef]
- Chen, A.; Chai, J.; Ren, X.; Li, M.; Yu, H.; Wang, G. A Novel Prediction Model for Thermal Conductivity of Open Microporous Metal Foam Based on Resonance Enhancement Mechanisms. Energies 2025, 18, 1529. [Google Scholar] [CrossRef]
- Lin, Z.; Lan, Y.; Huang, C. Reduced thermal conductivity of nanoparticle packed bed by hybrid design. Int. J. Heat Mass Transf. 2020, 162, 120340. [Google Scholar] [CrossRef]
- Lin, Z.Z.; Huang, C.L.; Luo, D.C.; Feng, Y.H.; Zhang, X.X.; Wang, G. Thermal performance of metallic nanoparticles in air. Appl. Therm. Eng. 2016, 105, 686–690. [Google Scholar] [CrossRef]
- Singh, R.; Kasana, H.S. Computational aspects of effective thermal conductivity of highly porous metal foams. Appl. Therm. Eng. 2004, 24, 1841–1849. [Google Scholar] [CrossRef]
- Shen, S.; Henry, A.; Tong, J.; Zheng, R.; Chen, G. Polyethylene nanofibres with very high thermal conductivities. Nat. Nanotechnol. 2010, 5, 251–255. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Wang, L.; Zhang, Z.M. Near-field thermal radiation: Recent progress and outlook. Nanoscale Microscale Thermophys. Eng. 2015, 19, 98–126. [Google Scholar] [CrossRef]
- Rytov, S.M.; Kravtsov, Y.A.; Tatarskii, V.I. Principles of Statistical Radiophysics; Springer: Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Basu, S.; Zhang, Z.M.; Fu, C.J. Review of near-field thermal radiation and its application to energy conversion. Int. J. Energy Res. 2009, 33, 1203–1232. [Google Scholar] [CrossRef]
- Wu, X.; Fu, C.; Zhang, Z.M. Effect of orientation on the directional and hemispherical emissivity of hyperbolic metamaterials. Int. J. Heat Mass Transf. 2019, 135, 1207–1217. [Google Scholar] [CrossRef]
- Bernardo, V.; Martin-de Leon, J.; Pinto, J.; Schade, U.; Rodriguez-Perez, M.A. On the interaction of infrared radiation and nanocellular polymers: First experimental determination of the extinction coefficient. Colloids Surf. A Physicochem. Eng. Asp. 2020, 600, 124937. [Google Scholar] [CrossRef]
- Martín-de León, J.; Pura, J.L.; Bernardo, V.; Rodríguez-Pérez, M.Á. Transparent nanocellular PMMA: Characterization and modeling of the optical properties. Polymer 2019, 170, 16–23. [Google Scholar] [CrossRef]
- Mayerhöfer, T.G.; Pahlow, S.; Popp, J. The Bouguer-Beer-Lambert law: Shining light on the obscure. ChemPhysChem 2020, 21, 2029–2046. [Google Scholar] [CrossRef]
- Pelissari, P.I.; Angélico, R.A.; Salvini, V.R.; Vivaldini, D.O.; Pandolfelli, V.C. Analysis and modeling of the pore size effect on the thermal conductivity of alumina foams for high temperature applications. Ceram. Int. 2017, 43, 13356–13363. [Google Scholar] [CrossRef]
- Zhao, L. Radiative Transport in Transparent Aerogels for Solar Thermal Energy Applications. Doctoral Dissertation, Massachusetts Institute of Technology, Cambridge, MA, USA, 2019. [Google Scholar]
- Solórzano, E.; Reglero, J.A.; Rodríguez-Pérez, M.A.; Lehmhus, D.; Wichmann, M.; De Saja, J.A. An experimental study on the thermal conductivity of aluminium foams by using the transient plane source method. Int. J. Heat Mass Transf. 2008, 51, 6259–6267. [Google Scholar] [CrossRef]
- Calmidi, V.V.; Mahajan, R.L. The effective thermal conductivity of high porosity fibrous metal foams. J. Heat Transf. 1999, 121, 466–471. [Google Scholar] [CrossRef]
- Paek, J.W.; Kang, B.H.; Kim, S.Y.; Hyun, J.M. Effective thermal conductivity and permeability of aluminum foam materials. Int. J. Thermophys. 2000, 21, 453–464. [Google Scholar] [CrossRef]
- Takegoshi, E.; Hirasawa, Y.; Matsuo, J.; Okui, K. A study on effective thermal conductivity of porous metals. Trans. Jpn. Soc. Mech. Eng. Ser. B 1992, 58, 879–884. [Google Scholar] [CrossRef][Green Version]
- Rakić, A.D. Algorithm for the determination of intrinsic optical constants of metal films: Application to aluminum. Appl. Opt. 1995, 34, 4755–4767. [Google Scholar] [CrossRef]
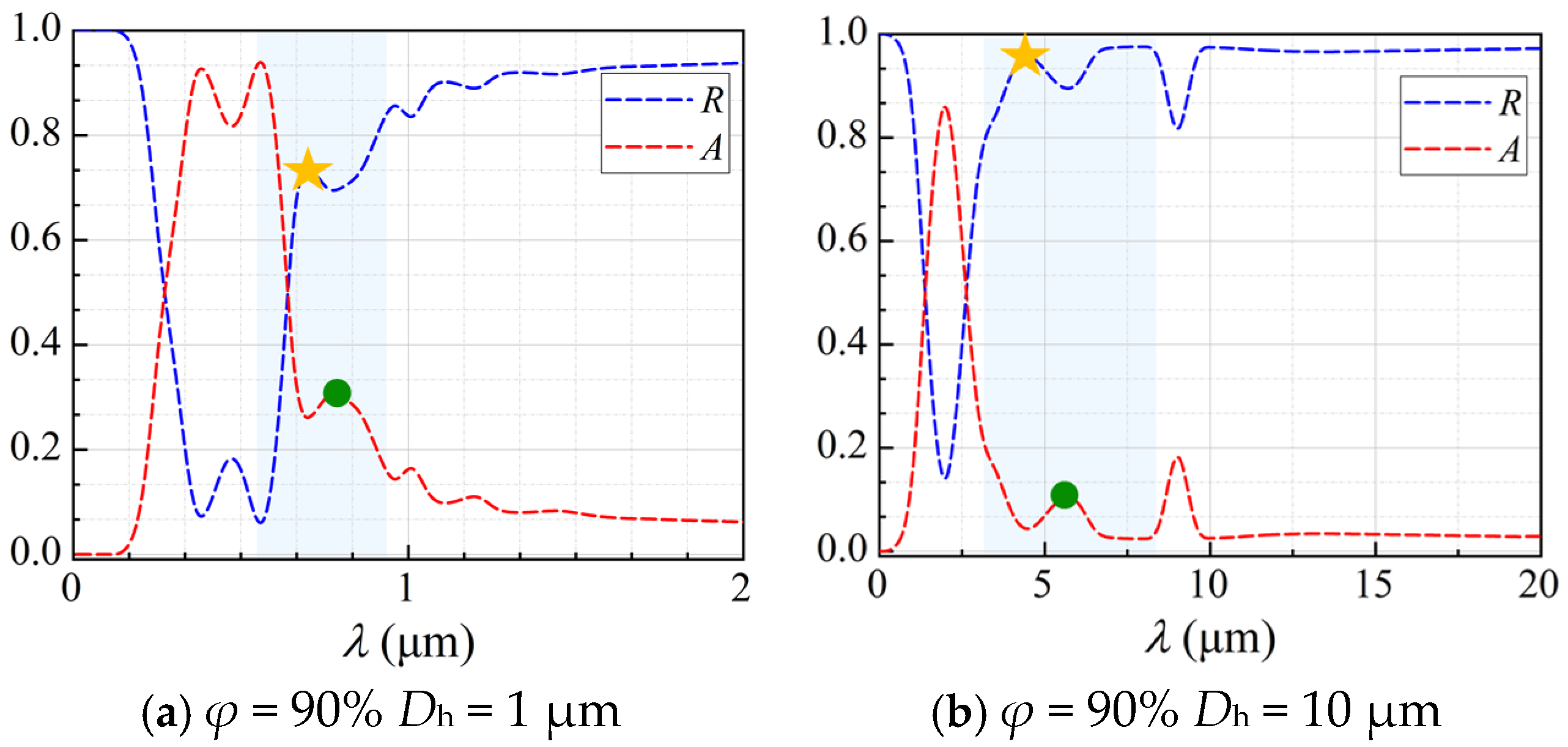
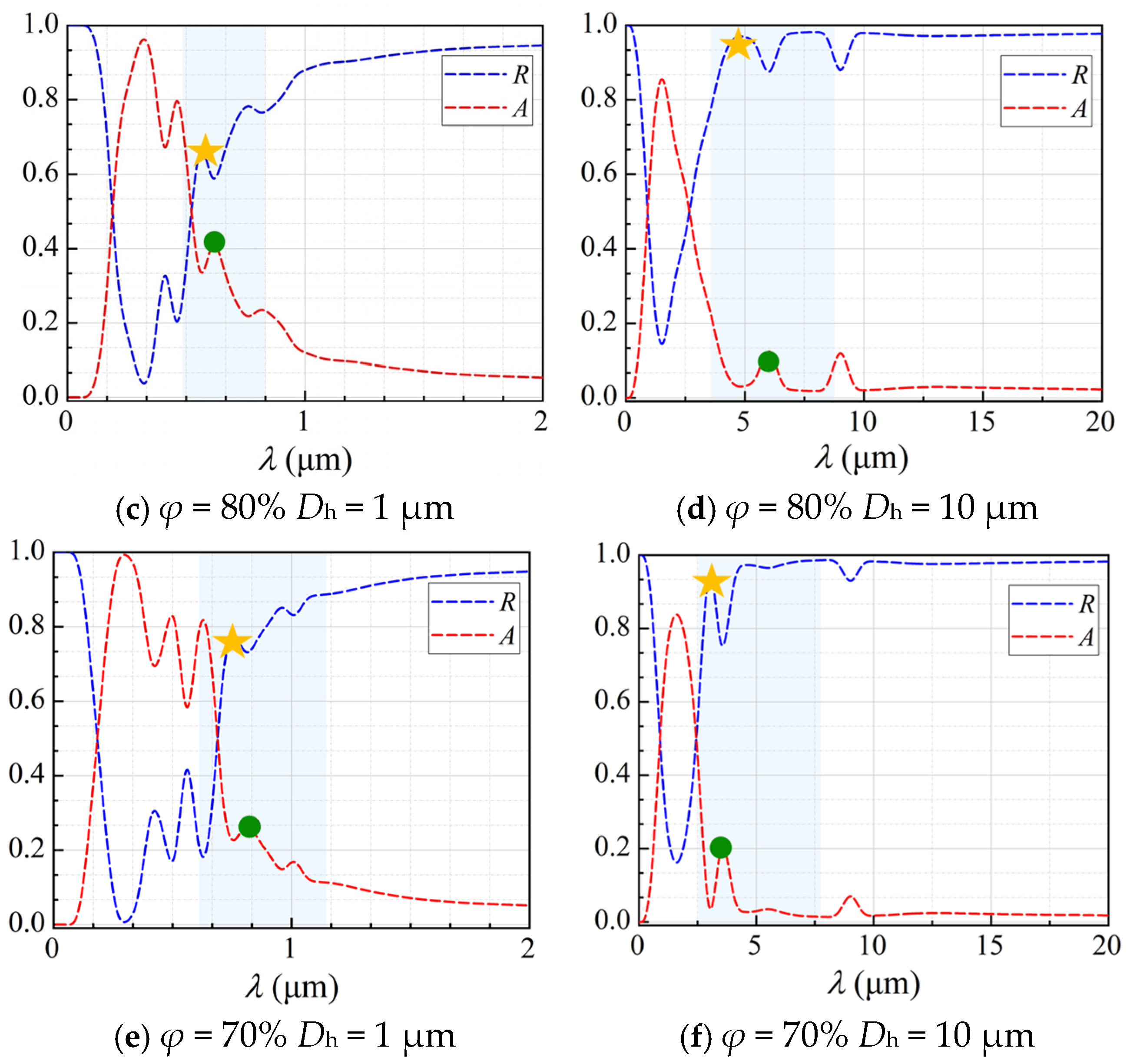

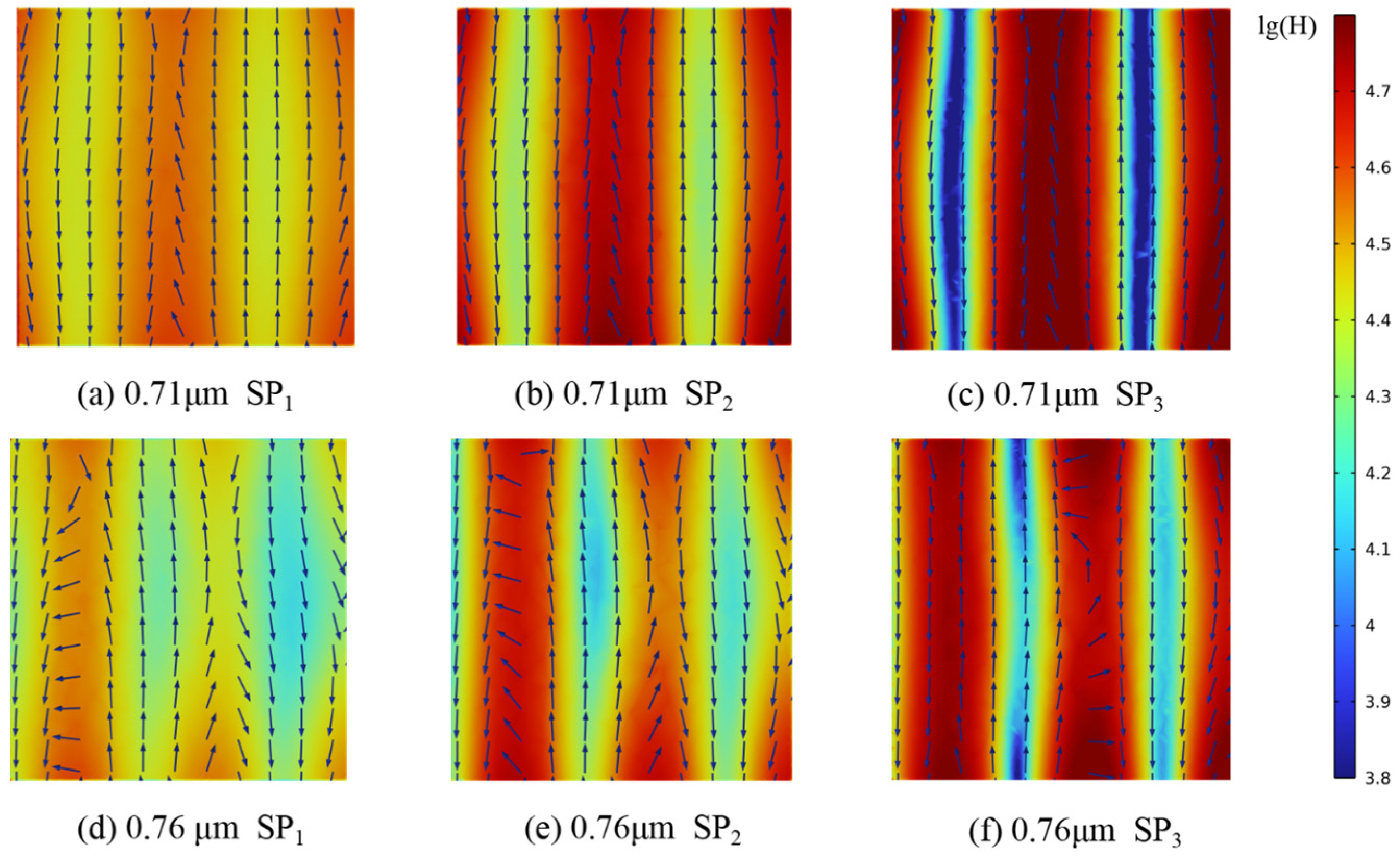
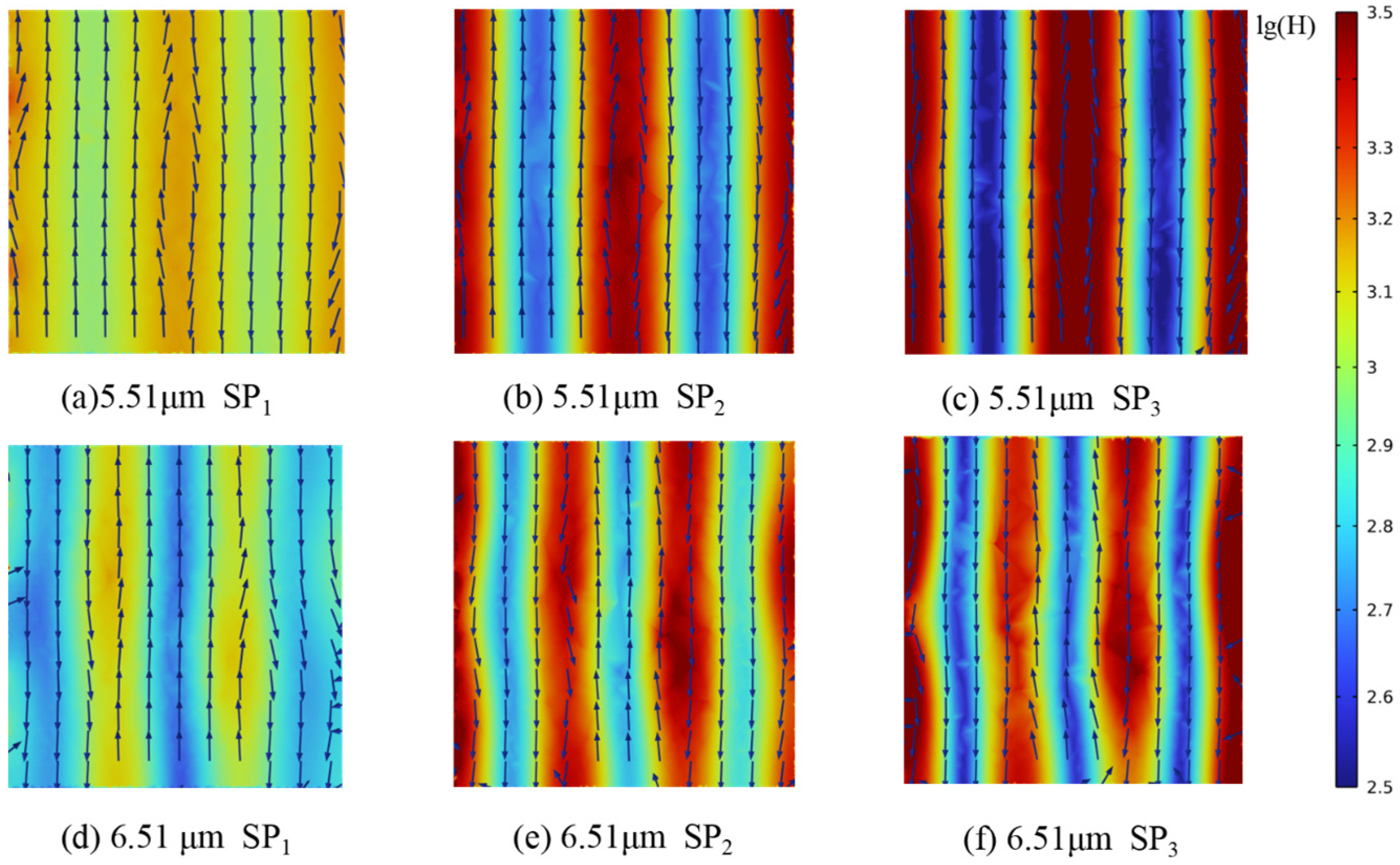
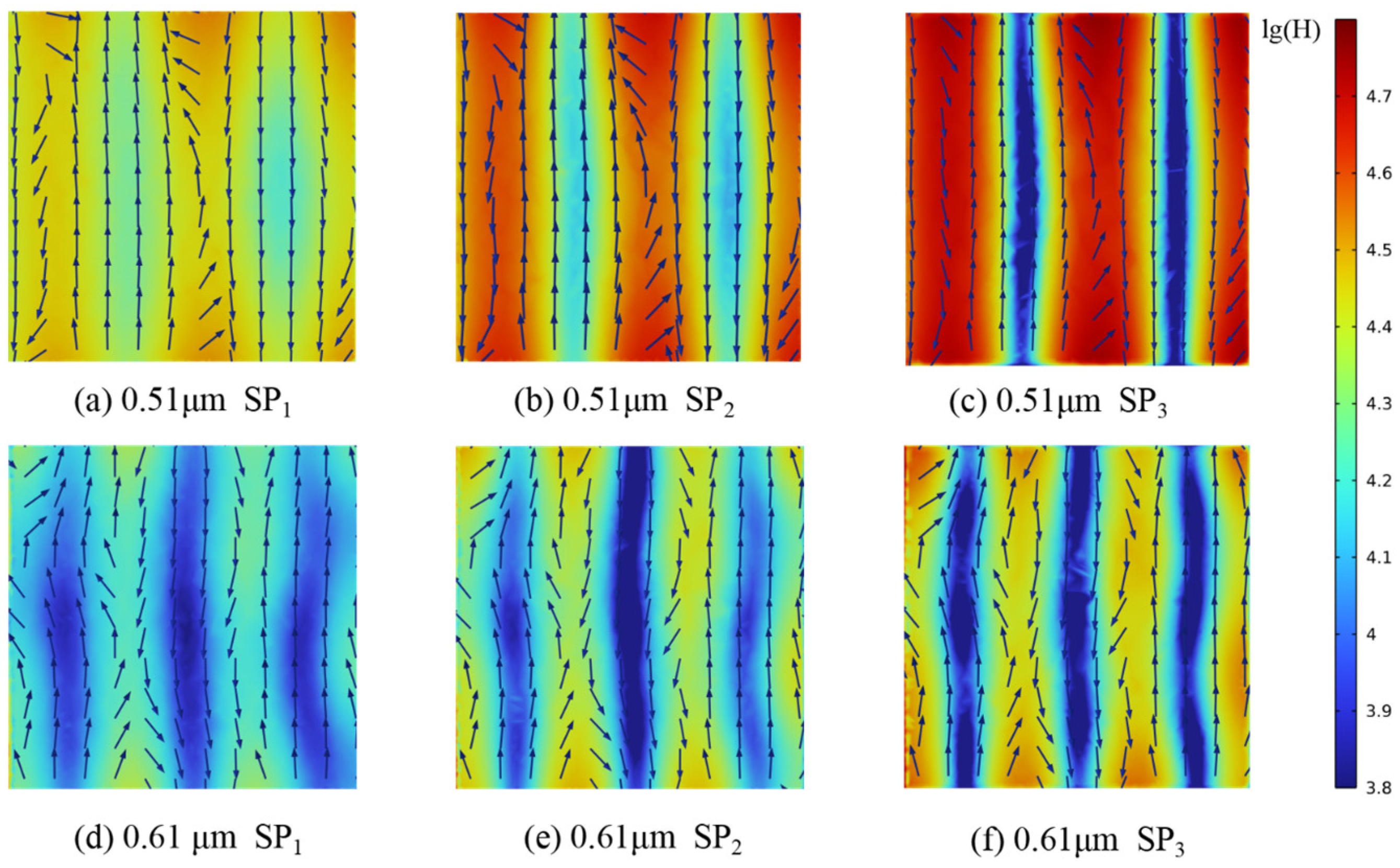
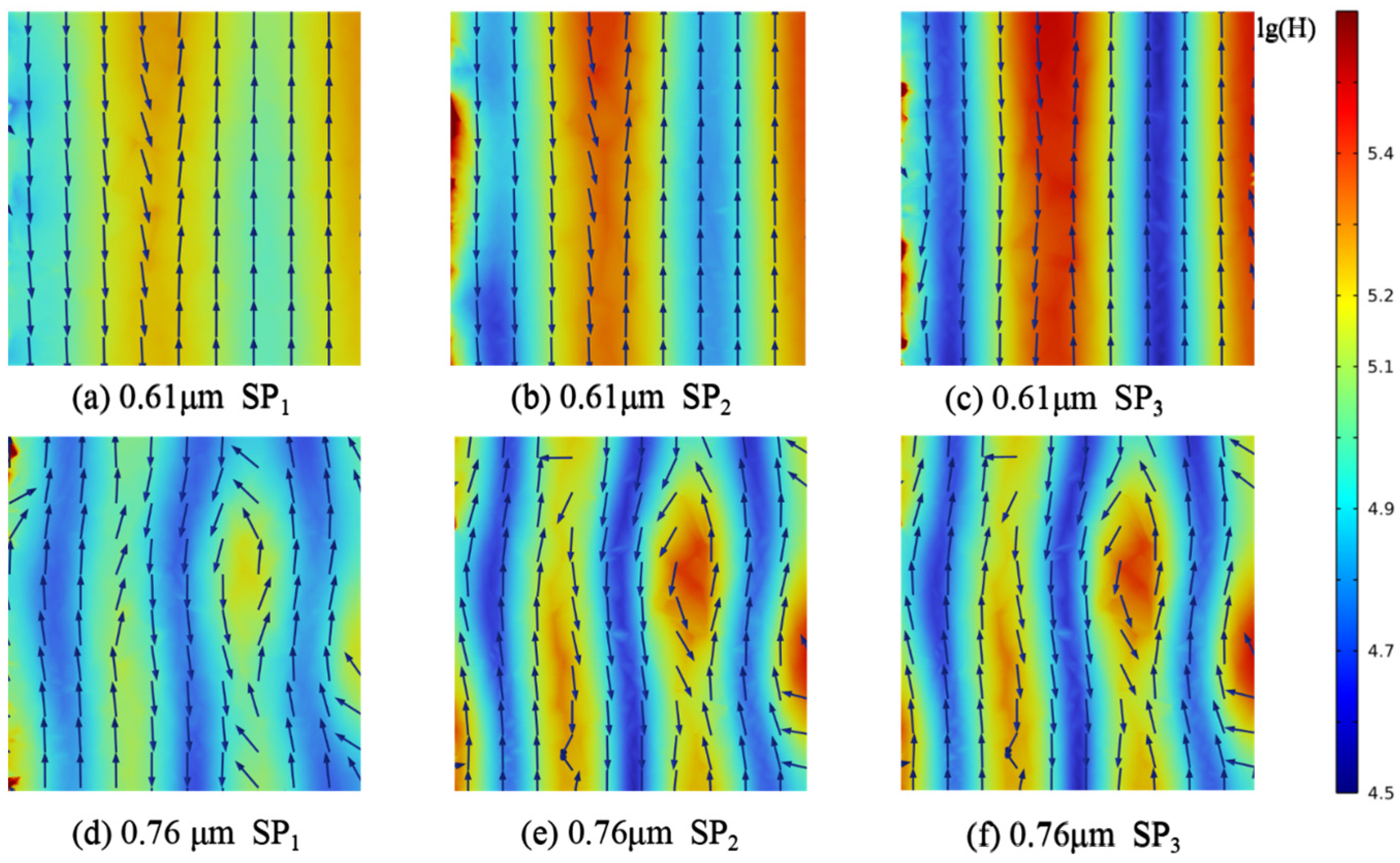
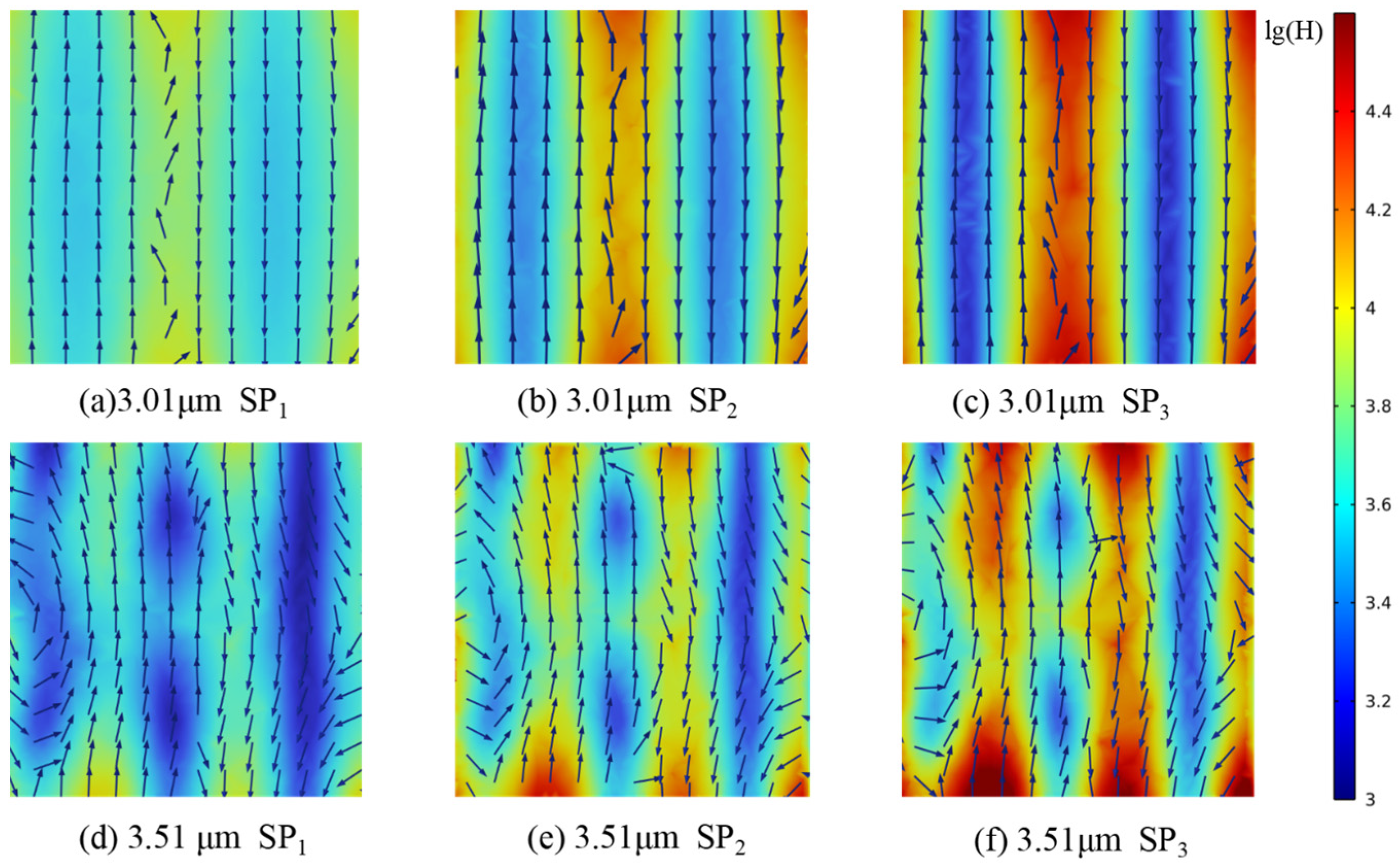
| λ | SP1 | SP2 | SP3 | φ | Dh |
|---|---|---|---|---|---|
| 0.71 μm | 24.43 | 29.13 | 36.75 | 90% | 1 μm |
| 0.76 μm | 30.88 | 34.43 | 42.78 | ||
| 5.51 μm | 10.72 | 12.46 | 23.28 | 10 μm | |
| 6.51 μm | 20.69 | 22.34 | 29.90 | ||
| 0.51 μm | 27.24 | 32.53 | 42.16 | 80% | 1 μm |
| 0.61 μm | 28.87 | 36.39 | 49.07 | ||
| 5.01 μm | 18.07 | 23.3 | 30.33 | 10 μm | |
| 6.01 μm | 22.73 | 27.84 | 33.39 | ||
| 0.61 μm | 29.42 | 34.71 | 45.66 | 70% | 1 μm |
| 0.76 μm | 31.34 | 36.75 | 49.43 | ||
| 3.01 μm | 18.27 | 26.13 | 38.37 | 10 μm | |
| 3.51 μm | 24.87 | 29.67 | 45.87 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Guo, N.; Chen, A.; Li, M.; Zhang, H.; Du, M. Microscopic Insight into Knudsen and Electromagnetic Effects on Thermal Conductivity of Closed Mesoporous Metal Gels. Gels 2025, 11, 739. https://doi.org/10.3390/gels11090739
Yu H, Guo N, Chen A, Li M, Zhang H, Du M. Microscopic Insight into Knudsen and Electromagnetic Effects on Thermal Conductivity of Closed Mesoporous Metal Gels. Gels. 2025; 11(9):739. https://doi.org/10.3390/gels11090739
Chicago/Turabian StyleYu, Haiyan, Ning Guo, Anqi Chen, Mingdong Li, Haochun Zhang, and Mu Du. 2025. "Microscopic Insight into Knudsen and Electromagnetic Effects on Thermal Conductivity of Closed Mesoporous Metal Gels" Gels 11, no. 9: 739. https://doi.org/10.3390/gels11090739
APA StyleYu, H., Guo, N., Chen, A., Li, M., Zhang, H., & Du, M. (2025). Microscopic Insight into Knudsen and Electromagnetic Effects on Thermal Conductivity of Closed Mesoporous Metal Gels. Gels, 11(9), 739. https://doi.org/10.3390/gels11090739









