Abstract
This study introduces a collaborative and open dataset designed to classify operational transconductance amplifiers (OTAs) in switched-capacitor applications. The dataset comprises a diverse collection of OTA designs sourced from the literature, facilitating benchmarking, analysis and innovation in analog and mixed-signal integrated circuit design. Various evaluation methodologies, implemented through a companion Python notebook script, are discussed to assess OTA performances across different operating conditions and specifications. Several Figures of Merit (FoMs) are utilized as performance metrics to achieve significant performance classification. This study also uncovers intriguing behaviors and correlations among FoMs, providing valuable insights into OTA design considerations. By making the dataset openly available on platforms like GitHub, this work encourages collaboration and knowledge sharing within the integrated circuit design community, thereby enhancing transparency, reproducibility and innovation in OTA design research.
Dataset License: Dataset available under the GNU General Public License (GPL) version 3.
1. Introduction
In the context of analog integrated circuit design, operational transconductance amplifiers (OTAs) play a crucial role in various electronic systems, including switched-capacitor (SC) applications. OTAs serve as fundamental building blocks in modern communication, sensing, driving and signal-processing systems [1,2,3].
The performance and efficiency of OTAs greatly influence the overall functionality of integrated circuits [4,5]. Therefore, the classification of OTAs is essential to optimize circuit design, enhancing performances, and to meet application-specific requirements such as settling time, slew rate, bandwidth at specific conditions of capacitive loading and settling accuracy [6].
Existing research concerning OTA design has primarily focused on the analysis of OTA circuits based on their circuital topology [7,8], design methodology [9,10,11,12] or CMOS technological node [13,14].
The design process of OTAs continues to demand significant technical expertise. Presently, this process is predominantly facilitated by Electronic Design Automation (EDA) tools; nevertheless, designers are often confronted with the challenging responsibility of meticulously selecting the appropriate circuit topology based on given requirements (e.g., process, power consumption, accuracy). Furthermore, reaching state-of-art performances still implies complex optimization procedures, stemming from an in-depth understanding of specific circuit topologies and related design trade-offs. Insofar, fully automated design procedures are still far from being available.
In pursuit of cost reduction and accelerated project timelines, future iterations of EDA tools are poised to integrate Artificial Intelligence (AI) to a greater extent [15,16]. AI algorithms will progressively assume responsibility for an expanding range of tasks, beginning with repetitive duties such as layout drawing. Subsequently, AI will advance to tasks involving the optimization of circuit parameters by exploring the design space, culminating in abstract endeavors such as synthesizing circuit sub-topologies to devise novel architectural solutions [17,18].
Nevertheless, the absence of high-quality datasets for training and evaluating classification models remains a significant challenge, with sparse information scattered throughout the scientific literature. This limitation impedes the progress of developing and bench-marking classification techniques.
In response to this challenge, this study presents a collaborative and open dataset for OTA classification in switched-capacitor applications. By leveraging contributions from multiple sources and fostering collaboration within the research community, this dataset aims to facilitate advancements in OTA classification and supports the optimization of the design process. Equally crucial is the necessity for this dataset to be openly accessible, fostering a democratic transition of society into the digital age [19].
2. Dataset Description
In the following, we provide comprehensive information about the various attributes of the proposed dataset, including its context, its structure and its contents.
The database title “OTA Settling Survey” conveys the focus and purpose of the dataset, drawing inspiration from the renowned “ADC Performance Survey” by Murmann [20]. The term “settling” pertains to the OTA performance, which is usually of greatest interest in switched-capacitor applications. With settling performance, we refer to the speed of the OTA output voltage in recovering from abrupt variations, up to settling to a desired voltage level (under specified accuracy requirements). SC circuits are discrete-time systems whose operations are based on charge transfers among capacitors, assisted by OTAs in closed-loop configurations. OTAs configured with negative feedback provide low-impedance nodes, allowing for almost ideal charge transfer processes. However, correct functionality is achieved as long as OTAs are able to charge/discharge their load capacitors quickly enough as to make transient duration substantially smaller than the clock period. In light of this, bandwidth, slew rate and, most importantly, settling time serve as cornerstone characteristics of such circuits in the above-mentioned applications [21].
2.1. Data Source
The dataset is built starting from sourcing the scientific literature accessible through various online search engines and platforms for the scientific and technical literature, including IEEE Xplore, MDPI, Springer, Elsevier and Wiley, among others. These platforms serve as valuable repositories of scholarly articles, research papers and publications, providing a rich pool of data for analysis and exploration.
An exhaustive search is conducted across these search engines, utilizing key phrases such as ‘OTA’, ‘settling time’ and ‘switched capacitors’. Each article retrieved in the search results undergoes meticulous manual extraction of quantitative information. This method ensures thoroughness and accuracy in capturing relevant data from the scientific literature, filtering out data of questionable quality.
At this juncture, it is essential to distinguish between two fundamental types of data obtained through electrical simulations performed with EDA tools: measured performances and simulated data. Measured results are deemed of higher quality as they demonstrate actual metrics obtained in real-world scenarios, thereby overcoming any potential inaccuracies inherent in electrical models of the devices and/or other non-idealities not accounted for during simulations. However, direct measurements may not always be feasible, especially for very fast operational transconductance amplifiers (OTAs) or those loaded with very small capacitance values (e.g., <1 pF). Moreover, several research works also only report simulated results because of the relatively high fabrication costs and long turn-around times of integrated circuit prototypes. However, simulated results can still be relevant if sufficiently accurate analyses are included (e.g., process–voltage–temperature corner simulations, Monte Carlo statistical simulations, post-layout simulations). Consequently, articles describing both experimental and simulation approaches are considered in the dataset compilation process. The nature of the results, however, is reported in the dataset as a specific data field (EXPM).
2.2. Data Structure
The dataset is structured in a tabular format within a spreadsheet (.xlsx), incorporating the fields outlined in Table 1. For each field, a short-named variable is associated, referenced for numerical calculations to assess the performance metrics described in Section 3. Units are also specified whenever pertinent. For better clarity, the data entry type is also indicated.

Table 1.
Spreadsheet headings of the “OTA Settling Survey” dataset (field, variable, units) and the corresponding entry type.
The Digital Object Identifier, title, first author, and year fields (denoted as DOI, TITL, AU1, YEAR, respectively) enable the unique identification of the research work. While the data are graphically represented in scatter plots, the design instances are labeled by combining the first author’s name and the year of publication (author + year format).
The CMOS technological node (CMOS) is relevant for investigating the impact of adopting different technology nodes on the performance.
The number of gain stages (NS) is related to the circuit topology of the OTA. Typically, the choice is limited to three major architectures: single-stage, two-stage or three-stage (i.e., NS ).
The signal configuration (SCFG), either single-ended or fully differential, is mainly determined by the application and is relevant in determining the intended use of the OTA
The test setup (TEST) is identified among the following possible choices: ‘Not specified’, ‘RC-beta’, ‘Switched-cap configuration’, ‘Unity-gain buffer’, and ‘Unity-gain R-beta’, as illustrated in Figure 1. Configurations (a) and (d) are used, respectively, for single-ended and fully differential setups to characterize the OTA in unity-gain configuration [22]. Configurations (b) and (e) are often used for very high-speed designs to resemble a switched-capacitor amplifier, applying a pulsed input as in the previous configuration case [23]. For these configurations, and . It is important to set , where G is the desired voltage gain. This condition imposes the compensation conditions: and . Configurations (c) and (f) represent the actual switched-capacitor amplifier/integrator configuration [24]. Direct measurements of these latter configurations are less straightforward.
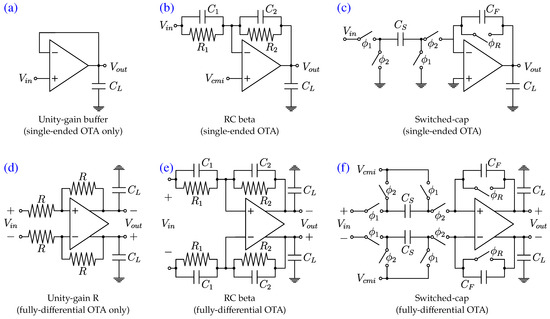
Figure 1.
Test setup configurations of OTAs (TEST): (a) Unity-gain buffer for single-ended OTAs; (b) RC beta feedback for single-ended OTAs; (c) Switched-capacitor feedback for single-ended OTAs; (d) Unity-gain resistive feedback for fully-differential OTAs; (e) RC beta feedback for fully-differential OTAs; (f) Switched-capacitor feedback for fully-differential OTAs.
The feedback factor, BETA, is derived from specific test setup configurations (see Table 2). As discussed in [6], this factor inherently impacts the evaluation of performance metrics and could potentially be utilized for additional normalizations of the Figures of Merit (FoMs) when comparing different OTA designs. However, for simplicity, the incorporation of BETA into the FoMs of Section 3 is not addressed in this context.

Table 2.
Correspondence between the circuital parameters relative to the configurations shown in Figure 1 and BETA and CLE.
The experimental method, denoted as EXPM, indicates whether the metrics are derived from measurements (‘Measured’) or electrical simulations (‘Simulated’).
The effective capacitive load, CLE, indicates the loading condition, considering also the feedback network (see Table 2).
The input voltage step, DVS, refers to the amplitude of the stimulus step used in the measurement of the settling parameters (specifically for what concerns SRP, SRN, TSP and TSN).
The overall supply voltage, SUP, refers to the supply configuration, which can either be a single supply () or a dual supply (with representing the highest supply voltage and representing the lowest supply voltage). For all data analyses, only the term is relevant (or , in the case of a single supply).
The remaining fields (SRP, SRN, UGF, TSP, TSN, SERR, PWR, AREA, A0, PM, OS, SNOI, INOI) pertain to characteristic performance metrics of OTAs, namely positive and negative slew rates, unity-gain frequency, low-to-high and high-to-low settling times, settling accuracy, power consumption, area occupation, phase margin, input referred offset (standard deviation), root-mean-squared noise density given at a specific frequency spot, and root-mean-squared noise integrated in the bandwidth from DC to the given frequency value, respectively.
2.3. Data Usage
The intended usage of the collected data should serve two primary purposes, listed as follows:
- Expanding the Reference Pool: Continuously updating the spreadsheet to encompass future research works, as well as incorporating previously published works not currently included in the database, thereby enriching the perspective on the state of the art of OTA designs.
- Data Analysis: Employing simple Python scripts (or equivalent script tools) to visualize, rank, or classify the design instances using the methods outlined and described in Section 3. Additionally, there is the possibility of introducing new methods tailored to more specific analyses.
The GNU General Public License (GPL) version 3 is applied to both the spreadsheet and the Python notebook associated with the ‘OTA Settling Survey’ dataset. This choice ensures that the dataset remains openly accessible and can be freely used, modified, and shared by all, while also guaranteeing that derivative works remain open. Interested readers are encouraged to make use of the proposed dataset according to these principles to foster novel widespread awareness in the subject of fast-settling OTA design.
3. Methodology
Perfromances of the designs are measured through the following set of FoMs [6]:
To calculate these quantities, the worst-case slew rate, SR, and the worst-case settling time, , are extracted from the parameters of Table 1 as follows:
The functions ‘fmin()’ and ‘fmax()’ correspond to element-wise max and min functions, respectively, between two arrays, taking care of NaN (not-a-number) cases. If one of the elements being compared is a NaN, the non-NaN element is returned [25,26]. A NaN value is present whenever the corresponding spreadsheet field is left blank. This could happen, for example, if only one value between SRP and SRN is annotated.
Finally, in Equation (4), indicates the static current drawn from the supply, derived from the dataset as follows:
The FoMs of Equations (1)–(4) are focused on classifying OTA performances in terms of settling speed vs. power efficiency at a given loading condition. In this respect, FOMN is the most descriptive since it also accounts for the amplitude of the input voltage step (DVS). A detailed discussion on the differences between the FoMs is developed in [6].
Clearly, new FoMs can be introduced to account for other design aspects as well, such as open-loop DC gain (A0), phase margin (PM) or silicon area occupation (AREA). This is left for possible future explorations of the dataset.
In this work, we explore the state-of-the-art literature using the FoMs of Equations (1)–(4), employing the following classification methods:
- Ranking the top-10 designs in terms of each FoM;
- Ranking the top-10 designs in terms of FOMN/CLE;
- Mapping the best FoM against the OTA architecture (NS);
- Placing each design case in a FoM vs. CLE scatter plot;
- Visualizing each design case in an FoM vs. technological node (CMOS) scatter plot;
- Analyzing the correlations between the four FoMs.
Data-elaboration functions used in the Python notebook script are described in Appendix A.
4. Results and Discussion
The results in both tabular and graphical formats are obtained by running the Python notebook script. A straightforward classification of each design with respect to each FoM is exhibited in Figure 2. The tabular output serves as a valuable tool for identifying specific publications by displaying key information such as the DOI (Digital Object Identifier) and other significant fields (AU1, YEAR).
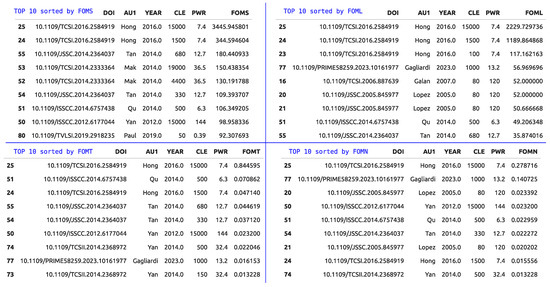
Figure 2.
Tabular output for the ranking of designs in terms of Figures of Merit (FoMs) values. CLE is expressed in [pF], PWR in [µW], FOMS in [MHz·pF/µW], FOML in [V·pF·s−1·µW−1], FOMT in [pF·ns−1·µW−1], and FOMN is a dimensionless number.
Classification by simple ranking, however, is not sufficient to deduce the best OTA design. It is worth noting that OTA design with fast-settling targets encompasses both topological choices and slew-rate-enhancing mechanisms [6]. The effectiveness of each solution is benchmarked against specific operating conditions and specifications (CLE, SUP, DVS, BETA, SERR). Therefore, a holistic evaluation of OTA designs requires considering a range of factors beyond just performance metrics. Further exploration of the dataset involves comprehensive benchmarking and analysis to identify optimal designs tailored to specific requirements and operating conditions. These considerations led us to explore 2D design spaces represented by the FoM vs. CLE axes of Figure 3.
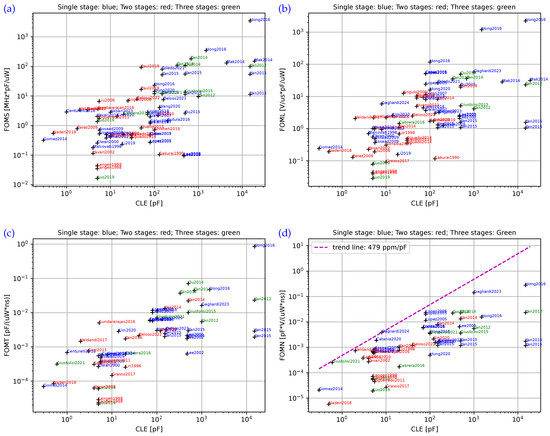
Figure 3.
Scatter plot outputs for each FoM: (a) FOMS vs. CLE; (b) FOML vs. CLE; (c) FOMT vs. CLE; (d) FOMN vs. CLE.
As discussed in [6], a trend line can be observed, which is particularly evident in the FOMN–CLE space. The tabular output shown in Figure 4 presents the ranking based on the trend-line slope coefficient, R_FOMN_CLE [ppm/pF], defined by
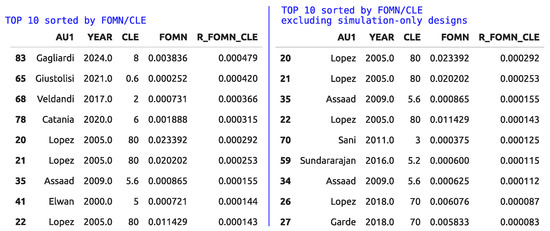
Figure 4.
Tabular output with respect to the ratio from (8), including all designs and including only experimental results. CLE is expressed in [pF], FOMN is a dimensionless number, and R_FONM_CLE is expressed in [pF−1].
The measured results report a lower maximum R_FOMN_CLE (292 ppm/pF) compared to simulation results (420 ppm/pF). As anticipated, this discrepancy can be attributed to the intrinsic difficulties of reproducing the operating conditions of a switched-capacitor stage in a test setup where the probe loading cannot be neglected. Additionally, it is worth mentioning that high-speed switched-capacitor stages are typically intended for uses in larger systems such as filters, modulators or pipeline analog-to-digital converters, where the stage under test is typically loaded by similar sub-circuits presenting an equivalent load capacitance well below the 10 pF level.
Figure 5 illustrates a potential classification based on the number of stages (NS) to evaluate the impact of architectural choices. A general trend of superiority for single-stage designs over multistage ones is observed. Multistage topologies are often utilized in low-voltage designs to address DC gain limitations resulting from the inability to employ cascode configurations. While the results presented in Figure 5 offer valuable insights, it is evident that further refinement is necessary to draw more robust conclusions. Enriching the dataset with additional references dedicated to this aspect would be advantageous and is earmarked for future developments.
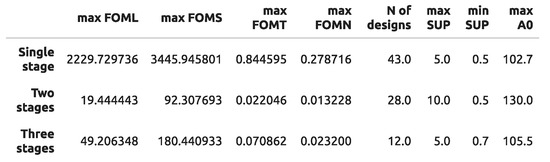
Figure 5.
Tabular output for FoM classification based on the OTA number of stages (NS). Maximum and minimum supply voltages (SUP) are expressed in [V], while A0 is expressed in [dB].
Regarding the impact of the CMOS technological node on performances, it is evident from Figure 6a that, currently, the 180 nm CMOS node collects the greatest number of designs, followed by the 500 nm CMOS and the 130 nm CMOS nodes. Apparently, implementations in 180 nm CMOS show superior performances in terms of FoMs. However, concerning absolute settling speed, the best result is obtained with the 40 nm CMOS node, as shown in the tabular output of Figure 6b.
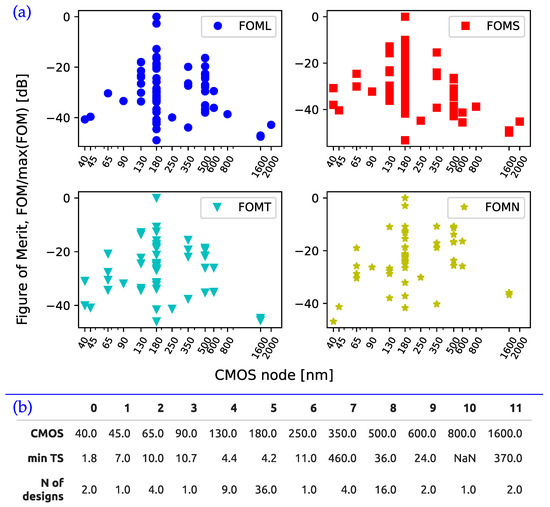
Figure 6.
(a) Scatter plot output of FoM vs. technological node; (b) minimum settling time [ns] obtained for each technological node.
Interdependences among the FoMs represent a crucial aspect in evaluating OTA performances. As previously introduced, transitioning to the unified FOMN seems to offer several advantages, leading to higher correlations in performance classification between designs featuring similar architectures, as proven by the clusters emerging in Figure 3d. These considerations were already discussed in [6] and are partially confirmed by the general trends shown in plots in Figure 7. However, a closer examination reveals the emergence of the following behaviors:
- In the FOMT–FOMN plot of Figure 7a, a high degree of correlation is evident. This can be easily understood by directly elaborating Equations (3), (4) and (7), resulting in the following relation:Moreover, the maximum input range DVS is related to the supply range SUP: , where is determined by specific design choices (e.g., stage gain, employment of cascode configurations or complementary input pairs). Hence,Equation (10) linearly relates FOMN and FOMT for a given SUP, through a coefficient equal to . However, since SUP may vary from design to design, a band appears in the bilogarithmic plot of Figure 7a. Under the same FOMT performance, a better FOMN is achieved for larger supplies and larger input steps. The upper limit of this band is clearly determined by the interpolation of (10) to the design case with the highest , whereas the lower limit of the band corresponds to the design case with the smaller value. This phenomenon suggests that a specific design with a given FOMN scales with law, when FOMT is considered. Clearly, this argument has some practical limitations: excessively up-scaling SUP may incur a violation of devices’ safe operating region, whereas excessive down-scaling SUP may cause the devices to exit the usual saturation region, degrading the gain of the amplification stages and finally heavily affecting the settling precision, as well as other OTA functionalities based on feedback action (e.g., bandwidth and/or slew-rate-enhancing). The two design points determining the total width of the dispersion band have been marked with APA-style labels: “Gagliardi2023” [22] and “Naderi2018” [23]. For the latter, we have the following specifications: and (). For “Gagliardi2023”, and (). Consequently, and .
- The FOML–FOMN plot in Figure 7b follows a similar trend as that of Figure 7a. In [6], it has been demonstrated that, if the asymptotic condition of settling time dominated by slew-rate settling holds, then the following simple relationship can be considered:where is the maximum output current of the OTA and k is a constant related to the capacitive feedback network. On the other hand, since , we can relate Equations (2) and (11) to find the following:Both k and SUP are specific to each design point. Hence, a band-like dispersion similar to that in Figure 7a is observed. In this case, the band dispersion is determined by the “Hong2016” [27] and the “Gagliardi2023” [22] designs. The observed maximum and minimum values of are V and V, respectively.
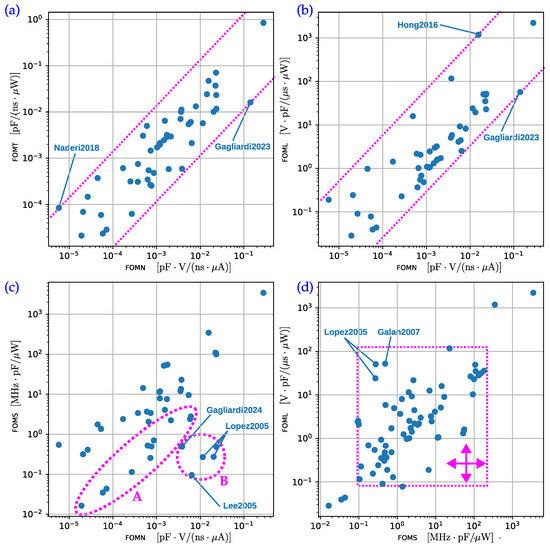 Figure 7. Annotated scatter plots for FoM interdependence analysis: Dots represent design entries in the dataset, while areas determined by dotted lines are meant to group and/or cluster design points with similar characteristics. (a) FOMT–FOMN plot; (b) FOML–FOMN plot; (c) FOMS–FOMN plot; (d) FOML–FOMS plot. The following references have been indicated in the plots: Gagliardi2023 [22], Naderi2018 [23], Gagliardi2024 [24], Hong2016 [27], Lopez2005 [28], Galan2007 [29], Lee2005 [30].
Figure 7. Annotated scatter plots for FoM interdependence analysis: Dots represent design entries in the dataset, while areas determined by dotted lines are meant to group and/or cluster design points with similar characteristics. (a) FOMT–FOMN plot; (b) FOML–FOMN plot; (c) FOMS–FOMN plot; (d) FOML–FOMS plot. The following references have been indicated in the plots: Gagliardi2023 [22], Naderi2018 [23], Gagliardi2024 [24], Hong2016 [27], Lopez2005 [28], Galan2007 [29], Lee2005 [30]. - A different behavior is observed in the FOMS–FOMN plot of Figure 7c, where subgroups A and B have been encircled for easier visual identification. These groups demonstrate the existence of sub-optimal designs in terms of bandwidth (UGF), which, however, are marked by high FOMN scores due to more efficient large-signal characteristics, such as input range and slew rate. Depending on the intended application, it may be reasonable to opt for such OTA solutions, but it should be considered that enhanced large-signal performance is achieved at the expense of small-signal characteristics. This is a typical design situation where a low-power operation is achieved by reducing the static OTA power consumption and relying on efficient class AB operation, which temporarily and on demand increases the instantaneous current in the OTA internal branches [31]. Designs labeled “Lopez2005” [28] and “Galan2007” [29] follow this trend with specific circuit implementations based on Super-Class AB OTAs.
- In the FOML–FOMS plot of Figure 7d, a distinct disposition of the design instances is evident. There is no strong correlation between FOML and FOMS. This plot has been annotated with a square to highlight the partial orthogonality of FOML with respect to FOMS, exhibiting complementary characteristics as for what concerns small-signal and large-signal behaviors. This aspect is intriguing as it challenges the generally accepted rule of thumb that unequivocally correlates slew rate to unity-gain bandwidth for basic OTA topologies [32], and it helps identifying optimal solutions for different application cases (e.g., standard-voltage vs. low-voltage contexts [33]). This consideration could potentially stimulate the creation of new OTA topologies with the aim of combining different characteristics for enhanced performance as for both small-signal and large-signal features.
5. Conclusions
This work offers the following contributions.
- Dataset Development: The creation of a collaborative and open dataset for the classification of OTAs represents a significant contribution to the field of analog and mixed-signal integrated circuit design. This dataset provides researchers with access to a comprehensive collection of OTA designs, facilitating benchmarking, analysis and innovation in OTA design methodologies.
- Evaluation Methodologies: The article discusses various evaluation methodologies, including the use of FoMs to assess OTA performances across different operating conditions and specifications. These methodologies enable researchers to systematically analyze and compare OTA designs, yielding a clearer picture of the state of the art and leading to insights into design trade-offs and performance optimization alternatives.
- Interdependence of FoMs: The study highlights the interdependence of FoMs and related implications for OTA design. Transitioning to a unified FoM, such as FOMN, offers advantages in terms of performance classification and correlation between performances and circuit architecture categories. Additionally, the proposed analysis reveals intriguing behaviors and correlations among FoMs, providing insights into design considerations.
- Open Access and Collaboration: By making the dataset openly available on platforms such as GitHub, the article promotes collaboration and knowledge sharing within the research community. This open access approach fosters transparency, reproducibility and innovation in OTA design research.
Author Contributions
Conceptualization, methodology, software, validation, formal analysis, data curation, writing, F.G. and M.D.; funding acquisition, M.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the NRRP, Mission 4 Component 2 Investment 1.2 of Italian MIUR funded by the EU-NextGenerationEU with the project HeMoWear. GA ID: 0004610/2022.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original data presented in the study are openly available on GitHub at https://github.com/michele-dei/OTA-settling-survey (accessed on 30 September 2024).
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Appendix A
In this section, we provide detailed descriptions of the auxiliary functions employed to process, analyze and visualize the data presented in this study. These functions are implemented within the companion Python notebook script, ensuring a systematic and reproducible approach to dataset manipulation and graphical representation.
Appendix A.1. “display_sorted” Function

The “display_sorted” function is designed to display tabular results sorted by a specified key. This function is particularly useful for ranking and presenting the top entries in the dataset based on a particular criterion. The function allows for the customization of the columns included in the display and the number of entries shown. This function is used to produce the tabular results in Figure 2.
Parameters:
- sort_key (str): The column name by which to sort the data.
- number (int): The number of top entries to display. Default is 10.
- print_key_list (list): A list of column names to include in the displayed table. Default includes [’DOI’, ‘AU1’, ‘YEAR’, ‘CLE’, ‘PWR’]. Any field from those listed in Table 1 may be used.
- df (DataFrame): The DataFrame containing the dataset. Default is x, which corresponds to the data imported from the “OTA Settling Survey” xlsx file through the Pandas “read_excel” function [34].
Appendix A.2. “apa_style_annotations” Function

The “apa_style_annotations” function is designed to create APA-style (author + year) annotations for use in scatter plots. This function is helpful for labeling data points in plots with a standardized citation format, making it easier to identify and reference specific studies.
Appendix A.3. “ns_to_color” Function

The “ns_to_color” function assigns colors to data points based on the number of stages (NS) of the OTA designs. This is useful for visually distinguishing between different architectural choices in scatter plots of Figure 3.
Appendix A.4. “design_id_in_fom” Function

The “design_id_in_fom” function identifies the design indices that fall within a specified range of a given FoM. This is useful for filtering designs based on their performance metrics. It returns the indices of the designs that meet the criteria. This function is employed in the function “design_id_in_fom1_2” described in Appendix A.5.
Parameters:
- fom: The array of Figure of Merit values. Defaults to FOMN.
- fom_range: A list specifying the lower and upper bounds of the FoM range. Defaults to [ , ].
Appendix A.5. “design_id_in_fom1_2” Function

The “design_id_in_fom1_2” function is designed to filter and identify design indices that fall within specified ranges of two FoMs. This function allows for more complex filtering criteria by considering two performance metrics simultaneously. This function is employed to identify designs in specific regions of plots of Figure 7. The function returns the indices of the designs that meet the criteria.
Parameters:
- fom1: The first array of Figure of Merit values. Defaults to FOMN.
- fom2: The second array of Figure of Merit values. Defaults to FOMT.
- range1: A list specifying the lower and upper bounds of the first FoM range. Defaults to [0, 1].
- range2: A list specifying the lower and upper bounds of the second FoM range. Defaults to [0, 1].
References
- Parveen, T. Textbook of Operational Transconductance Amplifier and Analog Integrated Circuits; IK International Pvt Ltd.: Delhi, India, 2013. [Google Scholar]
- Sanchez-Sinencio, E.; Ramirez-Angulo, J.; Linares-Barranco, B.; Rodriguez-Vazquez, A. Operational transconductance amplifier-based nonlinear function syntheses. IEEE J. Solid-State Circuits 1989, 24, 1576–1586. [Google Scholar] [CrossRef]
- Geiger, R.L.; Sánchez-Sinencio, E. Active filter design using operational transconductance amplifiers: A tutorial. IEEE Circuits Devices Mag. 1985, 1, 20–32. [Google Scholar] [CrossRef]
- Ramus, X. Demystifying the Operational Transconductance Amplifier; Application Report SBOA117A; Texas Instruments Inc.: Dallas, TX, USA, 2013; pp. 1–12. [Google Scholar]
- Smith, D.N. The performance of integrated transconductance amplifiers as variable current sources for bio-electric impedance measurements. Clin. Phys. Physiol. Meas. 1992, 13, 25. [Google Scholar] [CrossRef] [PubMed]
- Dei, M.; Gagliardi, F.; Bruschi, P. Slew-Rate Enhancement Techniques for Switched-Capacitors Fast-Settling Amplifiers: A Review. Chips 2024, 3, 98–128. [Google Scholar] [CrossRef]
- Kumari, U.; Yadav, R. A Review About Analysis and Design Methodology of Two-Stage Operational Transconductance Amplifier (OTA). In Lecture Notes in Networks and Systems, Proceedings of the International Conference on Data Science and Applications; Saraswat, M., Chowdhury, C., Kumar Mandal, C., Gandomi, A.H., Eds.; Springer: Singapore, 2023; Volume 552. [Google Scholar]
- Poddar, V.; Ali, Z.K. A Review on Low Power Designs of Operational Transconductance Amplifier with Linearity Techniques. Int. J. Eng. Res. Technol. 2015, 4, 417–423. [Google Scholar]
- Choi, J.; Kweon, S.-J.; Jeon, H. Single-Stage CMOS Operational Transconductance Amplifiers (OTAs): A Design Tutorial. Electronics 2023, 12, 3833. [Google Scholar] [CrossRef]
- Da Silva Braga, R.A.; Silva, P.M.M.; Karolak, D.B. Are CMOS operational transconductance amplifiers old fashioned? A systematic review. J. Integr. Circuits Syst. 2022, 17, 1–7. [Google Scholar] [CrossRef]
- Riad, J.; Estrada-López, J.J.; Sánchez-Sinencio, E. Classification and Design Space Exploration of Low-Power Three-Stage Operational Transconductance Amplifier Architectures for Wide Load Ranges. Electronics 2019, 8, 1268. [Google Scholar] [CrossRef]
- Sharma, S.; Kaur, P.; Singh, T.; Kumar, M. A Review of Different Architectures of Operational Transconductance Amplifier. Int. J. Electron. Commun. Technol. 2012, 3, 384–388. [Google Scholar]
- Pandey, R.; Kumar, S.; Sonia, V.; Singh, P.; Ghangas, S.; Bisariya, S. A Review on CMOS Operational Transconductance Amplifier on Different Technology Node. Proc. Adv. Electron. Commun. Eng. 2022, 584–587. [Google Scholar] [CrossRef]
- Vadodaria, M.U.; Patel, R.; Popat, J. A Review on Operational Transconductance Amplifier (OTA) Using 180nm Technology. Int. J. Adv. Eng. Res. Dev. 2014, 1, 215–219. [Google Scholar]
- Freund, K. AI Is Reshaping Chip Design. But Where Will It End? Forbes. 2023. Available online: https://www.forbes.com/sites/karlfreund/2023/12/19/ai-is-reshaping-chip-design-but-where-will-it-end/?sh=2618b79e5bed (accessed on 20 April 2024).
- Fayazi, M.; Taba, M.T.; Afshari, E.; Dreslinski, R. AnGeL: Fully-Automated Analog Circuit Generator Using a Neural Network Assisted Semi-Supervised Learning Approach. IEEE Trans. Circuits Syst. I Regul. Pap. 2023, 70, 4516–4529. [Google Scholar] [CrossRef]
- Unleashing the Power of Generative AI in Chip, System, and Product Design, White Papers. Available online: https://www.cadence.com/en_US/home/resources/white-papers/unleashing-the-power-of-generative-ai-in-chip-system-and-product-design-wp.html (accessed on 20 April 2024).
- What Is AI Chip Design? Available online: https://www.synopsys.com/ai/what-is-ai-chip-design.html (accessed on 20 April 2024).
- Kuroda, T. Slashing IC Power and Democratizing IC Access for the Digital Age. IPSJ Trans. Syst. LSI Des. Methodol. 2023, 17, 2–6. [Google Scholar] [CrossRef]
- Murmann, B. ADC Performance Survey 1997–2023. Available online: https://github.com/bmurmann/ADC-survey (accessed on 20 April 2024).
- Gregorian, R.; Martin, K.W.; Temes, G.C. Switched-capacitor circuit design. Proc. IEEE 1983, 71, 941–966. [Google Scholar] [CrossRef]
- Gagliardi, F.; Catania, A.; Piotto, M.; Bruschi, P.; Dei, M. A Novel High-Performance Parallel-Type Slew-Rate Enhancer for LCD-Driving Applications. In Proceedings of the 2023 18th Conference on Ph.D Research in Microelectronics and Electronics (PRIME), Valencia, Spain, 18–21 June 2023; pp. 65–68. [Google Scholar] [CrossRef]
- Naderi, M.H.; Prakash, S.; Silva-Martinez, J. Operational Transconductance Amplifier With Class-B Slew-Rate Boosting for Fast High-Performance Switched-Capacitor Circuits. IEEE Trans. Circuits Syst. I Regul. Pap. 2018, 65, 3769–3779. [Google Scholar] [CrossRef]
- Gagliardi, F.; Catania, A.; Piotto, M.; Bruschi, P.; Dei, M. Parallel Slew-Rate Enhancer With Current-Recycling Core for Switched-Capacitors Circuits. IEEE Trans. Circuits Syst. II Express Briefs 2024. [Google Scholar] [CrossRef]
- NumPy Documentation. Available online: https://numpy.org/doc/stable/reference/generated/numpy.fmin.html (accessed on 23 April 2024).
- NumPy Documentation. Available online: https://numpy.org/doc/stable/reference/generated/numpy.fmax.html (accessed on 23 April 2024).
- Hong, S.-W.; Cho, G.-H. A Pseudo Single-Stage Amplifier With an Adaptively Varied Medium Impedance Node for Ultra-High Slew Rate and Wide-Range Capacitive-Load Drivability. IEEE Trans. Circuits Syst. I Regul. Pap. 2016, 63, 1567–1578. [Google Scholar] [CrossRef]
- Lopez-Martin, A.J.; Baswa, S.; Ramirez-Angulo, J.; Carvajal, R.G. Low-Voltage Super class AB CMOS OTA cells with very high slew rate and power efficiency. IEEE J. Solid-State Circuits 2005, 40, 1068–1077. [Google Scholar] [CrossRef]
- Galan, J.A.; Lopez-Martin, A.J.; Carvajal, R.G.; Ramirez-Angulo, J.; Rubia-Marcos, C. Super Class-AB OTAs With Adaptive Biasing and Dynamic Output Current Scaling. IEEE Trans. Circuits Syst. I Regul. Pap. 2007, 54, 449–457. [Google Scholar] [CrossRef]
- Lee, H.; Mok, P.K.T.; Leung, K.N. Design of low-power analog drivers based on slew-rate enhancement circuits for CMOS low-dropout regulators. IEEE Trans. Circuits Syst. II Express Briefs 2005, 52, 563–567. [Google Scholar] [CrossRef]
- Catania, A.; Cicalini, M.; Dei, M.; Piotto, M.; Bruschi, P. Performance Analysis and Design Optimization of Parallel-Type Slew-Rate Enhancers for Switched-Capacitor Applications. Electronics 2020, 9, 1949. [Google Scholar] [CrossRef]
- Solomon, J.E. The monolithic op amp: A tutorial study. IEEE J. Solid-State Circuits 1974, 9, 314–332. [Google Scholar] [CrossRef]
- Catania, A.; Cicalini, M.; Piotto, M.; Bruschi, P.; Dei, M. Energy Efficiency in Slew-Rate Enhanced Single-Stage OTAs for Switched-Capacitor Applications. J. Low Power Electron. Appl. 2021, 11, 1. [Google Scholar] [CrossRef]
- Pandas Documentation. Available online: https://pandas.pydata.org/docs/reference/api/pandas.read_excel.html (accessed on 27 July 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).