Abstract
The Boltzmann equation is applied to fit data of volume loss for evaporation (in %) during spirit ageing in northern white oak (Quercus Alba) standard barrels of 205 L (+/− 10 L) using a temperature and humidity controlled cellar. The Boltzmann equation satisfactory fitted to the experimental data of the volume loss against temperature at constant humidity. Two parameters of the Boltzmann equation showed a linear dependency on the relative humidity of the air, while the other two parameters exhibited a constant value independently of the air humidity. The found empirical mathematical model can be used to calculate the volume loss for evaporation of spirits (40% v/v of ethanol) during ageing in terms of relative humidity (range: 40%–95%) and temperature (range: 10–30 °C) with significant accuracy.
1. Introduction
Rum is a fairly tasteless and neutral spirit, traditionally (but not exclusively) produced in the Caribbean and Central America countries. The distilled product (as primary rum), known in Cuba as “Aguardiente”, is a colorless liquid which is aged in barrels of white oak wood (Quercus Alba) during a timed period in order to transform and improve its sensorial characteristics [1]. Oak barrels impart flavor, aroma, and color to spirits that are completely clear at the time of distillation, and lacking many of the most familiar and desirable sensory qualities of aged spirits. Freshly distilled primary rum typically has some unpleasant characteristics that require maturation time to moderate some of their pungency and acquire many of the characteristic flavors that are desirable in a mature product. When spirits age, the alcohol extracts and reacts with constituents in the barrel wood, producing its distinctive color, taste, and aroma. Constituents in the wood are transferred to the bulk liquid in the barrel by simple diffusion, by convection currents in the bulk liquid, and by temperature cycling. As the barrel heats up, the gas above the liquid increases in pressure and forces liquid into the barrel wood. When the barrel cools and the gas pressure drops, the liquid flows out of the wood into the bulk liquid, carrying with it the wood constituents [1,2,3,4].
Additionally, the concentration of flavors that is the consequence of evaporation is an important factor in maturation [5]. In that sense, the volume loss is an inherent part of the ageing process. The barrel acts as a semi permeable membrane that allows evaporation from the cask and migration of air into the barrel, because of its porous structure [3]. Angel’s share is an industry term used to describe percent volume lost from the barrel owing to evaporation, which (among other variables) increases in function of the cask surface area/capacity ratio [6]. Environmental conditions in barrel storage facilities (rack houses, cellars) are frequently not controlled, which leads to differences in ageing effects in the variety of climatic conditions in which spirits are aged [3,7,8,9].
The annual ageing loss not only depends on external factors such as climatic conditions of the cellar (air humidity, velocity, and temperature), but also internal factors corresponding to the wood and liquid properties (porosity, density, stave preparation, and morphology of the wood fiber), as well as the alcoholic content, have a significant influence [10,11,12]. The spirit evaporation during the ageing process is an unquestionable economic issue for producers. Therefore, efforts to diminish and/or control the loss during ageing are crucial in order to optimize the production process and to reduce the associated costs. The most frequent solutions for diminishing the evaporation loss are focused on temperature and humidity controlled cellars. However, for large cellars, a further detailed economic analysis is needed in order to evaluate the cost–benefit of installing a controlled air conditioning system [13,14]. In general, ineffective design criteria for cellar conditioning are applied for spirits and wine producers because of the challenging complexity of the diffusional process involved, having a multifactorial and combined effect, which generates difficulties to accurately calculate the ageing loss using an integrated mathematical model [13].
Different phenomenological-based models have been explored in order to describe the liquid evaporation from barrels with a tight-linked basis in wood drying process studies [10,11,12,13]. However, despite the efforts, the large number of variables involved and their interactions lead to simplifications and theoretical assumptions that hinder the generalization of the proposed models from being successfully applied at the different conditions reported by spirit producers, thus being rather specific for a dedicated case. For traditional spirit producers, the empirical models and the ageing loss statistical records are still the emergent tools to calculate the Angel’s share for their cellars.
In that direction, this work is focused on obtaining an empirical Boltzmann-based mathematical model to describe the ageing loss reported data in a conditioned cellar. The fitted model is used to calculate the annual percent volume loss during spirit (40% v/v alcoholic content) ageing in standard white oak barrels under controlled conditions of temperature and air humidity, which are the only two variables considered for this study. The analysis in this paper is expressed in terms of total loss in volume, instead of the changes in the alcohol concentration during ageing. The reasons for this are as follows. During the spirit ageing, water and ethanol are evaporated at the same time. Therefore, the total volume loss in the barrel depends not only on the contribution of the evaporated volume of water and ethanol, but also on other volatile compounds present in the spirit. However, the evaporation rate of both (water and ethanol) is a complex process that depends not only on environmental conditions of air temperature and humidity, but also highly on the wood properties such as wood porosity, thickness of the staves, size of the cask (represented by its ratio of capacity/wood surface), and the physical-chemical characteristics of the spirit. Additionally, spirits are not only formed by ethanol and water, they are a very complex mixture of other congeners gathered in a very diverse families of esters, aldehydes, alcohols, and acids, which in turn react with wood extractables (poly-phenolics compounds) during ageing, thus changing the original characteristics of the spirits over time. This complex and changing chemical composition not only defines the organoleptic features of the spirit, making it possible to differentiate them, but also affects the mass-diffusional properties of each compound through the oak wood into the air (according to the Fick law). The math modeling of spirit evaporation by integrating all the involved variables described above is thus quite complex, and thus simplifications and theoretical assumptions are frequently considered. In this research, (spirit (rum) 40% v/v) the changes found in real ethanol content in the rum after the experiments ranged between 37.3% and 39.5% v/v, but without following a “useful” correlational trend, as was found in the case of the total volume loss. That is why it is preferred to not include this analysis at the moment. Perhaps, this “random” behavior in the ethanol content is the result of the complexity in the chemical-wood diffusional scenario interacting with the environmental variables of temperature and humidity, but this needs further study. Although very specific, this work constitutes one discrete step in the attempt to describe the complex process of spirit loss during the ageing process. The found results should be interesting for researchers and producers working on the aged alcoholic beverages technology.
2. Materials and Methods
2.1. Experimental Data
Experimental data were provided by a major rum producer in Cuba. The volume loss per year (in %) at different conditions of air temperature and relative humidity is presented in Table 1. An air-conditioned cellar was used to establish the temperature and humidity controlled environment. The studied ranges of relative humidity and temperature were 40%–95% and 10–30 °C, respectively.

Table 1.
Volume loss per year (in %) at different conditions of air temperature and relative humidity (HR).
A total of 225 experimental data points were recorded. Selected white oak standard barrels of 205 L (+/− 10 L) were used and conveniently prepared to accurately measure the volume loss during the ageing process of a product of 40% of ethanol content (40% v/v).
2.2. Mathematical Model and Data Fitting
The Boltzmann sigmoidal classical model of four parameters (Equation (1)) was used to fit the experimental data using Origin software (version 8.0, OriginLab®, Northampton, MA, US).
where A1, A2, x0, and dx are the Boltzmann’s model constants.
3. Results and Discussion
Figure 1 depicts the plots of volume loss for evaporation during 40% v/v spirit ageing as a function of the temperature at constant relative air humidity (HR in %) plotted from the data presented in Table 1.
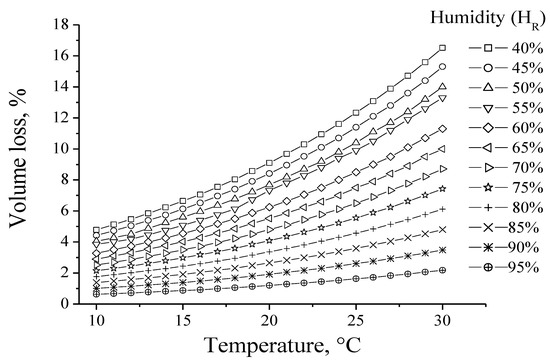
Figure 1.
Volume loss for evaporation during ageing as function of the temperature at constant relative air humidity (HR in %). Ethanol content of the spirit: (40% v/v). White oak standard barrels of 205 L (+/− 10 L).
In this case, a family of twelve curves is obtained at constant relative humidity in the range of 40%–95%. As expected, air humidity significantly influences the evaporation from the barrel. The higher the water content in the air, the lower the volume loss during ageing. In contrast, with the increment of the temperature, an increase in the volume loss is also confirmed [1,5,6,10,11,12,13,14]. On the basis of the data presented in Table 1 and its corresponding plots in Figure 1, the effect of the temperature on the volume evaporated is more significant at a lower humidity. After 20 °C, an increment in the growing slope of the (40%–55%) curves is more noticeable, indicating a significant effect of both parameters on the evaporation. Furthermore, at 95%, an almost linear relationship between the temperature and volume loss can be observed. As the air humidity decreases, an exponential or polynomial correlation between temperature and the evaporated volume becomes more evident.
Although other math models can be explored, in this study, the Boltzmann model (Equation (1)) was applied for fitting the data presented in Table 1, modifying the variables as presented in Equation (2), where T is the air temperature (independent variable) and T0, A1, A2, and dT are model constants. Notice the general independent variable “x” in this case is the temperature, so x0 and dx were changed to T0 and dT, respectively.
The selection of this model was based on the following conveniences: (1) the model fitted satisfactorily for all the twelve curves family at constant relative humidity, with a correlation coefficient over 0.999 for all the cases (see fitting parameters in Supplementary Materials); and (2) the Boltzmann model constants obtained after fitting each independent curve of volume loss (VLOSS) versus temperature (Figure 1) can be satisfactorily linearly-correlated with the humidity of the air, with the highest correlation coefficient in comparison with the other explored models.
Table 2 presents the fitting parameters for Equation (2) obtained for each curve at different relative humidity. Parameters A1 and A2 presented a decreasing tendency with the increment of the air humidity. In contrast, the other parameter dT and k () exhibited values that are independent on the air humidity. Fisher’s lower significant difference (LSD) method was applied to demonstrate that there is no statistical difference between the dT and k values found at different HR. Additionally, normal distribution of the parameters dT and k was confirmed, and their means are presented in Table 2.

Table 2.
Fitting parameters of Equation (2) obtained for the different curves at constant HR.
The found correlation coefficients (R2) were higher than 0.999 for all the cases (see the complete fitting data in Supplementary Materials). and are the mean of the correspondent parameters.
Figure 2 displays the linear correlation fitting plots of the A1 and A2 parameters in terms of HR. As an interesting feature of both linear correlations A1 and A2, the fitting linear goodness is better in the range of 70%–95% of HR, while in the range of 40%–70%, the found dispersion is higher, as previously demonstrated in Figure 1.
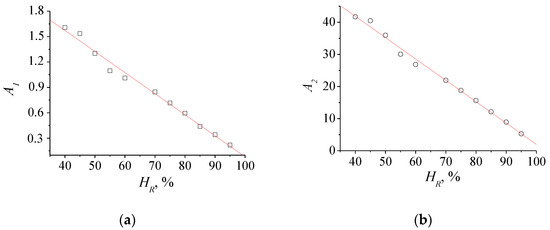
Figure 2.
Linear correlation plots of the Boltzmann A1 (a) and A2 (b) constants in terms of HR.
Table 3 shows the linear fitting parameters between the A1 and A2 Boltzmann constants and HR. Both parameters present comparable correlation coefficients of around 0.99.

Table 3.
Linear fitting parameters between the Boltzmann A1 and A2 constants and HR.
Combining the constant values ( and ) in Table 2, the linear correlations presented in Table 3 (A1 and A2 vs. HR) and Equation (2) yield Equation (3).
Equation (3) is the found empirical equation to determine the volume loss during 40% v/v spirit ageing in white oak standard barrels of 205 L (+/− 10 L), just considering relative humidity and temperature of the air as variables.
Figure 3 presents the correlation between experimental data and the proposed model (Equation (3)). According to the found correlation, the model satisfactorily reproduces the experimental data at the specified conditions. On the basis of the errors of the linear fitting parameters, the experimental and model-predicted values are statistically equal, with a reproducibility of 99.9% and a standard deviation of 0.11% of the calculated volume loss.
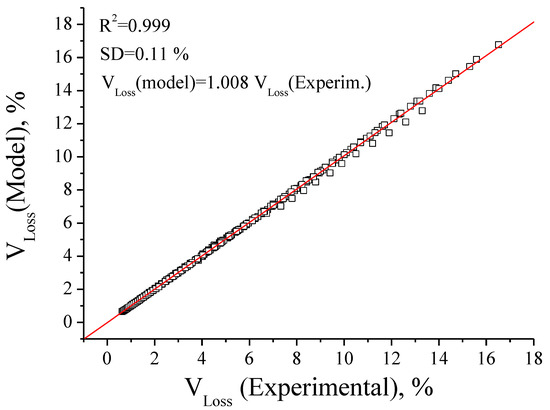
Figure 3.
Correlation plot between experimental data and the proposed empiric model (Equation (3)). SD = standard deviation in % of volume loss.
One of the advantages of using the proposed empirical model is the calculation of the volume loss at unsteady state conditions of weather variables of temperature and humidity in non-controlled cellars. For different year seasons, temperature and air humidity changes with the time (t). Therefore, the calculating of the total volume loss at the reported conditions in a yearly time period “t” of unsteady environmental conditions can be determined by numerically integrating the model (Equation (4)) using recorded data of air temperature and humidity at different moments (t) in the cellar (Equation (5)) and including a correcting discreet factor “n”, which depends on the discreet time laps when the humidity and temperature measurement are recorded. For instance, if the environmental measurements are recorded monthly (30 days), then n = 12; on weekly basis (7 days), n = 52; and on daily basis, n = 365.
4. Conclusions
It can be stated that a four-constants classical Boltzmann sigmoidal model can be successfully correlated (with a fitting goodness over 99.9%) with experimental volume loss data of spirit (40% v/v ethanol content) from 205 L standard white oak barrels in terms of temperature (in a range of 10–30 °C) and relative humidity (in a range of 40%–95%).
Two of the Boltzmann constants are linear functions of the relative air humidity and the other two are not affected by changes in the humidity content of the air. The found correlations can be combined in a single function to calculate the volume loss in terms of temperature and humidity at the specified conditions.
The best results in terms of accuracy and reproducibility of the experimental data are obtained at relative humidity in the range of 70%–95%. In contrast, the variability is higher when the model is used at a lower relative humidity (40%–70%). Therefore, caution is advised during extrapolation of ageing loss at lower air humidity than the specified values in this study.
The proposed model is a suitable tool for assessing/predicting the evaporation volume loss for spirit producers in view of an in-time controlling strategy needed within the ageing process in alcoholic beverages production and cellar air-conditioning design and evaluation. Additionally, the model can be used to calculate the volume loss at unsteady conditions of temperature and air humidity in a time period in non-conditioned cellars.
Supplementary Materials
The following are available online at https://www.mdpi.com/2306-5710/5/4/60/s1, Table S1: Data parameters for the Boltzmann model for volume loss at constant relative Humidity.
Author Contributions
J.N.C., J.A.R. and N.d.T.d.T. conceived and designed the experiments; F.F.C. and M.C.P.G. performed the experiments; H.C.S., J.N.C., D.V., J.Y. and R.C. analyzed the data; N.d.T.d.T., H.C.S., J.Y. and R.C. wrote the paper.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank VLIR-UOS (Flemish Interuniversity Council for University Development Cooperation) project between Belgium and Cuba for providing funding and granting the support of the current and future studies.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Crespo Sariol, H.; Vanreppelen, K.; Yperman, J.; Brito Sauvanell, A.; Carleer, R.; Campa, J.N. A colorimetric method for the determination of the exhaustion level of granular activated carbons used in the rum production. Beverages 2016, 2, 24. [Google Scholar] [CrossRef]
- Mosedale, J.R. Effects of oak wood on the maturation of alcoholic beverages with particular reference to whisky. Forestry 1995, 68, 203–230. [Google Scholar] [CrossRef]
- Matsuyama, R.; Nishimura, K. Maturation and Maturation Chemistry: The Science and Technology of Whiskies; Chapter 3; Duncan, R.E.B., Piggott, J.R., Sharp, R., Eds.; Longman Scientific and Technical: Essex, UK, 1989. [Google Scholar]
- Mosedale, J.R.; Puech, J.L. Wood maturation of distilled beverages. Food Sci. Technol. 1998, 9, 95–101. [Google Scholar] [CrossRef]
- Singleton, V.L. Maturation of wines and spirits: Comparisons, facts and hypothesis. Am. J. Enol. Vitic. 1995, 46, 98–115. [Google Scholar]
- Connor, J.M.; Paterson, A.; Piggott, J.R.; Withers, S.J. Comparison of Scotch malt whisky maturation in oak miniature casks and American standard barrels. J. Inst. Brew. 1995, 101, 359–364. [Google Scholar]
- Conner, J.; Jack, F.; Reid, K. Maturation and blending: Whisky Technology, Production and Marketing; Chapter 7; Russel, I., Ed.; Academic Press: London, UK, 2003. [Google Scholar]
- Clyne, J.; Conner, J.M.; Paterson, A.; Piggott, J.R. The effect of cask charring on Scotch whisky maturation. Int. J. Food Sci. Technol. 1993, 28, 69–81. [Google Scholar] [CrossRef]
- Philp, J.M. Cask Quality and Warehouse Conditions: The Science and Technology of Whiskies; Chapter 9; Duncan, R.E.B., Piggott, J.R., Sharp, R., Eds.; Longman Scientific and Technical: Essex, UK, 1989. [Google Scholar]
- Blazer, R.M. Influence of environment on wine evaporation from barrels. Pract. Winery Wineyard 1991, 5, 20–22. [Google Scholar]
- Kamke, F.A.; Yvanek, M. Computer models for wood drying. Drying pacific northwest species for quality markets. In Proceedings of the Conference Sponsored by the Forest Products Society, Washington, DC, USA, 30 October–1 November 1995. [Google Scholar]
- Liu, J.Y. A new method for separating diffusion coefficient and surface emission coefficient. Wood Fiber Sci. 1989, 21, 133–141. [Google Scholar]
- Ruiz, A.M. Aplicación de Dinámica de los Fluidos Computacional al Control de Mermas en Vinos en Naves de Crianza Climatizadas. Ph.D. Thesis, Universidad de la Rioja, Logroño, Spain, 2004. [Google Scholar]
- Jeffery, A.M. Aging of Whiskey Spirits in Barrels of Non-Traditional Volume. Master’s Thesis, Michigan State University, East Lansing, Michigan, 2012. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).