The Role of Machine Learning and Design of Experiments in the Advancement of Biomaterial and Tissue Engineering Research
Abstract
1. Introduction
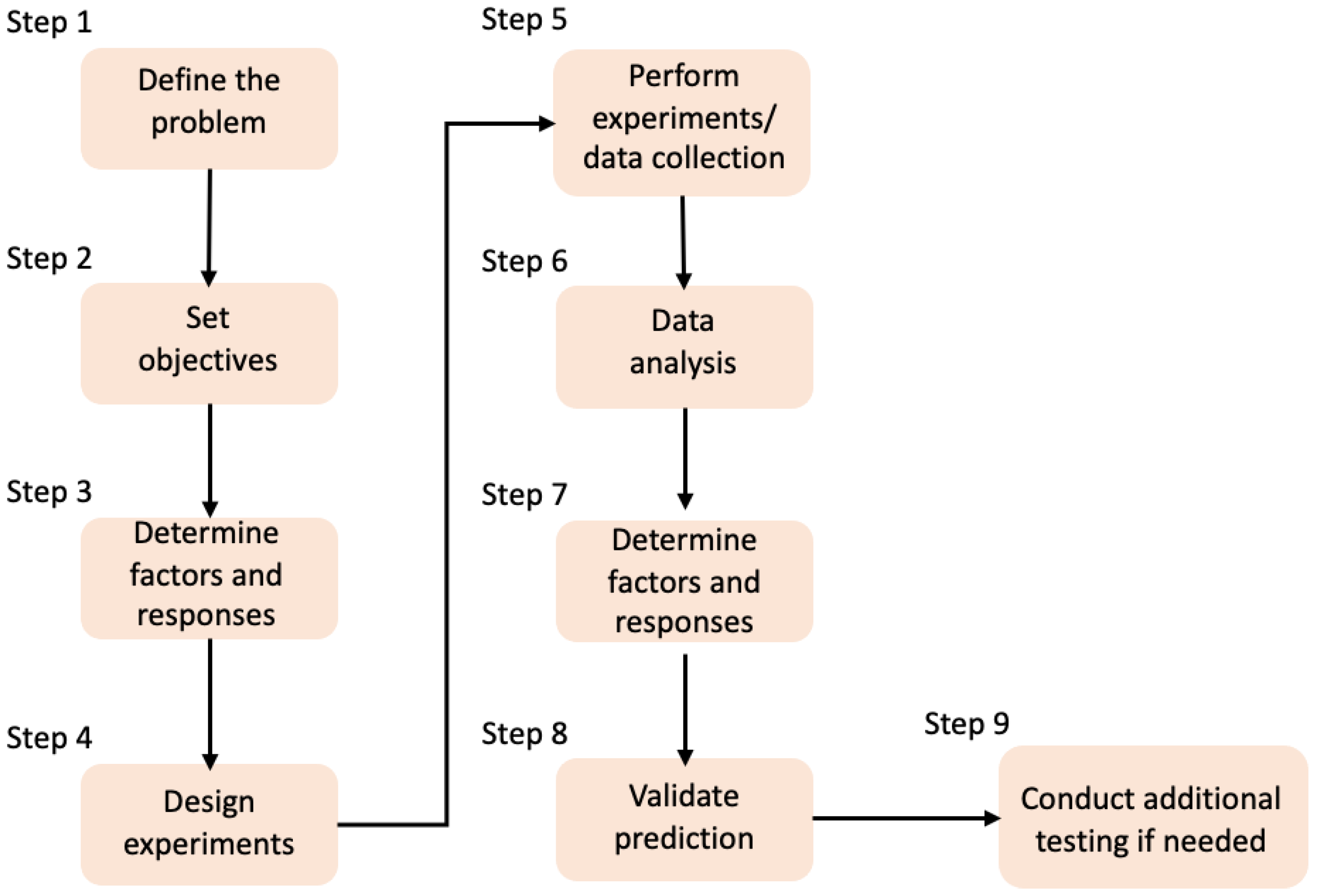
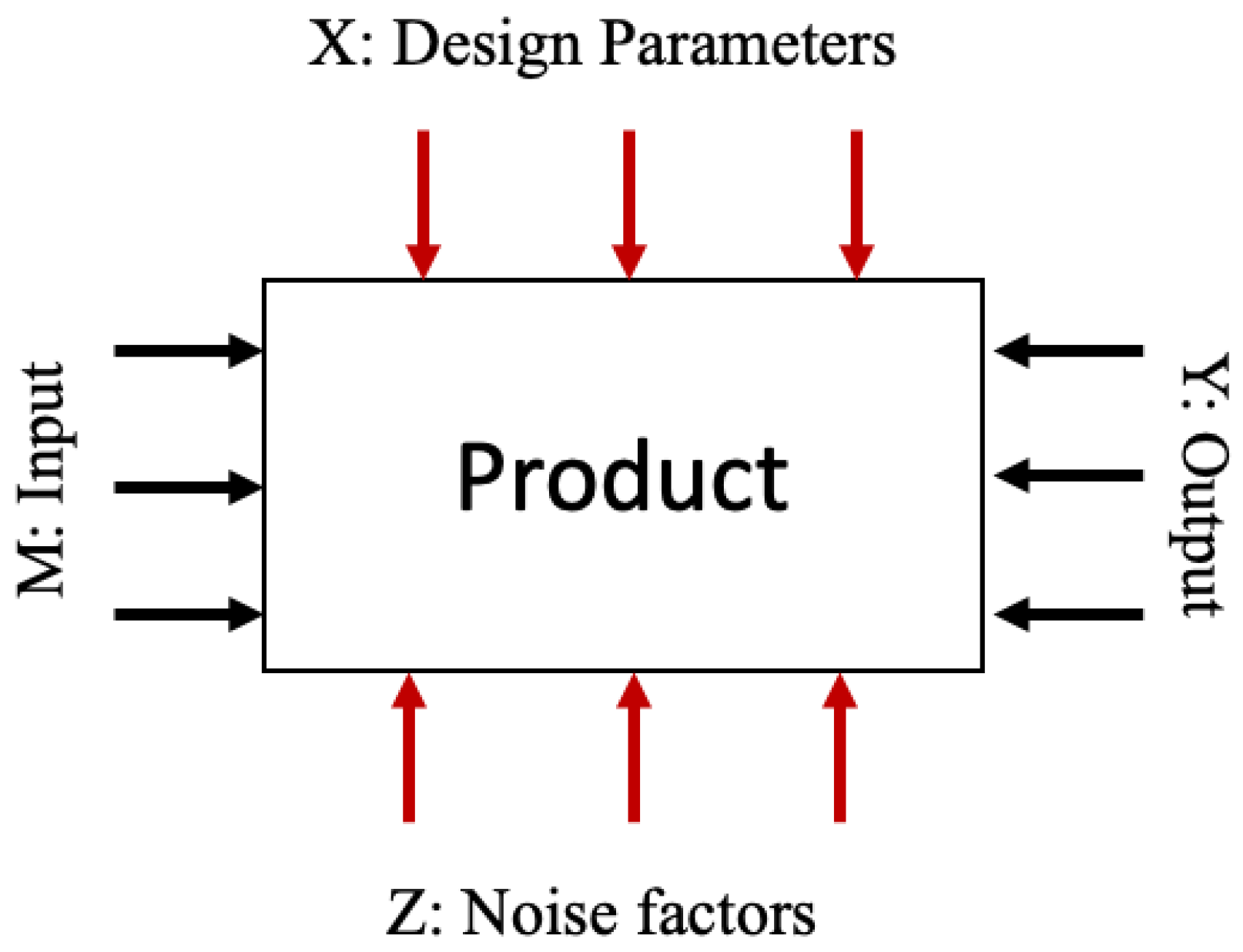
2. Design of Experiments (DoE)
2.1. Factorial Experiments
2.2. Latin Square
2.3. Taguchi Designs
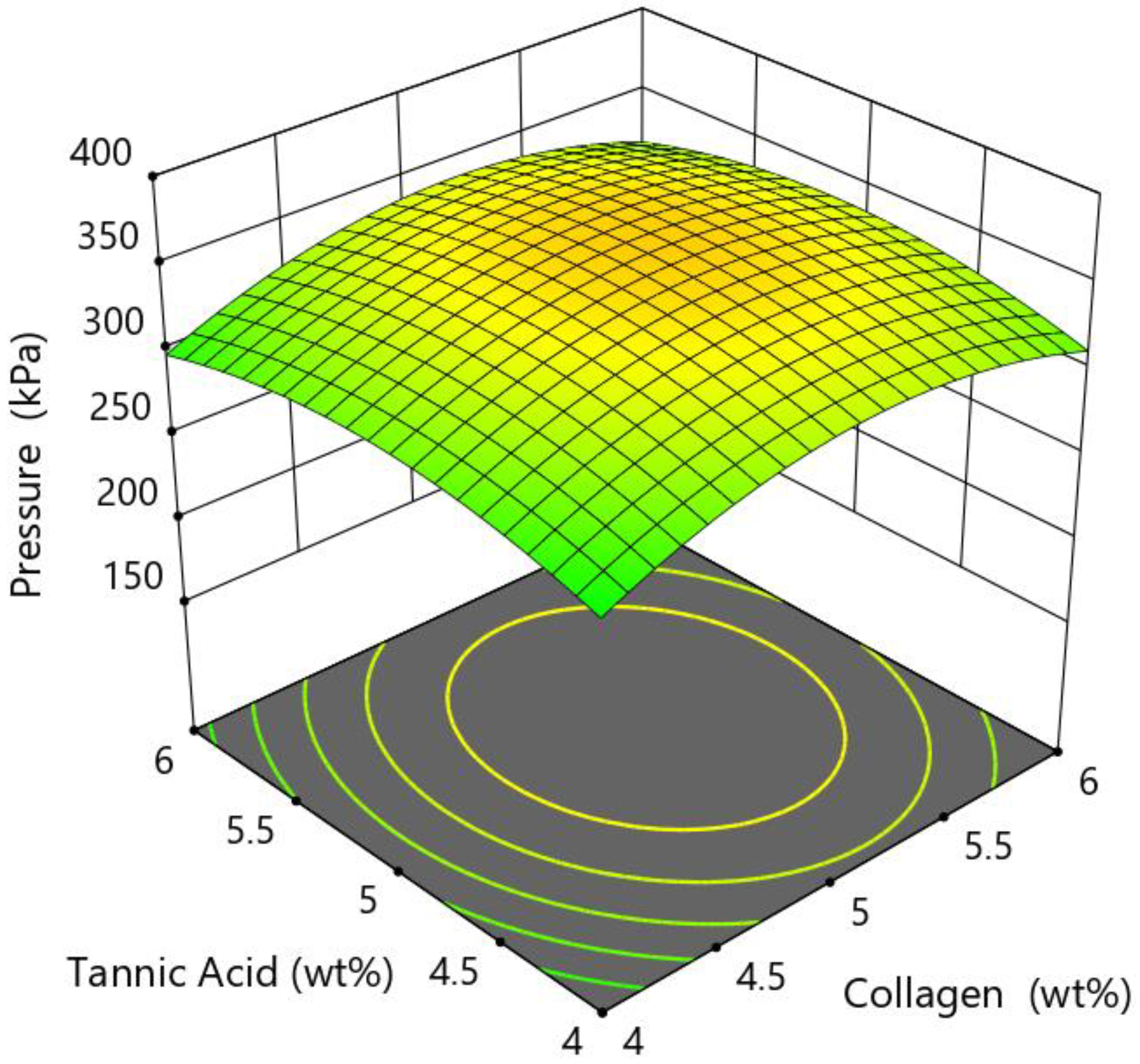
2.4. Response Surface Methodology (RSM)
2.5. Statistical Tools
| Techniques | Overview | Methodology | Benefits | Ref |
|---|---|---|---|---|
| Factorial designs | All factors are assessed as all possible combinations of ‘high’ and ‘low’ levels. Fractional factorial designs can be used to reduce the number of experimental runs. | Usually involve two or more factors assessed at two levels. | Useful for determining the main effects in screening experiments; Straight-forward to design; Robust. | [29] |
| Latin square | Ideally used for experiments in which it is possible to test subjects individually under every treatment. | Number of experimental conditions is required to equal the number of different labels | High control of the variation from the different experimental runs and labels Better efficiency compared to other techniques. | [34,36] |
| Taguchi designs | Determination of the best combination of inputs to produce a design or a product. | Determines parameter levels. | Identifies the right input; High-quality product; Robust design perspective. | [30,37] |
| Response Surface Methodology (RSM) | An offline optimisation method, which usually involves studying two factors. However, this technique can be used to study three or more factors. The method is usually employed in optimisation experiments. | RSM merges mathematical and statistical methods with experimental designs, to develop models that relate to the response and control factors. | Represents relationship between the responses and control factors; Allows response values to be predicted using a range of control factors; Provides optimum values for control variables; Uses statistical testing to determine a significant control variable. | [37,38] |
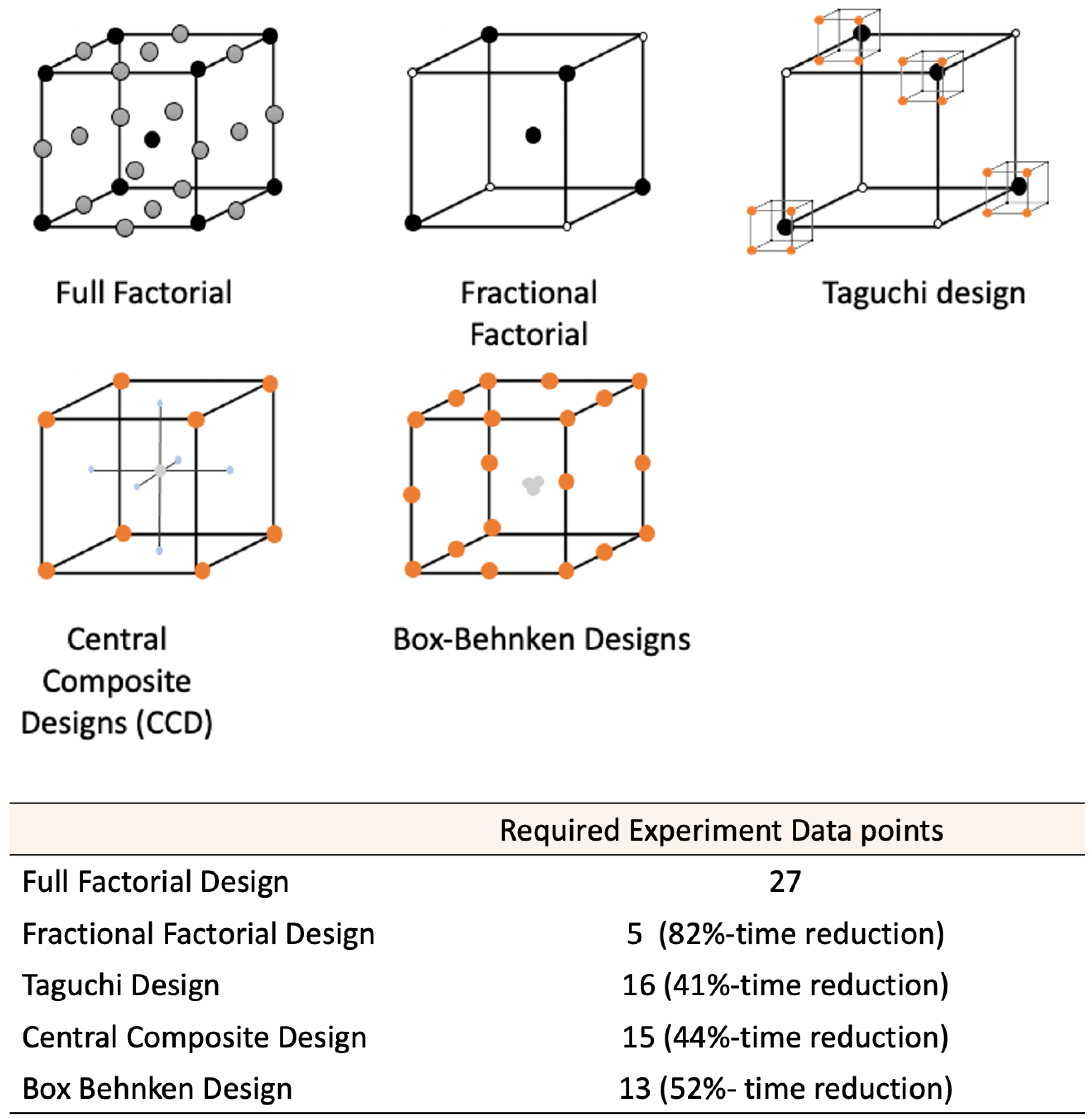
2.6. Comparison of the DoE Techniques
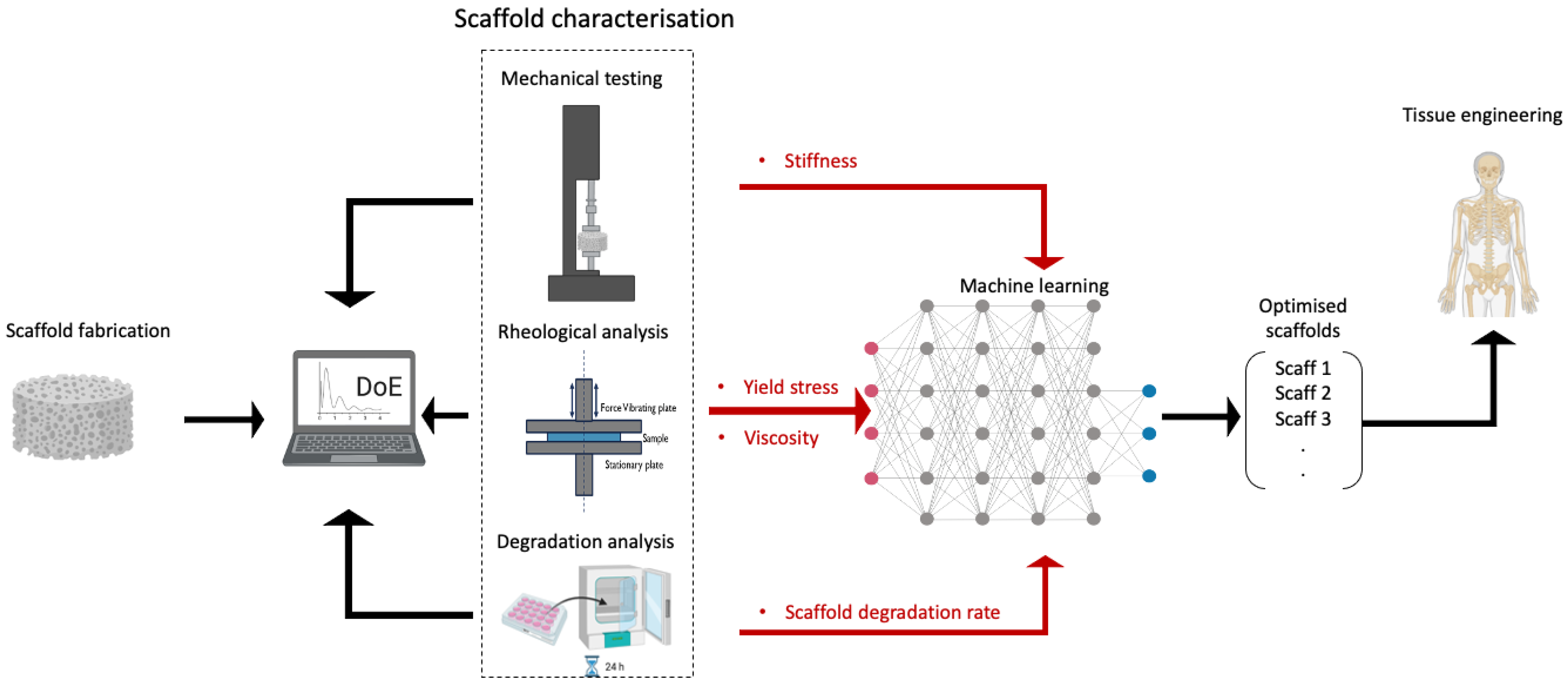
2.7. Application of DoE Methods in Biomaterials and TE Research
3. Machine Learning (ML)
3.1. Supervised Learning
3.1.1. Linear Regression
3.1.2. Decision Tree and Random Forest
3.1.3. Neural Networks
3.1.4. Support Vector Machines (SVMs)
3.1.5. Kernel Ridge Regression (KRR)
3.1.6. Bayesian Optimisation (BO)
3.1.7. Hierarchical Machine Learning (HML)
3.2. Unsupervised and Reinforcement Learning
Inductive Logic Programming (ILP)
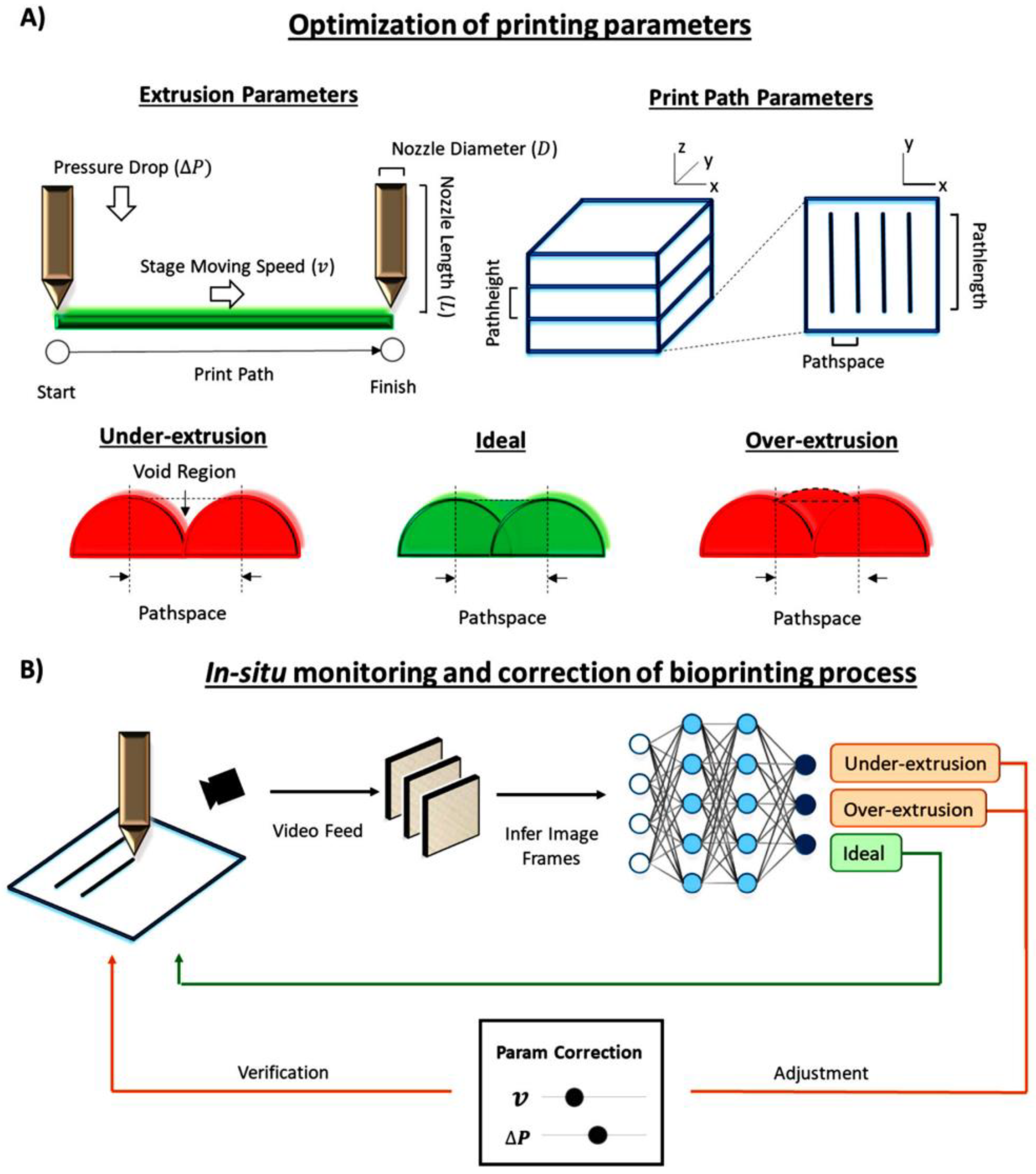
3.3. Applications of ML in Biomaterials and TE Research
4. Classical ML Techniques Compared with DoE Methods
5. Summary and Future Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, D.; Santos, H.Z.H.A. Droplet-based microfluidics for cell encapsulation and delivery. In Micro-fluidics for Pharmaceutical Applications; William Andrew: Hangzhou, China, 2019; pp. 307–335. [Google Scholar]
- Mark, A.A.; Furth, E. Principles of Tissue Engineering, 5th ed.; Elsevier Science Publishing Co Inc.: San Diego, CA, USA, 2014. [Google Scholar]
- Ghaemi, R.V.; Siang, L.C.; Yadav, V.G. Improving the Rate of Translation of Tissue Engineering Products. Adv. Healthc. Mater. 2019, 8, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Saunders, L.; Ma, P.X. Self-Healing Supramolecular Hydrogels for Tissue Engineering Applications. Macromol. Biosci. 2018, 19, e1800313. [Google Scholar] [CrossRef] [PubMed]
- Goldfracht, I.; Efraim, Y.; Shinnawi, R.; Kovalev, E.; Huber, I.; Gepstein, A.; Arbel, G.; Shaheen, N.; Tiburcy, M.; Zimmermann, W.H.; et al. Engineered heart tissue models from hiPSC-derived cardiomyocytes and cardiac ECM for disease modeling and drug testing applications. Acta Biomater. 2019, 92, 145–159. [Google Scholar] [CrossRef]
- Heo, D.N.; Hospodiuk, M.; Ozbolat, I.T. Synergistic interplay between human MSCs and HUVECs in 3D spheroids laden in collagen/fibrin hydrogels for bone tissue engineering. Acta Biomater. 2019, 95, 348–356. [Google Scholar] [CrossRef] [PubMed]
- Montgomery, D.C. Design and Analysis of Experiments, 8th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Zhang, S.; Vijayavenkataraman, S.; Lu, W.F.; Fuh, J.Y.H. A review on the use of computational methods to characterize, design, and optimize tissue engineering scaffolds, with a potential in 3D printing fabrication. J. Biomed. Mater. Res.-Part B Appl. Biomater. 2019, 107, 1329–1351. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.; McKee, J.A.; Fontenot, J.J.; Jung, J.P. Engineering Tissue Fabrication With Machine Intelligence: Generating a Blueprint for Regeneration. Front. Bioeng. Biotechnol. 2020, 7, 443. [Google Scholar] [CrossRef] [PubMed]
- Hakimi, O.; Krallinger, M.; Ginebra, M.-P. Time to kick-start text mining for biomaterials. Nat. Rev. Mater. 2020, 5, 553–556. [Google Scholar] [CrossRef]
- Sharpe, C.; Wiest, T.; Wang, P.; Seepersad, C.C. A Comparative Evaluation of Supervised Machine Learning Classification Techniques for Engineering Design Applications. J. Mech. Des. 2019, 141, 1–38. [Google Scholar] [CrossRef]
- Ng, W.L.; Chan, A.; Ong, Y.S.; Chua, C.K. Deep learning for fabrication and maturation of 3D bioprinted tissues and organs. Virtual Phys. Prototyp. 2020, 15, 340–358. [Google Scholar] [CrossRef]
- Yu, C.; Jiang, J. A perspective on using machine learning in 3D bioprinting. Int. J. Bioprinting 2020, 6, 4–11. [Google Scholar] [CrossRef] [PubMed]
- Ruberu, K.; Senadeera, M.; Rana, S.; Gupta, S.; Chung, J.; Yue, Z.; Venkatesh, S.; Wallace, G. Coupling machine learning with 3D bioprinting to fast track optimisation of extrusion printing. Appl. Mater. Today 2021, 22, 100914. [Google Scholar] [CrossRef]
- Bone, J.M.; Childs, C.M.; Menon, A.; Póczos, B.; Feinberg, A.W.; LeDuc, P.R.; Washburn, N.R. Hierarchical Machine Learning for High-Fidelity 3D Printed Biopolymers. ACS Biomater. Sci. Eng. 2020, 6, 7021–7031. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Oh, S.J.; An, S.H.; Kim, W.-D.; Kim, S.-H. Machine learning-based design strategy for 3D printable bioink: Elastic modulus and yield stress determine printability. Biofabrication 2020, 12, 035018. [Google Scholar] [CrossRef] [PubMed]
- Cao, B.; Adutwum, L.A.; Oliynyk, A.O.; Luber, E.J.; Olsen, B.C.; Mar, A.; Buriak, J.M. How To Optimize Materials and Devices via Design of Experiments and Machine Learning: Demonstration Using Organic Photovoltaics. ACS Nano 2018, 12, 7434–7444. [Google Scholar] [CrossRef] [PubMed]
- Entekhabi, E.; Nazarpak, M.H.; Sedighi, M.; Kazemzadeh, A. Predicting degradation rate of genipin cross-linked gelatin scaffolds with machine learning. Mater. Sci. Eng. C 2020, 107, 110362. [Google Scholar] [CrossRef] [PubMed]
- Koeppe, A.; Padilla, C.A.H.; Voshage, M.; Schleifenbaum, J.H.; Markert, B. Efficient numerical modeling of 3D-printed lattice-cell structures using neural networks. Manuf. Lett. 2018, 15, 147–150. [Google Scholar] [CrossRef]
- Kareem, M.M.; Tanner, K.E. Optimising micro-hydroxyapatite reinforced poly(lactide acid) electrospun scaffolds for bone tissue engineering. J. Mater. Sci. Mater. Med. 2020, 31, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Han, J.; Cao, T.; Lam, W.; Fan, B.; Tang, W.; Chen, S.; Fok, K.L.; Li, L. Design of self-assembly dipeptide hydrogels and machine learning via their chemical features. Proc. Natl. Acad. Sci. USA 2019, 116, 11259–11264. [Google Scholar] [CrossRef]
- Robles-Bykbaev, Y.; Naya, S.; Díaz-Prado, S.; Calle-López, D.; Robles-Bykbaev, V.; Garzón, L.; Sanjurjo-Rodríguez, C.; Tarrío-Saavedra, J. An artificial-vision- And statistical-learning-based method for studying the bio-degradation of type I collagen scaffolds in bone regeneration systems. PeerJ 2019, 7, 1–39. [Google Scholar] [CrossRef]
- Durakovic, B. Design of experiments application, concepts, examples: State of the art. Period. Eng. Nat. Sci. 2017, 5, 421–439. [Google Scholar] [CrossRef]
- Pietraszek, J.; Radek, N.; Goroshko, A.V. Challenges for the DOE methodology related to the introduction of Industry 4.0. Prod. Eng. Arch. 2020, 26, 190–194. [Google Scholar] [CrossRef]
- Horaningoga, A.U.; Kinsella, G.K.; Henehan, G.T.; Ryan, B.J. The goldilocks approach: A review of employing design of experiments in prokaryotic recombinant protein production. Bioengineering 2018, 5, 1–27. [Google Scholar]
- Sukthomya, W.; Tannock, J. The optimisation of neural network parameters using Taguchi’s design of ex-periments approach: An application in manufacturing process modelling. Neural Comput. Appl. 2005, 14, 337–344. [Google Scholar] [CrossRef]
- Sarvin, B.; Fedorova, E.; Shpigun, O.; Titova, M.; Nikitin, M.; Kochkin, D.; Rodin, I.; Stavrianidi, A. LC-MS determination of steroidal glycosides from Dioscorea deltoidea Wall cell suspension culture: Optimization of pre-LC-MS procedure parameters by Latin Square design. J. Chromatogr. B 2018, 1080, 64–70. [Google Scholar] [CrossRef] [PubMed]
- Vaut, L.; Juszczyk, J.J.; Kamguyan, K.; Jensen, K.E.; Tosello, G.; Boisen, A. 3D Printing of Reservoir Devices for Oral Drug Delivery: From Concept to Functionality through Design Improvement for Enhanced Mucoadhesion. ACS Biomater. Sci. Eng. 2020, 6, 2478–2486. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology. NIST/SEMATECH e-Handbook of Statistical Methods. 2012. Available online: http://www.itl.nist.gov/div898/handbook/ (accessed on 12 September 2022).
- Ng, E.Y.K.; Ng, W.K. Parametric study of the biopotential equation for breast tumour identification us-ing ANOVA and Taguchi method. Med. Biol. Eng. Comput. 2006, 44, 131–149. [Google Scholar] [CrossRef] [PubMed]
- Enoch, O.F.; Shuaib, A.A.; Bin Hasbullah, A.H. Applying P-Diagram in Product Development Process: An Approach towards Design for Six Sigma. Appl. Mech. Mater. 2015, 789, 1187–1191. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, G.; Bjerg, B. Assessments of experimental designs in response surface modelling process: Estimating ventilation rate in naturally ventilated livestock buildings. Energy Build. 2013, 62, 570–580. [Google Scholar] [CrossRef]
- Karimifard, S.; Moghaddam, M.R.A. Application of response surface methodology in physicochemical removal of dyes from wastewater: A critical review. Sci. Total Environ. 2018, 640, 772–797. [Google Scholar] [CrossRef] [PubMed]
- Scaffaro, R.; Sutera, F.; Lopresti, F. Using Taguchi method for the optimization of processing variables to prepare porous scaffolds by combined melt mixing/particulate leaching. Mater. Des. 2017, 131, 334–342. [Google Scholar] [CrossRef]
- Hoefsloot, H.C.J.; Vis, D.J.; Westerhuis, J.A.; Smilde, A.K.; Jansen, J.J. Multiset Data Analysis: ANOVA Simultaneous Component Analysis and Related Methods. Compr. Chemom. 2009, 2, 453–472. [Google Scholar]
- Yu, F.; Qiu, F.; Meza, J. Design and Statistical Analysis of Mass-Spectrometry-Based Quantitative Proteomics Data. In Proteomic Profiling and Analytical Chemistry: The Crossroads, 2nd ed.; Ciborowski, P., Silberring, J., Eds.; Elsevier: Amsterdam, The Netherlands, 2016; pp. 211–237. [Google Scholar]
- Davis, R.; John, P. Application of Taguchi-Based Design of Experiments for Industrial Chemical Processes. In Statistical Approaches with Emphasis on Design of Experiments Applied to Chemical Processes; Silva, V., Ed.; InTech: Rijeka, Croatia, 2018; pp. 137–156. [Google Scholar]
- Huerta-Ochoa, S.; Castillo-Araiza, C.O.; Guerrero, A.R.; Prado-Barragán, A. Whole-Cell Bioconversion of Citrus Flavonoids to Enhance Their Biological Properties. Stud. Nat. Prod. Chem. 2019, 61, 335–367. [Google Scholar]
- Garakani, S.S.; Khanmohammadi, M.; Atoufi, Z.; Kamrava, S.K.; Setayeshmehr, M.; Alizadeh, R.; Faghihi, F.; Bagher, Z.; Davachi, S.M.; Abbaspourrad, A. Fabrication of chitosan/agarose scaffolds containing extracellular matrix for tissue engineering applications. Int. J. Biol. Macromol. 2019, 143, 533–545. [Google Scholar] [CrossRef]
- Tan, L.; Gong, M.; Zheng, F.; Zhang, B.; Yang, K. Study on compression behavior of porous magnesium used as bone tissue engineering scaffolds. Biomed. Mater. 2009, 4, 015016. [Google Scholar] [CrossRef] [PubMed]
- Levingstone, T.J.; Barron, N.; Ardhaoui, M.; Benyounis, K.; Looney, L.; Stokes, J. Application of response surface methodology in the design of functionally graded plasma sprayed hydroxyapatite coatings. Surf. Coatings Technol. 2017, 313, 307–318. [Google Scholar] [CrossRef]
- Levingstone, T.J.; Ardhaoui, M.; Benyounis, K.; Looney, L.; Stokes, J.T. Plasma sprayed hydroxyapatite coatings: Understanding process relationships using design of experiment analysis. Surf. Coatings Technol. 2015, 283, 29–36. [Google Scholar] [CrossRef]
- Kehoe, S.; Ardhaoui, M.; Stokes, J. Design of experiments study of hydroxyapatite synthesis for orthopae-dic application using fractional factorial design. J. Mater. Eng. Perform. 2011, 20, 1423–1437. [Google Scholar] [CrossRef]
- Lam, J.; Carmichael, S.T.; Lowry, W.E.; Segura, T. Hydrogel design of experiments methodology to optimize hydrogel for iPSC-NPC culture. Adv. Healthc. Mater. 2015, 4, 534–539. [Google Scholar] [CrossRef]
- Blanco, M.; Vázquez, J.A.; Pérez-Martín, R.I.; Sotelo, C.G. Collagen extraction optimization from the skin of the small-spotted catshark (S. Canicula) by response surface methodology. Mar. Drugs 2019, 17, 40. [Google Scholar] [CrossRef] [PubMed]
- Ruiter, F.A.A.; Alexander, C.; Rose, F.R.A.J.; Segal, J.I. A design of experiments approach to identify the influencing parameters that determine poly-D,L-lactic acid (PDLLA) electrospun scaffold morphologies. Biomed. Mater. 2017, 12, 5. [Google Scholar] [CrossRef] [PubMed]
- Marchiori, G.; Berni, M.; Boi, M.; Petretta, M.; Grigolo, B.; Bellucci, D.; Cannillo, V.; Garavelli, C.; Bianchi, M. Design of a novel procedure for the optimization of the mechanical performances of 3D printed scaffolds for bone tissue engineering combining CAD, Taguchi method and FEA. Med Eng. Phys. 2019, 69, 92–99. [Google Scholar] [CrossRef] [PubMed]
- Bhargav, A.; Rosa, V.; Feng, L.W.; Fuh, J.Y.H. Optimization of Surface Scaffold Morphology and Structure Using Taguchi’s Design of Experiments. Front. Biomed. Devices 2018, 18, 6813. [Google Scholar] [CrossRef]
- Shirzad, M.; Zolfagharian, A.; Matbouei, A.; Bodaghi, M. Design, evaluation, and optimization of 3D printed truss scaffolds for bone tissue engineering. J. Mech. Behav. Biomed. Mater. 2021, 120, 104594. [Google Scholar] [CrossRef] [PubMed]
- Trachtenberg, J.E.; Placone, J.K.; Smith, B.T.; Piard, C.M.; Santoro, M.; Scott, D.W.; Fisher, J.P.; Mikos, A.G. Extrusion-Based 3D Printing of Poly(propylene fumarate) in a Full-Factorial Design. ACS Biomater. Sci. Eng. 2016, 2, 1771–1780. [Google Scholar] [PubMed]
- Zheng, Z.; Eglin, D.; Alini, M.; Richards, G.R.; Qin, L.; Lai, Y. Visible Light-Induced 3D Bioprinting Tech-nologies and Corresponding Bioink Materials for Tissue Engineering: A Review. Engineering 2021, 7, 966–978. [Google Scholar] [CrossRef]
- Lee, A.; Hudson, A.R.; Shiwarski, D.J.; Tashman, J.W.; Hinton, T.J.; Yerneni, S.; Bliley, J.M.; Campbell, P.G.; Feinberg, A.W. 3D bioprinting of collagen to rebuild components of the human heart. Science 2019, 365, 482–487. [Google Scholar] [CrossRef]
- Gopinathan, J.; Noh, I. Recent trends in bioinks for 3D printing. Biomater. Res. 2018, 22, 11. [Google Scholar] [CrossRef]
- McGivern, S.; Boutouil, H.; Al-Kharusi, G.; Little, S.; Dunne, N.J.; Levingstone, T.J. Translational Applica-tion of 3D Bioprinting for Cartilage Tissue Engineering. Bioengineering 2021, 8, 144. [Google Scholar] [CrossRef]
- Bi, Z. Applications—Solid Mechanics Problems. In Finite Element Analysis Applications; Elsevier Inc.: Bloomington, IA, USA, 2018; pp. 281–339. [Google Scholar]
- Williams, B.A.; Cremaschi, S. Surrogate Model Selection for Design Space Approximation And Surrogate-based Optimization; Elsevier Masson SAS: Amsterdam, The Netherlands, 2019; Volume 47. [Google Scholar]
- Jankovic, A.; Chaudhary, G.; Goia, F. Designing the design of experiments (DOE) – An investigation on the influence of different factorial designs on the characterization of complex systems. Energy Build. 2021, 250, 111298. [Google Scholar] [CrossRef]
- Dehghan, M.; Mehrizi, M.K.; Nikukar, H. Modeling and optimizing a polycaprolac-tone/gelatin/polydimethylsiloxane nanofiber scaffold for tissue engineering: Using response surface methodology. J. Text. Inst. 2021, 112, 482–493. [Google Scholar] [CrossRef]
- Li, Z. Predicting bone regeneration from machine learning. Nat. Comput. Sci. 2021, 1, 509–510. [Google Scholar] [CrossRef]
- Alpaydin, E. Introduction to Machine Learning, 4th ed.; The MIT Press: Cambridge, MA, USA, 2020. [Google Scholar]
- Park, C.; Took, C.C.; Seong, J.-K. Machine learning in biomedical engineering. Biomed. Eng. Lett. 2018, 8, 1–3. [Google Scholar] [CrossRef] [PubMed]
- Murdoch, W.J.; Singh, C.; Kumbier, K.; Abbasi-Asl, R.; Yu, B. Definitions, methods, and applications in in-terpretable machine learning. Proc. Natl. Acad. Sci. USA 2019, 116, 22071–22080. [Google Scholar] [CrossRef] [PubMed]
- Talabis, M.R.M.; McPherson, R.; Miyamoto, I.; Martin, J.L.; Kaye, D. Analytics Defined. In Information Security Analytics: Finding Security Insights, Patterns, and Anomalies in Big Data; Elsevier Inc.: Waltham, MA, USA, 2015; pp. 1–12. [Google Scholar]
- De Ridder, D.; de Ridder, J.; Reinders, M.J.T. Pattern recognition in bioinformatics. Briefings Bioinform. 2013, 14, 633–647. [Google Scholar] [CrossRef] [PubMed]
- Balasubramanyam, S. New Technologies and Environments. IFPUG Guid. IT Softw. Meas. 2012, 385, 28. [Google Scholar]
- Conev, M.A.; Litsa, M.E.; Perez, M.M.; Diba, M.; Mikos, A.G.; Kavraki, L.E. Machine Learning-Guided Three-Dimensional Printing of Tissue Engineering Scaffolds. Tissue Eng. Part A 2020, 26, 1359–1368. [Google Scholar] [CrossRef] [PubMed]
- Shaikhina, T.; Lowe, D.; Daga, S.; Briggs, D.; Higgins, R.; Khovanova, N. Machine Learning for Predictive Modelling based on Small Data in Biomedical Engineering. IFAC-PapersOnLine 2015, 48, 469–474. [Google Scholar] [CrossRef]
- Tigga, N.P.; Garg, S. Prediction of Type 2 Diabetes using Machine Learning Classification Methods. Procedia Comput. Sci. 2020, 167, 706–716. [Google Scholar] [CrossRef]
- Shobha, S.R.G. Chapter 8-Machine Learning. in Computational Analysis and Understanding of Natural Languages: Principles, Methods and Applications; Gudivada, V.N., Rao, C.R., Eds.; Elsevier: Waltham, MA, USA, 2018; Volume 38, pp. 197–228. [Google Scholar]
- Patterson, J.; Gibson, A. Deep Learning: A Practitioner’s Approach, First; O’Reilly Media: Sebastopol, CA, USA, 2017. [Google Scholar]
- Suryachandra, P. Comparison of Machine Learning Algorithms. In Proceedings of the 3rd International Conference on Science and Technology-Computer (ICST) Comparison, Yogyakarta, Indonesia, 11–12 July 2017; Volume 8, pp. 2241–2247. [Google Scholar]
- Mashayekhi, M.; Gras, R. Rule Extraction from Random Forest: The RF+HC Methods. In Advances in Artificial Intelligence: Lecture Notes in Artificial Intelligence Subseries 9091; Barbosa, D., Milios, E., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 223–237. [Google Scholar]
- Witten, I.H.; Frank, E.; Hall, M.A.; Pal, C.J. Extending instance-based and linear models. In Data Mining: Practical Machine Learning Tools and Techniques; Elsevier: Amsterdam, The Netherlands, 2017; pp. 243–284. [Google Scholar] [CrossRef]
- Vu, K.; Snyder, J.C.; Li, L.; Rupp, M.; Chen, B.F.; Khelif, T.; Müller, K.-R.; Burke, K. Understanding kernel ridge regression: Common behaviors from simple functions to density functionals. Int. J. Quantum Chem. 2015, 115, 1115–1128. [Google Scholar] [CrossRef]
- Zhu, D.; Linke, N.M.; Benedetti, M.; Landsman, K.A.; Nguyen, N.H.; Alderete, C.H.; Perdomo-Ortiz, A.; Korda, N.; Garfoot, A.; Brecque, C.; et al. Training of quantum circuits on a hybrid quantum computer. Sci. Adv. 2019, 5, eaaw9918. [Google Scholar] [CrossRef] [PubMed]
- Shahriari, B.; Swersky, K.; Wang, Z.; Adams, R.P.; de Freitas, N. Taking the Human Out of the Loop: A Review of Bayesian Optimization Citation Taking the Human Out of the Loop: A Review of Bayesian Optimization. Proc. IEEE 2016, 104, 148–175. [Google Scholar] [CrossRef]
- Siegel, A. Chapter 11—Correlation and Regression: Measuring and Predicting Relationships. In Practical Business Statistics; Elsevier Inc.: Seattle, WA, USA, 2016; pp. 299–354. [Google Scholar]
- Kotu, V.; Deshpande, B. Predictive Analytics and Data Mining; University of California: San Diego, CA, USA, 2015; Volume 329, p. 2. [Google Scholar] [CrossRef]
- Mushtaq, M.-S.; Mellouk, A. Methodologies for Subjective Video Streaming QoE Assessment. Qual. Exp. Paradig. Multimed. Serv. 2017, 2, 27–57. [Google Scholar] [CrossRef]
- Gholami, R.; Fakhari, N. Support Vector Machine: Principles, Parameters, and Applications. In Hand-book of Neural Computation; Samui, P., Sekhar, S., Balas, V.E., Eds.; Elsevier Inc.: Amsterdam, The Netherlands, 2017; pp. 515–535. [Google Scholar]
- Misra, S.; Li, H. Noninvasive fracture characterization based on the classification of sonic wave travel times. Mach. Learn. Subsurf. Charact. 2019, 90, 243–287. [Google Scholar] [CrossRef]
- Mao, W.; Wang, F.-Y. Cultural Modeling for Behavior Analysis and Prediction. In New Advances in Intelligence and Security Informatics; Mao, W., Wang, F.-Y., Eds.; Academic Press: Cambridge, MA, USA, 2012; pp. 91–102. [Google Scholar]
- Reinders, C.; Ackermann, H.; Yang, M.Y.; Rosenhahn, B. Chapter 4—Learning Convolutional Neural Networks for Object Detection with Very Little Training Data. In Multimodal Scene Understanding; Yang, M.Y., Rosenhahn, B., Murino, V., Eds.; Academic Press: Cambridge, MA, USA, 2019; pp. 65–100. [Google Scholar]
- Nagarajan, H.P.; Mokhtarian, H.; Jafarian, H.; Dimassi, S.; Bakrani-Balani, S. Knowledge-based design of artificial neural network topology for additive manu-facturing process modeling: A new approach and case study for fused deposition modeling. J. Mech. Des. Trans. ASME 2019, 141, 1–12. [Google Scholar] [CrossRef]
- Jin, Z.; Zhang, Z.; Gu, G.X. Autonomous in-situ correction of fused deposition modeling printers using computer vision and deep learning. Manuf. Lett. 2019, 22, 11–15. [Google Scholar] [CrossRef]
- Singh, S.A.; Desai, K.A. Automated surface defect detection framework using machine vision and con-volutional neural networks. J. Intell. Manuf. 2022, 6, 1–17. [Google Scholar]
- Nguyen, T.P.; Choi, S.; Park, S.-J.; Yoon, J. Inspecting Method for Defective Casting Products with Convolutional Neural Network (CNN). Int. J. Precis. Eng. Manuf. Technol. 2020, 8, 583–594. [Google Scholar] [CrossRef]
- Gove, R.; Faytong, J. Machine Learning and Event-Based Software Testing: Classifiers for Identifying In-feasible GUI Event Sequences. In Advances in Computers; Hurson, A., Memon, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2012; Volume 86, pp. 109–135. [Google Scholar]
- Verrelst, J.; Camps-Valls, G.; Muñoz-Marí, J.; Rivera, J.P.; Veroustraete, F.; Clevers, J.G.P.W.; Moreno, J. Optical remote sensing and the retrieval of terrestrial vegetation bio-geophysical properties—A review. ISPRS J. Photogramm. Remote Sens. 2015, 108, 273–290. [Google Scholar] [CrossRef]
- Wu, J.; Hao, X.C.; Xiong, Z.L.; Lei, H. Hyperparameter Optimization for Machine Learning Models Based on Bayesian Optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar]
- Nguyen, V.; Kingdom, U. Bayesian Optimization for Accelerating Hyper-parameter Tuning. In Proceedings of the IEEE Second International Conference on Artificial Intelligence and Knowledge Engineering (AIKE), Sardinia, Italy, 3–5 June 2019. [Google Scholar]
- Zhang, L.; Zhang, B. Hierarchical Machine Learning—A Learning Methodology Inspired by Human Intel-ligence. In Rough Sets and Knowledge Technology; Wang, G., Peters, J.F., Skowron, A., Yao, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 28–30. [Google Scholar]
- Subendran, S. Using Natural Language Processing to Detect Breast Cancer Recurrence in Clinical Notes: A Hierarchical Machine Learning Approach. Masters thesis, University of Waterloo, Waterloo, Canada, 2021. [Google Scholar]
- Wu, M.; Song, Z.; Moon, Y.B. Detecting cyber-physical attacks in CyberManufacturing systems with machine learning methods. J. Intell. Manuf. 2019, 30, 1111–1123. [Google Scholar] [CrossRef]
- Notingher, I.; Jell, G.; Lohbauer, U.; Salih, V.; Hench, L.L. In situ non-invasive spectral discrimination be-tween bone cell phenotypes used in tissue engineering. J. Cell. Biochem. 2004, 92, 1180–1192. [Google Scholar] [CrossRef] [PubMed]
- Simek, K.; Fujarewicz, K.; Świerniak, A.; Kimmel, M.; Jarząb, B.; Wiench, M.; Rzeszowska, J. Using SVD and SVM methods for selection, classification, clustering and modeling of DNA microarray data. Eng. Appl. Artif. Intell. 2004, 17, 417–427. [Google Scholar] [CrossRef]
- El Bouchefry, K.; de Souza, R.S. Learning. In Knowledge Discovery in Big Data from Astronomy and Earth Observation: Astrogeoinformatics; Škoda, P., Adam, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 225–249. [Google Scholar]
- Sengupta, A.; Naresh, G.; Mishra, A.; Parashar, D.; Narad, P. Chapter Five—Proteome analysis using ma-chine learning approaches and its applications to diseases. In Advances in Protein Chemistry and Structural Biology; Donev, O., Karabencheva-Christova, T., Eds.; Academic Press: Cambridge, MA, USA, 2021; Volume 127, pp. 161–216. [Google Scholar]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. Deep Reinforcement Learning: A Brief Survey. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- Nguyen, T.; Nguyen, N.D.; Bello, F.; Nahavandi, S. A New Tensioning Method using Deep Reinforcement Learning for Surgical Pattern Cutting. IEEE Int. Conf. Ind. Technol. 2019, 55, 1339–1344. [Google Scholar] [CrossRef]
- Jiang, Y.; Jiang, Z.P. Robust adaptive dynamic programming and feedback stabilization of nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 882–893. [Google Scholar] [CrossRef] [PubMed]
- Cropper, A.; Dumančić, S.; Evans, R.; Muggleton, S.H. Inductive logic programming at 30. Mach. Learn. 2022, 111, 147–172. [Google Scholar] [CrossRef]
- Cropper, A.; Dumancic, S.; Muggleton, S.H. Turning 30: New ideas in inductive logic programming. In Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence (IJCAI-20) Survey, Yokohama, Japan, 11–17 July 2020; pp. 4833–4839. [Google Scholar]
- Panigrahy, S.K.; Chiang, K.-N. Study on an Artificial Intelligence Based Kernel Ridge Regression Algo-rithm for Wafer Level Package Reliability Prediction. In Proceedings of the 71st Electronic Components and Technology Conference (ECTC), San Diego, CA, USA, 1 June–4 July 2021; pp. 1435–1441. [Google Scholar]
- Khadilkar, A.; Wang, J.; Rai, R. Deep learning–based stress prediction for bottom-up SLA 3D printing process. Int. J. Adv. Manuf. Technol. 2019, 102, 2555–2569. [Google Scholar] [CrossRef]
- Freiesleben, J.; Keim, J.; Grutsch, M. Machine learning and Design of Experiments: Alternative approaches or complementary methodologies for quality improvement? Qual. Reliab. Eng. Int. 2020, 36, 1837–1848. [Google Scholar] [CrossRef]
- Kording, A.K.P.; Benjamin, A.S.; Farhoodi, R.; Glaser, J.I. The Roles of Machine Learning in Biomedical Science. In Frontiers of Engineering; National Academy of Sciences: Washington, DC, USA, 2017; pp. 61–71. [Google Scholar]
- Arboretti, R.; Ceccato, R.; Pegoraro, L.; Salmaso, L. Design of Experiments and machine learning for prod-uct innovation: A systematic literature review. Qual. Reliab. Eng. Int. 2021, 38, 1131–1156. [Google Scholar] [CrossRef]
- Khoshnevisan, L.; Hourfar, F.; Alhameli, F.; Elkamel, A. Combining design of experiments, machine learning, and principal component analysis for predicting energy consumption and product quality of a natural gas processing plant. Int. J. Energy Res. 2021, 45, 5974–5987. [Google Scholar] [CrossRef]
- Huang, J.; Segura, L.J.; Wang, T.; Zhao, G.; Sun, H.; Zhou, C. Unsupervised learning for the droplet evolu-tion prediction and process dynamics understanding in inkjet printing. Addit. Manuf. 2020, 35, 101197. [Google Scholar]
- Olsson, F. A Literature Survey of Active Machine Learning in the Context of Natural Language Processing; Swedish Institute of Computer Science: Kista, Sweden, 2009. [Google Scholar]
- Duquesnoy, M.; Lombardo, T.; Chouchane, M.; Primo, E.N.; Franco, A.A. Data-driven assessment of elec-trode calendering process by combining experimental results, in silico mesostructures generation and machine learning. J. Power Sources 2020, 480, 229103. [Google Scholar] [CrossRef]
- Sommer, C.; Gerlich, D.W. Machine learning in cell biology-teaching computers to recognize pheno-types. J. Cell Sci. 2013, 126, 5529–5539. [Google Scholar] [PubMed]
- Reiter, D.A.; Irrechukwu, O.; Lin, P.-C.; Moghadam, S.; Von Thaer, S.; Pleshko, N.; Spencer, R.G. Improved MR-based characterization of engineered cartilage using multiexponential T2 relaxation and multivariate analysis. NMR Biomed. 2012, 25, 476–488. [Google Scholar] [CrossRef] [PubMed]





| Algorithms | Category | Assumptions | Benefits | Limitations | Ref |
|---|---|---|---|---|---|
| Linear regression | Regression | Linearity, fixed features, independence, normality; Error variance is assumed to be constant. | Simple application; Guaranteed to find the optimal solution. | Only works for linear relationship data. | [69,70] |
| Random forest | Classification | Assume model errors are uncorrelated and uniform. | Provides fast learning and highly accurate predictions; Can intake large set of data without variable deletion; Can work with unbalanced data sets. | Time-consuming to form predictions. | [71,72] |
| Decision tree | Classification, Regression | The classes must be mutually exclusive. | Easy to use and to understand, efficient algorithm (especially for predictions). | Depending on the selection order, missing factors from the characteristic overfitting. | [71] |
| Neural networks | Classification, Regression | Variable independence, linearity. | Can be used for classification and regression, able to use the Boolean functions; Allows inputs with noise. | Overfitting due to too many attributes; Hard to understand the algorithm structure. | [71] |
| Support vector machines (SVM) | Classification, Regression | Model assumptions depend on the probability of default (PD). | Complexity of the model can be easily controlled; The models use non-linear boundaries. | Hard to understand the algorithm structure; Data training is slow. | [69,71] |
| Kernel ridge regression (KRR) | Regression | Linear or nonlinear function. | Computational simplicity; Prevents overfitting. | Computationally expensive. | [73,74] |
| Bayesian optimisation (OP) | Optimisation | A non-convex problem; No access to derivative. | Hyperparameter tuning; Cost-efficient. | The objective function can’t be modelled; High dimension problem. | [75,76] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Kharusi, G.; Dunne, N.J.; Little, S.; Levingstone, T.J. The Role of Machine Learning and Design of Experiments in the Advancement of Biomaterial and Tissue Engineering Research. Bioengineering 2022, 9, 561. https://doi.org/10.3390/bioengineering9100561
Al-Kharusi G, Dunne NJ, Little S, Levingstone TJ. The Role of Machine Learning and Design of Experiments in the Advancement of Biomaterial and Tissue Engineering Research. Bioengineering. 2022; 9(10):561. https://doi.org/10.3390/bioengineering9100561
Chicago/Turabian StyleAl-Kharusi, Ghayadah, Nicholas J. Dunne, Suzanne Little, and Tanya J. Levingstone. 2022. "The Role of Machine Learning and Design of Experiments in the Advancement of Biomaterial and Tissue Engineering Research" Bioengineering 9, no. 10: 561. https://doi.org/10.3390/bioengineering9100561
APA StyleAl-Kharusi, G., Dunne, N. J., Little, S., & Levingstone, T. J. (2022). The Role of Machine Learning and Design of Experiments in the Advancement of Biomaterial and Tissue Engineering Research. Bioengineering, 9(10), 561. https://doi.org/10.3390/bioengineering9100561










