Quasi-3D Mechanistic Model for Predicting Eye Drop Distribution in the Human Tear Film
Abstract
1. Introduction
2. Materials and Methods
2.1. Approach
2.2. Tear Film Anatomy
2.3. Q3D Design and Assumptions
2.4. Modeling Blink Cycles
2.5. Modeling Tear Fluid Drainage
2.6. Modeling Tear Fluid Evaporation
2.7. Tear Film Species Transport Validation
3. Results
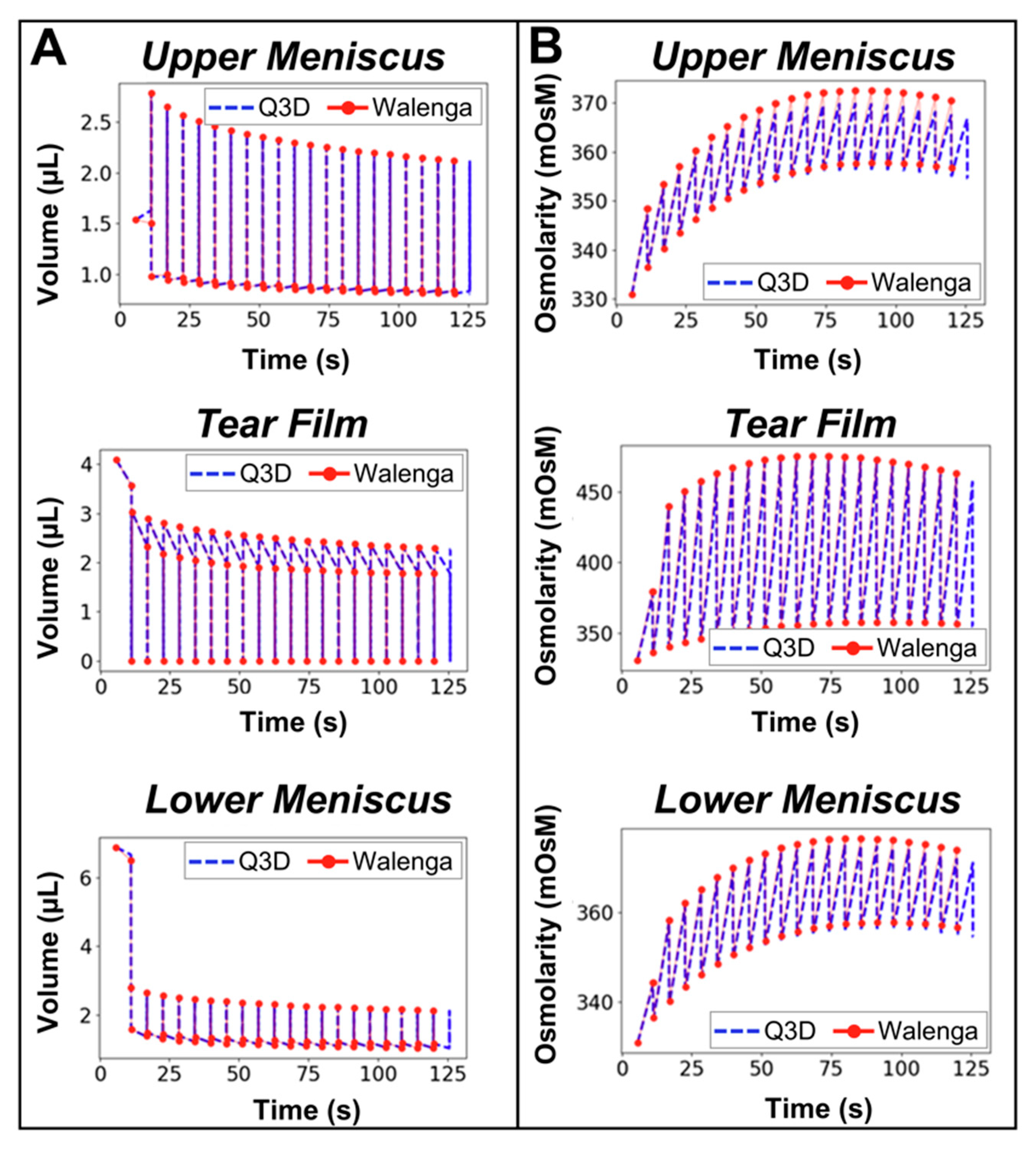
3.1. Verification of Blink Cycle Volume and Osmolarity Dynamics
3.2. Assessment of Computational Performance
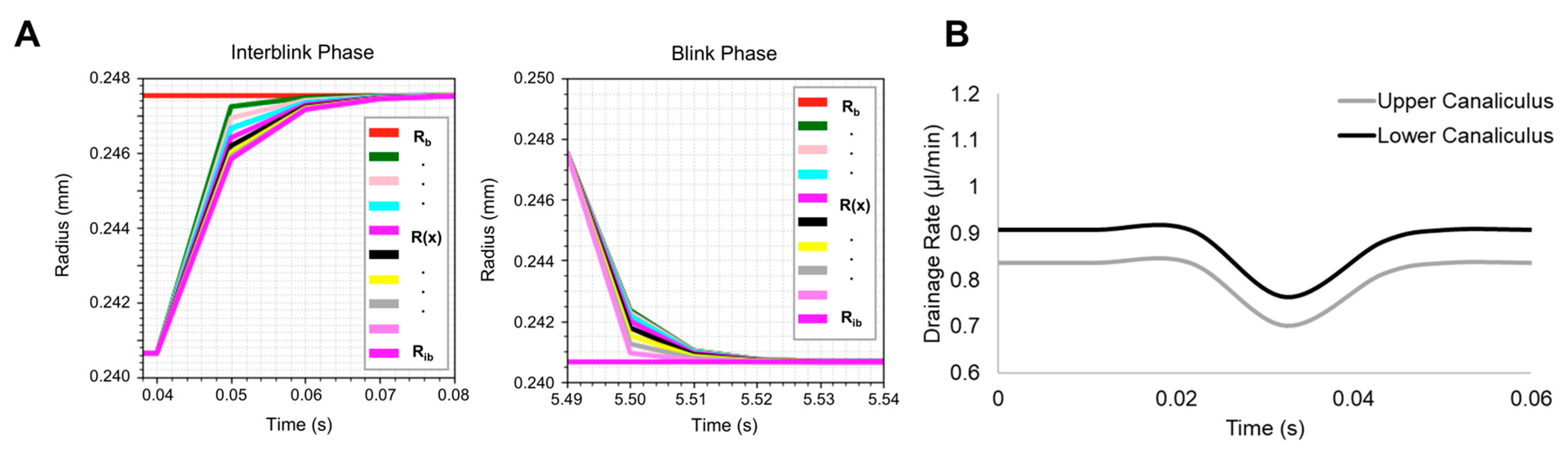
3.3. Verification of Nasolacrimal Drainage Rates
3.4. Validation of Tear Film Species Transport
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PBPK | Physiologically based pharmacokinetic |
| Q3D | Quasi-three-dimensional |
| R2 | Coefficient of determination |
| RMSE | Root-Mean-Square Error |
| AARD | Average Absolute Relative Deviation |
| CPU | Central Processing Unit |
| FDA | Food and Drug Administration |
| ODE | Ordinary Differential Equation |
| PDE | Partial Differential Equation |
| FEM | Finite Element Model |
| 3D | Three-dimensional |
| CoBi | Computational Biology |
| HHS | Health and Human Services |
References
- Nijm, L.M.; Schweitzer, J.; Gould Blackmore, J. Glaucoma and dry eye disease: Opportunity to assess and treat. Clin. Ophthalmol. 2023, 17, 3063–3076. [Google Scholar] [CrossRef]
- Sleath, B.; Blalock, S.; Covert, D.; Stone, J.L.; Skinner, A.C.; Muir, K.; Robin, A.L. The relationship between glaucoma medication adherence, eye drop technique, and visual field defect severity. Ophthalmology 2011, 118, 2398–2402. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, M.B.; Zhang, H. The emerging role of topical ocular drugs to target the posterior eye. Ophthalmol. Ther. 2021, 10, 465–494. [Google Scholar] [CrossRef]
- Jacob, S.; Nair, A.B.; Shah, J.; Gupta, S.; Boddu, S.H.; Sreeharsha, N.; Joseph, A.; Shinu, P.; Morsy, M.A. Lipid nanoparticles as a promising drug delivery carrier for topical ocular therapy—An overview on recent advances. Pharmaceutics 2022, 14, 533. [Google Scholar] [CrossRef]
- Palakuru, J.R.; Wang, J.; Aquavella, J.V. Effect of blinking on tear volume after instillation of midviscosity artificial tears. Am. J. Ophthalmol. 2008, 146, 920–924. [Google Scholar] [CrossRef]
- Harrell, C.R.; Feulner, L.; Djonov, V.; Pavlovic, D.; Volarevic, V. The molecular mechanisms responsible for tear hyperosmolarity-induced pathological changes in the eyes of dry eye disease patients. Cells 2023, 12, 2755. [Google Scholar] [CrossRef]
- Food and Drug Administration, Department of Health and Human Services. 21 CFR Part 355. 1995. Available online: https://www.ecfr.gov/current/title-21/part-355 (accessed on 18 March 2025).
- Azhdari, E.; Emami, A.; Ferreira, J.A. Drug delivery to the anterior segment of the eye enhanced by ultrasound—Modeling and simulation. Comput. Math. Appl. 2023, 144, 51–61. [Google Scholar] [CrossRef]
- Azhdari, E.; Emami, A. Mathematical model of drug release to the posterior segment of the eye after topical drug delivery. Appl. Math. 2022, 49, 35–58. [Google Scholar] [CrossRef]
- Khoobyar, A.; Penkova, A.N.; Humayun, M.S.; Sadhal, S.S. Mathematical model of macromolecular drug transport in a partially liquefied vitreous humor. J. Heat Transf. 2022, 144, 031208. [Google Scholar] [CrossRef] [PubMed]
- Abootorabi, S.; Tripathi, A.; Yu, H.W.; Dávila, L.P. Computational modeling of intraocular drug delivery supplied by porous implants. Drug Deliv. Transl. Res. 2021, 11, 2134–2143. [Google Scholar] [CrossRef]
- Toffoletto, N.; Saramago, B.; Serro, A.P.; Chauhan, A. A physiology-based mathematical model to understand drug delivery from contact lenses to the back of the eye. Pharm. Res. 2023, 40, 1939–1951. [Google Scholar] [CrossRef]
- Agrahari, V.; Mandal, A.; Agrahari, V.; Trinh, H.M.; Joseph, M.; Ray, A.; Hadji, H.; Mitra, R.; Pal, D.; Mitra, A.K. A comprehensive insight on ocular pharmacokinetics. Drug Deliv. Transl. Res. 2016, 6, 735–754. [Google Scholar] [CrossRef]
- Sadeghi, A.; Subrizi, A.; del Amo, E.M.; Urtti, A. Mathematical models of ocular drug delivery. Investig. Ophthalmol. Vis. Sci. 2024, 65, 28. [Google Scholar] [CrossRef]
- Le Merdy, M.; Spires, J.; Lukacova, V.; Tan, M.-L.; Babiskin, A.; Xu, X.; Zhao, L.; Bolger, M.B. Ocular physiologically based pharmacokinetic modeling for ointment formulations. Pharm. Res. 2020, 37, 245. [Google Scholar] [CrossRef] [PubMed]
- Le Merdy, M.; AlQaraghuli, F.; Tan, M.-L.; Walenga, R.; Babiskin, A.; Zhao, L.; Lukacova, V. Clinical ocular exposure extrapolation for ophthalmic solutions using PBPK modeling and simulation. Pharm. Res. 2023, 40, 431–447. [Google Scholar] [CrossRef] [PubMed]
- Kannan, R.; Chen, Z.J.; Singh, N.; Przekwas, A.; Delvadia, R.; Tian, G.; Walenga, R. A quasi-3D wire approach to model pulmonary airflow in human airways. Int. J. Numer. Methods Biomed. Eng. 2017, 33, e2838. [Google Scholar] [CrossRef] [PubMed]
- Kannan, R.; Singh, N.; Przekwas, A. A quasi-3D compartmental multi-scale approach to detect and quantify diseased regional lung constriction using spirometry data. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e2973. [Google Scholar] [CrossRef]
- Kannan, R.; Singh, N.; Przekwas, A. A compartment–quasi-3D multiscale approach for drug absorption, transport, and retention in the human lungs. Int. J. Numer. Methods Biomed. Eng. 2018, 34, e2955. [Google Scholar] [CrossRef]
- Kannan, R.R.; Przekwas, A.J.; Singh, N.; Delvadia, R.; Tian, G.; Walenga, R. Pharmaceutical aerosols deposition patterns from a Dry Powder Inhaler: Euler Lagrangian prediction and validation. Med. Eng. Phys. 2017, 42, 35–47. [Google Scholar] [CrossRef]
- Pak, J.; Chen, Z.; Sun, K.; Przekwas, A.; Walenga, R.; Fan, J. Computational modeling of drug transport across the in vitro cornea. Comput. Biol. Med. 2018, 92, 139–146. [Google Scholar] [CrossRef]
- Jumelle, C.; Gholizadeh, S.; Annabi, N.; Dana, R. Advances and limitations of drug delivery systems formulated as eye drops. J. Control. Release 2020, 321, 1–22. [Google Scholar] [CrossRef]
- Ghate, D.; Edelhauser, H.F. Ocular drug delivery. Expert Opin. Drug Deliv. 2006, 3, 275–287. [Google Scholar] [CrossRef]
- Peng, C.-C.; Cerretani, C.; Braun, R.J.; Radke, C.J. Evaporation-driven instability of the precorneal tear film. Adv. Colloid Interface Sci. 2014, 206, 250–264. [Google Scholar] [CrossRef]
- German, C.; Chen, Z.; Przekwas, A.; Walenga, R.; Babiskin, A.; Zhao, L.; Fan, J.; Tan, M.-L. Computational model of in vivo corneal pharmacokinetics and pharmacodynamics of topically administered ophthalmic drug products. Pharm. Res. 2023, 40, 961–975. [Google Scholar] [CrossRef]
- German, C.; Pilvankar, M.; Przekwas, A. Computational framework for predictive PBPK-PD-Tox simulations of opioids and antidotes. J. Pharmacokinet. Pharmacodyn. 2019, 46, 513–529. [Google Scholar] [CrossRef] [PubMed]
- German, C.; Boyer, A.; Przekwas, A.; Bader, S.E.; Cabal, A. A physiologically based model to capture species-dependent differences in oxygen distribution in the posterior eye. Model. Artif. Intell. Ophthalmol. 2021, 3, 10–42. [Google Scholar] [CrossRef]
- Somayaji, M.R.; Das, D.; Garimella, H.T.; German, C.L.; Przekwas, A.J.; Simon, L. An integrated biophysical model for predicting the clinical pharmacokinetics of transdermally delivered compounds. Eur. J. Pharm. Sci. 2021, 167, 105924. [Google Scholar] [CrossRef]
- Przekwas, A.; Garimella, H.T.; Chen, Z.J.; Zehnbauer, T.; Gupta, R.K.; Skotak, M.; Carr, W.S.; Kamimori, G.H. Fast-running tools for personalized monitoring of blast exposure in military training and operations. Mil. Med. 2021, 186, 529–536. [Google Scholar] [CrossRef] [PubMed]
- Gharahi, H.; Garimella, H.T.; Chen, Z.J.; Gupta, R.K.; Przekwas, A. Mathematical model of mechanobiology of acute and repeated synaptic injury and systemic biomarker kinetics. Front. Cell. Neurosci. 2023, 17, 1007062. [Google Scholar] [CrossRef]
- Przekwas, A.; Friend, T.; Teixeira, R.; Chen, Z.; Wilkerson, P. Spatial modeling tools for cell biology. CFD Res. Corp. Huntsville AL 2006. Available online: https://apps.dtic.mil/sti/html/tr/ADA460852/ (accessed on 18 March 2025).
- Tsubota, K.; Nakamori, K. Effects of ocular surface area and blink rate on tear dynamics. Arch. Ophthalmol. 1995, 113, 155–158. [Google Scholar] [CrossRef]
- Wang, J.; Aquavella, J.; Palakuru, J.; Chung, S. Repeated measurements of dynamic tear distribution on the ocular surface after instillation of artificial tears. Investig. Ophthalmol. Vis. Sci. 2006, 47, 3325–3329. [Google Scholar] [CrossRef]
- Walenga, R.L.; Babiskin, A.H.; Zhang, X.; Absar, M.; Zhao, L.; Lionberger, R.A. Impact of vehicle physicochemical properties on modeling-based predictions of cyclosporine ophthalmic emulsion bioavailability and tear film breakup Time. J. Pharm. Sci. 2018, 108, 620–629. [Google Scholar] [CrossRef] [PubMed]
- Mishima, S.; Gasset, A.; Klyce, S.D., Jr.; Baum, J.L. Determination of tear volume and tear flow. Investig. Ophthalmol. Vis. Sci. 1966, 5, 264–276. [Google Scholar]
- Kawakita, T.; Kawashima, M.; Murat, D.; Tsubota, K.; Shimazaki, J. Measurement of fornix depth and area: A novel method of determining the severity of fornix shortening. Eye 2009, 23, 1115–1119. [Google Scholar] [CrossRef] [PubMed]
- Cerretani, C.F.; Ho, N.H.; Radke, C.J. Water-evaporation reduction by duplex films: Application to the human tear film. Adv. Colloid Interface Sci. 2013, 197, 33–57. [Google Scholar] [CrossRef]
- Jones, L.T. Anatomy of the tear system. Int. Ophthalmol. Clin. 1973, 13, 3–22. [Google Scholar] [CrossRef]
- Jones, L.T. Epiphora: II. Its relation to the anatomic structures and surgery of the medial canthal region. Am. J. Ophthalmol. 1957, 43, 203–212. [Google Scholar] [CrossRef]
- Palakuru, J.R.; Wang, J.; Aquavella, J.V. Effect of blinking on tear dynamics. Investig. Ophthalmol. Vis. Sci. 2007, 48, 3032–3037. [Google Scholar] [CrossRef]
- Cruz, A.A.; Garcia, D.M.; Pinto, C.T.; Cechetti, S.P. Spontaneous eyeblink activity. Ocul. Surf. 2011, 9, 29–41. [Google Scholar] [CrossRef]
- Braun, R.J.; King-Smith, P.E.; Begley, C.; Li, L.; Gewecke, N. Dynamics and function of the tear film in relation to the blink cycle. Prog. Retin. Eye Res. 2015, 45, 132–164. [Google Scholar] [CrossRef]
- Doane, M.G. Blinking and the mechanics of the lacrimal drainage system. Ophthalmology 1981, 88, 844–851. [Google Scholar] [CrossRef]
- Cerretani, C.F.; Radke, C.J. Tear dynamics in healthy and dry eyes. Curr. Eye Res. 2014, 39, 580–595. [Google Scholar] [CrossRef]
- Pflugfelder, S.C.; Stern, M.E. Biological functions of tear film. Exp. Eye Res. 2020, 197, 108115. [Google Scholar] [CrossRef]
- Zhu, H.; Chauhan, A. A mathematical model for tear drainage through the canaliculi. Curr. Eye Res. 2005, 30, 621–630. [Google Scholar] [CrossRef]
- Zhu, H.; Bhatia, S.; Chauhan, A. Dynamic mechanical properties of porcine lacrimal canaliculus. Curr. Eye Res. 2007, 32, 829–835. [Google Scholar] [CrossRef] [PubMed]
- Wilson, G.; Merrill, R. The lacrimal drainage system: Pressure changes in the canaliculus. Optom. Vis. Sci. 1976, 53, 55–59. [Google Scholar] [CrossRef]
- Tomlinson, A.; Doane, M.G.; Mcfadyen, A. Inputs and outputs of the lacrimal system: Review of production and evaporative loss. Ocul. Surf. 2009, 7, 186–198. [Google Scholar] [CrossRef] [PubMed]
- Yalkowsky, S.H.; He, Y.; Jain, P. Handbook of Aqueous Solubility Data; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- O’Neil, M.J. The Merck Index: An Encyclopedia of Chemicals, Drugs, and Biologicals; RSC Publishing: Cambridge, UK, 2013. [Google Scholar]
- Le Merdy, M.; Fan, J.; Bolger, M.B.; Lukacova, V.; Spires, J.; Tsakalozou, E.; Patel, V.; Xu, L.; Stewart, S.; Chockalingam, A. Application of mechanistic ocular absorption modeling and simulation to understand the impact of formulation properties on ophthalmic bioavailability in rabbits: A case study using dexamethasone suspension. AAPS J. 2019, 21, 65. [Google Scholar] [CrossRef]
- Malhotra, M.; Majumdar, D. Permeation through cornea. Indian J. Exp. Biol. 2001, 39, 11–24. [Google Scholar]
- Balla, A.; Auriola, S.; Grey, A.C.; Demarais, N.J.; Valtari, A.; Heikkinen, E.M.; Toropainen, E.; Urtti, A.; Vellonen, K.-S.; Ruponen, M. Partitioning and spatial distribution of drugs in ocular surface tissues. Pharmaceutics 2021, 13, 658. [Google Scholar] [CrossRef] [PubMed]
- Karami, T.K.; Hailu, S.; Feng, S.; Graham, R.; Gukasyan, H.J. Eyes on Lipinski’s Rule of Five: A new “rule of thumb” for physicochemical design space of ophthalmic drugs. J. Ocul. Pharmacol. Ther. 2022, 38, 43–55. [Google Scholar] [CrossRef]
- Jóhannesson, G.; Moya-Ortega, M.D.; Ásgrímsdóttir, G.M.; Lund, S.H.; Thorsteinsdóttir, M.; Loftsson, T.; Stefánsson, E. Kinetics of γ-cyclodextrin nanoparticle suspension eye drops in tear fluid. Acta Ophthalmol. 2014, 92, 550–556. [Google Scholar] [CrossRef] [PubMed]
- Zhu, H.; Chauhan, A. Effect of viscosity on tear drainage and ocular residence time. Optom. Vis. Sci. 2008, 85, E715–E725. [Google Scholar] [CrossRef] [PubMed]
- Tyson, S.L.; Campbell, P.; Biggins, J.; Driscoll, A.; Jarrett, P.; Gibson, A.; Vantipalli, S.; Metzinger, J.L.; Goldstein, M.H. Punctum and canalicular anatomy for hydrogel-based intracanalicular insert technology. Ther. Deliv. 2020, 11, 173–182. [Google Scholar] [CrossRef]
- Osborne, J.M. An adaptive numerical method for multi-cellular simulations of tissue development and maintenance. J. Theor. Biol. 2024, 594, 111922. [Google Scholar] [CrossRef]
- Jafari, S.; Park, J.; Lu, Y.; Demer, J.L. Finite element model of ocular adduction with unconstrained globe translation. Biomech. Model. Mechanobiol. 2024, 23, 601–614. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Z.; Li, Y.; Du, J.; Gao, X.; Li, Y.; Lai, L. A combination of machine learning and PBPK modeling approach for pharmacokinetics prediction of small molecules in humans. Pharm. Res. 2024, 41, 1369–1379. [Google Scholar] [CrossRef]
- Ramasubramanian, D.; Hernández-Verdejo, J.L.; López-Alonso, J.M. Contact lens fitting and changes in the tear film dynamics: Mathematical and computational models review. Graefes Arch. Clin. Exp. Ophthalmol. 2024, 262, 2751–2764. [Google Scholar] [CrossRef]
- Paulsen, F.; Schaudig, U.; Thale, A.B. Drainage of tears: Impact on the ocular surface and lacrimal system. Ocul. Surf. 2003, 1, 180–191. [Google Scholar] [CrossRef]
- Poetker, D.M.; Reh, D.D. A comprehensive review of the adverse effects of systemic corticosteroids. Otolaryngol. Clin. N. Am. 2010, 43, 753–768. [Google Scholar] [CrossRef] [PubMed]






| Description | Parameter | Value | Reference |
|---|---|---|---|
| Exposed eye surface area | SAexp | 220 mm2 | [32] |
| Tear film width | wTF | 18.59 µm | [33,34] |
| Eyelid length | Llid | 57 mm | [35] |
| Initial tear film volume | VTF0 | 4.09 mm3 | Calculated; SAexp × wTF |
| Tear film depth | d | 28.5 mm | Calculated; Llid/2 |
| Upper tear film height | hTF | 7.72 mm | Calculated; SAexp/d |
| Upper fornical sac height | hUF | 14.1 mm | [36] |
| Upper meniscus height | hUM | 0.934 mm | [33,34] |
| Lower meniscus height | hLM | 3.02 mm | [33,34] |
| Lower fornical sac height | hLF | 10.2 mm | [36] |
| Upper meniscus surface area | SAUM | 0.0539 mm2 | [33,34] |
| Lower meniscus surface area | SALM | 0.242 mm2 | [33,34] |
| Lacrimal duct entrance width | wLA | 2 µm | [37] |
| Base of fornical sac width | wBF | 7 µm | [37] |
| Undeformed canaliculi radius | R0 | 0.25 mm | [38] |
| Canaliculi length | Lc | 0.012 m | [39] |
| Description | Parameter | Value | Reference |
|---|---|---|---|
| Canalicular wall thickness × elastic modulus | bE | 2.57 Pa-m | [47] |
| Eyelid closure time | tblink | 0.04 s | [43] |
| End of interblink phase | tinterblink | 5.54 s | [40] |
| Initial pressure in canaliculi | 400 Pa | [48] | |
| Pressure in the lacrimal sac | 0 Pa (atmospheric) | [46] | |
| Viscosity of the instilled fluid | μ | 0.0015 Pa-s | [46] |
| Steady-State Assumptions Governing Drainage | ||
|---|---|---|
| Phase | Blink Phase | Interblink Phase |
| Limits | 0 < t < tblink | tblink < t < tblinkcycle |
| Radius | ||
| Flow rate | ||
| Pressure | ||
| Description | Parameter | Maxidex® |
|---|---|---|
| Drug concentration [mg/mL] | C | 1 |
| Solubility limit [µg/mL] | Cs | 100 |
| Octanol–water partition coefficient | LogP | 1.83 |
| Drug mass [mg] | Mdrug | 0.035 |
| Drug molecular weight [g/mol] | MW | 392.5 |
| Drug density [kg/m3] | ρ | 1300 |
| Distribution coefficient | KD | 2.5 |
| Particle radius [µm] | r | 1.5 |
| Case Label a | Timestep | Q3D CPU Time | Total No. of Timesteps |
|---|---|---|---|
| A | Uniform dt = 0.001 | 13 m 47 s | 57,200 |
| B | 3 m 53 s | 14,072 | |
| C | 2 m 13 s | 8673 | |
| D | 1 m 09 s | 4281 | |
| E | 1 m 02 s * | 3741 | |
| F | 2 m 06 s | 7800 | |
| G | 1 m 58 s | 8263 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garimella, H.T.; Norris, C.; German, C.; Przekwas, A.; Walenga, R.; Babiskin, A.; Tan, M.-L. Quasi-3D Mechanistic Model for Predicting Eye Drop Distribution in the Human Tear Film. Bioengineering 2025, 12, 825. https://doi.org/10.3390/bioengineering12080825
Garimella HT, Norris C, German C, Przekwas A, Walenga R, Babiskin A, Tan M-L. Quasi-3D Mechanistic Model for Predicting Eye Drop Distribution in the Human Tear Film. Bioengineering. 2025; 12(8):825. https://doi.org/10.3390/bioengineering12080825
Chicago/Turabian StyleGarimella, Harsha T., Carly Norris, Carrie German, Andrzej Przekwas, Ross Walenga, Andrew Babiskin, and Ming-Liang Tan. 2025. "Quasi-3D Mechanistic Model for Predicting Eye Drop Distribution in the Human Tear Film" Bioengineering 12, no. 8: 825. https://doi.org/10.3390/bioengineering12080825
APA StyleGarimella, H. T., Norris, C., German, C., Przekwas, A., Walenga, R., Babiskin, A., & Tan, M.-L. (2025). Quasi-3D Mechanistic Model for Predicting Eye Drop Distribution in the Human Tear Film. Bioengineering, 12(8), 825. https://doi.org/10.3390/bioengineering12080825






