Numerical Modeling and Simulation of Non-Invasive Acupuncture Therapy Utilizing Near-Infrared Light-Emitting Diode
Abstract
1. Introduction
2. Materials and Methods
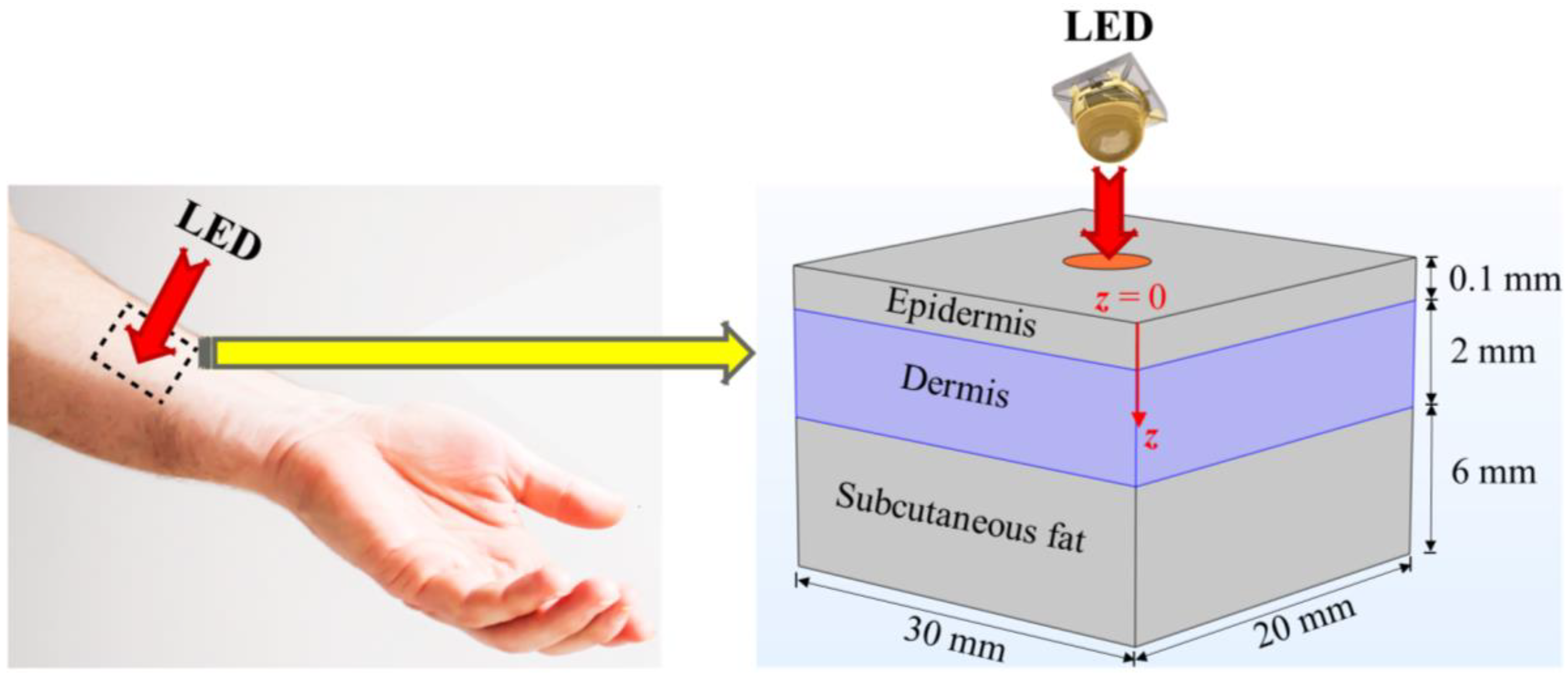
2.1. Finite-Element-Method (FEM)-Based Model
2.2. LED Irradiance Profile
2.3. Experimental Setup for Testing the LEDs
3. Results
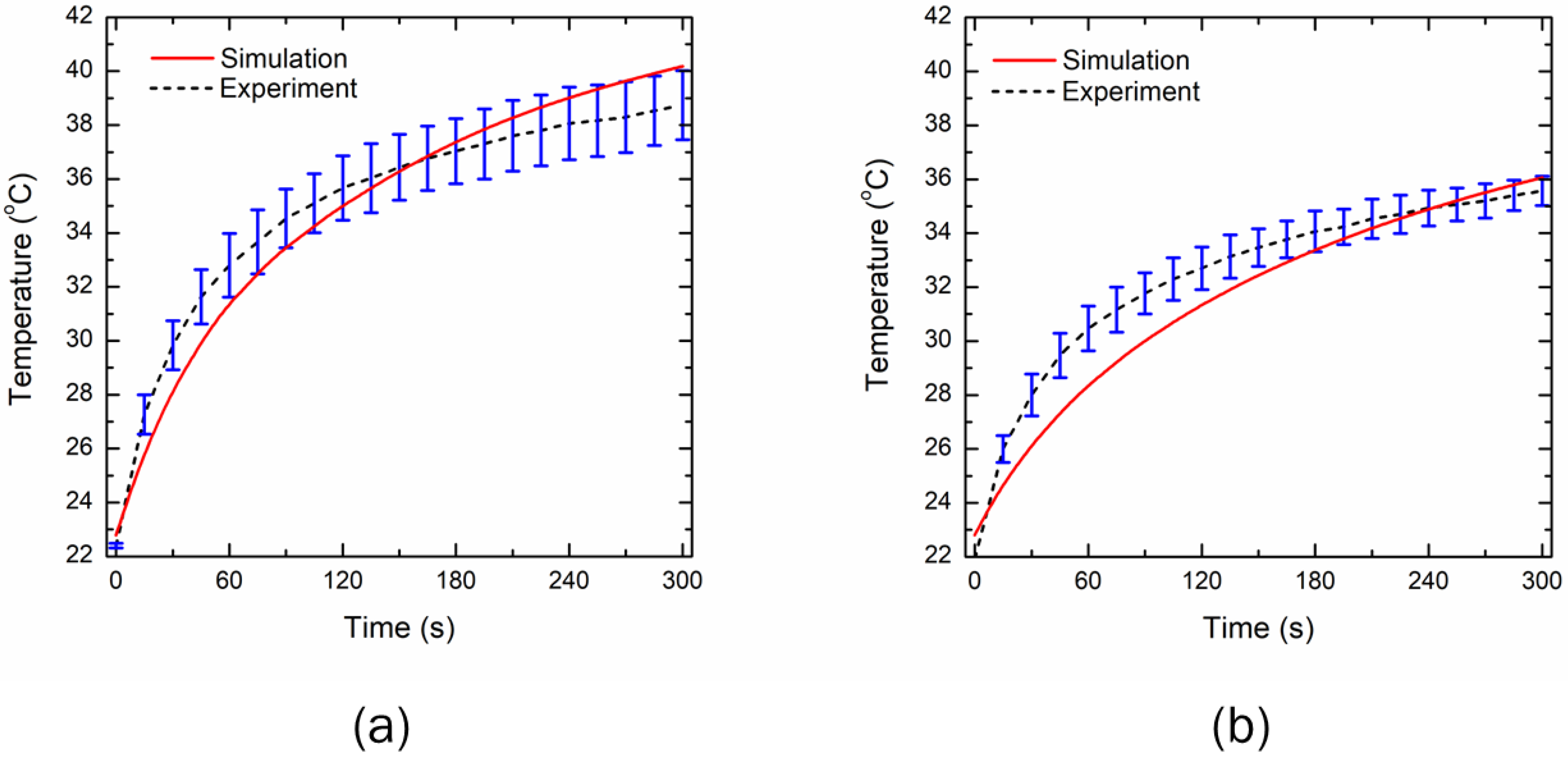
3.1. Experimental Validation
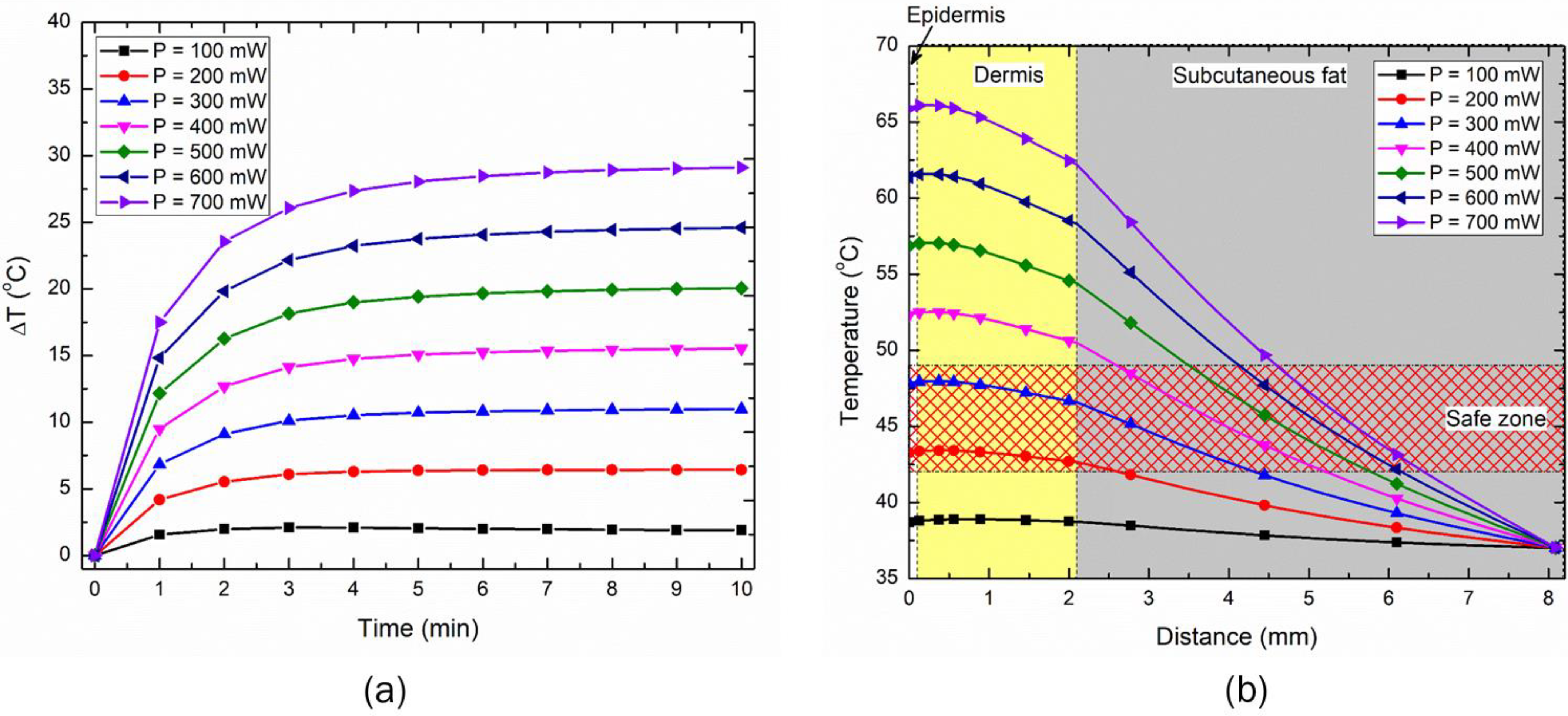
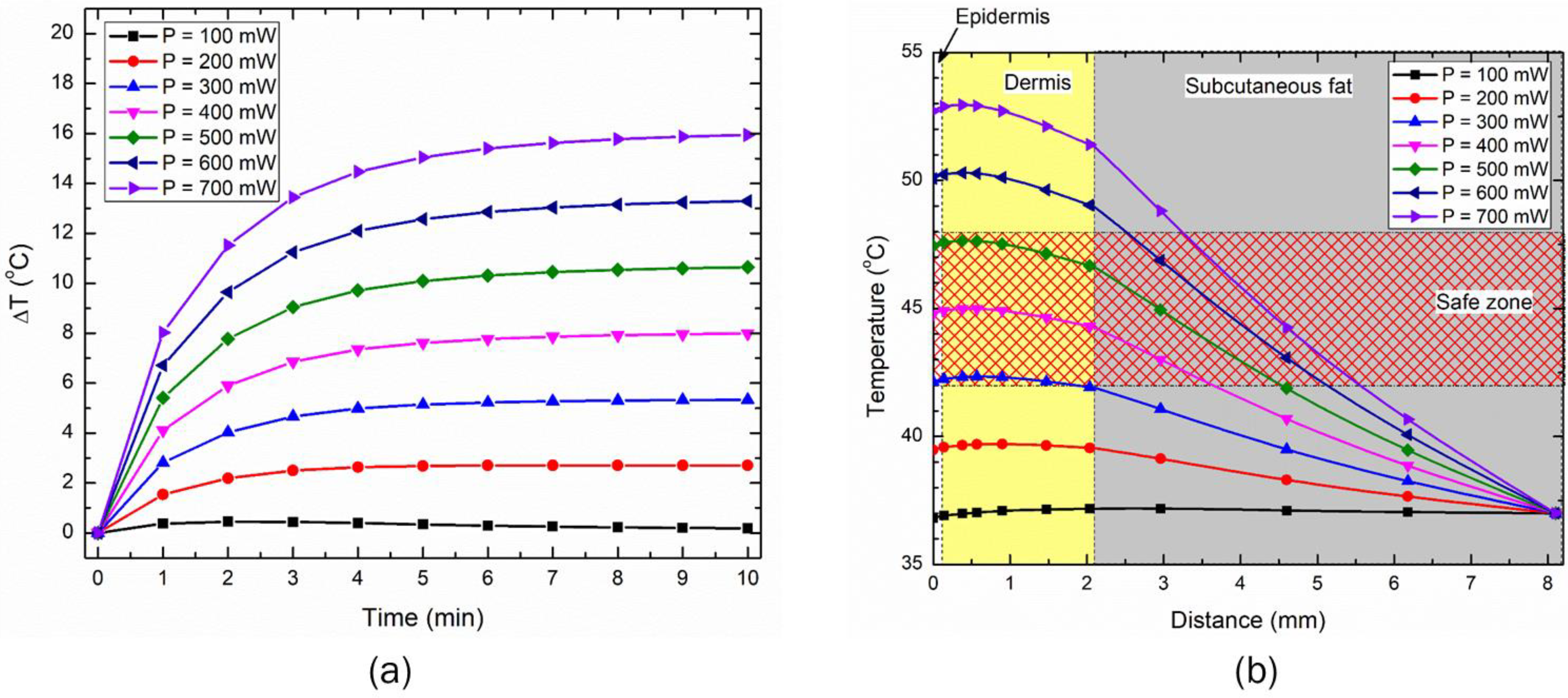
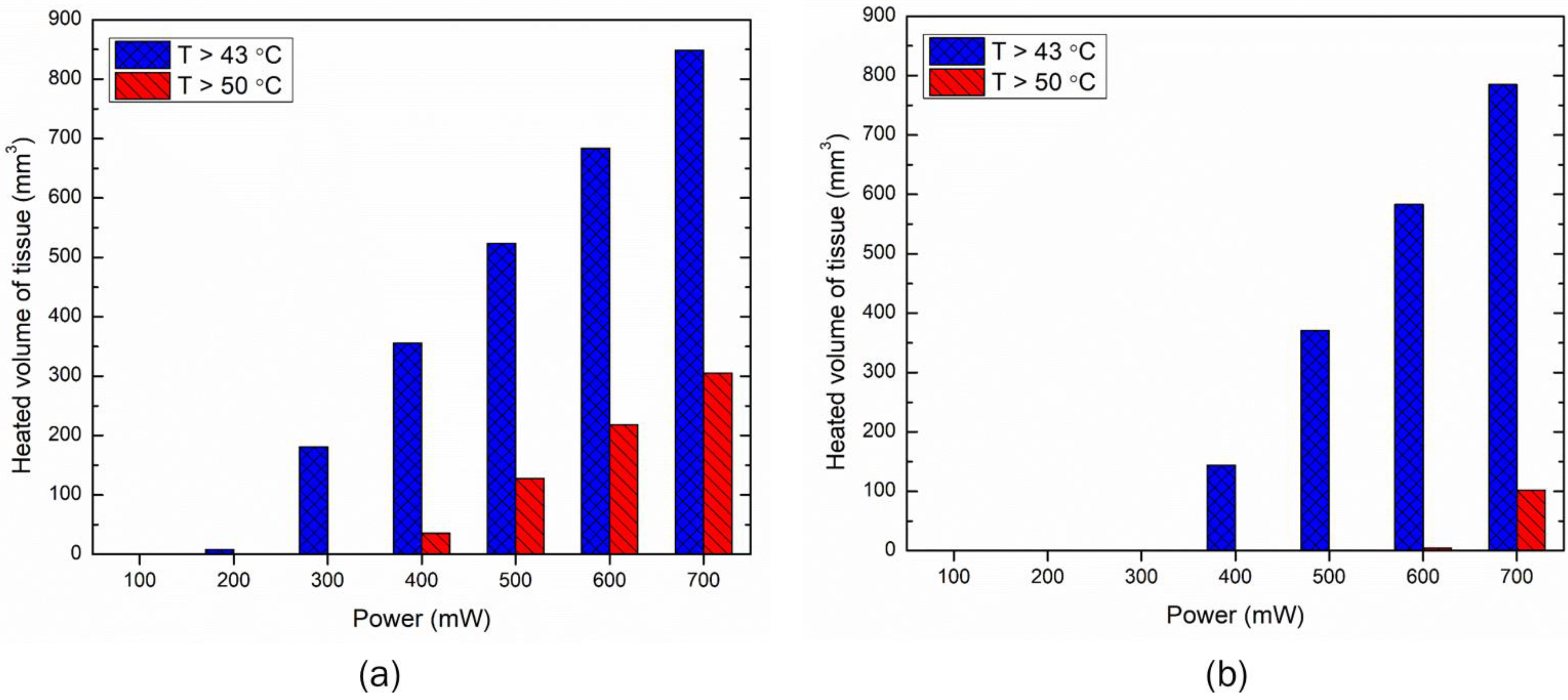
3.2. Effect of Input LED Power on Temperature Rise within the Skin
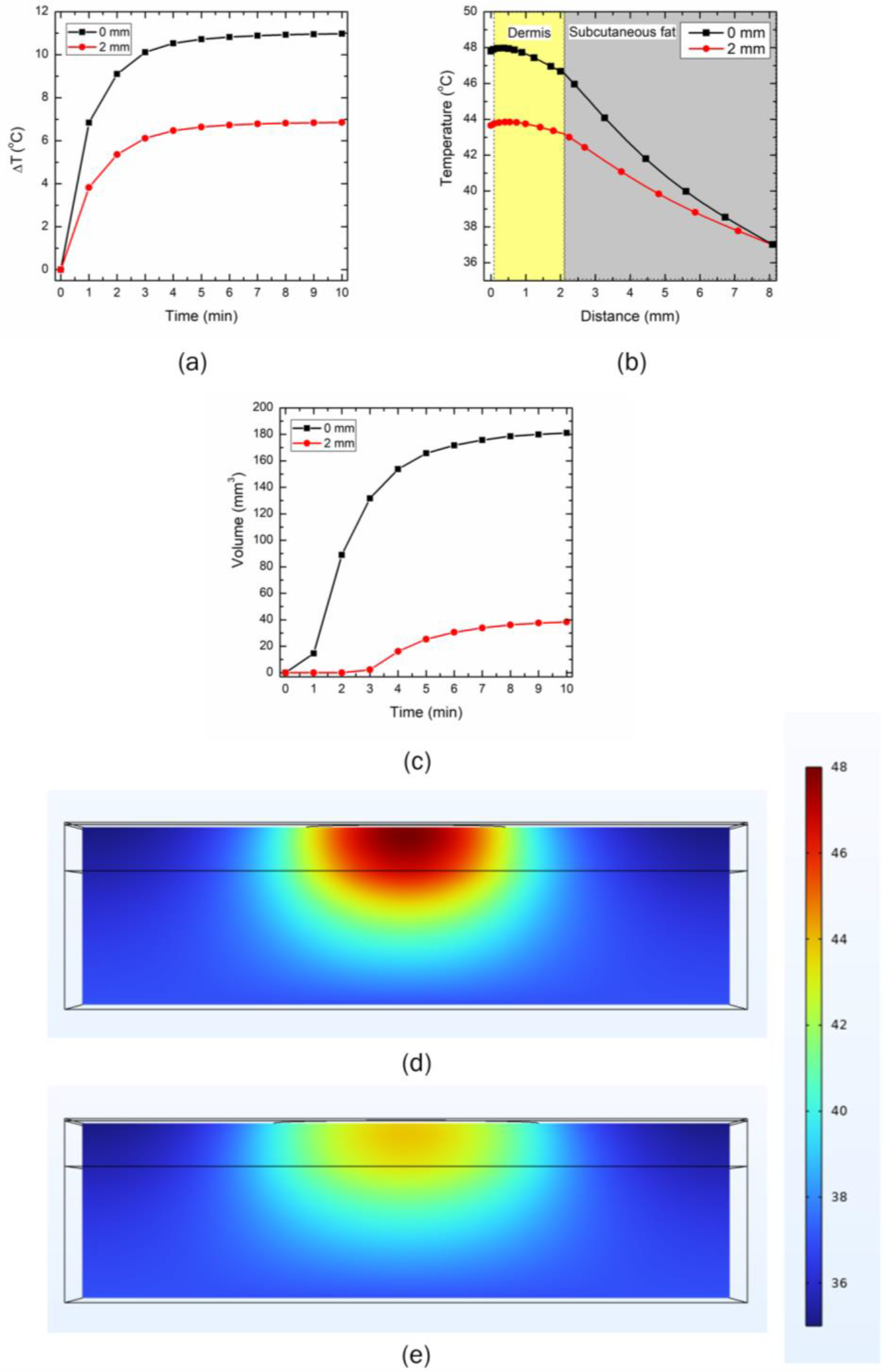
3.3. Effect of Distance between the LED and Skin Surface on Heat Transport
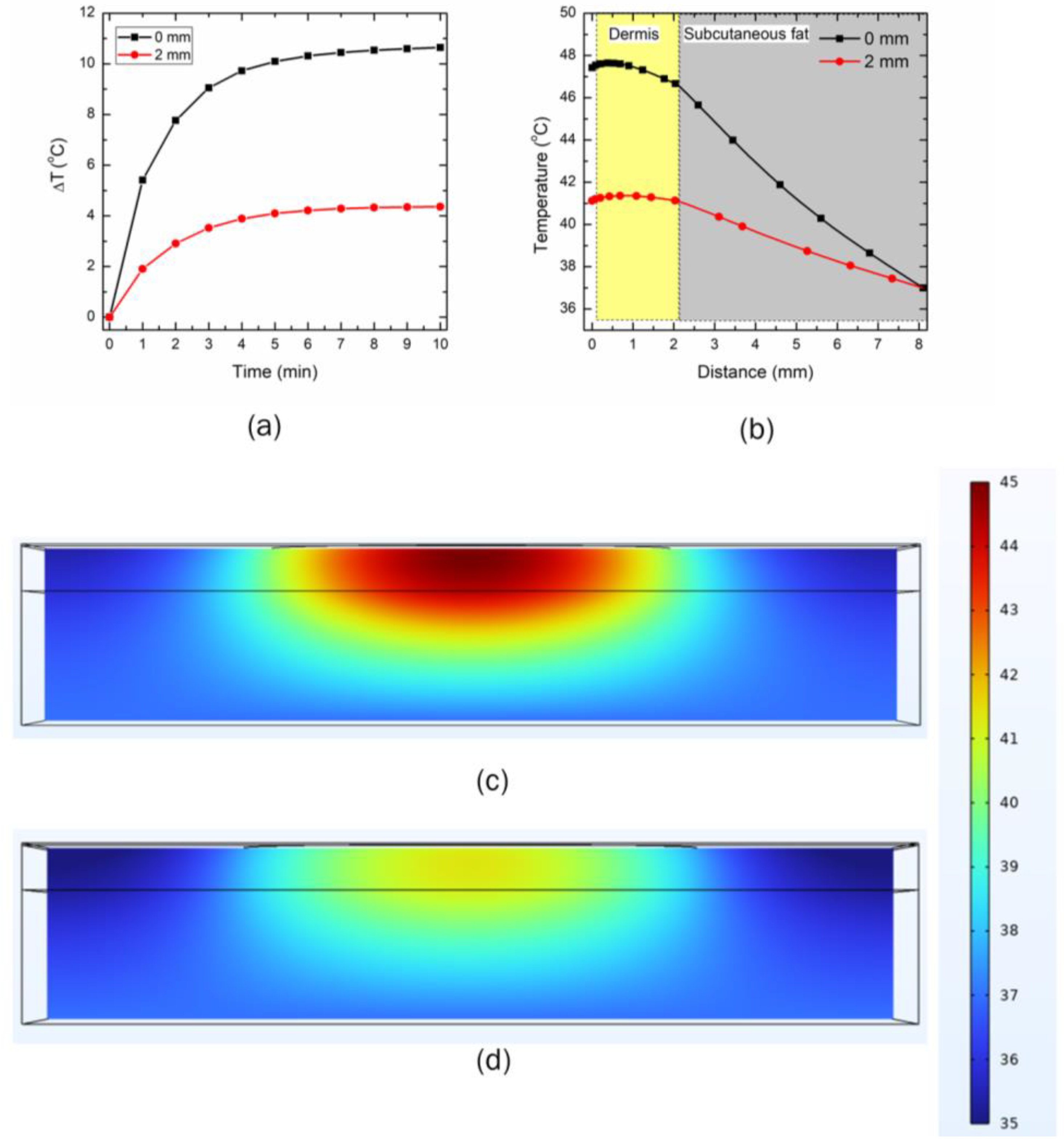
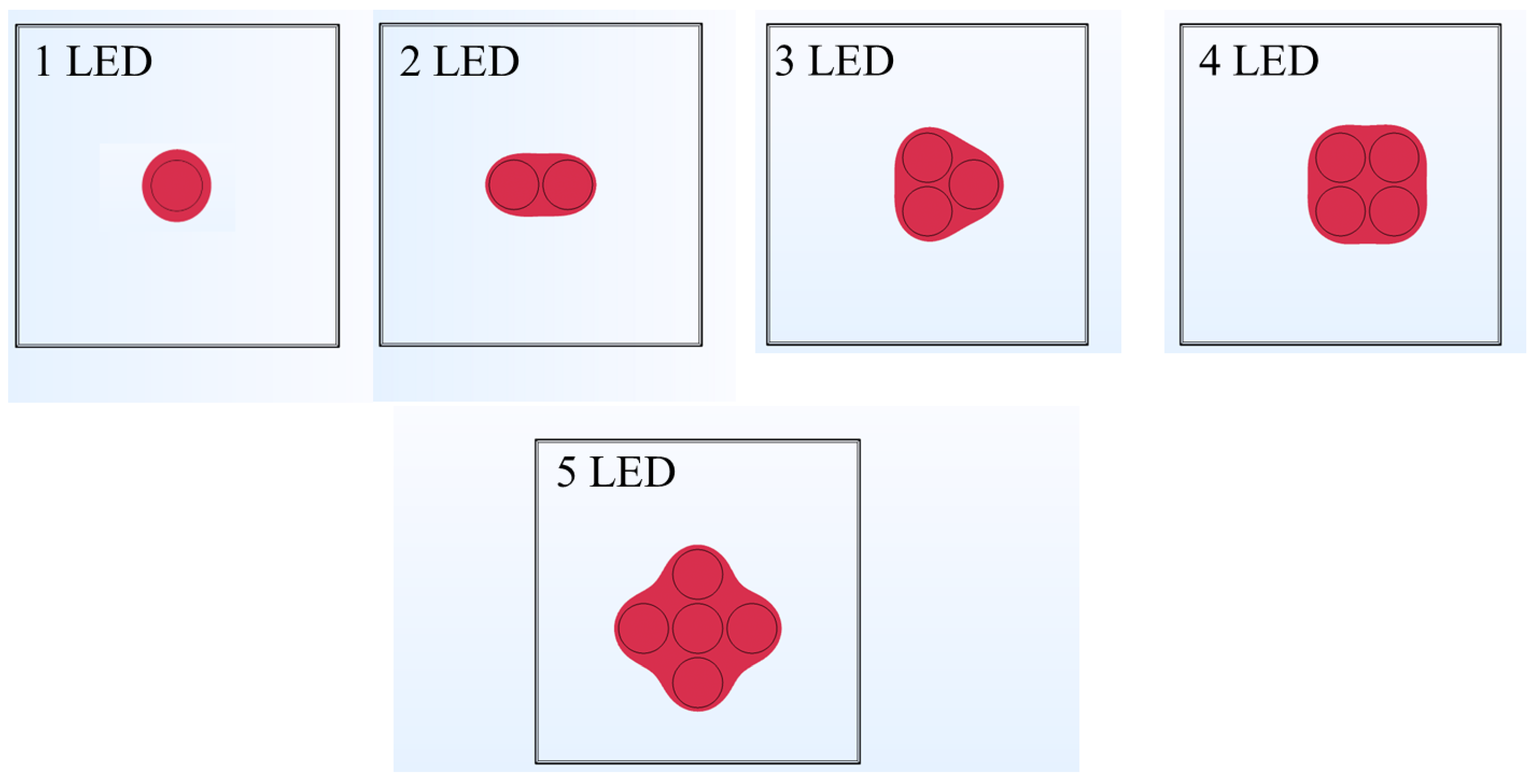
3.4. Effect of Increase in the Number of LEDs on Temperature Rise within Skin Tissue
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chow, S.L.; Bozkurt, B.; Baker, W.L.; Bleske, B.E.; Breathett, K.; Fonarow, G.C.; Greenberg, B.; Khazanie, P.; Leclerc, J.; Morris, A.A. Complementary and Alternative Medicines in the Management of Heart Failure: A Scientific Statement From the American Heart Association. Circulation 2023, 147, e4–e30. [Google Scholar] [CrossRef]
- Esmail, N. Complementary and Alternative Medicine; Fraser Institute: Vancouver, BC, Canada, 2017. [Google Scholar]
- Keene, M.R.; Heslop, I.M.; Sabesan, S.S.; Glass, B.D. Complementary and alternative medicine use in cancer: A systematic review. Complement. Ther. Clin. Pract. 2019, 35, 33–47. [Google Scholar] [CrossRef] [PubMed]
- Milenkovic, J. Complementary and alternative medicine in European countries-legislative framework. Tradit. Med. Res. 2020, 5, 125. [Google Scholar] [CrossRef]
- Ng, J.Y.; Bhatt, H.A.; Raja, M. Complementary and alternative medicine mention and recommendations in pancreatic cancer clinical practice guidelines: A systematic review and quality assessment. Integr. Med. Res. 2023, 12, 100921. [Google Scholar] [CrossRef]
- Sunjka, M.L.; Pejcic, A.; Jakovljevic, M. Utilization patterns of complementary and alternative medicine in Australia, Canada and the United States: Popularity of dietary supplements, mind-body and manipulative therapies. Farmeconomia Health Econ. Ther. Pathw. 2017, 18, 15–20. [Google Scholar]
- Wode, K.; Henriksson, R.; Sharp, L.; Stoltenberg, A.; Hök Nordberg, J. Cancer patients’ use of complementary and alternative medicine in Sweden: A cross-sectional study. BMC Complement. Altern. Med. 2019, 19, 62. [Google Scholar] [CrossRef] [PubMed]
- Austin, S.; Ramamonjiarivelo, Z.; Qu, H.; Ellis-Griffith, G. Acupuncture use in the United States: Who, where, why, and at what price? Health Mark. Q. 2015, 32, 113–128. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Zhang, Y.; Tang, X.; Ge, S.; Wen, H.; Zeng, J.; Wang, L.; Zeng, Z.; Rada, G.; Ávila, C. Evidence on acupuncture therapies is underused in clinical practice and health policy. BMJ 2022, 376, e067475. [Google Scholar] [CrossRef]
- Xia, Y.; Ding, G.; Wu, G.-C. Current Research in Acupuncture; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Jun, M.-H.; Kim, Y.-M.; Kim, J.U. Modern acupuncture-like stimulation methods: A literature review. Integr. Med. Res. 2015, 4, 195–219. [Google Scholar] [CrossRef]
- Longhurst, J.C. Defining meridians: A modern basis of understanding. J. Acupunct. Meridian Stud. 2010, 3, 67–74. [Google Scholar] [CrossRef]
- Ma, Y.; Dong, M.; Zhou, K.; Mita, C.; Liu, J.; Wayne, P.M. Publication trends in acupuncture research: A 20-year bibliometric analysis based on PubMed. PLoS ONE 2016, 11, e0168123. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Yu, Y.; Liu, Y.; Yao, W. Mast cells and acupuncture analgesia. Cells 2022, 11, 860. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Wang, Y.; Meng, H.; Li, S.; Jiang, H.; Zhang, Z.; He, J.; Zhao, Y.; Zhang, S.; Zhai, W. Acupuncture for brain diseases: Conception, application, and exploration. Anat. Rec. 2022. [CrossRef] [PubMed]
- Kim, K.-W.; Hong, S.; Kim, H.S.; Kim, T.; Ahn, J.; Song, H.-S.; Kim, Y.-K.; Oh, J.-Y.; Hwang, T.-Y.; Lee, H. Physiological impact of nanoporous acupuncture needles: Laser Doppler perfusion imaging in healthy volunteers. PLoS ONE 2019, 14, e0226304. [Google Scholar] [CrossRef]
- Zhu, J.; Li, J.; Yang, L.; Liu, S. Acupuncture, from the ancient to the current. Anat. Rec. 2021, 304, 2365–2371. [Google Scholar] [CrossRef]
- Yang, W.; Liu, X.; Zhang, X.; Li, C.; Li, Z.; Li, Y.; Li, M. Bibliometric analysis of acupuncture and moxibustion treatment for mild cognitive impairment. Front. Neurosci. 2023, 17, 1209262. [Google Scholar] [CrossRef]
- Zhang, Z.-J.; Wang, X.-M.; McAlonan, G.M. Neural acupuncture unit: A new concept for interpreting effects and mechanisms of acupuncture. Evid. Based Complement. Altern. Med. 2012, 2012, 429412. [Google Scholar] [CrossRef]
- Deng, H.; Shen, X. The mechanism of moxibustion: Ancient theory and modern research. Evid. Based Complement. Altern. Med. 2013, 2013, 379291. [Google Scholar] [CrossRef]
- Liu, H.; Huang, Z.; Wei, L.; Huang, H.; Li, Q.; Peng, H.; Liu, M. Uncertainty analysis and optimization for mild moxibustion. PLoS ONE 2023, 18, e0282355. [Google Scholar] [CrossRef]
- Li, Y.; Sun, C.; Kuang, J.; Ji, C.; Feng, S.; Wu, J.; You, H. An in vitro and numerical study of moxibustion therapy on biological tissue. IEEE Trans. Biomed. Eng. 2017, 65, 779–788. [Google Scholar] [CrossRef]
- Sun, C.; Ji, C.; Li, Y.; Kuang, J.; Wu, J. A comparison study of photothermal effect between moxibustion therapy and laser irradiation on biological tissue. Int. J. Therm. Sci. 2021, 164, 106924. [Google Scholar] [CrossRef]
- Liu, H.; Huang, Z.; Wei, L.; Huang, H.; Li, Q.; Peng, H.; Liu, M. Numerical Simulation of Temperature Distribution during Mild Moxibustion. Evid. Based Complement. Altern. Med. 2022, 2022, 6604372. [Google Scholar] [CrossRef] [PubMed]
- Kim, G.; Hwang, Y.-I.; Ryu, Y.; Kim, H.-J.; Bae, Y.-M.; Kim, K.-B. Ultrasonic device developed for non-invasive moxibustion therapy. Integr. Med. Res. 2021, 10, 100729. [Google Scholar] [CrossRef]
- Solovchuk, M.; Deng, H.-A.; Sheu, T.W. Experimental and numerical study on the temperature elevation in tissue during moxibustion therapy. Evid. Based Complement. Altern. Med. 2020, 2020, 7514302. [Google Scholar] [CrossRef]
- Sun, C.; Li, Y.; Kuang, J.; Liang, X.; Wu, J.; Ji, C. The thermal performance of biological tissue under moxibustion therapy. J. Therm. Biol. 2019, 83, 103–111. [Google Scholar] [CrossRef]
- Tsuruoka, N.; Watanabe, M.; Seki, T.; Matsunaga, T.; Hagaa, Y. Acupoint stimulation device using focused ultrasound. In Proceedings of the 2010 Annual International Conference of the IEEE Engineering in Medicine and Biology, Buenos Aires, Argentina, 31 August–4 September 2010; pp. 1258–1261. [Google Scholar]
- Tsuruoka, N.; Watanabe, M.; Takayama, S.; Seki, T.; Matsunaga, T.; Haga, Y. Brief effect of acupoint stimulation using focused ultrasound. J. Altern. Complement. Med. 2013, 19, 416–419. [Google Scholar] [CrossRef] [PubMed]
- Calderhead, R.G.; Vasily, D.B. Low level light therapy with light-emitting diodes for the aging face. Clin. Plast. Surg. 2016, 43, 541–550. [Google Scholar] [CrossRef] [PubMed]
- Rossi, F.; Pini, R.; De Siena, G.; Massi, D.; Pavone, F.S.; Alfieri, D.; Cannarozzo, G. A blue-LED-based device for selective photocoagulation of superficial abrasions: Theoretical modeling and in vivo validation. In Photonic Therapeutics and Diagnostics VI: 23–25 January 2010, San Francisco, CA, USA; SPIE: Bellingham, DC, USA, 2010; pp. 53–59. [Google Scholar]
- Sorbellini, E.; Rucco, M.; Rinaldi, F. Photodynamic and photobiological effects of light-emitting diode (LED) therapy in dermatological disease: An update. Lasers Med. Sci. 2018, 33, 1431–1439. [Google Scholar] [CrossRef]
- Nasouri, B.; Murphy, T.E.; Berberoglu, H. Simulation of laser propagation through a three-layer human skin model in the spectral range from 1000 to 1900 nm. J. Biomed. Opt. 2014, 19, 075003. [Google Scholar] [CrossRef]
- Dremin, V.; Novikova, I.; Rafailov, E. Simulation of thermal field distribution in biological tissue and cell culture media irradiated with infrared wavelengths. Opt. Express 2022, 30, 23078–23089. [Google Scholar] [CrossRef]
- Wongchadakul, P.; Rattanadecho, P.; Wessapan, T. Implementation of a thermomechanical model to simulate laser heating in shrinkage tissue (effects of wavelength, laser irradiation intensity, and irradiation beam area). Int. J. Therm. Sci. 2018, 134, 321–336. [Google Scholar] [CrossRef]
- Andreozzi, A.; Brunese, L.; Iasiello, M.; Tucci, C.; Vanoli, G.P. Modeling heat transfer in tumors: A review of thermal therapies. Ann. Biomed. Eng. 2019, 47, 676–693. [Google Scholar] [CrossRef] [PubMed]
- Bhowmik, A.; Singh, R.; Repaka, R.; Mishra, S.C. Conventional and newly developed bioheat transport models in vascularized tissues: A review. J. Therm. Biol. 2013, 38, 107–125. [Google Scholar] [CrossRef]
- Singh, S.; Melnik, R. Thermal ablation of biological tissues in disease treatment: A review of computational models and future directions. Electromagn. Biol. Med. 2020, 39, 49–88. [Google Scholar] [CrossRef]
- Hasgall, P.; Di Gennaro, F.; Baumgartner, C.; Neufeld, E.; Lloyd, B.; Gosselin, M.; Payne, D.; Klingenböck, A.; Kuster, N. IT’IS Database for Thermal and Electromagnetic Parameters of Biological Tissues. Available online: itis.swiss/database (accessed on 7 March 2023).
- Mohammadi, A.; Bianchi, L.; Korganbayev, S.; De Landro, M.; Saccomandi, P. Thermomechanical modeling of laser ablation therapy of tumors: Sensitivity analysis and optimization of influential variables. IEEE Trans. Biomed. Eng. 2021, 69, 302–313. [Google Scholar] [CrossRef]
- Salomatina, E.; Jiang, B.; Novak, J.; Yaroslavsky, A.N. Optical properties of normal and cancerous human skin in the visible and near-infrared spectral range. J. Biomed. Opt. 2006, 11, 064026. [Google Scholar] [CrossRef] [PubMed]
- Proskurnin, M.A.; Khabibullin, V.R.; Usoltseva, L.O.; Vyrko, E.; Mikheev, I.V.; Volkov, D.S. Photothermal and optoacoustic spectroscopy: State of the art and prospects. Phys. Uspekhi 2022, 65, 270. [Google Scholar] [CrossRef]
- Paul, A.; Narasimhan, A.; Kahlen, F.J.; Das, S.K. Temperature evolution in tissues embedded with large blood vessels during photo-thermal heating. J. Therm. Biol. 2014, 41, 77–87. [Google Scholar] [CrossRef] [PubMed]
- Patapoutian, A.; Peier, A.M.; Story, G.M.; Viswanath, V. ThermoTRP channels and beyond: Mechanisms of temperature sensation. Nat. Rev. Neurosci. 2003, 4, 529–539. [Google Scholar] [CrossRef] [PubMed]
- Adriaensen, H.; Gybels, J.; Handwerker, H.; Van Hees, J. Response properties of thin myelinated (A-delta) fibers in human skin nerves. J. Neurophysiol. 1983, 49, 111–122. [Google Scholar] [CrossRef]
- Wang, G.-Y.; Wang, L.-L.; Xu, B.; Zhang, J.-B.; Jiang, J.-F. Effects of moxibustion temperature on blood cholesterol level in a mice model of acute hyperlipidemia: Role of TRPV1. Evid. Based Complement. Altern. Med. 2013, 2013, 871704. [Google Scholar] [CrossRef] [PubMed]



| Parameters | Epidermis | Dermis | Subcutaneous Fat |
|---|---|---|---|
| Density, ρ (kg/m3) | 1200 | 1090 | 1210 |
| Specific heat capacity, cp (J/kg/K) | 3950 | 3350 | 2240 |
| Thermal conductivity, k (W/m·K) | 0.24 | 0.42 | 0.194 |
| Blood perfusion rate, ωb (1/s) | - | 0.002 | 0.002 |
| Absorption coefficient @ 850 nm, µa (1/cm) | 0.9 | 0.95 | 1 |
| Reduced scattering coefficient @ 850 nm, µ′s (1/cm) | 30 | 20 | 18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, S.; Escobar, A.; Wang, Z.; Zhang, Z.; Ramful, C.; Xu, C.-Q. Numerical Modeling and Simulation of Non-Invasive Acupuncture Therapy Utilizing Near-Infrared Light-Emitting Diode. Bioengineering 2023, 10, 837. https://doi.org/10.3390/bioengineering10070837
Singh S, Escobar A, Wang Z, Zhang Z, Ramful C, Xu C-Q. Numerical Modeling and Simulation of Non-Invasive Acupuncture Therapy Utilizing Near-Infrared Light-Emitting Diode. Bioengineering. 2023; 10(7):837. https://doi.org/10.3390/bioengineering10070837
Chicago/Turabian StyleSingh, Sundeep, Andres Escobar, Zexi Wang, Zhiyi Zhang, Chundra Ramful, and Chang-Qing Xu. 2023. "Numerical Modeling and Simulation of Non-Invasive Acupuncture Therapy Utilizing Near-Infrared Light-Emitting Diode" Bioengineering 10, no. 7: 837. https://doi.org/10.3390/bioengineering10070837
APA StyleSingh, S., Escobar, A., Wang, Z., Zhang, Z., Ramful, C., & Xu, C.-Q. (2023). Numerical Modeling and Simulation of Non-Invasive Acupuncture Therapy Utilizing Near-Infrared Light-Emitting Diode. Bioengineering, 10(7), 837. https://doi.org/10.3390/bioengineering10070837








