From Spatial-Temporal Multiscale Modeling to Application: Bridging the Valley of Death in Industrial Biotechnology
Abstract
1. Introduction
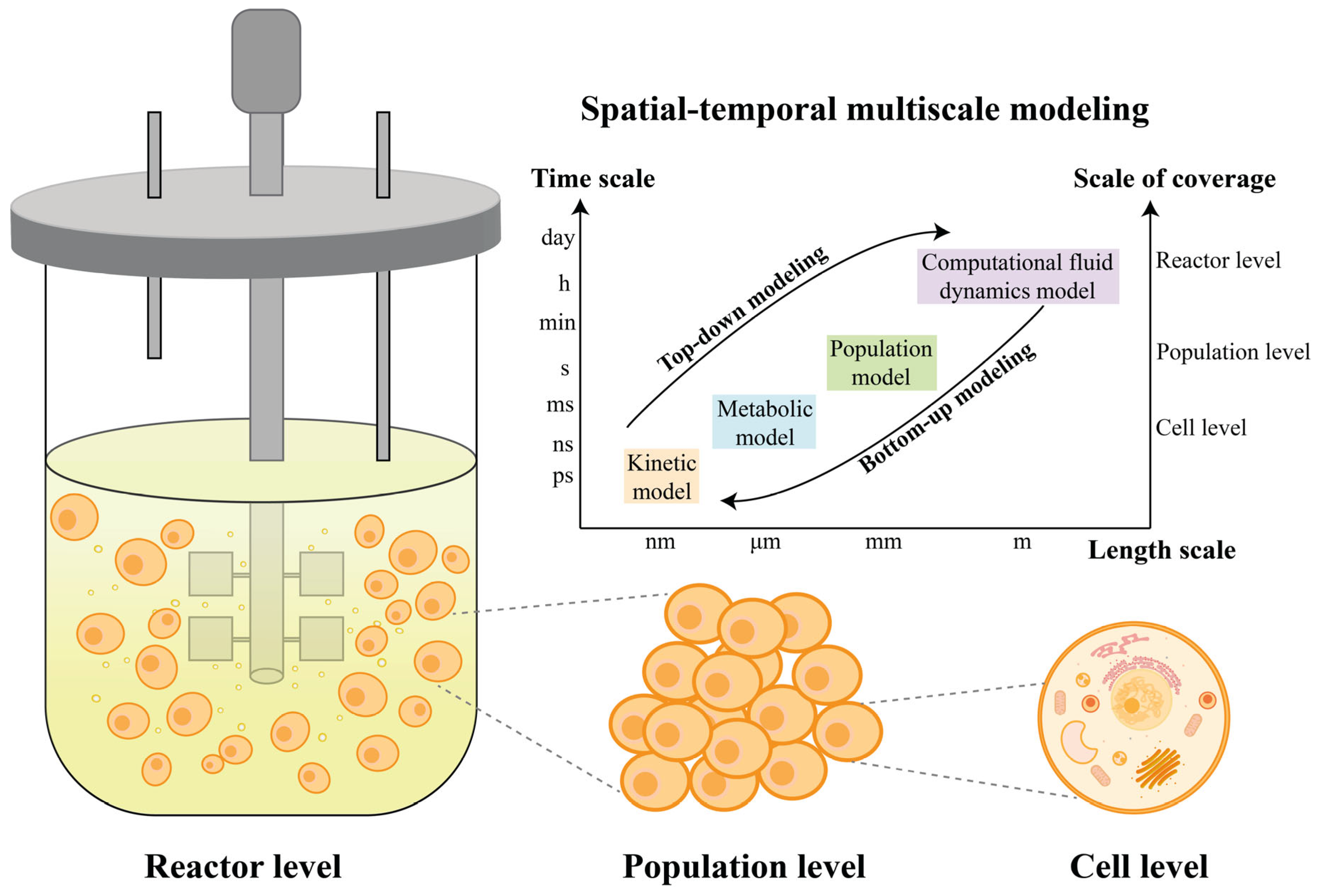
2. Development of Modeling
2.1. Mechanistic Models
2.1.1. Unstructured Unsegregated Models
2.1.2. Structured Unsegregated Models
2.1.3. Segregated Models
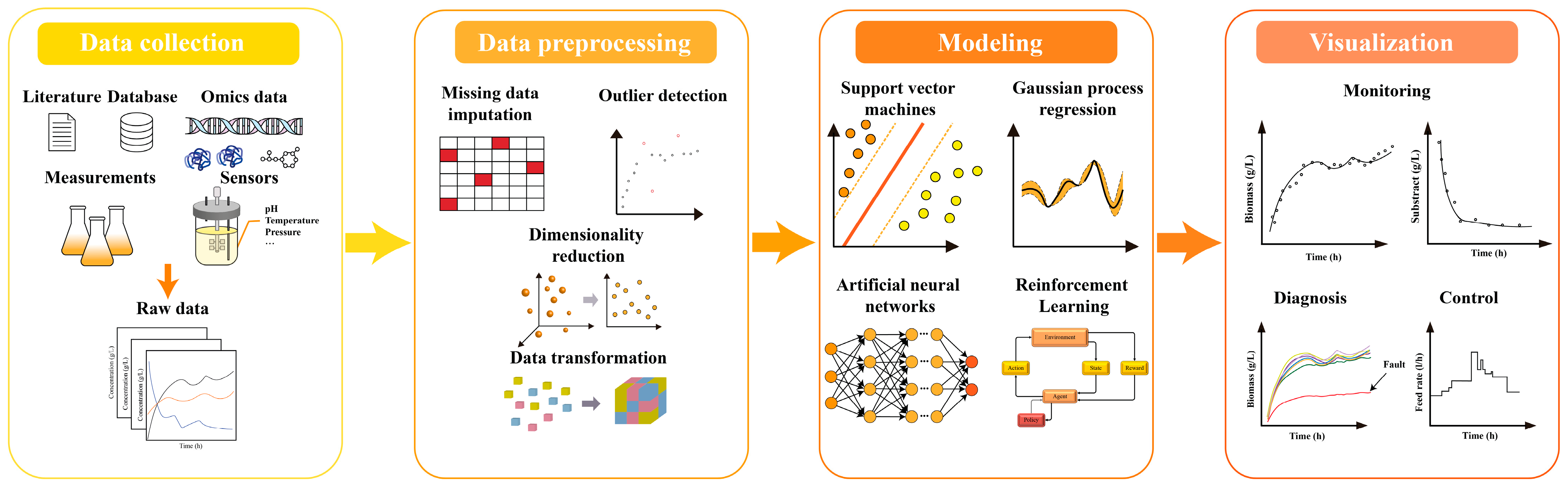
2.2. Data-Driven Modeling
2.2.1. Support Vector Machine (SVM)
2.2.2. Artificial Neural Network (ANN)
2.2.3. Gaussian Process (GP)
2.2.4. Reinforcement Learning (RL)
| Method | Advantages | Disadvantages |
|---|---|---|
| Support vector machine (SVM) | Suitable for high-dimensional datasets; Suitable for solving non-linear problems; Various kernel functions for different problems. | Not suitable for large datasets; High requirements on data; Preprocessing and selections of hyperparameters. |
| Artificial neural network (ANN) | Suitable for solving non-linear problems; Robustness to noise; Suitable for large datasets. | High requirements on the integrity of datasets; Hyperparameter optimization at a high computational cost; Poor generalization capability. |
| Gaussian process (GP) | Suitable for solving non-linear problems; Capacity of predictive values and their uncertainty; Various kernel functions for different problems. | Not suitable for large datasets; High computational costs. |
| Reinforcement learning (RL) | Suitable for decision problems in time-series models; Suitable for optimization problems; Good generalization capability. | High requirements on data quantity and quality; Difficulty to design the reward function. |
2.3. Multi-Scale Hybrid Modeling
3. Applications of Hybrid Models in Bioprocess Development
3.1. Metabolic Engineering
3.1.1. Metabolic Model Reconstruction for Better Performance
3.1.2. Metabolic Model-BASED Guidance for Strain Design
3.2. Bioprocess Engineering
3.2.1. Monitoring and Control of Bioprocess
3.2.2. Diagnosis and Analysis of Bioprocesses
3.2.3. Optimization and Scale-Up of Bioprocesses
4. Challenges and Future Perspectives
4.1. Challenges
4.2. Future Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gropp, R.E. COVID-19 and the Bioeconomy. Bioscience 2020, 70, 443. [Google Scholar] [CrossRef] [PubMed]
- Frohling, M.; Hiete, M. Sustainability and Life Cycle Assessment in Industrial Biotechnology: A Review of Current Approaches and Future Needs. Adv. Biochem. Eng. Biotechnol. 2020, 173, 143–203. [Google Scholar] [CrossRef] [PubMed]
- Lerner, J.; Nanda, R. Venture Capital’s Role in Financing Innovation: What We Know and How Much We Still Need to Learn. J. Econ. Perspect. 2020, 34, 237–261. [Google Scholar] [CrossRef]
- Koch, M.; Duigou, T.; Faulon, J.L. Reinforcement Learning for Bioretrosynthesis. ACS Synth. Biol. 2020, 9, 157–168. [Google Scholar] [CrossRef]
- Hutmacher, D.W.; Singh, H. Computational fluid dynamics for improved bioreactor design and 3D culture. Trends Biotechnol. 2008, 26, 166–172. [Google Scholar] [CrossRef]
- Mears, L.; Stocks, S.M.; Albaek, M.O.; Sin, G.; Gernaey, K.V. Application of a mechanistic model as a tool for on-line monitoring of pilot scale filamentous fungal fermentation processesThe importance of evaporation effects. Biotechnol. Bioeng. 2017, 114, 589–599. [Google Scholar] [CrossRef]
- Antonakoudis, A.; Barbosa, R.; Kotidis, P.; Kontoravdi, C. The era of big data: Genome-scale modelling meets machine learning. Comput. Struct. Biotec. 2020, 18, 3287–3300. [Google Scholar] [CrossRef]
- Gernaey, K.V.; Lantz, A.E.; Tufvesson, P.; Woodley, J.M.; Sin, G. Application of mechanistic models to fermentation and biocatalysis for next-generation processes. Trends Biotechnol. 2010, 28, 346–354. [Google Scholar] [CrossRef]
- Saa, P.A.; Nielsen, L.K. Formulation, construction and analysis of kinetic models of metabolism: A review of modelling frameworks. Biotechnol. Adv. 2017, 35, 981–1003. [Google Scholar]
- Ghosh, A.; Ransinchung, G.D.R.N. Application of machine learning algorithm to assess the efficacy of varying industrial wastes and curing methods on strength development of geopolymer concrete. Constr. Build. Mater. 2022, 341, 127828. [Google Scholar] [CrossRef]
- Zhao, Y.Q.; Fu, S.Y.; Bielinski, S.J.; Decker, P.; Chamberlain, A.M.; Roger, V.L.; Liu, H.F.; Larson, N.B. Using Natural Language Processing and Machine Learning to Identify Incident Stroke From Electronic Health Records. Circulation 2020, 141, AP259. [Google Scholar] [CrossRef]
- Ousmane, A.M.; Djara, T.; Zoumarou, W.F.J.; Vianou, A. Automatic recognition system of emotions expressed through the face using machine learning: Application to police interrogation simulation. In Proceedings of the 2019 3rd International Conference on Bio-Engineering for Smart Technologies (Biosmart), Paris, France, 24–26 April 2019. [Google Scholar]
- Byeloborodov, Y.; Rashad, S. Design of Machine Learning Algorithms for Behavioral Prediction of Objects for Self-Driving Cars. In Proceedings of the 2020 11th IEEE Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (Uemcon), New York, NY, USA, 28–31 October 2020; pp. 101–105. [Google Scholar]
- Krishnaveni, P.R.; Kishore, G.N. Image Based Group Classifier for Brain Tumor Detection Using Machine Learning Technique. Trait. Signal 2020, 37, 865–871. [Google Scholar] [CrossRef]
- Nielsen, J.; Keasling, J.D. Engineering Cellular Metabolism. Cell 2016, 164, 1185–1197. [Google Scholar] [CrossRef]
- del Rio-Chanona, E.A.; Wagner, J.L.; Ali, H.; Fiorelli, F.; Zhang, D.D.; Hellgardt, K. Deep learning-based surrogate modeling and optimization for microalgal biofuel production and photobioreactor design. AIChE J. 2019, 65, 915–923. [Google Scholar] [CrossRef]
- Michaelis, L.; Menten, M.L. The kinetics of invertin action. FEBS Lett. 2013, 587, 2712–2720. [Google Scholar] [CrossRef]
- Fernandes, R.L.; Bodla, V.K.; Carlquist, M.; Heins, A.L.; Lantz, A.E.; Sin, G.; Gernaey, K.V. Applying Mechanistic Models in Bioprocess Development. Adv. Biochem. Eng. Biot. 2013, 132, 137–166. [Google Scholar] [CrossRef]
- Jin, Q.; Wu, Q.; Shapiro, B.M.; McKernan, S.E. Limited Mechanistic Link Between the Monod Equation and Methanogen Growth: A Perspective from Metabolic Modeling. Microbiol. Spectr. 2022, 10, e02259-21. [Google Scholar] [CrossRef]
- Lopez, P.C.; Udugama, I.A.; Thomsen, S.T.; Roslander, C.; Junicke, H.; Mauricio-Iglesias, M.; Gernaey, K.V. Towards a digital twin: A hybrid data-driven and mechanistic digital shadow to forecast the evolution of lignocellulosic fermentation. Biofuels Bioprod. Biorefining 2020, 14, 1046–1060. [Google Scholar] [CrossRef]
- Muloiwa, M.; Nyende-Byakika, S.; Dinka, M. Comparison of unstructured kinetic bacterial growth models. S. Afr. J. Chem. Eng. 2020, 33, 141–150. [Google Scholar] [CrossRef]
- Costa, R.S.; Hartmann, A.; Vinga, S. Kinetic modeling of cell metabolism for microbial production. J. Biotechnol. 2016, 219, 126–141. [Google Scholar]
- Kerkhoven, E.J.; Lahtvee, P.J.; Nielsen, J. Applications of computational modeling in metabolic engineering of yeast. FEMS Yeast Res. 2015, 15, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Tang, W.J.; Deshmukh, A.T.; Haringa, C.; Wang, G.; van Gulik, W.; van Winden, W.; Reuss, M.; Heijnen, J.J.; Xia, J.Y.; Chu, J.; et al. A 9-pool metabolic structured kinetic model describing days to seconds dynamics of growth and product formation by Penicillium chrysogenum. Biotechnol. Bioeng. 2017, 114, 1733–1743. [Google Scholar] [CrossRef]
- Schmidt, H.; Jirstrand, M. Systems Biology Toolbox for MATLAB: A computational platform for research in systems biology. Bioinformatics 2006, 22, 514–515. [Google Scholar] [PubMed]
- Schomburg, I.; Jeske, L.; Ulbrich, M.; Placzek, S.; Chang, A.; Schomburg, D. The BRENDA enzyme information system-From a database to an expert system. J. Biotechnol. 2017, 261, 194–206. [Google Scholar] [PubMed]
- Wittig, U.; Kania, R.; Golebiewski, M.; Rey, M.; Shi, L.; Jong, L.; Algaa, E.; Weidemann, A.; Sauer-Danzwith, H.; Mir, S.; et al. SABIO-RK-database for biochemical reaction kinetics. Nucleic Acids Res. 2012, 40, D790–D796. [Google Scholar]
- Doan, S.; Lin, K.W.; Conway, M.; Ohno-Machado, L.; Hsieh, A.; Feupe, S.F.; Garland, A.; Ross, M.K.; Jiang, X.; Farzaneh, S.; et al. PhenDisco: Phenotype discovery system for the database of genotypes and phenotypes. J. Am. Med. Inform. Assoc. 2014, 21, 31–36. [Google Scholar] [CrossRef]
- Ramirez-Gaona, M.; Marcu, A.; Pon, A.; Guo, A.C.; Sajed, T.; Wishart, N.A.; Karu, N.; Djoumbou Feunang, Y.; Arndt, D.; Wishart, D.S. YMDB 2.0: A significantly expanded version of the yeast metabolome database. Nucleic Acids Res. 2017, 45, D440–D445. [Google Scholar] [CrossRef]
- Haug, K.; Cochrane, K.; Nainala, V.C.; Williams, M.; Chang, J.; Jayaseelan, K.V.; O’Donovan, C. MetaboLights: A resource evolving in response to the needs of its scientific community. Nucleic Acids Res. 2020, 48, D440–D444. [Google Scholar] [CrossRef]
- Perez-Riverol, Y.; Bai, J.; Bandla, C.; Garcia-Seisdedos, D.; Hewapathirana, S.; Kamatchinathan, S.; Kundu, D.J.; Prakash, A.; Frericks-Zipper, A.; Eisenacher, M.; et al. The PRIDE database resources in 2022: A hub for mass spectrometry-based proteomics evidences. Nucleic Acids Res. 2022, 50, D543–D552. [Google Scholar] [CrossRef]
- Mochao, H.; Barahona, P.; Costa, R.S. KiMoSys 2.0: An upgraded database for submitting, storing and accessing experimental data for kinetic modeling. Database 2020, 2020, baaa093. [Google Scholar] [CrossRef]
- Cotten, C.; Reed, J.L. Mechanistic analysis of multi-omics datasets to generate kinetic parameters for constraint-based metabolic models. BMC Bioinform. 2013, 14, 32. [Google Scholar] [CrossRef]
- Bi, X.Y.; Liu, Y.F.; Li, J.H.; Du, G.C.; Lv, X.Q.; Liu, L. Construction of Multiscale Genome-Scale Metabolic Models: Frameworks and Challenges. Biomolecules 2022, 12, 721. [Google Scholar] [CrossRef]
- Xu, N.; Ye, C.; Liu, L.M. Genome-scale biological models for industrial microbial systems. Appl. Microbiol. Biot. 2018, 102, 3439–3451. [Google Scholar] [CrossRef]
- Rejc, Z.; Magdevska, L.; Trselic, T.; Osolin, T.; Vodopivec, R.; Mraz, J.; Pavliha, E.; Zimic, N.; Cvitanovic, T.; Rozman, D.; et al. Computational modelling of genome-scale metabolic networks and its application to CHO cell cultures. Comput. Biol. Med. 2017, 88, 150–160. [Google Scholar] [CrossRef]
- McCloskey, D.; Palsson, B.O.; Feist, A.M. Basic and applied uses of genome-scale metabolic network reconstructions of Escherichia coli. Mol. Syst. Biol. 2013, 9, 661. [Google Scholar] [CrossRef]
- Chen, Y.; Li, F.; Nielsen, J. Genome-scale modeling of yeast metabolism: Retrospectives and perspectives. FEMS Yeast Res. 2022, 22, foac003. [Google Scholar] [CrossRef]
- Gu, C.; Kim, G.B.; Kim, W.J.; Kim, H.U.; Lee, S.Y. Current status and applications of genome-scale metabolic models. Genome Biol. 2019, 20, 121. [Google Scholar] [CrossRef]
- Fleischmann, R.D.; Adams, M.D.; White, O.; Clayton, R.A.; Kirkness, E.F.; Kerlavage, A.R.; Bult, C.J.; Tomb, J.F.; Dougherty, B.A.; Merrick, J.M.; et al. Whole-genome random sequencing and assembly of Haemophilus influenzae Rd. Science 1995, 269, 496–512. [Google Scholar] [CrossRef]
- Orth, J.D.; Thiele, I.; Palsson, B.O. What is flux balance analysis? Nat. Biotechnol. 2010, 28, 245–248. [Google Scholar] [CrossRef]
- Gomez, J.A.; Hoffner, K.; Barton, P.I. DFBAlab: A fast and reliable MATLAB code for dynamic flux balance analysis. BMC Bioinform. 2014, 15, 409. [Google Scholar] [CrossRef]
- Seaver, S.M.D.; Liu, F.; Zhang, Q.Z.; Jeffryes, J.; Faria, J.P.; Edirisinghe, J.N.; Mundy, M.; Chia, N.; Noor, E.; Beber, M.E.; et al. The ModelSEED Biochemistry Database for the integration of metabolic annotations and the reconstruction, comparison and analysis of metabolic models for plants, fungi and microbes. Nucleic Acids Res. 2021, 49, D575–D588. [Google Scholar] [CrossRef] [PubMed]
- Chindelevitch, L.; Stanley, S.; Hung, D.; Regev, A.; Berger, B. MetaMerge: Scaling up genome-scale metabolic reconstructions with application to Mycobacterium tuberculosis. Genome Biol. 2012, 13, r6. [Google Scholar] [CrossRef] [PubMed]
- Lieven, C.; Beber, M.E.; Olivier, B.G.; Bergmann, F.T.; Ataman, M.; Babaei, P.; Bartell, J.A.; Blank, L.M.; Chauhan, S.; Correia, K.; et al. MEMOTE for standardized genome-scale metabolic model testing. Nat. Biotechnol. 2020, 38, 272–276. [Google Scholar] [CrossRef] [PubMed]
- Heirendt, L.; Arreckx, S.; Pfau, T.; Mendoza, S.N.; Richelle, A.; Heinken, A.; Haraldsdóttir, H.S.; Wachowiak, J.; Keating, S.M.; Vlasov, V.; et al. Creation and analysis of biochemical constraint-based models using the COBRA Toolbox v.3.0. Nat. Protoc. 2019, 14, 639–702. [Google Scholar] [CrossRef]
- Wang, H.; Marcisauskas, S.; Sanchez, B.J.; Domenzain, I.; Hermansson, D.; Agren, R.; Nielsen, J.; Kerkhoven, E.J. RAVEN 2.0: A versatile toolbox for metabolic network reconstruction and a case study on Streptomyces coelicolor. PLoS Comput. Biol. 2018, 14, e1006541. [Google Scholar] [CrossRef]
- Kanehisa, M.; Goto, S. KEGG: Kyoto Encyclopedia of Genes and Genomes. Nucleic Acids Res. 2000, 28, 27–30. [Google Scholar] [CrossRef]
- Caspi, R.; Foerster, H.; Fulcher, C.A.; Hopkinson, R.; Ingraham, J.; Kaipa, P.; Krummenacker, M.; Paley, S.; Pick, J.; Rhee, S.Y.; et al. MetaCyc: A multiorganism database of metabolic pathways and enzymes. Nucleic Acids Res. 2006, 34, D511–D516. [Google Scholar] [CrossRef]
- O’Brien, E.J.; Lerman, J.A.; Chang, R.L.; Hyduke, D.R.; Palsson, B.O. Genome-scale models of metabolism and gene expression extend and refine growth phenotype prediction. Mol. Syst. Biol. 2013, 9, 693. [Google Scholar] [CrossRef]
- Henry, C.S.; Jankowski, M.D.; Broadbelt, L.J.; Hatzimanikatis, V. Genome-Scale Thermodynamic Analysis of Escherichia coli Metabolism. Biophys. J. 2006, 90, 1453–1461. [Google Scholar] [CrossRef]
- Adadi, R.; Volkmer, B.; Milo, R.; Heinemann, M.; Shlomi, T. Prediction of Microbial Growth Rate versus Biomass Yield by a Metabolic Network with Kinetic Parameters. PLoS Comput. Biol. 2012, 8, e1002575. [Google Scholar] [CrossRef]
- Sanchez, B.J.; Zhang, C.; Nilsson, A.; Lahtvee, P.J.; Kerkhoven, E.J.; Nielsen, J. Improving the phenotype predictions of a yeast genome-scale metabolic model by incorporating enzymatic constraints. Mol. Syst. Biol. 2017, 13, 935. [Google Scholar] [CrossRef]
- Domenzain, I.; Sanchez, B.; Anton, M.; Kerkhoven, E.J.; Millan-Oropeza, A.; Henry, C.; Siewers, V.; Morrissey, J.P.; Sonnenschein, N.; Nielsen, J. Reconstruction of a catalogue of genome-scale metabolic models with enzymatic constraints using GECKO 2.0. Nat. Commun. 2022, 13, 3766. [Google Scholar] [CrossRef]
- Khodayari, A.; Maranas, C.D. A genome-scale Escherichia coli kinetic metabolic model k-ecoli457 satisfying flux data for multiple mutant strains. Nat. Commun. 2016, 7, 13806. [Google Scholar] [CrossRef]
- Andreozzi, S.; Miskovic, L.; Hatzimanikatis, V. iSCHRUNK: In silico approach to characterization and reduction of uncertainty in the kinetic models of genome-scale metabolic networks. Metab. Eng. 2016, 33, 158–168. [Google Scholar] [CrossRef]
- Huang, Z.R.; Yoon, S. Integration of Time-Series Transcriptomic Data with Genome-Scale CHO Metabolic Models for mAb Engineering. Processes 2020, 8, 331. [Google Scholar] [CrossRef]
- Wang, G.; Haringa, C.; Noorman, H.; Chu, J.; Zhuang, Y.P. Developing a Computational Framework To Advance Bioprocess Scale-Up. Trends Biotechnol. 2020, 38, 846–856. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, X.B.; Luo, Z.H. A CFD-PBM Coupled Method to Optimize a Pilot-Scale Stirred Bioreactor. Ind. Eng. Chem. Res. 2022, 61, 8302–8312. [Google Scholar] [CrossRef]
- Lapin, A.; Muller, D.; Reuss, M. Dynamic behavior of microbial populations in stirred bioreactors simulated with Euler-Lagrange methods: Traveling along the lifelines of single cells. Ind. Eng. Chem. Res. 2004, 43, 4647–4656. [Google Scholar] [CrossRef]
- Seidel, S.; Maschke, R.W.; Werner, S.; Jossen, V.; Eibl, D. Oxygen Mass Transfer in Biopharmaceutical Processes: Numerical and Experimental Approaches. Chem. Ing. Tech. 2021, 93, 42–61. [Google Scholar]
- Kanwar, L.; Rathore, A.; Sarkar, J.; Loomba, V. CFD of mixing of multi-phase flow in a bioreactor using population balance model. Abstr. Pap. Am. Chem. Soc. 2017, 253, 613–628. [Google Scholar] [CrossRef]
- Morchain, J.; Gabelle, J.C.; Cockx, A. A Coupled Population Balance Model and CFD Approach for the Simulation of Mixing Issues in Lab-Scale and Industrial Bioreactors. AIChE J. 2014, 60, 27–40. [Google Scholar] [CrossRef]
- Pigou, M.; Morchain, J. Investigating the interactions between physical and biological heterogeneities in bioreactors using compartment, population balance and metabolic models. Chem. Eng. Sci. 2015, 126, 267–282. [Google Scholar] [CrossRef]
- Karimian, E.; Motamedian, E. ACBM: An Integrated Agent and Constraint Based Modeling Framework for Simulation of Microbial Communities. Sci. Rep. 2020, 10, 8695. [Google Scholar] [CrossRef] [PubMed]
- Lapin, A.; Klann, M.; Reuss, M. Multi-Scale Spatio-Temporal Modeling: Lifelines of Microorganisms in Bioreactors and Tracking Molecules in Cells. Biosyst. Eng. II 2010, 121, 23–43. [Google Scholar] [CrossRef]
- Du, Y.H.; Tong, L.L.; Wang, Y.; Liu, M.Z.; Yuan, L.; Mu, X.Y.; He, S.J.; Wei, S.X.; Zhang, Y.D.; Chen, Z.L.; et al. Development of a kinetics-integrated CFD model for the industrial scale-up of DHA fermentation using Schizochytrium sp. AIChE J. 2022, 68, e17750. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Z.J.; Xia, J.Y.; Haringa, C.; Liu, Y.P.; Chu, J.; Zhuang, Y.P.; Zhang, S.L. Application of Euler-Lagrange CFD for quantitative evaluating the effect of shear force on Carthamus tinctorius L. cell in a stirred tank bioreactor. Biochem. Eng. J. 2016, 114, 212–220. [Google Scholar] [CrossRef]
- Haringa, C.; Tang, W.J.; Wang, G.; Deshmukh, A.T.; van Winden, W.A.; Chu, J.; van Gulik, W.M.; Heijnen, J.J.; Mudde, R.F.; Noorman, H.J. Computational fluid dynamics simulation of an industrial P. chrysogenum fermentation with a coupled 9-pool metabolic model: Towards rational scale-down and design optimization. Chem. Eng. Sci. 2018, 175, 12–24. [Google Scholar] [CrossRef]
- Haringa, C.; Tang, W.J.; Noorman, H.J. Stochastic parcel tracking in an Euler-Lagrange compartment model for fast simulation of fermentation processes. Biotechnol. Bioeng. 2022, 119, 1849–1860. [Google Scholar] [CrossRef]
- Kuschel, M.; Fitschen, J.; Hoffmann, M.; von Kameke, A.; Schlüter, M.; Wucherpfennig, T. Validation of Novel Lattice Boltzmann Large Eddy Simulations (LB LES) for Equipment Characterization in Biopharma. Processes 2021, 9, 950. [Google Scholar] [CrossRef]
- Haringa, C. An analysis of organism lifelines in an industrial bioreactor using Lattice-Boltzmann CFD. Eng. Life Sci. 2022, 23, e2100159. [Google Scholar] [CrossRef]
- Witz, C.; Treffer, D.; Hardiman, T.; Khinast, J. Local gas holdup simulation and validation of industrial-scale aerated bioreactors. Chem. Eng. Sci. 2016, 152, 636–648. [Google Scholar] [CrossRef]
- Li, M.; Lu, X.F.; Wang, X.D.; Lu, S.F.; Zhong, N. Biomedical classification application and parameters optimization of mixed kernel SVM based on the information entropy particle swarm optimization. Comput. Assist. Surg. 2016, 21, 133–142. [Google Scholar] [CrossRef]
- Li, Y.F.; Yuan, J.Q. Prediction of key state variables using support vector machines in bioprocesses. Chem. Eng. Technol. 2006, 29, 313–319. [Google Scholar] [CrossRef]
- Cui, J.L.; Wang, X.F. Bioprocess Soft Sensing Based on Multiple Kernel Support Vector Machine. In Proceedings of the 2011 Chinese Control and Decision Conference, Mianyang, China, 23–25 May 2011; pp. 3984–3988. [Google Scholar]
- Zhang, L.H.; Chao, B.; Zhang, X. Modeling and optimization of microbial lipid fermentation from cellulosic ethanol wastewater by Rhodotorula glutinis based on the support vector machine. Bioresour. Technol. 2020, 301, 122781. [Google Scholar] [CrossRef]
- Gao, X.J.; Pu, W.; Qi, Y.S.; Zhang, Y.T.; Zhang, H.Q.; Yan, A.J. An Optimal Control Strategy Combining SVM with RGA for Improving Fermentation Titer. Chin. J. Chem. Eng. 2010, 18, 95–101. [Google Scholar] [CrossRef]
- Robles-Rodriguez, C.E.; Bideaux, C.; Roux, G.; Molina-Jouve, C.; Aceves-Lara, C.A. Soft-Sensors for Lipid Fermentation Variables Based on PSO Support Vector Machine (PSO-SVM). Adv. Intell. Syst. 2016, 474, 175–183. [Google Scholar] [CrossRef]
- Urtubia, A.; Leon, R.; Vargas, M. Identification of chemical markers to detect abnormal wine fermentation using support vector machines. Comput. Chem. Eng. 2021, 145, 107158. [Google Scholar] [CrossRef]
- Peng, J.; Meng, F.; Ai, Y. Time-dependent fermentation control strategies for enhancing synthesis of marine bacteriocin 1701 using artificial neural network and genetic algorithm. Bioresour. Technol. 2013, 138, 345–352. [Google Scholar] [CrossRef]
- Zhang, A.H.; Zhu, K.Y.; Zhuang, X.Y.; Liao, L.X.; Huang, S.Y.; Yao, C.Y.; Fang, B.S. A robust soft sensor to monitor 1,3-propanediol fermentation process by Clostridium butyricum based on artificial neural network. Biotechnol. Bioeng. 2020, 117, 3345–3355. [Google Scholar] [CrossRef]
- Ding, Y.H.; Liu, G.H.; Dai, X.Z. Soft-sensing method based on modified ANN inversion and its application in erythromycin fermentation. In Proceedings of the IEEE International Conference on Information and Automation, Shenyang, China, 6–8 June 2012; pp. 900–905. [Google Scholar]
- Guselnikova, O.; Trelin, A.; Skvortsova, A.; Ulbrich, P.; Postnikov, P.; Pershina, A.; Sykora, D.; Svorcik, V.; Lyutakov, O. Label-free surface-enhanced Raman spectroscopy with artificial neural network technique for recognition photoinduced DNA damage. Biosens. Bioelectron. 2019, 145, 111718. [Google Scholar] [CrossRef]
- Antwi, P.; Li, J.Z.; Boadi, P.O.; Meng, J.; Shi, E.; Deng, K.W.; Bondinuba, F.K. Estimation of biogas and methane yields in an UASB treating potato starch processing wastewater with backpropagation artificial neural network. Bioresour. Technol. 2017, 228, 106–115. [Google Scholar] [CrossRef] [PubMed]
- Ding, J.; Jia, L.; Mpofu, E.; Gao, M.; Ren, X. An on-line adaptive glucose feeding system incorporating patterns recognition for glucose concentration control in glutamate fermentations. Biotechnool. Bioproc. Eng. 2016, 21, 758–766. [Google Scholar] [CrossRef]
- Beznik, T.; Smyth, P.; de Lannoy, G.; Lee, J.A. Deep learning to detect bacterial colonies for the production of vaccines. Neurocomputing 2022, 470, 427–431. [Google Scholar] [CrossRef]
- Senior, A.W.; Evans, R.; Jumper, J.; Kirkpatrick, J.; Sifre, L.; Green, T.; Qin, C.L.; Zidek, A.; Nelson, A.W.R.; Bridgland, A.; et al. Improved protein structure prediction using potentials from deep learning. Nature 2020, 577, 706–710. [Google Scholar] [CrossRef]
- Bao, Y.; Wang, B.; Guo, P.D.; Wang, J.T. Chemical process fault diagnosis based on a combined deep learning method. Can. J. Chem. Eng. 2022, 100, 54–66. [Google Scholar] [CrossRef]
- Beiroti, A.; Hosseini, S.N.; Aghasadeghi, M.R.; Norouzian, D. Comparative study of mu-stat methanol feeding control in fed-batch fermentation of Pichia pastoris producing HBsAg: An open-loop control versus recurrent artificial neural network-based feedback control. J. Chem. Technol. Biot. 2019, 94, 3924–3931. [Google Scholar] [CrossRef]
- Beiroti, A.; Aghasadeghi, M.R.; Hosseini, S.N.; Norouzian, D. Application of recurrent neural network for online prediction of cell density of recombinant Pichia pastoris producing HBsAg. Prep. Biochem. Biotechnol. 2019, 49, 352–359. [Google Scholar] [CrossRef]
- Yuan, X.; Li, L.; Wang, Y. Nonlinear Dynamic Soft Sensor Modeling With Supervised Long Short-Term Memory Network. IEEE Trans. Ind. Inform. 2020, 16, 3168–3176. [Google Scholar] [CrossRef]
- Tulsyan, A.; Garvin, C.; Undey, C. Advances in industrial biopharmaceutical batch process monitoring: Machine-learning methods for small data problems. Biotechnol. Bioeng. 2018, 115, 1915–1924. [Google Scholar] [CrossRef]
- Wang, X.; Liu, H.; Li, L.; Zhang, Y. Dual adversarial learning-based virtual sample generation method for data expansion of soft senors. Measurement 2022, 198, 111409. [Google Scholar] [CrossRef]
- Mei, C.L.; Yang, M.; Shu, D.X.; Jiang, H.; Liu, G.H.; Liao, Z.L. Soft Sensor Based on Gaussian Process Regression and Its Application in Erythromycin Fermentation Process. Chem. Ind. Chem. Eng. Q. 2016, 22, 127–135. [Google Scholar] [CrossRef]
- Bradford, E.; Imsland, L.; Zhang, D.D.; Chanona, E.A.D. Stochastic data-driven model predictive control using gaussian processes. Comput. Chem. Eng. 2020, 139, 106844. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Mowbray, M.; Petsagkourakis, R.; del Rio-Chanona, E.A.; Zhang, D. Safe chance constrained reinforcement learning for batch process control. Comput. Chem. Eng. 2022, 157, 107630. [Google Scholar] [CrossRef]
- Mowbray, M.; Smith, R.; Del Rio-Chanona, E.A.; Zhang, D.D. Using process data to generate an optimal control policy via apprenticeship and reinforcement learning. AIChE J. 2021, 67, e17306. [Google Scholar] [CrossRef]
- Li, D.Z.; Zhu, F.Q.; Wang, X.; Jin, Q.B. Multi-objective reinforcement learning for fed-batch fermentation process control. J. Process. Contr. 2022, 115, 89–99. [Google Scholar] [CrossRef]
- Pandian, B.J.; Noel, M.M. Control of a bioreactor using a new partially supervised reinforcement learning algorithm. J. Process. Contr. 2018, 69, 16–29. [Google Scholar] [CrossRef]
- Lu, S.W.; Lee, J.H.; You, F.Q. Soft-constrained model predictive control based on data-driven distributionally robust optimization. AIChE J. 2020, 66, e16546. [Google Scholar] [CrossRef]
- Kim, J.W.; Park, B.J.; Oh, T.H.; Lee, J.M. Model-based reinforcement learning and predictive control for two-stage optimal control of fed-batch bioreactor. Comput. Chem. Eng. 2021, 154, 107465. [Google Scholar] [CrossRef]
- Oh, T.H.; Park, H.M.; Kim, J.W.; Lee, J.M. Integration of reinforcement learning and model predictive control to optimize semi-batch bioreactor. AIChE J. 2022, 68, e17658. [Google Scholar] [CrossRef]
- Ma, Y.; Noreña-Caro, D.A.; Adams, A.J.; Brentzel, T.B.; Romagnoli, J.A.; Benton, M.G. Machine-learning-based simulation and fed-batch control of cyanobacterial-phycocyanin production in Plectonema by artificial neural network and deep reinforcement learning. Comput. Chem. Eng. 2020, 142, 107016. [Google Scholar] [CrossRef]
- Karimi Alavijeh, M.; Baker, I.; Lee, Y.Y.; Gras, S.L. Digitally enabled approaches for the scale up of mammalian cell bioreactors. Digit. Chem. Eng. 2022, 4, 100040. [Google Scholar] [CrossRef]
- Vega-Ramon, F.; Zhu, X.F.; Savage, T.R.; Petsagkourakis, P.; Jing, K.J.; Zhang, D.D. Kinetic and hybrid modeling for yeast astaxanthin production under uncertainty. Biotechnol. Bioeng. 2021, 118, 4854–4866. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; Yuan, L.; Lu, H.; Li, G.; Chen, Y.; Engqvist, M.K.M.; Kerkhoven, E.J.; Nielsen, J. Deep learning-based kcat prediction enables improved enzyme-constrained model reconstruction. Nat. Catal. 2022, 5, 662–672. [Google Scholar] [CrossRef]
- Culley, C.; Vijayakumar, S.; Zampieri, G.; Angione, C. A mechanism-aware and multiomic machine-learning pipeline characterizes yeast cell growth. Proc. Natl. Acad. Sci. USA 2020, 117, 18869–18879. [Google Scholar]
- Ryu, J.Y.; Kim, H.U.; Lee, S.Y. Deep learning enables high-quality and high-throughput prediction of enzyme commission numbers. Proc. Natl. Acad. Sci. USA 2019, 116, 13996–14001. [Google Scholar]
- Yang, K.K.; Wu, Z.; Arnold, F.H. Machine-learning-guided directed evolution for protein engineering. Nat. Methods 2019, 16, 687–694. [Google Scholar] [CrossRef]
- Lawson, C.E.; Marti, J.M.; Radivojevic, T.; Jonnalagadda, S.V.R.; Gentz, R.; Hillson, N.J.; Peisert, S.; Kim, J.; Simmons, B.A.; Petzold, C.J.; et al. Machine learning for metabolic engineering: A review. Metab. Eng. 2021, 63, 34–60. [Google Scholar] [CrossRef]
- Yugi, K.; Nakayama, Y.; Kinoshita, A.; Tomita, M. Hybrid dynamic/static method for large-scale simulation of metabolism. Theor. Biol. Med. Model. 2005, 2, 42. [Google Scholar] [CrossRef]
- Gerken-Starepravo, L.; Zhu, X.; Cho, B.A.; Vega-Ramon, F.; Pennington, O.; Antonio del Río-Chanona, E.; Jing, K.; Zhang, D. An MIQP framework for metabolic pathways optimisation and dynamic flux analysis. Digit. Chem. Eng. 2022, 2, 100011. [Google Scholar] [CrossRef]
- Carinhas, N.; Bernal, V.; Teixeira, A.P.; Carrondo, M.J.T.; Alves, P.M.; Oliveira, R. Hybrid metabolic flux analysis: Combining stoichiometric and statistical constraints to model the formation of complex recombinant products. BMC Syst. Biol. 2011, 5, 34. [Google Scholar] [CrossRef]
- HamediRad, M.; Chao, R.; Weisberg, S.; Lian, J.Z.; Sinha, S.; Zhao, H.M. Towards a fully automated algorithm driven platform for biosystems design. Nat. Commun. 2019, 10, 5150. [Google Scholar] [CrossRef]
- Vigneshvar, S.; Sudhakumari, C.C.; Senthilkumaran, B.; Prakash, H. Recent Advances in Biosensor Technology for Potential Applications—An Overview. Front. Bioeng. Biotechnol. 2016, 4, 11. [Google Scholar] [CrossRef]
- Classen, J.; Aupert, F.; Reardon, K.F.; Solle, D.; Scheper, T. Spectroscopic sensors for in-line bioprocess monitoring in research and pharmaceutical industrial application. Anal. Bioanal. Chem. 2017, 409, 651–666. [Google Scholar] [CrossRef]
- Liu, G.H.; Jiang, H.; Xiao, X.H.; Zhang, D.J.; Mei, C.L.; Ding, Y.H. Determination of Process Variable pH in Solid-State Fermentation by FT-NIR Spectroscopy and Extreme Learning Machine (ELM). Spectrosc. Spect. Anal. 2012, 32, 970–973. [Google Scholar] [CrossRef]
- Kozma, B.; Hirsch, E.; Gergely, S.; Parta, L.; Pataki, H.; Salgo, A. On-line prediction of the glucose concentration of CHO cell cultivations by NIR and Raman spectroscopy: Comparative scalability test with a shake flask model system. J. Pharm. Biomed. 2017, 145, 346–355. [Google Scholar] [CrossRef]
- Mehdizadeh, H.; Lauri, D.; Karry, K.M.; Moshgbar, M.; Procopio-Melino, R.; Drapeau, D. Generic Raman-based calibration models enabling real-time monitoring of cell culture bioreactors. Biotechnol. Progr. 2015, 31, 1004–1013. [Google Scholar] [CrossRef]
- Zhang, D.D.; Savage, T.R.; Cho, B.A. Combining model structure identification and hybrid modelling for photo-production process predictive simulation and optimisation. Biotechnol. Bioeng. 2020, 117, 3356–3367. [Google Scholar] [CrossRef]
- Antonakoudis, A.; Strain, B.; Barbosa, R.; del Val, I.J.; Kontoravdi, C. Synergising stoichiometric modelling with artificial neural networks to predict antibody glycosylation patterns in Chinese hamster ovary cells. Comput. Chem. Eng. 2021, 154, 107471. [Google Scholar] [CrossRef]
- Zhu, X.L.; Rehman, K.U.; Wang, B.; Shahzad, M. Modern Soft-Sensing Modeling Methods for Fermentation Processes. Sensors 2020, 20, 1771. [Google Scholar] [CrossRef]
- Ding, J.; Cao, Y.; Mpofu, E.; Shi, Z.P. A hybrid support vector machine and fuzzy reasoning based fault diagnosis and rescue system for stable glutamate fermentation. Chem. Eng. Res. Des. 2012, 90, 1197–1207. [Google Scholar] [CrossRef]
- Yang, Q.; Yao, J.T.; Zhang, X.; Chao, X.J. FICA-PNN Fault Diagnosis for Penicillin Fermentation Process. In Proceedings of the 2011 30th Chinese Control Conference (CCC), Yantai, China, 22–24 July 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 4351–4354. [Google Scholar]
- Abbasi, M.A.; Khan, A.Q.; Mustafa, G.; Abid, M.; Khan, A.S.; Ullah, N. Data-Driven Fault Diagnostics for Industrial Processes: An Application to Penicillin Fermentation Process. IEEE Access 2021, 9, 65977–65987. [Google Scholar] [CrossRef]
- Yang, C.M.; Hou, J. Fed-batch fermentation penicillin process fault diagnosis and detection based on support vector machine. Neurocomputing 2016, 190, 117–123. [Google Scholar] [CrossRef]
- Oyetunde, T.; Liu, D.; Martin, H.G.; Tang, Y.J.J. Machine learning framework for assessment of microbial factory performance. PLoS ONE 2019, 14, e0210558. [Google Scholar] [CrossRef]
- Pinto, J.; de Azevedo, C.R.; Oliveira, R.; von Stosch, M. A bootstrap-aggregated hybrid semi-parametric modeling framework for bioprocess development. Bioproc. Biosyst. Eng. 2019, 42, 1853–1865. [Google Scholar] [CrossRef]
- Bayer, B.; Diaz, R.D.; Melcher, M.; Striedner, G.; Duerkop, M. Digital Twin Application for Model-Based DoE to Rapidly Identify Ideal Process Conditions for Space-Time Yield Optimization. Processes 2021, 9, 1109. [Google Scholar] [CrossRef]
- Kiran, A.U.M.; Jana, A.K. Control of continuous fed-batch fermentation process using neural network based model predictive controller. Bioproc. Biosyst. Eng. 2009, 32, 801–808. [Google Scholar] [CrossRef]
- Kuschel, M.; Siebler, F.; Takors, R. Lagrangian Trajectories to Predict the Formation of Population Heterogeneity in Large-Scale Bioreactors. Bioengineering 2017, 4, 27. [Google Scholar] [CrossRef]
- Bayer, B.; Duerkop, M.; Striedner, G.; Sissolak, B. Model Transferability and Reduced Experimental Burden in Cell Culture Process Development Facilitated by Hybrid Modeling and Intensified Design of Experiments. Front. Bioeng. Biotechnol. 2021, 9, 740215. [Google Scholar] [CrossRef]
- Yeoh, J.W.; Jayaraman, S.S.; Tan, S.G.; Jayaraman, P.; Holowko, M.B.; Zhang, J.; Kang, C.W.; Leo, H.L.; Poh, C.L. A model-driven approach towards rational microbial bioprocess optimization. Biotechnol. Bioeng. 2021, 118, 305–318. [Google Scholar] [CrossRef]
- Brunk, E.; George, K.W.; Alonso-Gutierrez, J.; Thompson, M.; Baidoo, E.; Wang, G.; Petzold, C.J.; McCloskey, D.; Monk, J.; Yang, L.; et al. Characterizing Strain Variation in Engineered E. coli Using a Multi-Omics-Based Workflow. Cell Syst. 2016, 2, 335–346. [Google Scholar] [CrossRef]
- Zampieri, G.; Vijayakumar, S.; Yaneske, E.; Angione, C. Machine and deep learning meet genome-scale metabolic modeling. PLoS Comput. Biol. 2019, 15, e1007084. [Google Scholar] [CrossRef]
- Dickinson, Q.; Aufschnaiter, A.; Ott, M.; Meyer, J.G. Multi-omic integration by machine learning (MIMaL). Bioinformatics 2022, 38, 4908–4918. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Mohsin, A.; Sun, Y.; Li, C.; Zhuang, Y.; Wang, G. From Spatial-Temporal Multiscale Modeling to Application: Bridging the Valley of Death in Industrial Biotechnology. Bioengineering 2023, 10, 744. https://doi.org/10.3390/bioengineering10060744
Wang X, Mohsin A, Sun Y, Li C, Zhuang Y, Wang G. From Spatial-Temporal Multiscale Modeling to Application: Bridging the Valley of Death in Industrial Biotechnology. Bioengineering. 2023; 10(6):744. https://doi.org/10.3390/bioengineering10060744
Chicago/Turabian StyleWang, Xueting, Ali Mohsin, Yifei Sun, Chao Li, Yingping Zhuang, and Guan Wang. 2023. "From Spatial-Temporal Multiscale Modeling to Application: Bridging the Valley of Death in Industrial Biotechnology" Bioengineering 10, no. 6: 744. https://doi.org/10.3390/bioengineering10060744
APA StyleWang, X., Mohsin, A., Sun, Y., Li, C., Zhuang, Y., & Wang, G. (2023). From Spatial-Temporal Multiscale Modeling to Application: Bridging the Valley of Death in Industrial Biotechnology. Bioengineering, 10(6), 744. https://doi.org/10.3390/bioengineering10060744








