Semantic Segmentation of Medical Images Based on Runge–Kutta Methods
Abstract
1. Introduction
- We abandoned the encoder–decoder structure and considered the design of the segmentation network holistically from the dynamical systems perspective.
- We introduced RK methods into the segmentation network and inventively used various dimensions within one time step of RK methods.
- We proposed a novel segmentation network architecture called RKSeg.
1.1. Related Work
1.1.1. Segmentation Networks
1.1.2. RKCNNs
2. Materials and Methods
2.1. Architecture of RKSegs
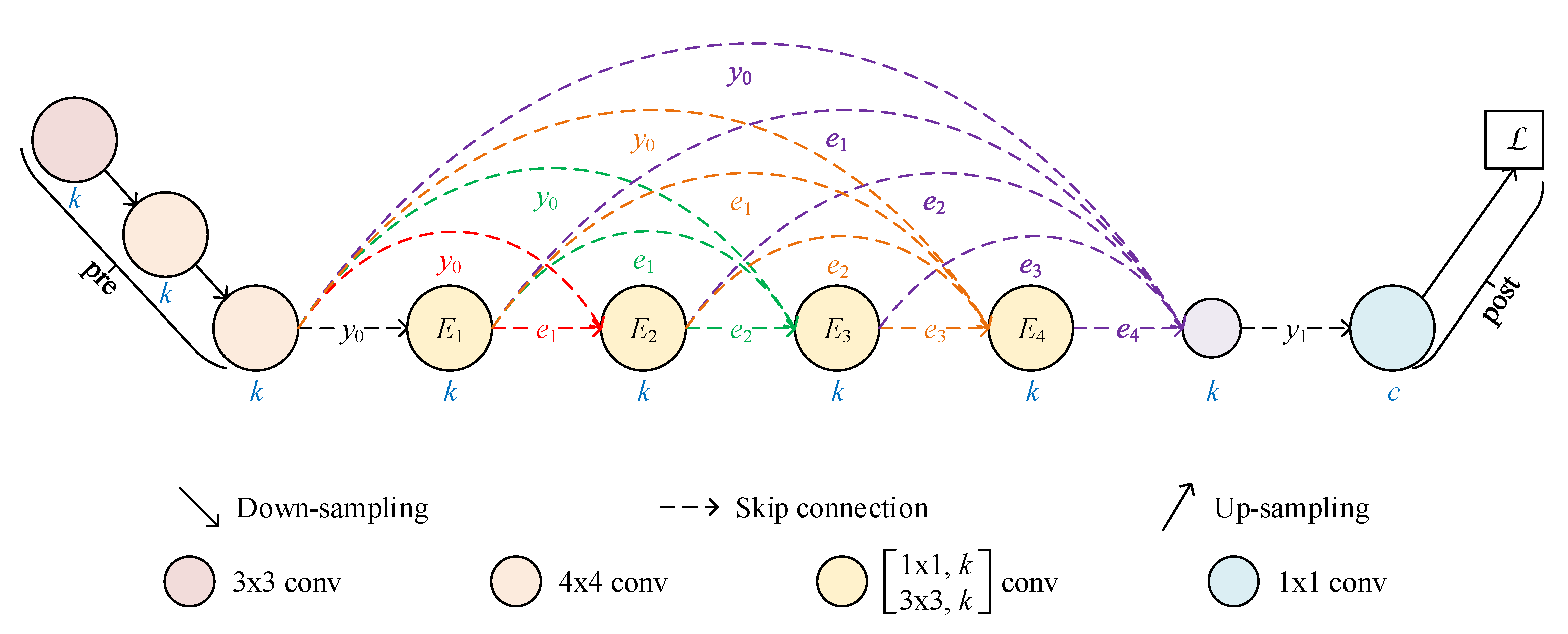
2.1.1. RKCNN-Based FCN
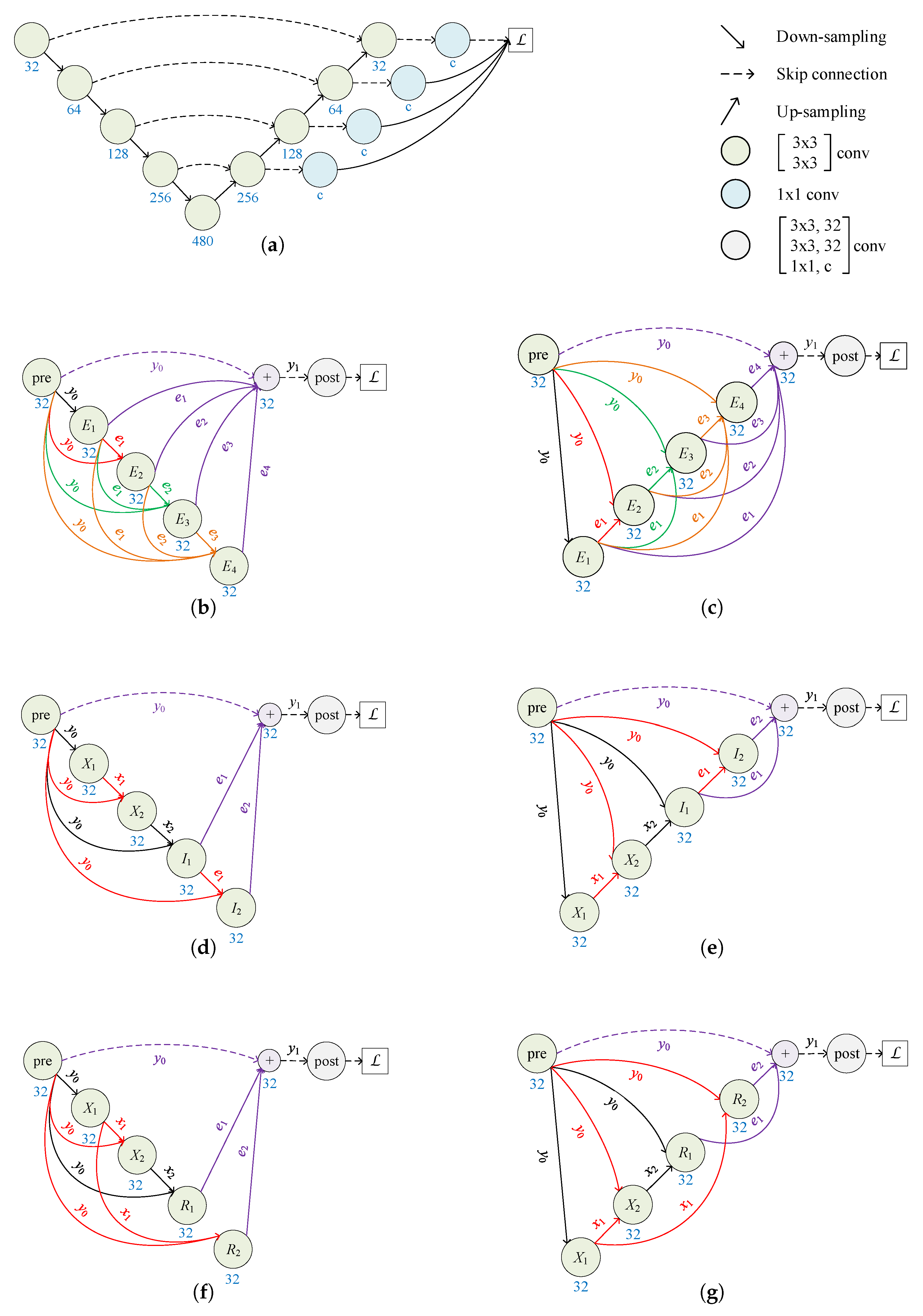
2.1.2. From FCN to RKSeg
2.1.3. More Variants
2.2. Experiments
3. Results
3.1. Comparison of Backbones
3.2. Compared to State-of-the-Art Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MNIST | Modified National Institute of Standards and Technology |
| MSD | Medical Segmentation Decathlon |
| RK | Runge–Kutta |
| ODE | Ordinary Differential Equation |
| MRI | Magnetic Resonance Imaging |
| CT | Computerized Tomography |
Appendix A
| Math Symbols | Introduction |
|---|---|
| t | A scalar representing time. |
| y | A vector representing the state of a dynamical system. |
| y is a function of t. | |
| The rate of change of the system state. | |
| The nth moment. | |
| The initial time. | |
| The system state at . | |
| An approximation of . | |
| The initial state of the system. | |
| h | The size of the time step from to . |
| s | The stages of RK methods. |
| The slope in the ith stage. | |
| A coefficient of RK methods. It indicates the dependence of the stages on the derivatives found at other stages. | |
| A coefficient of RK methods. All are quadrature weights, showing how the final result depends on the derivatives computed at the various stages. | |
| A coefficient of RK methods. It indicates the position of the stage value within the time step. | |
| The weighted average of as the estimated slope. | |
| The increment of the system state after the duration h. | |
| The weighted increment of the ith stage. | |
| It stands for . | |
| The initial value of in RKCNN-I and RKCNN-R. | |
| The convolutional subnetwork to get in RKCNN-E. | |
| The convolutional subnetwork to get in RKCNN-I or RKCNN-R. | |
| The convolutional subnetwork to get in RKCNN-I. | |
| The convolutional subnetwork to get in RKCNN-R. | |
| m | The number of convolution filters. It is variable. |
| k | The number of convolution filters. It is constant. |
| c | The number of classes. |
References
- Long, M.; Peng, F.; Zhu, Y. Identifying natural images and computer generated graphics based on binary similarity measures of PRNU. Multi. Tools Appl. 2019, 78, 489–506. [Google Scholar] [CrossRef]
- Chen, C.; Li, K.; Teo, S.G.; Zou, X.; Li, K.; Zeng, Z. Citywide traffic flow prediction based on multiple gated spatio-temporal convolutional neural networks. ACM Trans. Knowl. Discov. Data TKDD 2020, 14, 1–23. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, D.; Tang, Q.; Tang, S.; Yang, K. Local and nonlocal constraints for compressed sensing video and multi-view image recovery. Neurocomputing 2020, 406, 34–48. [Google Scholar] [CrossRef]
- Cao, D.; Ren, X.; Zhu, M.; Song, W. Visual question answering research on multi-layer attention mechanism based on image target features. Hum.-Centr. Comput. Inform. Sci. 2021, 11, 11. [Google Scholar] [CrossRef]
- Bu, H.; Kim, N.; Kim, S. Content-based image retrieval using a combination of texture and color features. Hum.-Centr. Comput. Inform. Sci. 2021, 11, 23. [Google Scholar] [CrossRef]
- Bibi, S.; Abbasi, A.; Haq, I.U.; Baik, S.W.; Ullah, A. Digital Image Forgery Detection Using Deep Autoencoder and CNN Features. Hum.-Centr. Comput. Inform. Sci. 2021, 11, 32. [Google Scholar] [CrossRef]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar] [CrossRef]
- Ronneberger, O.; Fischer, P.; Brox, T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention—MICCAI 2015, Munich, Germany, 5–9 October 2015; Navab, N., Hornegger, J., Wells, W.M., Frangi, A.F., Eds.; Springer: Cham, Switzerland, 2015; pp. 234–241. [Google Scholar] [CrossRef]
- Zhou, Z.; Rahman Siddiquee, M.M.; Tajbakhsh, N.; Liang, J. UNet++: A Nested U-Net Architecture for Medical Image Segmentation. In Proceedings of the Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support; Stoyanov, D., Taylor, Z., Carneiro, G., Syeda-Mahmood, T., Martel, A., Maier-Hein, L., Tavares, J.M.R., Bradley, A., Papa, J.P., Belagiannis, V., et al., Eds.; Springer: Cham, Switzerland, 2018; pp. 3–11. [Google Scholar] [CrossRef]
- Huang, H.; Lin, L.; Tong, R.; Hu, H.; Zhang, Q.; Iwamoto, Y.; Han, X.; Chen, Y.W.; Wu, J. UNet 3+: A Full-Scale Connected UNet for Medical Image Segmentation. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 1055–1059. [Google Scholar] [CrossRef]
- Weinan, E. A Proposal on Machine Learning via Dynamical Systems. Commun. Math. Stat. 2017, 5, 1–11. [Google Scholar] [CrossRef]
- Haber, E.; Ruthotto, L.; Holtham, E.; Jun, S.H. Learning Across Scales—Multiscale Methods for Convolution Neural Networks. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LO, USA, 2–7 February 2018; Volume 32. [Google Scholar] [CrossRef]
- Chang, B.; Meng, L.; Haber, E.; Ruthotto, L.; Begert, D.; Holtham, E. Reversible Architectures for Arbitrarily Deep Residual Neural Networks. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LO, USA, 2–7 February 2018; Volume 32. [Google Scholar] [CrossRef]
- Chang, B.; Meng, L.; Haber, E.; Tung, F.; Begert, D. Multi-level Residual Networks from Dynamical Systems View. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Lu, Y.; Zhong, A.; Li, Q.; Dong, B. Beyond Finite Layer Neural Networks: Bridging Deep Architectures and Numerical Differential Equations. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; Dy, J., Krause, A., Eds.; PMLR: Stockholm Sweden, 2018. Volume 80: Proceedings of Machine Learning Research. pp. 3276–3285. [Google Scholar]
- Zhu, M.; Chang, B.; Fu, C. Convolutional neural networks combined with Runge–Kutta methods. Neur. Comput. Appl. 2023, 35, 1629–1643. [Google Scholar] [CrossRef]
- Butcher, J.C. Numerical Differential Equation Methods. In Numerical Methods for Ordinary Differential Equations; John Wiley & Sons Ltd.: Chichester, UK, 2008; Chapter 2; pp. 51–135. [Google Scholar] [CrossRef]
- Simpson, A.L.; Antonelli, M.; Bakas, S.; Bilello, M.; Farahani, K.; Van Ginneken, B.; Kopp-Schneider, A.; Landman, B.A.; Litjens, G.; Menze, B.; et al. A large annotated medical image dataset for the development and evaluation of segmentation algorithms. arXiv 2019, arXiv:1902.09063. [Google Scholar] [CrossRef]
- Antonelli, M.; Reinke, A.; Bakas, S.; Farahani, K.; Kopp-Schneider, A.; Landman, B.A.; Litjens, G.; Menze, B.; Ronneberger, O.; Summers, R.M.; et al. The medical segmentation decathlon. Nat. Commun. 2022, 13, 4128. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. In Proceedings of the International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar] [CrossRef]
- Jégou, S.; Drozdzal, M.; Vazquez, D.; Romero, A.; Bengio, Y. The One Hundred Layers Tiramisu: Fully Convolutional DenseNets for Semantic Segmentation. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1175–1183. [Google Scholar] [CrossRef]
- Isensee, F.; Jaeger, P.F.; Kohl, S.A.; Petersen, J.; Maier-Hein, K.H. nnU-Net: A self-configuring method for deep learning-based biomedical image segmentation. Nat. Methods 2021, 18, 203–211. [Google Scholar] [CrossRef]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Semantic image segmentation with deep convolutional nets and fully connected crfs. arXiv 2014, arXiv:1412.7062. [Google Scholar] [CrossRef]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. DeepLab: Semantic Image Segmentation with Deep Convolutional Nets, Atrous Convolution, and Fully Connected CRFs. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 834–848. [Google Scholar] [CrossRef]
- Chen, L.C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking atrous convolution for semantic image segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar] [CrossRef]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-Decoder with Atrous Separable Convolution for Semantic Image Segmentation. In Proceedings of the Computer Vision—ECCV 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Springer: Cham, Switzerland, 2018; pp. 833–851. [Google Scholar] [CrossRef]
- Butcher, J.C. Differential and Difference Equations. In Numerical Methods for Ordinary Differential Equations; John Wiley & Sons Ltd.: Chichester, UK, 2008; Chapter 1; pp. 1–49. [Google Scholar] [CrossRef]
- Süli, E.; Mayers, D.F. An Introduction to Numerical Analysis; Cambridge University Press: Cambridge, UK, 2003; pp. 351–352. [Google Scholar] [CrossRef]
- Netzer, Y.; Wang, T.; Coates, A.; Bissacco, A.; Wu, B.; Ng, A.Y. Reading Digits in Natural Images with Unsupervised Feature Learning. In Proceedings of the NIPS Workshop on Deep Learning and Unsupervised Feature Learning 2011, Granada, Spain, 16 December 2011. [Google Scholar]
- Krizhevsky, A. Learning Multiple Layers of Features from Tiny Images, Unpublished work. 2009.
- Butcher, J.C. Runge–Kutta Methods. In Numerical Methods for Ordinary Differential Equations; John Wiley & Sons Ltd.: Chichester, UK, 2008; Chapter 3; pp. 137–316. [Google Scholar] [CrossRef]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar] [CrossRef]

| Organs | Segmentation Target | Training Cases | Validation Cases | Testing Cases | Modality | Type |
|---|---|---|---|---|---|---|
| Brain | 1: edema | |||||
| 2: non-enhancing tumor | 387 | 97 | 266 | Multimodal multisite MRI data | 4D | |
| 3: enhancing tumor | ||||||
| Heart | left atrium | 16 | 4 | 10 | Mono-modal MRI | 3D |
| Liver | 1: liver | 104 | 27 | 70 | Portal venous phase CT | 3D |
| 2: cancer | ||||||
| Hippocampus | 1: anterior | 208 | 52 | 130 | Mono-modal MRI | 3D |
| 2: posterior | ||||||
| Prostate | 1: peripheral zone | 25 | 7 | 16 | Multimodal MR | 4D |
| 2: transition zone | ||||||
| Lung | cancer | 50 | 13 | 32 | CT | 3D |
| Pancreas | 1: pancreas | 224 | 57 | 139 | Portal venous phase CT | 3D |
| 2: cancer | ||||||
| Hepatic Vessel | 1: vessel | 242 | 61 | 140 | CT | 3D |
| 2: tumour | ||||||
| Spleen | spleen | 32 | 9 | 20 | CT | 3D |
| Colon | colon cancer primaries | 100 | 26 | 64 | CT | 3D |
| Heart | Prostate | ||||||
|---|---|---|---|---|---|---|---|
| Models | Backbones | Params | Left Atrium | Params | Peripheral Zone | Transition Zone | Mean |
| RKSeg-L | RKCNN-E | 0.28 | 0.9137 (0.9101 ± 0.0032) | 0.28 | 0.6642 (0.6522 ± 0.0105) | 0.8715 (0.8709 ± 0.0042) | 0.7678 (0.7615 ± 0.0068) |
| RKCNN-I | 0.22 | 0.8983 (0.8937 ± 0.0033) | 0.22 | 0.6430 (0.6392 ± 0.0071) | 0.8641 (0.8604 ± 0.0027) | 0.7535 (0.7498 ± 0.0040) | |
| RKCNN-R | 0.22 | 0.9028 (0.9008 ±0.0022) | 0.22 | 0.6563 (0.6510 ±0.0039) | 0.8703 (0.8663 ±0.0055) | 0.7633 (0.7587 ±0.0044) | |
| RKSeg-R | RKCNN-E | 0.28 | 0.9136 (0.9108 ± 0.0020) | 0.28 | 0.6608 (0.6486 ± 0.0088) | 0.8740 (0.8717 ± 0.0023) | 0.7674 (0.7602 ± 0.0051) |
| RKCNN-I | 0.22 | 0.9117 (0.9102 ± 0.0015) | 0.22 | 0.6553 (0.6382 ± 0.0144) | 0.8694 (0.8587 ± 0.0076) | 0.7624 (0.7485 ± 0.0104) | |
| RKCNN-R | 0.22 | 0.9086 (0.9060 ± 0.0029) | 0.22 | 0.6601 (0.6439 ±0.0115) | 0.8733 (0.8723 ± 0.0023) | 0.7667 (0.7581 ±0.0063) | |
| (a) Brain | ||||||
|---|---|---|---|---|---|---|
| Models | Params | Edema | Non-Enhancing Tumor | Enhancing Tumor | Mean | Time |
| nnU-Net [25] | 18.67 | 0.7876 () | 0.6046 () | 0.7527 () | 0.7150 () | 3:22:49 |
| UNet++ [9] | 24.00 | 0.7840 (0.7870 ± 0.0023) | 0.6084 () | 0.7580 (0.7578 ± 0.0004) | 0.7168 (0.7163 ± 0.0006) | 4:42:23 |
| UNet 3+ [10] | 11.98 | 0.6218 () | 0.4137 () | 0.4782 () | 0.5046 () | 22:01:57 |
| DeepLabv3+ [29] | 5.22 | 0.7820 () | 0.5737 () | 0.7235 () | 0.6931 () | 2:52:06 |
| FC-DenseNet56 [24] | 2.50 | 0.7773 () | 0.6045 () | 0.7556 () | 0.7124 () | 2:19:45 |
| RKSeg-L (ours) | 0.21 | 0.7865 () | 0.6091 () | 0.7628 () | 0.7194 () | 6:10:22 |
| RKSeg-R (ours) | 0.21 | 0.7787 () | 0.6092 (0.6061 ± 0.0024) | 0.7566 () | 0.7148 () | 2:42:23 |
| (b) Heart | ||||||
| Models | Params | Left Atrium | Time | |||
| nnU-Net [25] | 29.97 | 0.9191 (0.9190 ± 0.0001) | 2:29:16 | |||
| UNet++ [9] | 49.35 | 0.9138 () | 2:59:31 | |||
| UNet 3+ [10] | 18.13 | 0.6555 () | 36:17:41 | |||
| DeepLabv3+ [29] | 5.22 | 0.9000 () | 1:15:27 | |||
| FC-DenseNet56 [24] | 2.49 | 0.9230 () | 2:36:19 | |||
| RKSeg-L (ours) | 0.28 | 0.9137 () | 11:19:51 | |||
| RKSeg-R (ours) | 0.28 | 0.9136 () | 1:40:39 | |||
| (c) Liver | ||||||
| Models | Params | Liver | Cancer | Mean | Time | |
| nnU-Net [25] | 41.26 | 0.9586 (0.9563 ± 0.0017) | 0.5662 (0.5560 ± 0.0121) | 0.7624 (0.7562 ± 0.0064) | 2:33:14 | |
| UNet++ [9] | 86.77 | 0.9514 () | 0.4861 () | 0.7187 () | 4:42:29 | |
| UNet 3+ [10] | 25.01 | 0.0000 () | 0.0000 () | 0.0000 () | 55:50:10 | |
| DeepLabv3+ [29] | 5.22 | 0.9569 () | 0.5523 () | 0.7546 () | 1:32:43 | |
| FC-DenseNet56 [24] | 2.49 | 0.8545 () | 0.2645 () | 0.5595 () | 2:37:57 | |
| RKSeg-L (ours) | 0.35 | 0.9517 () | 0.5454 () | 0.7485 () | 17:22:25 | |
| RKSeg-R (ours) | 0.35 | 0.9461 () | 0.4597 () | 0.7029 () | 1:57:55 | |
| (d) Hippocampus | ||||||
| Models | Params | Anterior | Posterior | Mean | Time | |
| nnU-Net [25] | 1.93 | 0.8866 () | 0.8691 () | 0.8778 () | 1:06:31 | |
| UNet++ [9] | 2.21 | 0.8878 () | 0.8698 () | 0.8788 () | 1:19:40 | |
| UNet 3+ [10] | 2.07 | 0.8627 () | 0.8372 () | 0.8500 () | 4:11:23 | |
| DeepLabv3+ [29] | 5.22 | 0.8752 () | 0.8588 () | 0.8670 () | 1:03:57 | |
| FC-DenseNet56 [24] | 2.49 | 0.8932 (0.8922 ± 0.0008) | 0.8751 (0.8745 ± 0.0005) | 0.8841 (0.8833 ± 0.0006) | 2:15:51 | |
| RKSeg-L (ours) | 0.11 | 0.8894 () | 0.8731 () | 0.8813 () | 0:49:29 | |
| RKSeg-R (ours) | 0.11 | 0.8892 () | 0.8736 () | 0.8814 () | 0:49:21 | |
| (e) Prostate | ||||||
| Models | Params | Peripheral Zone | Transition Zone | Mean | Time | |
| nnU-Net [25] | 29.97 | 0.6747 () | 0.8827 () | 0.7787 () | 2:34:08 | |
| UNet++ [9] | 49.35 | 0.7129 () | 0.8855 (0.8842 ± 0.0012) | 0.7992 () | 3:03:04 | |
| UNet 3+ [10] | 18.15 | 0.5402 () | 0.8381 () | 0.6892 () | 36:37:15 | |
| DeepLabv3+ [29] | 5.22 | 0.6409 () | 0.8726 () | 0.7568 () | 1:29:24 | |
| FC-DenseNet56 [24] | 2.50 | 0.7149 (0.7026 ± 0.0090) | 0.8875 () | 0.8012 (0.7929 ± 0.0062) | 3:14:00 | |
| RKSeg-L (ours) | 0.28 | 0.6642 () | 0.8715 () | 0.7678 () | 11:31:27 | |
| RKSeg-R (ours) | 0.28 | 0.6608 () | 0.8740 () | 0.7674 () | 1:45:07 | |
| (f) Lung | ||||||
| Models | Params | Cancer | Time | |||
| nnU-Net [25] | 41.26 | 0.5620 () | 2:34:18 | |||
| UNet++ [9] | 86.77 | 0.4915 () | 4:15:01 | |||
| UNet 3+ [10] | 24.99 | 0.0000 () | 55:12:41 | |||
| DeepLabv3+ [29] | 5.22 | 0.5929 () | 1:18:37 | |||
| FC-DenseNet56 [24] | 2.49 | 0.4302 () | 2:21:04 | |||
| RKSeg-L (ours) | 0.35 | 0.5302 () | 17:09:48 | |||
| RKSeg-R (ours) | 0.35 | 0.5961 (0.5763 ± 0.0219) | 1:45:26 | |||
| (g) Pancreas | ||||||
| Models | Params | Pancreas | Cancer | Mean | Time | |
| nnU-Net [25] | 41.26 | 0.7418 (0.7434 ± 0.0015) | 0.3644 (0.3533 ± 0.0093) | 0.5531 (0.5484 ± 0.0039) | 2:40:00 | |
| UNet++ [9] | 86.77 | 0.6906 () | 0.3393 () | 0.5150 () | 4:23:14 | |
| UNet 3+ [10] | 25.01 | 0.0000 () | 0.0000 () | 0.0000 () | 55:29:29 | |
| DeepLabv3+ [29] | 5.22 | 0.6982 () | 0.2964 () | 0.4973 () | 1:24:22 | |
| FC-DenseNet56 [24] | 2.49 | 0.3575 () | 0.2067 () | 0.2821 () | 2:25:15 | |
| RKSeg-L (ours) | 0.35 | 0.7090 () | 0.3395 () | 0.5242 () | 17:13:50 | |
| RKSeg-R (ours) | 0.35 | 0.6798 () | 0.3193 () | 0.4995 () | 1:49:43 | |
| (h) Hepatic Vessel | ||||||
| Models | Params | Vessel | Tumour | Mean | Time | |
| nnU-Net [25] | 41.26 | 0.6631 (0.6603 ± 0.0026) | 0.6548 (0.6500 ± 0.0035) | 0.6590 (0.6552 ± 0.0027) | 2:38:24 | |
| UNet++ [9] | 86.77 | 0.6522 () | 0.6419 () | 0.6471 () | 4:20:34 | |
| UNet 3+ [10] | 25.01 | 0.1120 () | 0.2638 () | 0.1879 () | 55:24:44 | |
| DeepLabv3+ [29] | 5.22 | 0.6392 () | 0.6473 () | 0.6432 () | 1:23:00 | |
| FC-DenseNet56 [24] | 2.49 | 0.5923 () | 0.3963 () | 0.4943 () | 2:29:33 | |
| RKSeg-L (ours) | 0.35 | 0.6522 () | 0.6372 () | 0.6447 () | 17:13:56 | |
| RKSeg-R (ours) | 0.35 | 0.6475 () | 0.5971 () | 0.6223 () | 1:49:12 | |
| (i) Spleen | ||||||
| Models | Params | Spleen | Time | |||
| nnU-Net [25] | 41.26 | 0.9082 () | 2:27:17 | |||
| UNet++ [9] | 86.77 | 0.9101 () | 3:47:19 | |||
| UNet 3+ [10] | 24.99 | 0.5711 () | 54:49:08 | |||
| DeepLabv3+ [29] | 5.22 | 0.9228 () | 1:13:43 | |||
| FC-DenseNet56 [24] | 2.49 | 0.5632 () | 2:07:48 | |||
| RKSeg-L (ours) | 0.35 | 0.9222 () | 17:09:42 | |||
| RKSeg-R (ours) | 0.35 | 0.9171 (0.9165 ± 0.0006) | 1:41:05 | |||
| (j) Colon | ||||||
| Models | Params | Colon Cancer Primaries | Time | |||
| nnU-Net [25] | 41.26 | 0.2718 () | 2:32:09 | |||
| UNet++ [9] | 86.77 | 0.2088 () | 3:01:07 | |||
| UNet 3+ [10] | 24.99 | 0.0000 () | 36:55:21 | |||
| DeepLabv3+ [29] | 5.22 | 0.2082 () | 1:17:03 | |||
| FC-DenseNet56 [24] | 2.49 | 0.1496 () | 1:38:18 | |||
| RKSeg-L (ours) | 0.35 | 0.2960 (0.2857 ± 0.0122) | 17:07:55 | |||
| RKSeg-R (ours) | 0.35 | 0.2311 () | 1:43:32 | |||
| Models | Brain | Heart | Liver | Hippocampus | Prostate | Lung | Pancreas | Hepatic Vessel | Spleen | Colon |
|---|---|---|---|---|---|---|---|---|---|---|
| nnU-Net [25] | 2.93 | 5.60 | 42.25 | 0.42 | 0.93 | 24.18 | 8.82 | 6.16 | 8.07 | 7.53 |
| UNet++ [9] | 5.47 | 8.35 | 135.64 | 0.58 | 1.55 | 108.13 | 40.60 | 27.21 | 36.84 | 35.43 |
| UNet 3+ [10] | 5.62 | 8.85 | 136.35 | 0.64 | 1.75 | 111.54 | 40.41 | 27.77 | 37.60 | 35.21 |
| DeepLabv3+ [29] | 3.61 | 4.83 | 43.39 | 0.81 | 0.91 | 22.24 | 8.28 | 5.71 | 7.42 | 7.31 |
| FC-DenseNet56 [24] | 4.60 | 6.10 | 82.42 | 0.98 | 1.21 | 60.08 | 23.37 | 15.85 | 21.27 | 20.31 |
| RKSeg-L (ours) | 2.06 | 3.48 | 37.55 | 0.31 | 0.75 | 18.63 | 6.49 | 4.56 | 5.89 | 5.55 |
| RKSeg-R (ours) | 2.21 | 3.46 | 37.00 | 0.33 | 0.71 | 20.34 | 7.08 | 4.93 | 6.34 | 5.90 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, M.; Fu, C.; Wang, X. Semantic Segmentation of Medical Images Based on Runge–Kutta Methods. Bioengineering 2023, 10, 506. https://doi.org/10.3390/bioengineering10050506
Zhu M, Fu C, Wang X. Semantic Segmentation of Medical Images Based on Runge–Kutta Methods. Bioengineering. 2023; 10(5):506. https://doi.org/10.3390/bioengineering10050506
Chicago/Turabian StyleZhu, Mai, Chong Fu, and Xingwei Wang. 2023. "Semantic Segmentation of Medical Images Based on Runge–Kutta Methods" Bioengineering 10, no. 5: 506. https://doi.org/10.3390/bioengineering10050506
APA StyleZhu, M., Fu, C., & Wang, X. (2023). Semantic Segmentation of Medical Images Based on Runge–Kutta Methods. Bioengineering, 10(5), 506. https://doi.org/10.3390/bioengineering10050506






