Towards Informed Water Resources Planning and Management
Abstract
:1. Introduction
1.1. Management under Stationary Conditions
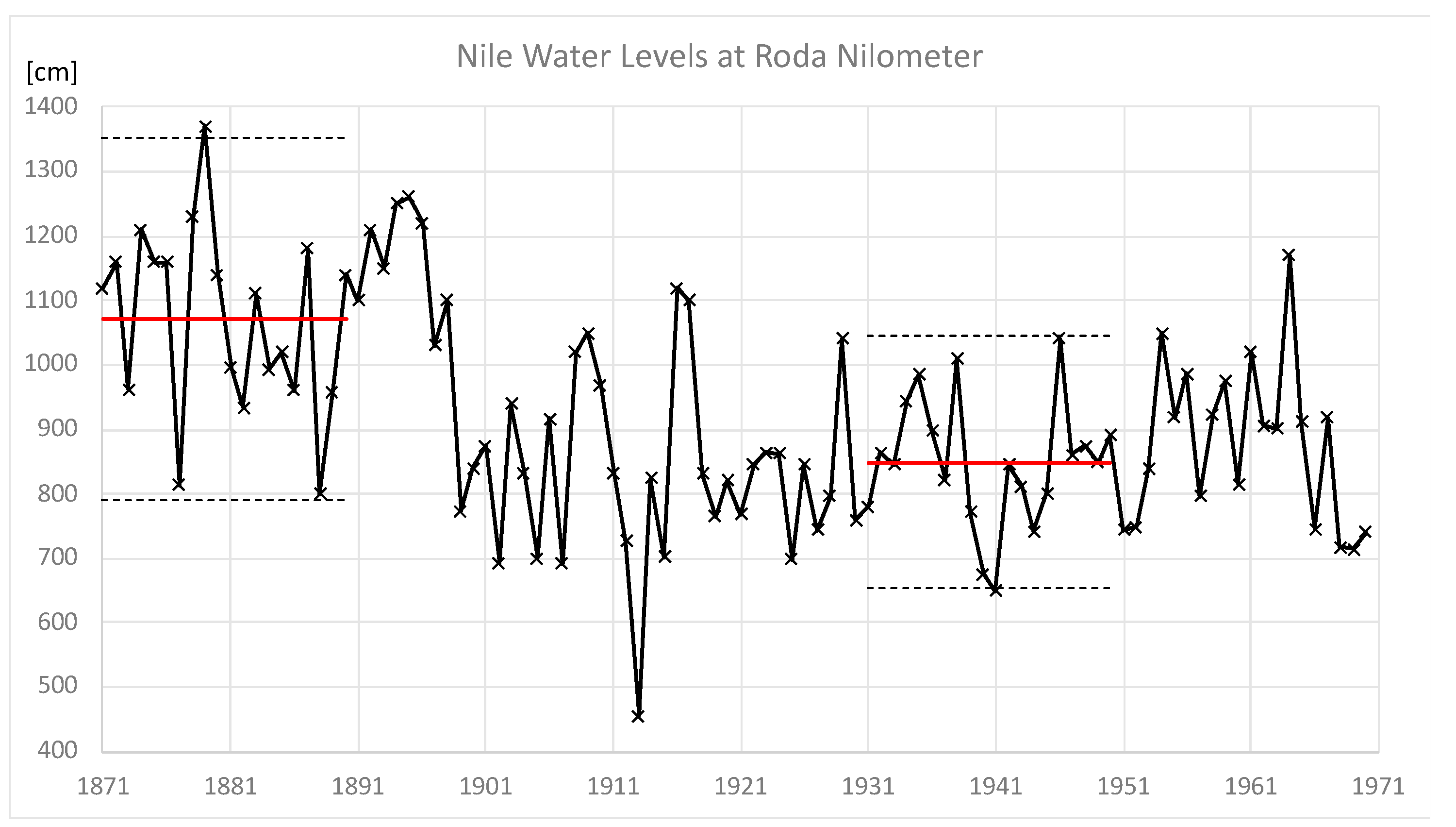
1.2. Management under Non-Stationary Conditions
2. Basic Concepts
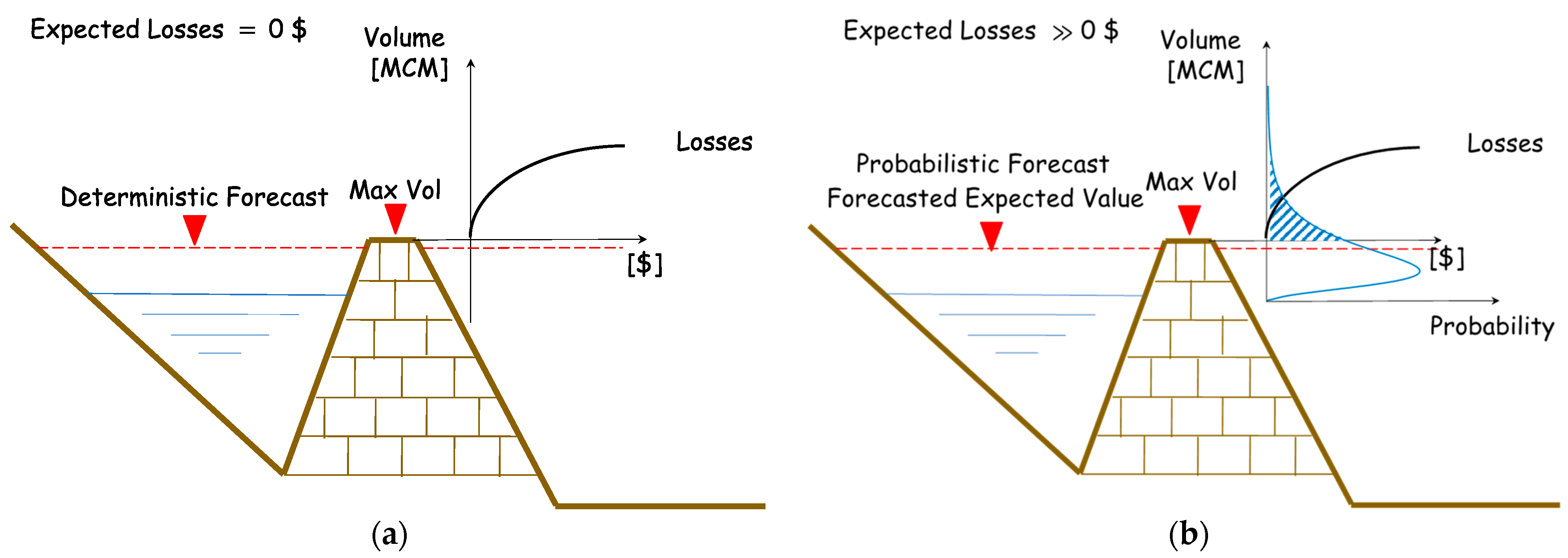
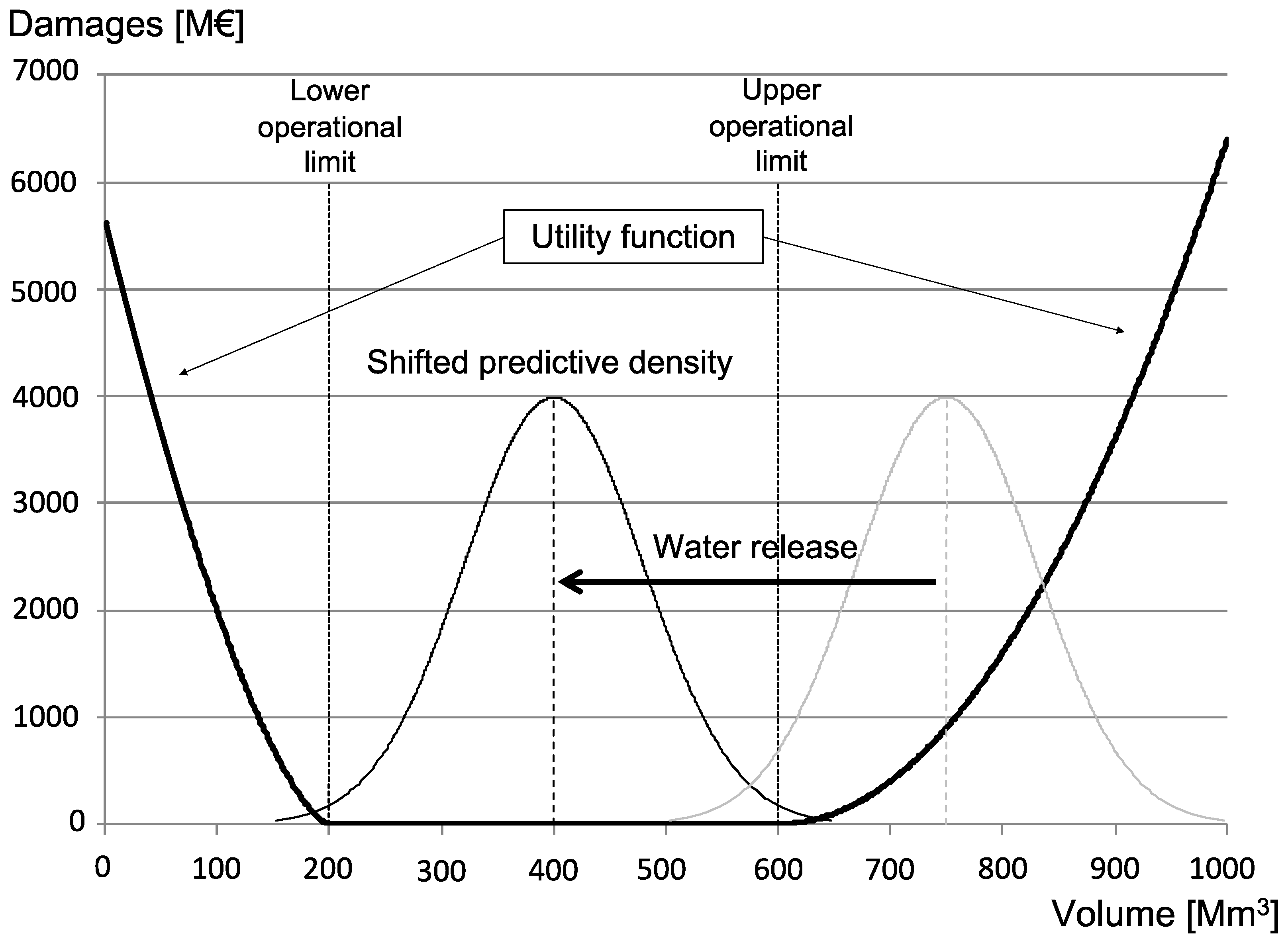
2.1. Decisions under Uncertainty
2.2. The Mathematical Representation of Knowledge
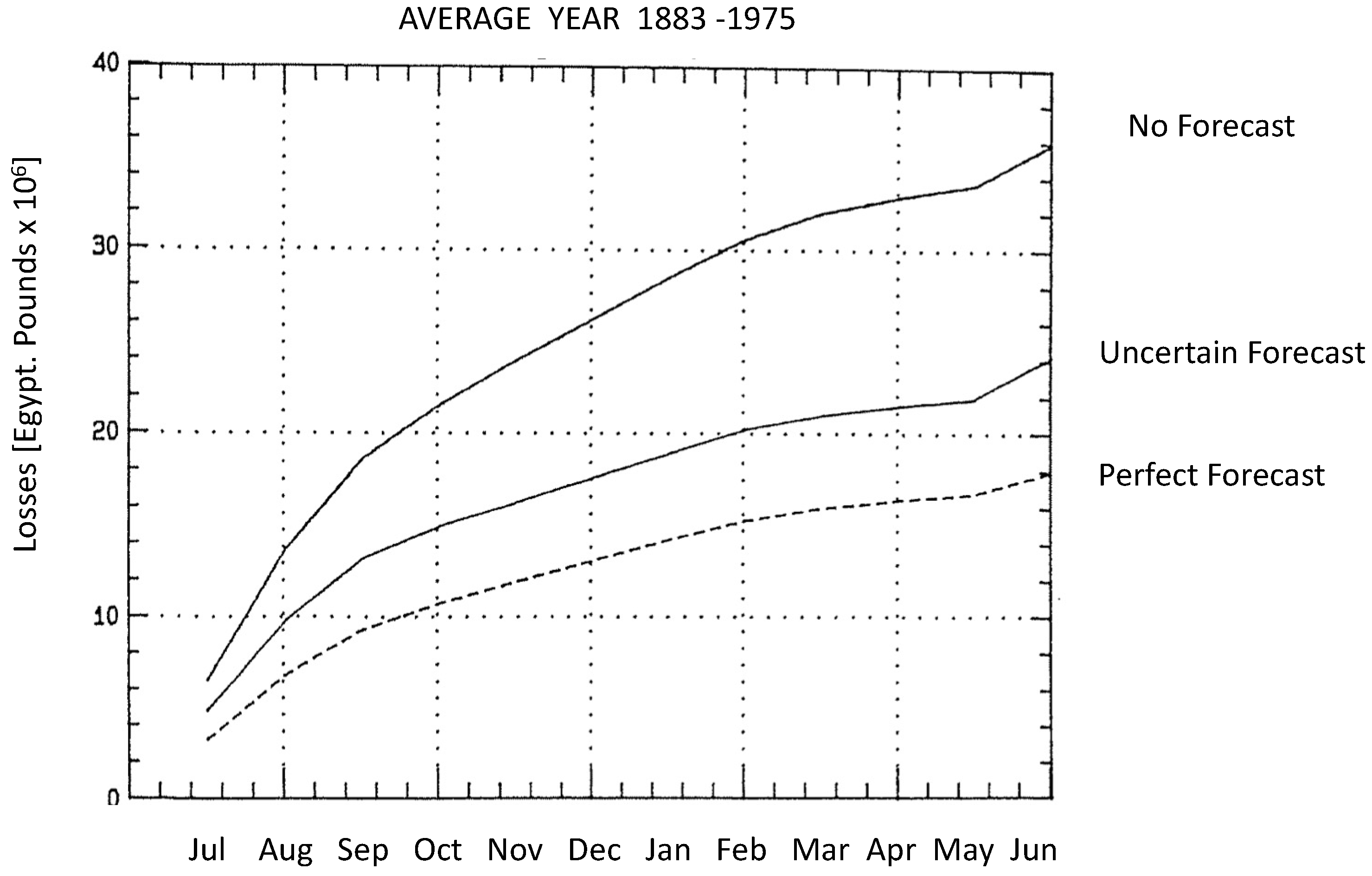
2.3. Deterministic versus Probabilistic Forecasts
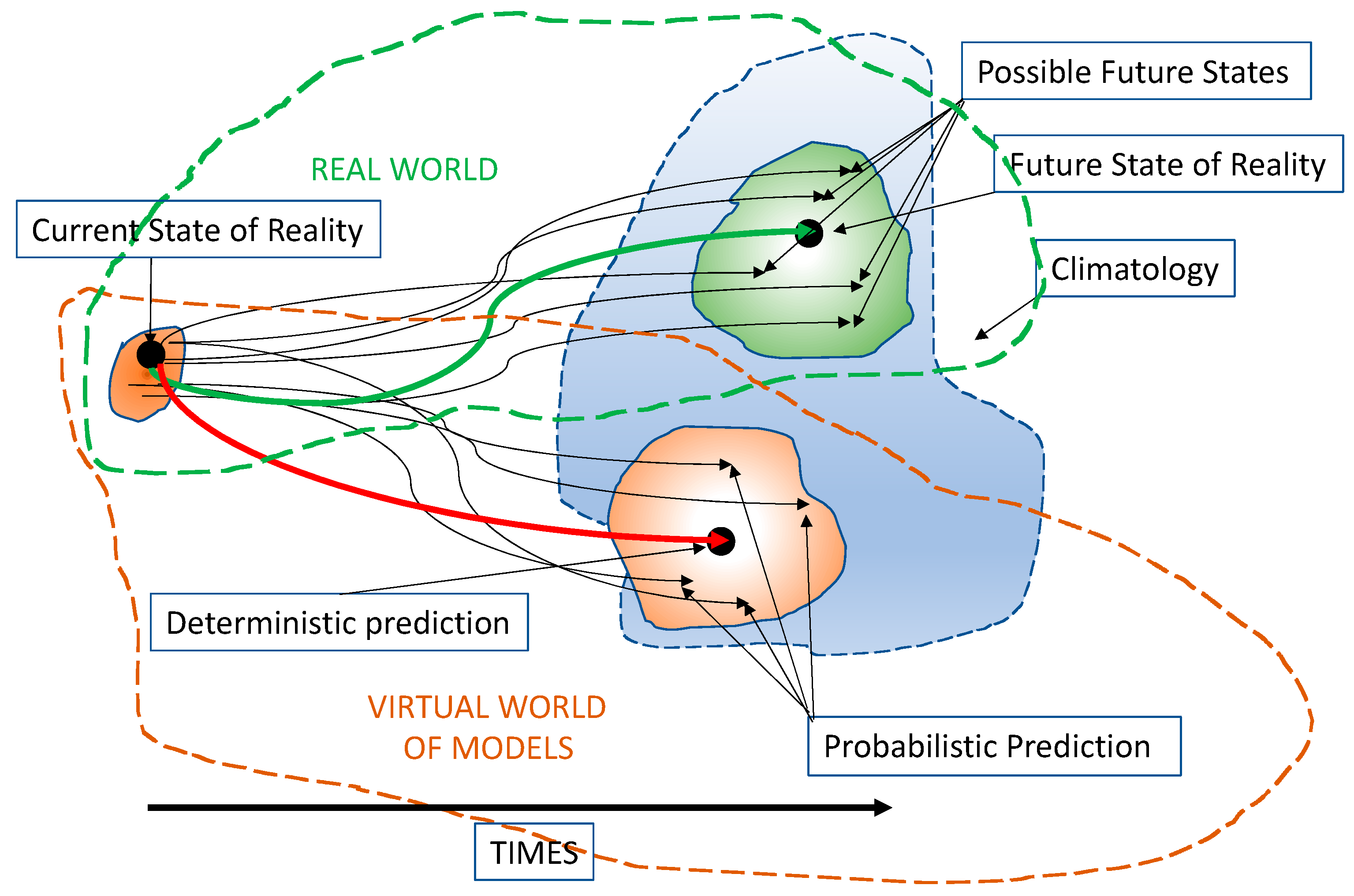
3. Probabilistic Predictions
3.1. Short Term Probabilistic Forecasts
3.2. Medium Term Probabilistic Forecasts
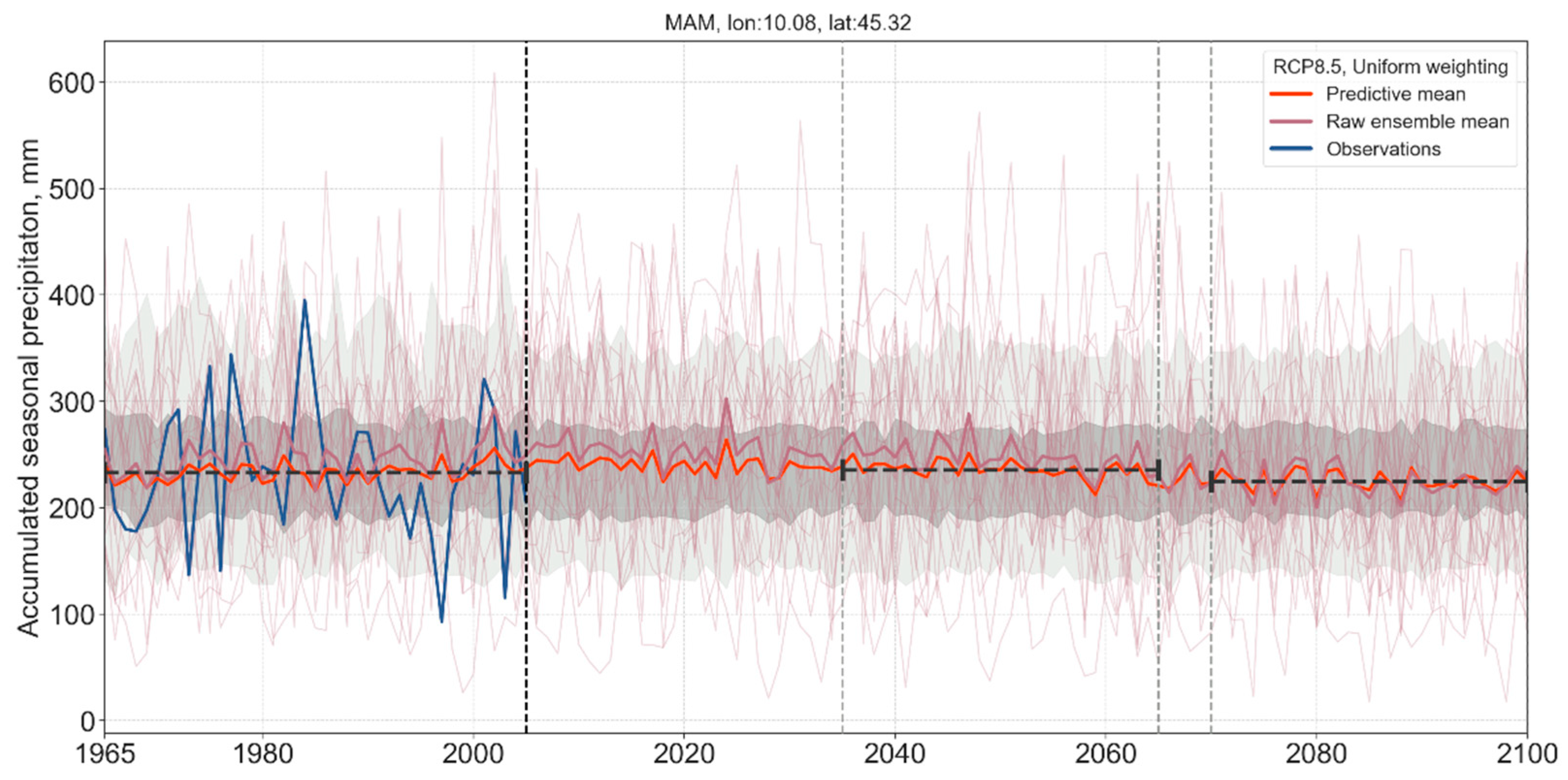
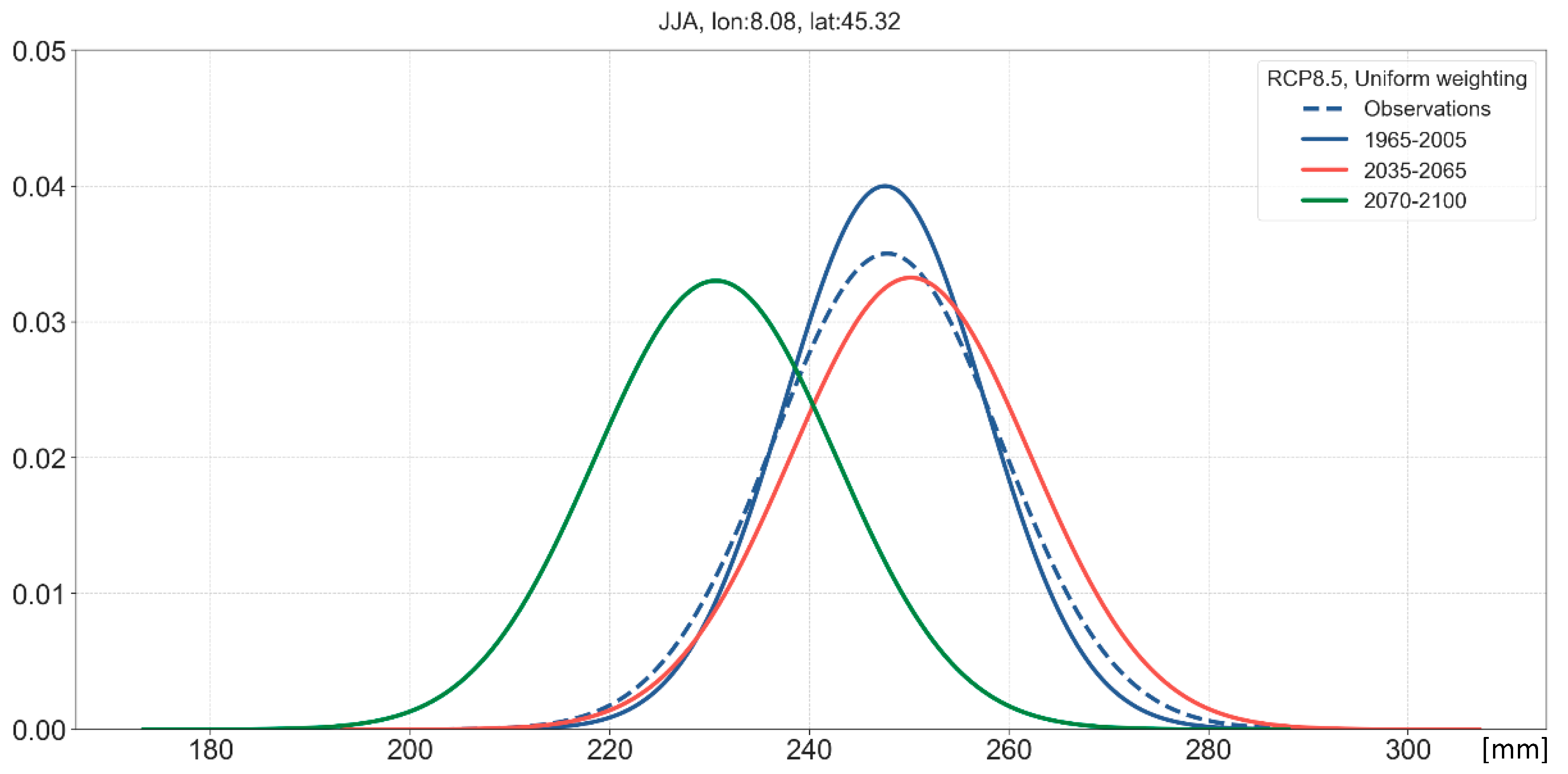
3.3. Long-Term Probabilistic Climate Projections
4. Attracting the Interest of Decision Makers
- inappropriate definition of predictive uncertainty;
- misunderstanding of the meaning of predictive uncertainty and of its role in decision-making;
- unclear role and use of epistemic uncertainty (such as parameter uncertainty), which is often confused with predictive uncertainty;
- incorrect use of ensembles in the assessment of predictive uncertainty;
- misunderstanding of the mechanism and of the advantages for using predictive uncertainty in the Bayesian decision-making process.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schwanenberg, D.; Fan, F.M.; Naumann, S.; Kuwajima, J.I.; Montero, R.A.; dos Reis, A.A. Short-Term Reservoir Optimization for Flood Mitigation under Meteorological and Hydrological Forecast Uncertainty. Water Resour. Manag. 2015, 29, 1635–1651. [Google Scholar] [CrossRef] [Green Version]
- Todini, E. Paradigmatic changes required in water resources management to benefit from probabilistic forecasts. Water Secur. 2018, 3, 9–17. [Google Scholar] [CrossRef]
- Todini, E. Coupling real time forecasting in the Aswan Dam reservoir management. In Proceedings of the Workshop on Monitoring, Forecasting and Simulation of River Basins for Agricultural Production, FAO and Centro IDEA, Bologna, Italy, 18–23 March 1991; Land and Water Development Division, FAO: Rome, Italy, 1991. Report N. FAO-AGL-RAF/8969. [Google Scholar]
- Reggiani, P.; Todini, E.; Boyko, O.; Buizza, R. Assessing uncertainty for decision-making in climate adaptation and risk mitigation. Int. J. Clim. 2021, 41, 2891–2912. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef] [Green Version]
- Deng, J.L. Control problems of grey systems. Syst. Control Lett. 1982, 5, 288–294. [Google Scholar]
- Todini, E. The role of predictive uncertainty in the operational management of reservoirs. In Evolving Water Resources Systems: Understanding, Predicting and Managing Water–Society Interactions, 2014 Proceedings of ICWRS2014, Bologna, Italy, 4–6 June 2014; IAHS Publ. 36X; IAHS Press: Wallingford, UK, 2014. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The Principles of Quantum Mechanics, 4th ed.; International Series of Monographs on Physics 27; Oxford University Press: New York, NY, USA, 1958; p. 328. ISBN 978-0-19-852011-5. [Google Scholar]
- Glahn, H.R.; Lowry, D.A. The Use of Model Output Statistics (MOS) in Objective Weather Forecasting. J. Appl. Meteorol. 1972, 11, 1203–1211. Available online: http://www.jstor.org/stable/26176961 (accessed on 28 June 2022). [CrossRef] [Green Version]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences: An Introduction; International Geophysics Series; Elsevier: San Diego, CA, USA, 1995; Volume 59, 467p. [Google Scholar]
- Raftery, A.E. Bayesian model selection in structural equation models. In Testing Structural Equation Models; Bollen, K.A., Long, J.S., Eds.; Sage: Newbury Park, CA, USA, 1993; pp. 163–180. [Google Scholar]
- Krzysztofowicz, R. Bayesian theory of probabilistic forecasting via deterministic hydrologic model. Water Resour. Res. 1999, 35, 2739–2750. [Google Scholar] [CrossRef] [Green Version]
- Koenker, R. Quantile Regression. In Econometric Society Monographs; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- Todini, E. A model conditional processor to assess predictive uncertainty in flood forecasting. Int. J. River Basin Manag. 2008, 6, 123–137. [Google Scholar] [CrossRef]
- Coccia, G.; Todini, E. Recent developments in predictive uncertainty assessment based on the model conditional processor approach. Hydrol. Earth Syst. Sci. 2011, 15, 3253–3274. [Google Scholar] [CrossRef] [Green Version]
- Coccia, G. Analysis and Developments of Uncertainty Processors for Real Time Flood Forecasting. Ph.D. Thesis, University of Bologna, Bologna, Italy, 2011. Available online: http://amsdottorato.unibo.it/id/eprint/3423 (accessed on 24 January 2019). [CrossRef]
- Krzysztofowicz, R. Probabilistic flood forecasts: Exact and approximate predictive distributions. J. Hydrol. 2014, 517, 643–651. [Google Scholar] [CrossRef]
- Barbetta, S.; Coccia, G.; Moramarco, T.; Brocca, L.; Todini, E. The multi temporal/multi-model approach to predictive uncertainty assessment in real-time flood forecasting. J. Hydrol. 2017, 551, 555–576. [Google Scholar] [CrossRef]
- Matthews, G.; Barnard, C.; Cloke, H.; Dance, S.L.; Jurlina, T.; Mazzetti, C.; Prudhomme, C. Evaluating the impact of post-processing medium-range ensemble streamflow forecasts from the European Flood Awareness System. Hydrol. Earth Syst. Sci. 2022, 26, 2939–2968. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M. Time Series Analysis: Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1970. [Google Scholar]
- Wang, Q.; Shao, Y.; Song, Y.; Schepen, A.; Robertson, D.E.; Ryu, D.; Pappenberger, F. An evaluation of ECMWF SEAS5 seasonal climate forecasts for Australia using a new forecast calibration algorithm. Environ. Model. Softw. 2019, 122, 104550. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A.E.; Westveld, A.H.; Goldman, T. Calibrated Probabilistic Forecasting Using Ensemble Model Output Statistics and Minimum CRPS Estimation. Mon. Weather Rev. 2005, 133, 1098–1118. [Google Scholar] [CrossRef]
- Evensen, G. The Ensemble Kalman Filter: Theoretical formulation and practical implementation. Ocean Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; Available online: https://www.climatechange2013.org (accessed on 28 June 2022).
- Meehl, G.A.; Boer, G.J.; Covey, C.; Latif, M.; Stouer, R.J. The coupled model inter-comparison project (CMIP). Bull. Am. Meteorol. Soc. 2000, 81, 313–318. [Google Scholar] [CrossRef] [Green Version]
- Meehl, G.A.; Covey, C.; Delworth, T.; Latif, M.; McAvaney, B.; Mitchell, J.F.B.; Stouffer, R.J.; Taylor, K.E. The WCRP CMIP3 multi-model dataset: A new era in climate change research. Bull. Am. Meteorol. Soc. 2007, 88, 1383–1394. [Google Scholar] [CrossRef] [Green Version]
- Taylor, K.E.; Stouer, R.J.; Meehl, G.A. Summary of the CMIP5 experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef] [Green Version]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef] [Green Version]
- Giorgi, F.; Francisco, R. Uncertainties in regional climate change prediction: A regional analysis of ensemble simulations with the HADCM2 coupled AOGCM. Clim. Dyn. 2000, 16, 169–182. [Google Scholar] [CrossRef]
- Palmer, T. Predicting uncertainty in forecasts of weather and climate. Rep. Prog. Phys. 2000, 63, 71–116. [Google Scholar] [CrossRef] [Green Version]
- Krzysztofowicz, R. The case for probabilistic forecasting in hydrology. J. Hydrol. 2001, 249, 2–9. [Google Scholar] [CrossRef]
- Hamill, T.M.; Whitaker, J.S. Probabilistic Quantitative Precipitation Forecasts Based on Reforecast Analogs: Theory and Application. Mon. Weather Rev. 2006, 134, 3209–3229. [Google Scholar] [CrossRef]
- Montanari, A. What do we mean by ‘uncertainty’? The need for a consistent wording about uncertainty assessment in hydrology. Hydrol. Process. 2007, 21, 841–845. [Google Scholar] [CrossRef]
- Beven, K.J.; Alcock, R.E. Modelling everything everywhere: A new approach to decision-making for water management under uncertainty. Freshw. Biol. 2011, 57, 124–132. [Google Scholar] [CrossRef] [Green Version]
- Beven, K.J. Facets of uncertainty: Epistemic uncertainty, non-stationarity, likelihood, hypothesis testing, and communication. Hydrol. Sci. J. 2016, 61, 1652–1665. [Google Scholar] [CrossRef] [Green Version]
- Clark, M.P.; Wilby, R.L.; Gutmann, E.D.; Vano, J.A.; Gangopadhyay, S.; Wood, A.W.; Fowler, H.J.; Prudhomme, C.; Arnold, J.R.; Brekke, L.D. Characterizing Uncertainty of the Hydrologic Impacts of Climate Change. Curr. Clim. Chang. Rep. 2016, 2, 55–64. [Google Scholar] [CrossRef] [Green Version]
- Draper, D.; Krnjajic, M. Calibration Results for Bayesian Model Specification; Technical Report; Department of Applied Mathematics and Statistics, University of California: Santa Cruz, CA, USA, 2013; Available online: https://users.soe.ucsc.edu/~draper/draper-krnjajic-2013-draft.pdf (accessed on 1 June 2022).



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reggiani, P.; Talbi, A.; Todini, E. Towards Informed Water Resources Planning and Management. Hydrology 2022, 9, 136. https://doi.org/10.3390/hydrology9080136
Reggiani P, Talbi A, Todini E. Towards Informed Water Resources Planning and Management. Hydrology. 2022; 9(8):136. https://doi.org/10.3390/hydrology9080136
Chicago/Turabian StyleReggiani, Paolo, Amal Talbi, and Ezio Todini. 2022. "Towards Informed Water Resources Planning and Management" Hydrology 9, no. 8: 136. https://doi.org/10.3390/hydrology9080136
APA StyleReggiani, P., Talbi, A., & Todini, E. (2022). Towards Informed Water Resources Planning and Management. Hydrology, 9(8), 136. https://doi.org/10.3390/hydrology9080136







