Determination of the Z-R Relationship through Spatial Analysis of X-Band Weather Radar and Rain Gauge Data

Abstract

In weather radar applications, the Z-R relationship is considered one of the most crucial factors for providing quality quantitative precipitation estimates. However, the relationship’s parameters vary in time and space, making the derivation of an optimal relationship for a specific weather radar system challenging. This research focused on the analysis of the spatiotemporal variability of the parameters for a newly installed X-Band weather radar in Athens, Greece, by performing correlation and optimization analyses between high temporal resolution weather radar and rain gauge datasets. The correlation analysis was performed to assess the available datasets and provide the base of quality control. Multiple Z-R relationships were then derived for the following three optimization procedures; event-based relationships, station-based relationships, and a single area-based relationship. The results highlighted the region’s spatial variability regarding the Z-R relationship and the correlation between the station location and its parameter values. Moreover, it was found that stations near the coast and the front end of precipitation systems featured parameter values typical of convective type events. Finally, a single Z-R relationship was determined under a calibration and validation scheme, Z = 321R^1.53,, which was validated with good agreement.

1. Introduction

Radar technology, as a means to estimate precipitation, has been used for over 50 years. Advances in radar and computer technology have increased the number of applications that can use high-quality Quantitative Precipitation Estimates (QPEs) [1,2]. This telemetric method has substantial advantages over traditional rainfall measuring, through rain gauges, since it can provide datasets with the following advantages: (a) the datasets can cover a significantly large area, against a single point measurement, and, thus, measure in inaccessible areas, and (b) the datasets operate on high temporal scales [3,4,5]. Compared to traditional rain gauge stations, weather radars provide better spatial and temporal resolutions, and, therefore, the use of radar-based rainfall data has seen increased interest in numerous applications [2,6,7,8]. Such applications include, first and foremost, hydrological modeling and simulation, where the rainfall’s spatial variability highly affects a basin’s hydrological output [5]. Another area where weather radar measurements have been exploited is in weather monitoring, specifically in severe weather assessment and forecasting [2,9,10]. In the era of climate change, protection against floods and flash floods has become a significant target, due to the increased socioeconomic and fatality rates associated with recent events. To that end, Early Warning Systems (EWSs) are designed to provide the necessary information to assist decision-making and allow targeted actions by civil protection agencies for a lower cost than flood protection works, especially in highly urbanized areas. These systems process weather measurements to provide high-quality feeds to nowcasts, forecasts, and hydrological models. Since such EWSs are usually as good as the input they are provided with, the higher temporal and spatial resolution input of weather radar data to the nowcasting algorithms, compared with those available from a rain gauge, satellite, or lightning networks [11,12], are considered vital. Therefore, weather radar measurements are usually the cornerstones of modern EWS implementations.

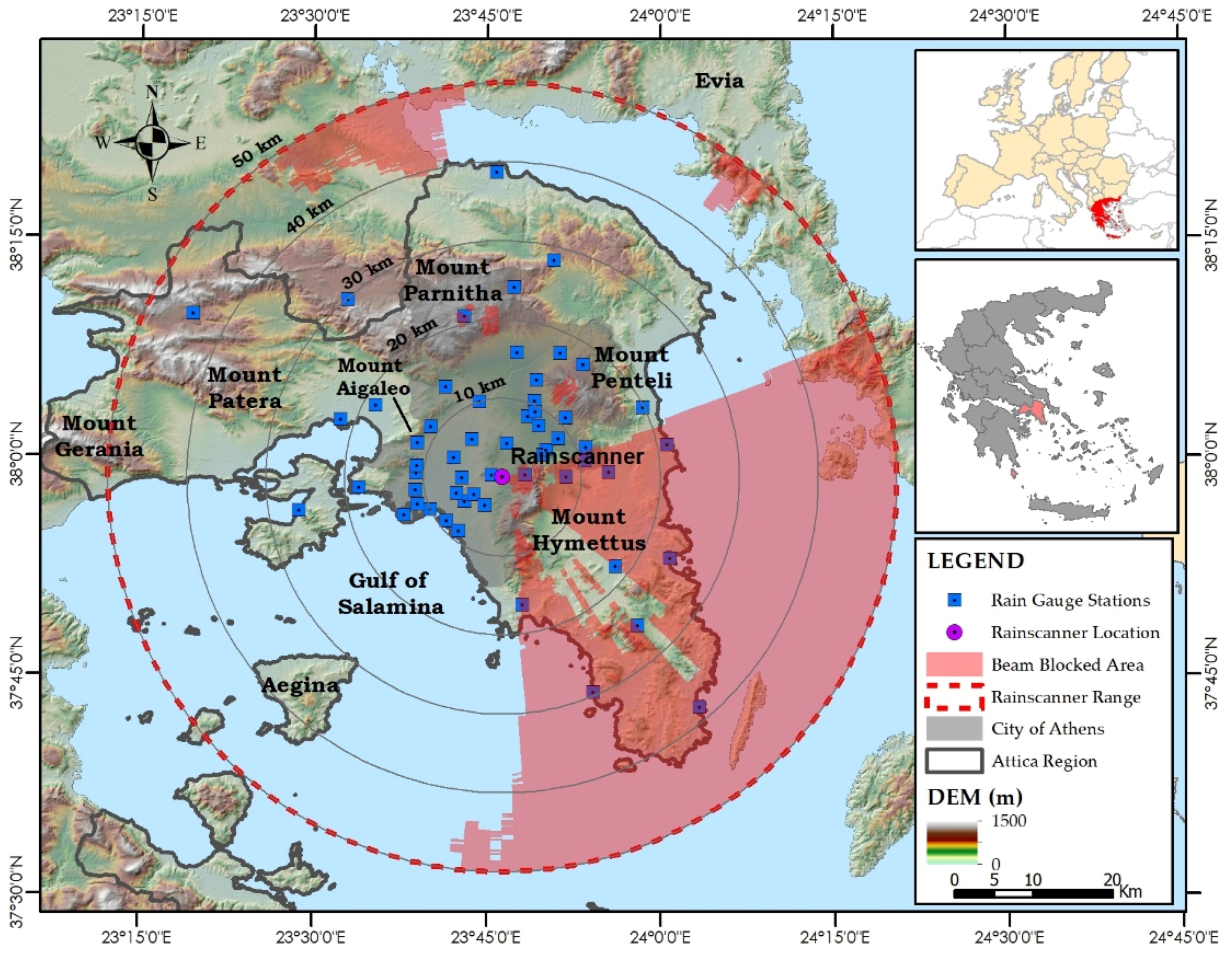
While weather radar measurements showcase many advantages over rain gauges, they are prone to non-negligible and sometimes even significant errors [2,13,14]. These errors are mainly a result of the measurement’s nature, i.e., the transmission of microwave radiation pulses and their reception when they are reflected after hitting rain droplets, in conjunction with other meteorological factors [1,15,16]. The main problem is usually signal attenuation caused by the signal’s scattering, absorption, and the addition of signal interferences like noise, such as second trip echoes or ground-generated echoes, also referred to as ground clutter. Signal attenuation limits the effective scanning range of a weather radar but can be mitigated when a higher wavelength and signal power are used. Typical radiation wavelengths of operational weather radar systems are 3, 5, and 10 cm, referred to as X-Band, C-Band, and S-Band radar systems. S-Band systems feature the highest power and, therefore, can operate at long distances. However, this usually comes at the cost of spatial resolution since the higher wavelength cannot detect small particles, which can be detectable by a versatile X-Band system that features smaller wavelengths in conjunction with high pulse repetition. The configurations feature in X-Band systems, which are also smaller in size and more cost-effective than the respected S-Band and C-Band systems [17], have made them popular for local-based solutions, such as weather monitoring in diverse mountainous regions and urban areas, which feature high beam blockage and vertical profile variability [2,4,8].

Apart from the radar-based technical parameters, errors to the estimated QPE usually occur on the measured reflectivity, Z [mm⁶/m³], into rainfall intensity, R [mm/h], a conversion performed using the so-called Z-R relationship. This relationship is an exponential equation of the following form:

$$Z=a{R}^{\mathrm{b}}$$

(1)

where a and b are parameters, usually ranging from 1 to 2000 for parameter a and 1 to 3 for parameter b. This relationship was first established in the work of Marshal and Palmer [18]. They proposed the values of 200 and 1.6 for parameters a and b, respectively, after analyzing the raindrop distribution of multiple rainfall events. However, it is well documented that these parameters show high variability [5,19,20]. Factors that affect the parameter values can be the spatial and temporal resolution of the analysis, the radar-specific calibration properties, and the characteristics of the precipitation systems, e.g., stratiform, convective, haze, or snowfall events [21,22,23]. In order to estimate the values of these parameters, also referred to as radar system calibration, two principal methodologies can be followed. The first is the use of disdrometer measurements, an instrument that measures the raindrop diameter distribution [24,25,26,27], while the second is through the correlation between radar and rain gauge measurements, assuming that the rain gauge measurements are the ground truth [24]. While the first method can produce more in-depth results, the latter method is preferred since disdrometer data are scarce and do not offer as complete an area coverage as an already established rain gauge station, while the rainfall variability is so high that it is difficult to reproduce/observe a concrete pattern twice.

Two methodologies can be followed regarding the rain gauge—radar optimization procedure. The first is utilizing a known Z-R relationship and performing a bias-driven statistical analysis at either station level [28,29] or area level, based on specific geostatistical interpolation algorithms, such as inverse distance or co-kriging [25,26,27]. This method does not rely on the Z-R relationship but mainly on the quality of available datasets, such as rain gauges, weather radar, and satellite measurements, to provide a merging algorithm to calculate and minimize any bias applicable to the QPE generated from the radar. While this method has numerous applications, new research in this domain seems to have limited value in operational applications since they can be time-consuming and provide little benefit compared with simpler methods [2]. The second method is by optimizing the Z-R parameters. The optimum set is determined by fitting either historical or real-time datasets. In this case, a calibration and validation scheme, with the use of multiple radar-rain gauge data pairs, is adopted after quality control, such as the removal of low to zero values of either reflectivity, e.g., less than 15 dBZ, or rainfall intensity, depending on the scope and temporal resolution of the analysis [28,29,30,31]. The following different approaches can also be taken concerning the optimization procedure: (a) linear optimizing methods of a single parameter, usually parameter a, with parameter b kept as a constant, (b) performing nonlinear calibration and optimizing both parameters [32], and (c) adding more parameters to the equation, such as the rain gauge-radar distance [29,33,34]. The temporal evolution of the rainfall event is usually addressed by adopting seasonal or rainfall-based characteristic Z-R relationships [35,36], although dynamic approaches, i.e., where the parameters are continuously changing based on the current or short-term measurements in a single event, have shown promising results [37,38].

There are numerous approaches to deal with the problem. However, the solution highly depends upon the available dataset’s quantity, quality, and scale. For instance, the results may vary when utilizing either different temporal scales, e.g., 10 min or lower against hourly, or different spatial scales, radar pixels size. Moreover, the Z-R relationship is highly related to storm characteristics which, in turn, are related to the topography of a given study area [39]. Therefore, the Z-R relationship is expected to vary in diverse topographies, where high and low elevation areas are found within a study area.

In this work, we addressed the problem by focusing on the values of the derived Z-R parameters for the following three cases: (a) event-based, using multiple rain gauge stations, (b) station-based, using multiple events, and (c) combining all available datasets to derive a single Z-R for the region. With this framework, we highlighted the differences generated in each case to utilize the best-correlated datasets for providing robust Z-R relationships for operational usage. The research was performed using datasets from the newly installed X-Band weather radar system, herein referred to as rainscanner, located in the facilities of the National Technical University of Athens (NTUA) near the center of Athens, Greece [20]. The aim was to explore the properties of the Z-R relationship within the city of Athens, which features diverse geomorphological characteristics, such as a long coastline and high elevation mountains surrounding the city, which affect the generation, the movement, and the discharge of rainfall storms.

2. Materials and Methods

2.1. Study Area and Data used

The NTUA X-Band radar system, herein referred to as rainscanner, is located within the facilities of the NTUA complex in the Zografou municipality, only 5 km distance from the center of Athens at an elevation height of 200 m. The rainscanner technical specifications are presented in

Table 1. Technical Specifications of the NTUA RAINSCANNER^® weather radar installed system.

RAINSCANNER® RS 90	Value
Peak Power	25 kW
Wave Length	X-Band 3.2 cm
Frequency	9410 (±30 MHz)
PRF	833–1500 Hz
Pulse Duration	1200–500 ns
Rotation Rate	12 rpm
Azimuth & Elevation Beamwidth	2.5°
Azimuth Accuracy	±0.5°
Scanning Range	50 km
Maximum Spatial Resolution	100 m × 100 m

. The rainscanner range is 50 km, which is more than enough to cover the entire metropolitan area of Athens, Greece’s capital, which is surrounded by the mountains of Penteli, Parnitha, Hymettus, and Aigaleo, and in the southeast has the Saronic gulf, which leads to the Aegean Sea. The rainscanner range extends the distance of the mountains, but the line-of-sight obstruction and radio antenna installations on the top of Hymettus and Parnitha make measurements on the east and south unreliable. The radar operates at a fixed angle of two degrees, set to be as low as possible while still overcoming mountainous objects in the center and west of Athens, providing an unobstructed view to the west. This setting, along with the high elevation at Zographou, at approximately 200 m, makes the sight’s location favorable for observing and producing nowcasts of precipitation systems generated on the west and over the city of Athens. At the 10 to 20 km distance of the rainscanner, where most of the Athens is located, the rainscanner beam height is 550 to 900 m from sea level, with the elevation in the center of Athens and Mount Aigaleo being 60 m and 400 m, respectively.

The rainscanner measurements are first processed by the rainscanner system software, RainView Analyzer^® [40], where the analog to digital signal conversion and other hardware-based transformations are made. Moreover, apart from the signal digital transformation, corrections due to signal obstruction and ground clutter are also applied through a user performed pre-process. Error-prone areas are identified in weather-free conditions and flagged by the user for either removal or automatic interpolation, as shown in Figure 1 as the beam blockage and clutter area. The system then creates a two-minute reflectivity field by analyzing 24 measured instances, thus limiting unexpected signal errors. The system does not perform other vertical or weather-related corrections since it does not feature a vertical rotating axis or dual-polarization signal generation. The raw products generated by the system are gridded reflectivity measurements with a spatial resolution of 100 m × 100 m pixel size and a two-minute temporal resolution stored in a georeferenced ASCII text file. These are further processed as discussed in Section 2.2 to match the temporal resolution of the rain gauge stations.

Concerning the rain gauge station datasets, a total of 52 stations of the National Observatory of Athens Automatic Network (NOAAN) [41] are found within the scanning area, where 40 of them are located within the city of Athens. The datasets consist of 10 min precipitation measurements, which have been quality controlled, concerning spatial and temporal inconsistencies against neighboring stations [41].

Finally, 13 events that occurred between 2018 and 2020 are examined in this study, which are the highest rainfall events with available datasets from both instruments. Most of them occurred during the wet season, in the winter months, from November to February, featuring convective type characteristics, such as small durations and high intensities in selected parts of the area.

2.2. Methodological Framework

The methodological framework follows the entire process, from data collection to the estimation of the Z-R relationships, as displayed in Figure 2. The data collection concerned the identification of each dataset’s spatial and temporal resolution. A process was then applied to transform the above scales into a comparable form for further analysis. This process was performed by aggregating the highest temporal scale dataset into the scale of the other dataset, i.e., the 2 min rainscanner datasets were aggregated into 10 min, while the area measurements were extracted into single timeseries. These processes were performed through a developed MATLAB^® programming code, as presented in the works of Bournas and Baltas [20] and Pappa et al. [19]. Specifically, a pre-process was first applied where the rainscanner cell within each station was identified. This was achieved by performing a nearest neighbor proximity search between the station coordinates and the rainscanner cell’s centroid coordinates. The matching cell was the centroid that lay in the nearest the station, which was then flagged to extract the recorded timeseries of the entire rainscanner field.

Following this match, for each event, the timeseries of the matched cells were extracted and correlated with the same time zone as the rain gauge measurements, being the Eastern European Time (EET) (UTC + 02:00) during winter and (UTC + 03:00) during summer. The aggregation of the rainscanner datasets was then performed along with a data curing process, where any inconsistencies, such as missing timesteps or inconsistent data, were corrected. The 10 min reflectivity was calculated as the average value of the five two-minute instances that lay within the same 10 min time interval of the rain gauge. If a timestep was missing, the aggregated value was calculated as the average of the remaining four instances. Moreover, when a single two-minute value had values unrelated to the other instances, such as NaN, zero, or extreme values, these values would be excluded from the aggregation. Finally, if a complete 10 min interval was missing, a zero value would be added instead, although that never occurred. Measurements that featured significant time gaps, due to power failures of the rainscanner system, were not included in this work. Therefore, in the studied events, missing data was rarely found, albeit there were some situations where some instances were lost when the system had to create a new date folder to store the files.

The next step of the analysis involved the calculation of the Pearson correlation coefficient for each station per event. The correlation coefficient evaluated whether the two datasets followed the same pattern, i.e., they were measuring the same rainfall volume at the same time interval and, therefore, did not become significantly altered by the Z-R applied. For providing station-based relationships, the use of multiple event datasets was incorporated into a single dataset. For quality control, the poor-correlated rainfall events were excluded from the dataset for each station. In rainfall events where the correlation was high, it was evident that both instruments were recording the correct measurements, whereas in events where a poor correlation featured, it was assumed that systematic errors or temporal inconsistencies were present. Therefore, we opted to remove the entire event dataset in favor of better-correlated rainfall events.

In most cases, poor correlation was observed when one instrument, usually the rainscanner, recorded a significant amount of rainfall, whereas the other did not record rainfall at all. Therefore, the correlation coefficient value, above which a rainfall event was deemed a well-correlated event, was set at 0.60, although a 0.70 limit was also tested. By applying a higher threshold, the number of events that featured within the multi-event dataset of each station reduced, therefore limiting the number of available data pairs that would be used for the latter optimization procedure. While a higher correlation would most likely reach better-fitted optimization results, by reducing the number of data pairs, it reduced the number of samples and, thus, risked being overfitted to few Z-R relationship data that might not be an appropriate fit. Furthermore, it was essential that, since this analysis was performed on a high temporal scale, i.e., of 10 min, the 0.60 threshold could be considered conservative. In high temporal scales, datasets show higher variability between each time step; thus, the error in each time step could be considerably higher than in coarser scales, e.g., 1-h, where the data variability is mitigated through the aggregation process [5].

Finally, the last procedure consisted of the optimization, where the parameters a and b were determined through optimization by minimizing the Root Mean Square Error (RMSE) of the selected rainscanner to obtain rain gauge pairs. The optimization procedures were performed in three groups of datasets: event-based, station-based, and a single Z-R. In each case, various Z-R relationships were derived, with the primary purpose of extracting different characteristics. The first incorporated datasets from multiple stations to derive event-based Z-R relationships. This analysis was performed to assess the quality of a Z-R derived when a single event was used and whether a storm classification could be made. The second optimization involved the station-based Z-R relationships, which highlighted the variability of the Z-R relationship in space. Finally, a single Z-R relationship was derived through an all-size-fits-all optimization utilizing the entire well-correlated datasets. The optimization was performed in two stages: first, using the entire dataset, and, second, with calibration and validation groups. The calibration stations were selected based on their correlation coefficients, i.e., the best-correlated stations in conjunction with an even spatial distribution of calibration and validation stations within the study area. The results were compared with the derived Z-R relationships from the Marshal n Palmer Z = 200R^1.60, and with two derived from disdrometer measurements for Athens, a convective based, Z = 431R^1.25 [42] and Z = 261R^1.53 based on datasets consisting of both stratiform and convective events [43]. The Bias, the Normalized Mean Bias (NMB), and the Normalized Mean Absolute Error (NMAE) were calculated as well, described in equations 2, 3, and 4, where R_i was the rainscanner estimate, G_i the rain gauge rainfall height and n the number of data pairs. The NMAE highlighted the actual percentage error, while the NMB and Bias highlighted whether an overestimation or underestimation of rainfall was performed by the rainscanner [19].

$$BIAS=\frac{{{\displaystyle \sum }}_{i=1}^n{R}_i-G_i}{n}.$$

(2)

$${\rm N}{\rm M}{\rm B}=\frac{{{\displaystyle \sum }}_{i=1}^n\left(R_i-G_i\right)}{{{\displaystyle \sum }}_{i=1}^n{G}_i}\mathrm{x}100\%$$

(3)

$$NMAE=\frac{{{\displaystyle \sum }}_{i=1}^n\left|R_i-G_i\right|}{{{\displaystyle \sum }}_{i=1}^n{G}_i}\mathrm{x}100\%$$

(4)

3. Results and Discussion

3.1. Rain Gauge—Rainscanner Correlation

The first step of the analysis consisted of evaluating the available datasets, by calculating the correlation coefficient, r, between the rainscanner and rain gauge datasets, at the station level and for each event. The results are shown in Figure 3 and Figure 4. Figure 3 shows the number of events with an above-average correlation, over 0.6 shown in panel a and over 0.7 in panel b. This comparison was made to justify the usage of the 0.6 correlation limit. In both cases, stations located in the northeast area, i.e., the mountainous regions at Penteli and Hymettus, or stations located near, or within, the cluttered area, featured an overall low correlation, evidenced by the small number of events that featured high correlation. However, in the 0.7 limit, several stations located on the coastal front did not meet the threshold, reducing the number of data pairs that would otherwise have been used in the optimization procedures. From a total of 13 events, reducing the available data pairs to only a few events would substantially decrease the number of data pairs used. Therefore, since the higher the correlation, the better the optimization, in the limited available sample, it was considered best to provide as many well-correlated datasets as possible. The effect of utilizing only well-correlated datasets is reflected in Figure 4, where the mean correlation coefficient when all datasets were used, shown in panel a, was compared with the mean correlation coefficient derived when utilizing the events featured for each station above the 0.6 correlation.

By combining the results shown in Figure 3 and Figure 4, we could extract some information regarding the quality of the rainscanner in terms of rain gauge datasets correlation at the station level. First, it was noticeable that there was a considerably high number of stations featuring low correlation values. These stations were found mainly within the beam blockage and clutter area, i.e., at the Hymettus area, east of the rainscanner location, where substantial noise interferes with the reflectivity measurements, making these stations unsuitable. Moreover, station 2, located within 1 km from the rainscanner location, similar to stations on the west, No. 38 and No. 29, also seemed to feature poor correlation. However, in the latter case, for station 29, as seen in panel b of Figure 4, the correlation was strong when few events were utilized.

Next, we focused on the well-correlated stations, i.e., those with a mean correlation above 0.6, such as stations 15, 21, and 53. A total of 15 stations featured above 0.6 correlation in 7 out of the 13 events, as shown in panel a of Figure 4. When considering only events that featured good correlation, shown in panel b of Figure 4, a total of 32 stations featured correlation above 0.6, 29 stations above 0.7, and 15 above 0.8. These results were encouraging, especially for the stations featuring high correlation in multiple events, e.g., stations 21, 42, and 53, as they could be used as control points for any other hydrological applications regarding rainfall field bias correction.

Finally, it was noticeable that some stations featured high correlation, but only in a limited number of rainfall events. Specifically, stations 28, 29, and 50, located in the north and southwest, respectively, featured a high correlation in a few events, less than 4, but the correlation in these events was relatively strong, above 0.8. This result highlighted that the rain gauge—rainscanner correlation in these specific areas, located within 20 km from the rainscanner, was not crippled by systematic errors, such as ground clutter or signal error, but from storm-based characteristics. Such characteristics can be the actual storm trajectory in conjunction with the station location, the presence of strong winds, especially in events where light rain is observed, overshoot or undershoot of the storm cloud by the rainscanner, due to the high beam elevation, or bright band effects. Identifying and correcting these effects requires an in-detail analysis concerning the rainscanner grid size, wind conditions, knowledge of the vertical profile of the storm, and time-series analysis between the rain gauge and rainscanner measurements. This study did not focus on this aspect, since few stations featured these issues. Thus, the derivation of Z-R relationships was deemed feasible with the rest of the data used. Overall, stations located away from high elevation or ground clutter regions, and within 15 km from the rainscanner range, i.e., stations near the coastal front of Athens city, featured the best correlation.

3.2. Event-Based Calibration

An event-based calibration was then performed to reach valuable conclusions regarding the studied events, such as whether an event-based Z-R relationship could be established or any differences found between each event. For the optimization of the Z-R parameters, only stations that featured above-average correlation, above 0.6, were used, as shown in Figure 3b. The results are shown in

Table 2. Z-R Optimization results per rainfall event.

Event	Date	Stations Used	Calibration on Parameters a and b				Calibration on Parameter a with Fixed b
			a	b	RMSE	r	a	b	RMSE
E1	30 September 2018	6	452	2.50	0.130	0.42	343	1.60	0.419
E2	16 December 2018	28	1486	2.50	0.445	0.60	771	1.60	0.169
E3	18 December 2018	31	301	1.95	0.210	0.66	306	1.60	0.450
E4	10 January 2019	23	758	2.42	0.197	0.67	551	1.60	0.237
E5	7 February 2019	26	956	2.50	0.290	0.54	540	1.60	0.225
E6	15 February 2019	27	1628	2.50	0.378	0.25	1070	1.60	0.329
E7	15 April 2019	25	340	1.41	0.304	0.88	292	1.60	0.392
E8	21 November 2019	19	369	2.50	0.308	0.71	402	1.60	0.356
E9	25 November 2019	22	206	1.05	0.216	0.95	118	1.60	0.625
E10	30 November 2019	27	1556	2.50	0.524	0.35	944	1.60	0.258
E11	1 June 2020	19	439	1.05	0.742	0.90	201	1.60	0.744
E12	8 August 2020	25	190	2.28	0.493	0.62	271	1.60	0.768
E13	4 December 2020	14	302	2.50	0.425	0.38	344	1.60	0.550

. Two calibration strategies were used. The first one involved the calibration of parameters a and b simultaneously. In the second one, parameter b was fixed at a default value, 1.6, and parameter a was calibrated to highlight the differences between the events.

As seen from the values of the featured table, in most cases, the parameter values varied, while in the first calibration, in some cases, parameter b was found to be fixed on the selected upper boundary of 2.50. This maximum value demonstrated that in these cases, the rainfall measured by the rain gauge was considerably lower than the reflectivity measured by the rainscanner, showing overall overestimation made by the rainscanner. Furthermore, when parameter b was fixed, although parameter a continued to vary, compared to the previous optimization, small changes were noticed in the correlation of the calculated RMSE. This effect highlighted that parameter b had little effect on the correlation, due to the small reflectivity and rainfall volumes correlated by using multiple station datasets in events with a small coverage.

Depending on the parameter a value, two main groupings could be extracted: (a) where the parameter was between the typical bounds of 50 to 500 and (b) when the parameter acquired larger values of up to 2000. Concerning the first group, based on commonly used Z-R relationships, when parameter a ranged above 400 this was a strong indication of a convective storm, while lower values, such as 200 and lower, featured in stratiform events, and, therefore, a quick storm classification could be performed, based on the results. However, this should be taken lightly, since more information is needed before making such statements. Concerning the latter grouping, it was found that the joint statement that a parameter a value of over 1000 suggested snowfall events was accurate. Events E2, E6, and E10 that featured such values were indeed snowfall events based on the temperature conditions at the time and local weather reports. Therefore, the snow events, which required a different Z-R relationship, were excluded from further analysis to avoid disrupting the station-based Z-R derived relationships. Overall, performing a single event Z-R optimization was not optimal since the parameters correlated with rainfall characteristics could vary substantially in space due to storm trajectory, thus, poor results were obtained by the optimization, especially in cases where the event had small coverage.

3.3. Station-Based Z-R Calibration

For stations with a correlation coefficient over 0.6, as shown in Figure 3b, the Z-R determination was then performed but this time by optimizing both a and b parameters. The results are shown in

Table 3. Z-R Optimization results for each station.

Calibration Stations
Index	Station	a	b	RMSE	r	Events	NMAE%	NMB%
4	Ano Liosia	168	1.79	0.58	0.79	7	57.1	17.0
5	Athens	316	1.68	0.33	0.78	5	40.1	−11.7
17	Patissia	423	2.15	0.23	0.76	4	42.2	−4.1
27	Athens-Marina	430	1.78	0.42	0.65	3	58.2	52.8
28	Tatoi	209	1.52	1.67	0.79	3	54.6	−17.2
30	Korydalos	304	1.57	0.27	0.85	7	41.5	−14.0
32	Alimos	317	1.14	0.38	0.72	2	39.2	28.9
42	Imittos-Dafni	292	1.05	0.58	0.79	6	41.0	−14.0
43	Harokopio-Athens	297	1.98	0.35	0.77	6	44.6	−8.0
45	Pireas-Pedagogiki	192	1.87	0.32	0.81	4	30.7	−9.6
47	Chaidari	257	1.87	0.80	0.87	2	17.8	0.4
48	Pireas	261	1.34	0.34	0.83	4	33.8	−2.2
52	Delacroix-Attiki	448	1.05	0.36	0.87	6	46.5	−16.4
Validation Stations
6	Dionysos	183	1.86	0.36	0.90	6	35.5	0.8
8	Faliro	433	2.26	0.30	0.75	5	36.4	−1.5
15	Neasmyrni	239	2.18	0.67	0.75	4	56.5	3.0
16	Neos Kosmos	402	1.83	0.39	0.84	8	40.1	−1.6
19	Peristeri	261	1.31	0.21	0.73	5	29.7	−4.1
21	Phychiko	271	1.42	0.45	0.81	8	37.0	−5.1
29	Aspropirgos	310	1.42	0.43	0.92	4	34.6	−10.2
34	Petroupoli	272	1.81	1.12	0.78	3	40.3	−6.8
35	Vrilissia	371	1.23	0.27	0.92	7	31.7	−10.1
38	Elefsina	275	1.05	0.25	0.77	3	41.6	−0.5
39	Nikaia	419	2.42	0.44	0.69	6	46.7	12.5
40	Salamina	490	1.08	0.00	0.83	2	0.1	−0.1
41	Ska	298	1.63	0.32	0.75	7	40.4	−1.4
45	Pireas-Pedagogiki	192	1.87	0.32	0.81	4	30.7	−9.6
51	Ano Korydallos	315	1.84	0.43	0.91	7	32.0	−2.6

. Based on the results, it was noticeable that parameter a was within the 168–490 range, while parameter b was within the 1.05–2.42 range. The correlation coefficient in all stations was high, since only the well-correlated events were utilized. This selection was performed to maximize the number of available data pairs, which was crucial for the optimization process. The mean values, used as an estimate of the parameters, were 312 and 1.64 for parameters a and b, respectively. In Figure 5, the spatial variability of both parameters could be observed, specifically in panel a of Figure 5, parameter a, and in panel b of Figure 5, parameter b. It was observed that higher parameter a values were observed on the coastal front, while lower values were observed in the north. The same results could be found for parameter b, although the lower values were observed in the east, while medium to high values were located in the southwest. High parameter a and b values indicated, according to the Z-R relationship, that lower rain intensity was to be estimated for the same amount of reflectivity.

In order to better comprehend the spatial variability of the Z-R relationship, we selected to lock parameter b to the average value of 1.64 and perform the optimization only on parameter a. As discussed earlier, the Z-R relationship showed higher variability in parameter a, especially on small temporal resolution datasets. Moreover, the average value of parameter b was found close to the value of 1.6 used by the Marshal n Palmer equation, and, thus, it was deemed a reliable order. Performing the new optimization, parameter a’s average value changed slightly at the value 293. However, differences were observed at the station level, especially in stations where parameter b varied from the 1.6 value. The results are plotted in Figure 6, where the station names are also shown for better indexing.

The results are equivalent to panel a of Figure 5, i.e., the higher parameter a values were calculated in the southwest, at the coastal front of Athens, while the lower values were calculated in the north section. A high parameter a value and a low parameter b are found in Z-R relationships better suited to convective type events. In such events, the reflectivity values are much higher, e.g., 35–40 dBZ [9,44], and therefore unrealistic extreme rain intensity can be estimated when parameter b is large, for instance. Since this study did not perform an event classification, Figure 6 indicates that high reflectivity was measured on the coastal front and less on the northeast. This fact also correlated with the typical trajectory of rainstorms in Athens, which tend to have west to east direction, as in most studied events. Specifically, through observations made by the rainscanner measurements concerning the trajectory of the studied rainfall events, it was found that the majority of rainfall events has their core generated either within the sea, in the Gulf of Salamina, or at the Mount Aigaleo area. Following through, they head to the east, where they discharge the largest amount of rainfall, depending on the weather conditions and their formation location, in either south Athens, where Faliro and Alimos stations are located, or at the center of Athens. Finally, they follow either an easterly direction towards Mount Hymettus or a northeasterly direction towards Mounts Parthitha and Penteli. These observations match the spatial variability of parameter a since its value decreased from the coastal areas towards the north in the same trajectory pattern as a typical rainfall system discharges rainfall. Areas first affected by a rainfall system usually record higher rainfall intensities, matching those of the convective type, than those in the northern areas, where most of the water has been discharged.

3.4. Single Z-R Calibration

In this section, a single Z-R relationship was derived for universal usage for Athens. A one-size-fits-all process was performed, where the use of all datasets from multiple stations and multiple events were used. As in the previous optimizations, data pairs of all stations for well correlated events were used, excluding zero value pairs. Two Z-R relationships were extracted, one where all available data were used and one where a calibration/validation grouping was made, with the scope of evaluating the relationship. In the first case, the derived Z-R relationship was the following:

$$Z=300R^{1.69}$$

(5)

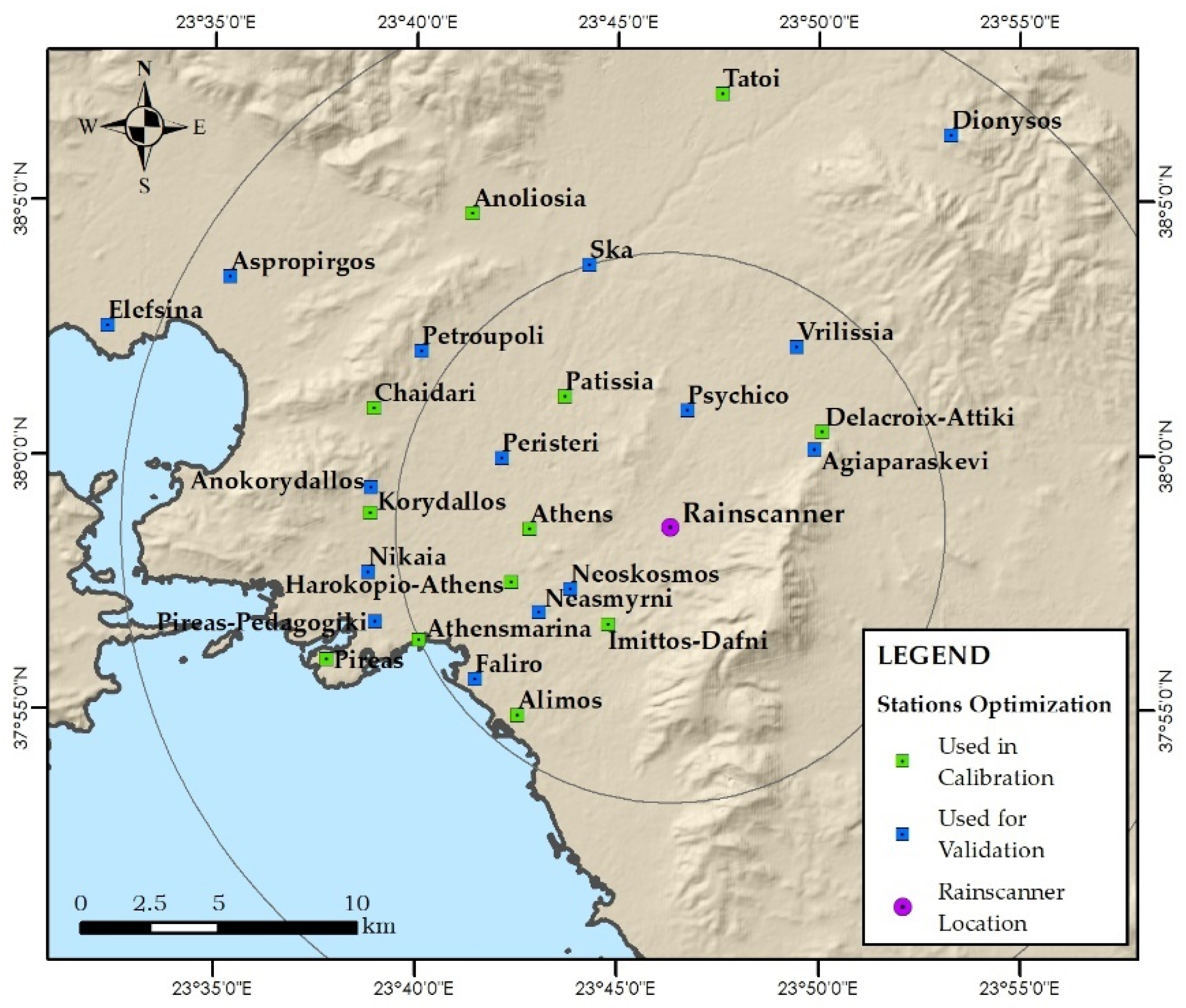
This result was in line with most of the individual station optimizations, since the parameters approached the average values of 312 and 1.64 calculated earlier, shown in Table 3. This approach is the simplest and most common way to extract a Z-R relationship but does not consider spatial or temporal variability. In the calibration-validation scheme, first, selection of control stations, i.e., stations to be used for calibration, was performed by applying a simple selecting strategy. Stations preferred for calibration were those that featured high correlation in multiple events, as shown in Figure 3 and Figure 4, while maintaining a good distribution over the entire study area, i.e., the city of Athens, for both calibration and validation. Half of the available stations were used for calibration and half for validation, as shown in Figure 7, while the scatter plots of the data pairs are shown in Figure 8. The derived Z-R relationship was the following:

$$Z=321R^{1.53}$$

(6)

In

Table 4. Z-R validation station statistics using the Z = 321R^1.53 relationship.

Index	Station	Individual Optimization				Validation
		a	b	RMSE	r	RMSE	r
6	Dionysos	183	1.86	0.36	0.90	0.45	0.90
8	Faliro	433	2.26	0.30	0.75	0.37	0.75
15	Neasmyrni	239	2.18	0.67	0.75	0.72	0.75
16	Neos Kosmos	402	1.83	0.39	0.84	0.42	0.84
19	Peristeri	261	1.31	0.21	0.73	0.23	0.73
21	Phychiko	271	1.42	0.45	0.81	0.47	0.81
29	Aspropirgos	310	1.42	0.43	0.92	0.46	0.92
31	Agia Paraskevi	290	1.21	0.24	0.95	0.70	0.95
34	Petroupoli	272	1.81	1.12	0.78	1.19	0.78
35	Vrilissia	371	1.23	0.27	0.92	0.30	0.92
38	Elefsina	275	1.05	0.25	0.77	0.28	0.77
39	Nikaia	419	2.42	0.44	0.69	0.46	0.69
40	Salamina	490	1.08	0.30	0.83	0.32	0.83
41	Ska	298	1.63	0.32	0.75	0.32	0.75
45	Pireas-Pedagogiki	192	1.87	0.32	0.81	0.40	0.81
51	Ano Korydallos	315	1.84	0.43	0.91	0.60	0.91

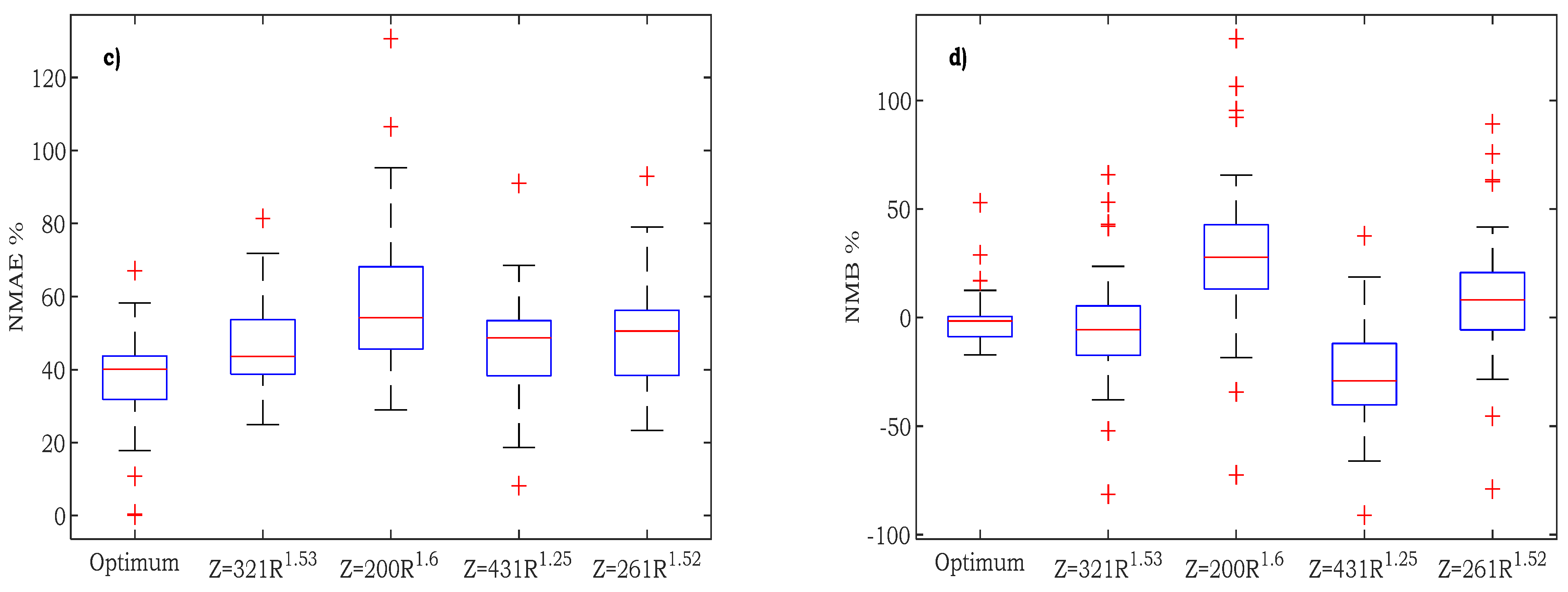
, the validation station’s RMSE and r correlation coefficient are displayed, in contrast with the individual optimization performed in Section 3.3. As expected, the r correlation was unaffected, since it does alter significantly with the used Z-R, while the RMSE of each station seemed to differ slightly but did not impact the results. Most stations showed little changes, apart from some stations with high a and b values, such as Neos Kosmos and Ano Korydallos. The boxplots for the RMSE, the BIAS, the NMAE, and NMB are presented in Figure 9 to compare the determined Z-R relationship and other used relationships. The optimum Z-R relationship is the one that has been derived for the specific station and rainfall event, and therefore, features the best results. However, this solution was not feasible for implementation, since it relied on multiple Z-R relationships at the station level and was shown for comparison purposes alone. The proposed Z-R relationship, Z = 321R^1.53, showed the second-best results compared to the others, since it features the smallest values in all metrics and the smallest variation. The Marshal n Palmer Z = 200R^1.6 showed the worst results in all metrics. The convective-based Z = 431R^1.25 showed good results but underestimated the actual rainfall since the NMB value had a significant negative value, which was inappropriate, especially for early warning applications. Finally, the Z = 261R^1.52, which featured equal parameter b but much less parameter a value than the one proposed, showed promising results but was still worse than the one proposed. This change of the parameter a value also highlighted how sensitive the rainfall estimation is, highlighted by the change of the mean BIAS and NMB values between the two Z-R relationships used.

Finally, another validation of the derived Z-R relationships of this study is shown in Figure 10 and Figure 11, where the rainfall and accumulative rainfall timeseries for two of the validation stations, the Psychiko and Neos Kosmos, for two rainfall events, E4 and E8, are presented. The figures assist in the visualization of the differences between the use of each optimized Z-R previously derived. Within the figures, with blue bars, the rain gauge measurements are displayed. The colors displaying the rainscanner measurements accord with the following: (a) a green line indicates rainscanner measurements through the use of the Marshal n Palmar, Z = 200R^1.6, equation, (b) a red line indicates rainscanner measurements through the all data calibration Equation (3), Z = 321R^1.53, (c) with a purple line through the Event-based Z-R, as shown in Table 2 for each event, (d) with a black line through the Station Based Z-R, as shown in Table 3, and (e) with a blue line through the optimized relationship by utilizing the station dataset for the particular event. From the above, the best-fit result should be option (e), where Z-R parameters were derived from the specific datasets, and, therefore, the fit should be the optimum. At the same time, the station-based Z-R, black line, should follow suit, as the Z-R was calibrated for the specific station data. As seen in Figure 10, for Psychiko station, while the optimized fit better in each 10 min rainfall height, the rainfall accumulation did not feature the best result, mainly because of the gap of the rainscanner dataset at 02:00, which disrupted the rainfall accumulation timeseries. On the other hand, the station-based relationship, black line, seemed better suited, while the all-data calibration and event-based were all tagging well. Finally, the Marshal n Palmer equation showed a higher deviation, highlighting the need for calibrated Z-R relationships.

In Figure 11, the optimized and station-based relationships were similar, showcased by the Z-R a value parameter, while even if parameter b varied 0.15, the difference was relatively insignificant. Again, the Marshal n Palmer equation showed the worst correlation, showcased by the 10 mm accumulation precipitation bias, while the calibration-based was slightly better. The calibrated Z-R correlated well with small biases in the accumulative precipitation diagram, highlighting that it could be used for different stations and events. It is essential to notice that incorporating a single Z-R cannot describe the spatial variability of the rainfall field; therefore, bias is expected. However, it is movement in a positive direction that a single Z-R relationship could be used that minimizes this bias. Moreover, this work showcases the importance of calibrating a weather radar system’s Z-R relationship, since utilizing a literature-based relationship may lead to substantial systematic errors.

4. Conclusions

In this research work, a framework was applied to assess the variability of the Z-R relationship. Specifically, for a newly installed weather radar system in Athens, Greece, a series of radar and rain gauge measurements were utilized in an optimization procedure to estimate the parameters a and b of the Z-R relationship, which governs the conversion of measured reflectivity into rainfall intensity. First, a correlation analysis was performed to extract information regarding the characteristics of the studied events and to assess the quality of the rainscanner measurements against the rain gauge measurements, which are assumed to be the ground truth. It was shown that the correlation between the two datasets, even in a single event, showed high variability, which originated from two reasons. The first was the proximity of each station to the areas that were affected by ground clutter, which generally featured low to zero correlation. The second was the actual rainfall intensity, where the correlation was found to be higher when higher rather than lower rainfall was recorded by the rain gauge. Conversely, areas where little rainfall was measured, near the accuracy of the rain gauge, featured low correlation. Overall, stations on low elevations, such as those found on the coastline, showed the highest correlation in multiple events. Specifically, 15 stations featured above 0.60 correlation in 7 out of 13 events. By applying the 0.60 correlation limit, excluding poorly correlated events at the station level, it was found that a total of 32 out of 52 stations featured an average correlation of more than 0.60.

The optimization procedures highlighted important findings. First, a single event for calibration is most likely to reach a poor Z-R and should be avoided when calibrating a weather radar system. However, it still has its value, since, by examining the a and b parameters values, one can conclude whether the event examined was a stratiform, a convective, or a snowfall event. Notably, snowfall events featured a large parameter a value, e.g., above 1000, and could be easily identified and excluded from further analysis when rainfall was being analyzed. In the station-based optimization, although high variability concerning the values of the Z-R parameters was found in space, a pattern could be drawn, where high parameter a values, 300 to 500, were found in the west and southwest areas near the coast, while lower values characterized the northern areas. Such high values were a characteristic of convective-type events, which feature high rainfall intensities. Therefore, it can be said that these areas are affected by higher rainfall intensities than the northern areas. This finding followed suit with the topographic characteristics and the west to east storm trajectory seen in Athens. The sea of the Salamina Gulf fuels a precipitation system which later on discharges with high intensity on the first mainland areas it hits, i.e., the coastal areas, also aided by the presence of nearby high elevation points, such as Mount Aigaleo and Mount Hymettus. Stations in the north and northwest are found in higher elevations, and rainfall is mainly due to orography, thus, it may feature higher quantities, but with less intensity, i.e., the duration is much larger. Finally, a single Z-R relationship was established through a calibration and validation process. The proposed Z-R showed good agreement in multiple stations and featured better metrics than other previously derived Z-R relationships, two of which were derived for Athens through disdrometer measurements. Moreover, compared with other Z-R relationships derived in this analysis, i.e., station and event-based relationships, it showed good application when used for two stations. Finally, based on its parameter values, the derived Z-R highlighted the fact that in the city of Athens, most storm events are of the convective type.

It is essential to notice that the derived Z-R relationships were better used for the spatial and temporal resolution of the datasets used in this study. Moreover, usage with a different radar system should be performed with awareness of some risk, since a radar system’s calibration does not only rely on the Z-R relationship used. A limitation of the study was the number of datasets. Using more datasets would increase the quality of the determined Z-R. Research focused on a bias-driven analysis could be additionally applied to reach corrected weather radar rainfall fields for hydrological and nowcasting applications. Furthermore, an in-depth analysis of storm trajectory patterns to explore their impact on the temporal evolution of the Z-R relationship and rainfall intensity in the studied area was also pursued. This research paves the way for a holistic approach to the understanding and application of weather radar rainfall estimation.