Multiple Linear Regression Models with Limited Data for the Prediction of Reference Evapotranspiration of the Peloponnese, Greece
Abstract
1. Introduction
2. Materials and Methods
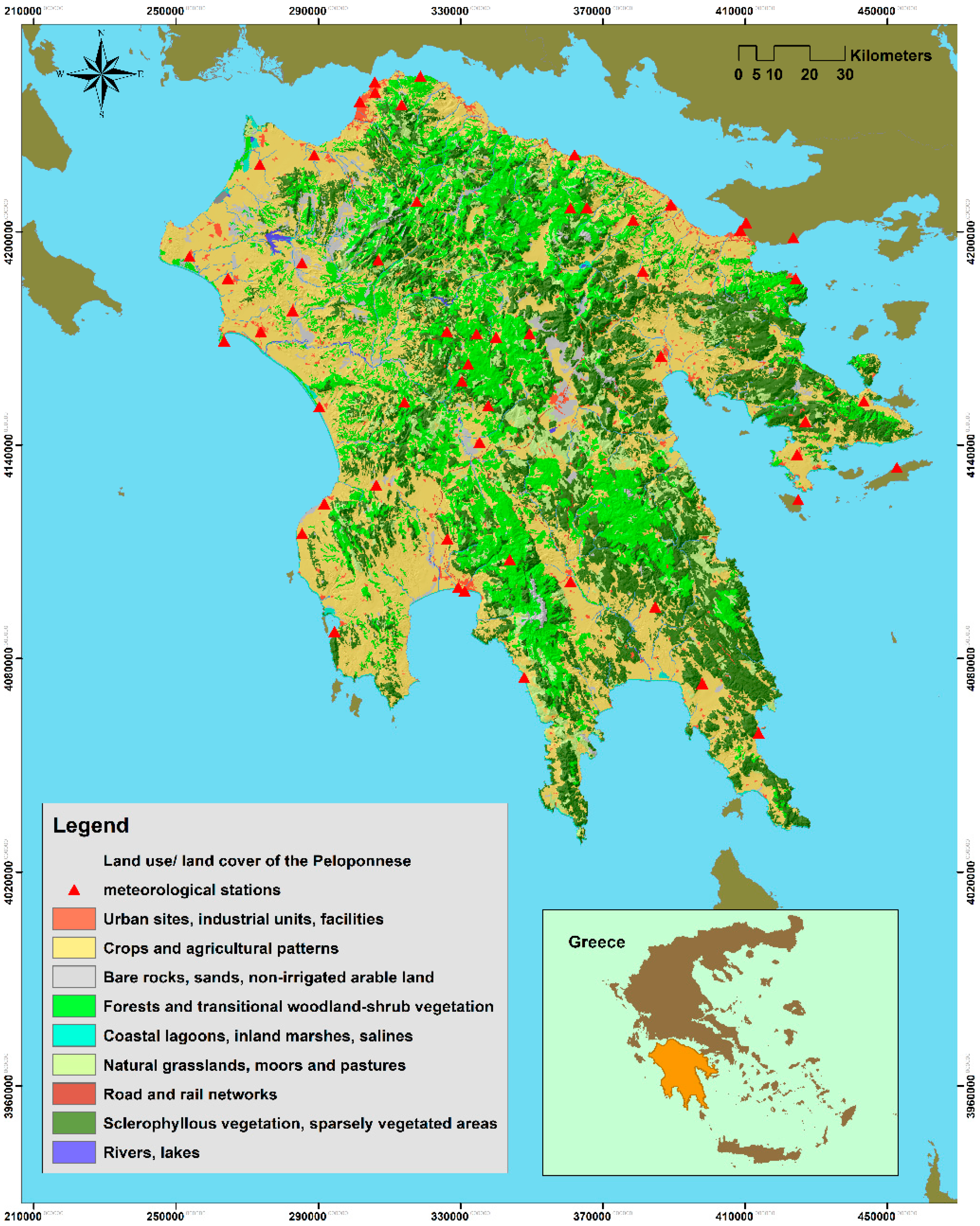
2.1. The Study Area
2.2. Methods
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| ID | Station | X | Y | Elevation (m) | Municipality | ID | Station | X | Y | Elevation (m) | Municipality |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Meteorological Stations for the 3 Empirical Methods (ETo) | Meteorological Stations for the 3 Empirical Methods (ETo) | ||||||||||
| 1 | Kalavrita | 334,349.9 | 4,210,128 | 781 | Achaia | 32 | Oleni | 282,783.4 | 4,177,872 | 61 | Ilia |
| 2 | Kato Vlassia | 317,683.4 | 4,2085,58 | 773 | Achaia | 33 | Pineia | 285,425.3 | 4,191,240 | 184 | Ilia |
| 3 | Lappa | 273,550 | 4,218,928 | 15 | Achaia | 34 | Pirgos | 273,886.9 | 4,171,891 | 22 | Ilia |
| 4 | Olenia | 288,845.1 | 4,221,654 | 34 | Achaia | 35 | Vartholomio | 253,773.8 | 4,193,127 | 15 | Ilia |
| 5 | Panachaiko | 313,491.4 | 4,235,800 | 1588 | Achaia | 36 | Zacharo | 290,302.6 | 4,150,806 | 5 | Ilia |
| 6 | Panagopoula | 318,709.5 | 4,243,842 | 15 | Achaia | 37 | Amoni Sofikou | 424,227.5 | 4,186,898 | 55 | Korinthia |
| 7 | Panepistimio | 305,972.3 | 4,239,289 | 66 | Achaia | 38 | Derveni | 362,057.1 | 4,221,737 | 5 | Korinthia |
| 8 | Patra | 301,697.8 | 4,236,694 | 6 | Achaia | 39 | Isthmos | 408,645.4 | 4,200,499 | 6 | Korinthia |
| 9 | Rio | 305,898.1 | 4,242,177 | 2 | Achaia | 40 | Kiato | 389,163.5 | 4,207,722 | 15 | Korinthia |
| 10 | Romanos | 313,476.1 | 4,235,744 | 228 | Achaia | 41 | Krioneri | 378,491.9 | 4,203,310 | 887 | Korinthia |
| 11 | Sageika | 280,638.4 | 4,219,575 | 26 | Achaia | 42 | Loutraki | 410,248.7 | 4,202,636 | 30 | Korinthia |
| 12 | Argos | 386,329.1 | 4,165,059 | 38 | Argolida | 43 | Nemea | 381,197.9 | 4,188,976 | 290 | Korinthia |
| 13 | Didima | 426,936.9 | 4,146,702 | 175 | Argolida | 44 | Perigiali | 397,303.1 | 4,199,344 | 38 | Korinthia |
| 14 | Kranidi | 424,615.7 | 4,137,411 | 110 | Argolida | 45 | Trikala Korinthias | 365,493.7 | 4,206,835 | 1077 | Korinthia |
| 15 | Lagadia | 326,139.9 | 4,172,057 | 970 | Arkadia | 46 | Agioi Theodoroi | 423,533.6 | 4,198,395 | 37 | Korinthia |
| 16 | Levidi | 349,386.5 | 4,171,330 | 853 | Arkadia | 47 | Apidia | 392,819.7 | 4,082,655 | 230 | Lakonia |
| 17 | Lykochia | 337,772.6 | 4,151,113 | 870 | Arkadia | 48 | Asteri | 386,527.1 | 4,076,757 | 8 | Lakonia |
| 18 | Magouliana | 334,497.7 | 4,171,275 | 1256 | Arkadia | 49 | Geraki | 384,706.6 | 4,094,508 | 330 | Lakonia |
| 19 | Megalopoli | 335,363 | 4,140,782 | 432 | Arkadia | 50 | Krokees | 371,576.2 | 4,082,640 | 241 | Lakonia |
| 20 | Stemnitsa | 330,377.8 | 4,157,967 | 1094 | Arkadia | 51 | Molaoi | 397,984.6 | 4,072,957 | 128 | Lakonia |
| 21 | Tripoli | 359,989.3 | 4,152,250 | 650 | Arkadia | 52 | Monemvasia | 413,811.4 | 4,059,051 | 17 | Lakonia |
| 22 | Vytina | 339,989.8 | 4,170,409 | 1013 | Arkadia | 53 | Sparti | 360,929.9 | 4,101,670 | 204 | Lakonia |
| 23 | Spetses | 424,919.5 | 4,124,662 | 3 | Attiki | 54 | Alagonia | 343,840.9 | 4,107,863 | 765 | Messinia |
| 24 | Taktikoupoli Troizinias | 443,373.2 | 4,152,374 | 15 | Attiki | 55 | Arfara | 326,299.4 | 4,113,666 | 96 | Messinia |
| 25 | Ydra | 452,645.8 | 4,133,727 | 2 | Attiki | 56 | Filiatra | 285,439.9 | 4,115,175 | 65 | Messinia |
| 26 | Amaliada | 264,604.9 | 4,186,923 | 26 | Ilia | 57 | Kalamata | 331,127 | 4,098,974 | 5 | Messinia |
| 27 | Andritsaina | 314,220.3 | 4,152,125 | 731 | Ilia | 58 | Kalamata Dytika | 329,347.3 | 4,100,001 | 10 | Messinia |
| 28 | Archaia Olympia | 287,981.3 | 4,163,856 | 45 | Ilia | 59 | Kardamili | 347,857.7 | 4,074,651 | 13 | Messinia |
| 29 | Foloi | 297,082.7 | 4,174,732 | 600 | Ilia | 60 | Kopanaki | 306,288.6 | 4,128,741 | 184 | Messinia |
| 30 | Katakolo | 263,537.2 | 4,169,327 | 2 | Ilia | 61 | Kyparissia | 291,691 | 4,123,584 | 36 | Messinia |
| 31 | Lampeia | 306,840.3 | 4,192,041 | 840 | Ilia | 62 | Pylos | 294,556.8 | 4,087,590 | 5 | Messinia |
References
- Malamos, N.; Tegos, A. Advances in Evaporation and Evaporative Demand. Hydrology 2022, 9, 78. [Google Scholar] [CrossRef]
- Shamshirband, S.; Hashemi, S.; Salimi, H.; Samadianfard, S.; Asadi, E.; Shadkani, S.; Kargar, K.; Mosavi, A.; Nabipour, N.; Chau, K.W. Predicting Standardized Streamflow index for hydrological drought using machine learning models. Eng. Appl. Comput. Fluid Mech. 2020, 14, 339–350. [Google Scholar] [CrossRef]
- Xu, S.; Yu, Z.; Yang, C.; Ji, X.; Zhang, K. Trends in evapotranspiration and their responses to climate change and vegetation greening over the upper reaches of the Yellow River Basin. Agric. For. Meteorol. 2018, 263, 118–129. [Google Scholar] [CrossRef]
- Dimitriadou, S.; Nikolakopoulos, K.G. Evapotranspiration Trends and Interactions in Light of the Anthropogenic Footprint and the Climate Crisis: A Review. Hydrology 2021, 8, 163. [Google Scholar] [CrossRef]
- Djaman, K.; Balde, A.B.; Sow, A.; Muller, B.; Irmak, S.; N’Diaye, M.K.; Manneh, B.; Moukoumbi, Y.D.; Futakuchi, K.; Saito, K. Evaluation of sixteen reference evapotranspiration methods under sahelian conditions in the Senegal River Valley. J. Hydrol. Reg. Stud. 2015, 3, 139–159. [Google Scholar] [CrossRef]
- Pereira, L.S.; Perrier, A.; Allen, R.G.; Alves, I. Evapotranspiration: Concepts and Future Trends. J. Irrig. Drain. Eng. 1999, 125, 45–51. [Google Scholar] [CrossRef]
- Malamos, N.; Tsirogiannis, I.L.; Tegos, A.; Efstratiadis, A.; Koutsoyiannis, D. Spatial interpolation of potential evapotranspiration for precision irrigation purposes. Eur. Water 2017, 59, 303–309. Available online: https://www.researchgate.net/publication/323030147_Spatial_interpolation_of_potential_evapotranspiration_for_precision_irrigation_purposes (accessed on 19 May 2022).
- Saggi, M.K.; Jain, S. Reference evapotranspiration estimation and modelling of the Punjab Northern India using deep learning. Comput. Electron. Agric. 2019, 156, 387–398. [Google Scholar] [CrossRef]
- Zhang, Y.; Wei, Z.; Zhang, L.; Du, J. Applicability evaluation of different algorithms for daily reference evapotranspiration model in KBE system. Int. J. Comput. Sci. Eng. 2019, 18, 361–374. [Google Scholar] [CrossRef]
- Skarlatos, D.; Kalavrouziotis, I.K.; Montes, C.R.; Melfi, A.J.; Pereira, B.F.F. Wastewater reuse in citrus: A fuzzy logic model for optimum evapotranspiration. Desalination Water Treat. 2015, 55, 315–324. [Google Scholar] [CrossRef]
- Ma, N.; Szilagyi, J.; Zhang, Y. Calibration-free complementary relationship estimates terrestrial evapotranspiration globally. Water Resour. Res. 2021, 57, e2021WR029691. [Google Scholar] [CrossRef]
- Ma, N.; Szilagyi, J.; Zhang, Y.; Liu, W. Complementary-relationship-based modeling of terrestrial evapotranspiration across China during 1982–2012: Validations and spatiotemporal analyses. J. Geophys. Res. Atmos. 2019, 124, 4326–4351. [Google Scholar] [CrossRef]
- Li, M.; Chu, R.; Islam, A.R.M.T.; Shen, S. Reference Evapotranspiration Variation Analysis and Its Approaches Evaluation of 13 Empirical Models in Sub-Humid and Humid Regions: A Case Study of the Huai River Basin, Eastern China. Water 2018, 10, 493. [Google Scholar] [CrossRef]
- Tabari, H.; Grismer, M.E.; Trajkovic, S. Comparative analysis of 31 reference evapotranspiration methods under humid conditions. Irrig. Sci. 2013, 31, 107–117. [Google Scholar] [CrossRef]
- Roy, D.K.; Sarkar, T.K.; Kamar, S.S.A.; Goswami, T.; Muktadir, M.A.; Al-Ghobari, H.M.; Alataway, A.; Dewidar, A.Z.; El-Shafei, A.A.; Mattar, M.A. Daily Prediction and Multi-Step forward Forecasting of Reference Evapotranspiration Using LSTM and Bi-LSTM Models. Agronomy 2022, 12, 594. [Google Scholar] [CrossRef]
- Ferreira, L.B.; da Cunha, F.F. Multi-step ahead forecasting of daily reference evapotranspiration using deep learning. Comput. Electron. Agric. 2020, 178, 105728. [Google Scholar] [CrossRef]
- Ravindran, S.M.; Bhaskaran, S.K.; Ambat, S.K. A Deep Neural Network Architecture to Model Reference Evapotranspiration Using a Single Input Meteorological Parameter. Environ. Process. 2021, 8, 1567–1599. [Google Scholar] [CrossRef]
- Granata, F.; Di Nunno, F. Forecasting evapotranspiration in different climates using ensembles of recurrent neural networks. Agric. Water Manag. 2021, 255, 107040. [Google Scholar] [CrossRef]
- Mosavi, A.; Edalatifar, M. A Hybrid Neuro-Fuzzy Algorithm for Prediction of Reference Evapotranspiration. In Recent Advances in Technology Research and Education; INTER-ACADEMIA 2018; Lecture Notes in Networks and Systems; Laukaitis, G., Ed.; Springer: Cham, Switzerland, 2019; Volume 53. [Google Scholar]
- Andreu, A.; Kustas, W.P.; Polo, M.J.; Carrara, A.; González-Dugo, M.P. Modeling Surface Energy Fluxes over a Dehesa (Oak Savanna) Ecosystem Using a Thermal Based Two Source Energy Balance Model (TSEB) II—Integration of Remote Sensing Medium and Low Spatial Resolution Satellite Images. Remote Sens. 2018, 10, 558. [Google Scholar] [CrossRef]
- Silva, A.M.; da Silva, R.M.; Santos, C.A.G. Automated surface energy balance algorithm for land (ASEBAL) based on automating end member pixel selection for evapotranspiration calculation in MODIS orbital images. Int. J. Appl. Earth Obs. Geoinf. 2019, 79, 1–11. [Google Scholar] [CrossRef]
- Sidiropoulos, P.; Dalezios, N.R.; Loukas, A.; Mylopoulos, N.; Spiliotopoulos, M.; Faraslis, I.N.; Alpanakis, N.; Sakellariou, S. Quantitative Classification of Desertification Severity for Degraded Aquifer Based on Remotely Sensed Drought Assessment. Hydrology 2021, 8, 47. [Google Scholar] [CrossRef]
- Raoufi, R.; Beighley, E. Estimating Daily Global Evapotranspiration Using Penman–Monteith Equation and Remotely Sensed Land Surface Temperature. Remote Sens. 2017, 9, 1138. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)—Model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar] [CrossRef]
- Dimitriadou, S.; Nikolakopoulos, K.G. Remote sensing methods to estimate evapotranspiration incorporating MODIS derived data and applications over Greece: A review. In Proceedings of the SPIE 11524, Eighth International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2020), Paphos, Cyprus, 26 August 2020; p. 1152405. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, S.; Jiahua Zhang, J.; Tang, L.S.; Bai, Y. Assessment and Comparison of Six Machine Learning Models in Estimating Evapotranspiration over Croplands Using Remote Sensing and Meteorological Factors. Remote Sens. 2021, 13, 3838. [Google Scholar] [CrossRef]
- Proias, G.; Gravalos, I.; Papageorgiou, E.; Poczęta, K.; Sakellariou-Makrantonaki, M. Forecasting Reference Evapotranspiration Using Time Lagged Recurrent Neural Network. Wseas Trans. Environ. Dev. 2020, 16, 699–707. [Google Scholar] [CrossRef]
- Kitsara, G.; Papaioannou, G.; Retalis, A.; Paronis, D.; Kerkides, P. Estimation of air temperature and reference evapotranspiration using MODIS land surface temperature over Greece evapotranspiration using MODIS land surface temperature. Int. J. Remote Sens. 2018, 39, 924–948. [Google Scholar] [CrossRef]
- Falalakis, G.; Gemitzi, A. A simple method for water balance estimation based on the empirical method and remotely sensed evapotranspiration estimates. J. Hydroinform. 2020, 22, 440–451. [Google Scholar] [CrossRef]
- Tsouni, A.; Kontoes, C.; Koutsoyiannis, D.; Elias, P. Estimation of Actual Evapotranspiration by Remote Sensing. Sensors 2008, 8, 3586–3600. [Google Scholar] [CrossRef]
- Vasiliades, L.; Spiliotopoulos, M.; Tzabiras, J.; Loukas, A.; Mylopoulos, N. Estimation of crop water requirements using remote sensing for operational water resources management. In Proceedings of the Third International Conference on Remote Sensing and Geoinformation of the Environment (RSCy2015), Paphos, Cyprus, 19 June 2015; Volume 9535. [Google Scholar] [CrossRef]
- Dimitriadou, S.; Nikolakopoulos, K.G. Development of GIS models via optical programming and python scripts to implement four empirical methods of reference and actual evapotranspiration (ETo, ETa) incorporating MODIS LST inputs. In Proceedings of the SPIE 11856, Remote Sensing for Agriculture, Ecosystems, and Hydrology XXIII, 118560K, Madrid, Spain, 12 September 2021. [Google Scholar] [CrossRef]
- Allen, R.; Pereira, L.; Raes, D.; Smith, M. Crop evapotranspiration–Guidelines for computing crop water requirements. In Irrigation and Drainage, Paper No. 56; FAO: Rome, Italy, 1998; Volume 300. [Google Scholar]
- Pereira, L.S.; Allen, R.G.; Smith, M.; Raes, D. Crop evapotranspiration estimation with FAO 56: Past and future. Agric. Water Manag. 2015, 147, 4–20. [Google Scholar] [CrossRef]
- Samani, Z. Estimating solar radiation and evapotranspiration using minimum climatological data. J. Irrig. Drain. Eng. 2000, 126, 265–267. [Google Scholar] [CrossRef]
- Dimitriadou, S.; Nikolakopoulos, K.G. Reference Evapotranspiration (ETo) Methods Implemented as ArcMap Models with Remote-Sensed and Ground-Based Inputs, Examined along with MODIS ET, for Peloponnese, Greece. ISPRS Int. J. Geo-Inf. 2021, 10, 390. [Google Scholar] [CrossRef]
- Djaman, K.; Rudnick, D.; Mel, V.C.; Mutiibwa, D.; Diop, L.; Sall, M.; Kabenge, I.; Bodian, A.; Tabari, H.; Irmak, S. Evaluation of Valiantzas’ Simplified Forms of the FAO-56 Penman-Monteith Reference Evapotranspiration Model in a Humid Climate. J. Irrig. Drain. Eng. 2017, 143, 0001191. [Google Scholar] [CrossRef]
- Tegos, A.; Efstratiadis, A.; Malamos, N.; Mamassis, N.; Koutsoyiannis, D. Evaluation of a Parametric Approach for Estimating Potential Evapotranspiration across Different Climates. Agric. Agric. Sci. Procedia 2015, 4, 2–9. [Google Scholar] [CrossRef]
- Valiantzas, J.D. Simplified Reference Evapotranspiration Formula Using an Empirical Impact Factor for Penman’s Aerodynamic Term. J. Irrig. Drain. Eng. 2013, 18, 108–114. [Google Scholar] [CrossRef]
- Zanetti, S.S.; Sousa, E.F.; Oliveira, V.P.S.; Almeida, F.T.; Bernardo, S. Estimating evapotranspiration using artificial neural network and minimum climatological data. J. Irrig. Drain. Eng. 2007, 133, 83–89. [Google Scholar] [CrossRef]
- Noi, P.T.; Degener, J.; Kappas, M. Comparison of Multiple Linear Regression, Cubist Regression, and Random Forest Algorithms to Estimate Daily Air Surface Temperature from Dynamic Combinations of MODIS LST Data. Remote Sens. 2017, 9, 398. [Google Scholar] [CrossRef]
- Paparrizos, S.; Matzarakis, A. Present and future responses of growing degree days for Crete Island. Adv. Sci. Res. 2017, 14, 1–5. [Google Scholar] [CrossRef]
- Taki, M.; Rohani, A.; Yildizhan, H. Application of machine learning for solar radiation modeling. Theor. Appl. Climatol. 2021, 143, 1599–1613. [Google Scholar] [CrossRef]
- Alvarez-Mendoza, C.; Teodoro, A.; Ramirez-Cando, L. Spatial estimation of surface ozone concentrations in Quito Ecuador with remote sensing data, air pollution measurements and meteorological variables. Environ. Monit. Assess. 2019, 191, 155. [Google Scholar] [CrossRef]
- Almeida, C.R.D.; Teodoro, A.C.; Gonçalves, A. Study of the Urban Heat Island (UHI) Using Remote Sensing Data/Techniques: A Systematic Review. Environments 2021, 8, 105. [Google Scholar] [CrossRef]
- Ghosh, A.; Joshi, P.K. Hyperspectral imagery for disaggregation of land surface temperature with selected regression algorithms over different land use land cover scenes. ISPRS J. Photogramm. Remote Sens. 2014, 96, 76–93. [Google Scholar] [CrossRef]
- Mohammad, P.; Goswami, A. A Spatio-Temporal Assessment and Prediction of Surface Urban Heat Island Intensity Using Multiple Linear Regression Techniques Over Ahmedabad City, Gujarat. J. Indian Soc. Remote Sens. 2021, 49, 1091–1108. [Google Scholar] [CrossRef]
- ASCE Task Committee on Application of Artificial Neural Networks in Hydrology. Artificial neural networks in hydrology. I: Preliminary concepts. J. Hydrol. Eng. 2000, 5, 115–123. [Google Scholar] [CrossRef]
- Perugu, M.; Singam, A.J.; Kamasani, C.S.R. Multiple Linear Correlation Analysis of Daily Reference Evapotranspiration. Water Resour. Manag. 2013, 27, 1489–1500. [Google Scholar] [CrossRef]
- Mallikarjuna, P.; Jyothy, S.A.; Sekhar Reddy, K.C. Daily Reference Evapotranspiration Estimation using Linear Regression and ANN Models. J. Inst. Eng. India Ser. A 2012, 93, 215–221. [Google Scholar] [CrossRef]
- Khoshravesh, M.; Sefidkouhi, M.A.G.; Valipour, M. Estimation of reference evapotranspiration using multivariate fractional polynomial, Bayesian regression, and robust regression models in three arid environments. Appl. Water Sci. 2015, 7, 1911–1922. [Google Scholar] [CrossRef]
- Tabari, H.; Kisi, O.; Ezani, A.; Talaee, P.H. SVM, ANFIS, regression and climate based models for reference evapotranspiration modeling using limited climatic data in a semi-arid highland environment. J. Hydrol. 2012, 444–445, 78–89. [Google Scholar] [CrossRef]
- Shirsath, P.B.; Singh, A.K. A Comparative Study of Daily Pan Evaporation Estimation Using ANN, Regression and Climate Based Models. Water Resour. Manag. 2010, 24, 1571–1581. [Google Scholar] [CrossRef]
- Sanford, W.E.; Nelms, D.L.; Selnick, J.; Pope, J.P. Quantifying Components of the Hydrologic Cycle in Virginia Using Chemical Hydrograph Separation and Multiple Regression Analysis; U.S. Geological Survey Scientific Investigations Report 2011-5198; USGS Science Publishing Network: Raleigh, NC, USA, 2011; p. 152. [Google Scholar]
- Sanford, W.E.; Selnick, D.L. Estimation of Evapotranspiration across the Conterminous United States Using a Regression with Climate and Land-Cover Data. J. Am. Water Resour. Assoc. 2013, 49, 217–230. [Google Scholar] [CrossRef]
- Niaghi, A.R.; Hassanijalilian, O.; Shiri, J. Estimation of Reference Evapotranspiration Using Spatial and Temporal Machine Learning Approaches. Hydrology 2021, 8, 25. [Google Scholar] [CrossRef]
- Ohana-Levi, N.; Ben-Gal, A.; Munitz, S.; Netzer, Y. Grapevine crop evapotranspiration and crop coefficient forecasting using linear and non-linear multiple regression models. Agric. Water Manag. 2022, 262, 107317. [Google Scholar] [CrossRef]
- Sharafi, S.; Ghaleni, M.M. Evaluation of multivariate linear regression for reference evapotranspiration modeling in different climates of Iran. Theor. Appl. Climatol. 2021, 143, 1409–1423. [Google Scholar] [CrossRef]
- Soni, A.; Syed, T.H. Analysis of variations and controls of evapotranspiration over major Indian River Basins (1982–2014). Sci. Total Environ. 2021, 754, 141892. [Google Scholar] [CrossRef] [PubMed]
- Bian, Y.; Dai, H.; Zhang, Q.; Yang, L.; Du, W. Spatial distribution of potential evapotranspiration trends in the Inner Mongolia Autonomous Region (1971–2016). Theor. Appl. Climatol. 2020, 140, 1161–1169. [Google Scholar] [CrossRef]
- Yirga, S.A. Modelling reference evapotranspiration for Megecha catchment by multiple linear regression. Modeling Earth Syst. Environ. 2019, 5, 471–477. [Google Scholar] [CrossRef]
- Dimitriadou, S.; Katsanou, K.; Charalabopoulos, S.; Lambrakis, N. Interpretation of the Factors Defining Groundwater Quality of the Site Subjected to the Wildfire of 2007 in Ilia Prefecture, South-Western Greece. Geosciences 2018, 8, 108. [Google Scholar] [CrossRef]
- Copernicus Land Monitoring Service. CLC 2018. © European Union, Copernicus Land Monitoring Service 2018, European Environment Agency (EEA). Available online: https://land.copernicus.eu/pan-european/corine-land-cover/clc2018 (accessed on 11 April 2022).
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Wang, K.; Xu, Q.; Li, T. Does recent climate warming drive spatiotemporal shifts in functioning of high-elevation hydrological systems? Sci. Total Environ. 2020, 719, 137507. [Google Scholar] [CrossRef]
- Rahimikhoob, A. Estimation of evapotranspiration based on only air temperature data using artificial neural networks for a subtropical climate in Iran. Theor. Appl. Climatol. 2010, 101, 83–91. [Google Scholar] [CrossRef]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Gokmen, M.; Vekerdy, Z.; Verhoef, A.; Verhoef, W.; Batelaan, O.; van der Tol, C. Integration of soil moisture in SEBS for improving evapotranspiration estimation under water stress conditions. Remote Sens. Environ. 2012, 121, 261–274. [Google Scholar] [CrossRef]
- Chen, M.; Senay, G.B.; Singh, R.K.; Verdin, J.P. Uncertainty analysis of the Operational Simplified Surface Energy Balance (SSEBop) model at multiple flux tower sites. J. Hydrol. 2016, 536, 384–399. [Google Scholar] [CrossRef]
- Krishnashetty, P.H.; Balasangameshwara, J.; Sreeman, S.; Desai, S.; Kantharaju, A.B. Cognitive computing models for estimation of reference evapotranspiration: A review. Cogn. Syst. Res. 2021, 70, 109–116. [Google Scholar] [CrossRef]
- Maroufpoor, S.; Bozorg-Haddad, O.; Maroufpoor, E. Reference evapotranspiration estimating based on optimal input combination and hybrid artificial intelligent model: Hybridization of artificial neural network with grey wolf optimizer algorithm. J. Hydrol. 2020, 588, 125060. [Google Scholar] [CrossRef]
- Sattari, M.T.; Apaydin, H.; Band, S.S.; Mosavi, A.; Prasad, R. Comparative analysis of kernel-based versus ANN and deep learning methods in monthly reference evapotranspiration estimation. Hydrol. Earth Syst. Sci. 2021, 25, 603–618. [Google Scholar] [CrossRef]
- Dimitriadou, S.; Nikolakopoulos, K.G. Artificial Neural Networks for the Prediction of the Reference Evapotranspiration of the Peloponnese Peninsula, Greece. Water 2022, 14, 2027. [Google Scholar] [CrossRef]
- Seifi, A.; Riahi, H. Estimating daily reference evapotranspiration using hybrid gamma test-least square support vector machine, gamma test-ANN, and gamma test-ANFIS models in an arid area of Iran. J. Water Clim. Chang. 2020, 11, 217–240. [Google Scholar] [CrossRef]
- Ferreira, L.B.; da Cunha, F.F.; de Oliveira, R.A.; Fernandes Filho, E.I. Estimation of reference evapotranspiration in Brazil with limited meteorological data using ANN and SVM—A new approach. J. Hydrol. 2019, 572, 556–570. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Oxford, UK; Waltham, MA, USA, 2006. [Google Scholar]
- Willmott, C.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- McVicar, T.R.; Roderick, M.L.; Donohue, R.J.; Li, L.T.; Van Niel, T.G.; Thomas, A.; Grieser, J.; Jhajharia, D.; Himri, Y.; Mahowald, N.M.; et al. Global review and synthesis of trends in observed terrestrial near-surface wind speeds: Implications for evaporation. J. Hydrol. 2012, 416–417, 182–205. [Google Scholar] [CrossRef]
| Formulae of the Indices | |
|---|---|
| (2) | (3) |
| (4) | (5) |
| (6) | (7) |
| Models | Independent Variables | Sig. | Adj. R2 | D–W | Cook’s D | C. Leverage | SE | RMSE | NRMS | MAE | IoA |
|---|---|---|---|---|---|---|---|---|---|---|---|
| MLR1 | N | <0.001 | 0.960 | 1.742 | 0.003 ± 0.006 | 0.003 ± 0.0001 | 0.034 ± 0.0003 | 0.409 | 0.121 | 0.320 | 0.990 |
| MLR2 | N, Tmean | <0.001 | 0.971 | 1.732 | 0.004 ± 0.010 | 0.007 ± 0.004 | 0.035 ± 0.006 | 0.343 | 0.102 | 0.248 | 0.993 |
| MLR3 | N, Tmean, u2 | <0.001 | 0.975 | 1.675 | 0.004 ± 0.011 | 0.010 ± 0.015 | 0.036 ± 0.011 | 0.321 | 0.095 | 0.238 | 0.994 |
| MLR4 | N, Tmean, u2, es − ea | <0.001 | 0.980 | 1.784 | 0.005 ± 0.014 | 0.014 ± 0.016 | 0.036 ± 0.011 | 0.286 | 0.085 | 0.214 | 0.995 |
| MLR5 | N, Tmean, u2, es − ea, Rn | <0.001 | 0.981 | 1.738 | 0.004 ± 0.014 | 0.017 ± 0.018 | 0.039 ± 0.011 | 0.280 | 0.083 | 0.206 | 0.995 |
| MLR6 | N, Tmean, u2, es − ea, Rn, Z | <0.001 | 0.981 | 1.746 | 0.005 ± 0.014 | 0.021 ± 0.019 | 0.044 ± 0.012 | 0.276 | 0.082 | 0.206 | 0.995 |
| MLR7 | Rn | <0.001 | 0.955 | 2.093 | 0.003 ± 0.006 | 0.003 ± 0.001 | 0.036 ± 0.003 | 0.429 | 0.127 | 0.323 | 0.989 |
| MLR8 | Rn, u2 | <0.001 | 0.969 | 1.949 | 0.004 ± 0.007 | 0.007 ± 0.011 | 0.035 ± 0.010 | 0.357 | 0.106 | 0.280 | 0.992 |
| MLR9 | Rn, u2, Tmean | <0.001 | 0.975 | 1.952 | 0.005 ± 0.019 | 0.010 ± 0.013 | 0.036 ± 0.011 | 0.321 | 0.095 | 0.251 | 0.994 |
| MLR10 | Rn, u2, Tmean, Z | <0.05 | 0.975 | 1.904 | 0.005 ± 0.015 | 0.014 ± 0.014 | 0.041 ± 0.011 | 0.318 | 0.094 | 0.249 | 0.994 |
| MLR11 | Rn, u2, Tmean, Z, Rs | <0.05 | 0.976 | 1.922 | 0.005 ± 0.016 | 0.017 ± 0.016 | 0.042 ± 0.012 | 0.313 | 0.093 | 0.245 | 0.994 |
| MLR12 | Tmean | <0.001 | 0.918 | 1.857 | 0.003 ± 0.004 | 0.003 ± 0.002 | 0.048 ± 0.008 | 0.582 | 0.172 | 0.461 | 0.978 |
| MLR13 | Tmean, u2 | <0.05 | 0.920 | 1.842 | 0.007 ± 0.046 | 0.007 ± 0.012 | 0.056 ± 0.018 | 0.574 | 0.170 | 0.467 | 0.979 |
| MLR14 | Rs | <0.001 | 0.918 | 2.098 | 0.003 ± 0.006 | 0.003 ± 0.002 | 0.048 ± 0.006 | 0.582 | 0.172 | 0.442 | 0.978 |
| MLR15 | u2 | <0.05 | 0.030 | 0.122 | 0.003 ± 0.003 | 0.003 ± 0.012 | 0.154 ± 0.064 | 2.001 | 0.592 | 1.953 | 0.120 |
| MLR16 | es − ea | <0.001 | 0.817 | 1.884 | 0.003 ± 0.007 | 0.003 ± 0.003 | 0.071 ± 0.014 | 0.868 | 0.257 | 0.637 | 0.947 |
| Model | Multiple Linear Regression Equation | Adj. R2 |
|---|---|---|
| MLR5 | (2) | 0.981 * |
| MLR1 | (3) | 0.960 * |
| MLR7 | (4) | 0.955 * |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dimitriadou, S.; Nikolakopoulos, K.G. Multiple Linear Regression Models with Limited Data for the Prediction of Reference Evapotranspiration of the Peloponnese, Greece. Hydrology 2022, 9, 124. https://doi.org/10.3390/hydrology9070124
Dimitriadou S, Nikolakopoulos KG. Multiple Linear Regression Models with Limited Data for the Prediction of Reference Evapotranspiration of the Peloponnese, Greece. Hydrology. 2022; 9(7):124. https://doi.org/10.3390/hydrology9070124
Chicago/Turabian StyleDimitriadou, Stavroula, and Konstantinos G. Nikolakopoulos. 2022. "Multiple Linear Regression Models with Limited Data for the Prediction of Reference Evapotranspiration of the Peloponnese, Greece" Hydrology 9, no. 7: 124. https://doi.org/10.3390/hydrology9070124
APA StyleDimitriadou, S., & Nikolakopoulos, K. G. (2022). Multiple Linear Regression Models with Limited Data for the Prediction of Reference Evapotranspiration of the Peloponnese, Greece. Hydrology, 9(7), 124. https://doi.org/10.3390/hydrology9070124







