Abstract
This study of the Quantitative Estimation Precipitation (QEP) of rainfall, detected by two Meteorology Radars over Chi Basin, North-east Thailand, used data from the Thai Meteorological Department (TMD). The rainfall data from 129 rain gauge stations in the Chi Basin area, covering a period of two years, was also used. The study methodology consists of: firstly, deriving the QPE between radar and rainfall based on meteorological observations using the Marshall Palmer Stratiform, the Summer Deep Convection, and Regression Model and calibrating with rain gauge station data; secondly, Bias Correction using statistical method; thirdly, determining spatial variation using three methods, namely Kriging, Inverse Distance Weight (IDW), and the Minimum Curvature Method. The results of the study demonstrated the accuracy of estimating precipitation using meteorological radar. Estimated precipitation compared against an equivalent of 2 years of rain station measurement had a probability of detection (POD) of 0.927, where a value of 1 indicated perfect agreement, demonstrating the effectiveness of the method used to calibrate the radar data. The bias correction method gave high accuracy compared with measured rainfall. Furthermore, of the spatial estimation of rainfall methods, the Kriging methodology showed the best fit between estimation of rainfall distribution and measured rainfall distribution. Therefore, the results of this study showed that the rainfall estimation, using data from a meteorology radar, has good accuracy and can be useful, especially in areas where it is not possible to install and operate rainfall measurement stations, such as in heavily forested areas and/or in steep terrain. Additionally, good accuracy rainfall data derived from radar data can be integrated with other data used for water management and natural disasters for applications to reduce economic losses, as well as losses of life and property.
1. Introduction
In Thailand, several hydrology models have been applied (e.g., SWAT, HEC-HMS) for a variety of water resource purposes. These hydrology models play a major role in developing an understanding of the hydrological dynamics of catchments, and they are widely used in water resources management, flood control, drainage design, water supply, and irrigation. In these models, rainfall data are an indispensable input necessary to operate the models. Traditionally, rainfall datasets obtained from rain gauges were used as input to hydrological models. There is an opportunity to use meteorological radars to derive rainfall data, which, if successful, can be used as input in hydrology models.
The radar type used in this study was Weather Radar Double Polarization, which emits electromagnetic transmissions. These emissions are back scattered by atmospheric hydrometeors in the form of reflectivity.
where Z is radar reflectivity (mm6.m−3), R is rainfall Rate (mm.hr−1), and a and b are the coefficients, which depend on climate and location, including season and type of rain. For equilibrium rainfall condition, a linear Z-R relationship is observed, i.e., b =1.
Z = a.R.b
Marshall et al. [1] derived the values a = 200 and b = 1.6, and in this form, it is commonly known as the Marshall Palmer Stratiform method. It has been indiscriminately used regardless of climatic region. These parameters, in fact, do change (Wilson et al. [2]) and appear to depend on the size and distribution of atmospheric hydrometeors. Atmospheric hydrometeors’ size distribution varies with the type and phase of the precipitation (Joss et al. [3]; Uijlenhoet [4]; Chumchean et al. [5]). Errors and uncertainties in the measurement of reflectivity, as well as the conversion of reflectivity to rainfall rates on the ground, have meant that the advances in and the advantages of radar precipitation data have not been fully realized in many hydrology applications (Chumchean et al. [6]; Berne et al. [7]).
Ciach et al. [8] employed the non-parametric kernel regression method to model radar rainfall uncertainty. Fewer assumptions about the processes being modelled need to be invoked when sufficient observational data exist, so this method can be more effective than parametric methods (Silverman [9]; Mehrotra et al. [10]). While nonparametric techniques have the ability to adjust to data on a local level, outliers can cause local biases.
The advantage of the extensive spatial coverage of weather radars is that they are able to monitor many small catchments in some areas, which may remain unmonitored and therefore without precipitation records (Berne et al., [7]). Additionally, the various difficulties in measuring spatial variability of precipitation and intermittent precipitation, as well as measuring under some types of catchment cover (forest) and terrain (mountains), makes estimation of spatial distribution of rainfall in a catchment with a sparse rain gauge network very difficult (Hwang et al. [11]). This translates to modeling using hydrological distributed models. Their accuracy is limited by the availability of reliable spatial rainfall input data. (Syed et al. [12]). Spatial interpolation techniques can be useful in catchments where rain gauges are unevenly distributed. Such methods include simple ones: Kriging, Inverse distance weighting, and Minimum curvature. A review of different interpolation methods was presented by Hwang et al. [11], where the rain gauge was a single sensor. Obtaining a distributed precipitation field over various river gauged areas over Chi basin remained a challenging task to undertake. Taking advantage of the spatial variability of radar, by focusing on merging radar and gauge data, could further improve the spatial interpolation of gauges. Rabiei et al. [13], demonstrated that the main factor determining the quality of the result is if the quantitative radar data are good. Hasan et al. [14,15], showed that rain gauge and radar could be merged when errors associated with the precipitation field derived of both can be quantified correctly. This approach is promising because, in sparsely gauged regions, the error structure developed from radar and rain gauge data and translated to nearby ungauged regions.
This study used data from the Chi Basin located on the north-eastern Thailand. The catchment has two dams: Lampao Dam and Ubonrat Dam. The purpose of this study is to obtain high accuracy rainfall data from weather radars that may be input to hydrological models for dam operations, flood, and agriculture-related applications and catchment management, especially in areas which are poorly gauged.
2. Data and Methods
2.1. Study Area and Data
The Chi River is the longest river that wholly flows within Thailand. The river sources from the Phetchabun mountains. The river flows from east to west before joining the Mun River, which ultimately runs into the Mekong River. The Chi Basin (Figure 1) covers an area of approximately 49,132 km2, is located in north-eastern Thailand, and extends over 14 provinces in Thailand, namely Chaiyaphum, Khon Kaen, Nongbua lamphu, Udonthani, Mahasarakham, Nakonratchasima, Loei, Phetchabun, Kalasin, Roiet, Yasothon, Ubon Ratchathani, Sisaket, and Mukdahan. The Chi Basin is located between latitude 15°30′ north and 17°30′ north, as well as between longitude 101°30′ east and longitude 104°30′ east.
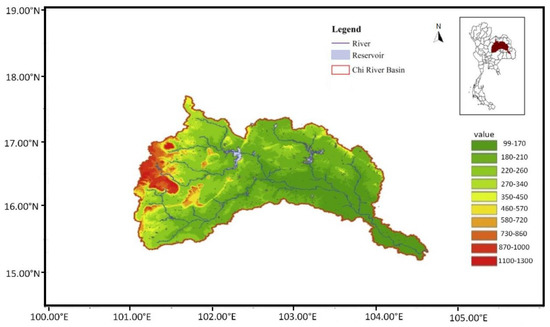
Figure 1.
Chi River Basin, including its major rivers, is located in north-eastern Thailand. An inset map of Thailand shows the location of the Chi Basin within Thailand.
The elevation of the land varies from 1250 m in the Phetchabun mountains to 150 m in the river flood plains. Most of the land is predominantly flat with land slope of less than 10%. The dominant land use is agricultural (rice, sugar cane, rubber, orchards, vegetables, and pastures. Other land uses are urbans areas and forests in the mountain regions and in some lowland areas.
2.2. Radar Data
The Khon Kaen radar station is located at latitude 17.1564 degrees north and longitude 104.1326 degrees east. The Sakon–Nakhon radar station is located at latitude 16.4625 degrees north and longitude 102.7859 degrees east. Both antenna are 196 m above sea level and measure at radar angles of 0.5, 1, 1.5, and 2. The radial coverage (as shown in Figure 2) is 240 km. Radar data were measured every 15 min. The rainfall radar data were measured in units of plan position indicator (PPI).

Figure 2.
Coverage of Khon Kaen radar (green) and Sakon–Nakhon radar (purple) over the Chi Basin, showing the overlap between the two radars. Dots mark the center of the coverage where the radars are located.
The Khon Kaen and Sakon–Nakhon radars have common coverage of several provinces, such as Chaiyapoom, Nakorn Ratchasim, Loei, Burirum, etc. (see Figure 2), and here, the composite data were used to reduce error and increase the accuracy in reflectivity of the radar. In the common coverage area in the Chi Basin, the average values of the radar data were used to calculate a dataset at 2 km altitude. The Barnes filter is used for this purpose. Barnes [16,17] assumed that a Fourier was integral to describe the distribution of an atmospheric variable. A filter based on a Gaussian weighting function was proposed to separate different-scale signals from a 2D field to reduce calculation and computational time. There are several studies demonstrating its performance in separating signal with different scales from 2D meteorological field (Morris et al. [18]; Zhang et al. [19]).
2.3. Rainfall Data
The raw dataset used in this study comes in two parts. The first part is the raw data downloaded from the radars located at Khon Kaen and Sakon–Nakhon. The second part is rainfall data from meteorological rain gauge stations.
The UF (Universal format) data from radars was developed to the lowest PPI (plan position index). The reflectivity data at various elevations are projected down to a reference elevation (2 km) from the ground. The projection, known as a VPR (vertical profile of reflectivity) correction, is applied to account for the variability in the vertical profile and for the bright band effect (Elo [20]). A single Z–R relationship was applied at 15 min intervals to convert reflectivity into precipitation rates. The 15 min precipitation rates were then accumulated to hourly rates and distributed to the end user as an hourly radar precipitation rate surface rainfall intensity (SRI) product. This SRI product was used in the present study.
The rainfall data used in this study were from the Thailand Meteorological Department (TMD) rain gauges at locations shown in Figure 3. There are 129 rain gauge stations in Chi Basin generally within latitude 15–18° North and longitude 101–105° East.

Figure 3.
Location of 129 rain gauge stations in the Chi Basin study area.
The reflectivity is measured by the radar and can be converted to rates of ground precipitation, typically, using Equation (1).
2.4. Methodology
The two sources of rainfall data from the radar and from rain gauges were merged using a procedure outlined in the flow diagram shown in Figure 4. The framework shows the data used and the methods applied in the merging process which was conducted in a two-step process.

Figure 4.
Flow diagram for processing and merging radar and rain gauge rainfall to create spatial rainfall map and data for the Chi Basin.
Before merging, it is first necessary to apply possible corrections that could enhance the estimates of radar rainfall rates (Goudenhoofdt et al. [21]). The hourly rainfall rates were first adjusted with a non-parametric method using data from rain gauges. Since the rainfall gauge data are at specific positions, a spatial interpolation is required to estimate rainfall values at grid points. At grid points, rainfall data from the two sources (radar and gauge) were merged using the estimated combination weights and the 1D-Var bias correction (see Figure 4). Each step is described in detail in the following subsections.
2.4.1. Rain Gauge Interpolation
The rainfall data from 129 rain gauge stations over the Chi Basin are used to determine rainfall at specific locations using the Kriging-based interpolation method. The method uses the spatial association from the radar data to interpolate and determine the rain values at specific grid points. The equation of ordinary Kriging is shown as Equation (2).
where z0 = estimated value at the unobserved location; zx = observed value at the location x; wx = weight mean average; s = the number of locations used for observation.
The Kriging-based interpolation method predict rain values at ungauged locations by applying linear weights derived at gauged locations obtained by minimizing the variance of the error. The rainfall data at various positions are characterized as Gaussian random variables.
2.4.2. Radar Dataset Development
The meteorological radar dataset between June and September each year, from 2018 to 2019, was used to estimate rainfall in the study. The Khon Kaen and Sakon–Nakhon radar data, in the form of text files (.uf files), were used. The .uf files were converted to CAPPI (constant altitude plan position indicator), which, in this study, was set at an altitude of 2 km. This altitude was set to be clear of rainfall clouds. The conversion was done using python script and kept in the form of .cdf files.
2.4.3. Z-R Relationship Development
In this study, the Z–R parameters were derived by considering the scattering regime calculation, which is the profile drop of rainfall size distribution. Radar and rain gauge station rainfall intensity were at different time periods—the former every 15 min and the latter every hour. The radar dataset was maintained at 1 h, while rain gauge station data within 1 h periods were accumulated, so it could be compared appropriately with the former. In this study, two methods were used. The first method used the radar datasets and rain gauge station data for the entire year. The second method used a discontinuous dataset comprising only data from the rainy season (June to September). In both methods, the radar reflectivity data were filtered for negative values and not a number (NaN) values, and both were ignored in the processing. Similarly, rainfall NaN values or negative ones were replaced with unknown and similarly ignored. The aim of trialing the two different methods is to determine which method gives the smaller error.
Linear regression of the log transformation of R and Z (logR vs logZ) was applied to find the constants (a, b) of the nonlinear power law equation Z = aRb. Several methods were used to find the Z–R relationship in this study, namely the Marshall Palmer Stratiform method (Equation (3)), Summer Deep Convection method (Equation (4)), and Regression Model:
Summer deep Convection→ Z = 300R1.4
Marshall Palmer Stratiform→ Z = 200R1.6
2.4.4. Validation Methods
‘Continuous statistics’ means criteria that use the full range of values of data distribution functions of the observed and the forecasted values. This comparison is not sensitive to the space structure of the fields being compared. It can be complemented by the use of scatter diagrams, which take into account the structure. The comparison can be reduced to obtain bulk scores, such as the bias (BIAS), the root mean square error (RMSE), or the square of the correlation coefficient (R2), as defined in Section 2.4.5.
To determine how well the radar forecast compares, qualitatively, with rain gauge stations, four different verification indices, i.e., POD, POFD, FAR, and CSI, were studied. Table 1 defines the parameters used for deriving these verification indices, which were used for testing the qualitative accuracy of the relationship between radar data (forecast) and rain gauge station data (observed). A decision threshold for radar was set at <0.1 mm (for no rain) and ≥0.1 mm (for rain). POD, POFD, FAR, and CSI can be computed as follows.

Table 1.
Binary Contingency table for whether or not rain is forecast.
- 1.
- Probability of Detection (POD) (Berens et al. [22]) is the ratio of hits (a) to the total number of hits and miss (a + b).
POD = a/(a +b)
For a perfect forecast, POD is equal to 1, i.e., b, the number of miss, is equal to zero.
- 2.
- False-alarm ratio (FAR) (Mason et al. [23]) accounts for the number of false alarms (c) compared to the number of hits and false alarms (a + c).
FAR = c/(a + c)
For a perfect forecast FAR equal to 0 i.e., c, the number of false alarms, is equal to zero.
- 3.
- Probability of false detection (POFD) (Berens et al. [22]) is the ratio of false alarms (c) to the number of false alarms and correct rejections (c + d).
POFD = c/(c + d)
- 4.
- Threat score (TS) (Wilks, [24]) is ratio of hits (a) to observed yes (rain) events plus false alarms (a + b + c)
TS = CSI = a/(a+ b + c)
The POD, FAR, and CSI scores are qualitative in nature and generally need to be examined together with quantitative validators. For this purpose, ME, MAE, and RMSE were calculated.
2.4.5. Rain Gauge Interpolation Category Merging using Spatial Association of Radar
Radar rainfall is well known for its superior coverage both spatially and temporally. Methods to merge radar and rainfall gauge data are generally classed as bias reduction and error variance minimization (Ochoa-Rodriguez et al. [25]). In the merging process, the most important step is to find the spatial correlation in the error structure model. This process takes the form that is described in three steps. First, bias adjustment of radar rainfall was applied; second, radar rainfall and rain gauge data integration methods were applied; third, rain gauge interpolation methods were applied using radar spatial association as a guide (Wang. et al. [26]).
In this study, three methods were used as merging interpolation, which are Kriging, Inverse distance weighting (IDW), and minimum curvature. Several statistical metrics have been used in literature to assess the performance of the models (or datasets) and to compare them (Villarini et al. [27]; Hasan et al. [15]). In this study, the performance of spatial interpolation between rain gauge and radar was also tested using root mean square error (RMSE), mean absolute error (MAE), mean error (ME), and correlation coefficient (CC). The mathematical equations of these are described below:
where = Rainfall intensity (mm/hr); = Average rainfall (mm/h); = rainfall intensity from measurement (mm/h); = average rainfall (mm/h); = number of data.
RMSE represents the forecasting error and estimates the sample standard deviation of the differences between predicted values and observed values. A RMSE value of zero indicates a perfect match, whereas higher values represent a smaller match between the observed and modelled output. It is a good measure when large model errors are not desirable. The RMSE is a good measure of overall performance (Hasan et al. [15]). CC indicates the statistical relationship between two variables (Boddy [28]), conformity with each other, and their linear dependence. The CC lies between 0 and 1, where 0 means no correlation, whereas 1 means that the dispersion of prediction is equal to that of the observation. In general, high CC values and low values for RMSE indicate good model predictions.
2.4.6. Statistical Verification and Evaluation Methods to Compare Radar with Rain Gauge Stations
Bias correction for 1D-Var is used, in this study, to decrease the error between radar and rain gauge station data. The bias and variance is given by
where Bi = Bias of rainfall quantity between the rain gauge station and radar data; var R = variance of set of rain gauge station data; var S = variance of radar data; Si = Estimation of quantity of rainfall from radar data; Ri = Estimation of rainfall from rain gauge station.
3. Results
The study of rainfall intensity was conducted using meteorological radar data from the Chi Basin collected between June and September in the years 2018 to 2019. The radar coverage at Khon Kaen and Sakon–Nakhon is shown in Figure 5a,b. Each radar covers a circular area of a 240 km radius. The composite radar coverage (shown in Figure 2) shows the area of overlap radar data. In the area where the two radar coverage areas overlap, the mean average data were calculated and used as inputs for CAPPI. After that, the composite radar over the Chi Basin, in constant altitude plan position indicator (CAPPI) form, was found by applying a python script to the two radar input dataset in *.utf file format. Where there are two radar readings available, the noise from reflectivity radar data, based on different topography and degree of radar, can be reduced.
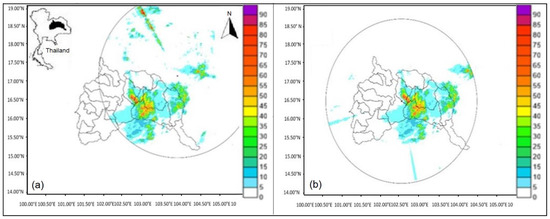
Figure 5.
The output of radar at (a) Khon Kaen weather meteorological radar station and (b) Sakon–Nakhon weather meteorological radar station on the date of 25 Sep 2019.
Figure 6 shows the relationship between rainfall rate and reflectivity in parabolic form Z = aRb. The figure also shows the comparison between the three relationships: Marshall Palmer Stratiform, Summer Deep Convection, and one derived by Regression Analysis for reflectivity and rainfall rate. Linear regression of the log transformation was applied to find the constants (a, b) in the equation Z= aRb. While the trend in each relationship is the same, there is a large scatter in the data, which prevents any one relationship from representing the data well.
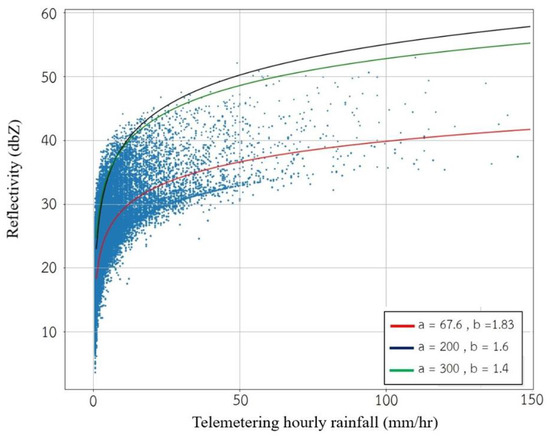
Figure 6.
The distribution of the telemetered rainfall rate (rain gauge data), with reflectivity for Marshall Palmer Stratiform (blue line), Summer Deep Convection (green), and Linear Log Regression (red). Data are for the years 2018 and 2019.
The new approach was taken by filtering (outlined in Section 2.4.3) the discontinuous rainfall data (June to September) of rain gauge stations and meteorological radar to reduce the error. Data after filtering were used for regression analysis to develop the Z–R equation. Figure 7 shows the relationship between rainfall rate and reflectivity after filtering. The scatter in the data is greatly reduced. Figure 7a also shows the comparison between the three relationships—Marshall Palmer Stratiform, Summer Deep Convection, and the Regressed Equation Z = 137.8R1.124—for reflectivity and rainfall rate. The data exclusively fits the latter relationship and the accuracy significantly improved. This is because small errors significantly affect small rainfall depths that occur during the dry season and significantly affect the overall accuracy. The relationship between telemetered rainfall intensity and estimated rainfall derived from reflectivity and the Regressed Equation is shown in Figure 7b. It shows a significant improvement over the results shown in Figure 6. At higher intensities, there exist few pieces of data to define the Z–R relationship, and the scatter is more evident (Figure 7b). This undoubtedly will improve with the collection of more data that will adequately define the Z–R relationship for high rainfall intensities.
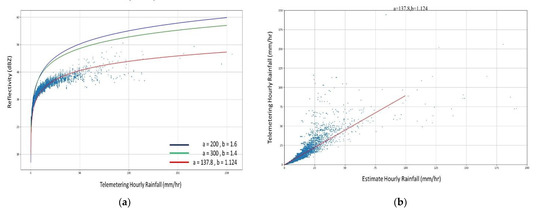
Figure 7.
The relationship between rainfall rate (R) (mm/hr) and reflectivity (Z) in parabolic form. Data are for between June and September for the years 2018 and 2019. (a) The distribution of telemetered rainfall rate (rain gauge data) with reflectivity for Marshall Palmer Stratiform (blue line), Summer Deep Convection (green), and Linear Regression (red). (b) The distribution of telemetered rainfall (rain gauge data) and estimated rainfall rate based on Regression Equation, Z = 137.8R1.124, and radar reflectivity.
Table 2 shows that the equation Z = 137.8R1.124 has the lowest RMSE equal to 3.54 with R2 0.795. By comparison, the Marshall Palmer and Summer Deep Convention methods had much larger RMSE values. From Table 2, MAE and RMSE are calculated by using estimating hourly rainfall and telemetering hourly rainfall.

Table 2.
Results of statistical testing of composite radar, comparing with three methods.
3.1. Statistics Validation based Contingency Tables
Analysis of data, based on the contingency table (Table 1), gives a qualitative evaluation of the data. Table 3 shows the values of hit, miss, etc., and statistical validation using POD, TS, etc., for daily cumulative rainfall (24 hrs) during the period 2018–2019.

Table 3.
Statistical validation using POD, TS (CSI), FAR, POFD for the period 2018–2019. Only months between June and September were analyzed.
Table 3 shows that the hits (a) are much larger than misses (b), and correct rejection (d) is much larger than false alarm (c), as should be expected. Misses are much smaller than false alarms by up to 15 times. False alarms occur when rain is detected by radar and not by rain gauge, with the latter being more reliable. Rainfall rates derived from reflectivity, from meteorological radar, are accumulated over 24 h periods and carry errors which accumulate over that period. Note that an accumulated rainfall intensity over the threshold 0.1 mm/day is counted as rain and can lead to a larger number of false alarms than if a higher rain threshold was adopted for radar detection. False alarms (c) are more prone to error than misses (b) (Yates et al. [29]).
The score of POD was high for all months shown and was close to a perfect forecast in July 2018 (0.921). For a perfect forecast, POD = 1. However FAR was as high as 0.73. For a perfect forecast, FAR = 0. FAR is the ratio of poorly predicted locations to the locations where the forecast is above the threshold (0.1 mm/day) (Yates et al. [29]). Except for the month of August 2019, when FAR was 0.16, values were generally high. When comparing hit (a) vs false alarms (c) in (Table 3), false alarms were generally high except for August and September 2019, leading to large FAR values. This was exacerbated in 2018 when hits (a) were generally low because of fewer incidents of rain events compared to 2019. False alarms are more prone to error, as noted above, and less reliable than misses (b). In this respect, POD, which uses misses (b), is a better indicator of reliability than FAR based on false alarms (c).
POFDs were generally low, which are good results, indicating false alarms (c) are low relative to correct rejections (d). Even though false alarms are prone to error, their occurrence is still relatively small compared to correct rejection.
TS were generally higher in 2019 and lower in 2018. This reflects a higher occurrence of precipitation events in 2019, i.e., hits (a) are higher. Further TS are high when hits (a) are high, e.g., in August 2019.
3.2. Result of using Spatial Methods to Interpolate Rainfall over Chi Basin
There were three methods used to interpolate rainfall station data: inverse distance weighting (IDW), minimum curvature, and Kriging. The statistical tests used to evaluate and compare the three methods were MAE and RMSE. The results show that Kriging gave the lowest RMSE and MAE compared with IDW and minimum curvature.
The correlation coefficient (CC) (Equation (10)) is a binary class performance assessment of the methods used in this study. A value closer to 1 means a better fit. In this study, Kriging gave the highest correlation coefficient of 0.9577 (Table 4). The MAE and RMSE calculation data are provided by accumulated rainfall radar data after validation for 24 h.

Table 4.
Comparison of validation statistical test for spatial interpolation using Kriging, Minimum curvature (Min. C.), and IDW methods.
The statistical test shows that spatial interpolation using Kriging is more suited and, therefore, was used for the Chi Basin.
3.3. Bias Correction Validation Results
Bias correction was applied by reducing the bias and variance error (Equations (12) and (13)) between radar data and rain gauge station data. The difference after bias correction was tested using statistical test ME, MAE, and RMSE and the results are summarized in Table 5.

Table 5.
The validation of bias correction using statistical test ME, MAE, and RMSE.
Table 5 shows how much improvement bias correction made to the values of MAE and RMSE compared to before bias correction. Bias correction reduced the errors inherent in the data and, consequently, reduced the residual error in merging spatial interpolation data in the Chi Basin region. The results of MAE and RMSE in August and September 2018 and, similarly, in August and September 2019 are high because of the extreme events that occurred (cyclones and typhoons). A part of the reason can be attributed to the few pieces of data that exist to define the Z–R relationship for high rainfall intensities and, later, the resulting scatter (Figure 7b). A better definition of Z–R in this region will improve estimates.
3.4. Rainfall Intensities Maps Derived from Meteorology Radar
Figure 8 shows spatial rainfall maps derived from spatial maps based on rain gauges, together with those from meteorology radar, before and after bias correction. Maps are shown for three events: 25 June 2018 (Figure 8a–c), 17 July 2018 (Figure 8d–f), and 3 September 2019 (Figure 8g–i).

Figure 8.
(a–i) 24 h spatial rain maps based on rain gauge after Kriging, based on radar, and after bias correction for the Chi Basin for 25 June 2018, 17 July 2018, and 3 September 2019.
Figure 8a–c shows the rainfall spatial distribution maps for the event 25 June 2018. The distribution of rainfall intensity, based on rain gauge station measurement, varied between 10–90 mm/h (Figure 8a). The spatial interpolation map derived from radar reflectivity measurements (Figure 8b) was generally similar, although distinct difference in the locations of the boundaries of each rainfall intensity contour is evident. After bias correction (Figure 8c), the spatial rainfall distribution based on rain gauge and based on radar more closely aligned with evidence from the movement of boundaries of each rainfall intensity contour shown when Figure 8b,c are compared.
Figure 8d–f shows the rainfall spatial distribution maps for the event 17 July 2018. The spatial distribution of rainfall intensity, based on rain gauge station measurement varied, more markedly with the maps based on radar data. The spatial rainfall maps after bias correction (Figure 8f) more closely resembled the spatial rainfall distribution based on rain gauge. Radar is better at detecting the spatial distribution of rainfall, although its actual rainfall intensities are less accurate. Bias correction brings these rainfall intensities to be more aligned with those based on rain gauge measurement. In this way, the strength of both measurement methods (radar and rain gauge) is combined where a rainfall spatial map is produced with the methods used here (i.e., Figure 4).
On 3 September 2019, a cyclone occurred in the Chi Basin (Figure 8g–h). The spatial rainfall distribution shows that the rain gauge rainfall intensity was very high in the area south-east of the Chi Basin (Figure 8g). Radar spatial rain intensity resembled the rain gauge derived distribution, although the high intensity region of the former was more extensive (Figure 8h). After bias correction, the rainfall intensity based on radar improved to become similar to that based on rain gauge station measurement (Figure 8i). Even so, some differences are still evident, particularly in the north-east, which is a mountainous region. Topography such as mountainous terrain can obstruct the angle of the radar and limit the effectiveness of radar measurement. The Pupan (north-eastern boundary of Chi Basin) and Petchaboon (western boundary of Chi Basin) mountains are the upstream sources of the Chi River Basin. The Pupan (north-east of Chi Basin) mountains are located near the location of Sakon–Nakhon radar (see Figure 2). Therefore, at some angles, radar reflectivity may be obstructed. At these locations, spatial distribution maps based on radar may be compromised. Merging methods between rain stations and radar are better suited for areas where radar measurement is not limited by terrain such mountainous areas that can obstruct some radar angles at some locations. A part of the reason can also be attributed to the few pieces of data that exist to define the Z–R relationship for high rainfall intensities.
Figure 8a–i demonstrates how rainfall intensity spatial maps based on radar reflectivity data, developed using the method outlined in this paper, showed good agreement with those derived with rain gauge station data. It is assumed that spatial rainfall distribution is better, although the magnitude of rainfall may not be as good. In all cases, the spatial rainfall distribution after bias correct moves closer to the spatial rainfall distribution based on gauged rainfall that are shown in the first column. This is what can be expected as the method builds on the better, the magnitude of rainfall measured by gauged rainfall stations and the better spatial rainfall distribution based on radar rainfall.
The new approach of using the discontinuous rainfall data (June to September) of rain gauge stations and meteorological radar made it possible to derive the Z–R relation using the regression method that significantly improved the outcome of spatial rainfall estimates. The methods of filtering and merging rainfall radar data and rainfall rain gauge station by ignoring NaN, not recorded and negative value data also helped. The use of Kriging methods and 1D-Var bias correction data assimilation also made a significant improvement. Other studies [30,31] observed that, in terms of the scattergram, when the raindrop diameter was less than 0.7 mm, DSDs of the two rainfalls basically coincided, while when the raindrop diameter was greater than 0.7 mm, DSDs of convective rainfall were located above the stratiform rain, including Z–R relationship of radar reflectivity. Adoption of this approach could help further improve the result.
4. Conclusions and Discussions
The statistical tools for validation using RMSE, MAE, bias correction, and two contingency table underpinned the model framework used in this study. The use of Kriging to interpolate rain gauge station data and the application of bias correction to merge with radar measurement is helpful for small catchments. The interpolation and merging methods applied gave spatial maps that displayed the same trend in rainfall intensity, including both those derived from rainfall gauge station and radar measurement.
In this study, a new approach was taken by using the discontinuous rainfall data (June to October) of rain gauge stations and meteorological radar to reduce the error. This made it possible to derive the Z–R relation using the regression method that significantly improved the outcome of spatial rainfall estimates.
The use of NAN filtering between rain gauge station and rainfall radar data also improved spatial merging between radar and rain gauge station. The 1D-Var data assimilation bias correction showed better results than using spatial merging methods between radar and rain gauge station alone.
The use of radar rainfall to improve the spatial accuracy of gauged rainfall has not been shown in the topography and type of rainfall experienced, in regions such as Thailand, with the infrastructure that is available there. This paper provides the evidence of what is possible and provides a useful case study.
The radar angle, the radar’s proximity to mountainous regions, and how it can be affected by mountainous topography are barriers that can limit the accuracy of radar for the measurement of rain intensities. Furthermore, an improvement to the Z–R relationship for high rainfall intensities, with the collection of more data, will also provide better outcomes.
Author Contributions
Conceptualization N.A., S.P. and P.L.; methodology, N.A. and P.L.; formal analysis, P.L.; investigation, N.A. and P.L.; resources, N.A.; curation, P.L.; writing— original draft preparation, N.A. and S.P.; writing—review and editing, J.K.; supervision, N.A.; project administration, N.A.; funding acquisition, N.A. and S.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Research Council of Thailand, grant number 106/2563.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank Thai Meteorological Department for providing the data and Suansunandha Rajhabhat University of Thailand for supporting this project.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Marshall, J.S.; Palmer, W.M.K. The distribution of raindrops with size. J. Meteorol. 1948, 5, 165–166. [Google Scholar] [CrossRef]
- Wilson, J.W.; Brandes, E.A. Radar measurement of rainfall a summary. Bull. Am. Meteorol. Soc. 1979, 60, 1048–1058. [Google Scholar] [CrossRef]
- Joss, J.; Waldvogel, A.; Collier, C. Precipitation measurement and hydrology. In Radar in Meteorology: Battan Memorial and 40th Anniversary Radar Meteorology Conference; American Meteorological Society: Boston, MA, USA, 1990; pp. 577–606. [Google Scholar]
- Uijlenhoet, R. Raindrop size distribution and radar reflectivity-rain rate relationships for radar hydrology. Hydrol. Earth Syst. Sci. 2001, 5, 615–627. [Google Scholar] [CrossRef]
- Chumchean, S.; Seed, A.; Sharma, A. An operational approach for classifying storms in real-time radar rainfall estimation. J. Hydrol. 2008, 363, 1–17. [Google Scholar] [CrossRef]
- Chumchean, S.; Sharma, A.; Seed, A. Radar rainfall error variance and its impact on radar rainfall calibration. Phys. Chem. Earth Parts A/B/C 2003, 28, 27–39. [Google Scholar] [CrossRef]
- Berne, A.; Krajewski, W.F. Radar for hydrology: Unfulfilled promise or unrecognized potential? Adv. Water Resour. 2013, 51, 357–366. [Google Scholar] [CrossRef]
- Ciach, G.J.; Krajewski, W.F.; Villarini, G. Product-error-driven uncertainty model for probabilistic quantitative precipitation estimation with nexrad data. J. Hydrometeorol. 2007, 8, 1325–1347. [Google Scholar] [CrossRef]
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; CRC Press: Boca Raton, FL, USA, 1986; Volume 26. [Google Scholar]
- Mehrotra, R.; Sharma, A. A nonparametric stochastic downscaling framework for daily rainfall at multiple locations. J. Geophys. Res. Atmos. 2006, 111, D15101. [Google Scholar] [CrossRef]
- Hwang, Y.; Clark, M.; Rajagopalan, B.; Leavesley, G. Spatial interpolation schemes of daily precipitation for hydrologic modeling. Stoch. Environ. Res. Risk Assess. 2012, 26, 295–320. [Google Scholar] [CrossRef]
- Syed, K.H.; Goodrich, D.C.; Myers, D.E.; Sorooshian, S. Spatial characteristics of thunderstorm rainfall fields and their relation to runoff. J. Hydrol. 2003, 271, 1–21. [Google Scholar] [CrossRef]
- Rabiei, E.; Haberlandt, U. Applying bias correction for merging rain gauge and radar data. J. Hydrol. 2015, 522, 544–557. [Google Scholar] [CrossRef]
- Hasan, M.M.; Sharma, A.; Johnson, F.; Mariethoz, G.; Seed, A. Merging radar and in situ rainfall measurements: An assessment of different combination algorithms. Water Resour. Res. 2016, 52, 8384–8398. [Google Scholar] [CrossRef]
- Hasan, M.M.; Sharma, A.; Mariethoz, G.; Johnson, F.; Seed, A. Improving radar rainfall estimation by merging point rainfall measurements within a model combination framework. Adv. Water Resour. 2016, 97, 205–218. [Google Scholar] [CrossRef]
- Barnes, S.L. A technique for maximizing details in numerical weather map analysis. J. Appl. Meteor. 1963, 3, 396–409. [Google Scholar] [CrossRef]
- Barnes, S.L. Mesoscale objective analysis using weighted time-series observations. In NOAA Technical Memorandum; National Severe Storms Laboratory: Norman, OK, USA, 1964. [Google Scholar]
- Morris, W.E.; Smith, P.J. Cyclolysis: A diagnosis of two extratropical cyclones. Mon. Weather Rev. 2001, 129, 2714. [Google Scholar] [CrossRef]
- Zhang, S.; Liang, X.; Yi, X. Improvement in the methods for removing isolated non-meteorological echoes and ground clutter in CINRAD. J. Meteor. Res. 2018, 32, 584–597. [Google Scholar] [CrossRef]
- Elo, C.A. Correcting and Quantifying Radar Data; Technical Report; Norwegian Meteorological Institute: Oslo, Norway, 2012. [Google Scholar]
- Goudenhoofdt, E.; Delobbe, L. Evaluation of radar-gauge merging methods for quantitative precipitation estimates. Hydrol. Earth Syst. Sci. 2009, 13, 195–203. [Google Scholar] [CrossRef]
- Berens, A.P. NDE Reliability Data Analysis. In ASM Handbook; ASM International: Materials Park, OH, USA, 1994; Volume 17. [Google Scholar]
- Mason, I. Dependence of the critical success index on sample climate and threshold probability. Aust. Meteorol. Mag. 1989, 37, 75–81. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 3rd ed.; Academic Press: Cambridge, MA, USA, 2011; 676p. [Google Scholar]
- Ochoa-Rodriguez, S.; Wang, L.P.; Willems, P.; Onof, C. A review of radar-rain gauge data merging methods and their potential for urban hydrological applications. Water Resour. Res. 2019, 55, 6356–6391. [Google Scholar] [CrossRef]
- Wang, L.P.; Ochoa-Rodríguez, S.; Simões, N.E.; Onof, C.; Maksimović, C. Radar-rain gauge data combination techniques: A revision and analysis of their suitability for urban hydrology. Water Sci. Technol. 2013, 68, 737–747. [Google Scholar] [CrossRef]
- Villarini, G.; Serinaldi, F.; Krajewski, W.F. Modeling radar-rainfall estimation uncertainties using parametric and non-parametric approaches. Adv. Water Resour. 2008, 31, 1674–1686. [Google Scholar] [CrossRef]
- Boddy, R.; Gordon, S. Statistical Methods in Practice: For Scientists and Technologists. In Statistical Methods in Practice; John Wiley & Sons, Ltd.: Chichester, UK, 2009. [Google Scholar]
- Yates, E.; Anquetin, S.; Ducrocq, V.; Creutin, J.-D.; Ricard, D.; Chancibault, K. Point and areal validation of forecast precipitation fields. Meteorol. Appl. 2006, 13, 1–20. [Google Scholar] [CrossRef]
- Zeng, Y.; Yang, L.; Tong, Z.; Jiang, Y.; Zhang, Z.; Zhang, J.; Zhou, Y.; Li, J.; Liu, F.; Liu, J. Statistical Characteristics of Raindrop Size Distribution during Rainy Seasons in Northwest China, Hindawi. Adv. Meteorol. 2021, 2021, 6667786. [Google Scholar] [CrossRef]
- Thurai, M.; Gatlin, P.N.; Bringi, V.N. Separating stratiform and convective rain types based on the drop size distribution characteristics using 2D video disdrometer data. Atmos. Res. 2016, 169, 416–423. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).