Development of Rating Curves: Machine Learning vs. Statistical Methods
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Statistical Approach—PINAX
- A test of the null hypothesis that the DC is equal to a selected value ρ0 against the alternative hypothesis to be less than ρ0 at a significance level α1.
- A test that the standardised departures from the regression estimations are less than an upper threshold (the acceptable threshold corresponds to a significance level α2).
- A test of the null hypothesis that the standardised deviation of the residuals is equal to a value σ0 against the alternative to be greater with a significance level α3.
- An upper threshold for consecutive positive or negative residuals (the acceptable threshold corresponds to a significance level α4).
- An upper threshold for standardised departures of inputs (stage) and outputs (discharge) from their corresponding mean values (the acceptable threshold corresponds to a significance level α5).
- An upper threshold b6 for the number of clusters.
- The known outliers and breakpoints.
2.2. The Machine Learning Approach
2.2.1. Data Clustering and Filtering
2.2.2. Approximate the Rating Curve with MLP
3. Results
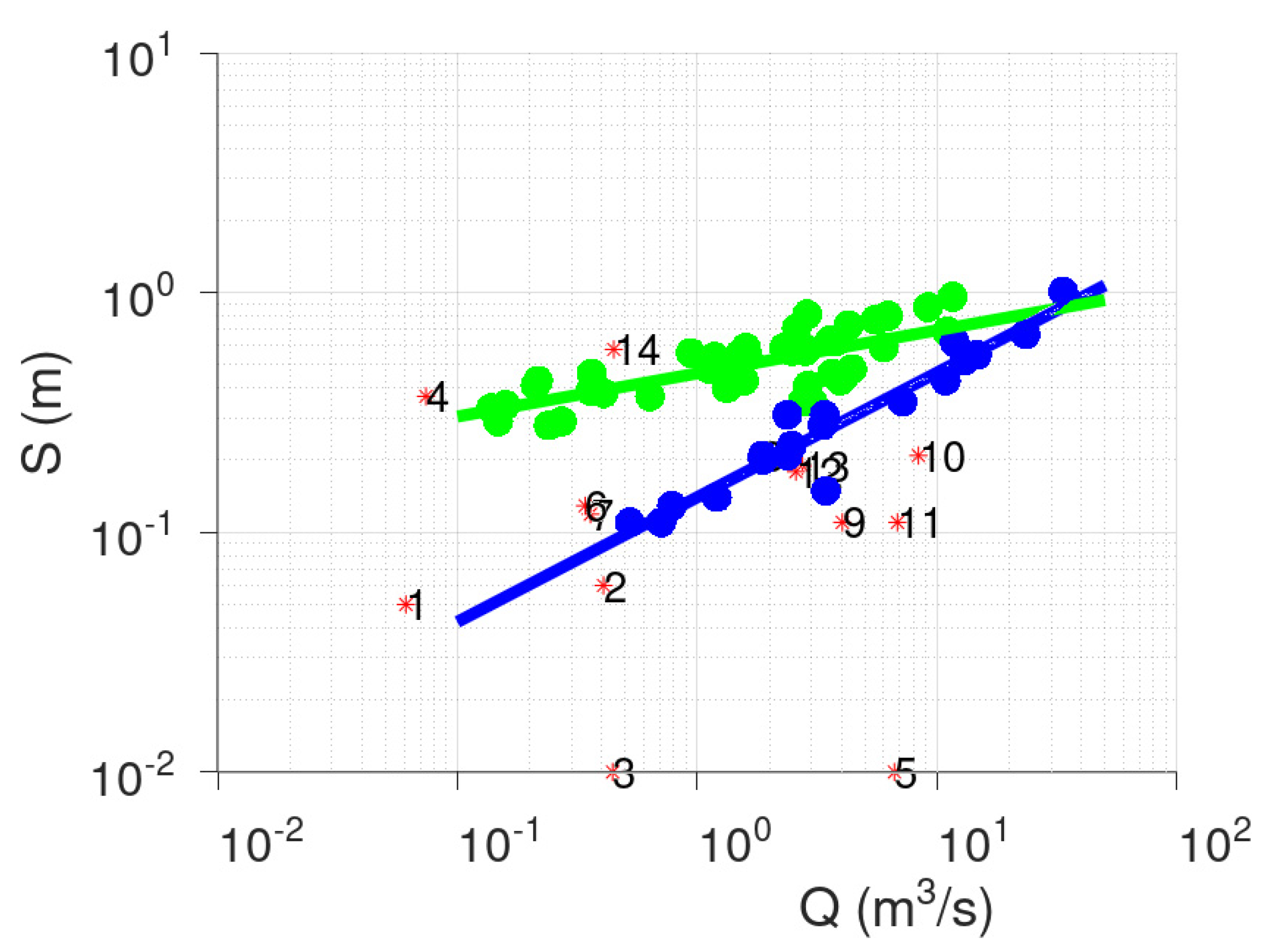
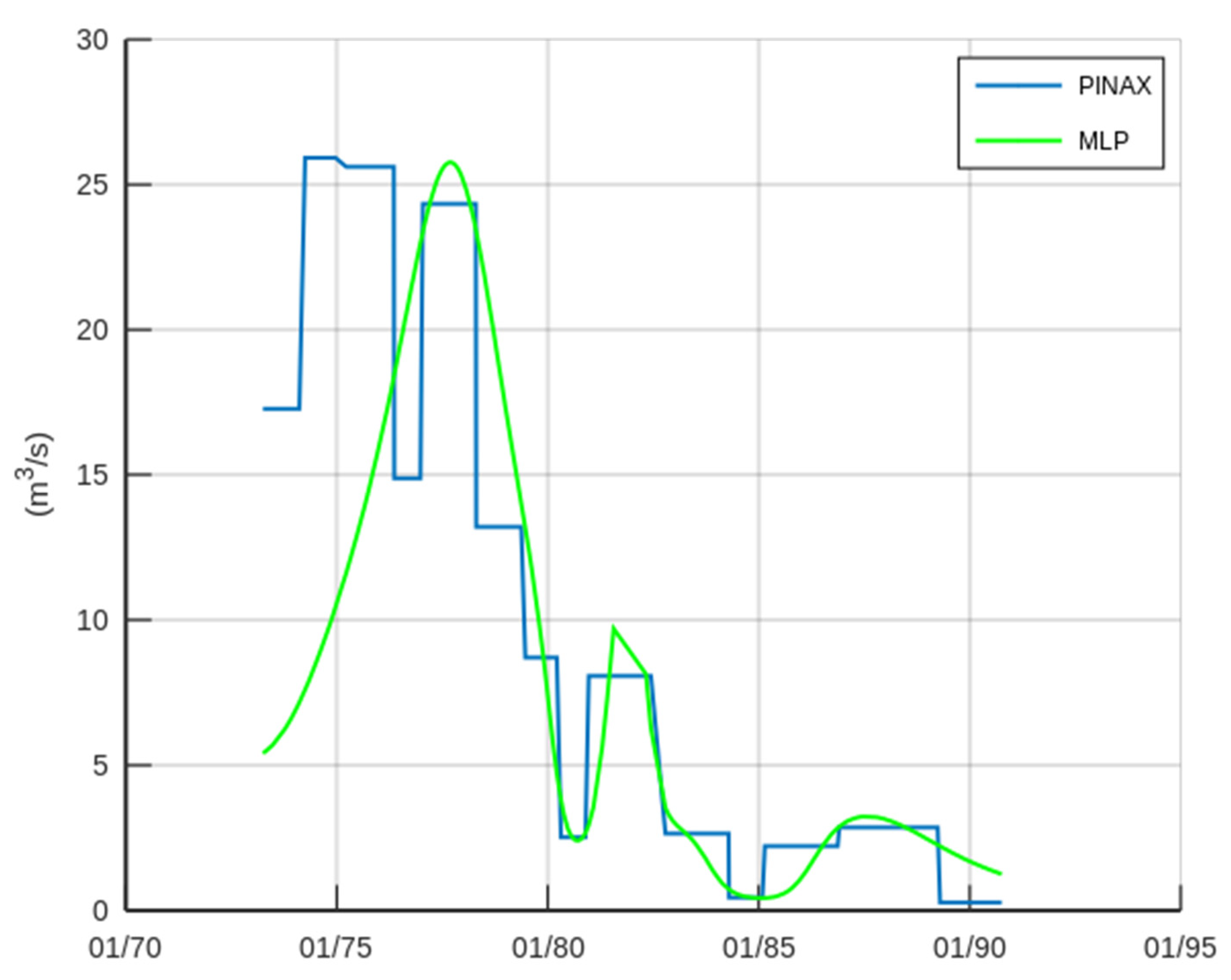
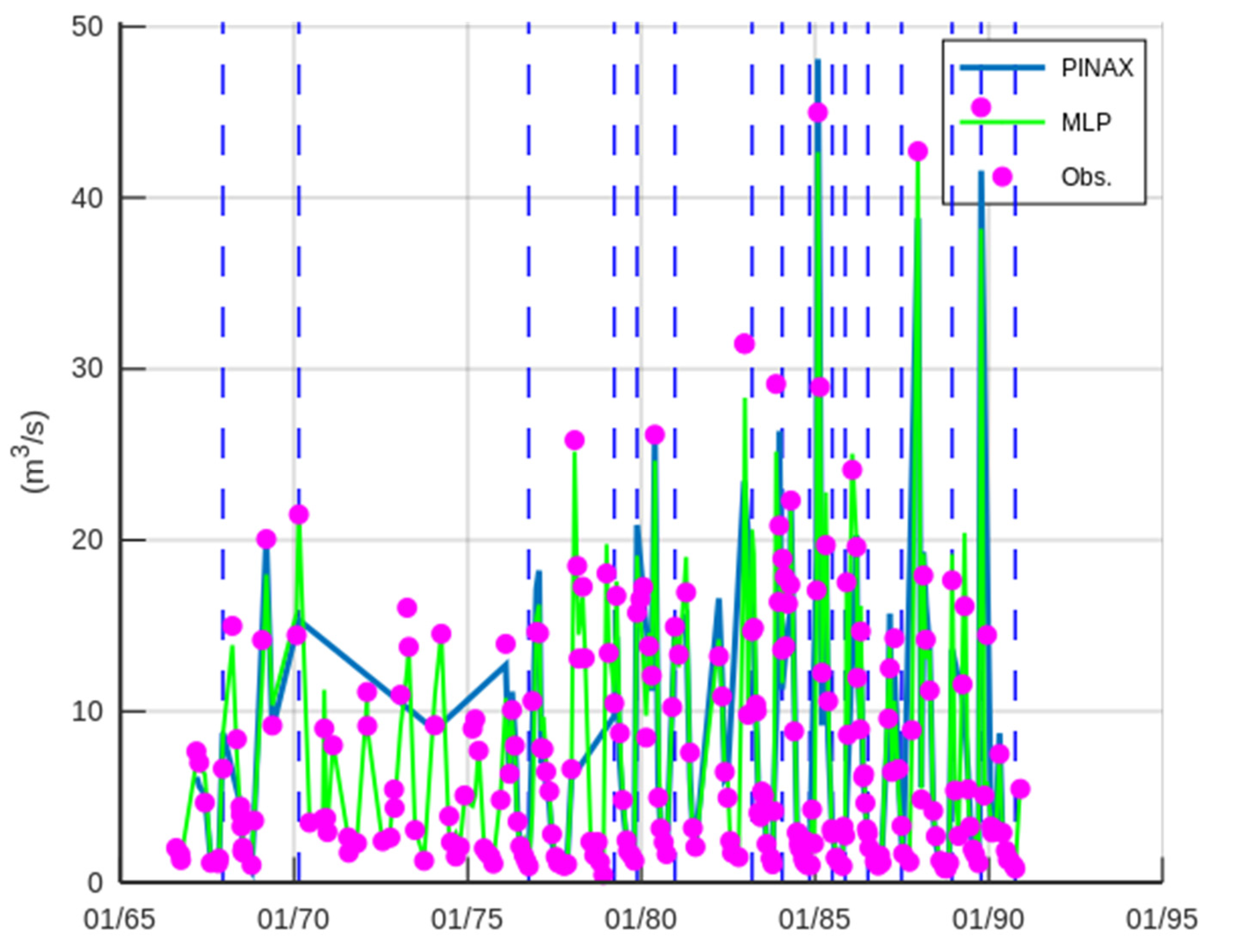
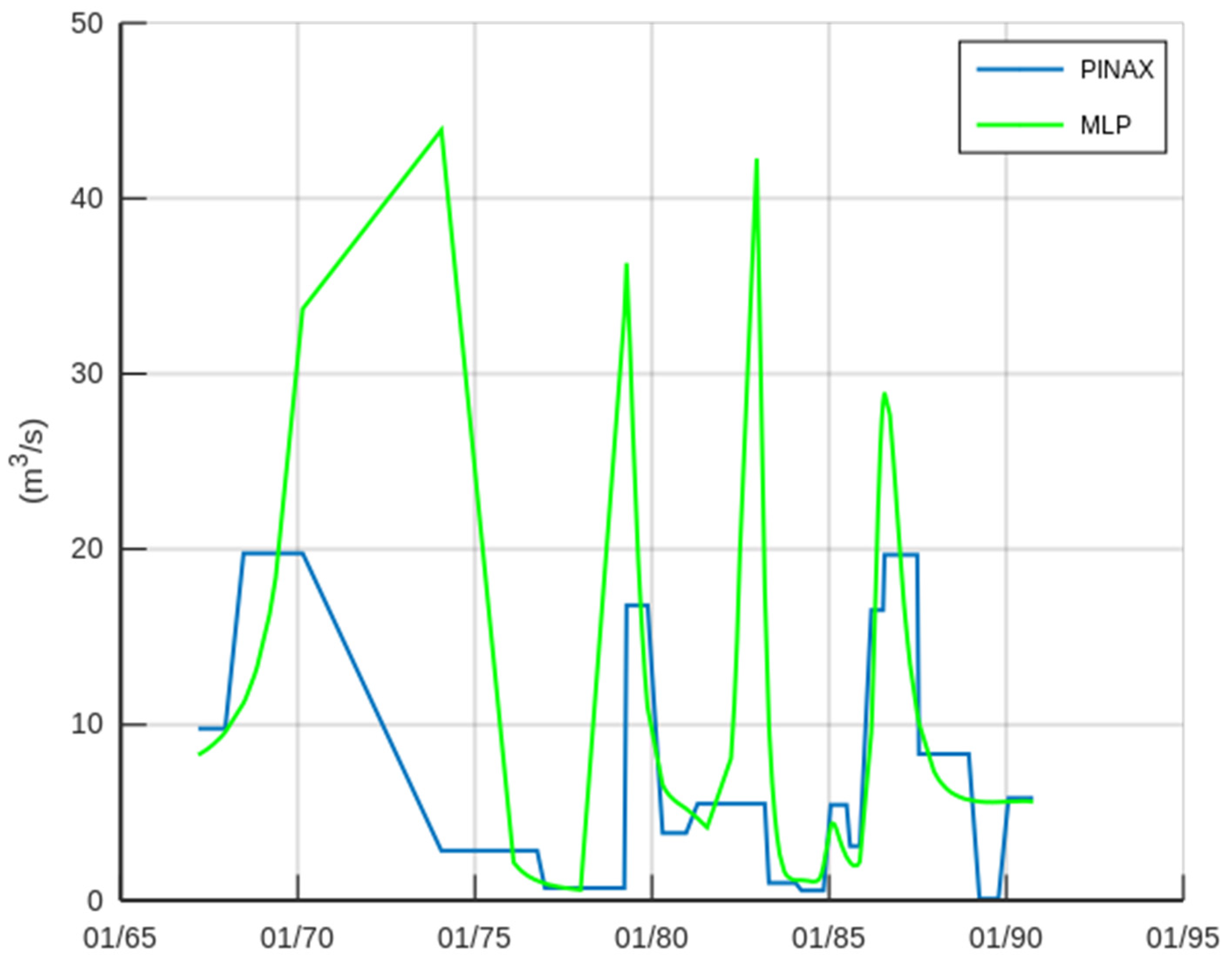
3.1. Case Study—Sakoulevas River
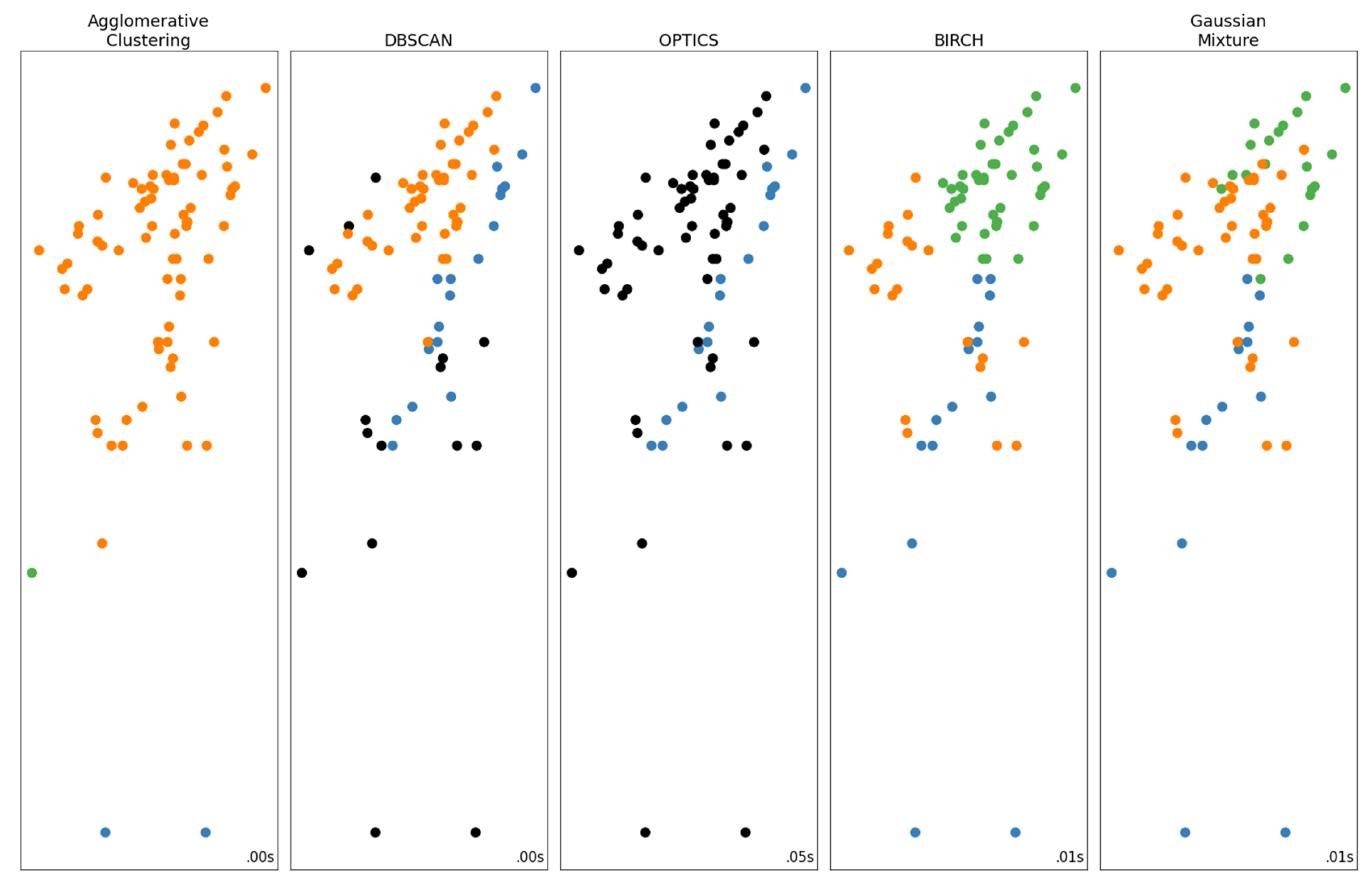
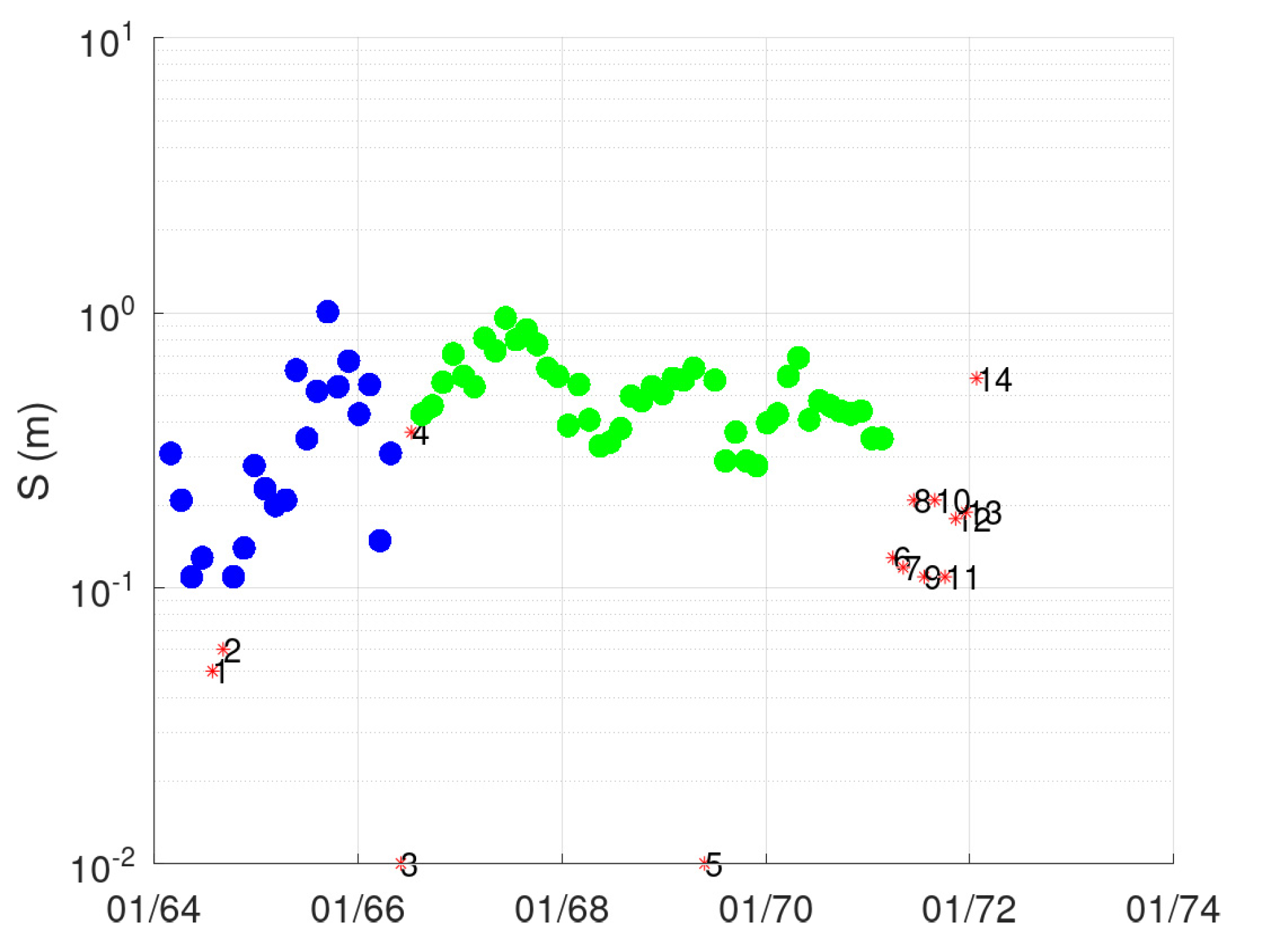
- Points 3 and 5. It is evident from Figure 5 that these two points lie far away from the cloud of the remaining points.
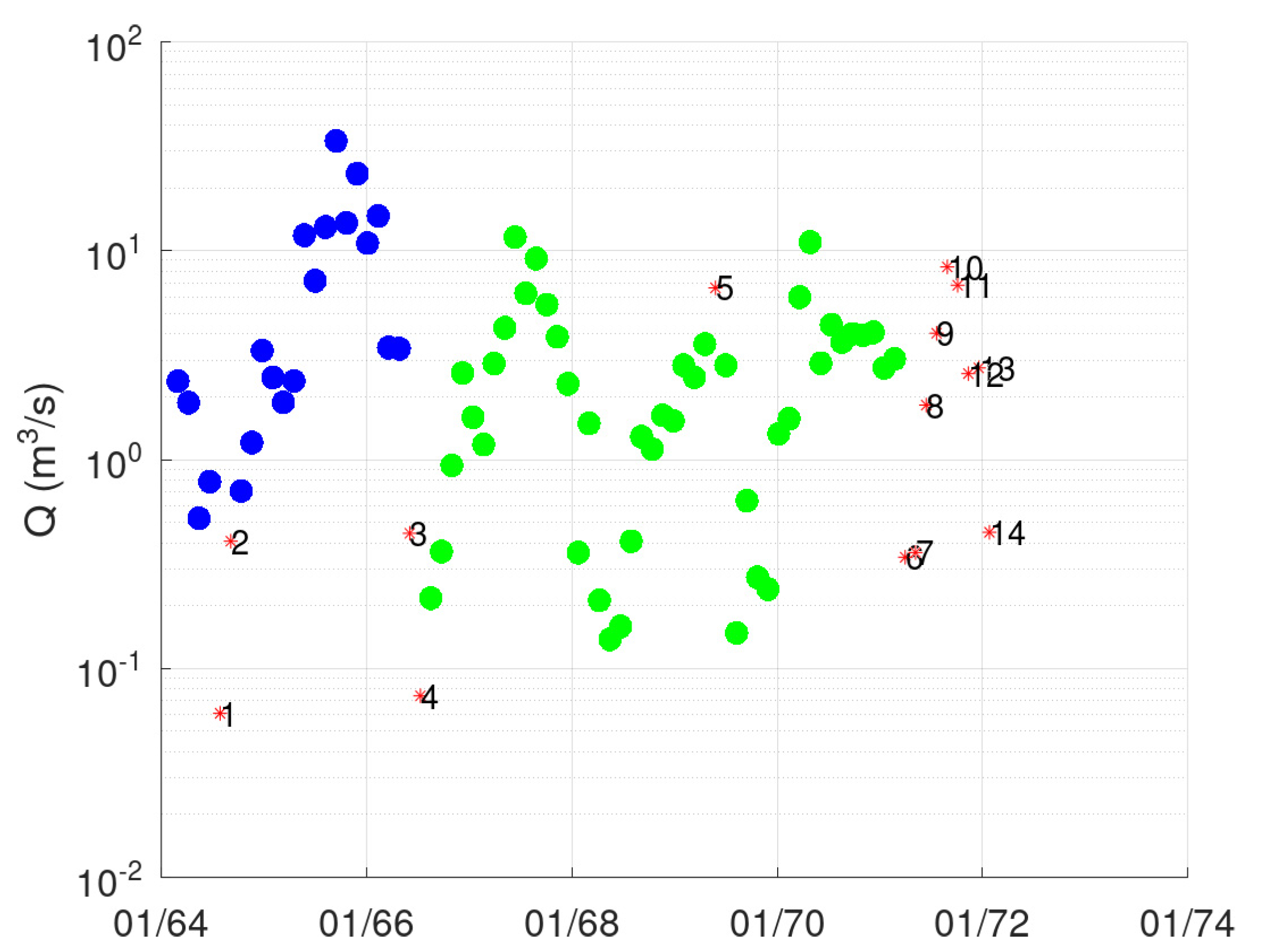
- Point 4. This point corresponds to a measurement with very low discharge (the second lowest, see Figure 3), which, however, has a significant stage (Figure 4). This is the only point of DBSCAN that was not deemed an outlier by PINAX. Indeed, geometrically, it looks like an outlier, but from a hydraulic perspective, this judgement can be disputed.
- Points 8, 12, and 13. These points could have formed a category on their own, but the lower limit to form a new category is 6 points (this was verified by setting m equal to 3).
- Points 1, 2, 6, and 7. The reason for this decision of DBSCAN is not obvious for these points.
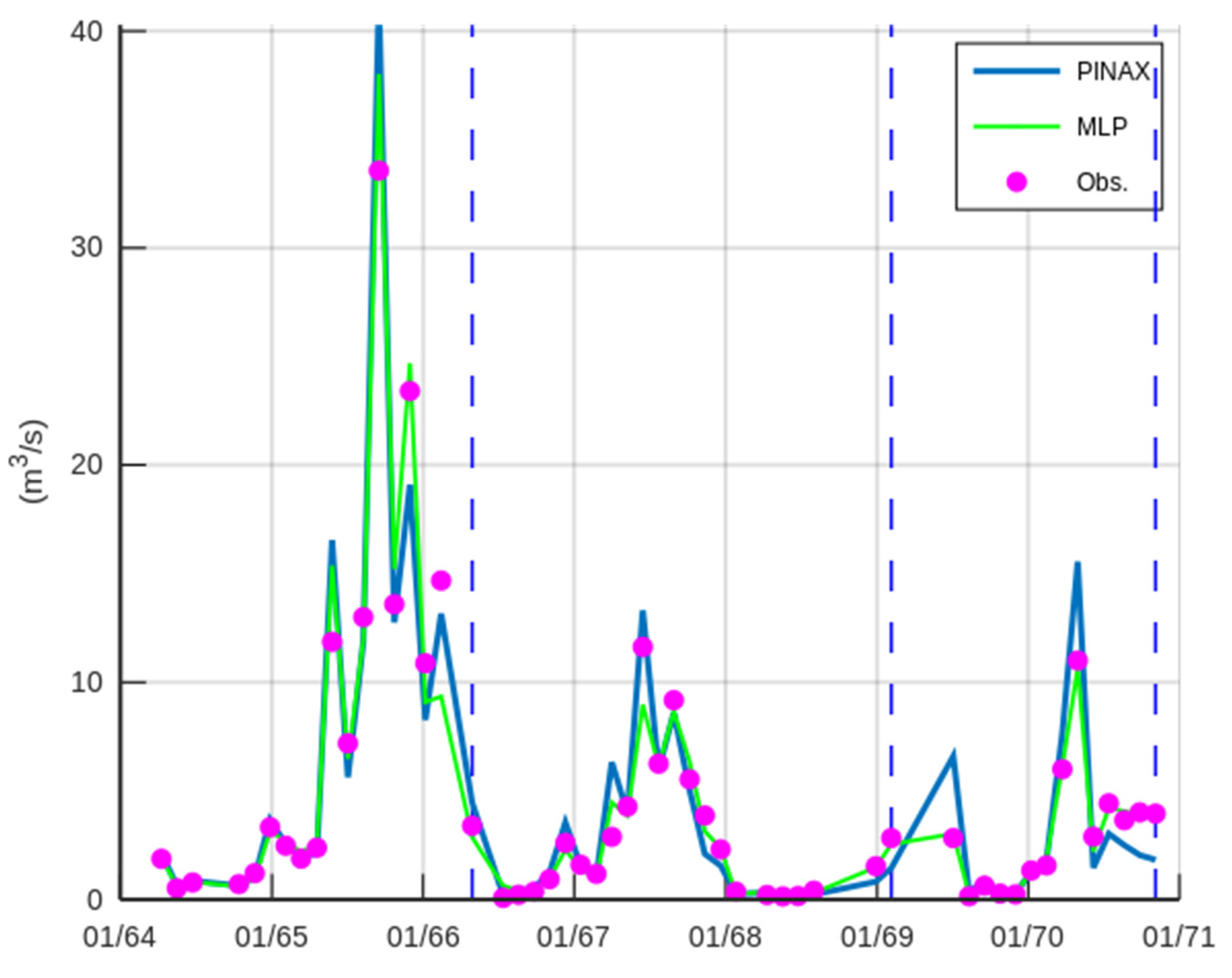
3.2. Case Study—Trikeriotis River
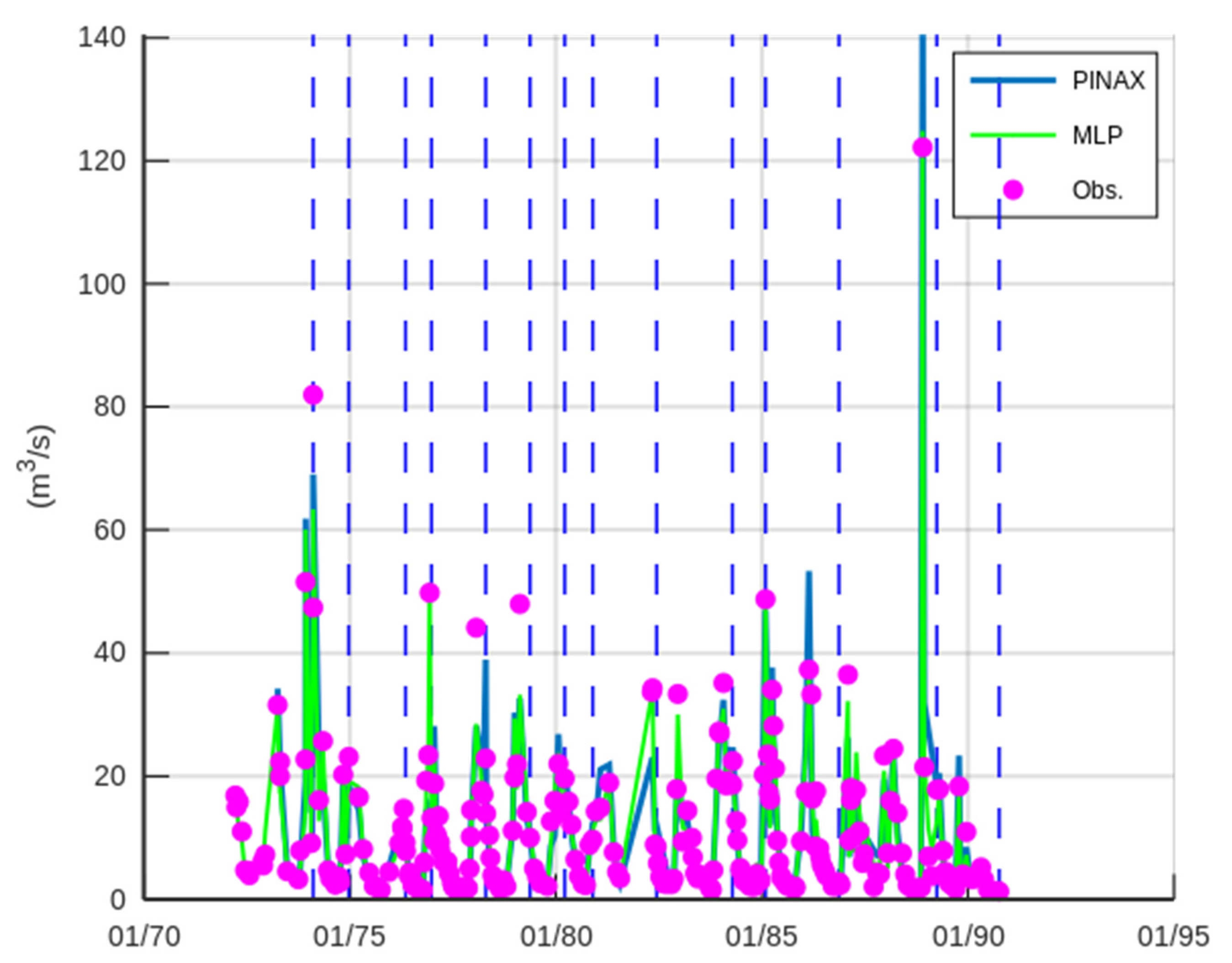
3.3. Case Study—Agrafiotis River
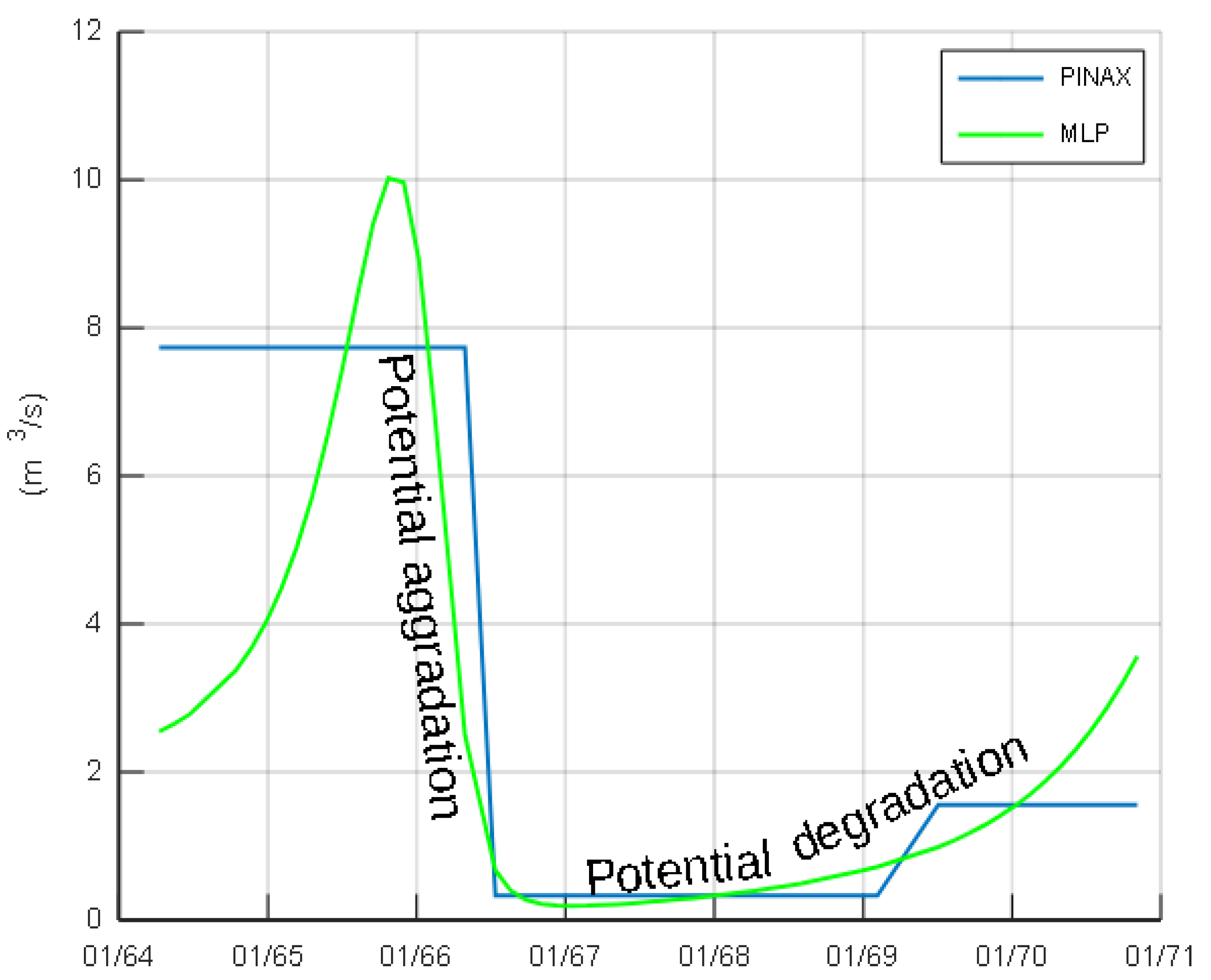
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

Appendix B

References
- Yin, J.; Guo, S.; Gentine, P.; Sullivan, S.; Gu, L.; He, S.; Chen, J.; Liu, P. Does the Hook Structure Constrain Future Flood Intensification Under Anthropogenic Climate Warming? Water Resour. Res. 2021, 57, e2020WR028491. [Google Scholar] [CrossRef]
- USGS. Stage-Discharge Relation Example. Available online: https://www.usgs.gov/media/images/usgs-stage-discharge-relation-example (accessed on 20 June 2022).
- Mosley, M.P.; McKerchar, A.I. Streamflow. In Handbook of Hydrology, 2nd ed.; Maidment, D.R., Ed.; McGraw Hill: New York, NY, USA, 1993; p. 267. [Google Scholar]
- Dogulu, N. Clustering Algorithms: Perspectives from the Hydrology Literature. Abstract IUGG19-3031. In Proceedings of the 27th IUGG General Assembly, IAHS Symposia, Montréal, QC, Canada, 9–14 July 2019. [Google Scholar]
- Vantas, K.; Sidiropoulos, E. Knowledge discovery using clustering analysis of rainfall timeseries. In Proceedings of the EGU General Assembly 2021, Online, 19–30 April 2021. [Google Scholar]
- El Hachem, A.; Bárdossy, A.; Seidel, J.; Goshtsasbpour, G.; Haberlandt, U. Clustering CDF and IDF curves of rainfall extremes. In Proceedings of the EGU General Assembly 2021, Online, 19–30 April 2021. [Google Scholar]
- Brunner, M.I.; Furrer, R.; Gilleland, E. Functional data clustering as a powerful tool to group streamflow regimes and flood hydrographs. In Proceedings of the EGU General Assembly 2021, Online, 19–30 April 2021. [Google Scholar]
- Sicaud, E.; Franssen, J.; Dedieu, J.P.; Fortier, D. Clustering analysis for the hydro-geomorphometric characterization of the George River watershed (Nunavik, Canada). In Proceedings of the EGU General Assembly 2021, Online, 19–30 April 2021. [Google Scholar]
- Zhou, Y.; Zhang, Q.; Singh, V. An adaptive multilevel correlation analysis: A new algorithm and case study. Hydrol. Sci. J. 2016, 61, 2718–2728. [Google Scholar] [CrossRef]
- Bernaola-Galván, P.; Ivanov, P.; Nunes Amaral, L.; Stanley, H. Scale Invariance in the Nonstationarity of Human Heart Rate. Phys. Rev. Lett. 2001, 87, 168105. [Google Scholar] [CrossRef] [PubMed]
- Fukuda, K.; Eugene Stanley, H.; Nunes Amaral, L. Heuristic segmentation of a nonstationary time series. Phys. Rev. E 2004, 69, 021108. [Google Scholar] [CrossRef] [PubMed]
- Tsakalias, G.; Koutsoyiannis, D. A comprehensive system for the exploration and analysis of hydrological data. Water Resour. Manag. 1999, 13, 269–302. [Google Scholar] [CrossRef]
- Bhattacharya, B.; Solomatine, D.P. Application of artificial neural network in stage-discharge relationship. In Proceedings of the 4th International Conference on Hydroinformatics, Iowa City, IA, USA, 23–27 July 2000; pp. 1–7. [Google Scholar]
- Al-Abadi, A. Modeling of stage–discharge relationship for Gharraf River, southern Iraq using backpropagation artificial neural networks, M5 decision trees, and Takagi–Sugeno inference system technique: A comparative study. Appl. Water Sci. 2016, 6, 407–420. [Google Scholar] [CrossRef]
- Goel, A.; Pal, M. Stage-discharge modeling using support vector machines. Int. J. Eng. 2011, 25, 1–9. [Google Scholar] [CrossRef]
- Londhe, S.; Panse-Aglave, G. Modelling Stage–Discharge Relationship using Data-Driven Techniques. ISH J. Hydraul. Eng. 2015, 21, 207–215. [Google Scholar] [CrossRef]
- Jiang, Z.; Wang, H.Y.; Song, W.W. Discharge estimation based on machine learning. Water Sci. Eng. 2013, 6, 145–152. [Google Scholar] [CrossRef]
- Alizadeh, F.; Faregh Gharamaleki, A.; Jalilzadeh, R. A two-stage multiple-point conceptual model to predict river stage-discharge process using machine learning approaches. J. Water Clim. Change 2020, 12, 278–295. [Google Scholar] [CrossRef]
- Kumar, M.; Kumari, A.; Kushwaha, D.; Kumar, P.; Malik, A.; Ali, R.; Kuriqi, A. Estimation of Daily Stage–Discharge Relationship by Using Data-Driven Techniques of a Perennial River, India. Sustainability 2020, 12, 7877. [Google Scholar] [CrossRef]
- Luo, Y.; Dong, Z.; Liu, Y.; Wang, X.; Shi, Q.; Han, Y. Research on stage-divided water level prediction technology of rivers-connected lake based on machine learning: A case study of Hongze Lake, China. Stoch. Environ. Res. Risk Assess. 2021, 35, 2049–2065. [Google Scholar] [CrossRef]
- Geron, A. Hands-On Machine Learning with Scikit-Learn & Tensorflow, 1st ed.; O’Reilly Media: Sebastopol, CA, USA, 2017; p. 10. [Google Scholar]
- Hayes-Roth, B.; Hewett, M. BB1: An Implementation of the Blackboard Control Architecture. In Blackboard Systems; Engelmore, R., Morgan, T., Eds.; Addison-Wesley: Reading, MA, USA, 1988; pp. 297–313. [Google Scholar]
- Comparing Different Clustering Algorithms on Toy Datasets. Available online: https://scikit-learn.org/stable/auto_examples/cluster/plot_cluster_comparison.html (accessed on 18 June 2022).
- DATEVALUE Function. Available online: https://support.microsoft.com/en-us/office/datevalue-function-df8b07d4-7761-4a93-bc33-b7471bbff252 (accessed on 28 June 2022).
- Jordan, J. Normalizing Your Data (Specifically, Input and Batch Normalization). Available online: https://www.jeremyjordan.me/batch-normalization/ (accessed on 28 June 2022).
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. Kdd 1996, 96, 226–231. [Google Scholar]
- DBSCAN. Available online: https://en.wikipedia.org/wiki/DBSCAN (accessed on 22 June 2022).
- ISO 1100; Liquid Flow Measurements in Open Channels—Establishment and Operation of a Gauging Station and Determination of the Stage–Discharge Relation. International Organization for Standardization: Geneva, Switzerland, 1973.
- How to Master the Popular DBSCAN Clustering Algorithm for Machine Learning. Available online: https://www.analyticsvidhya.com/blog/2020/09/how-dbscan-clustering-works/ (accessed on 3 July 2022).
- Dhhan, W.; Rana, S.; Alshaybawee, T.; Midi, H. The single-index support vector regression model to address the problem of high dimensionality. Commun. Stat.–Simul. Comput. 2018, 47, 2792–2799. [Google Scholar] [CrossRef]
- Rozos, E.; Dimitriadis, P.; Mazi, K.; Koussis, A. A Multilayer Perceptron Model for Stochastic Synthesis. Hydrology 2021, 8, 67. [Google Scholar] [CrossRef]
- Rozos, E.; Dimitriadis, P.; Bellos, V. Machine Learning in Assessing the Performance of Hydrological Models. Hydrology 2021, 9, 5. [Google Scholar] [CrossRef]
- Zeiler, M.D. ADADELTA: An Adaptive Learning Rate Method. arXiv 2012, arXiv:1212.5701. [Google Scholar]
- Szandała, T. Bio-Inspired Neurocomputing. In Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- XLSTAT Machine Learning. Available online: https://help.xlstat.com/6458-dbscan-clustering-excel (accessed on 25 July 2022).
- NEUROXL. Available online: http://neuroxl.com/ (accessed on 25 July 2022).


| Statistical Test | PINAX | MLP |
|---|---|---|
| (attained significance level of DC equal 0.9) > α1 = 0.05 | ✓ | ✓ |
| (standardised departures) < b2 = 2.58 | ✓ | X |
| (standard deviation of residuals) < σ0 = 0.35, with α3 = 0.05 | ✓ | ✓ |
| (number of consecutive runs) < 9 | ✓ | ✓ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rozos, E.; Leandro, J.; Koutsoyiannis, D. Development of Rating Curves: Machine Learning vs. Statistical Methods. Hydrology 2022, 9, 166. https://doi.org/10.3390/hydrology9100166
Rozos E, Leandro J, Koutsoyiannis D. Development of Rating Curves: Machine Learning vs. Statistical Methods. Hydrology. 2022; 9(10):166. https://doi.org/10.3390/hydrology9100166
Chicago/Turabian StyleRozos, Evangelos, Jorge Leandro, and Demetris Koutsoyiannis. 2022. "Development of Rating Curves: Machine Learning vs. Statistical Methods" Hydrology 9, no. 10: 166. https://doi.org/10.3390/hydrology9100166
APA StyleRozos, E., Leandro, J., & Koutsoyiannis, D. (2022). Development of Rating Curves: Machine Learning vs. Statistical Methods. Hydrology, 9(10), 166. https://doi.org/10.3390/hydrology9100166








