Development of Predictive Models for Water Budget Simulations of Closed-Basin Lakes: Case Studies of Lakes Azuei and Enriquillo on the Island of Hispaniola
Abstract
:1. Introduction
2. Materials and Methods
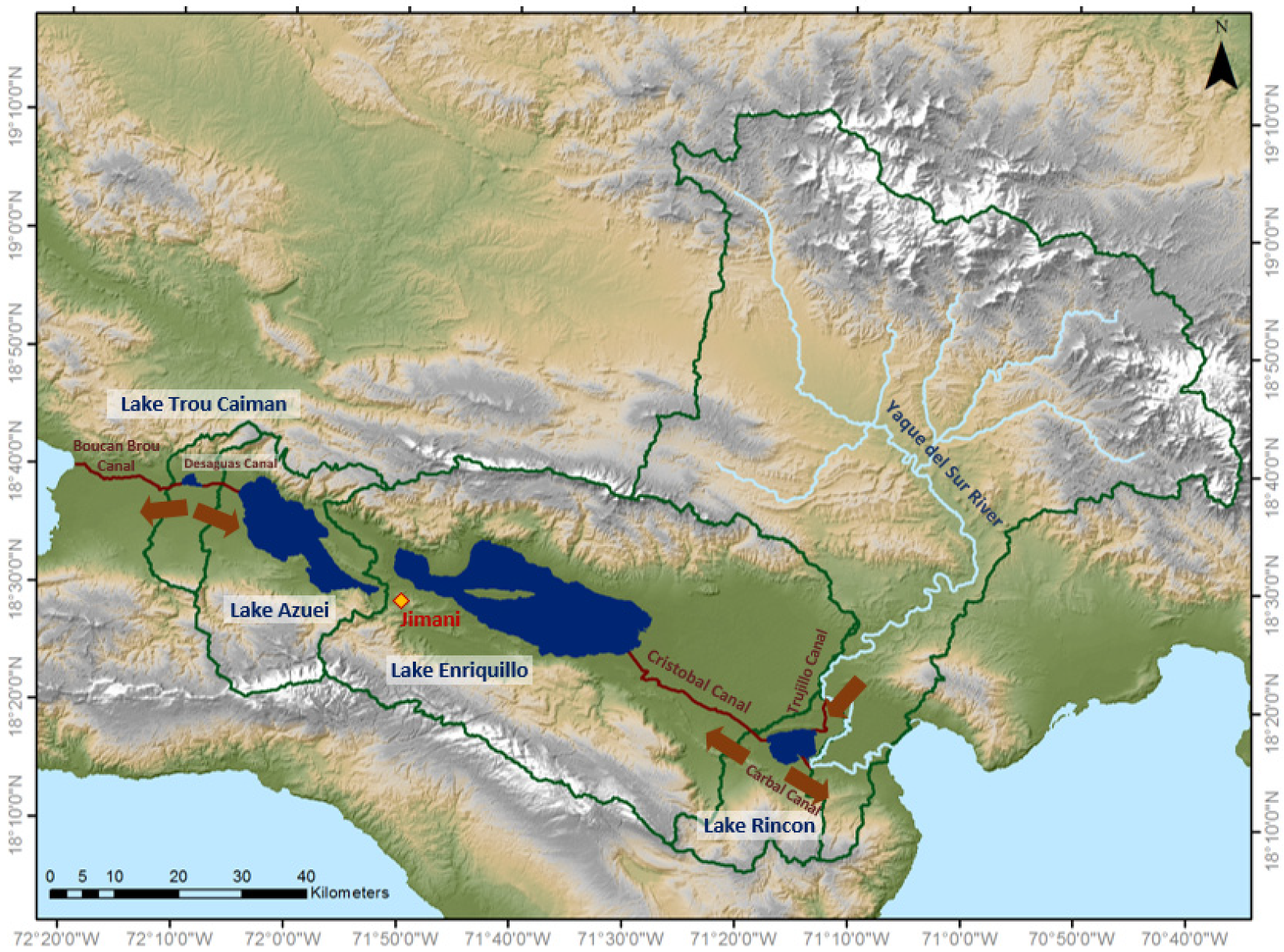
2.1. Study Area
2.2. Data Availibility
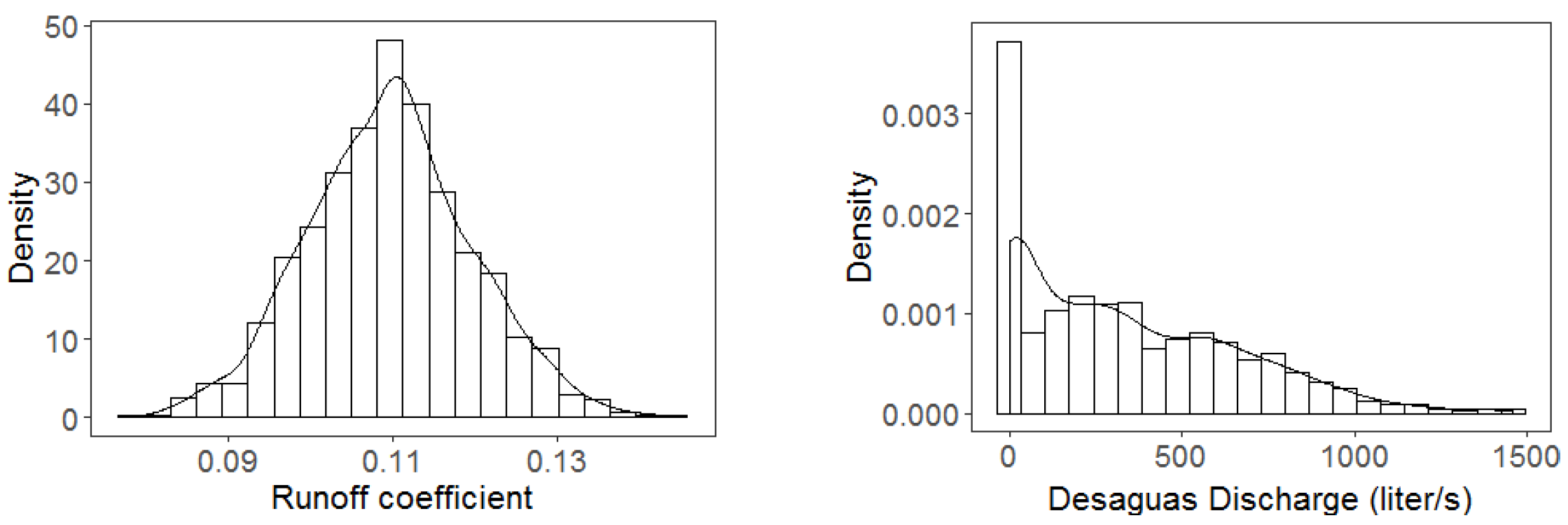
2.3. Model Development
2.4. Model Calibration, Validation, and Uncertainty Analysis
2.4.1. Lake Enriquillo-Model
2.4.2. Lake Azuei-Model
3. Results
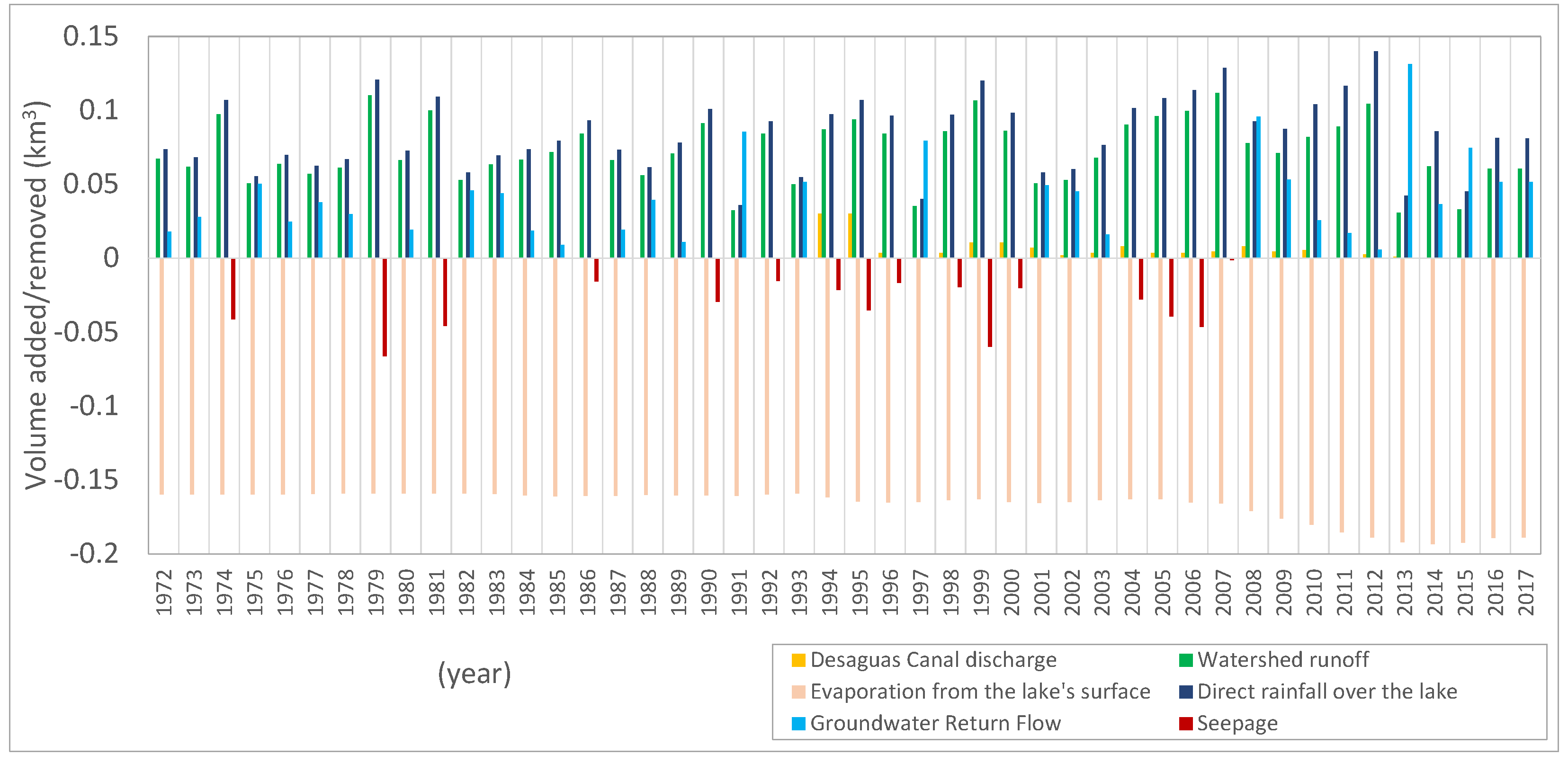
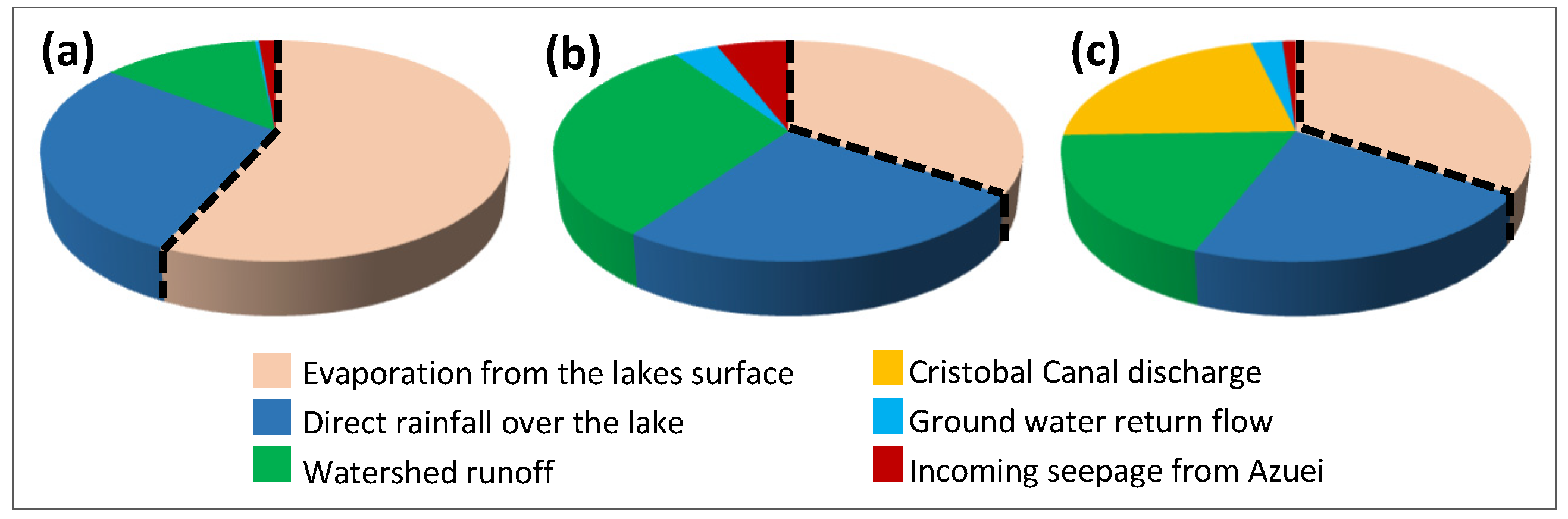
3.1. Water Budget Assessment
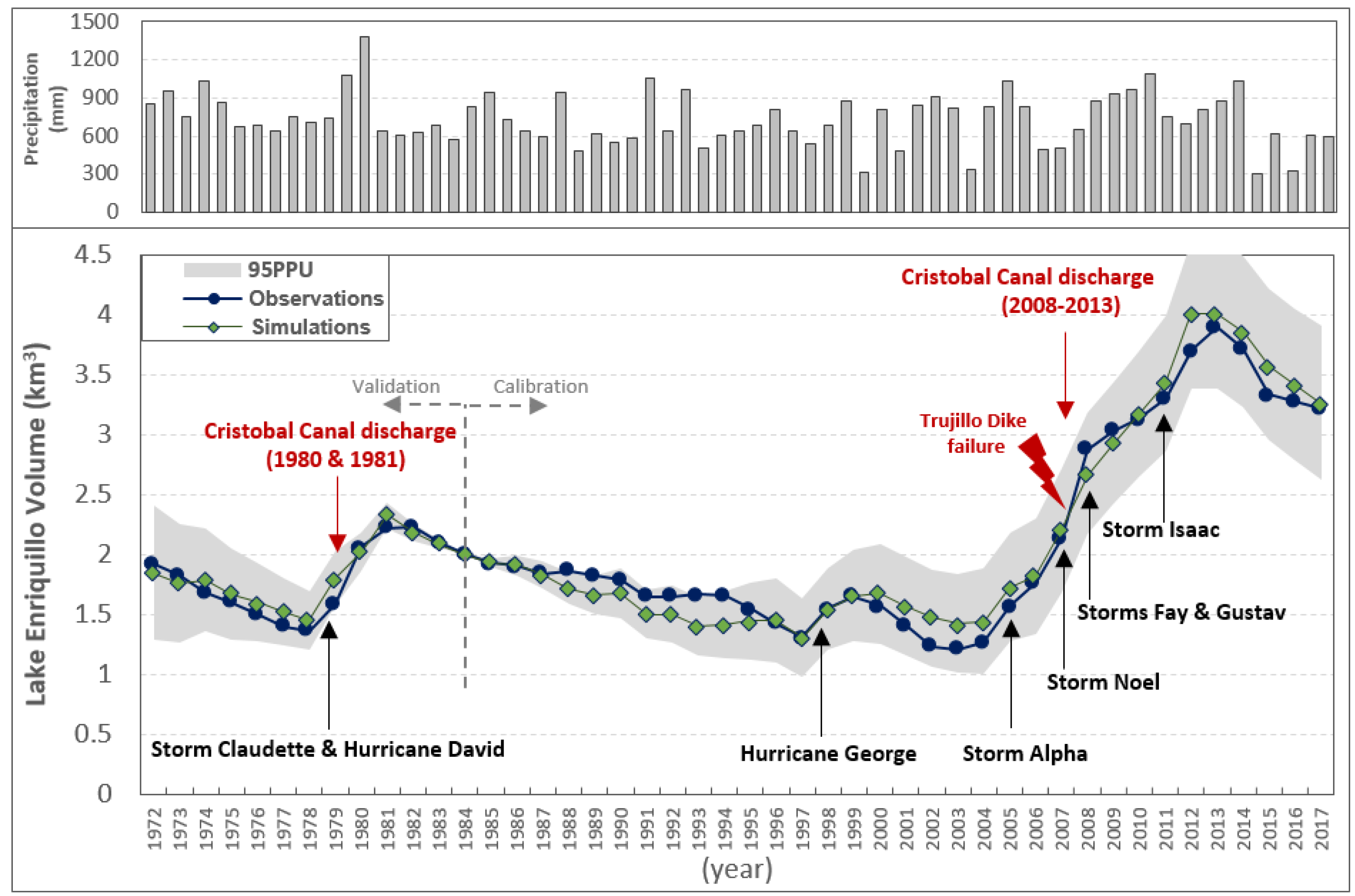
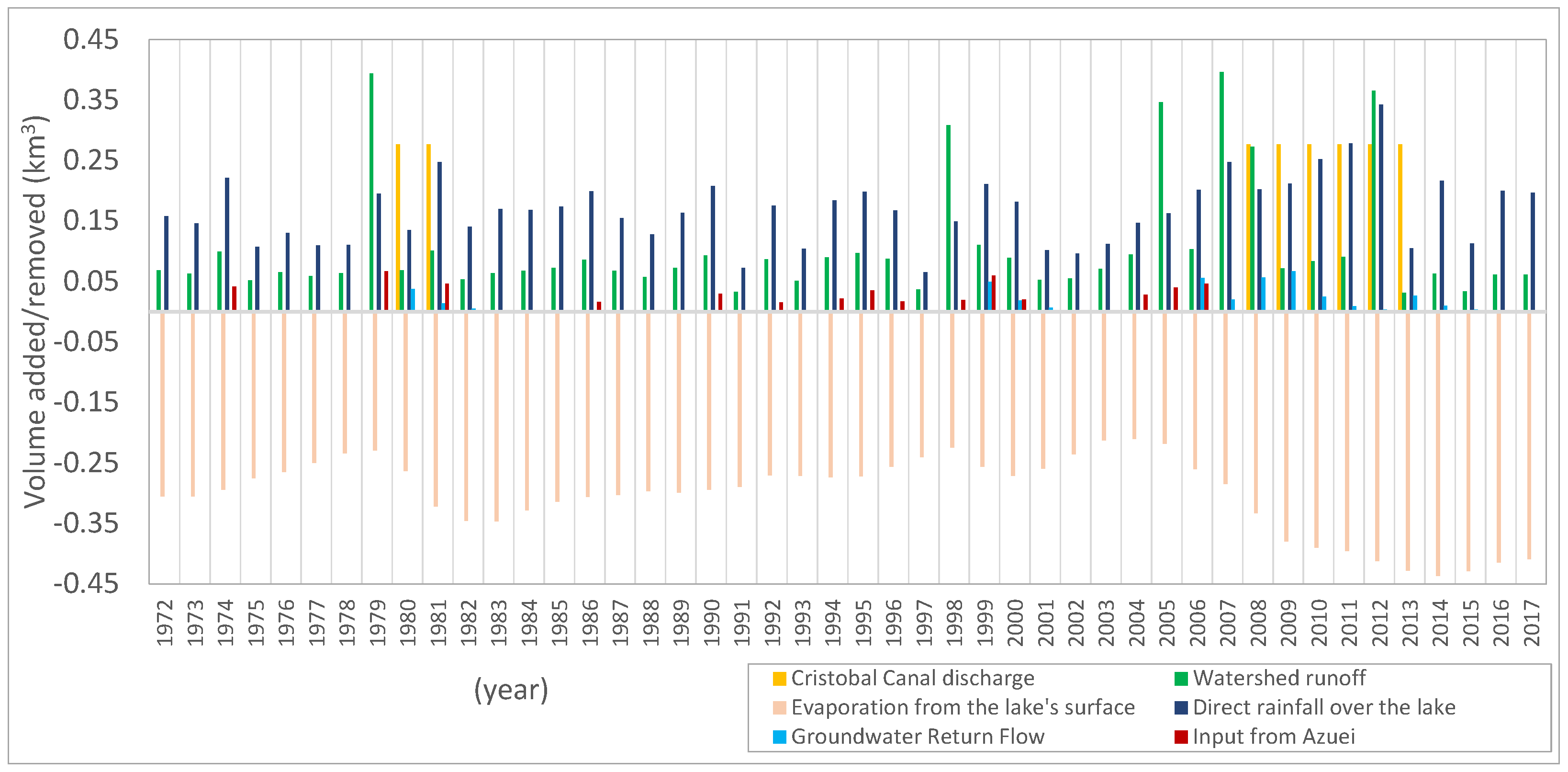
3.1.1. Lake Enriquillo
- 1972–1978:
- This period was characterized by a shrinkage pattern. No storm activities occurred close to the region, and the evaporation rate surpassed inflow to the lake from rainfall and surface runoff (with direct rainfall volume being higher than runoff). Therefore, the lake’s water budget was negative, and the lake was shrinking. For this period, the average direct rainfall volume rate was 0.14 km3/yr, the runoff was 0.07 km3/yr, and evaporation was 0.28 km3/yr.
- 1979–1981:
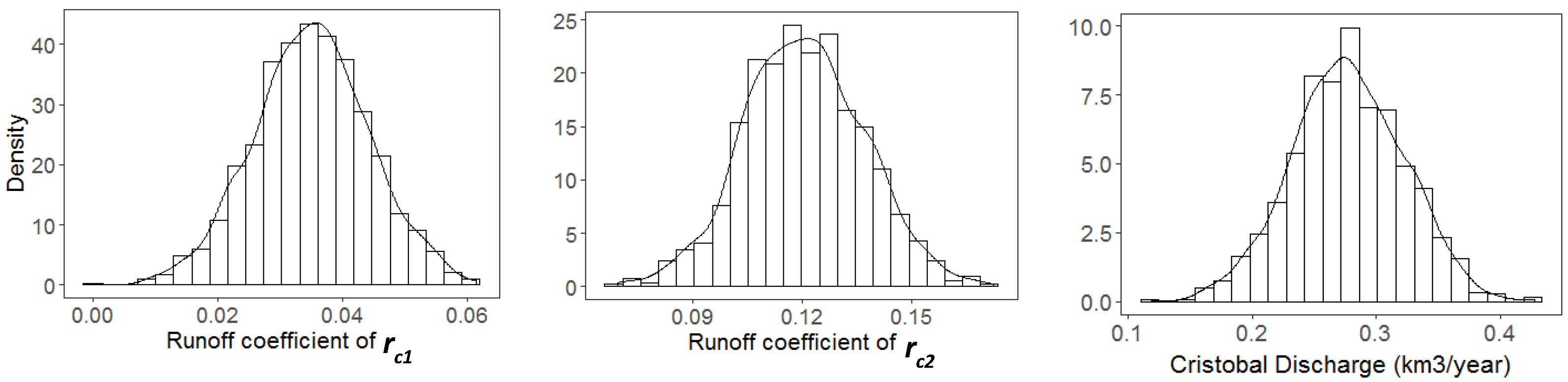
- In 1979, Storm Claudette and Hurricane David hit the area close to the lakes within a few months, causing the lake to grow due to high surface runoff volume. Later, flow brought by the Cristobal Canal from the neighboring watershed (Lake Rincon) added to the expansion, causing the lake level to rise by 4 m in total (which, otherwise, would have been 2.5 m). The amount of runoff caused by storms in 1979 was estimated to be 0.39 km3, while the cumulative volume of water from the Cristobal Canal was 0.55 km3 between 1980 and 1981. The average evaporation volume removed from the lake for this period was 0.27 km3/yr.
- 1982–1997:
- The shrinkage pattern observed for this period was due to the absence of storm activity and inter-basin water transfer. Therefore, the water budget of the lake system was dominated by evaporation (~0.29 km3/yr), causing it to shrink. Based on water budget estimations, the volume gathered by direct rainfall over the lake (~0.15 km3/yr) was higher than the volume received from surface runoff (~0.07 km3/yr).Differences between simulations and observations (1987–1996) could be due to assumptions taken and simplifications made during the modeling phase, such as the inclusion of constant evaporation and the choice of storm events. In 1988 and 1993, two storm incidents (Chris and Cindy) were reported with less than 87 mm of monthly rain, which may have slightly offset the graphs. Due to the lack of detailed data, the decision was made to carry on with the initial constraint that only storms occurring in months with a rainfall rate of more than 87 mm/month (within 80 km striking distance) [29] should be considered for the simulations.
- 1998–1999:
- The main event impacting the lake was Hurricane George, which caused a 1.3 m rise in LE’s surface level. In 1998, the runoff volume (~0.31 km3) was twice that of direct rainfall over the lake (~0.15 km3). In 1999, the lake grew mainly due to a high rainfall rate (~0.21 km3) and partially from groundwater return flow (0.05 km3).
- 2000–2004:
- In the absence of storm activity and inter-basin flow, the lake shrank. The primary inflows were coming from direct rainfall (~0.13 km3/yr) and runoff (~0.07 km3/yr), which was considerably less than the evaporation rate (~0.24 km3/yr). Comparison of observations and simulations showed an overestimation of volume, which could be attributed to inaccurate evaporation rates for these years.
- 2005–2006:
- In late 2005, Storm Alpha caused the lake to grow again (~1.6 m). The growth continued in 2006 due to direct rainfall, runoff, groundwater contribution, and incoming seepage from Azuei. The growth of the lake continued until mid-2007 (~1 m level rise), which might be a sign of the Cristobal Canal’s contribution (transferring Lake Rincon’s water) to LE’s water budget. However, this factor was not included in the simulations due to unreliable and more detailed information. The average volume of the water budget contributors was as follows: 0.24 km3/yr due to evaporation, 0.18 km3/yr added by direct rainfall, 0.22 km3/yr accumulated runoff, 0.03 km3/yr via groundwater contribution, and 0.04 km3/yr seepage coming from LA.
- 2007–2013:
- During this period, four storms (Noel, 2007; Fay, 2008; Gustav, 2008; and Isaac, 2012) passed in the vicinity of the LE watershed, with precipitation higher than 100 mm/month and uncontrolled water from the Cristobal Canal flowing towards LE, causing it to rise seven more meters.In December 2007, Storm Noel passed close to the region, introducing water to LE from direct rainfall and runoff. In late 2007 and early 2008, the Trujillo Dike failed due to the Yaque del Sur flood, at which time most of the river flow began to drain indirectly into LE, first through the Trujillo Canal into Lake Rincon and then through the Cristobal Canal into LE. In 2008, Storms Fay and Gustav struck the lake in December, adding to its volume. In April 2011, Trujillo Dike was repaired; however, water leakage from the dyke did not entirely stop. In 2012, another storm passed through, and LE expanded due to the extra volume originating from rainfall and runoff. These additions, however, did not account for all the LE growth, pointing to the existence of the continued extra flows in the Cristobal Canal. Without Cristobal’s contributions, the lake might have risen by only 2.5 m between 2007 and 2013.Based on water budget estimations, 0.24 km3/yr of added volume to the lake came from the Cristobal Canal’s discharge. The contributions of other factors were 0.37 km3/yr due to evaporation, 0.23 km3/yr as direct rainfall, 0.19 km3/yr accumulated runoff, and 0.03 km3/yr via groundwater contributions.The noticeable deviation between simulated and actual time-series for 2012–2014 was attributed to the assumption of a constant value for evaporation and discharge.
- 2014–2017:
- No external force was exerted on the lake’s water budget. Therefore, added precipitation and runoff could not compensate for the water lost through evaporation. As a result, LE showed a shrinkage pattern. For this period, evaporation, direct rainfall, and runoff rates were 0.42, 0.18, and 0.05 km3/yr, respectively. The high rate of evaporation during this period was due to the extent of the lake’s surface.
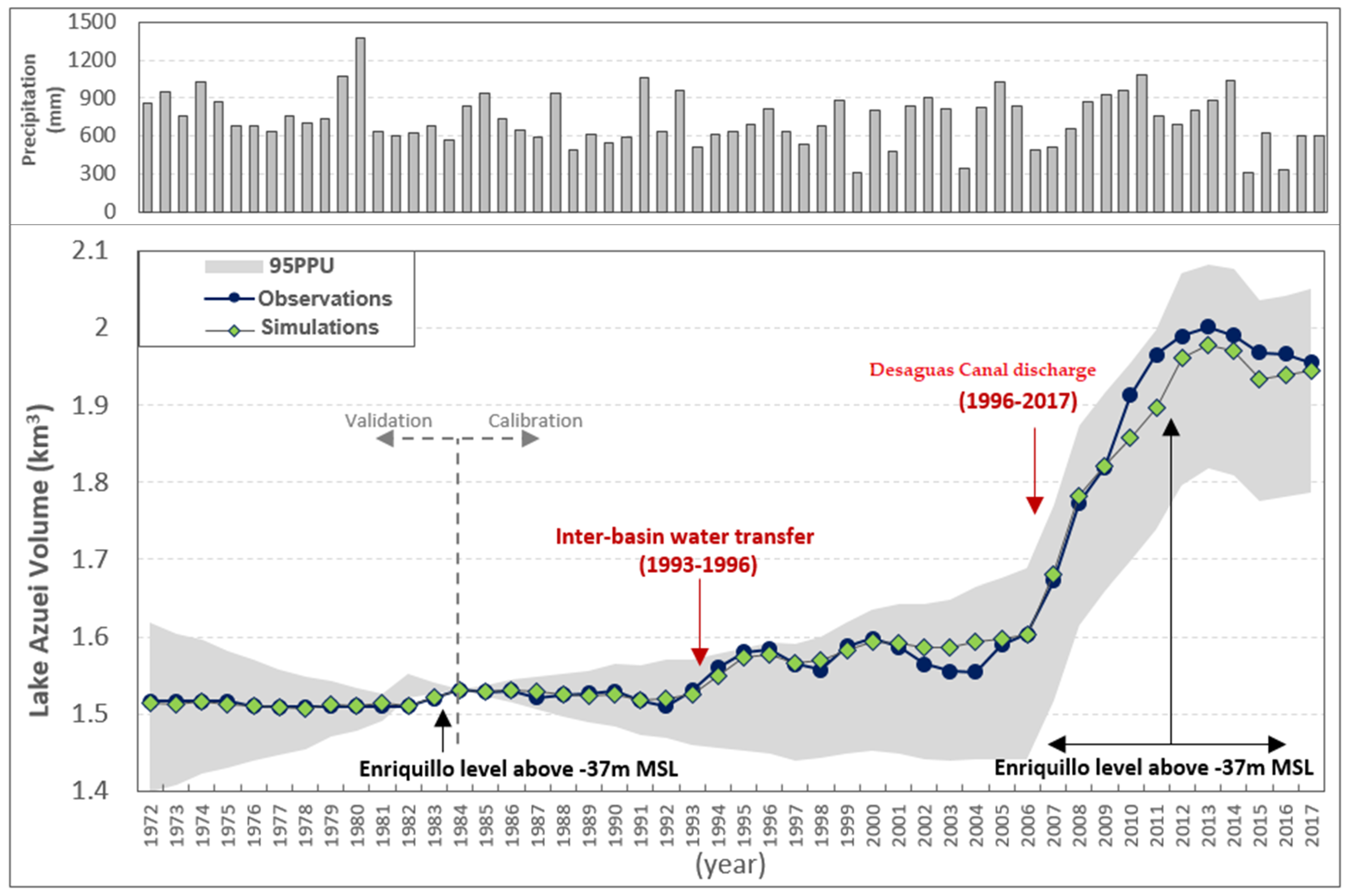
3.1.2. Lake Azuei
- 1972–1982:
- During this period, LA exhibited a stable behavior, and the amount of inflow and outflow to/from the lake was balanced. Average volumes estimated in this period were: 0.16 km3/yr due to evaporation, 0.08 km3/yr as direct rainfall, 0.07 km3/yr from runoff, 0.02 km3/yr via groundwater return flow, and 0.01 km3/yr as outgoing seepage from Azuei.
- 1983–1984:
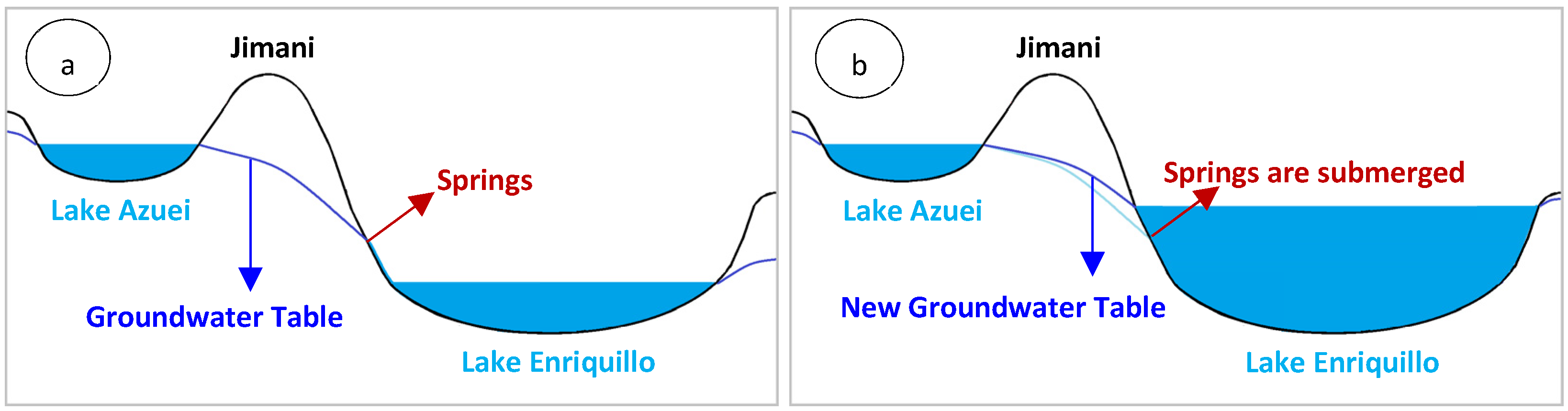
- During this short period, LA expanded slightly (~20 cm level rise) in response to LE’s level rising above –37 m MSL, which lasted for only a few years. For this period, groundwater return flow was approximately 0.03 km3/yr, while outgoing seepage was estimated to be close to zero, thus explaining the lake’s growth. Other elements of the water budget were: evaporation (~0.16 km3/yr), direct rainfall (~0.07 km3/yr), and runoff (~0.06 km3/yr).
- 1985–1992:
- Soon after the expansion in 1982–1984, LA stabilized and attained its previous equilibrium, which was owed to removing LE’s influence. This period lasted for eight years, during which direct precipitation, runoff, groundwater return flow, and seepage values from Azuei were the same as the 1972–1982 period.
- 1993–1996:
- A 5% expansion in the lake’s volume was observed, causing it to rise by 79 cm. This increase correlated with inter-basin water transfer without a significant precipitation event or LE’s influence. Based on water budget calculations, a total of 0.06 km3 had been added to the lake. Satellite imagery showed a possible water volume transfer from the Desaguas Canal to LA for 12 months during 1993 and 1996. To match the growth of LA, the Desaguas Canal would have had to supply 2.9 m3/s. The validity of this assumption would have to be investigated further.
- 1997–2000:
- For these years, LA was experiencing stability. Based on satellite imagery, water budget estimations showed a discharge of 338 lit/s for 28 months. The values of water budget constituents were 0.16, 0.09, 0.08, 0.006, 0.02, and 0.02 km3/yr for evaporation, direct rainfall, runoff, Desaguas discharge, groundwater return flow, and outgoing seepage.
- 2001–2006:
- Similar to LE observations, significant differences between observed and model simulations existed. These differences were attributed to the assumption of constant evaporation rate because those years coincided with a dry period. Satellite imagery showed 31 months of the Desaguas Canal flow (~0.005 km3/yr).
- 2007–2013:
- LA’s surface-level rose by approximately 3.7 m in seven years. This synchronous expansion was a result of LE’s rapid surface level rise influencing Azuei’s system. Desaguas Canal flow continued to contribute to LA’s water budget for 29 months (~0.004 km3/yr). The water budget calculations showed an outgoing seepage value of close to zero from Azuei’s system. The calculation of other factors yielded: 0.18, 0.10, 0.08, and 0.05 km3/yr for evaporation, direct rainfall, runoff, and groundwater return flow, respectively. The higher rate of evaporation and direct rainfall was due to the significant expansion of the lake’s surface area. The discrepancies between simulations and observations for the years after 2009 are due to the inaccurate prediction of the equilibrium modifier, which changed during the rising leg of the time series. Assessments using the LA model showed that the lake would never have expanded if it were not for the influence of LE on its system.
- 2014–2017:
- Synchronous with LE, LA was shrinking due to the gradual removal of LE’s impact on its dynamic. As mentioned before, the difference between simulations and observations was because of the simplifications applied to estimate the equilibrium modifier.
3.2. Lake Dynamics Description
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mason, I.M.; Guzkowska, M.A.J.; Rapley, C.G.; Street-Perrott, F.A. The response of lake levels and areas to climatic change. Clim. Change 1994, 27, 161–197. [Google Scholar] [CrossRef]
- Shanahan, T.M.; Overpeck, J.T.; Sharp, W.E.; Scholz, C.A.; Arko, J.A. Simulating the response of a closed-basin lake to recent climate changes in tropical West Africa (Lake Bosumtwi, Ghana). Hydrol. Process. 2007, 21, 1678–1691. [Google Scholar] [CrossRef]
- Mercier, F. Interannual lake level fluctuations (1993–1999) in Africa from Topex/Poseidon: Connections with ocean–atmosphere interactions over the Indian Ocean. Glob. Planet. Change 2002, 32, 141–163. [Google Scholar] [CrossRef]
- Ricko, M.; Carton, J.A.; Birkett, C. Climatic effects on lake basins. Part I: Modeling tropical lake levels. J. Clim. 2011, 24, 2983–2999. [Google Scholar] [CrossRef] [Green Version]
- Mohammed, I.N.; Tarboton, D.G. An examination of the sensitivity of the Great Salt Lake to changes in inputs. Water Resour. Res. 2012, 48, 11. [Google Scholar] [CrossRef] [Green Version]
- Todhunter, P.E. Mean hydroclimatic and hydrological conditions during two climatic modes in the Devils Lake Basin, North Dakota (USA). Lakes Reserv. Res. Manag. 2016, 21, 338–350. [Google Scholar] [CrossRef] [Green Version]
- Troin, M.; Vallet-Coulomb, C.; Sylvestre, F.; Piovano, E. Hydrological modelling of a closed lake (Laguna Mar Chiquita, Argentina) in the context of 20th century climatic changes. J. Hydrol. 2010, 393, 233–244. [Google Scholar] [CrossRef]
- Moknatian, M.; Piasecki, M.; Gonzalez, J. Development of geospatial and temporal characteristics for Hispaniola’s Lake Azuei and Enriquillo using Landsat imagery. Remote Sens. 2017, 9, 510. [Google Scholar] [CrossRef] [Green Version]
- Jones, R.; McMahon, T.; Bowler, J. Modelling historical lake levels and recent climate change at three closed lakes, Western Victoria, Australia (c.1840–1990). J. Hydrol. 2001, 246, 159–180. [Google Scholar] [CrossRef]
- Phan, V.H.; Lindenbergh, R.C.; Menenti, M. Geometric dependency of Tibetan lakes on glacial runoff. Hydrol. Earth Syst. Sci. Discuss. 2013, 10, 729–768. [Google Scholar]
- Kaiser, K.; Heinrich, I.; Heine, I.; Natkhin, M.; Dannowski, R.; Lischeid, G.; Schneider, T.; Henkel, J.; Küster, M.; Heussner, K.-U.; et al. Multi-decadal lake-level dynamics in north-eastern Germany as derived by a combination of gauging, proxy-data and modelling. J. Hydrol. 2015, 529, 584–599. [Google Scholar] [CrossRef] [Green Version]
- Morrill, C.; Small, E.E.; Sloan, L.C. Modeling orbital forcing of lake level change: Lake Gosiute (Eocene), North America. Glob. Planet. Change 2001, 29, 57–76. [Google Scholar] [CrossRef]
- Todhunter, P.E.; Fietzek-DeVries, R. Natural hydroclimatic forcing of historical lake volume fluctuations at Devils Lake, North Dakota (USA). Nat. Hazards 2016, 81, 1515–1532. [Google Scholar] [CrossRef] [Green Version]
- Kebede, S.; Travi, Y.; Alemayehu, T.; Marc, V. Water balance of Lake Tana and its sensitivity to fluctuations in rainfall, Blue Nile basin, Ethiopia. J. Hydrol. 2006, 316, 233–247. [Google Scholar] [CrossRef]
- Huybers, K.; Rupper, S.; Roe, G.H. Response of closed basin lakes to interannual climate variability. Clim. Dyn. 2016, 46, 3709–3723. [Google Scholar] [CrossRef]
- Bracht-Flyr, B.; Istanbulluoglu, E.; Fritz, S. A hydro-climatological lake classification model and its evaluation using global data. J. Hydrol. 2013, 486, 376–383. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.; Wang, L.; Zhang, Y.; Guo, Y.; Li, X.; Liu, W. Exploring the water storage changes in the largest lake ( Selin Co) over the Tibetan Plateau during 2003–2012 from a basin--wide hydrological modeling. Water Resour. Res. 2015, 51, 8060–8086. [Google Scholar] [CrossRef] [Green Version]
- Langbein, W.B. Salinity and Hydrology of Closed Lakes; U.S. Geological Survey Professional Paper 412; U.S. Goverment Printing Office: Washington, DC, USA, 1961.
- Rosenberry, D.O.; Lewandowski, J.; Meinikmann, K.; Nützmann, G. Groundwater-the disregarded component in lake water and nutrient budgets. Part 1: Effects of groundwater on hydrology. Hydrol. Process. 2015, 29, 2895–2921. [Google Scholar] [CrossRef]
- Deus, D.; Gloaguen, R.; Krause, P. Water balance modeling in a semi-arid environment with limited in situ data using remote sensing in Lake Manyara, East African Rift, Tanzania. Remote Sens. 2013, 5, 1651–1680. [Google Scholar] [CrossRef] [Green Version]
- Turner, B.F.; Gardner, L.R.; Sharp, W.E. The hydrology of Lake Bosumtwi, a climate-sensitive lake in Ghana, West Africa. J. Hydrol. 1996, 183, 243–261. [Google Scholar] [CrossRef]
- Mohammed, I.N.; Tarboton, D.G. On the interaction between bathymetry and climate in the system dynamics and preferred levels of the Great Salt Lake. Water Resour. Res. 2011, 47, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Clark, J.A.; Befus, K.M.; Sharman, G.R. A model of surface water hydrology of the Great Lakes, North America during the past 16,000 years. Phys. Chem. Earth 2012, 53–54, 61–71. [Google Scholar] [CrossRef]
- Vallet-Coulomb, C.; Legesse, D.; Gasse, F.; Travi, Y.; Chernet, T. Lake evaporation estimates in tropical Africa (Lake Ziway, Ethiopia). J. Hydrol. 2001, 245, 1–18. [Google Scholar] [CrossRef]
- Legesse, D.; Vallet-Coulomb, C.; Gasse, F. Analysis of the hydrological response of a tropical terminal lake, Lake Abiyata(Main Ethiopian Rift Valley) to changes in climate and human activities. Hydrol. Process. 2004, 18, 487–504. [Google Scholar] [CrossRef]
- Scheffers, A.; Browne, T. Encyclopedia of the World’s Coastal Landforms: Hispaniola (Haiti and the Dominican Republic); Bird, E.C.F., Ed.; Springer: Dordrecht, The Netherlands, 2010; Volume 2, pp. 7–10. ISBN 978-1-4020-8638-0. [Google Scholar]
- Moknatian, M.; Piasecki, M.; Moshary, F.; Gonzalez, J. Development of digital bathymetry maps for Lakes Azuei and Enriquillo using sonar and remote sensing techniques. Trans. GIS 2019, 23, 841–859. [Google Scholar] [CrossRef] [Green Version]
- Moknatian, M.; Piasecki, M. Observational Time Series for Lakes Azuei and Enriquillo: Surface Area, Volume, and Elevation; Research Report; CUNY Academic Works: New York, NY, USA, 2019. [Google Scholar]
- Moknatian, M.; Piasecki, M. Lake Volume Data Analyses: A Deep Look into the Shrinking and Expansion Patterns of Lakes Azuei and Enriquillo, Hispaniola. Hydrology 2019, 7, 1. [Google Scholar] [CrossRef] [Green Version]
- González, R.; Brito, D.R.; González, J. Estudio Hidrogeológico de la Zona del Lago Enriquillo, Determinación de las Causas del Aumento de Nivel de Sus Aguas e Intervenciones Requeridas Para su Control; Project Progress Report NO.1; Instituto Tecnológico de Santo Domingo (INTEC) and the City College of New York (CCNY): New York, NY, USA, 2010. [Google Scholar]
- Vlaminck, B. La Pecherie de L’etang Saumatre: Recherche Appliquee et Activites Periode Octobre 88–Septembre 89; Project Report HAI/88/003; United Nations Development Programme/Food and Agriculture Organization (PNUD/FAO): Haiti, Indonesia, 1989. [Google Scholar]
- Perrissol, M.; Lescoulier, C. Etude Hydrologique et Hydrogéologique de la Montée des eaux du lac Azueï; Project Repor; Version 2; Egis International: Haiti, Indonesia, 2011. [Google Scholar]
- Buck, D.G.; Brenner, M.; Hodell, D.A.; Curtis, J.H.; Martin, J.B.; Pagani, M. Physical and chemical properties of hypersaline Lago Enriquillo, Dominican Republic. SIL Proc. 2005, 29, 725–731. [Google Scholar] [CrossRef]
- Pichardo, F.D.G.; Conte, L.L.; Regio, G. Alternativas Productivas a Mediano y Largo Plazo Para las Familias Afectadas por la Crecida del Nivel del Lago Enriquillo; Project Report prepared by OXFAM-Italy; OXFAM-Italy: Santo Domingo, Dominican Republic, 2012. [Google Scholar]
- Martínez-Batlle, J.R. Sierra de Bahoruco Occidental, República Dominicana: Estudio Biogeomorfológico y Estado de Conservación de su Parque Nacional. Ph.D. Thesis, Departamento de Geografía Física y Análisis Geográfico Regional, Universidad de Sevilla, Sevilla, Spain, 2012. [Google Scholar]
- Gilboa, Y. The aquifer systems of the Dominican Republic. Hydrol. Sci. Bull. 1980, 25, 379–393. [Google Scholar] [CrossRef]
- Schubert, A. El Lago Enriquillo: Gran Patrimonio Natural y Cultural del Caribe, 2nd ed.; Secretaría de Medio Ambiente y Recursos Naturales Consorcio Ambiental Dominicano CAD: Jimani, Dominican Republic, 2003; ISBN 99934-0-110-2. [Google Scholar]
- Mendez-Tejeda, R.; Delanoy, R.A. Influence of climatic phenomena on sedimentation and increase of Lake Enriquillo in Dominican Republic, 1900–2014. J. Geogr. Geol. 2017, 9, 19. [Google Scholar] [CrossRef]
- Méndez-tejeda, R.; Rosado, G.; Rivas, D.V.; Montilla, T.; Hernández, S.; Ortiz, A.; Santos, F. Climate variability and its effects on the increased level of Lake Enriquillo in the Dominican Republic, 2000–2013. Appl. Ecol. Environ. Sci. 2016, 4, 26–36. [Google Scholar]
- Logan, W.S.; Enfield, D.B.; Division, P.O.; Capdevila, A.S. Rising Water Levels at Lake Enriquillo, Dominican Republic: Advice on Potential Causes and Pathways forward. Report by the International Center for Integrated Water Resources Management (ICIWaRM) to the Instituto Nacional de Recursos Hidráulicos (INDRHI), Government of the Dominican Republic. 2012. Available online: https://s3.amazonaws.com/sitesusa/wp-content/uploads/sites/422/2015/12/Lake_Enriquillo_report_1-26-2012.pdf (accessed on 12 August 2021).
- Araguás Araguás, L.; Mchelen, C.; Garcia, A.; Medina, J.; Febrillet, J. Estudio de la Dinamica del Lago Enriquillo: Segundo Informe de Avance; Project Report DOM/8/006; International Atomic Energy Agency: Vienna, Austria, 1995. [Google Scholar]
- Arboleda, J. Independencia: Perfil Socio-Economico y Medioambiental; Programa de las Naciones Unidas para el Desarrollo (PNUD): Santo Domingo, Dominican Republic, 2013; ISBN 978-9945-8741-4-3. [Google Scholar]
- Programa de Naciones Unidas para el Desarrollo (PNUD). Plan Estratégico de Recuperación y Transición al Desarrollo Para la Zona del Lago Enriquillo; Editora Búho, Proyecto Frontera-UNDP: Santo Domingo, Dominican Republic, 2013. [Google Scholar]
- Mejía, V.A.M.; León, Y.; Quintana, C.; Rosario, A. Contribution of surface water sources in the eastern part of Lake Enriquillo and the impact of these waters to the growth of the lake. Cienc. Soc. 2015, 40, 425–448. [Google Scholar]
- Quezada, A.C. El ciclo Hidrologico del Lago Enriquillo y la Crecida Extrema del 2009; Report available at Acqweather.com; Acqweather: Santo Domingo, Dominican Republic, 2009. [Google Scholar]
- Ducoudray, F.S. Dominican Nature, Article Published in the Saturday Supplement of the Newspaper El Caribe (1978–1989); Southern, R., Ed.; Aristides Inchaustegui, Blanca Delgado Malagón; Grupo León Jiménez: Santo Domingo, Dominican Republic, 2006; Volume 2, pp. 273–274. [Google Scholar]
- Sheller, M.; León, Y.M. Uneven socio-ecologies of Hispaniola: Asymmetric capabilities for climate adaptation in Haiti and the Dominican Republic. Geoforum 2016, 73, 32–46. [Google Scholar] [CrossRef]
- Piasecki, M.; Moknatian, M.; Moshary, F.; Cleto, J.; Leon, Y.; Gonzalez, J.; Comarazamy, D. Bathymetric Survey for Lakes Azuei and Enriquillo, Hispaniola; Research Report; CUNY Academic Works: New York, NY, USA, 2016. [Google Scholar]
- Dale, V.H.; Beyeler, S.C. Challenges in the development and use of ecological indicators. Ecol. Indic. 2001, 1, 3–10. [Google Scholar] [CrossRef] [Green Version]
- Patrício, J.; Neto, J.M.; Teixeira, H.; Salas, F.; Marques, J.C. The robustness of ecological indicators to detect long-term changes in the macrobenthos of estuarine systems. Mar. Environ. Res. 2009, 68, 25–36. [Google Scholar] [CrossRef] [Green Version]
- Choubak, M.; Pereira, R.; Sawatzky, A. Indicators of Ecological Behaviour Change; Community Engaged Scholarship Institute: Guelph, ON, Canada, 2019. [Google Scholar]
- Harmsen, E.W. Puerto Rico Agricultural Water Management (PEAGWATER). Available online: https://pragwater.com/ (accessed on 18 February 2018).
- Szesztay, K. Water balance and water level fluctuations of lakes. Hydrol. Sci. 1974, 19, 73–84. [Google Scholar] [CrossRef]
- Izzo, M.; Aucelli, P.P.C.; Javier, Y.; Pérez, C.; Rosskopf, C.M. The tropical storm Noel and its effects on the territory of the Dominican Republic. Nat. Hazards 2010, 53, 139–158. [Google Scholar] [CrossRef]
- Kieniewicz, J.M.; Smith, J.R. Paleoenvironmental reconstruction and water balance of a mid-Pleistocene pluvial lake, Dakhleh Oasis, Egypt. GSA Bull. 2009, 121, 1154–1171. [Google Scholar] [CrossRef]
- Eptisa Internacional Grupo EP. Unidad Hidrogeológica de la Sierra de Bahoruco y Península Sur de Barahona; Informe de la Estudio Hidrogeológico Nacional de la República Dominicana Fase II.; Santo Domingo, Dominican Republic, 2004; Available online: https://gymrd.com/hidro/estudio/Estudio%20Hidrogeol%C3%B3gico%20de%20la%20Sierra%20de%20Bahoruco%20y%20Pen%C3%ADnsula%20Sur%20de%20Barahona.pdf (accessed on 12 August 2021).
- Smucker, G.R.; Bannister, M.; D’Agnes, H.; Gossin, Y.; Portnof, M.; Timyan, J.; Tobias, S.; Toussaint, R. Environmental Vulnerability in Haiti: Findings & Recommendations; Report prepared by Chemonics International Inc. and the U.S. Forest Service for for review by the United States Agency for International Development (USAID); USAID: Haiti, Indonesia, 2007.
- International Resources Group Ltd. Dominican Republic Environmental Assessment; Report prepared for the United States Agency for International Development (USAID); United States Agency for International Development (USAID): Santo Domingo, Domonican Republic, 2001.
- Versluis, A.; Rogan, J. Mapping land-cover change in a Haitian watershed using a combined spectral mixture analysis and classification tree procedure. Geocarto Int. 2010, 25, 85–103. [Google Scholar] [CrossRef]
- Mora, S.; Roumagnac, A.; Asté, J.-P.; Calais, E.; Haase, J.; Saborío, J.; Marcello, M.; Milcé, J.-E.; Zahibo, N. Analysis of Multiple Natural Hazards in Haiti; Report prepared by the Government of Haiti, with support from the World Bank, the Inter-American Development Bank, and the United Nations System; Government of Haiti: Port-au-Prince, Haiti, 2010. [Google Scholar]
- Emmanuel, E. Atelier sur la Gestion et la Legislation de l’Eau, Haiti; Pre-Workshop Report; Technical cooperation BID No. ATN/SF-5485-HA, Programme de Formulation de la Politique de l’Eau; Ministère de l’Environnement: Port-au-Prince, Haiti, 1998. [Google Scholar]
- Abbaspour, K.C.; Johnson, C.A.; van Genuchten, M.T. Estimating uncertain flow and transport parameters using a sequential uncertainty fitting procedure. Vadose Zo. 2004, 3, 1340–1352. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]

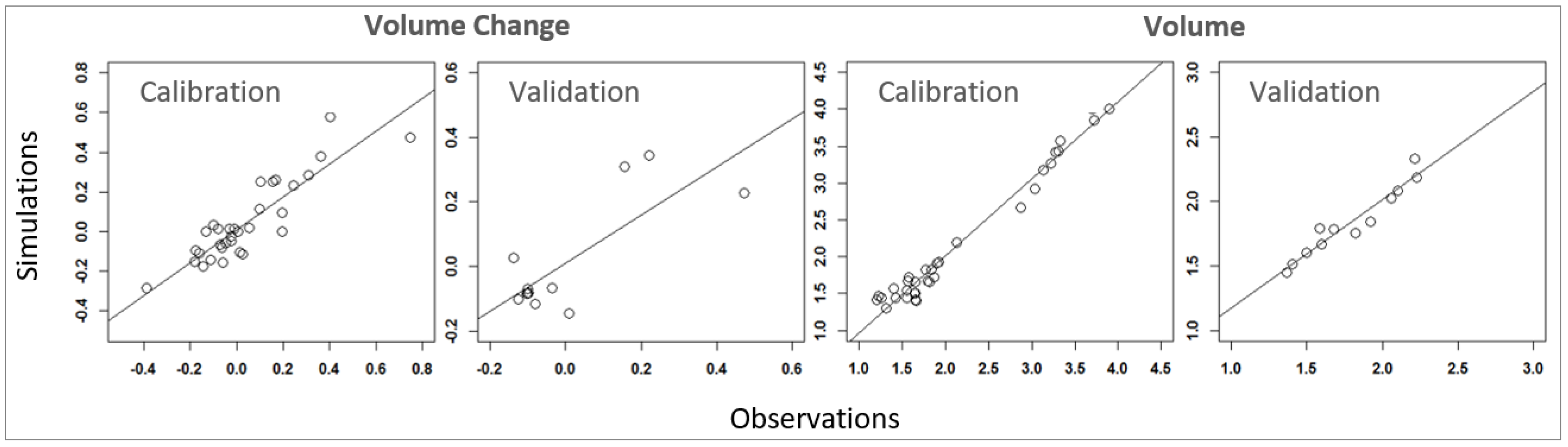


| NSE | RSS | RMSE | MAE | RE | p-factor | r-factor | ||
|---|---|---|---|---|---|---|---|---|
| Calibration | Volume Change | 0.78 | 0.276 | 0.091 | 0.074 | −9.2% | 33% | 0.41 |
| Volume | 0.97 | 0.662 | 0.142 | 0.122 | 0.9% | 94% | 0.92 | |
| Validation | Volume Change | 0.58 | 0.130 | 0.104 | 0.085 | 16.7% | 50% | 0.66 |
| Volume | 0.92 | 0.062 | 0.072 | 0.084 | 3.1% | 92% | 1.78 |
| NSE | RSS | RMSE | MAE | RE | p-factor | r-factor | ||
|---|---|---|---|---|---|---|---|---|
| Calibration | Volume Change | 0.71 | 0.0065 | 0.0141 | 0.011 | −14% | 45% | 0.59 |
| Volume | 0.99 | 0.0073 | 0.0149 | 0.015 | −0.18% | 100% | 0.97 | |
| Validation | Volume Change | 0.63 | 8.92 × 10−5 | 0.00262 | 0.002 | 12% | 83% | 5.54 |
| Volume | 0.87 | 5.52 × 10−5 | 0.00206 | 0.002 | 0.01% | 83% | 2.51 |
| Parameter | Lake Enriquillo | Lake Azuei |
|---|---|---|
| (km3/yr) * | Lake volume change time series [–0.39, +0.75] ** | Lake volume change time series [–0.02, +0.1] |
| (km2) * | Lake surface area time series [168.1, 349.6] | Lake surface area time series [113.7, 138.1] |
| (km2) * | ||
| (mm/yr) | Jimani station annual records [306, 1084] | Jimani station annual records [306, 1084] |
| (mm/yr) | ||
| (mm/yr) | 1250 | 1400 |
| (mm/yr) | not applicable | 733 or f (LE’s elev) |
| 0.19 | 0.21 | |
| *** | [0, 0.6] | [0, 0.6] |
| 0 or 1 | [0, 1] | |
| *** (m3/s) * | [0, 25] | No range is available |
| (mm/yr) | term from LA’s water budget when it is negative | not applicable |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moknatian, M.; Piasecki, M. Development of Predictive Models for Water Budget Simulations of Closed-Basin Lakes: Case Studies of Lakes Azuei and Enriquillo on the Island of Hispaniola. Hydrology 2021, 8, 148. https://doi.org/10.3390/hydrology8040148
Moknatian M, Piasecki M. Development of Predictive Models for Water Budget Simulations of Closed-Basin Lakes: Case Studies of Lakes Azuei and Enriquillo on the Island of Hispaniola. Hydrology. 2021; 8(4):148. https://doi.org/10.3390/hydrology8040148
Chicago/Turabian StyleMoknatian, Mahrokh, and Michael Piasecki. 2021. "Development of Predictive Models for Water Budget Simulations of Closed-Basin Lakes: Case Studies of Lakes Azuei and Enriquillo on the Island of Hispaniola" Hydrology 8, no. 4: 148. https://doi.org/10.3390/hydrology8040148
APA StyleMoknatian, M., & Piasecki, M. (2021). Development of Predictive Models for Water Budget Simulations of Closed-Basin Lakes: Case Studies of Lakes Azuei and Enriquillo on the Island of Hispaniola. Hydrology, 8(4), 148. https://doi.org/10.3390/hydrology8040148







