Next Article in Journal
Effect of Projected Land Use and Climate Change on Water Quality of Old Woman Creek Watershed, Ohio
Next Article in Special Issue
Interdisciplinary Water Development in the Peruvian Highlands: The Case for Including the Coproduction of Knowledge in Socio-Hydrology
Previous Article in Journal
Water Budget Analysis Considering Surface Water–Groundwater Interactions in the Exploitation of Seasonally Varying Agricultural Groundwater
Previous Article in Special Issue
Common Pool Resource Management: Assessing Water Resources Planning for Hydrologically Connected Surface and Groundwater Systems
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Hydrology
Volume 8
Issue 2
10.3390/hydrology8020061
hydrology-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

System Dynamics Modeling for Evaluating Regional Hydrologic and Economic Effects of Irrigation Efficiency Policy

by
Yining Bai
1,*,
Saeed P. Langarudi
1 and
Alexander G. Fernald
1,2
1
College of Agricultural, and Environmental Sciences, New Mexico State University, Las Cruces, NM 88003, USA
2
New Mexico Water Resources Research Institute, New Mexico State University, Las Cruces, NM 88003, USA
*
Author to whom correspondence should be addressed.
Hydrology 2021, 8(2), 61; https://doi.org/10.3390/hydrology8020061
Submission received: 4 March 2021 / Revised: 28 March 2021 / Accepted: 30 March 2021 / Published: 2 April 2021
(This article belongs to the Special Issue Socio-Hydrology: The New Paradigm in Resilient Water Management)
Browse Figures
Versions Notes

Abstract

:
Exploring the dynamic mechanisms of coupled sociohydrologic systems is necessary to solve future water sustainability issues. This paper employs system dynamics modeling to determine hydrologic and economic implications of an irrigation efficiency (IE) policy (increased conveyance efficiency and field efficiency) in a coupled sociohydrologic system with three climate scenarios. Simulations are conducted within the lower Rio Grande region (LRG) of New Mexico for the years 1969 to 2099, including water, land, capital, and population modules. Quadrant analysis is utilized to compare the IE policy outcomes with the base case and to categorize results of simulations according to hydrologic and economic sustainability. The four categories are beneficial, unacceptable, unsustainable agricultural development, and unsustainable hydrology. Simulation results for the IE policy analyzed here fall into the categories of unsustainable agricultural development or unacceptable, suggesting there are long-term negative effects to regional economies in all scenarios with mixed results for hydrologic variables. IE policy can yield water for redistribution as increased unit water supply in the field produces more deep percolation; however, IE policy sacrifices regional connectivity. Specifically, simulation results show that the policy increases abundance by 4.7–74.5% and return flow by −3.0–9.9%. These positive results, however, come at the cost of decreased hydrologic connectivity (−31.5 to −25.1%) and negative economic impacts (−32.7 to −5.7%). Long-term net depletions in groundwater are also observed from loss of hydrologic connectivity and increased agricultural water demand from projections of increased consumptive use of crops. Adaptive water management that limits water use in drought years and replenishes groundwater in abundant years as well as economic incentives to offset the costs of infrastructure improvements will be necessary for the IE policy to result in sustainable agriculture and water resources.

1. Introduction

The inclusion of the social component in hydrologic modeling is necessary for considering the implications of water management decisions in coupled socio-hydrologic systems. Sivapalan et al. [1] presented the importance of socio-hydrology to illustrate the evolution of coupled socio-hydrologic systems, potential co-evolution tracks, and emerging or even unexpected patterns that depart from the previous framework setting for scenario analyses. System dynamics modeling is a particularly useful method to simulate the dynamic mechanisms within a coupled system [2]. By properly modeling the interactions within a coupled socio-hydrologic system, proposed changes such as policy implementation may be included to model future impacts on varying aspects of both systems. In this way, simulations can offer insights as to which components of the system may benefit or be negatively impacted, which may contribute to water policy decision-making processes.

1.1. System Dynamics and Its Application for Sociohydrology

Communicating a coupled socio-hydrologic system’s complexity is difficult when considering the dynamics of the system, varied perspectives of water stakeholders, and potential conflicts among water users. Local changes to a system result in unexpected changes to the broader system and interconnected systems such as economies [3]. A change in the system can yield nonlinear and indirect effects [4,5,6]. The causes for an outcome with a management strategy are varied due to delays between actions and effects, making it challenging to identify policy options.
System dynamics modeling is one approach to represent the key feedback structures of a coupled system with a social component. Key feedback structures in socio-hydrologic modeling track systematic impacts that arise due to anthropogenic factors. Liu et al. [7] used one exploratory and simplified conceptual model to depict the socio-hydrologic system’s co-evolution processes. Gober et al. [8] stated that system dynamics view human activities as internal driving factors and include the interaction between social and hydrologic processes that threatens current water systems’ viability through feedbacks and unintended consequences.
System dynamics modeling has long been recognized as an approach to realize socio-hydrology research since Forrester developed the concept [9,10]. System dynamics modeling can long-term reflecting the impacts of social components. Then influence of social components may not have been obtained by modeling of the individual parts of the system separately. In this method, systems are represented through feedback loops, stocks, and flows. Feedback loops dictate the behavior of the system based upon physical processes and thresholds. Stocks depict the state of the system and maintain stepwise trends. Flows affect the stocks as inflow and outflow and interlink the stocks within a system [11].
System dynamics modeling is categorized as either qualitative and quantitative or conceptual and numerical [12,13]. Feedback loops improve the understanding of a system qualitatively [14]. Stocks and flows visualize the effects of system behavior through simulation quantitatively. Meanwhile, system dynamics modeling aggregates a wide range of input parameters as key factors in a meaningful way [15]. In particular, it can incorporate different forms of human decision-making processes and behavioral rules [16]. These characteristics can guide water management strategies responding to the crucial changes in an adaptive way [17,18]. System dynamics modeling can dynamically simulate the consequences of evolutionary systems as a decision support tool for strategic policy testing [19,20].

1.2. Regional Irrigation Efficiency

Precautionary measures for ensuring future supply often focus on reducing future demand by increasing IE. IE’s formal definitions are explained in Appendix A. IE policy aims to maximize the consumptive use portion of water withdrawals to obtain “more crop per drop” [21]. The essential assumption about irrigation efficiency is that by reducing the portion of non-consumptive use (e.g., surface water diverted that percolates back to groundwater) of total diversions, water is being conserved. The investment in advanced irrigation systems leads IE’s increase, which keeps the root zone saturated with limited irrigation. The saving of water at the field scale impacts the whole socio-hydrology system. The water saved results from IE policy implementation; however, it is not aligned with regional sustainability in agriculture and water. Furthermore, IE’s investment and its impacts regionally are particularly of interest to agricultural development in dry regions with limited available water supplies. Agricultural water demand is affected by various factors. IE policy achieved in one study performed in New Mexico led to a reduction in water applied per hectare but increasing water depletion based on various basin data analyses [22].
Achieving real water savings requires understanding institutional, technical, and accounting measures that accurately track and economically reward reduced water depletions. Conservation programs that target reduced water diversions or applications provide no guarantee of saving water. The systematic understanding leads to cooperation on regional sustainability goals from diverse water users.
Implications of IE policy should be calculated in a broader context reflecting a mathematical perspective as well as a systematic perspective that includes uses that are traditionally classified as nonbeneficial. The mathematical perspective reflects IE policy’s performance based on IE’s definition; systematic perspective reflects the changes in the system’s components affected by IE policy. Encompassing water management calls for understanding the interconnections between potential solutions and systematic consequences [17].
This paper aims to examine the utility of system dynamics modeling by analyzing the costs and benefits of implementing an IE policy. To address the overall effect of IE policy on agriculture sustainability and water sustainability, this study couples the dynamics of the agricultural hydrologic cycle, irrigation management, population, and economic development with interconnected feedbacks through system dynamics modeling. IE policy’s impact is investigated with three climate scenarios through system dynamics simulations within New Mexico’s LRG region from 1969 to 2099. It is hypothesized that system dynamics modeling would provide useful insights for informing IE policy. Specifically, it is hypothesized that unintended consequences of IE policy would be illuminated, such as decreased hydrologic connectivity, groundwater depletion, and negative economic impacts. Simulation results report the model’s pertinent performance measures of irrigated agriculture and local economies in response to the policy scenario.

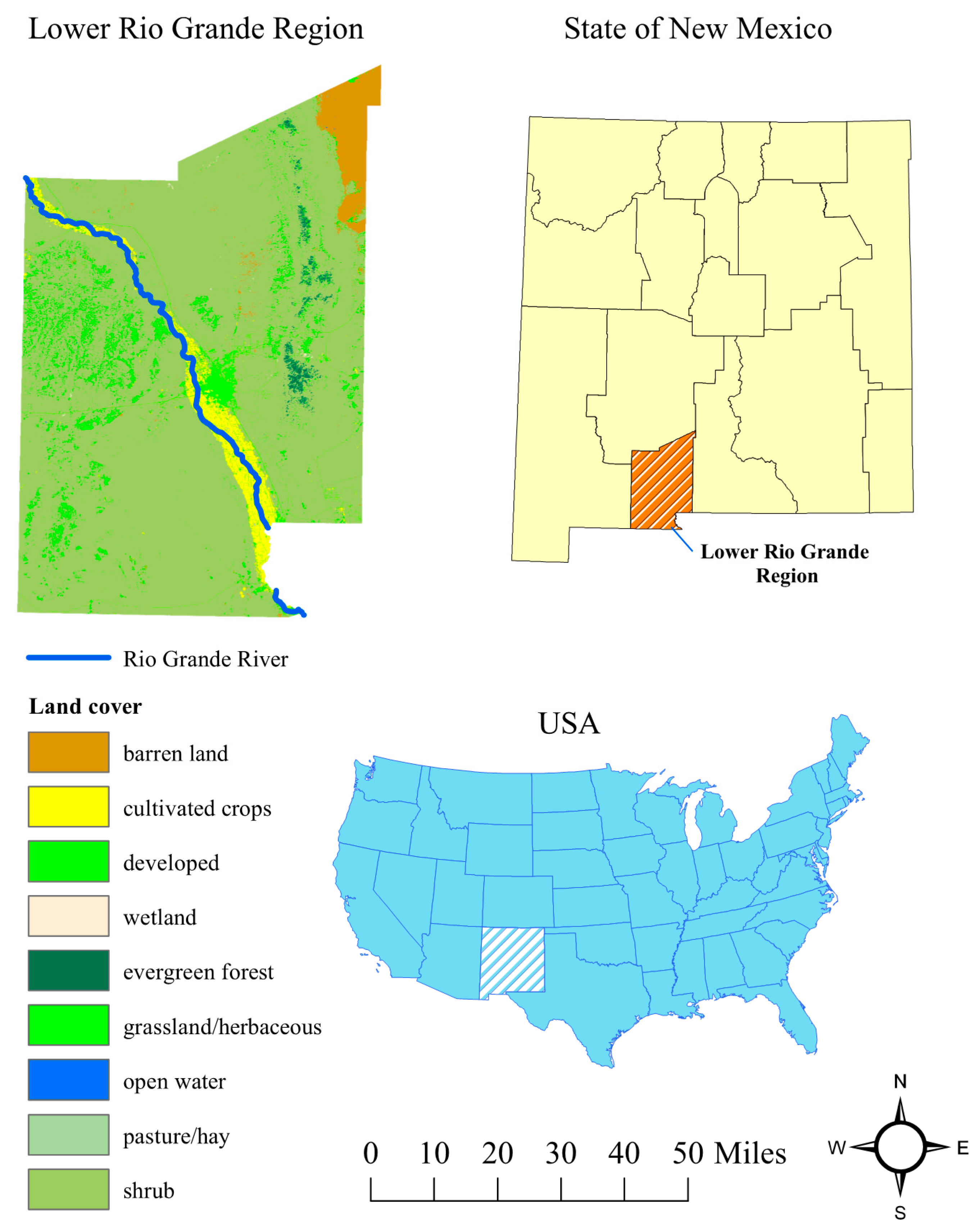
2. Overview of the Research Area

The Rio Grande River flows through three states (Colorado, New Mexico, and Texas) and forms the border between two countries (the Republic of Mexico and the United States of America). The Rio Grande has its headwaters in the San Juan Mountains of Colorado and terminates in the Gulf of Mexico. The river forms a valley through New Mexico; a large majority of the land use in the valley consists of irrigated agriculture [23]. The valleys surrounding the Rio Grande in New Mexico are categorized into three regions: upper Rio Grande, middle Rio Grande, and lower Rio Grande (LRG). The latter is focused on here (Figure 1). The LRG planning region includes all of Doña Ana County, and the total area of the planning region is 3814 square miles (9878 square km). Agriculture is the predominant land use adjacent to the Rio Grande in this area [23]. The climate is semi-arid, and annual precipitation ranges from 8 to 20 inches, depending on topography. The majority of precipitation falls as rainfall during the monsoon season. Geology surrounding the LRG consists of 150 to 400 feet of alluvium in which unconfined aquifers are highly connected with the river [24]. Fuchs et al. [25] stated that groundwater storage change is positively correlated with surface water use in the LRG region. The LRG region is located downstream of the Elephant Butte Reservoir, which supplies surface water to irrigators and happens to be experiencing a megadrought (drought persisting more than 20 years) [26].
The majority of water diverted from the Elephant Butte Reservoir is for agricultural use (87%), with only a small amount diverted for residential use [27]. Groundwater pumping is an indispensable supplement to surface irrigation supply impacting Rio Grande’s management operation. The current operating agreement since 2008 among the Elephant Butte Irrigation District, El Paso County Water Improvement District, and the U.S. Bureau of Reclamation has been to release 150,000 additional acre-ft from the reservoir in full-supply years to meet downstream delivery requirements of Texas and Mexico [28]. Because agriculture in this region plays a central role in the local economy, stakeholders’ perception and the economic value of crop yields jointly determine the water demand resulting in a low elasticity for water demand [29]. Water delivery requirements not met by surface water are supplied by groundwater. During drought, groundwater is presumably the crucial alternative water source.
The LRG region’s recorded population in 2010 was 209,000, which is continuing to increase [30]. The rising municipal water demand to match population growth creates the risk that water rights will be transferred from agriculture to urban areas, compressing the available agricultural water supply. New Mexico has been leading national pecan production after 2018. Hurricane Michael severely impacted the Georgia pecan industry [18]. Of the state’s 92 million pounds of pecans in 2017, Doña Ana county produced 66.9 million pounds. Pecan orchards comprise over 30% of the LRG region. During an irrigation season, pecan orchards need 3.6–6.6 ft irrigation in the southwestern United States [19,20]. Doña Ana also leads statewide pasture production [21]. A sufficient water supply is required to ensure profitable agricultural production, preventing substantial reallocation of water from agriculture to other sectors [31].

3. Methods

3.1. Model Structure

The model details are available from the accompanying Supplementary Material and Langarudi et al. [3]. This paper’s system dynamics model consists of 15 stocks and 33 flows and simulates from 1969 to 2099. The model is structured into four modules: water, capital, land, and population. All the details of the assumptions and modeling choices, including equations, parameter values, estimations and measurements, and data sources, are reported in the Supplementary Material. These modules interact with each other within a complex feedback system. The relationships among modules are constructed based on the literature, previous models, or empirical studies (black and blue linkages in Figure 2). The water module consists of surface water, soil moisture of irrigated and non-irrigated land, and groundwater as stocks. The primary physical processes are integrated into the model building, including surface inflow/outflow, river leakage, surface water withdrawal, canal leakage, field percolation, gaining flow from groundwater, and groundwater withdrawal. Income, capital development, irrigated land, and population growth contribute to water demand (Figure 2). Agricultural parameters, such as crop type and soil properties, are aggregated into the model design, addressing their impacts on the hydrologic cycle dynamics and water demand in socio-economic processes. Water availability is driven by precipitation, surface inflow, and groundwater storage. Water availability impacts income, capital development, irrigated land and population in turn. The model successfully passes the confidence building (validation) tests presented in the Supplementary Materials, supporting that this model can provide insights into regional water issues.

3.2. Scenarios

3.2.1. Climate Scenarios

Hydroclimate scenarios are introduced in a changing future. Model inputs (precipitation, temperature, and surface water inflow) are acquired from the New Mexico Dynamic Statewide Water Budget (DSWB) model [32]. The DSWB model generates data by using climate projections (Global Circulation Model), including GFDL (Geophysical Fluid Dynamics Laboratory), UKMO (United Kingdom Met Office), and NCAR (National Center for Atmospheric Research). Based on different greenhouse gas emission scenarios, each climate projection offers different drought conditions [26].
The GFDL, UKMO, and NCAR projections are used as inputs because they represent low, moderate and, high emission scenarios. The scenarios are listed in Table 1, where the prediction part of the simulation is divided between 2017–2050 and 2051–2099. The simulation interval is divided to illustrate the short and long-term results of the climate scenarios.

3.2.2. Climate Scenarios as Input

Precipitation has relatively high variability during 2017–2050 and 2051–2099 in the LRG planning region. Compared to historical average annual precipitation, the GFDL projection shows a decreasing trend, UKMO shows an increasing trend, and NCAR is similar to historical conditions.
Projections of temperature have relatively low variability in projections but show a potential increase of 5.1 °F in the long-term. All projections show temperature increasing to some degree as time progresses. Compared with historical average annual temperature (61.3 °F), GFDL shows a greatly increasing trend, UKMO shows a moderately increasing trend, and NCAR shows a mildly increasing trend.
Projections of surface inflow had high variability and no clear trends over time as all projections showed similar or increased values in the near-term which all decreased in the long-term. Compared with historical average annual surface inflow, the GFDL has similar then decreased flow, UKMO shows increased then slightly decreased flow, and NCAR shows greatly increased then moderately increased.

3.2.3. IE Policy

Canal lining and precision irrigation are strategies implemented here to represent IE policy. The scenario analysis is conducted with the cost of infrastructure development deducted from agricultural income. The deduction of cost counts as the impact of investment on agriculture or non-agriculture, which does not impact the cost of capital development. This means that agricultural income in the paper, in effect, represents a “net income” that reflects the impact of technological investment costs.
Canal lining aims to improve conveyance efficiency. Conveyance efficiency increases through investment in irrigation infrastructure that reduces canal seepage and increases water delivery to the fields relative to water released from the reservoir upstream. Improvement of conveyance efficiency necessitates irrigation infrastructure and involves deduction from profit. Canal lining cost varies depending on lining material, canal cross-section design, and installation approaches. Based on the Bureau of Reclamation’s historical record, the canal lining cost ranges from 14.9 to 37 dollars per square yard [33]. The canal lining cost ranges from up to 2000 dollars per acre-foot of water saved [34]. Multiplying the unit cost of canal lining and surface water divisions yields the total cost. More of surface water withdrawals will be delivered to the field with canal lining, and less water will be “lost” as canal seepage. In the model, as conveyance efficiency increases, the total cost for canal lining will be deducted from agriculture income. The regional canal lining project is a long-term process, so canal lining takes ten years to plan and ten more years to implement. The service life of the canal lining is deemed to be forty years [34]. The canal lining process continues until the total irrigation supply reaches the largest yearly water supply of surface water. The variables involved in the policy test are listed in Table 2.
Precision irrigation aims to improve field irrigation efficiency. Irrigation systems could be altered to improve field efficiency (e.g., through drip and sprinkler irrigation). High IE irrigation systems typically maintain the same productivity with less water applied or increase productivity with the same water application rate due to more water delivered to the fields being available to crops [35,36]. Field irrigation efficiency refers to irrigation technology and practices that attempt to apply only the water necessary to replenish the amount of water lost through ET and reduce percolation past the root zone. Costs associated with irrigation conservation have been cited for having varied installation costs per acre and operation costs [37]. As summarized in a report of drip irrigation experiments, the cost for design, materials, and installation of a drip irrigation system for the case of a farm in Rincon, New Mexico, which was a 26-acre farm, was 52,000 dollars [38]. The variables involved in the policy test are listed in Table 2.

3.3. Evaluation Framework

The simulated results are examined based on performance indicators such as water abundance, groundwater dependency, field IE, irrigation return, and hydrologic connectivity. These measures are described below.
  • Abundance: the difference between available water (sum of water supply from surface water, recharge or leakage from river channels and canals as well as percolation from the land surface) and total withdrawals (sum of withdrawals from surface water and groundwater for all uses);
  • Irrigation return: a proportion of irrigation drainage, which is excess water left in the root zone after soil saturation;
  • Connectivity: a measure for recharge connectivity of surface water and groundwater defined as the sum of river leakage, canal leakage, and deep percolation.
  • Groundwater dependency: the portion of agricultural groundwater withdrawals in total agricultural water withdrawals;
  • Agricultural water demand: water needed to be withdrawn from surface water and groundwater for sustaining the desired level of agricultural yield from irrigated land.
The policy performance is analyzed to measure water sustainability while investigating water economics. To understand the tradeoffs between the selected scenarios from both economical and hydrological perspectives, the above-described measures were employed. The percentage deviation is given by Equation (1):
Δ y i j = ∑ y i j t − ∑ y o j t ∑ y o j t × 100
The percentage deviation is given by Equation (1), where yij represents the value of measure j with scenario i. Note that i = 0 indicates the base case simulation whereas i = 1 represents irrigation efficiency. The values are then summed for t (time) during the periods 2017–2050 and 2051–2099. Policy notations are listed in Table 3. For each of these measures, we calculate their relative deviation from base run values. For each comparison, the climate scenario remains unchanged. For example, we do not compare a UKMO policy scenario (Ui) with a GFDL base scenario. These simulations provide three alternative future possibilities as benchmarks that the policy scenarios could be compared with.
The Δ y i j ’s value of hydrology performance indicators are plotted against percentage change in agriculture income on two-dimensional quadrant grids. On the presented quadrants, the x-axis always represents agricultural income, while the y-axis represents one of the hydrologic measures (IE, water abundance, irrigation return, and hydrologic connectivity). The title of each row in the figure indicates which hydrologic measures should be on the y-axis for the graphs in that column. Each column of the graphs is for a specific climate scenario. The first column indicates the results for GFDL, the second for UKMO, and the third for NCAR. Each point on the grid represents the discrepancy between a policy simulation run and a corresponding base run (no policy applied). Therefore, for each row of graphs, the origin of a grid represents an average steady-state, which is equivalent to a comparison of a base case and itself. Because there is no discrepancy between a simulation run and itself, such comparisons yield x = 0 and y = 0 . The analysis is broken into two periods being the years 2017–2050 and 2051–2099. The impact of policy implementation could be prolonged and yield unexpected consequences. The comparison between the two periods can illustrate the expected and unexpected performance.
A quadrant analysis is applied to interpret the hydrology performance indicators and agricultural income. Each quadrant represents a potential outcome: beneficial, unacceptable, unsustainable agriculture development, and unsustainable hydrology. The upper right quadrant (beneficial) represents policies that are beneficial both economically and hydrologically, which would be the most favorable state. Thus, results that are located in the lower-left quadrant (unacceptable) are neither economically beneficial nor sustainable, thus unacceptable. The upper left quadrant (unsustainable agriculture development) represents results with a positive effect on water system performance but a negative influence on agricultural income. The lower right quadrant (unsustainable hydrology) indicates results that would be beneficial economically but would need additional water management policies to offset associated negative hydrologic impacts. The following sections detail each grid presented in Figure 3 and demonstrate different performance measures of irrigated agriculture and how they deviate from the base runs due to the policy applications.

3.4. Model Suitability

The purpose of this modeling exercise is to determine long-term hydrologic and economic trends. Simulated results reveal implications of a specific water management policy. Only limited regional hydrologic and economic data are available in the literature from which model inputs and relationships are acquired. System dynamics modeling is specifically chosen for this application because it has the benefit over other modeling methods of being able to proficiently model long-term trends while having limited data as inputs [13].

4. Results

Basic behavior-over-time diagrams of the model’s outputs showed the strong relationships between independently measured variables (see Appendix A Figure A1 and Figure A2). These diagrams, along with formal statistical methods guided by practical examples [39], are used to validate the model outputs, including seven water variables and seven socioeconomic variables. These variables displaying the model’s outputs differ from the variables used for calibration that can be adjusted manually. Chapter 9 of the Supplementary Material offers a complete methodology. Results-over-time of base run and scenario tests are graphed in Figure A3. Results are interpreted in the quadrant analysis.

4.1. Policy Scenarios

The performance of water abundance, irrigation return, and connectivity are graphed in Figure 3. Black dots represent results during 2017–2050; blue dots represent results during 2051–2099.

4.1.1. Agricultural Income

Agricultural income is negatively affected by the IE policy. The results of simulations are constrained to the categories of unsustainable agricultural development or unacceptable in the quadrant analysis. Agriculture income reduces by 32.7% in G1, 19.1% in U1, 23.0% in N1 during 2017–2050, and 7.8% in G1, 5.7% in U1, and 10.0% in N1 during 2051–2099. The average reductions in agricultural income are −24.9% in the short-term and −7.8% in the long-term. The proposed infrastructure related to the IE policy is a long-term investment on a large scale, so reducing agricultural income is not surprising. It should be noted that the negative impacts to agricultural income are greatly reduced in the long-term but still have a consistently negative impact compared to the base case.

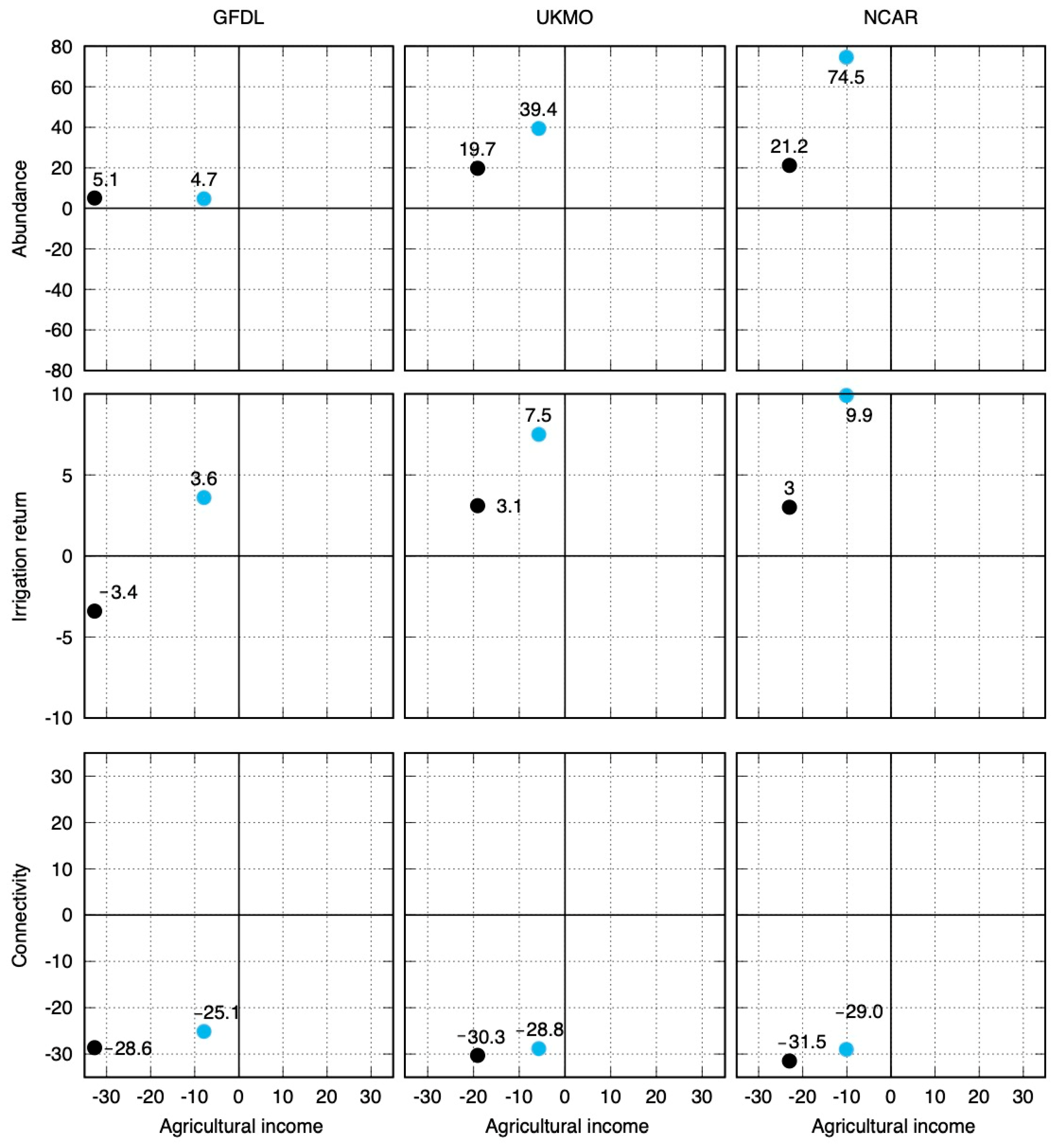
4.1.2. Abundance

Positive effects on water abundance in all scenarios are observed, and results fall within the category of unsustainable agricultural development. Abundance increases during 2017–2050 (5.1% in G1, 19.7% in U1, and 21.2% in N1) and 2051–2099 (4.7% in G1, 39.4% in U1, and 74.5% in N1). The average increase of abundance is 15.3% in the short-term and 39.5% in the long-term. The water “saved” positively affects water availability. An interesting result is that in the drought scenario (G1), the benefits of abundance show a slight decrease from the short-term to the long-term. The other two scenarios show a large increase from the short-term to the long-term. Copious precipitation in UKMO and surface inflow of NCAR during the long-term period contribute to a total agricultural water supply.

4.1.3. Irrigation Return

Irrigation return is affected positively for the majority of simulations, and results fall within the category of unsustainable agricultural development. An exception is the G1 scenario in the short-term, which falls into the category of unacceptable. The evaluated IE policy yields irrigation return changes (−3.4% in G1, 3.1% in U1, and 3.0% in N1) during 2017–2050. Irrigation return increases (3.6% in G1, 7.5% in U1, and 9.9% in N1) during 2051–2099. The average increase in irrigation return is 0.9% in the short-term and 7.0% in the long-term. The increasing irrigation return over the simulation period shows that the IE policy benefits the long-term irrigation supply.

4.1.4. Connectivity

The IE policy has consistently poor results regarding connectivity, and all simulations fell into the category of unacceptable. Decreases (over 25.1%) in connectivity (Figure 3) are due to a nearly complete reduction of canal seepage resulting from canal lining and the reduction of deep percolation in the field due to precision irrigation technologies. From 2017–2050 to 2051–2099, connectivity changes from −28.6% in G1, −30.3% in U1, and −31.5% in N1, to −25.1% in G1, −28.8% in U1, and −29.0% in N1. The average decrease in connectivity is −30.1% in the short-term and −27.6% in the long-term. These changes show that canal seepage and deep percolation are important sources of recharge to groundwater.

4.2. Water Resilience

In this paper, water resilience represents stable groundwater storage and agricultural water demand. Groundwater (GW) dependency and agricultural water demand are analyzed for exploring water resilience within efficiency-oriented management. Table 4 summarizes GW dependency and agricultural water demand in simulations.
IE policy lowered GW dependency under all three climate scenarios throughout the simulation. GW dependency reduction ranges from 10.7% to 39.1% during 2017–2050 and 1.7% to 14.1% during 2051–2099. The average change in GW dependency was −22.1% in the short-term and −6.2% in the long-term. GW dependency declined initially; however, after 2050, the benefits were consistently diminished.
Table 4 also suggests that IE policy failed to regulate agricultural water demand. Agricultural water demand changes are positive, which means more pressure would be put on the agricultural water supply. Agricultural water demand exhibited rising trends with precision irrigation policy in all three climate scenarios. The increase in agricultural demand ranges from 4.8% to 9.3% during 2017–2050 and 1.8% to 5.6% during 2051–2099. The average change in agricultural water demand was 6.8% in the short-term and 2.7% in the long-term.

5. Discussion

5.1. Regional Water Reuse

Water “lost” to irrigation return and groundwater through connectivity can be beneficial on the regional level for other users [40,41,42,43]. Results (Figure 3) show positive irrigation return (except G1 during 2017–2050) and negative connectivity. This suggests that, from one perspective, IE policy can yield water for redistribution as increasing unit water supply in the field. From another perspective, IE policy sacrifices regional connectivity. In general, groundwater at the regional scale is not sufficiently recharged. Since the 1960s, IE policy impacts of upstream areas upon downstream resources have been reported in the literature [44,45]. However, real savings at a regional scale require encompassing water management for downstream re-allocation. Simons et al. [45] showed that the recoverable flow from a water user could be reused multiple times by downstream water users. The “saved” amount in water conveyance impacts downstream uses that may rely on this portion of water.
Connectivity reductions indicate inadequacies of recharge from reduced irrigated agriculture on a regional scale. Similar to the irrigation return flow, the connectivity exhibits the time lag of mass movement in the water cycle. It buffers the disturbance of cumulative consequences such as water quality deterioration, soil contamination, edaphon alternation, and groundwater table depression. Declining connectivity and irrigation return reduce water availability for other users, as these non-consumptive flows play a vital role in instream water supplies [46,47].
In a broad context, connectivity contributes to groundwater resilience. In simulations, a loss of connectivity between surface water and groundwater is one of the unintended consequences of IE policy. Pringle [48] argued that human alterations of hydrologic processes that eliminate hydrologic connectivity have already influenced ecological patterns regionally and globally. As Gleick et al. [49] demonstrated, traditional IE improvement failed to depict the co-benefits, including water quality, reductions in water-related energy costs, ecosystem health, and improved crop quality. Although valuable, these benefits are not always as tangible as direct and immediate benefits because they do not yield “new water.” As Lexartza-Artza and Wainwright [50] suggested, practical studies should consider the opposite structural and functional components of connectivity and system boundaries. In water balance closure, any water use changes in one part of the region or basin will impact another water use. The consideration that water is “lost” when not applied directly to anthropogenic uses is a misleading perception. Applying these labels presents a lack of quantification of non-consumptive values. The definitions of natural and anthropogenic flows should be embedded in water management to represent multiple water users’ interdependency. IE may maximize water supply locally yet concurrently need synergies in a broader context. Synergistic practices such as aquifer storage and recovery should be included in future strategic water management alongside the efficiency practice to guarantee ecological benefits.

5.2. Groundwater Resilience

The evaluation of simulated scenarios indicates mixed results for groundwater resilience related to the policy tested. Folke et al. [51] defined resilience as both the capacity to undertake continuous changes and the ability to develop unceasingly. In light of this definition, groundwater resilience is not increased. Results suggest that IE policy could reduce groundwater dependency in the short-term, but this effect is diminished as time progresses. In simulations, net increases in agricultural water demand and reduced surface water supply and precipitation eventually lead to net groundwater mining and even reduced aquifer storage. Even though the GW dependency decreases, the total amount of groundwater withdrawals may increase because of increasing agricultural water demand. The incentives to grow higher water use crops lead to agricultural water demand increase in simulations for ensuring agricultural profits with increasing ET caused by higher temperature. The LRG region’s growing season is also longer than the surface water irrigation season. Regardless of surface water supply, irrigation in the LRG region is dependent upon groundwater at times. Increases in agricultural water demand (Table 4) show that IE policy fails to reduce total water withdrawals in times of drought without fundamental changes to current water delivery mechanisms.

5.3. Economic Implications

Reliance upon groundwater is costly in multiple aspects. Groundwater depletion, as a supplement to surface water supply, raises the cost of energy for pumping, the need for drilling new wells, and the need for deepening or repairing wells. Groundwater withdrawals need adequate energy facilities for pumping. Dehghanipour et al. [52] concluded that a reduction in surface water supply raises a challenge to groundwater pumping’s sustainable capacity. The sum of direct and indirect losses to agriculture in California was estimated at 2.2 billion dollars in 2014 [53] as the costs associated with groundwater pumping were an estimated 454 million dollars [54]. A farmer in the LRG Valley with a 325-acre farm had to spend about 150,000 dollars to drill a new well capable of producing sufficient quantities for irrigation [55]. The decreases in simulated agricultural income in this paper are in line with these observations.
The simulated initial costs for the IE policy are large during 2017–2050, as would be expected for infrastructure development. As such, the IE policy is a long-term policy that likely requires an up-front investment from the government [56]. Increased IE can support immediate irrigated agriculture requirements. Initial water supply security may encourage farmers to plant permanent crops such as orchards that yield higher profits. This may lead to inflexible production systems and expose the investment to increased risk [57]. In the long-term, irrigators have to cover the costs of maintaining the investment and cope with the returning drought. The investment for IE policy requires irrigation water productivity improvement to cover the costs in the long-term. Irrigated agriculture is not profitable for the majority of farmers when productivity remains low [58]. Enhancements in agricultural structure, such as cropland allotment and cropping intensity, promotion of resource conservation technologies, and farm mechanization, will ensure irrigated agriculture’s benefits. Turral et al. [59] reviewed global irrigation development and concluded that agricultural water use productivity is needed to achieve a higher value of agriculture. Constant adaptation and flexibility in water strategies and assorted economic incentives will enable regional agriculture development.

5.4. Management Strategies

Results in Figure 3 explain the sustainability stage in multiple aspects. In terms of abundance and irrigation return, results point to unsustainable agriculture development. Even though abundance and irrigation return increase, profits are decreased. From a connectivity perspective, the results show an unacceptable stage of sustainability where both connectivity and agricultural income suffer. Together these indicate that economic measures and alternative water management strategies are both lacking.
IE policy lays a foundation for ensuring irrigation supply as it maximizes the possible use of surface water. The investment in IE policy (loss in agricultural income in Figure 3) indicates that the next step is to increase agriculture benefits through various means, such as subsidies and technologies ensuring production and product quality to offset costs. Further, flexible water management strategies that focus on compensating for lost natural and historic flows during years with abundant water supply are necessary to prevent long-term consequences from the lost connectivity. If there are no assorted water management strategies to replenish the aquifer in wet years, recurring drought will still have an adverse impact on irrigation supply due to predicted increased and inelastic agricultural water demand. Scherberg et al. [60] applied modeling to verify that canal piping combined with an aquifer recharge program stabilized groundwater storage. Results suggested that canal piping alone failed to keep summer flows and could be detrimental to the local hydrology.
Economic incentives to offset costs of infrastructure investment such as subsidies or technologies that increase agricultural profits are necessary for the policy tested to be economically viable, particularly in the short-term. Maintaining a flexible cropping pattern could prevent groundwater reliance in times of drought, forgoing costs associated with well installation, repair, and pumping.

6. Summary and Conclusions

This study determined the systematic behavior of an arid region’s irrigation system within socio-hydrologic dynamics. A system dynamics model was developed for the lower Rio Grande region to determine the impacts of increased irrigation efficiency upon local hydrology and economics under different climate scenarios through 2099. The model simulated the variables’ dynamics with three climate projections and surface inflow that corresponded to the three climate projections as inputs. Regional IE policy was tested as a model scenario. Results showed that regional IE policy could yield water for redistribution as increasing unit water supply in the field; however, it may also have unintended consequences such as decreased hydrologic connectivity, groundwater depletion, and negative economic impacts. Regional IE policy fails to reverse the declining trends of groundwater and regulate agricultural water demand. Specifically, irrigation return flow and abundance are increased in the majority of simulations. These benefits come at the cost of decreased connectivity and overall economic losses in all scenarios.
In these scenarios, losses to agricultural economies are observed, particularly in the short-term. This suggests that subsidies, technologies, or management strategies that increase agricultural profits or decrease costs of IE infrastructure, particularly through the year 2050, are necessary for this IE policy to be economically viable. Water use in drought years and replenishment of groundwater in abundant years as well as economic incentives to offset the costs of infrastructure improvements will be necessary for the IE policy to result in sustainable agriculture and water resources.
Research on management strategies for increasing water sustainability is a prerequisite for future development. System dynamics modeling provides insights into interdependent water systems and how they may enable social and economic development. Further efforts may increase understanding of water management strategies, uncertainties of policy outcomes, and potential synergies. Successful implementation of this policy would include adaptive water management that limits water use in drought years and replenishes groundwater in abundant years. Economic policies or incentives to mitigate investment costs, particularly through 2050, are a necessary addition for this IE policy to be viable.

Supplementary Materials

The following are available online at https://www.mdpi.com/article/10.3390/hydrology8020061/s1.

Author Contributions

Conceptualization, Y.B. and S.P.L.; methodology, Y.B., S.P.L. and A.G.F.; software, Y.B. and S.P.L.; validation, S.P.L.; formal analysis, Y.B.; resources, A.G.F.; writing and original draft preparation, Y.B.; writing review and editing, Y.B., S.P.L. and A.G.F.; visualization, Y.B; supervision, A.G.F.; project administration, A.G.F.; funding acquisition, A.G.F. All authors have read and agreed to the published version of the manuscript.

Funding

This research was provided by the U.S. Bureau of Reclamation/New Mexico State University Cooperative Agreement R16AC00002 and the New Mexico Agricultural Experiment Station, New Mexico State University.

Acknowledgments

We thank Ian Hewitt for his constructive revisions. The authors wish to acknowledge the anonymous reviewers for their insightful comments and helpful suggestions which improved the earlier version of the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A

Appendix A.1. Irrigation Efficiency Equations

We define the regional irrigation efficiency as a product of two components: conveyance efficiency (IEc) and field irrigation efficiency (IEf). Conveyance efficiency is defined as
IE c = S D − C D S D
where SD is surface water diversion and CD is the amount of water that is lost through conveyance. Field irrigation efficiency is defined as follows:
IE f = E T − P a g S D − C D + G W D
where ET is evapotranspiration; Pag is effective precipitation during the growing season; GWD is groundwater diversion. Thus, the following may be deduced:
IE = E T S D + G W D
where IE is total irrigation efficiency.

Appendix A.2. Behavior over Time Diagrams of System Dynamics Model Outputs

The figures below show basic behavior-over-time diagrams of the model’s outputs results with complete methodology and full descriptions in the Supplementary Materials, pp. 81–82. Black lines represent the results simulated by the model applied in this paper. These results are plotted against the Dynamic Statewide Water Budget data (blue dots) and observations (red dots).
Hydrology 08 00061 g0a1 550
Figure A1. Behavior reproduction results (water variables).
Figure A1. Behavior reproduction results (water variables).
Hydrology 08 00061 g0a1
Hydrology 08 00061 g0a2 550
Figure A2. Behavior reproduction results (socioeconomic variables).
Figure A2. Behavior reproduction results (socioeconomic variables).
Hydrology 08 00061 g0a2

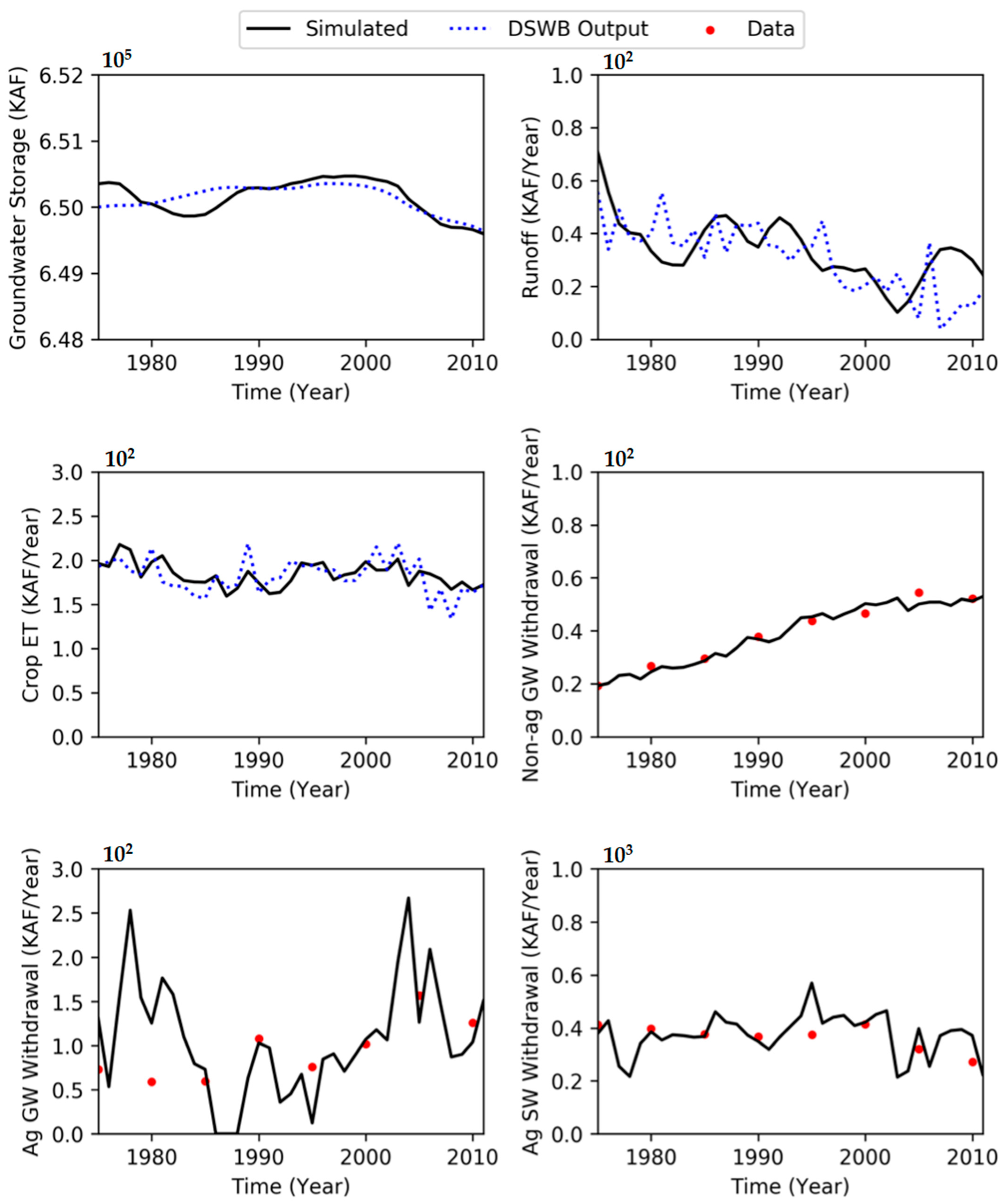
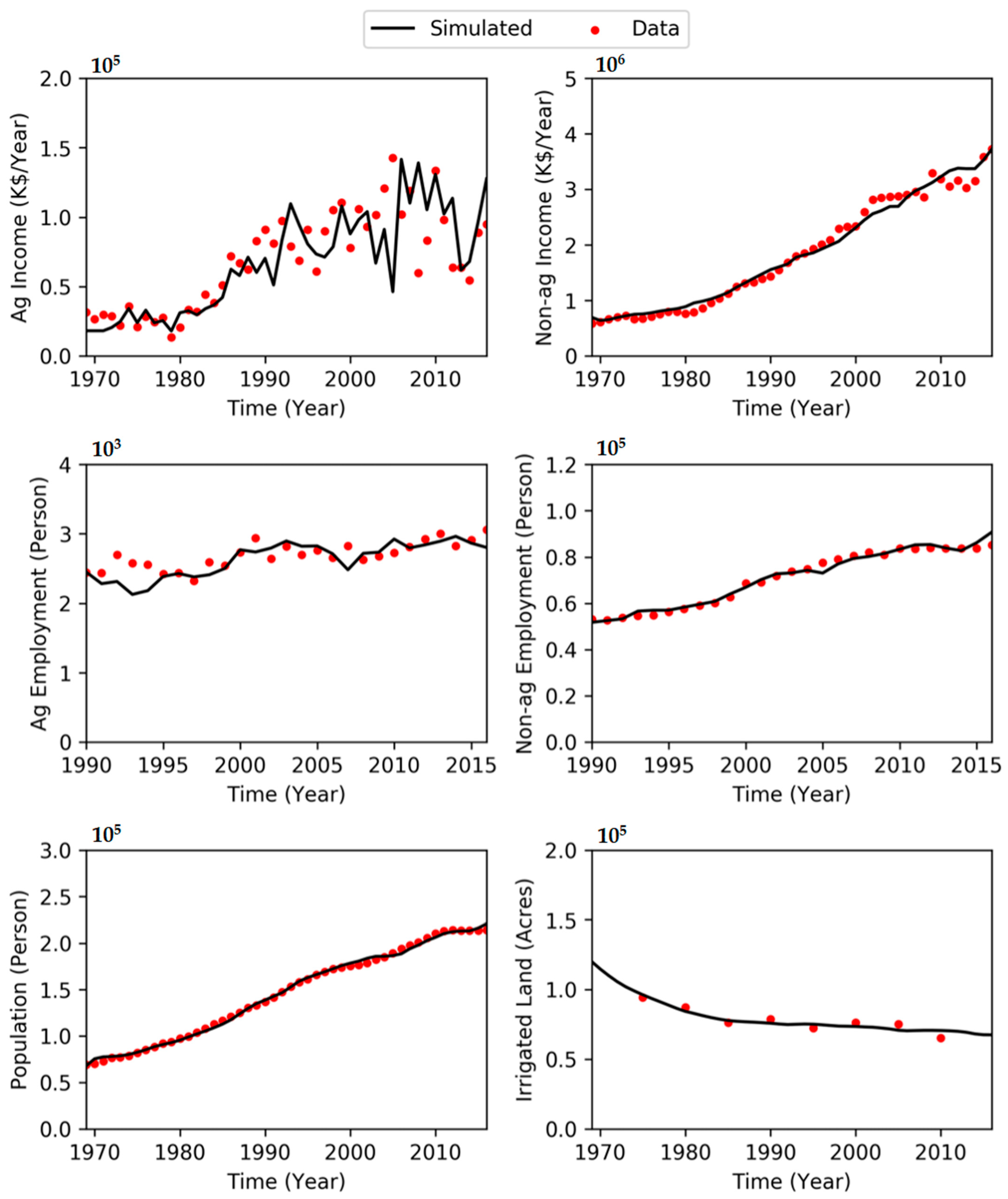
Appendix A.3. Result over Time Diagrams of Simulations

The figures below show simulation results-over-time of base runs and scenario tests of variables chosen in this paper. Simulation results show varied trends as climate inputs and model’s dynamics correspondingly.
Hydrology 08 00061 g0a3 550
Figure A3. Simulation results for selected variables with three climate projections.
Figure A3. Simulation results for selected variables with three climate projections.
Hydrology 08 00061 g0a3

References

  1. Sivapalan, M.; Savenije, H.H.G.; Blöschl, G. Socio-Hydrology: A New Science of People and Water. Hydrol. Process. 2012, 26, 1270–1276. [Google Scholar] [CrossRef]
  2. Mashaly, A.F.; Fernald, A.G. Identifying Capabilities and Potentials of System Dynamics in Hydrology and Water Resources as a Promising Modeling Approach for Water Management. Water 2020, 12, 1432. [Google Scholar] [CrossRef]
  3. Langarudi, S.P.; Maxwell, C.M.; Bai, Y.; Hanson, A.; Fernald, A. Does Socioeconomic Feedback Matter for Water Models? Ecol. Econ. 2019, 159, 35–45. [Google Scholar] [CrossRef]
  4. Sterman, J.D. All Models Are Wrong: Reflections on Becoming a Systems Scientist. Syst. Dyn. Rev. 2002, 18, 501–531. [Google Scholar] [CrossRef]
  5. House-Peters, L.A.; Chang, H. Urban Water Demand Modeling: Review of Concepts, Methods, and Organizing Principles. Water Resour. Res. 2011, 47, W05401. [Google Scholar] [CrossRef] [Green Version]
  6. An, L. Modeling Human Decisions in Coupled Human and Natural Systems: Review of Agent-Based Models. Ecol. Model. 2012, 229, 25–36. [Google Scholar] [CrossRef]
  7. Liu, D.; Tian, F.; Lin, M.; Sivapalan, M. A Conceptual Socio-Hydrological Model of the Co-Evolution of Humans and Water: Case Study of the Tarim River Basin, Western China. Hydrol. Earth Syst. Sci. 2015, 19, 1035–1054. [Google Scholar] [CrossRef] [Green Version]
  8. Gober, P.; Wheater, H.S. Debates—Perspectives on Socio-Hydrology: Modeling Flood Risk as a Public Policy Problem. Water Resour. Res. 2015, 51, 4782–4788. [Google Scholar] [CrossRef]
  9. Forrester, J.W. Industrial Dynamics; Productivity Press: Cambridge, MA, USA, 1961; ISBN 0-915299-88-7. [Google Scholar]
  10. Forrester, J.W. System Dynamics, Systems Thinking, and Soft OR. Syst. Dyn. Rev. 1994, 10, 245–256. [Google Scholar] [CrossRef]
  11. Sterman, J.D. System Dynamics Modeling: Tools for Learning in a Complex World. Calif. Manag. Rev. 2001, 43, 8–25. [Google Scholar] [CrossRef]
  12. Wolstenholme, E.F. Qualitative vs Quantitative Modelling: The Evolving Balance. Null 1999, 50, 422–428. [Google Scholar] [CrossRef]
  13. Coyle, G. Qualitative and Quantitative Modelling in System Dynamics: Some Research Questions. Syst. Dyn. Rev. 2000, 16, 225–244. [Google Scholar] [CrossRef]
  14. Clancy, T. Systems Thinking: Three System Archetypes Every Manager Should Know. IEEE Eng. Manag. Rev. 2018, 46, 32–41. [Google Scholar] [CrossRef]
  15. Forrester, J.W. Information Sources for Modeling the National Economy. J. Am. Stat. Assoc. 1980, 75, 555–566. [Google Scholar] [CrossRef]
  16. Langarudi, S.; Bar-On, I. Utility Perception in System Dynamics Models. Systems 2018, 6, 37. [Google Scholar] [CrossRef]
  17. Stave, K.A. A System Dynamics Model to Facilitate Public Understanding of Water Management Options in Las Vegas, Nevada. J. Environ. Manag. 2003, 67, 303–313. [Google Scholar] [CrossRef]
  18. Maxwell, C.M.; Langarudi, S.P.; Fernald, A.G. Simulating a Watershed-Scale Strategy to Mitigate Drought, Flooding, and Sediment Transport in Drylands. Systems 2019, 7, 53. [Google Scholar] [CrossRef] [Green Version]
  19. Konar, M.; Garcia, M.; Sanderson, M.R.; Yu, D.J.; Sivapalan, M. Expanding the Scope and Foundation of Sociohydrology as the Science of Coupled Human-Water Systems. Water Resour. Res. 2019, 55, 874–887. [Google Scholar] [CrossRef]
  20. Page, A.; Langarudi, S.P.; Forster-Cox, S.; Fernald, A. A Dynamic Hydro-Socio-Technical Policy Analysis of Transboundary Desalination Development. J. Environ. Account. Manag. 2019, 7, 87–114. [Google Scholar] [CrossRef]
  21. Luquet, D.; Vidal, A.; Smith, M.; Dauzat, J. ‘More Crop per Drop’: How to Make It Acceptable for Farmers? Agric. Water Manag. 2005, 76, 108–119. [Google Scholar] [CrossRef]
  22. Ward, F.A.; Pulido-Velazquez, M. Water Conservation in Irrigation Can Increase Water Use. Proc. Natl. Acad. Sci. USA 2008, 105, 18215–18220. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  23. Ackerly, N. Irrigation Systems in the Mesilla Valley: An Historical Overview; Center for Anthropological Research New Mexico State University: Las Cruces, NM, USA, 1992. [Google Scholar]
  24. New Mexico Bureau of Geology and Mineral Resources. Geologic Map of New Mexico; Geologic Map; New Mexico Bureau of Geology and Mineral Resources: Socorro, NM, USA, 2003. [Google Scholar]
  25. Fuchs, E.H.; Carroll, K.C.; King, J.P. Quantifying Groundwater Resilience through Conjunctive Use for Irrigated Agriculture in a Constrained Aquifer System. J. Hydrol. 2018, 565, 747–759. [Google Scholar] [CrossRef]
  26. NMWRRI. The New Mexico Dynamic Statewide Water Budget; New Mexico Water Resources and Research Institute, New Mexico State University: Las Cruces, NM, USA, 2018. [Google Scholar]
  27. Contor, B.A.; Taylor, R.G. Why Improving Irrigation Efficiency Increases Total Volume of Consumptive Use. Irrig. Drain. 2013, 62, 273–280. [Google Scholar] [CrossRef]
  28. Benson, M.H.; Morrison, R.R.; Llewellyn, D.; Stone, M. Governing the Rio Grande: Challenges and Opportunities for New Mexico’s Water Supply. In Practical Panarchy for Adaptive Water Governance: Linking Law to Social-Ecological Resilience; Cosens, B., Gunderson, L., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 99–114. ISBN 978-3-319-72472-0. [Google Scholar]
  29. Levidow, L.; Zaccaria, D.; Maia, R.; Vivas, E.; Todorovic, M.; Scardigno, A. Improving Water-Efficient Irrigation: Prospects and Difficulties of Innovative Practices. Agric. Water Manag. 2014, 146, 84–94. [Google Scholar] [CrossRef] [Green Version]
  30. OSE. Region 11-NM Regional Water Planning; State of New Mexico, Interstate Stream Commission, Office of the State Engineer: Albuquerque, NM, USA, 2017. [Google Scholar]
  31. Hooke, J. Coarse Sediment Connectivity in River Channel Systems: A Conceptual Framework and Methodology. Geomorphology 2003, 56, 79–94. [Google Scholar] [CrossRef]
  32. Peterson, K.; Hanson, A.; Roach, J.; Randall, J.; Thomson, B. A Dynamic Statewide Water Budget for New Mexico: Phase III—Future Scenario Implementation; New Mexico Water Resources Research Institute, New Mexico State University: Las Cruces, NM, USA, 2019. [Google Scholar]
  33. Hill, R. How Well Does Your Irrigation Canal Hold Water? Does It Need Lining? ENGR/BIE/WM 2000, 3, 1. [Google Scholar]
  34. King, P.; Hawley, J.; Hernandez, J.; Kennedy, J.; Martinez, E. Study of Potential Water Salvage on the Tucumcari Project Arch Hurley Conservancy District Phase I: A Pre-Appraisal-Level Study of the Potential Amount of Water that May Be Saved, and the Costs of Alternative Methods of Reducing Carriage Losses from District Canals. 2006. Available online: https://nmwrri.nmsu.edu/wp-content/uploads/2015/technical-reports/tr335.pdf (accessed on 17 September 2019).
  35. Burt, C.M.; O’Neill, B.P. Drip and Furrow on Processing Tomato-Field Performance. In Proceedings of the 28th Annual Irrigation Association Technical Conference, San Diego, CA, USA, 9 December 2007; p. 10. [Google Scholar]
  36. Perry, C.; Steduto, P.; Allen, R.G.; Burt, C.M. Increasing Productivity in Irrigated Agriculture: Agronomic Constraints and Hydrological Realities. Agric. Water Manag. 2009, 96, 1517–1524. [Google Scholar] [CrossRef] [Green Version]
  37. Wells, L. Cost of Pecan Production; UGA Pecan Extension: Athens, GA, USA, 2014. [Google Scholar]
  38. Bevacqua, R.F. Drip Irrigation for Row Crops; New Mexico State University: Las Cruces, NM, USA, 2001. [Google Scholar]
  39. Langarudi, S.P.; Radzicki, M.J. Resurrecting a Forgotten Model: Updating Mashayekhi’s Model of Iranian Economic Development. In Energy Policy Modeling in the 21st Century; Qudrat-Ullah, H., Ed.; Understanding Complex Systems; Springer: New York, NY, USA, 2013; pp. 197–233. ISBN 978-1-4614-8605-3. [Google Scholar]
  40. Perry, C. Efficient Irrigation; Inefficient Communication; Flawed Recommendations. Irrig. Drain. 2007, 56, 367–378. [Google Scholar] [CrossRef]
  41. Seckler, D.W. The New Era of Water Resources Management: From “Dry” to “Wet” Water Savings; IWMI: Gujarat, India, 1996; ISBN 978-92-9090-325-3. [Google Scholar]
  42. Burt, C.M.; Clemmens, A.J.; Strelkoff, T.S.; Solomon, K.H.; Bliesner, R.D.; Hardy, L.A.; Howell, T.A.; Eisenhauer, D.E. Irrigation Performance Measures: Efficiency and Uniformity. J. Irrig. Drain. Eng. 1997, 123, 423–442. [Google Scholar] [CrossRef] [Green Version]
  43. Guillet, D. Rethinking Irrigation Efficiency: Chain Irrigation in Northwestern Spain. Hum. Ecol. 2006, 34, 305–329. [Google Scholar] [CrossRef]
  44. Perry, C.J. The IWMI Water Resources Paradigm–Definitions and Implications. Agric. Water Manag. 1999, 40, 45–50. [Google Scholar] [CrossRef]
  45. Simons, G.W.H.; Bastiaanssen, W.G.M.; Immerzeel, W.W. Water Reuse in River Basins with Multiple Users: A Literature Review. J. Hydrol. 2015, 522, 558–571. [Google Scholar] [CrossRef]
  46. Conover, C.S. Ground-Water Conditions in the Rincon and Mesilla Valleys and Adjacent Areas in New Mexico; US Government Printing Office: Washington, DC, USA, 1950.
  47. Whittlesey, N. Improving irrigation efficiency through technology adoption: When will it Conserve water? In Developments in Water Science; Alsharhan, A.S., Wood, W.W., Eds.; Water Resources Perspectives: Evaluation, Management and Policy; Elsevier: Amsterdam, The Netherlands, 2003; Volume 50, pp. 53–62. [Google Scholar]
  48. Pringle, C. What Is Hydrologic Connectivity and Why Is It Ecologically Important? Hydrol. Process. 2003, 17, 2685–2689. [Google Scholar] [CrossRef]
  49. Gleick, P.H.; Christian-Smith, J.; Cooley, H. Water-Use Efficiency and Productivity: Rethinking the Basin Approach. Water Int. 2011, 36, 784–798. [Google Scholar] [CrossRef]
  50. Lexartza-Artza, I.; Wainwright, J. Hydrological Connectivity: Linking Concepts with Practical Implications. CATENA 2009, 79, 146–152. [Google Scholar] [CrossRef]
  51. Folke, C.; Carpenter, S.R.; Walker, B.; Scheffer, M.; Chapin, T.; Rockström, J. Resilience Thinking: Integrating Resilience, Adaptability and Transformability. Ecol. Soc. 2010, 15. [Google Scholar] [CrossRef]
  52. Dehghanipour, A.H.; Zahabiyoun, B.; Schoups, G.; Babazadeh, H. A WEAP-MODFLOW Surface Water-Groundwater Model for the Irrigated Miyandoab Plain, Urmia Lake Basin, Iran: Multi-Objective Calibration and Quantification of Historical Drought Impacts. Agric. Water Manag. 2019, 223, 105704. [Google Scholar] [CrossRef]
  53. Kerlin, K. Drought Impact Study: California Agriculture Faces Greatest Water Loss Ever Seen. Available online: https://www.ucdavis.edu/news/drought-impact-study-california-agriculture-faces-greatest-water-loss-ever-seen (accessed on 17 September 2019).
  54. McGhee, G. Understanding California’s Groundwater|Water in the West 2014. Available online: https://waterinthewest.stanford.edu/programs/groundwater/California-groundwater-overdraft (accessed on 17 September 2019).
  55. Guido, Z. The Costs of Drought on the Rio Grande|NOAA Climate.Gov 2012. Available online: https://www.climate.gov/news-features/features/costs-drought-rio-grandeseen (accessed on 17 September 2019).
  56. Inam, A.; Adamowski, J.; Prasher, S.; Halbe, J.; Malard, J.; Albano, R. Coupling of a Distributed Stakeholder-Built System Dynamics Socio-Economic Model with SAHYSMOD for Sustainable Soil Salinity Management. Part 2: Model Coupling and Application. J. Hydrol. 2017, 551, 278–299. [Google Scholar] [CrossRef]
  57. Adamson, D.; Loch, A. Possible Negative Feedbacks from ‘Gold-Plating’ Irrigation Infrastructure. Agric. Water Manag. 2014, 145, 134–144. [Google Scholar] [CrossRef]
  58. Hasan, F.u.; Fatima, B.; Heaney-Mustafa, S. A Critique of Successful Elements of Existing On-Farm Irrigation Water Management Initiatives in Pakistan. Agric. Water Manag. 2021, 244, 106598. [Google Scholar] [CrossRef]
  59. Turral, H.; Svendsen, M.; Faures, J.M. Investing in Irrigation: Reviewing the Past and Looking to the Future. Agric. Water Manag. 2010, 97, 551–560. [Google Scholar] [CrossRef]
  60. Scherberg, J.; Keller, J.; Patten, S.; Baker, T.; Milczarek, M. Modeling the Impact of Aquifer Recharge, in-Stream Water Savings, and Canal Lining on Water Resources in the Walla Walla Basin. Sustain. Water Resour. Manag. 2018, 4, 275–289. [Google Scholar] [CrossRef]
Hydrology 08 00061 g001 550
Figure 1. Generalized map of the lower Rio Grande region, its location in the US, and land cover.
Figure 1. Generalized map of the lower Rio Grande region, its location in the US, and land cover.
Hydrology 08 00061 g001
Hydrology 08 00061 g002 550
Figure 2. Causal structure of the model: positive or negative causality is marked as plus or minus; double sides arrows explains that two variables have mutual feedback; blue dash line represents where the policy implements.
Figure 2. Causal structure of the model: positive or negative causality is marked as plus or minus; double sides arrows explains that two variables have mutual feedback; blue dash line represents where the policy implements.
Hydrology 08 00061 g002
Hydrology 08 00061 g003 550
Figure 3. Tradeoff between selected performance measures and agriculture income; x-axis in all plots indicates agriculture income while the y-axis for each row of graphs from top to bottom are abundance, irrigation return, and connectivity; graph columns from left to right indicate climate scenarios GFDL, UKMO, and NCAR; value of hydrology indicators is labeled.
Figure 3. Tradeoff between selected performance measures and agriculture income; x-axis in all plots indicates agriculture income while the y-axis for each row of graphs from top to bottom are abundance, irrigation return, and connectivity; graph columns from left to right indicate climate scenarios GFDL, UKMO, and NCAR; value of hydrology indicators is labeled.
Hydrology 08 00061 g003
Table
Table 1. Climate inputs for scenario tests with average values of periods 2017–2050 and 2051–2099 (Units of surface inflow are in thousands of acre-feet, KAF).
Table 1. Climate inputs for scenario tests with average values of periods 2017–2050 and 2051–2099 (Units of surface inflow are in thousands of acre-feet, KAF).
Precipitation (in)Temperature (°F)Surface Inflow (KAF/Year)
Historical10.0 ± 2.761.3 ± 1.1675.9 ± 208.6
GFDL 2017–20509.5 ± 2.762.2 ±1.2679.1 ± 159.8
GFDL 2051–20999.2 ± 3.066.4 ± 2.0508.5 ± 178.6
UKMO 2017–205010.1 ± 2.762.6 ± 1.1775.4 ± 175.8
UKMO 2051–209910.9 ± 2.465.7 ± 1.3660.3 ± 150.1
NCAR 2017–205010.2 ± 2.362.1 ± 0.9818.7 ± 137.8
NCAR 2051–209910.1 ± 2.462.6 ± 0.7804.0 ± 139.3
Table
Table 2. Variables setting for IE policy.
Table 2. Variables setting for IE policy.
PolicyAffected ParametersSetting
IE policyIEc+20%
Canal lining cost$100 per acre-ft
Deep percolation fraction−50%
Precision irrigation cost$800 per acre
Table
Table 3. Notation of scenarios.
Table 3. Notation of scenarios.
NotationGFDLUKMONCAR
DefaultGFDLUKMONCAR
IE policyG1U1N1
Table
Table 4. Relative changes of groundwater dependency and agricultural water demand between scenarios and base runs (percent).
Table 4. Relative changes of groundwater dependency and agricultural water demand between scenarios and base runs (percent).
IE Policy
GW DependencyAgricultural Water Demand
GFDL 2017–2050−16.59.3
GFDL 2051–2099−1.72.7
UKMO 2017–2050−10.74.8
UKMO 2051–2099−2.71.8
NCAR 2017–2050−39.16.3
NCAR 2051–2099−14.13.6
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Bai, Y.; Langarudi, S.P.; Fernald, A.G. System Dynamics Modeling for Evaluating Regional Hydrologic and Economic Effects of Irrigation Efficiency Policy. Hydrology 2021, 8, 61. https://doi.org/10.3390/hydrology8020061

AMA Style

Bai Y, Langarudi SP, Fernald AG. System Dynamics Modeling for Evaluating Regional Hydrologic and Economic Effects of Irrigation Efficiency Policy. Hydrology. 2021; 8(2):61. https://doi.org/10.3390/hydrology8020061

Chicago/Turabian Style

Bai, Yining, Saeed P. Langarudi, and Alexander G. Fernald. 2021. "System Dynamics Modeling for Evaluating Regional Hydrologic and Economic Effects of Irrigation Efficiency Policy" Hydrology 8, no. 2: 61. https://doi.org/10.3390/hydrology8020061

APA Style

Bai, Y., Langarudi, S. P., & Fernald, A. G. (2021). System Dynamics Modeling for Evaluating Regional Hydrologic and Economic Effects of Irrigation Efficiency Policy. Hydrology, 8(2), 61. https://doi.org/10.3390/hydrology8020061

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop