Robust Vegetation Parameterization for Green Roofs in the EPA Stormwater Management Model (SWMM)
Abstract
1. Introduction
2. Materials and Methods
2.1. Field Campaign
2.1.1. Laboratory Tests
2.1.2. Perennial Plant Development
2.1.3. Runoff
- Summer period (from 1st of May to 30th of Sep) between 58% and 72%, subject to a decrease by 1/3 in cooler weather in
- Spring/autumn (from 16th of Mar to 30th of Apr and 01st of Oct to 15th of Nov) between 41% and 49%.
- Winter (from 16th of Nov to 15th of Mar) between 5% and 12%
2.2. Model Setup
2.2.1. Water Balance Simulation
2.2.2. Physically-Based ET Simulation
2.2.3. Coupled Modelling Approach
2.3. Calibration and Validation
- Calibration period: 28 Mar 2004–20 December 2004
- Validation period: 22 April 2005–25 November 2005 (due to missing weather data, 2006 was excluded from the analysis)
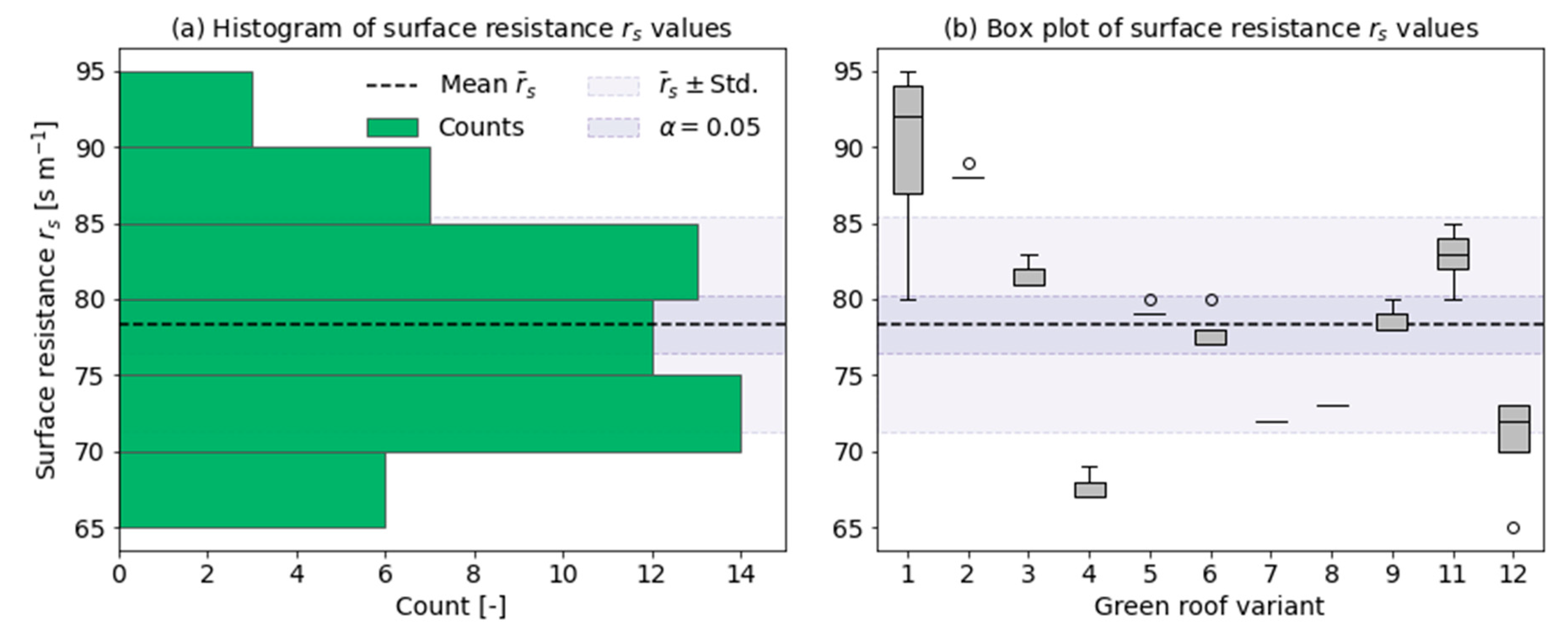
- 1st iteration: Run spotpy, applied to the coupled modelling approach with 5 repetitions for each test plot (to see how the stochastic nature of sampling affects results), in order to find a unique representative surface resistance value. Various evapotranspiration time series are calculated (with a surface resistance range from 60 to 300 s m−1). These files, or more specifically the file path in the EPA SWMM’s input file, are available as adjustable parameters to the calibration scheme. For this purpose, an existing EPA SWMM model driver in spotpy has been adjusted (https://github.com/mmmatthew/swmm_calibration (last access 24 Nov 2020)). This way, the surface resistance is estimated directly as a yearly average, suggesting that a seasonal variation is neglected.
- Based on the results of the previous step, a comparison of surface resistance values across the simulations for all test plots is carried out. An average value out of all surface resistance values is computed, in order to find a unique representative value.
- 2nd iteration: Rerun spotpy calibration with SCE-UA (Shuffled complex evolution method developed at The University of Arizona) for all green roof variants to calibrate the LID parameters in EPA SWMM (surface layer, soil layer, drainage mat), assuming a fixed surface resistance from the previous step. Compute performance measures for the calibration and validation period, respectively.
2.4. Global Sensitivity Analysis
3. Results
3.1. Representative Surface Resistance
3.2. Model Runs
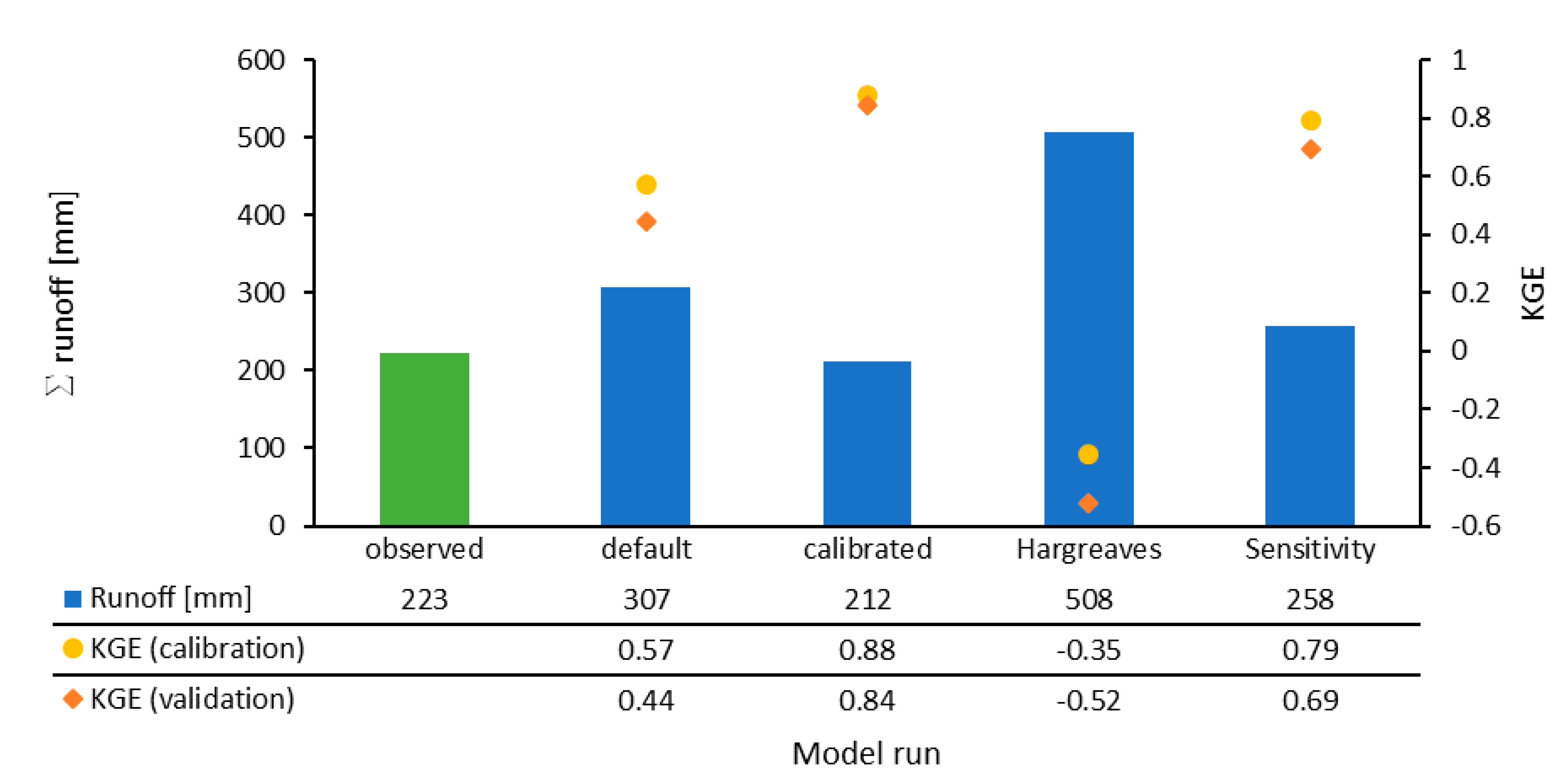
3.2.1. Model Run with Default Parameters
3.2.2. Calibrated Model
3.2.3. Model with the Integrated Hargreaves Method for ET
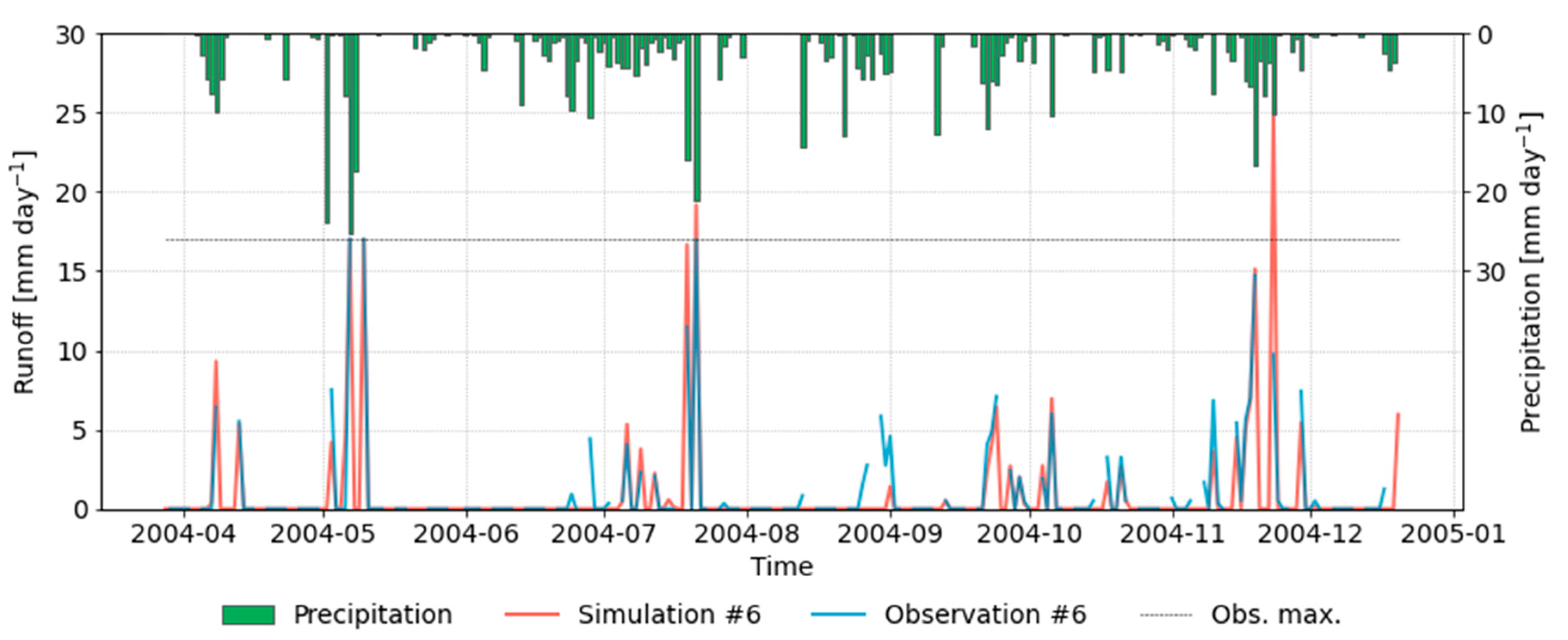
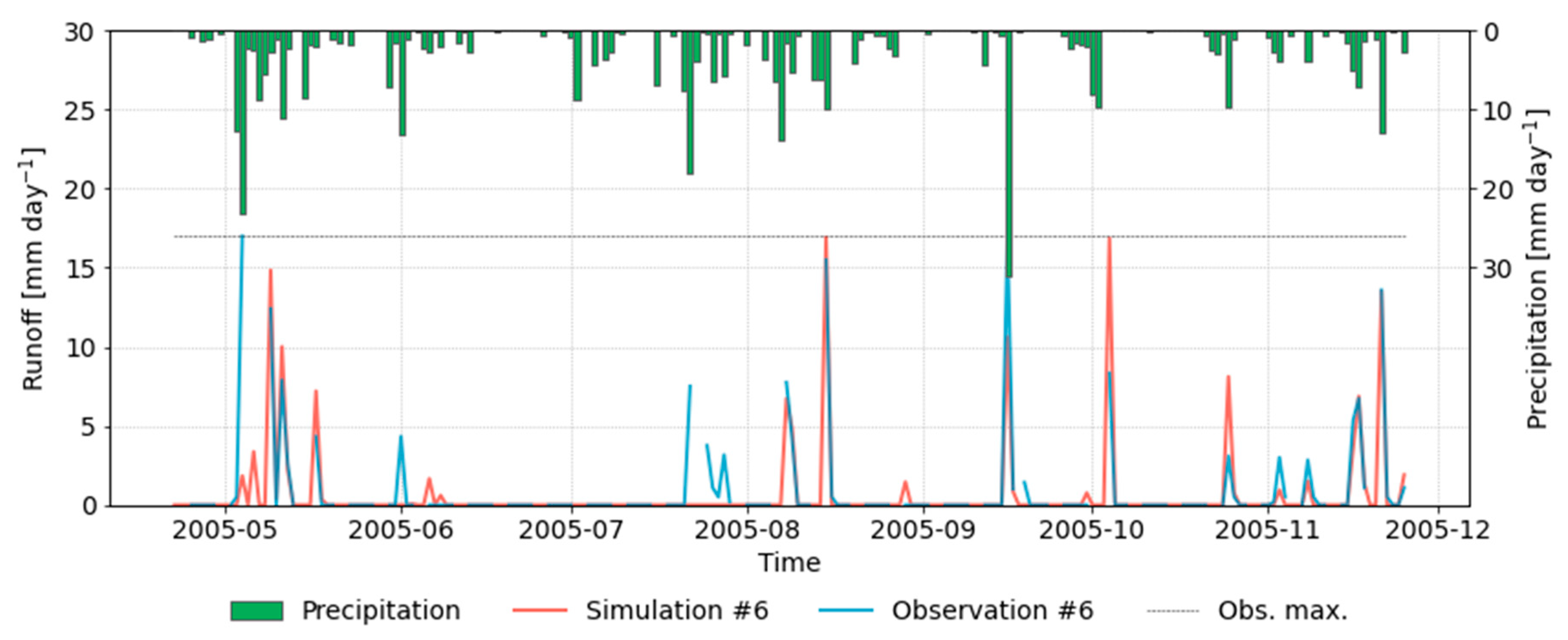
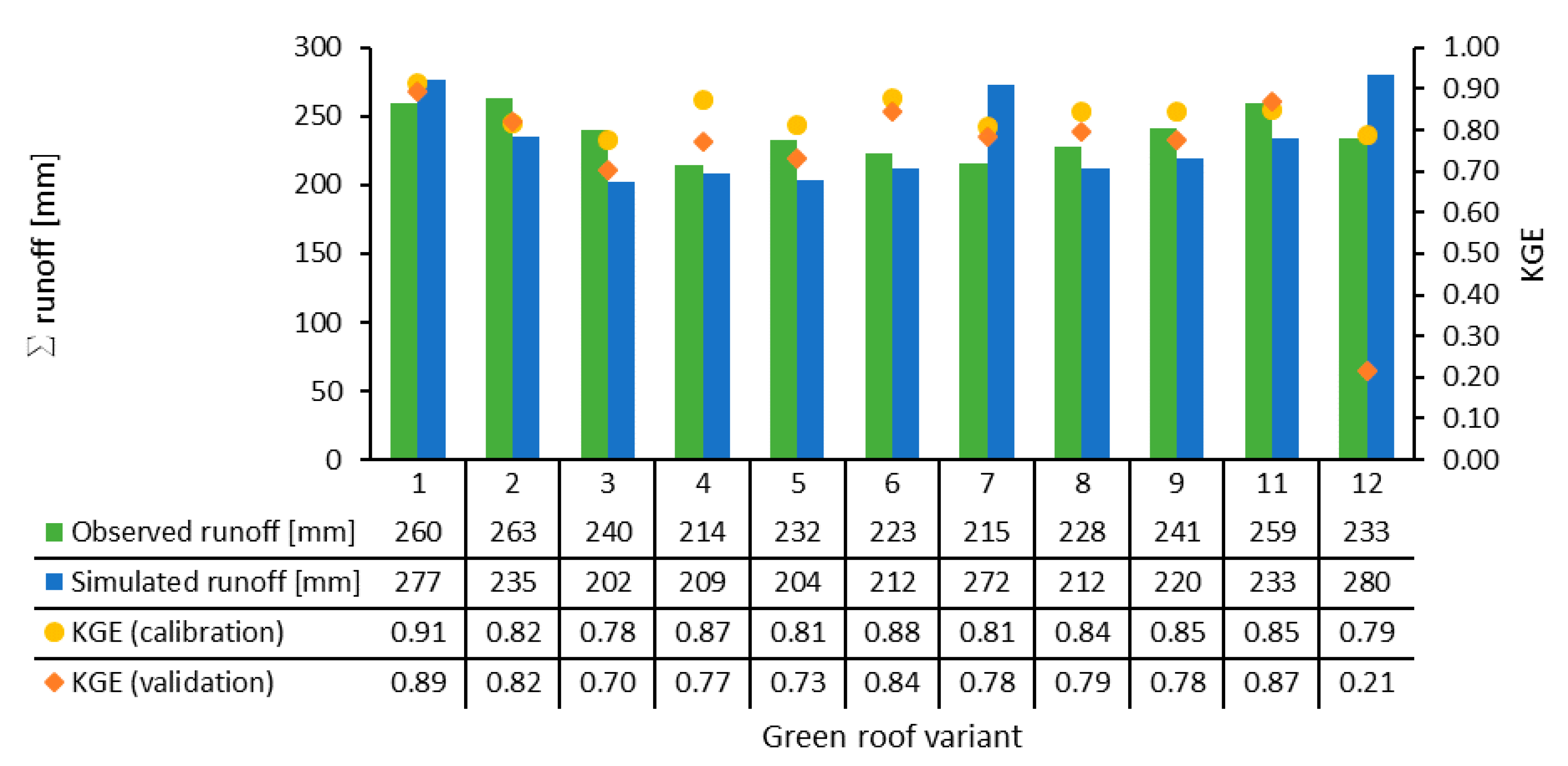
3.3. Validation
3.4. Global Sensitivity Analysis
3.5. Synthesis of Model Runs
4. Discussion
5. Conclusions
- (i)
- (ii)
- the coupled modelling approach outperforms the standard EPA SWMM model with Hargreaves ET computation, even without any further calibration of the ET component;
- (iii)
- a robust parametrization of the vegetation (or more specifically surface resistance) is possible for different green roof configurations with similar vegetation cover;
- (iv)
- only a subset of LID parameters in EPA SWMM are sensitive for continuous simulations, namely surface resistance, berm height, soil porosity and the drainage mat void fraction.
- (i)
- the design of the existing field campaign was not tailored to provide a basis for modelling studies. Hence, hydrological quantities that might complement constraining the model for dry and wet periods, such as soil moisture measurements, have not been addressed;
- (ii)
- The non-stationarity of vegetation characteristics was not considered in our study. For instance, Sedum tends to recover within one week after drought stress [54]. Moreover, surface resistance might undergo seasonal changes and might be subject to changes as a response to drought stress, as idealized irrigation experiments after drought might suggest [55];
- (iii)
- Equifinality (i.e., different parameter sets yield similar results or accuracy in terms of objective function) is still a source of uncertainty in studies aimed at parameter identification [56]. Some parameters are effective parameters, suggesting that their original physical meaning is not always given due to model uncertainty and scaling issues [51].
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Variant | Construction Technique and Material Description | Thickness (cm) | Water Retention (%) | Runoff Coefficient | |||
|---|---|---|---|---|---|---|---|
| Summer Period | Cooler Period | Winter Period | Average Over Time | ||||
| 1 | Vegetation mat | 2.5 | 61.3 | 42.3 | 10.4 | 44.8 | 0.55 |
| Protection fleece 300 g m−2 | |||||||
| Geotextile recycling | 0.2 | ||||||
| 2.7 | |||||||
| 2 | Vegetation mat | 2.5 | 58.3 | 41.9 | 7.6 | 42.4 | 0.58 |
| Drainage and filtration mat | |||||||
| Netting with filtration fleece | 1.5 | ||||||
| 4.0 | |||||||
| 3 | Vegetation mat | 2.5 | 64.9 | 47.4 | 7.6 | 47.1 | 0.53 |
| Water retention mat 800 g m−2 | |||||||
| Geotextile recycling | 0.6 | ||||||
| 3.1 | |||||||
| 4 | Vegetation mat | 2.5 | 68.9 | 49.1 | 11.5 | 50.6 | 0.49 |
| Water retention mat 1200 g m−2 | |||||||
| Geotextile recycling | 0.8 | ||||||
| 3.3 | |||||||
| 5 | Vegetation mat | 2.5 | 66.1 | 47.9 | 10.1 | 48.5 | 0.51 |
| Water retention mat 800 g m−2 | 0.6 | ||||||
| Drainage and filtration mat | |||||||
| Netting with filtration fleece | 1.5 | ||||||
| 4.6 | |||||||
| 6 | Vegetation mat | 2.5 | 68.1 | 48.2 | 9.5 | 49.5 | 0.51 |
| Water retention mat 1200 g m−2 | 0.8 | ||||||
| Drainage and filtration mat | |||||||
| Netting with filtration fleece | 1.5 | ||||||
| 4.8 | |||||||
| 7 | Vegetation mat | 2.5 | 71.7 | 46.3 | 7.8 | 50.6 | 0.49 |
| Single-layer substrate light | |||||||
| Pumice 2/8 mm | 4.0 | ||||||
| Protection fleece 300 g m−2 | |||||||
| Geotextile recycling | 0.2 | ||||||
| 6.7 | |||||||
| 8 | Vegetation mat | 2.5 | 69.9 | 44.7 | 9.2 | 49.6 | 0.50 |
| Single-layer substrate light | |||||||
| Expanded clay 2/10 mm | 4.0 | ||||||
| Protection fleece 300 g m−2 | |||||||
| Geotextile recycling | 0.2 | ||||||
| 6.7 | |||||||
| 9 | Vegetation mat | 2.5 | 67.1 | 44.4 | 5.7 | 47.2 | 0.53 |
| Single-layer substrate light | |||||||
| lava 2/8 mm | 4.0 | ||||||
| Protection fleece 300 g m−2 | |||||||
| Geotextile recycling | 0.2 | ||||||
| 6.7 | |||||||
| 10 | Vegetation mat | 2.5 | 61.3 | 41.1 | 6.7 | 43.6 | 0.56 |
| Gravel course | |||||||
| Granulation 16/32 mm | 5.0 | ||||||
| Protection fleece 300 g m−2 | |||||||
| Geotextile recycling | 0.2 | ||||||
| 7.7 | |||||||
| 11 | Vegetation mat | 2.5 | 63.4 | 41.9 | 4.7 | 44.4 | 0.56 |
| Multi-layer substrate | |||||||
| Lava with dolomite and organic matter | 3.0 | ||||||
| Drainage and filtration mat | |||||||
| Netting with filtration fleece | 1.5 | ||||||
| 7.0 | |||||||
| 12 | Vegetation mat | 2.5 | 67.3 | 43.7 | 4.7 | 46.9 | 0.53 |
| Multi-layer substrate | |||||||
| Lava with dolomite and organic matter | 6.0 | ||||||
| Drainage and filtration mat | |||||||
| Netting with filtration fleece | 1.5 | ||||||
| 10.0 | |||||||
| Default | Calibrated | Hargreaves | Sensitivity | |||
|---|---|---|---|---|---|---|
| NSE (Nash Sutcliffe Efficiency) | 0.72 | 0.85 | −0.19 | 0.83 | ||
| PBIAS (Percent Bias) | −37.15 | 6.15 | −125.33 | −14.87 | ||
| RMSE (Root-mean-square deviation) | 1.58 | 1.18 | 3.28 | 1.22 | ||
| KGE (Kling Gupta Efficiency) | 0.57 | 0.88 | −0.35 | 0.79 | ||
| R (Correlation coefficient) | 0.91 | 0.93 | 0.73 | 0.94 | ||
| Surface | Berm height | (mm) | 0 | 28.46 | 0.03 | 17.89 |
| Vegetation volume | (-) | 0.15 | 0.2 | 0.1 | 0.2 | |
| Surface Roughness | (-) | 0.15 | 0.19 | 0.08 | 0.19 | |
| Surface slope | (%) | 2 | 2 | 2 | 2 | |
| Soil | Thickness | (mm) | 33 | 33 | 33 | 33 |
| Porosity | (-) | 0.456 | 0.42 | 0.42 | 0.51 | |
| Field capacity | (-) | 0.35 | 0.3 | 0.24 | 0.3 | |
| Wilting point | (-) | 0.06 | 0.08 | 0.12 | 0.08 | |
| Conductivity | (mm hr−1) | 27.6 | 131.62 | 65.99 | 131.62 | |
| Conductivity slope | (-) | 5 | 41.83 | 24.19 | 41.83 | |
| Suction head | (mm) | 3 | 30.36 | 24.54 | 30.36 | |
| Drain | Thickness | (-) | 15 | 15 | 15 | 15 |
| Void fraction | (-) | 0.456 | 0.16 | 0.17 | 0.51 | |
| Roughness | (mm) | 0.02 | 0.17 | 0.27 | 0.17 | |
| FAO | Albedo | (-) | 0.20 | 0.20 | 0.20 | 0.20 |
| Wind exp. | (-) | 0.5 | 0.5 | 0.5 | 0.5 | |
| Crop height | (m) | 0.12 | 0.12 | 0.12 | 0.12 | |
| rs | (s m−1) | 170 | 78 | - | 78 |
| Objective Function | #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #11 | #12 | |
| Calibration | NSE | 0.87 | 0.77 | 0.80 | 0.85 | 0.82 | 0.85 | 0.88 | 0.83 | 0.85 | 0.87 | 0.85 |
| PBIAS | −2.51 | 14.63 | 20.15 | 7.14 | 16.63 | 6.15 | −13.82 | 11.33 | 13.03 | 13.88 | −15.29 | |
| RMSE | 1.16 | 1.57 | 1.38 | 1.14 | 1.31 | 1.18 | 1.05 | 1.23 | 1.22 | 1.16 | 1.20 | |
| KGE | 0.91 | 0.82 | 0.78 | 0.87 | 0.81 | 0.88 | 0.81 | 0.84 | 0.85 | 0.85 | 0.79 | |
| R | 0.94 | 0.89 | 0.91 | 0.93 | 0.92 | 0.93 | 0.96 | 0.93 | 0.93 | 0.94 | 0.94 | |
| Validation | NSE | 0.84 | 0.83 | 0.56 | 0.63 | 0.62 | 0.73 | 0.77 | 0.69 | 0.67 | 0.82 | 0.31 |
| PBIAS | −3.80 | 14.51 | 19.61 | 13.35 | 18.25 | 6.16 | −13.45 | 12.73 | 14.61 | 9.39 | −51.59 | |
| RMSE | 1.33 | 1.44 | 2.04 | 1.87 | 1.92 | 1.45 | 1.45 | 1.69 | 1.83 | 1.37 | 1.84 | |
| KGE | 0.89 | 0.82 | 0.70 | 0.77 | 0.73 | 0.84 | 0.78 | 0.79 | 0.78 | 0.87 | 0.21 | |
| R | 0.92 | 0.91 | 0.78 | 0.81 | 0.80 | 0.87 | 0.91 | 0.84 | 0.83 | 0.91 | 0.90 |
References
- Mentens, J.; Raes, D.; Hermy, M. Green roofs as a tool for solving the rainwater runoff problem in the urbanized 21st century? Landsc. Urban Plan. 2006, 77, 217–226. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Wetherald, R.T.; Dunne, K.A.; Delworth, T.L. Increasing risk of great floods in a changing climate. Nature 2002, 415, 514–517. [Google Scholar] [CrossRef]
- Shafique, M.; Kim, R. Low Impact Development Practices: A Review of Current Research and Recommendations for Future Directions. Ecol. Chem. Eng. S 2015, 22, 543–563. [Google Scholar] [CrossRef]
- Alfredo, K.; Montalto, F.; Goldstein, A. Observed and Modeled Performances of Prototype Green Roof Test Plots Subjected to Simulated Low- and High-Intensity Precipitations in a Laboratory Experiment. J. Hydrol. Eng. 2010, 15, 444–457. [Google Scholar] [CrossRef]
- She, N.; Pang, J. Physically Based Green Roof Model. J. Hydrol. Eng. 2010, 15, 458–464. [Google Scholar] [CrossRef]
- Carson, T.B.; Marasco, D.E.; Culligan, P.J.; McGillis, W.R. Hydrological performance of extensive green roofs in New York City: Observations and multi-year modeling of three full-scale systems. Environ. Res. Lett. 2013, 8, 24036. [Google Scholar] [CrossRef]
- Bolliger, J.; Silbernagel, J. Contribution of Connectivity Assessments to Green Infrastructure (GI). IJGI Int. J. Geo-Information 2020, 9, 212. [Google Scholar] [CrossRef]
- Oberndorfer, E.; Lundholm, J.; Bass, B.; Coffman, R.R.; Doshi, H.; Dunnett, N.; Gaffin, S.; Köhler, M.; Liu, K.K.Y.; Rowe, B. Green Roofs as Urban Ecosystems: Ecological Structures, Functions, and Services. BioScience 2007, 57, 823–833. [Google Scholar] [CrossRef]
- van Mechelen, C.; Dutoit, T.; Hermy, M. Adapting green roof irrigation practices for a sustainable future: A review. Sustain. Cities Soc. 2015, 19, 74–90. [Google Scholar] [CrossRef]
- Cascone, S.; Coma, J.; Gagliano, A.; Pérez, G. The evapotranspiration process in green roofs: A review. Build. Environ. 2019, 147, 337–355. [Google Scholar] [CrossRef]
- Li, Y.; Babcock, R.W. Green roof hydrologic performance and modeling: A review. Water Sci. Technol. 2014, 69, 727–738. [Google Scholar] [CrossRef] [PubMed]
- Cipolla, S.S.; Maglionico, M.; Stojkov, I. A long-term hydrological modelling of an extensive green roof by means of SWMM. Ecol. Eng. 2016, 95, 876–887. [Google Scholar] [CrossRef]
- Limos, A.G.; Mallari, K.J.B.; Baek, J.; Kim, H.; Hong, S.; Yoon, J. Assessing the significance of evapotranspiration in green roof modeling by SWMM. J. Hydroinformatics 2018, 20, 588–596. [Google Scholar] [CrossRef]
- Jayasooriya, V.M.; Ng, A.W.M. Tools for Modeling of Stormwater Management and Economics of Green Infrastructure Practices: A Review. Water Air Soil Pollut. 2014, 225. [Google Scholar] [CrossRef]
- Boughton, W.; Droop, O. Continuous simulation for design flood estimation—A review. Environ. Model. Softw. 2003, 18, 309–318. [Google Scholar] [CrossRef]
- Pathiraja, S.; Westra, S.; Sharma, A. Why continuous simulation? The role of antecedent moisture in design flood estimation. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Burszta-Adamiak, E.; Mrowiec, M. Modelling of green roofs’ hydrologic performance using EPA’s SWMM. Water Sci. Technol. 2013, 68, 36–42. [Google Scholar] [CrossRef]
- Palla, A.; Gnecco, I. Hydrologic modeling of Low Impact Development systems at the urban catchment scale. J. Hydrol. 2015, 528, 361–368. [Google Scholar] [CrossRef]
- Peng, Z.; Stovin, V. Independent Validation of the SWMM Green Roof Module. J. Hydrol. Eng. 2017, 22, 4017037. [Google Scholar] [CrossRef]
- Niazi, M.; Nietch, C.; Maghrebi, M.; Jackson, N.; Bennett, B.R.; Tryby, M.; Massoudieh, A. Storm Water Management Model: Performance Review and Gap Analysis. J. Sustain. Water Built Environ. 2017, 3. [Google Scholar] [CrossRef]
- Leimgruber, J.; Krebs, G.; Camhy, D.; Muschalla, D. Sensitivity of Model-Based Water Balance to Low Impact Development Parameters. Water 2018, 10, 1838. [Google Scholar] [CrossRef]
- Lee, H.S.J.; Griffiths, H. Induction and Repression of CAM in Sedum telephium L. in Response to Photoperiod and Water Stress. J. Exp. Bot. 1987, 38, 834–841. [Google Scholar] [CrossRef]
- Lüttge, U. Ecophysiology of Crassulacean Acid Metabolism (CAM). Ann. Bot. 2004, 93, 629–652. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Burian, S. Improving Evapotranspiration Mechanisms in the U.S. Environmental Protection Agency’s Storm Water Management Model. J. Hydrol. Eng. 2016, 21, 6016007. [Google Scholar] [CrossRef]
- Landscape Development and Landscaping Research Society–FLL. Green Roof Guidelines-Guidelines for the Planning, Construction and Maintenance of Green Roofs, 6th ed.; Landscape Development and Landscaping Research Society–FLL: Bonn, Germany, 2018. [Google Scholar]
- Liesecke, H.-J. Entwicklung Einer Dachsode für Extensive Dachbegrünung. Teil 2: Vegetationsentwicklung, Lastannahmen, Prozentuale Wasserrückhaltung; Dach + Grün; Patzer Verlag Berlin -Hannover. 2006, Volume 15. Available online: https://www.irb.fraunhofer.de/bauforschung/baufolit.jsp?s=Lastannahme (accessed on 19 January 2020).
- Liesecke, H.-J. Entwicklung Einer Dachsode für Extensive Dachbegrünung. Teil 1: Konzeption, Entwicklung, Substrateigenschaften, Anzuchtverfahren, Bauweisen; Dach + Grün; Patzer Verlag Berlin-Hannover. 2006, Volume 15. Available online: https://www.irb.fraunhofer.de/bauforschung/baufolit.jsp?s=Lastannahme (accessed on 19 January 2020).
- Strässer, M. Klimadiagramme zur Köppenschen Klimaklassifikation. Karten und Abbildungen Sowie 201 Klimadiagramme, 1st ed.; Klett-Perthes: Stuttgart, Germany, 1998; ISBN 3623007684. [Google Scholar]
- Rossman, L. Storm Water Management Model: User’s Manual Version 5.1. Available online: https://www.epa.gov/sites/production/files/2019-02/documents/epaswmm5_1_manual_master_8-2-15.pdf (accessed on 19 January 2020).
- Hargreaves, G.H.; Allen, R.G. History and Evaluation of Hargreaves Evapotranspiration Equation. J. Irrig. Drain. Eng. 2003, 129, 53–63. [Google Scholar] [CrossRef]
- Sumner, D.M.; Jacobs, J.M. Utility of Penman–Monteith, Priestley—Taylor, reference evapotranspiration, and pan evaporation methods to estimate pasture evapotranspiration. J. Hydrol. 2005, 308, 81–104. [Google Scholar] [CrossRef]
- Richards, M. PyETo. Available online: https://github.com/woodcrafty/PyETo (accessed on 19 January 2020).
- Allen, R.G.; Pereira, L.; Raes, D.; Smith, M. Crop. Evapotranspiration. In Guidelines for Computing Crop Water Requirements; FAO: Rome, Italy, 1998; ISBN 9251042195. [Google Scholar]
- Neale, L.C.; Price, R.E. Flow characteristics of PVC sewer pipe. J. Sanit. Eng. Div. 1964, 90, 109–132. [Google Scholar]
- Klemeš, V. Operational testing of hydrological simulation models. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Houska, T.; Kraft, P.; Chamorro-Chavez, A.; Breuer, L. SPOTting Model Parameters Using a Ready-Made Python Package. PLoS ONE 2015, 10, e0145180. [Google Scholar] [CrossRef]
- de Vitry, M.M. Swmm_Calibration. Available online: https://github.com/mmmatthew/swmm_calibration (accessed on 19 January 2020).
- Duan, Q.Y.; Gupta, V.K.; Sorooshian, S. Shuffled complex evolution approach for effective and efficient global minimization. J. Optim. Theory Appl. 1993, 76, 501–521. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Gupta, H.V.; Bastidas, L.A.; Bouten, W.; Sorooshian, S. Effective and efficient algorithm for multiobjective optimization of hydrologic models. Water Resour. Res. 2003, 39, 19481. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Pool, S.; Vis, M.; Seibert, J. Evaluating model performance: Towards a non-parametric variant of the Kling-Gupta efficiency. Hydrol. Sci. J. 2018, 63, 1941–1953. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Chan, K.P.-S. A Quantitative Model-Independent Method for Global Sensitivity Analysis of Model Output. Technometrics 1999, 41, 39–56. [Google Scholar] [CrossRef]
- Henkel, T.; Wilson, H.; Krug, W. Global sensitivity analysis of nonlinear mathematical models—An implementation of two complementing variance-based algorithms. In Proceedings of the 2012 Winter Simulation Conference (WSC). 2012 Winter Simulation Conference-(WSC 2012), Berlin, Germany, 9–12 December 2012; Laroque, C., Himmelspach, J., Pasupathy, R., Rose, O., Uhrmacher, A.M., Eds.; IEEE: Piscataway Township, NJ, USA, 2012; pp. 1–2, ISBN 978-1-4673-4782-2. [Google Scholar]
- Saltelli, A.; Annoni, P.; Azzini, I.; Campolongo, F.; Ratto, M.; Tarantola, S. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 2010, 181, 259–270. [Google Scholar] [CrossRef]
- Jansen, M.J. Analysis of variance designs for model output. Comput. Phys. Commun. 1999, 117, 35–43. [Google Scholar] [CrossRef]
- Rana, G.; Katerji, N. A Measurement Based Sensitivity Analysis of the Penman-Monteith Actual Evapotranspiration Model for Crops of Different Height and in Contrasting Water Status. Theor. Appl. Climatol. 1998, 60, 141–149. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Cristiano, E.; ten Veldhuis, M.-C.; van de Giesen, N. Spatial and temporal variability of rainfall and their effects on hydrological response in urban areas—A review. Hydrol. Earth Syst. Sci. 2017, 21, 3859–3878. [Google Scholar] [CrossRef]
- Todorov, D.; Driscoll, C.T.; Todorova, S. Long-term and seasonal hydrologic performance of an extensive green roof. Hydrol. Process. 2018, 32, 2471–2482. [Google Scholar] [CrossRef]
- Kirchner, J.W. Getting the right answers for the right reasons: Linking measurements, analyses, and models to advance the science of hydrology. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Grimaldi, S.; Nardi, F.; Piscopia, R.; Petroselli, A.; Apollonio, C. Continuous hydrologic modelling for design simulation in small and ungauged basins: A step forward and some tests for its practical use. J. Hydrol. 2020, 125664. [Google Scholar] [CrossRef]
- Poduje, A.C.C.; Haberlandt, U. Short time step continuous rainfall modeling and simulation of extreme events. J. Hydrol. 2017, 552, 182–197. [Google Scholar] [CrossRef]
- Kirschstein, C. Untersuchungen zum Wasserhaushalt von Sedum-Arten. In Insbesondere zur Bedeutung der Wurzeln und ihrer Saugkräfte; Kovač: Hamburg, Germany, 1996; ISBN 3860644270. [Google Scholar]
- Kaiser, D.; Köhler, M.; Wolff, F. Steigerung der Verdunstungsleistung von Extensivbegrünungen. GebäudeGrün 2019, 26–29. Available online: https://www.baufachinformation.de/steigerung-der-verdunstungsleistung-von-extensivbegruenungen/z/2019029001427 (accessed on 19 January 2020).
- Beven, K. Towards a coherent philosophy for modelling the environment. Proc. R. Soc. A Math. Phys. Eng. Sci. 2002, 458, 2465–2484. [Google Scholar] [CrossRef]
- Förster, K.; Gelleszun, M.; Meon, G. A weather dependent approach to estimate the annual course of vegetation parameters for water balance simulations on the meso- and macroscale. Adv. Geosci. 2012, 32, 15–21. [Google Scholar] [CrossRef][Green Version]






| Property | Set up |
|---|---|
| Sub-catchment | A sub-catchment represents a roof of 4 m2 (0.0004 ha) that is 100% impermeable (covered with PVC sheets; N-Imperv PVC: 0.01 [34]), has a slope of 2% and drains entirely to an outfall. It is covered by different low impact development (LIDs) (green roofs). |
| LID | The sub-catchment is covered by the LID type “Green Roof”. Different LID controls represent the different structures of the test setups. As long as the parameters are unknown, they were estimated and calibrated. |
| Precipitation | Hourly precipitation data are available. The data for the calibration period (28 Mar 2004–20 Dec 2004) have the following characteristics (Assuming a day from 8 A.M. to 8 A.M. (as observations were sampled at this time each day)): ● Total precipitation: 517.0 mm ● Number of days with precipitation: 153 ● Day with largest precipitation event: 25.29 mm on 7 May 2004 |
| Evapotranspiration (ET) | The Penman–Monteith approach is applied to calculate daily evapotranspiration rates. The data were introduced as external time series to EPA SWMM. The daily evaporation data for the calibration period (28 Mar 2004–20 Dec 2004) has the following characteristics (Using the Penman–Monteith approach, assuming a surface resistance of 78 s m−1): ● Total evapotranspiration: 321.65 mm ● Number of days with evapotranspiration: 266 ● Day with largest evapotranspiration rate: 4.95 mm on 10 Aug 2004 |
| Criteria | Calibration Period | Validation Period |
|---|---|---|
| ∑ Precipitation (mm) | 517.0 | 388.4 |
| Av. precipitation/d (mm) | 1.93 | 1.79 |
| # Days with prec. > 10 mm d−1 (-) | 13 | 8 |
| # Days with prec. > 20 mm d−1 (-) | 3 | 2 |
| Longest dry period(# days with 0 mm d−1) (d) | 12 | 7 |
| Av. temperature (°C) | 12.9 | 14.8 |
| Max. temperature (°C) | 31.4 | 33.8 |
| Av. ET (mm d−1) | 1.2 | 1.16 |
| ∑ ET (mm) | 231.65 | 251.3 |
| Max. ET (mm d−1) | 4.95 | 4.35 |
| Criteria | Calibration Period | Validation Period |
|---|---|---|
| Mean daily runoff (obs #6) (mm d−1) | 1.16 | 0.97 |
| Mean daily runoff (sim #6) (mm d−1) | 1.14 | 0.91 |
| Longest dry period (obs #6) (d) | 43 | 49 |
| Longest dry period (sim #6) (d) | 54 | 59 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iffland, R.; Förster, K.; Westerholt, D.; Pesci, M.H.; Lösken, G. Robust Vegetation Parameterization for Green Roofs in the EPA Stormwater Management Model (SWMM). Hydrology 2021, 8, 12. https://doi.org/10.3390/hydrology8010012
Iffland R, Förster K, Westerholt D, Pesci MH, Lösken G. Robust Vegetation Parameterization for Green Roofs in the EPA Stormwater Management Model (SWMM). Hydrology. 2021; 8(1):12. https://doi.org/10.3390/hydrology8010012
Chicago/Turabian StyleIffland, Ronja, Kristian Förster, Daniel Westerholt, María Herminia Pesci, and Gilbert Lösken. 2021. "Robust Vegetation Parameterization for Green Roofs in the EPA Stormwater Management Model (SWMM)" Hydrology 8, no. 1: 12. https://doi.org/10.3390/hydrology8010012
APA StyleIffland, R., Förster, K., Westerholt, D., Pesci, M. H., & Lösken, G. (2021). Robust Vegetation Parameterization for Green Roofs in the EPA Stormwater Management Model (SWMM). Hydrology, 8(1), 12. https://doi.org/10.3390/hydrology8010012






