Evaluation and Calibration of Alternative Methods for Estimating Reference Evapotranspiration in the Senegal River Basin
Abstract
1. Introduction
2. Materials and Methods
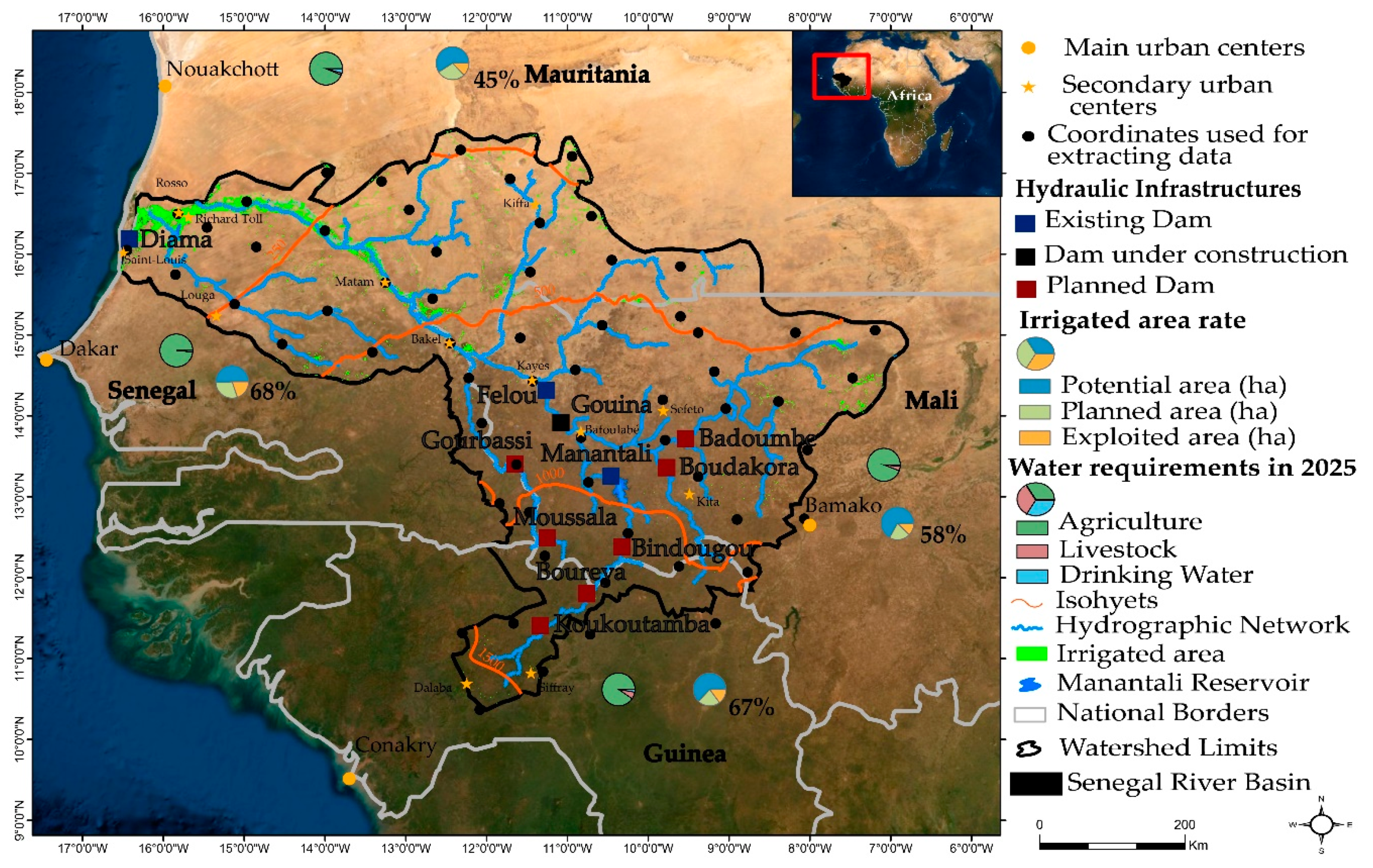
2.1. Study Area
2.2. Data
2.3. Method
2.3.1. Estimation of Reference Evapotranspiration
2.3.2. Performance of the Alternative Methods
2.3.3. Calibration and Validation
3. Results and Discussion
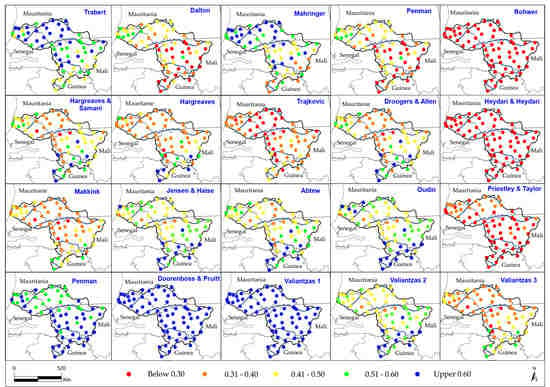
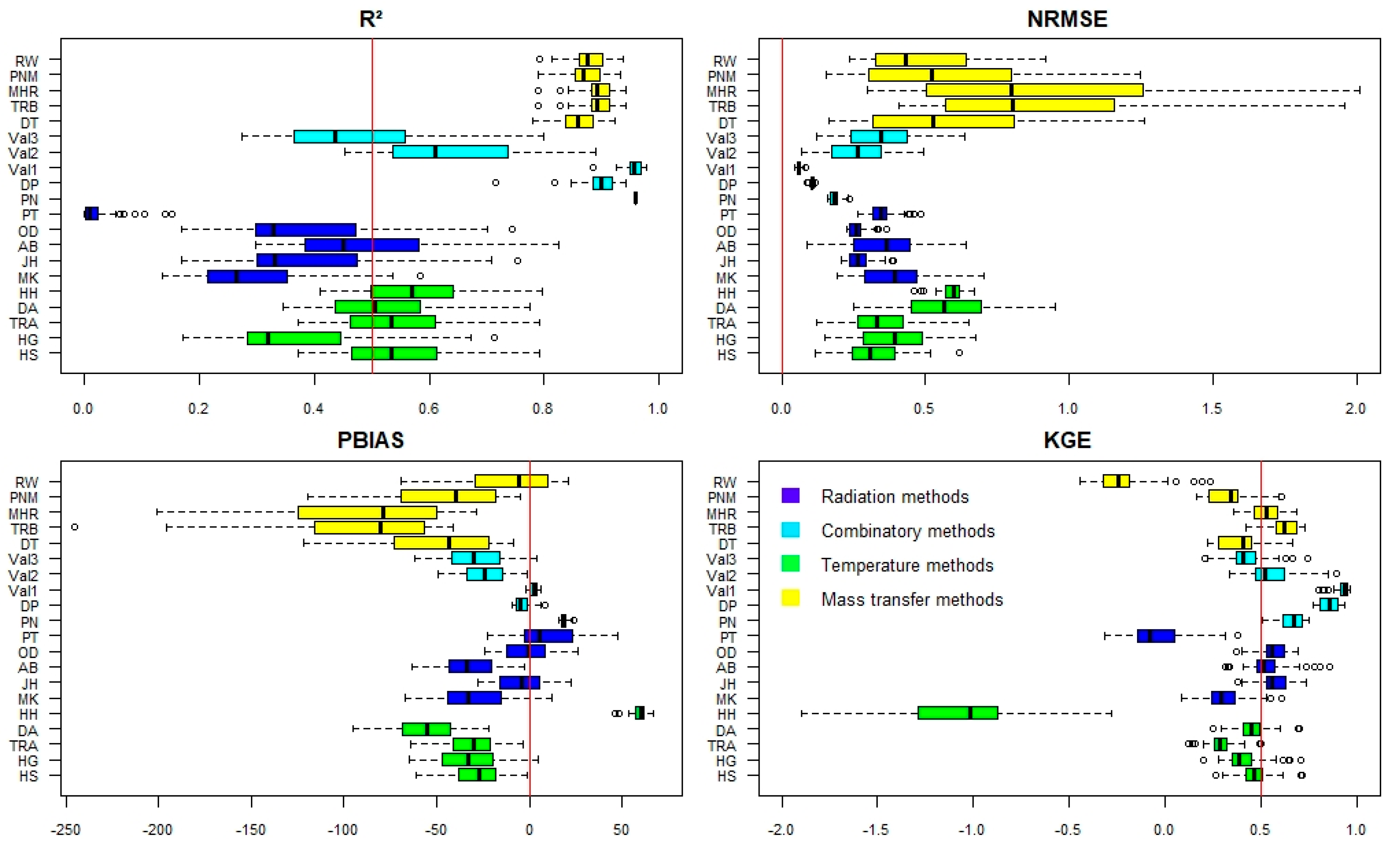
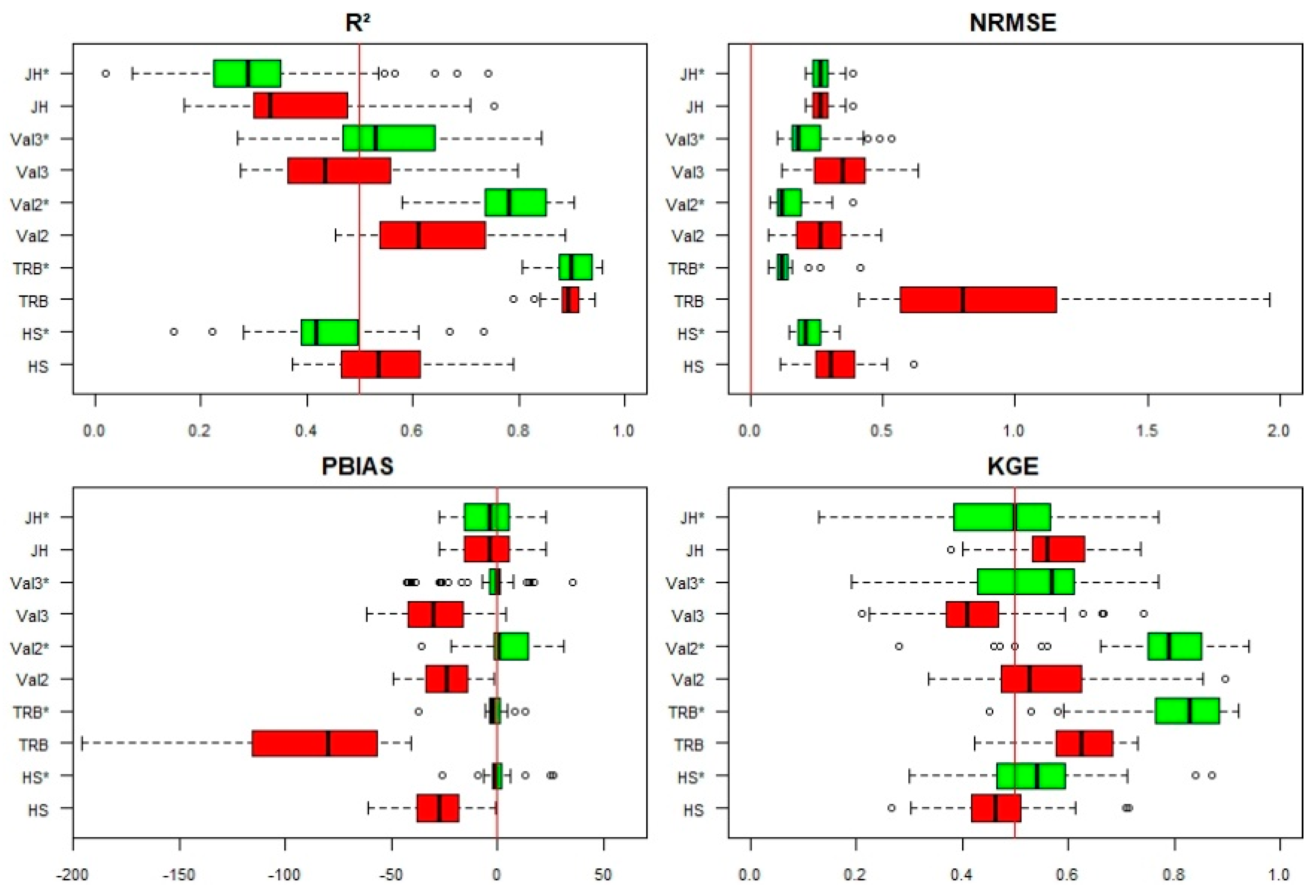
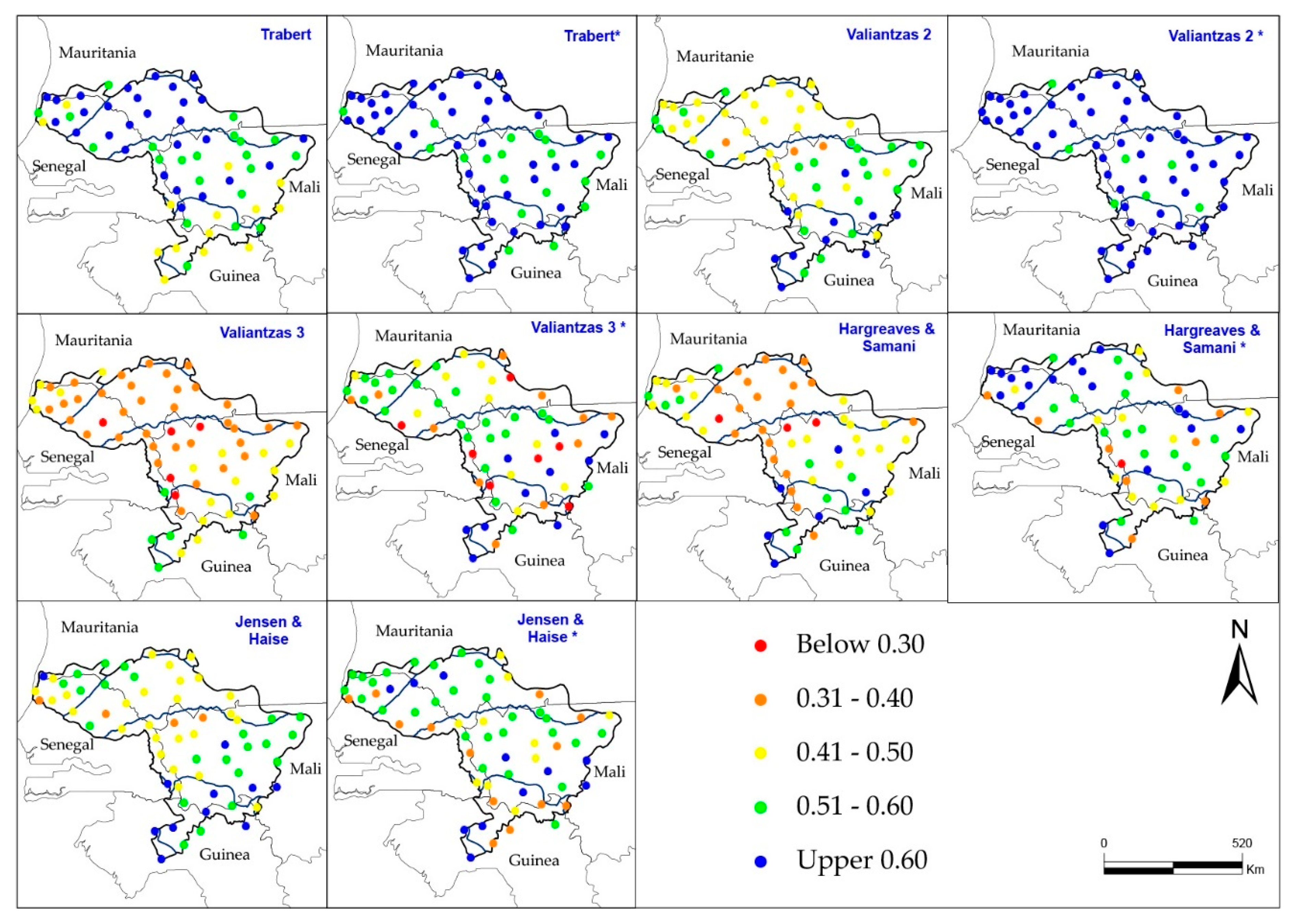
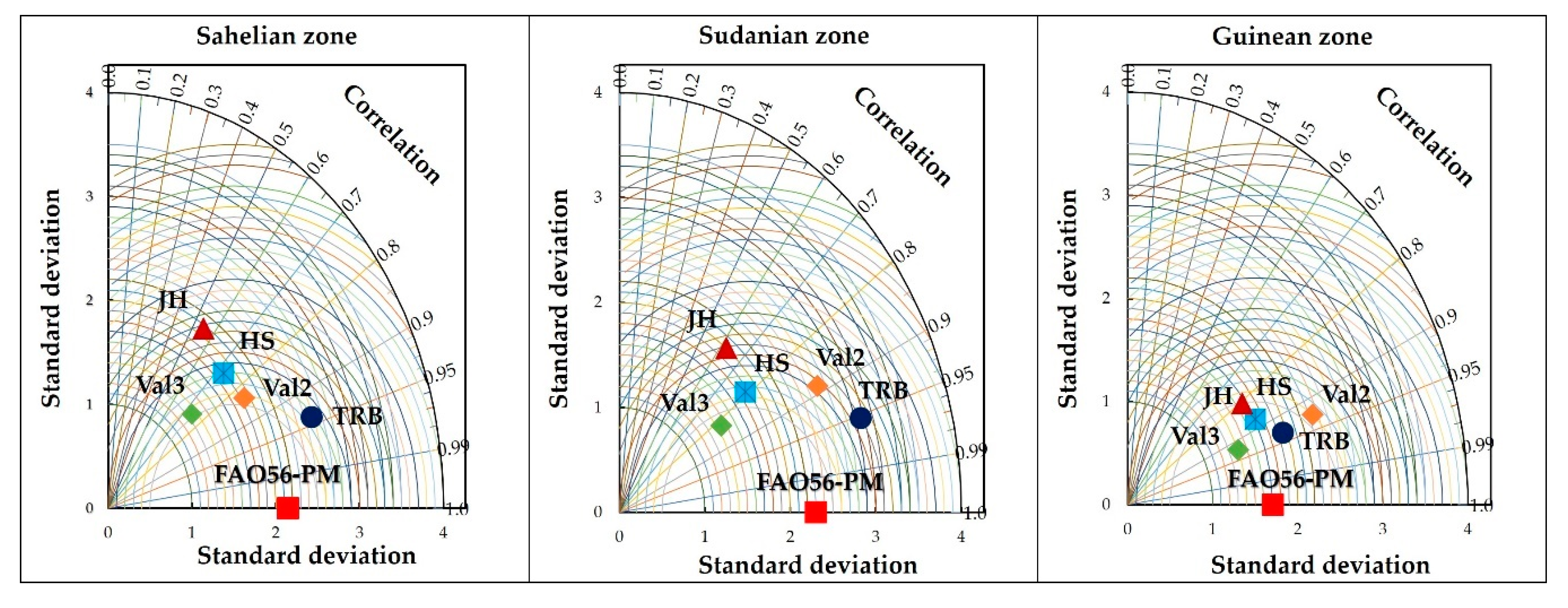
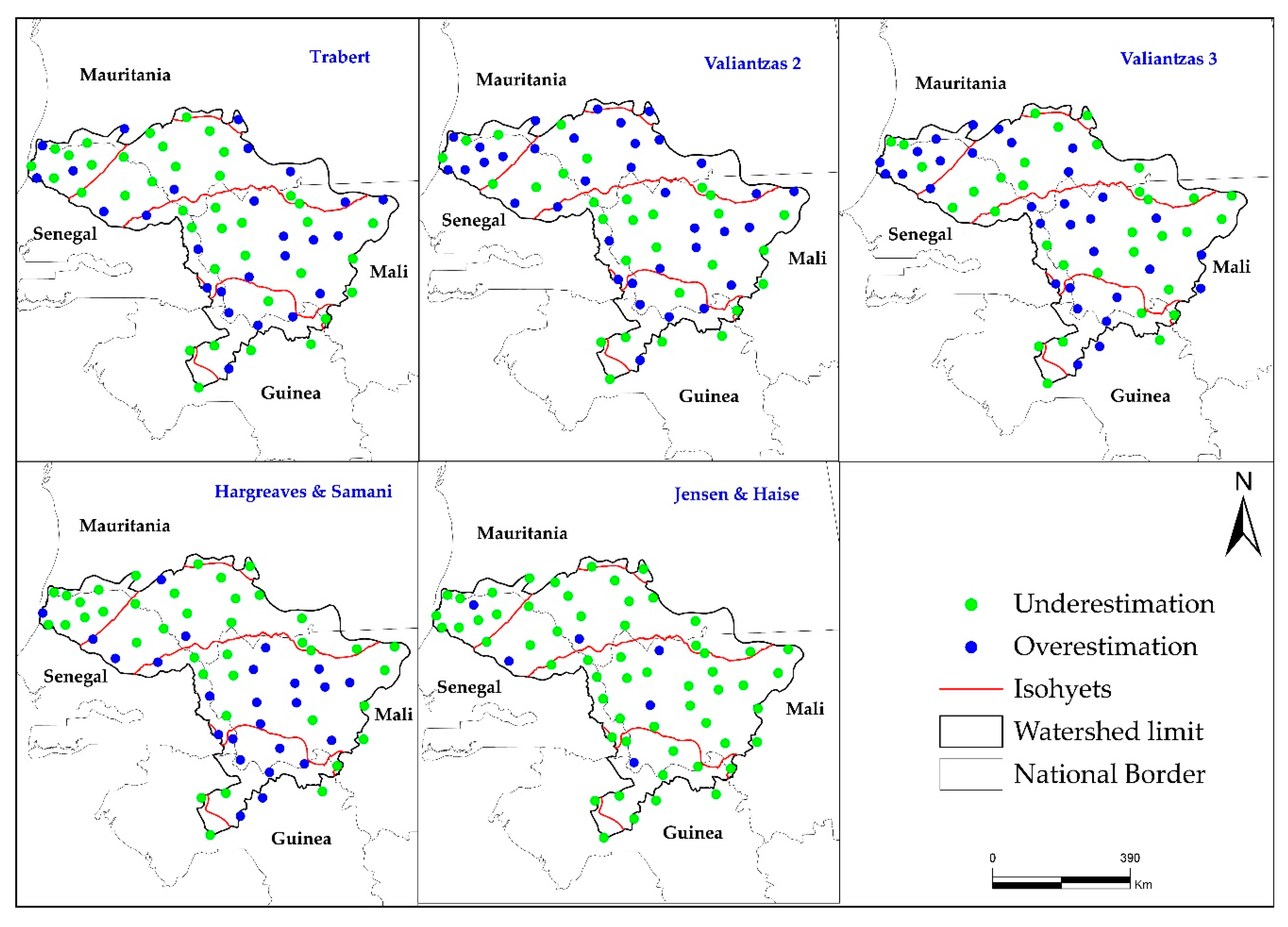
3.1. Performance of the Twenty Methods
3.2. Calibration and Validation of the Best Methods
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xu, C.Y.; Singh, V.P. Evaluation and generalization of temperature-based methods for calculating evaporation. Hydrol. Process. 2001, 14, 305–319. [Google Scholar]
- Oudin, L. Recherche d’un Modèle D’évapotranspiration Potentielle Pertinent Comme Entrée d’un Modèle Pluie-Débit Global (Search for a Relevant Potential Evapotranspiration Model as Input for a Global Rain-Flow Model). Ph.D. Thesis, L’école National de Génie Rural, des Eaux et Des Forêts (ENGREF), Paris, France, 2005; 496p. (In French). Available online: https://pastel.archives-ouvertes.fr/file/index/docid/499816/filename/memoire.pdf (accessed on 15 March 2020).
- Heydari, M.M.; Aghamajidi, R.; Beygipoor, G.; Heydari, M. Comparison and evaluation of 38 equations for estimating reference evapotranspiration in an arid region. FEB 2014, 23, 1985–1996. [Google Scholar]
- Jian, X.; Scherer, T.; Lin, D.; Zhang, X.; Refali, I. Comparison of reference evapotranspiration calculations for southeastern North Dakota. Irrig. Drain. Syst. Eng. 2013, 2, 1–9. [Google Scholar]
- Birhanu, D.; Kim, H.; Jang, C.; Park, S. Does the complexity of evapotranspiration and hydrological models enhance robustness? Sustainability 2018, 10, 2837. [Google Scholar] [CrossRef]
- Hong, T.; Tran, N.; Honti, M. Application of different evapotranspiration models to calculate total agricultural water demand in a tropical region. Period. Polytech. Civ. Eng. 2017, 61, 904–910. [Google Scholar] [CrossRef][Green Version]
- Li, Y.; Feng, A.; Liu, W.; Ma, X.; Dong, G. Variation of aridity index and the role of climate variables in the Southwest China. Water 2017, 9, 743. [Google Scholar] [CrossRef]
- Wen, J.; Wang, X.; Guo, M.; Xu, X. Impact of climate change on reference crop evapotranspiration in Chuxiong City, Yunnan Province. Procedia Earth Planet. Sci. 2012, 5, 113–119. [Google Scholar]
- Tao, X.; Hua, C.; Xu, C.; Hou, Y.; Jie, M. Analysis and prediction of reference evapotranspiration with climate change in Xiangjiang River Basin, China. Water Sci. Eng. 2015, 8, 273–281. [Google Scholar]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar]
- Bigeard, G. Estimation Spatialisée de L’évapotranspiration à l’aide de Données Infra-Rouge Thermique Multi-Résolutions (Spatialized Evapotranspiration Estimation Using Multi-Resolution Thermal Infrared Data). Ph.D. Thesis, Université Toulouse III Paul Sabatier (UT3 Paul Sabatier), Toulouse, France, 2014; 259p. (In French). Available online: https://tel.archives-ouvertes.fr/tel-01620222/document (accessed on 15 March 2020).
- Muhammad, M.K.I.; Nashwan, M.S.; Shahid, S.; Ismail, T.I.; Song, Y.H.; Chung, E. Evaluation of empirical reference evapotranspiration models using compromise programming: A case study of peninsular Malaysia. Sustainability 2019, 11, 4267. [Google Scholar] [CrossRef]
- Jiao, L.; Wang, D. Climate change, the evaporation paradox, and their effects on Streamflow in Lijiang Watershed. Pol. J. Environ. Stud. 2018, 27, 2585–2591. [Google Scholar] [CrossRef]
- Chu, R.; Li, M.; Shen, S.; Islam, A.; Cao, W.; Tao, S.; Gao, P. Changes in reference evapotranspiration and its contributing factors in Jiangsu, a major economic and agricultural province of Eastern China. Water 2017, 9, 486. [Google Scholar] [CrossRef]
- Aubin, A. Estimation de L’évapotranspiration par Télédétection Spatiale en Afrique de L’Ouest: Vers une Meilleure Connaissance de Cette Variable clé Pour la Région (English Title Estimation of Evapotranspiration using Space Remote Sensing in West Africa: Towards a Better Knowledge of this Key Variable for the Region). Ph.D. Thesis, L’Universite Montpellier, Montpellier, France, 2018; 431p. (In French). Available online: https://tel.archives-ouvertes.fr/tel-02045897/document (accessed on 15 March 2020).
- Cosandey, C.; Robinson, M. Hydrologie Continentale; Armand Colin: Paris, France, 2000; 353p. [Google Scholar]
- Pereira, L.S.; Allen, R.G.; Smith, M.; Raes, D. Crop evapotranspiration estimation with FAO56: Past and future. Agric. Water Manag. 2014, 1–16. [Google Scholar] [CrossRef]
- Allen, R.; Pereira, L.; Raes, D.; Smith, M. Crop Evapotranspiration. Guideline for Computing Crop Requirements; FAO-Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Gocic, M.; Trajkovic, S. Analysis of trends in reference evapotranspiration data in a humid climate. Hydrol. Sci. J. 2014, 59, 165–180. [Google Scholar]
- Diop, L.; Bodian, A.; Diallo, D. Use of atmometers to estimate reference evapotranspiration in Arkansas. Afr. J. Agric. Res. 2015, 10, 4376–4683. [Google Scholar] [CrossRef]
- Douar, A. Mesure de L’évapotranspiration par Eddy Covariance. Effet de la Hauteur de Mesure et Variabilité Spatiale (Measuring Evapotranspiration by Eddy Covariance. Effect of Measuring Height and Spatial Variability). Master’s Thesis, Université Pierre-Marie-Curie, Paris, France, 2017; 44p. (In French). Available online: http://m2hh.metis.upmc.fr/wp-content/uploads/Douar_Abdelhak_memoireHH1617.pdf (accessed on 11 March 2020).
- Dalton, J. Experimental essays on the constitution of mixed gases; on the force of steam of vapor from waters and other liquids in different temperatures, both in a Torricellian vacuum and in air on evaporation and on the expansion of gases by heat. Mem. Manch. Lit. Philos. Soc. 1802, 5, 535–602. [Google Scholar]
- Makkink, G.F. Testing the Penman formula by means of lysimeters. J. Inst. Water Eng. 1957, 11, 277–288. [Google Scholar]
- Penman, H.L. Vegetation and Hydrology; Technical Communication No. 53; Commonwealth Bureau of Soils: Harpenden, UK, 1963; 125p. [Google Scholar]
- Hargreaves, G.H. Moisture availability and crop production. Trans. ASAE 1975, 18, 980–984. [Google Scholar]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from temperature. Am. Soc. Agric. Eng. 1985, 1, 96–99. [Google Scholar]
- Valiantzas, J. Simple ET0 of Penman’s equation without wind/or humidity data. II: Comparisons Reduced Set-FAO and other methodologies. Am. Soc. Civ. Eng. 2013, 139, 9–19. [Google Scholar] [CrossRef]
- Tabari, H. Evaluation of reference crop evapotranspiration equations in various climates. Water Resour. Manag. 2010. [Google Scholar] [CrossRef]
- Djaman, K.; Balde, A.B.; Sow, A.; Muller, B.; Irmak, S.; Ndiaye, M.K.; Saito, K. Evaluation of sixteen reference evapotranspiration methods under sahelian conditions in Senegal River Valley. J. Hydrol. Reg. Stud. 2015, 3, 139–159. [Google Scholar] [CrossRef]
- Bodian, A.; Diop, L.; Panthou, G.; Dacosta, H.; Deme, A.; Dezetter, A.; Ndiaye, P.M.; Diouf, I.; Vichel, T. Recent trend in hydroclimatic conditions in the Senegal River Basin. Water 2020, 12, 436. [Google Scholar] [CrossRef]
- Trabert, W. Neue beobachtungen über verdampfungsgeschwindigkeiten (New observations about evaporation rates). Meteorol. Z. 1896, 13, 261–263. (In German) [Google Scholar]
- Penman, H.L. Natural evaporation from open water, bare soil and grass. Proc. R. Meteorol. Soc. 1948, 193, 120–145. [Google Scholar]
- Abtew, W. Evapotranspiration measurement and modeling for three wetland systems in South Florida. Water Resour. Bull. 1996, 32, 465–473. [Google Scholar]
- Rohwer, C. Evaporation from Free Water Surfaces; Technical Bulletin 271; US Department of Agriculture: Washington, DC, USA, 1931. [Google Scholar]
- Mahringer, W. Verdunstungsstudien am Neusiedler see. Arch. Meteorol. Geophys. Bioklimatol. Ser. B 1970, 18, 1–20. [Google Scholar]
- Trajkovic, S.; Stojvic, V. Effect of wind speed on accuracy of Turc method in humid climate. Archit. Civ. Eng. 2007, 5, 107–113. [Google Scholar]
- Droogers, P.; Allen, R.G. Estimating reference evapotranspiration under inaccurate data conditions. Irrig. Drain. Syst. 2002, 16, 33–45. [Google Scholar] [CrossRef]
- Heydari, M.M.; Heydari, M. Evaluation of pan coefficient equations for estimating reference crop evapotranspiration in the arid region. Arch. Agron. Soil Sci. 2014, 60, 715–731. [Google Scholar] [CrossRef]
- Jensen, M.E.; Haise, H.R. Estimating evapotranspiration from solar radiation. J. Irrig. Drain. Div. 1963, 89, 15–41. [Google Scholar]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large scale parameters. Mon. Weath. Rev. 1972, 100, 81–92. [Google Scholar]
- Doorenbos, J.; Pruitt, W.O. Guidelines for Predicting Crop Water Requirements; FAO Irrigation and Drainag, Paper No. 24; FAO: Rome, Italy, 1977. [Google Scholar]
- Xu, C.Y.; Singh, V.P. Evaluation and generalization of radiation-based methods for calculating evaporation. Hydrol. Process. 2000, 14, 339–349. [Google Scholar]
- Ahooghalandari, M.; Khiadani, M.; Jahromi, M.E. Calibration of Valiantzas’ reference evapotranspiration equations for the Pilbara region, Western Australia. Appl. Clim. 2016. [Google Scholar] [CrossRef]
- Čadro, S.; Uzunovi, M.; Žurovec, J.; Žurovec, O. Validation and calibration of various reference evapotranspiration alternative methods under the climate conditions of Bosnia and Herzegovina. Int. Soil Water Conserv. Res. 2017, 5, 309–324. [Google Scholar] [CrossRef]
- Djaman, K.; Tabari, H.; Balde, A.B.; Diop, L.; Futakuchi, K.; et Irmak, S. Analyses, calibration and validation of evapotranspiration models to predict grass-reference evapotranspiration in the Senegal river delta. J. Hydrol. Reg. Stud. 2016, 8, 82–94. [Google Scholar] [CrossRef]
- Bodian, A. Approche par Modélisation Pluie-Débit de la Connaissance Régionale de la Ressource en Eau: Application dans le Haut Bassin du Fleuve Sénégal ( Rain-Flow Modeling Approach to Regional Knowledge of Water Resources: Application in the Upper Basin of the Senegal River ). Ph.D. Thesis, Université Cheikh Anta Diop de Dakar, Dakar, Senegal, 2011; 211p. (In French). Available online: http://hydrologie.org/THE/BODIAN.pdf (accessed on 10 March 2020).
- Dione, O. Evolution Climatique Récente et Dynamique Fluviale dans les Hauts Bassins des Fleuves Sénégal et Gambie ( Recent Climate Evolution and Fluvial Dynamics in the High Basins of the Senegal and Gambia Rivers). Ph.D. Thesis, Université de Lyon 3 Jean Moulin, ORSTOM, Paris, France, 1996; 438p. (In French). Available online: http://horizon.documentation.ird.fr/exl-doc/pleins_textes/pleins_textes_7/TDM_7/010012551.pdf (accessed on 10 March 2020).
- SDAGE-OMVS. Etat des Lieux et Diagnostique; Rapport Provisoire 2009, Rapport de Phase III; SDAGE-OMVS: Dakar, Senegal, 2011. [Google Scholar]
- Bodian, A.; Dezetter, A.; Deme, A.; Diop, L. Hydrological evaluation of TRMM rainfall over the upper Senegal River Basin. Hydrology 2016, 3, 15. [Google Scholar] [CrossRef]
- Srivastava, P.; Han, D.; Ramirez, M.A.; Islam, T. Comparative assessment of evapotranspiration derived from NCEP and ECMWF global datasets through Weather Research and Forecasting model. Atmos. Sci. Lett. 2013, 14, 118–125. [Google Scholar] [CrossRef]
- Poccard-Leclercq, I. Etude Diagnostique de Nouvelles Données Climatiques: Les Réanalyses. Exemples D’application aux Précipitations en Afrique Tropicale (Diagnostic Study of New Climate Data: Reanalyses. Application to Precipitation in Tropical Africa). PhD. Thesis, Géographie. Université de Bourgogne, Dijon, France, 2000; 255p. (In French). [Google Scholar]
- Ruane, A.C.; Goldberg, R.; Chryssanthacopoulos, J. Climate forcing datasets for agricultural modeling: Merged products for gap-filling and historical climate series estimation. Agric. For. Meteorol. 2015, 200, 233–248. [Google Scholar]
- Martins, D.S.; Paredes, P.; Razia, T.; Pires, C.; Cadima, J.; Pereira, L. Assessing reference evapotranspiration from reanalysis weather products. An application to the Iberian Peninsula. Int. J. Climatol. 2016, 37, 1–20. [Google Scholar] [CrossRef]
- Stackhouse, P.W.; Westberg, D., Jr.; Chandler, W.S.; Zhang, T.; Hoell, J.M. Prediction of Worldwide Energy Resource (POWER): Agroclimatology Methodology. 2018; 52p. Available online: https://power.larc.nasa.gov/documents/POWER_Data_v9_methodology.pdf (accessed on 20 December 2018).
- Purnadurga, G.T.V.; Kumar, L.; Rao, K.K.; Barbosa, H.; Mall, R.K. Evaluation of evapotranspiration estimates from observed and reanalysis data sets over Indian region. Int. J. Climatol. 2019, 39, 5791–5800. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modeling. J. Hydrol. 2009, 377, 80–91. [Google Scholar]
- Valipour, M. Calibration of mass transfer-based methods to predict reference crop evapotranspiration. Appl. Water Sci. 2015, 1–11. [Google Scholar] [CrossRef]
- Bogawski, P.; Bednorz, E. Comparison and validation of selected evapotranspiration models for conditions in Poland (Central Europe). Water Resour. Manag. 2014, 28, 5021–5038. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2011, 106, 7183–7192. [Google Scholar] [CrossRef]
- Singh, V.P.; Xu, C.Y. Dependence of evaporation on meteorological variables at different time scales and intercomparison of estimation methods. Hydrol. Process. 1997, 12, 429–442. [Google Scholar]
- Djaman, K.; Koudahe, K.; Sall, M.; Kabenge, I.; Rudnick, D.; Irmak, S. Performance of twelve mass transfer based reference evapotranspiration models under humid climate. J. Water Resour. Prot. 2017, 9, 1347–1363. [Google Scholar] [CrossRef][Green Version]
- Ndiaye, P.M.; Bodian, A.; Diop, L.; Djaman, K. Evaluation de vingt méthodes d’estimation de l’évapotranspiration journalière de référence au Burkina Faso. Physio-Géo 2017, 11, 129–146. [Google Scholar]
- Tabari, H.; Talaee, P.H. Sensitivity of evapotranspiration to climatic change in different climates. Glob. Planet. Chang. 2014, 115, 16–23. [Google Scholar]
- Irmak, S.; Allen, R.G.; Whitty, E.B. Daily grass and alfalfa-reference evapotranspiration estimates and alfalfa-to-grass evapotranspiration ratios in Florida. J. Irrig. Drain. Eng. 2003, 129, 360–370. [Google Scholar] [CrossRef]
- Ambas, V.T.; Baltas, E. Sensitivity analysis of different evapotranspiration methods using a new sensitivity coefficient. Glob. Nest J. 2012, 14, 335–343. [Google Scholar]
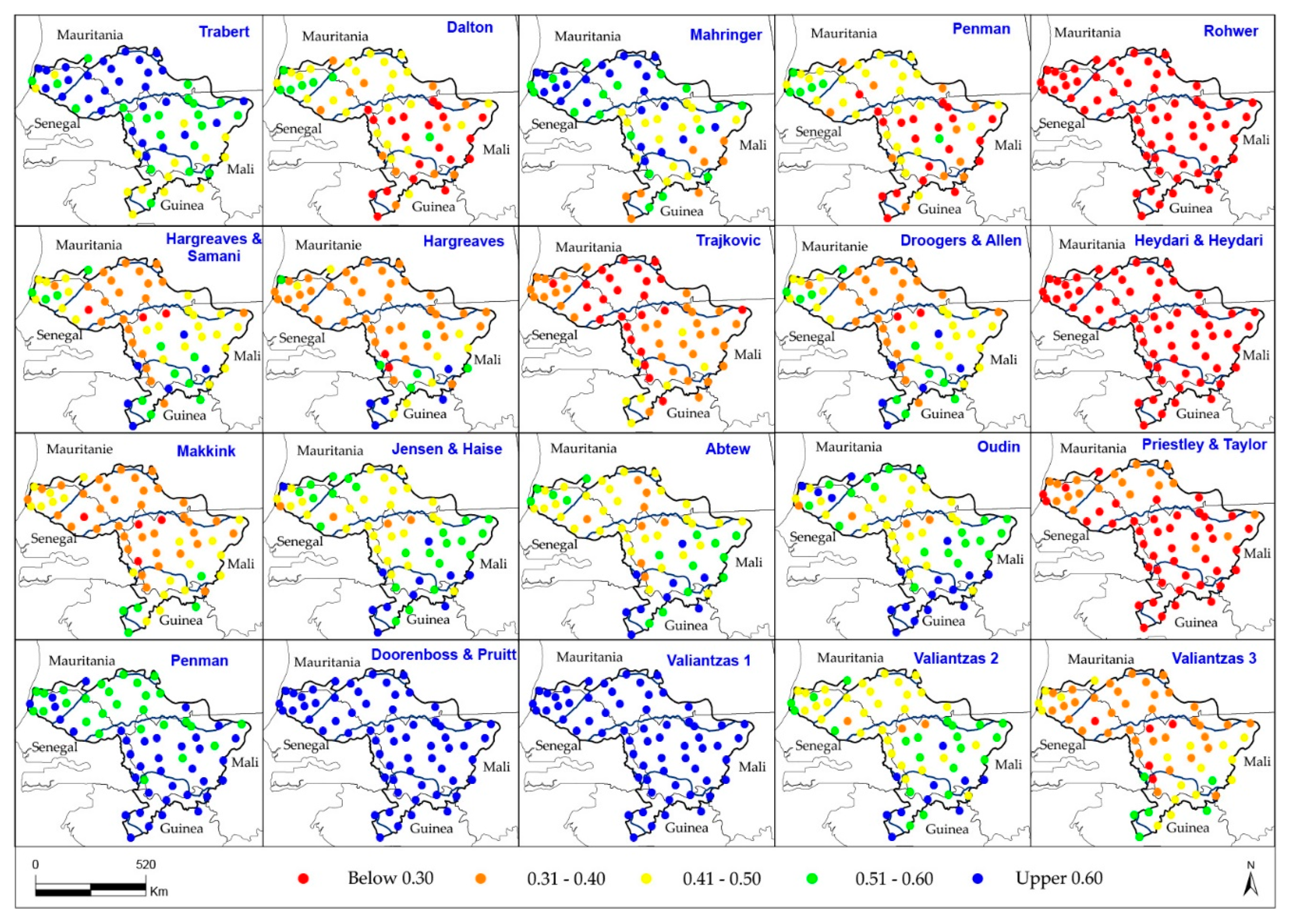
| Climate Zone * | u2 (m s−1) | Tmax (°C) | Tmin (°C) | Rh (%) | Rs (MJ m−2) | ET0 (mm day−1) |
|---|---|---|---|---|---|---|
| Guinean | 1.70 | 30.42 | 21.18 | 67.65 | 19.65 | 4.54 |
| Sudanian | 2.22 | 34.88 | 22.45 | 42.03 | 20.72 | 6.30 |
| Sahelian | 3.00 | 37.12 | 22.95 | 29.00 | 21.29 | 8.01 |
| Categories | References | Formula | Abbreviation | |
|---|---|---|---|---|
| Aerodynamic | Dalton [21] | DN | (2) | |
| Trabert [30] | TRB | (3) | ||
| Penman [31] | PNM | (4) | ||
| Rohwer [33] | RW | (5) | ||
| Mahringer [34] | MHR | (6) | ||
| Temperature | Hargreaves [24] | HG | (7) | |
| Hargreaves and Samani [25] | HS | (8) | ||
| Trajkovic [35] | TRA | (9) | ||
| Droogers and Allen [36] | DA | (10) | ||
| Heydari and Heydari [37] | HH | (11) | ||
| Radiation | Makkink [22] | MK | (12) | |
| Jensen and Haise [38] | JH | (13) | ||
| Priestley and Taylor [39] | PT | (14) | ||
| Abtew [32] | AB | (15) | ||
| Oudin [2] | OD | (16) | ||
| Combinatory | Penman [23] | PNM | (17) | |
| Doorenboss and Pruitt [40] | DP | (18) | ||
| Valiantzas [26] | Val 1 | (19) | ||
| Valiantzas [26] | Val 2 | (20) | ||
| Valiantzas [26] | Val 3 | (21) |
| Criteria. | Formula | Range | Optimum Value | |
|---|---|---|---|---|
| 0 to 1 | 1 | (22) | ||
| 0 to +∞ | 0 | (23) | ||
| −∞ to +∞ | 0 | (24) | ||
| −∞ to 1 | 1 | (25) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ndiaye, P.M.; Bodian, A.; Diop, L.; Deme, A.; Dezetter, A.; Djaman, K. Evaluation and Calibration of Alternative Methods for Estimating Reference Evapotranspiration in the Senegal River Basin. Hydrology 2020, 7, 24. https://doi.org/10.3390/hydrology7020024
Ndiaye PM, Bodian A, Diop L, Deme A, Dezetter A, Djaman K. Evaluation and Calibration of Alternative Methods for Estimating Reference Evapotranspiration in the Senegal River Basin. Hydrology. 2020; 7(2):24. https://doi.org/10.3390/hydrology7020024
Chicago/Turabian StyleNdiaye, Papa Malick, Ansoumana Bodian, Lamine Diop, Abdoulaye Deme, Alain Dezetter, and Koffi Djaman. 2020. "Evaluation and Calibration of Alternative Methods for Estimating Reference Evapotranspiration in the Senegal River Basin" Hydrology 7, no. 2: 24. https://doi.org/10.3390/hydrology7020024
APA StyleNdiaye, P. M., Bodian, A., Diop, L., Deme, A., Dezetter, A., & Djaman, K. (2020). Evaluation and Calibration of Alternative Methods for Estimating Reference Evapotranspiration in the Senegal River Basin. Hydrology, 7(2), 24. https://doi.org/10.3390/hydrology7020024