Deterministic Methodology for Determining the Optimal Sampling Frequency of Water Quality Monitoring Systems
Abstract
1. Introduction
2. Materials and Methods
2.1. Methodology
- The study area was specified and the topography data of the study area was collected, including locations of the preallocated MSs of the considered WQMN and recorded discharge, water depth and WQ datasets at the inlet, outlet, and within the water body;
- The hydraulic and WQ datasets were analyzed, in this research they were some effective physiochemical parameters (TDS, Ph, Turbidity, TH, DO, and BOD, Ca2+, Mg2+, Na+, SO42−, PO43− and NO3−Cd, Cr, and Pb), to specify all the potential cases and values of the boundary conditions for the study area. Consequently, the required calibration and verification datasets were specified according to these cases;
- The hydrodynamic and contaminant transport simulation models were implemented. Before applying these models for all potential cases of boundary conditions, the calibration and verification processes were performed;
- Based on the results of the contaminant transport simulation model, the spatiotemporal analysis tools of GIS were utilized to obtain the temporal changes in the considered WQ parameters distribution patterns within the considered water body. Subsequently, the minimum time interval of detecting a successive change in the concentration of the considered WQ parameters was computed at each MS with MA of each WQ parameter for each case of boundary conditions;
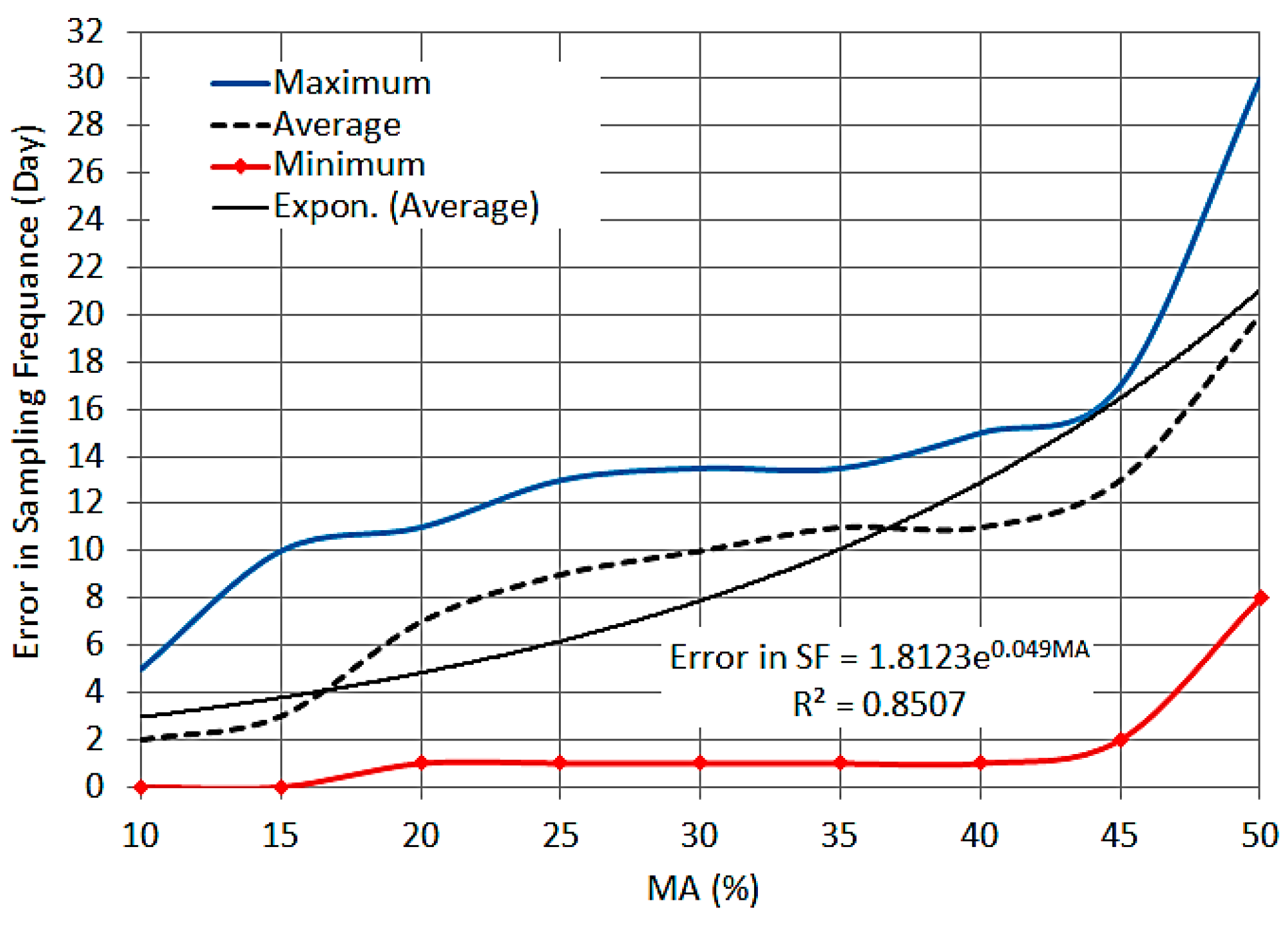
- To evaluate the effect of changing the MA, the results of the contaminants transport simulation models (for each WQ parameters) were reanalyzed using the spatiotemporal analysis approach and increasing the MA from ±5% to ±50% (stepwise 5%) for each WQ parameter for each case of boundary conditions;
- To verify the proposed methodology, a sampling schedule was implemented based on the criteria of the sampling frequency for GEMS/WATER stations UNEP/WHO [23] to compare with the results produced by using the proposed methodology;
- The results were analyzed and discussed, and the main conclusions and recommendations were presented.
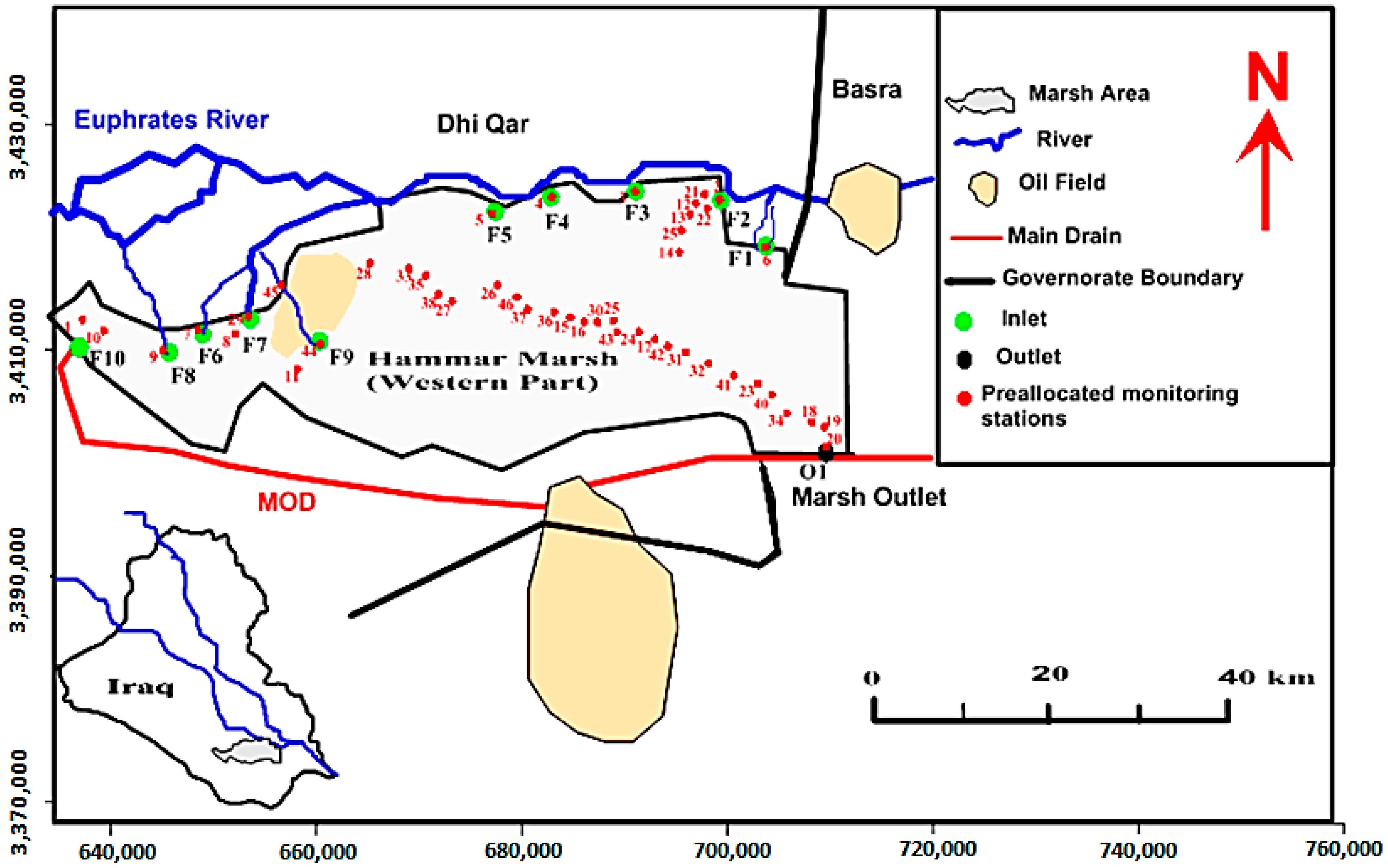
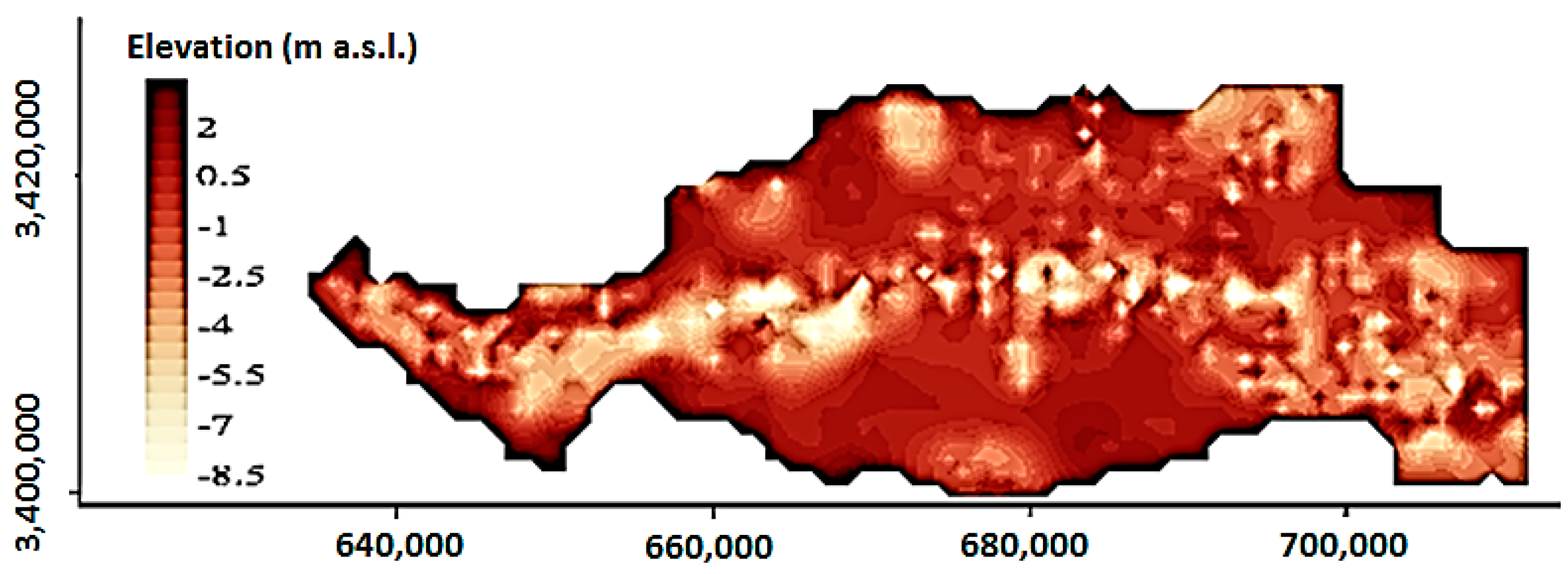
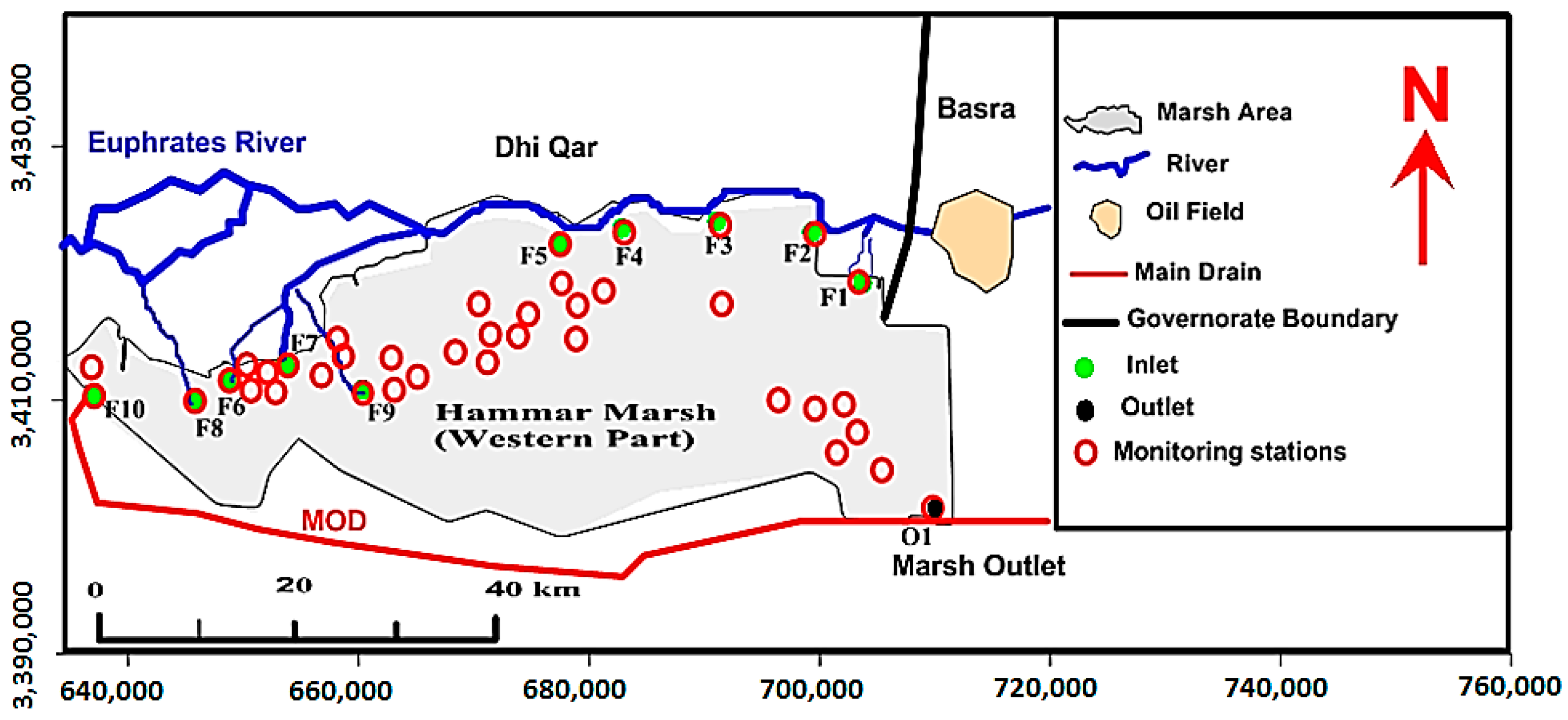
2.2. Study Area
2.3. Hydrodynamic and Contaminant Transport Simulation Models
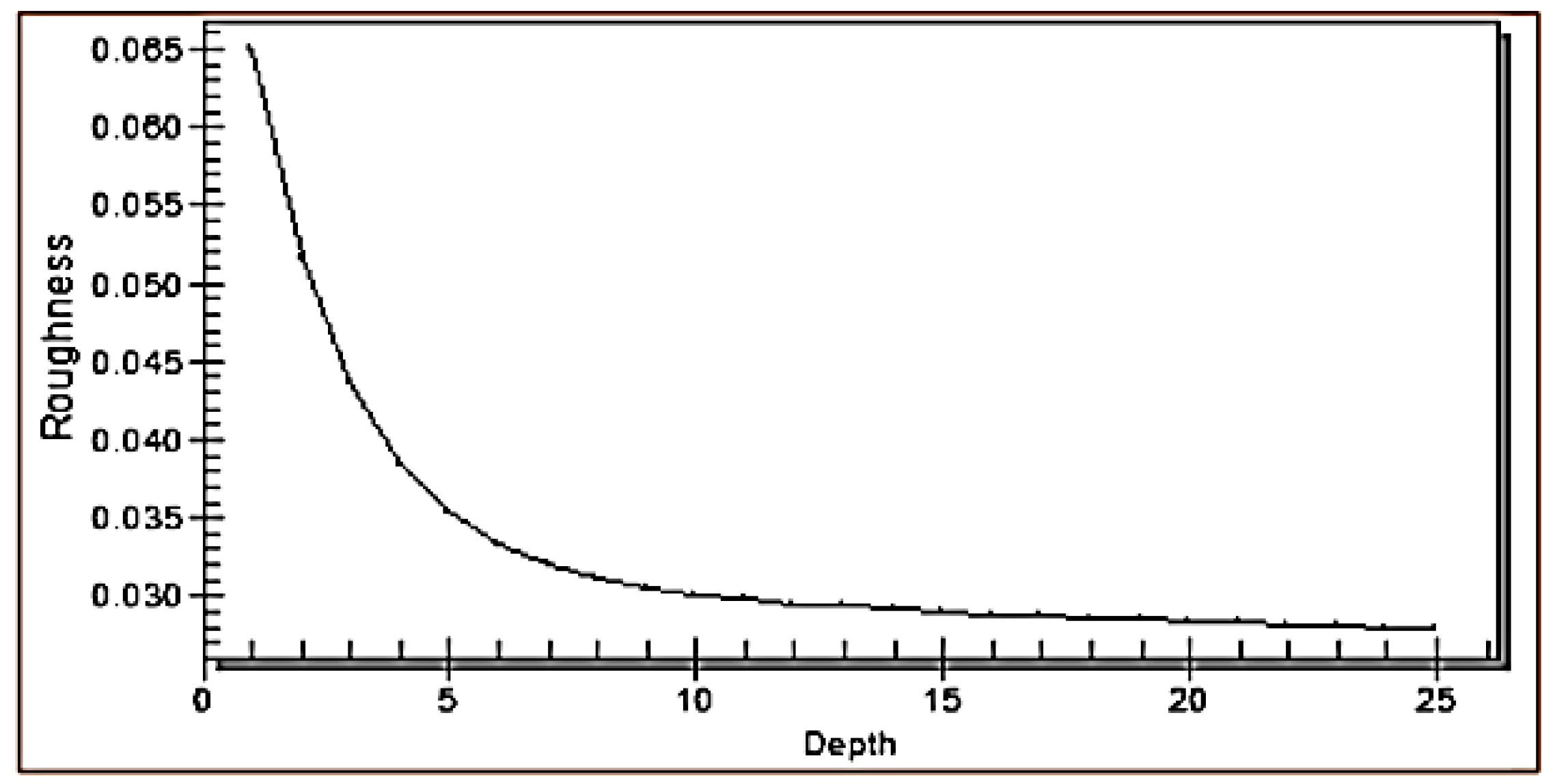
2.3.1. Hydrodynamic Model (RMA2)
2.3.2. Contaminant Transport Models (RMA4)
2.4. Spatial and Temporal Analysis
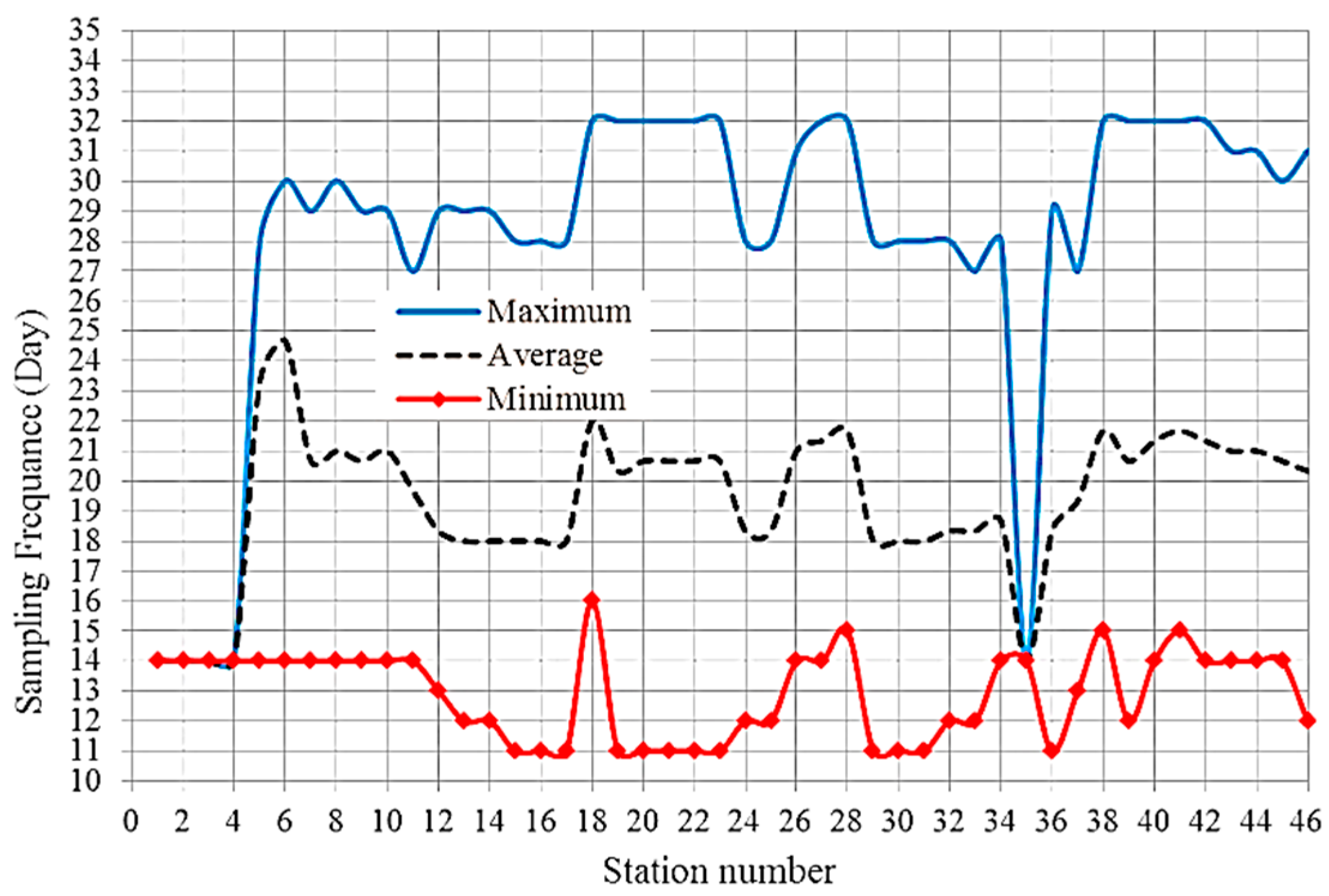
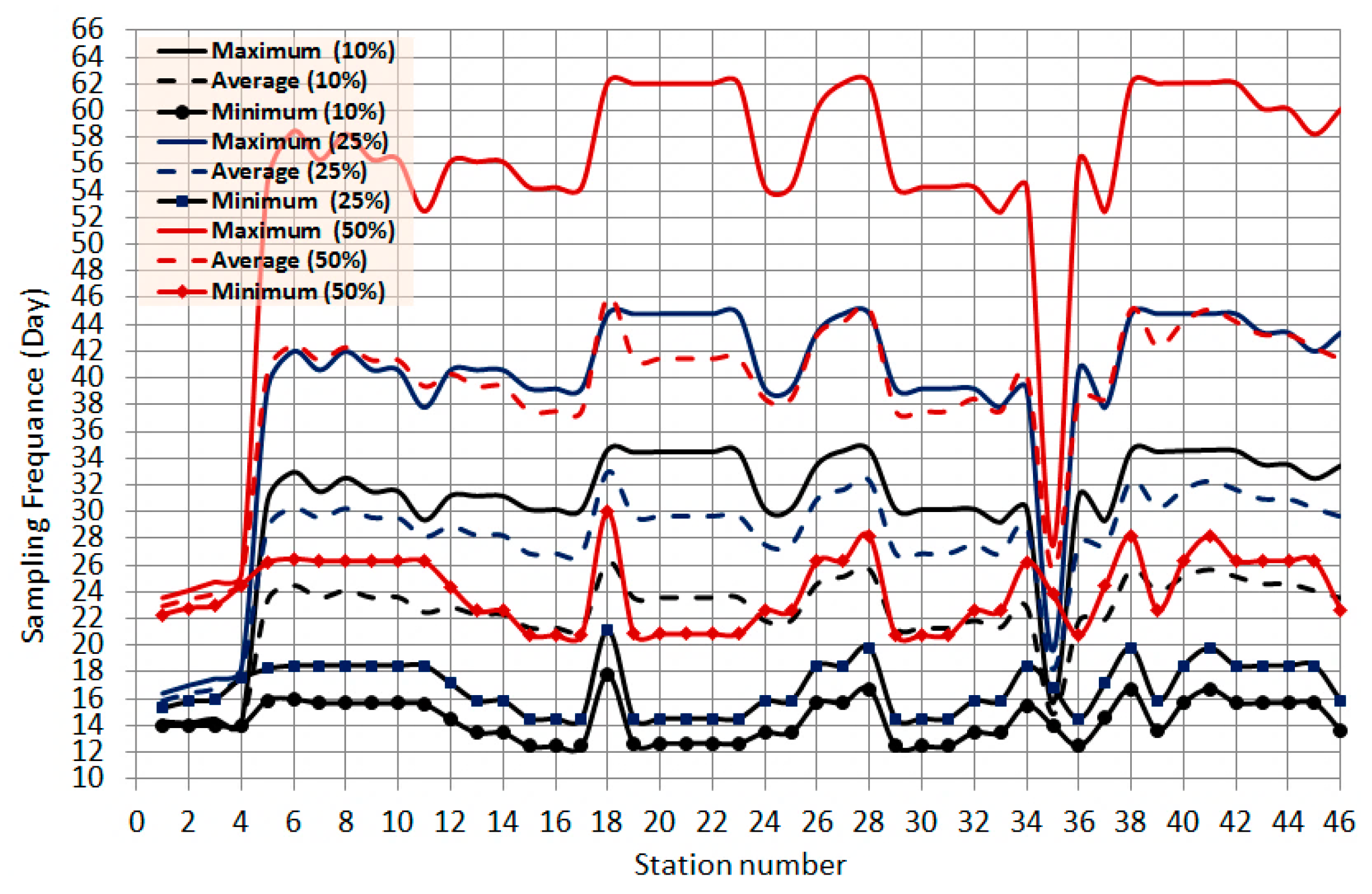
3. Results and Analysis
3.1. Verification of the RMA2 and RMA4 Models
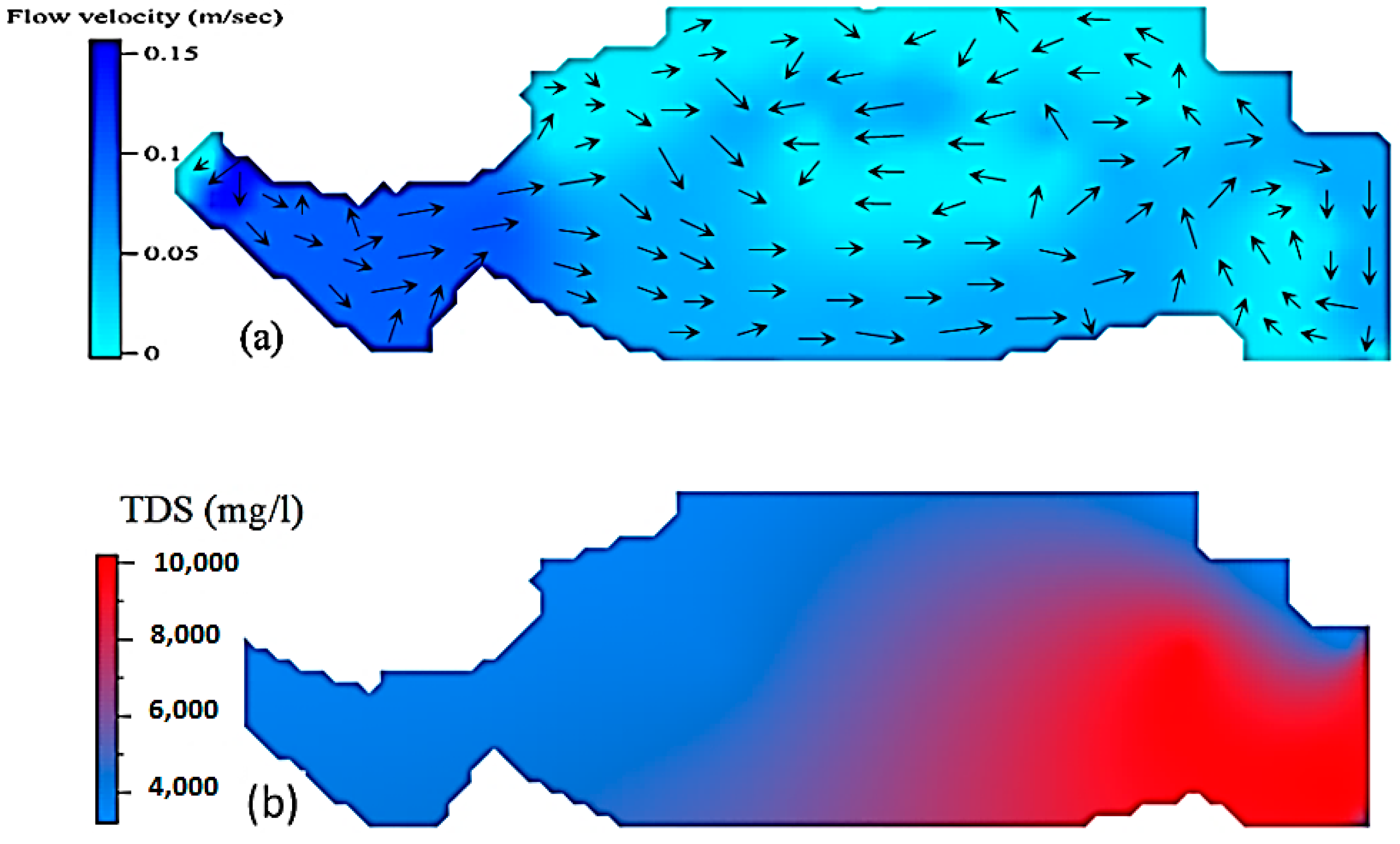
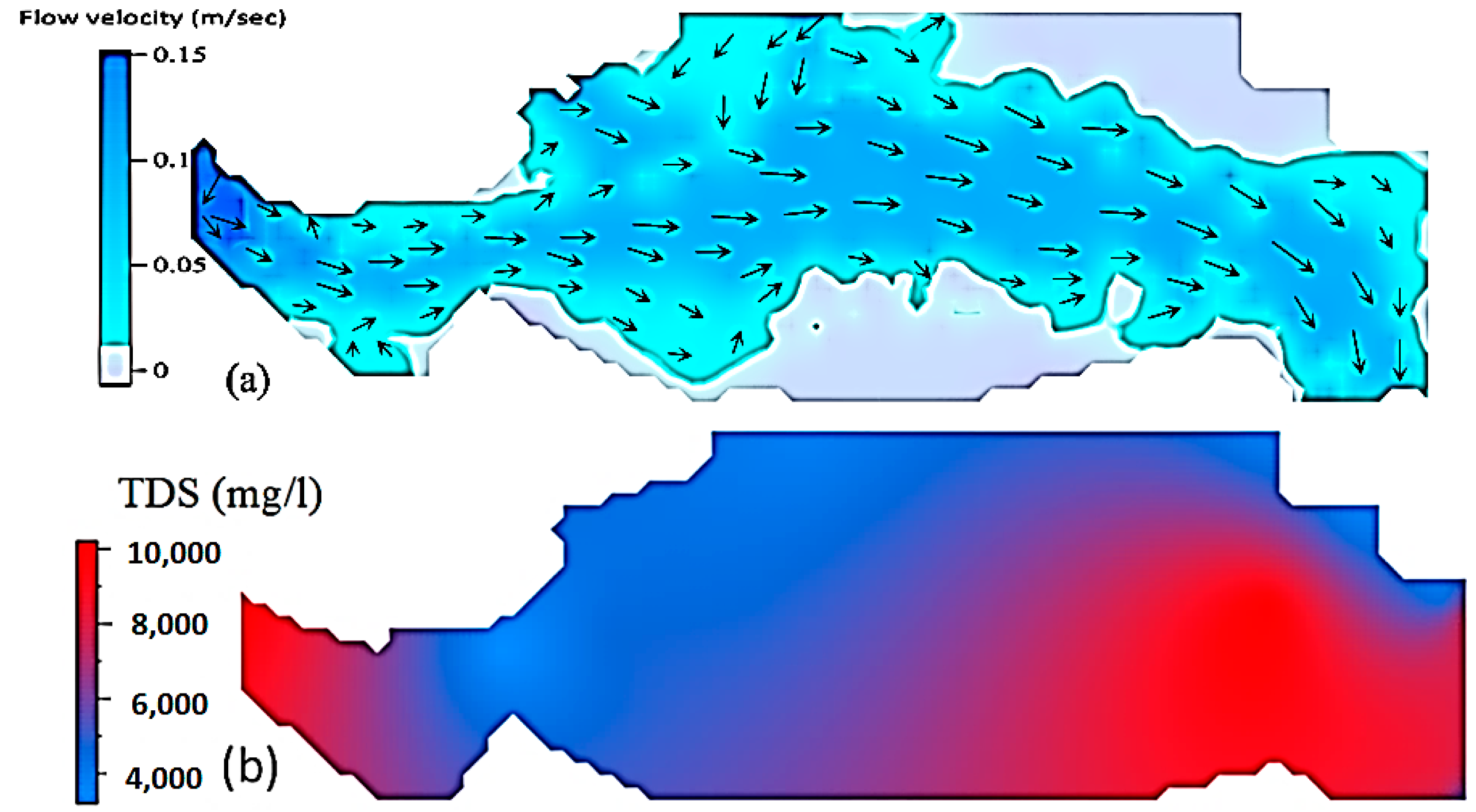
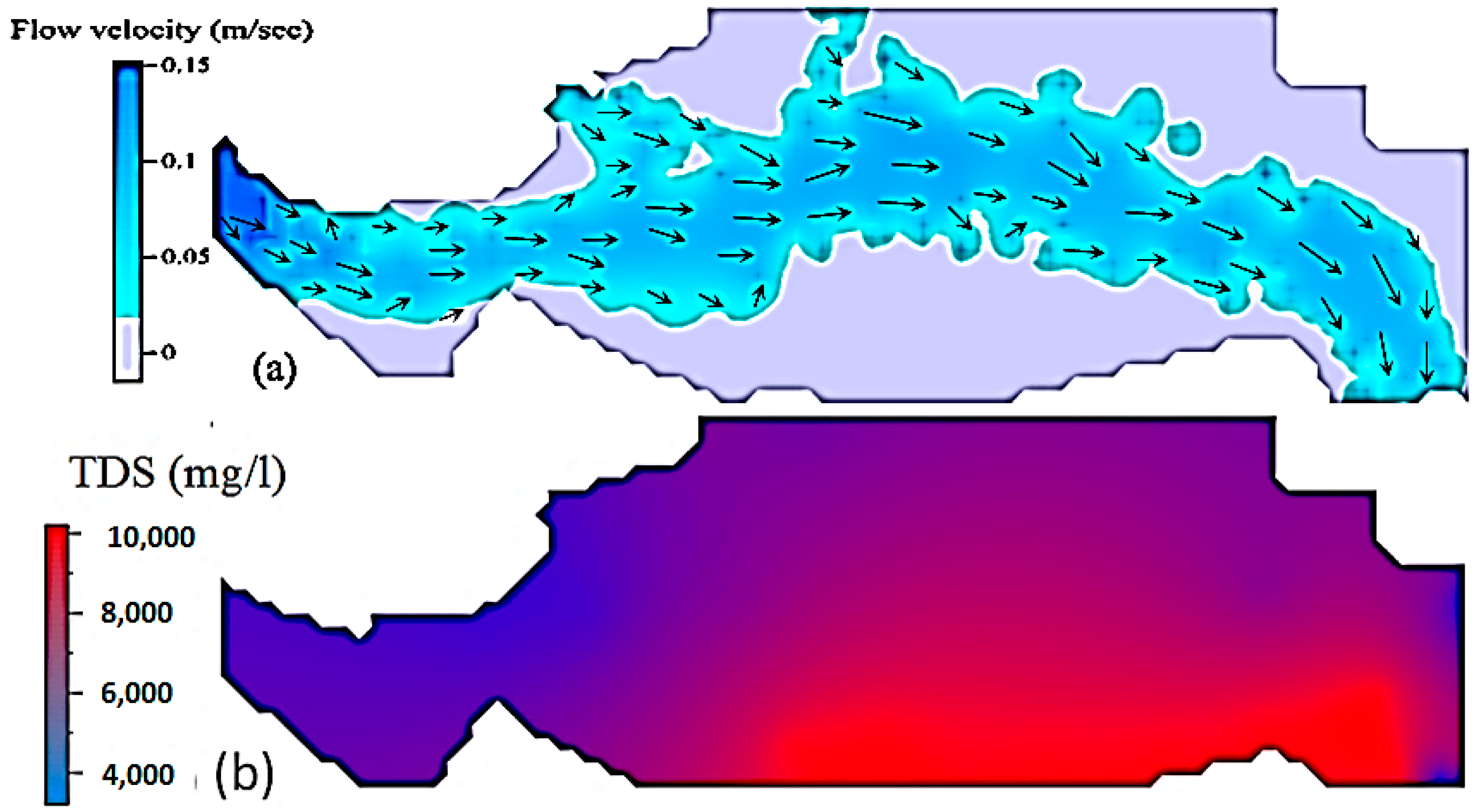
3.2. Application of the RMA2 and RMA4 Models
4. Conclusions
Supplementary Materials
Funding
Acknowledgments
Conflicts of Interest
References
- Bu, H.; Tan, X.; Li, S.; Zhang, Q. Temporal and spatial variations of water quality in the Jinshui River of the South Qinling Mts. Ecotoxicol. Environ. Saf. 2010, 73, 907–913. [Google Scholar] [CrossRef]
- Behmel, S.; Damour, M.; Ludwig, R.; Rodriguez, M.J. Water quality monitoring strategies—A review and future perspectives. Sci. Total Environ. 2016, 571, 1312–1329. [Google Scholar] [CrossRef]
- Thomas, G.S.; Adrian, D.D. Sampling frequency for river quality monitoring. Water Resour. Res. 1978, 14, 569–576. [Google Scholar]
- Loftis, J.C.; Ward, R.C. Water quality monitoring—Some practical sampling frequency considerations. Environ. Manag. 1980, 4, 521–526. [Google Scholar] [CrossRef]
- Robert, H.H.; Michael, J.B. Sampling Frequency for Water Quality Monitoring; Advanced Monitoring Systems Division, Environmental Monitoring Systems Laboratory: Las Vegas, NV, USA, 1981.
- Skalski, J.R.; Mackenzie, D.H. A design for aquatic monitoring programs. J. Environ. Manage. 1982, 14, 237–251. [Google Scholar]
- Don, C.; Peter, N.N.; Dean, H.U. Sampling frequency for water quality monitoring: Measures of effectiveness. Water Resour. Res. 1983, 19, 1107–1110. [Google Scholar] [CrossRef]
- Groot, S.; Schilperoort, T. Optimization of water quality monitoring networks. Water Sci. Technol. 1984, 16, 275–287. [Google Scholar] [CrossRef]
- Steven, P.M.; Dennis, P.L. Optimal design of biological sampling programs using the analysis of variance. Estuar. Coast. Shelf Sci. 1986, 22, 637–656. [Google Scholar] [CrossRef]
- Smith, D.G.; McBride, G.B. New Zealand’s National Water Quality Monitoring Network—Design and First Year’s Operation. Water Resour. Bull. 1990, 26, 767–775. [Google Scholar] [CrossRef]
- Loftis, J.C.; McBride, G.B.; Ellis, J.C. Considerations of scale in water quality monitoring and data analysis. Water Resour. Bull. 1991, 27, 255–264. [Google Scholar] [CrossRef]
- Esterby, S.R.; El-Shaarawi, A.H.; Block, H.O. Detection of water quality changes along a river system. Environ. Monit. Assess. 1992, 23, 219–242. [Google Scholar] [CrossRef]
- Zhou, Y. Sampling frequency for monitoring the actual state of groundwater systems. J. Hydrol. 1996, 180, 301–318. [Google Scholar] [CrossRef]
- Dixon, W.; Chiswell, B. Review of aquatic monitoring program design. Water Res. 1996, 30, 1935–1948. [Google Scholar] [CrossRef]
- Charles, G.H. Relationships between total phosphorus concentrations, sampling frequency, and wind velocity in a shallow, Polymictic Lake. Lake Reserv. Manag. 1999, 15, 39–46. [Google Scholar] [CrossRef][Green Version]
- Ning, S.K.; Chang, N.B. Multi-objective, decision-based assessment of a water quality monitoring network in a river system. J. Environ. Monit. 2002, 4, 121–126. [Google Scholar] [CrossRef]
- Su-Young, P.; Jung, H.C.; Sookyun, W.; Seok, S.P. Design of a water quality monitoring network in a large river system using the genetic algorithm. Ecol. Model. 2006, 199, 289–297. [Google Scholar] [CrossRef]
- Loftis, J.C.; Ward, R.C. Sampling frequency selection for regulatory water quality monitoring. J. Am. Water Resour. Assoc. 2007, 16, 501–507. [Google Scholar] [CrossRef]
- Harmancioglu, N.B.; Alpaslan, N. Water quality monitoring network design: A problem of multiobjective decision making. Water Resour. Bull. 1992, 28, 179–192. [Google Scholar] [CrossRef]
- Hudak, P.F.; Loaiciga, H.A.; Marino, M.A. Regional-scale ground water quality monitoring via integer programming. J. Hydrol. 1995, 164, 153–170. [Google Scholar] [CrossRef]
- Cieniawski, S.E.; Eheart, J.W.; Ranjithan, S. Using genetic algorithms to solve a multiobjective groundwater monitoring problem. Water Resour. Res. 1995, 31, 399–410. [Google Scholar] [CrossRef]
- Strobl, R.O.; Robillard, P.D. Network design for water quality monitoring of surface freshwaters: A review. J. Environ. Manag. 2008, 87, 639–648. [Google Scholar] [CrossRef] [PubMed]
- UNEP/WHO. Water Quality Monitoring—A Practical Guide to the Design and Implementation of Freshwater Quality Studies and Monitoring Programmes; Bartram, J., Balance, R., Eds.; United Nations Environment Programme (UNEP)/The World Health Organization (WHO): Nairobi, Kenya; Geneva, Switzerland, 1996; ISBN 0 419 22320 7 (Hbk); 0 419 21730 4 (Pbk). [Google Scholar]
- Timmerman, J.G.; Adriaanse, M.; Breukel, R.M.A.; Van Oirschot, M.C.M.; Ottens, J.J. Guidelines for water quality monitoring and assessment of transboundary rivers. Eur. Water Pollut. Control 1997, 7, 21–30. [Google Scholar]
- Dixon, W.; Smyth, G.K.; Chiswell, B. Optimized selection of river sampling sites. Water Res. 1999, 33, 971–978. [Google Scholar] [CrossRef]
- Khalil, B.; Ouarda, T.B. Statistical approaches used to assess and redesign surface water-quality-monitoring networks. J. Environ. Monit. 2009, 11, 1915–1929. [Google Scholar] [CrossRef]
- World Meteorological Organization. Planning of Water Quality Monitoring System; Technical Report; Series No. 3; World Meteorological Organization: Geneva, Switzerland, 2013; ISBN 978-92-63-11113-5. [Google Scholar]
- Kaya, I.; Kahraman, C. Multicriteria decision making in energy planning using a modified fuzzy TOPSIS methodology. Expert Syst. Appl. 2011, 38, 6577–6585. [Google Scholar] [CrossRef]
- Huu, T.D.; Shang-Lien, L.; Lan Anh, P.T. Calculating of river water quality sampling frequency by the analytic hierarchy process (AHP). Environ. Monit. Assess. 2013, 185, 909–916. [Google Scholar] [CrossRef]
- Holnicki, P.; Nahorski, Z.; Żochowski, A. Modelling of Environment Processes; Wydawnictwo Wyższej Szkoły Informatyki Stosowanej i Zarządzania: Warszawa, Poland, 2000. [Google Scholar]
- Balcerzak, W. Application of selected mathematical models to evaluate changes in water quality. In Proceedings of the International Conference on Water Supply, Water Quality and Protection, Kraków, Poland, 7–9 September 2000. [Google Scholar]
- Al-Khafaji, M.S.; Abdulraheem, Z.A. A deterministic algorithm for determination of optimal water quality monitoring stations. Water Resour. Manag. 2017, 31, 3575–3592. [Google Scholar] [CrossRef]
- WMO (World Metrological Organization). Guide to Hydrological Practice, 6th ed.; No. 168; World Metrological Organization: Geneva, Switzerland, 2008; Volume I. [Google Scholar]
- Alhamdani, J.S. Location of Outlet and Operation of the West Part of Al-Hammar Marsh. Ph.D. Thesis, University of Baghdad, Baghdad, Iraq, 2014. [Google Scholar]
- Iraqi Ministry of Environment. New Eden Master Plan for the Integrated Water Resources Management in the Marshland Area, Marshlands, Book 4; Iraqi Ministries of Environment, Water Resources Municipalities and Public Works with cooperation of the Italian Ministry for the Environment and Territory and Free Iraq Foundation: Baghdad, Iraq, 2006; p. 130. [Google Scholar]
- Al-Gburi, H.F.; Al-Tawash, B.S.; Al-Lafta, H.S. Environmental assessment of Al-Hammar Marsh, Southern Iraq. Heliyon 2017, 3, e00256. [Google Scholar] [CrossRef]
- Al-Musawi, N.O.; Al-Obaidi, S.K.; Al-Rubaie, F.M. Evaluating Water Quality Index of Al Hammar Marsh, South of Iraq with the Application of GIS Technique. J. Eng. Sci. Technol. 2018, 13, 4118–4130. [Google Scholar]
- APHA. Standard Methods, The Examination of Water and Wastewater, 22nd ed.; APHY: Washington, DC, USA, 2012; p. 1496. [Google Scholar]
- Young, J.C.; Mcdermott, G.N.; Jenkins, D. Alterations in the bod procedure for the 15th edition of standard methods for the examination of water and wastewater. J. Water Pollut. Control Fed. 1981, 53, 1253–1259. [Google Scholar]
- Harris, D.C. Quantitative Chemical Analysis, 4th ed.; W.H Freeman and Company: New York, NY, USA, 1995; Chapter 21. [Google Scholar]
- Raghavan, R.; Raha, S. A rapid turbidimetric method for the determination of total Sulphur in zinc concentrate. Talanta 1991, 38, 525–528. [Google Scholar] [CrossRef]
- Armstrong, F.A.J. Determination of nitrate in water by ultraviolet spectrophotometry. Anal. Chem. 1963, 35, 1292–1294. [Google Scholar] [CrossRef]
- Soltani, F.; Kerachian, R.; Shirangi, E. Developing operating rules for reservoirs considering the water quality issues: Application of ANFIS-based surrogate models. Expert Syst. Appl. 2010, 37, 6639–6645. [Google Scholar] [CrossRef]
- Donnell, B.P.; Letter, J.V.; McAnally, W.H. User Guide to WES-RMA2 Version 4.5; Waterways Experiment Station, Costal and Hydraulics Laboratory: Davis, CA, USA, 2004. [Google Scholar]
- Peuquet, D.J.; Duan, N. An event-based spatio-temporal data model (ESTDM) for temporal analysis of geographic data. Int. J. Geogr. Inf. Syst. 1995, 9, 2–24. [Google Scholar] [CrossRef]
- Peuquet, D.J.; Wentz, E. An approach for time-based analysis of spatio-temporal data. In Proceedings of the Sixth International Symposium on Spatial Data Handling, Edinburgh, UK, 5–9 September 1994; International Geographical Union: London, UK, 1994; pp. 489–504. [Google Scholar]
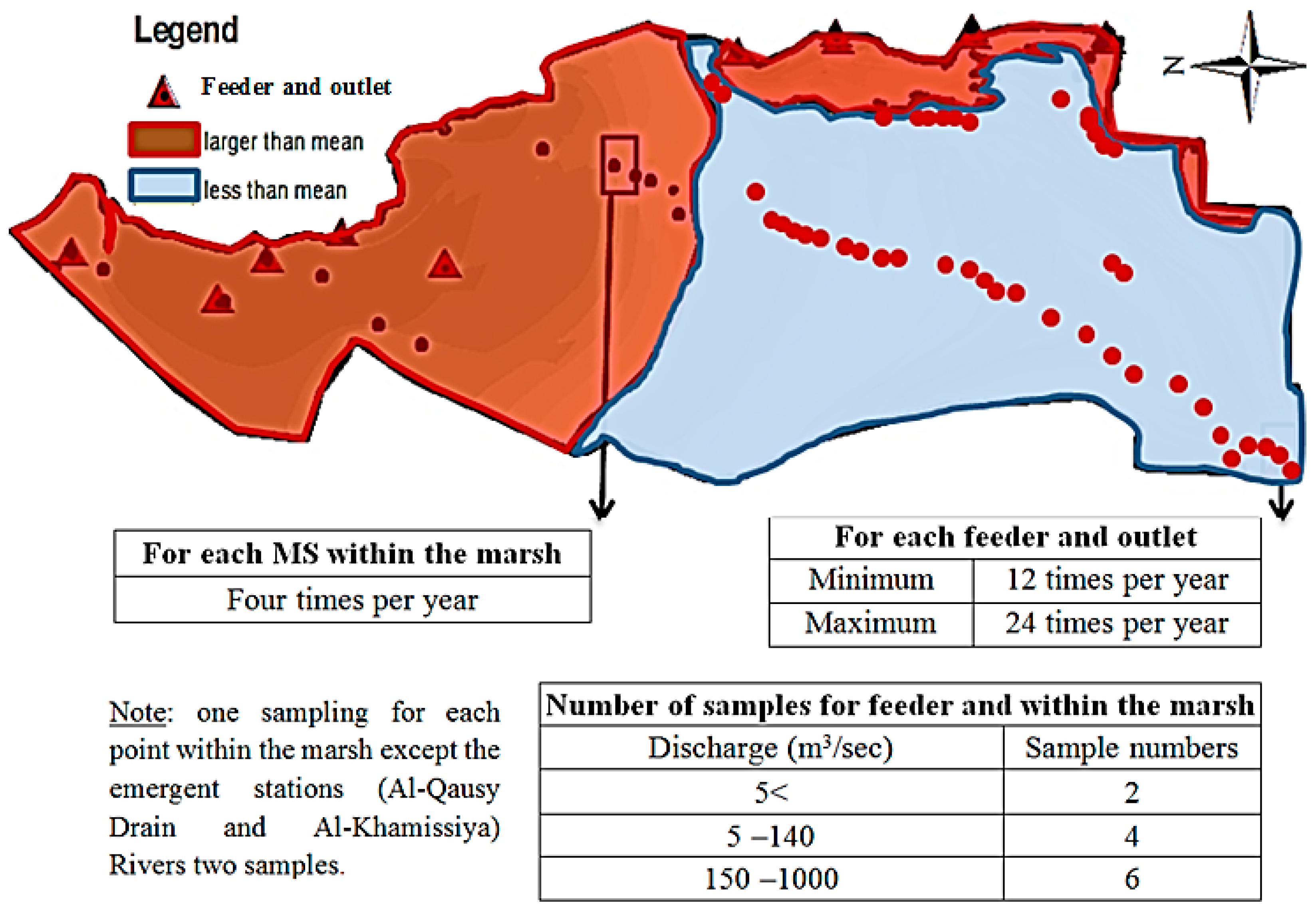
| Water Body | Sampling Frequency | |
|---|---|---|
| Baseline stations | Streams | Minimum: four per year, including high- and low-water stages. Optimum: 24 per year (every second week); weekly for total suspended solids. |
| Headwater lakes | Minimum: one per year at turnover; sampling at lake outlet. Optimum: one per year at turnover, and one vertical profile at the end of stratification season. | |
| Trend stations | Rivers | Minimum: 12 per year for large drainage areas (approximately 100,000 km2). Maximum: 24 per year for small drainage areas (approximately 10,000 km2). |
| Lakes and reservoirs | For issues other than eutrophication: Minimum: one per year at turnover. Maximum: two per year at turnover, and one at maximum thermal stratification. For eutrophication: 12 per year, including twice monthly during the summer. | |
| Groundwater | Minimum: one per year for large, stable aquifers. Maximum: four per year for small, alluvial aquifers. Karst aquifers: same as rivers. | |
| Case No. | Discharge (m3/sec) | WSE (m a.s.l.) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| BC3 | BC4 | FBC3 | FBC4 | FW | Um Nakhla | Al-Kurmashia | Al-Qausy Drain | Al-Hamedy | Al-Khamissiya | Hammar Outlet | |
| 1 | 3.93 | 3.83 | 4.60 | 5.50 | 10.00 | 6.85 | 3.85 | 29.63 | 5.30 | 56.55 | 1.90 |
| 2 | 3.93 | 3.83 | 4.60 | 5.50 | 10.00 | 6.85 | 3.85 | 29.63 | 5.30 | 26.38 | 1.90 |
| 3 | 3.93 | 3.83 | 4.60 | 5.50 | 10.00 | 6.85 | 3.85 | 29.63 | 5.30 | 9.70 | 1.90 |
| 4 | 1.82 | 2.19 | 1.87 | 1.95 | 2.08 | 3.14 | 1.76 | 13.25 | 1.97 | 56.55 | 1.90 |
| 5 | 1.82 | 2.19 | 1.87 | 1.95 | 2.08 | 3.14 | 1.76 | 13.25 | 1.97 | 26.38 | 1.90 |
| 6 | 1.82 | 2.19 | 1.87 | 1.95 | 2.08 | 3.14 | 1.76 | 13.25 | 1.97 | 9.70 | 1.90 |
| 7 | 0.43 | 0.50 | 0.50 | 0.45 | 0.35 | 0.85 | 0.35 | 3.00 | 0.20 | 56.55 | 1.90 |
| 8 | 0.43 | 0.50 | 0.50 | 0.45 | 0.35 | 0.85 | 0.35 | 3.00 | 0.20 | 26.38 | 1.90 |
| 9 | 0.43 | 0.50 | 0.50 | 0.45 | 0.35 | 0.85 | 0.35 | 3.00 | 0.20 | 9.70 | 1.90 |
| 10 | 3.93 | 3.83 | 4.60 | 5.50 | 10.00 | 6.85 | 3.85 | 29.63 | 5.30 | 56.55 | 1.67 |
| 11 | 3.93 | 3.83 | 4.60 | 5.50 | 10.00 | 6.85 | 3.85 | 29.63 | 5.30 | 26.38 | 1.67 |
| 12 | 3.93 | 3.83 | 4.60 | 5.50 | 10.00 | 6.85 | 3.85 | 29.63 | 5.30 | 9.70 | 1.67 |
| 13 | 1.82 | 2.19 | 1.87 | 1.95 | 2.08 | 3.14 | 1.76 | 13.25 | 1.97 | 56.55 | 1.67 |
| 14 | 1.82 | 2.19 | 1.87 | 1.95 | 2.08 | 3.14 | 1.76 | 13.25 | 1.97 | 26.38 | 1.67 |
| 15 | 1.82 | 2.19 | 1.87 | 1.95 | 2.08 | 3.14 | 1.76 | 13.25 | 1.97 | 9.70 | 1.67 |
| 16 | 0.43 | 0.50 | 0.50 | 0.45 | 0.35 | 0.85 | 0.35 | 3.00 | 0.20 | 56.55 | 1.67 |
| 17 | 0.43 | 0.50 | 0.50 | 0.45 | 0.35 | 0.85 | 0.35 | 3.00 | 0.20 | 26.38 | 1.67 |
| 18 | 0.43 | 0.50 | 0.50 | 0.45 | 0.35 | 0.85 | 0.35 | 3.00 | 0.20 | 9.70 | 1.67 |
| 19 | 3.93 | 3.83 | 4.60 | 5.50 | 10.00 | 6.85 | 3.85 | 29.63 | 5.30 | 56.55 | 1.35 |
| 20 | 3.93 | 3.83 | 4.60 | 5.50 | 10.00 | 6.85 | 3.85 | 29.63 | 5.30 | 26.38 | 1.35 |
| 21 | 3.93 | 3.83 | 4.60 | 5.50 | 10.00 | 6.85 | 3.85 | 29.63 | 5.30 | 9.70 | 1.35 |
| 22 | 1.82 | 2.19 | 1.87 | 1.95 | 2.08 | 3.14 | 1.76 | 13.25 | 1.97 | 56.55 | 1.35 |
| 23 | 1.82 | 2.19 | 1.87 | 1.95 | 2.08 | 3.14 | 1.76 | 13.25 | 1.97 | 26.38 | 1.35 |
| 24 | 1.82 | 2.19 | 1.87 | 1.95 | 2.08 | 3.14 | 1.76 | 13.25 | 1.97 | 9.70 | 1.35 |
| 25 | 0.43 | 0.50 | 0.50 | 0.45 | 0.35 | 0.85 | 0.35 | 3.00 | 0.20 | 56.55 | 1.35 |
| 26 | 0.43 | 0.50 | 0.50 | 0.45 | 0.35 | 0.85 | 0.35 | 3.00 | 0.20 | 26.38 | 1.35 |
| 27 | 0.43 | 0.50 | 0.50 | 0.45 | 0.35 | 0.85 | 0.35 | 3.00 | 0.20 | 9.70 | 1.35 |
| 28 | 3.93 | 3.83 | 4.60 | 5.50 | 10.00 | 6.85 | 3.85 | 29.63 | 5.30 | 0.00 | 1.90 |
| 29 | 1.82 | 2.19 | 1.87 | 1.95 | 2.08 | 3.14 | 1.76 | 13.25 | 1.97 | 0.00 | 1.67 |
| 30 | 0.43 | 0.50 | 0.50 | 0.45 | 0.35 | 0.85 | 0.35 | 3.00 | 0.20 | 0.00 | 1.35 |
| Case No. | TDS (ppm) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| BC3 | BC4 | FBC3 | FBC4 | FW | Um Nakhla | Al-Kurmashia | Al-Qausy Drain | Al-Hamedy | Al-Khamissiya | |
| 1 | 2130 | 2979 | 1790 | 1790 | 1790 | 1622 | 1618 | 3575 | 3319 | 3050 |
| 2 | 2130 | 2979 | 1790 | 1790 | 1790 | 1622 | 1618 | 3575 | 3319 | 4776 |
| 3 | 2130 | 2979 | 1790 | 1790 | 1790 | 1622 | 1618 | 3575 | 3319 | 7012 |
| 4 | 3299 | 4749 | 2879 | 2879 | 2879 | 2879 | 2879 | 5310 | 5624 | 3050 |
| 5 | 3299 | 4749 | 2879 | 2879 | 2879 | 2879 | 2879 | 5310 | 5624 | 4776 |
| 6 | 3299 | 4749 | 2879 | 2879 | 2879 | 2879 | 2879 | 5310 | 5624 | 7012 |
| 7 | 5155 | 8232 | 6750 | 6750 | 6750 | 6750 | 6750 | 8791 | 9102 | 3050 |
| 8 | 5155 | 8232 | 6750 | 6750 | 6750 | 6750 | 6750 | 8791 | 9102 | 4776 |
| 9 | 5155 | 8232 | 6750 | 6750 | 6750 | 6750 | 6750 | 8791 | 9102 | 7012 |
| 10 | 2130 | 2979 | 1790 | 1790 | 1790 | 1622 | 1618 | 3575 | 3319 | 3050 |
| 11 | 2130 | 2979 | 1790 | 1790 | 1790 | 1622 | 1618 | 3575 | 3319 | 4776 |
| 12 | 2130 | 2979 | 1790 | 1790 | 1790 | 1622 | 1618 | 3575 | 3319 | 7012 |
| 13 | 3299 | 4749 | 2879 | 2879 | 2879 | 2879 | 2879 | 5310 | 5624 | 3050 |
| 14 | 3299 | 4749 | 2879 | 2879 | 2879 | 2879 | 2879 | 5310 | 5624 | 4776 |
| 15 | 3299 | 4749 | 2879 | 2879 | 2879 | 2879 | 2879 | 5310 | 5624 | 7012 |
| 16 | 5155 | 8232 | 6750 | 6750 | 6750 | 6750 | 6750 | 8791 | 9102 | 3050 |
| 17 | 5155 | 8232 | 6750 | 6750 | 6750 | 6750 | 6750 | 8791 | 9102 | 4776 |
| 18 | 5155 | 8232 | 6750 | 6750 | 6750 | 6750 | 6750 | 8791 | 9102 | 7012 |
| 19 | 2130 | 2979 | 1790 | 1790 | 1790 | 1622 | 1618 | 3575 | 3319 | 3050 |
| 20 | 2130 | 2979 | 1790 | 1790 | 1790 | 1622 | 1618 | 3575 | 3319 | 4776 |
| 21 | 2130 | 2979 | 1790 | 1790 | 1790 | 1622 | 1618 | 3575 | 3319 | 7012 |
| 22 | 3299 | 4749 | 2879 | 2879 | 2879 | 2879 | 2879 | 5310 | 5624 | 3050 |
| 23 | 3299 | 4749 | 2879 | 2879 | 2879 | 2879 | 2879 | 5310 | 5624 | 4776 |
| 24 | 3299 | 4749 | 2879 | 2879 | 2879 | 2879 | 2879 | 5310 | 5624 | 7012 |
| 25 | 5155 | 8232 | 6750 | 6750 | 6750 | 6750 | 6750 | 8791 | 9102 | 3050 |
| 26 | 5155 | 8232 | 6750 | 6750 | 6750 | 6750 | 6750 | 8791 | 9102 | 4776 |
| 27 | 5155 | 8232 | 6750 | 6750 | 6750 | 6750 | 6750 | 8791 | 9102 | 7012 |
| 28 | 2130 | 2979 | 1790 | 1790 | 1790 | 1622 | 1618 | 3575 | 3319 | 3050 |
| 29 | 3299 | 4749 | 2879 | 2879 | 2879 | 2879 | 2879 | 5310 | 5624 | 3050 |
| 30 | 5155 | 8232 | 6750 | 6750 | 6750 | 6750 | 6750 | 8791 | 9102 | 7012 |
| Point No. | Location | Flow Velocity (m/sec) | Depth (m) | TDS (ppm) | |
|---|---|---|---|---|---|
| E | N | ||||
| 1 | 735,739 | 3,413,844 | 0.014 | 1.25 | 3603 |
| 2 | 640,266 | 3,411,446 | 0.031 | 1.25 | 3280 |
| 3 | 640,674 | 3,412,158 | 0.016 | 1.11 | 4046 |
| 4 | 641,115 | 3,412,073 | 0.027 | 1.40 | 4041 |
| 5 | 642,122 | 3,411,965 | 0.021 | 1.31 | 4041 |
| 6 | 641,479 | 3,411,141 | 0.017 | 0.75 | 3355 |
| 7 | 649,680 | 3,410,178 | 0.031 | 0.90 | 3525 |
| 8 | 653,389 | 3,410,968 | 0.024 | 0.75 | 1930 |
| 9 | 657,249 | 3,410,967 | 0.016 | 1.56 | 3543 |
| 10 | 657,072 | 3,410,796 | 0.008 | 2.80 | 3669 |
| 11 | 656,077 | 3,410,371 | 0.012 | 0.97 | 2802 |
| 12 | 655,028 | 3,410,202 | 0.028 | 0.93 | 3495 |
| 13 | 654,336 | 3,409,881 | 0.036 | 0.74 | 3700 |
| 14 | 653,581 | 3,409,873 | 0.031 | 1.84 | 3575 |
| 15 | 653,351 | 3,409,814 | 0.032 | 0.95 | 3609 |
| 16 | 652,953 | 3,410,096 | 0.029 | 1.24 | 3635 |
| 17 | 652,563 | 3,409,957 | 0.035 | 1.70 | 3640 |
| 18 | 652,055 | 3,409,220 | 0.031 | 1.06 | 4190 |
| 19 | 651,566 | 3,408,521 | 0.026 | 1.03 | 4250 |
| 20 | 650,961 | 3,408,808 | 0.024 | 0.58 | 4135 |
| 21 | 650,269 | 3,409,260 | 0.030 | 0.47 | 4076 |
| 22 | 649,773 | 3,409,601 | 0.029 | 1.06 | 4122 |
| 23 | 649,224 | 3,409,558 | 0.033 | 0.60 | 4190 |
| 24 | 648,657 | 3,409,673 | 0.031 | 1.02 | 4116 |
| 25 | 647,783 | 3,409,460 | 0.024 | 1.09 | 4297 |
| 26 | 646,142 | 3,409,343 | 0.023 | 0.64 | 4396 |
| 27 | 640,266 | 3,411,446 | 0.021 | 1.25 | 3280 |
| 28 | 640,674 | 3,412,158 | 0.020 | 1.11 | 4046 |
| 29 | 641,115 | 3,412,073 | 0.020 | 1.40 | 4041 |
| 30 | 642,122 | 3,411,965 | 0.023 | 1.31 | 4041 |
| 31 | 641,479 | 3,411,141 | 0.026 | 0.75 | 3355 |
| Station | Date | Discharge (m3/sec) | TDS (ppm) |
|---|---|---|---|
| BC3 | 3/5/2015 | 1.63 | 3151 |
| BC4 | 3/5/2015 | 1.52 | 3040 |
| FBC3 | 3/5/2015 | 1.81 | 3048 |
| FBC4 | 3/5/2015 | 2.26 | 2079 |
| FW | 3/5/2015 | 4.01 | 2454 |
| Um Nakhla | 4/5/2015 | 2.35 | 4350 |
| Al-Kurmashia | 4/5/2015 | 1.52 | 3318 |
| Al-Qausy Drain | 3/5/2015 | 3.32 | 8791 |
| Al-Hamedy | 4/5/2015 | 2.16 | 3236 |
| Al-Khamissiya | 4/5/2015 | 29.42 | 6635 |
| Outlet pipes | 3/5/2015 | 47.26 (water level = 1.56 m a.s.l.) | 9000 |
| BC3 | 27/5/2015 | 1.60 | 3240 |
| BC4 | 27/5/2015 | 1.54 | 3122 |
| FBC3 | 27/5/2015 | 1.78 | 3036 |
| FBC4 | 27/5/2015 | 2.22 | 2127 |
| FW | 27/5/2015 | 3.26 | 3025 |
| Um Nakhla | 28/5/2015 | 2.83 | 3850 |
| Al-Kurmashia | 28/5/2015 | 1.75 | 2800 |
| Al-Qausy Drain | 27/5/2015 | 3.60 | 8695 |
| Al-Hamedy | 28/5/2015 | 3.04 | 3314 |
| Al-Khamissiya | 28/5/2015 | 11.8 | 6817 |
| Outlet pipes | 27/5/2015 | 32.40 (water level = 1.48 m a.s.l.) | 8904 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Khafaji, M.S. Deterministic Methodology for Determining the Optimal Sampling Frequency of Water Quality Monitoring Systems. Hydrology 2019, 6, 94. https://doi.org/10.3390/hydrology6040094
Al-Khafaji MS. Deterministic Methodology for Determining the Optimal Sampling Frequency of Water Quality Monitoring Systems. Hydrology. 2019; 6(4):94. https://doi.org/10.3390/hydrology6040094
Chicago/Turabian StyleAl-Khafaji, Mahmoud Saleh. 2019. "Deterministic Methodology for Determining the Optimal Sampling Frequency of Water Quality Monitoring Systems" Hydrology 6, no. 4: 94. https://doi.org/10.3390/hydrology6040094
APA StyleAl-Khafaji, M. S. (2019). Deterministic Methodology for Determining the Optimal Sampling Frequency of Water Quality Monitoring Systems. Hydrology, 6(4), 94. https://doi.org/10.3390/hydrology6040094





