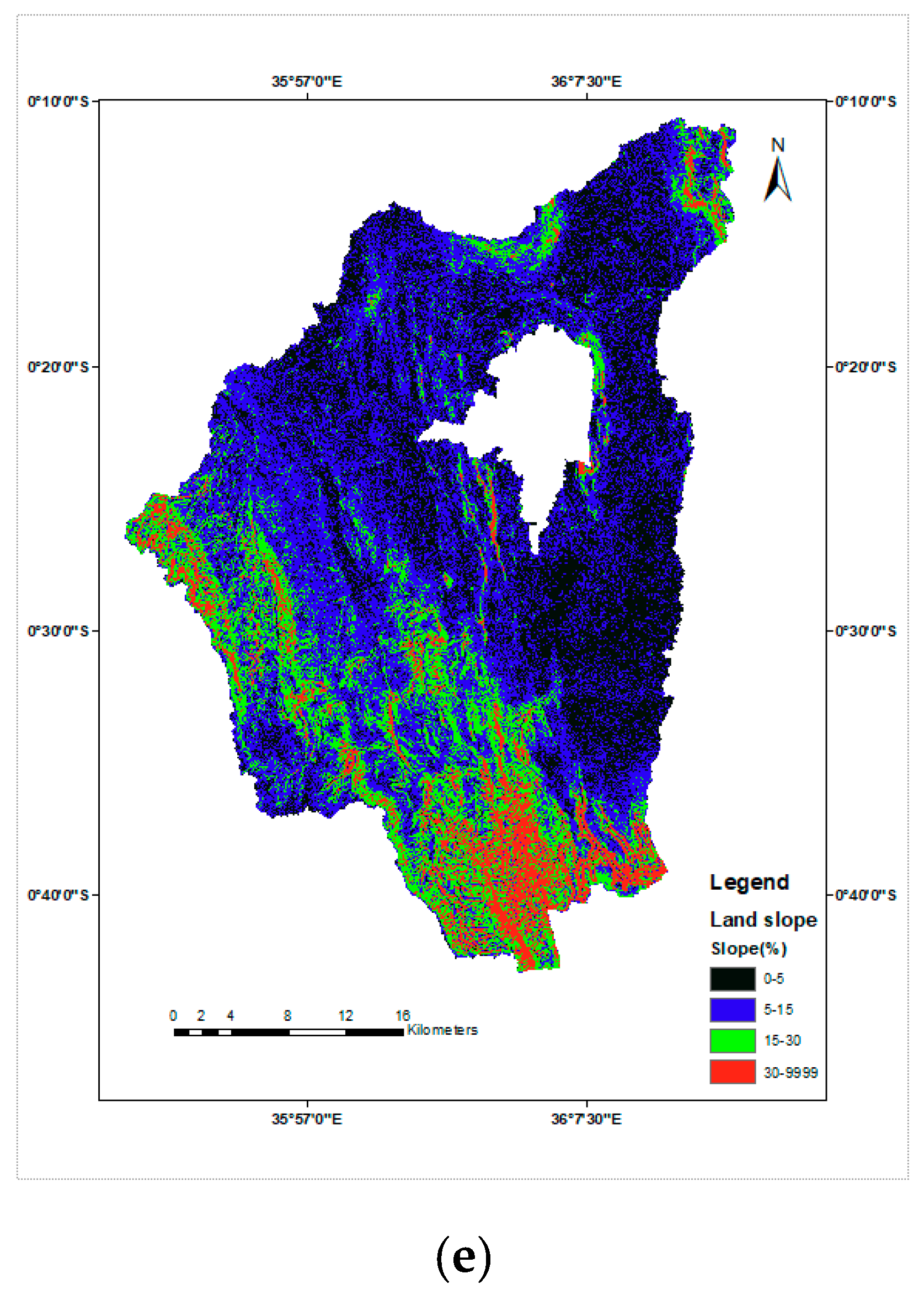
1. Introduction
Changes in the spatial configuration of runoff can occur as a result of changes in the spatial distribution and temporal variability of atmospheric precipitation, which are linked to climate change. Runoff, therefore, becomes a product of the interaction between climate and changes in land use in a basin [
1]. A water balance study of the Volta Basin in West Africa confirmed that runoff was extremely sensitive to precipitation [
2]. Rainfall exhibits high spatial and temporal variability globally and is one of the climatic factors affecting temporal patterns of water availability. The variability of rainfall can pose a major risk to water resources and reservoirs due to flooding, which impacts the population and properties in the basin [
3].The variability is attributed to climate variability, whose impact on water resources in terms of flooding or drought is felt globally [
4]. The likelihood of extreme drought or flooding is determined by a temporal variability analysis of rainfall and river discharges at defined timescales. This becomes necessary for enhancing water resource management, agriculture production, planning and designing hydraulic structures, and mitigating the negative effects of flooding [
5,
6]. Information on the temporal patterns of rainfall runoff is obtained by carrying out an analysis of historical datasets, which gives timely warnings to allow people to cope with or mitigate the negative effects of floods and droughts caused by climate change.
Hydrological models such as the hydrologic modeling system (HEC-HMS) [
7,
8], the Australian water balance model (AWBM) [
9], the soil moisture accounting and routing (SMAR) model [
10], the topography-based hydrological model (TOPMODEL) [
11,
12] and the soil and water assessment tool (SWAT) [
13] are useful for simulating the runoff from ungauged catchment based on the data availability and complexity of the hydrological system. Many studies have demonstrated that SWAT is an effective and promising tool to use for simulating flows and sediments for large-scale watersheds and complex basins with different land uses and various soil types (Access et al. [
14], Brouziyne et al. [
15], Palani et al. [
16], Amatya et al. [
17], and Tri et al. [
18], among others). The advantages of using SWAT include its applicability to larger watersheds with more than 100 km
2, its interface with a geographic information system (GIS), its ability to perform continuous simulations, and its ability to characterize a watershed in high spatial detail [
19].
Drought is categorized into four major types: agricultural, hydrological, meteorological, and socioeconomic. Meteorological drought occurs when precipitation is below normal based on its long-term average, while hydrological drought occurs when the surface water level or groundwater is low compared to the long-term average [
20]. Various indices are used to assess meteorological drought and hydrological drought, such as the rainfall anomaly index (RAI), deciles index (DI), drought area index (DAI), standardized precipitation index (SPI), standardized precipitation evaporation index (SPEI), surface humidity index, Palmer drought severity index (PDSI), and streamflow drought index (SDI) [
21,
22,
23]. Among the indices, SPI and SPEI are two outstanding meteorological drought indices used as descriptor(s) of rainfall variability, while SDI is a hydrological drought index. SPI and SPEI are described by Gurrapu et al. [
24] as multi-scale indices with the advantage of identifying the multitemporal nature of droughts. Okpara and Tarhule rank SPI first among the three drought indices evaluated in the Niger Basin of West Africa, describing it as robust and sensitive to dryness [
25]. SPI, developed by Mckee [
26], has the advantage of providing early warning of drought; it can be computed at different timescales, helps in assessing drought severity, and is not as complex as the Palmer index [
27]. The index also gives better spatial standardization in comparison to other drought indices such as PDSI [
28]. The SPI at one- and three-month timescales reflects short-term moisture conditions, while the six- and nine-month timescales reflect medium trends in rainfall. The SPI of the 12-month timescale reflects long-term precipitation patterns and is possibly tied to streamflow, reservoir levels, and groundwater levels [
29]. SPI is solely based on precipitation and ignores the role of evaporation; due to this limitation, SPEI was developed to complement the SPI drought index since it incorporates the effect of potential evaporation [
30]. SDI makes similar calculations to SPI and is widely used due to its simplicity and efficiency [
22].
Lake Nakuru undergoes major fluctuations, sometimes drying up completely [
31]. The lake experienced a prolonged drying period and falling water levels from the mid-1980s through 1996, and had associated increases in water salinity. The lake dried up completely in 1995 and 1996, resulting in most birds disappearing and tourism being greatly diminished. Following extreme El Niño-driven flooding in 1997 and 1998, the lake levels rebounded. Flamingoes returned in 2000, but were fewer in number than before [
32]. According to [
33], the lake has shown increasing water levels since 2011. This resulted in an increase in its flood area from a low area of 31.8 km
2 in January 2010 to a high of 54.67 km
2 in September 2013, corresponding to a 71.92% increase in area. Landsat images were used to determine the lake’s surface variations from 1984 to 2013 [
34]. The lake surface area had a steady increase of between 30.48 km
2 in November 2009 to 57.55 km
2 in January 2014—an increase of 27.09 km
2 or 88.94%. The lake swelled in 2013, submerging old buildings that had been abandoned. The negative effects of flooding translate to economic losses due to reduced tourism following reduced numbers of flamingoes and the loss of constructed buildings. There is limited information on rainfall variability within the Lake Nakuru Basin, and no study has investigated the variability in the streamflow into the lake.
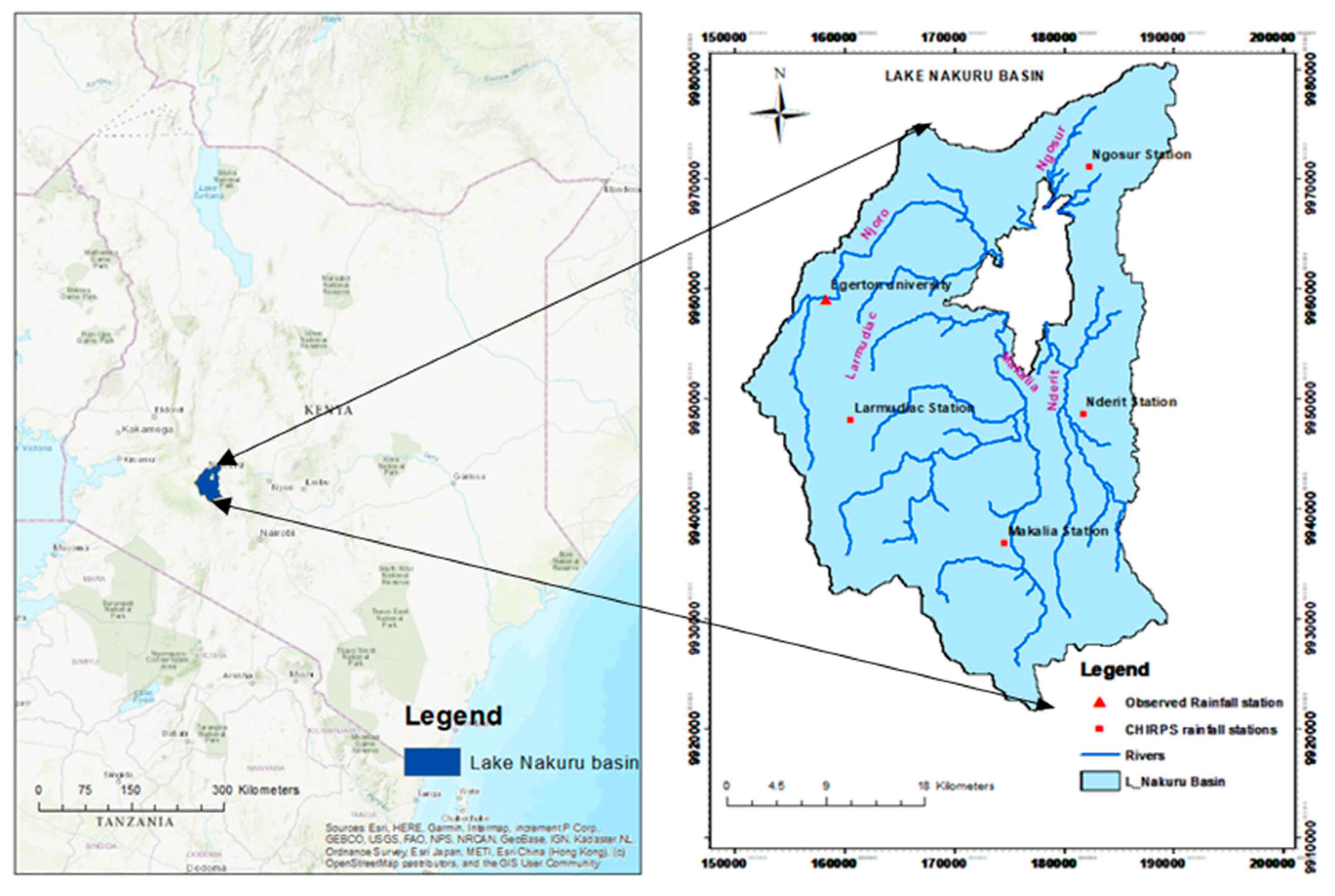
The objectives of the study were: (i) to simulate flow from the gauged subcatchment (Njoro) and ungauged subcatchments (Ngosur, Nderit, Larmudiac, and Makalia); (ii) to calculate the meteorological (SPI and SPEI) and hydrological (SDI) drought indices for the description of rainfall and streamflow variability at the 12-month scale; and (iii) to compare the results of SPI and SDI at the catchment scale and in individual subcatchments.
3. Results and Discussion
3.1. Rainfall Analysis for Lake Nakuru Catchment
3.1.1. Station (KE0863) and CHIRPS Rainfall Data Comparison
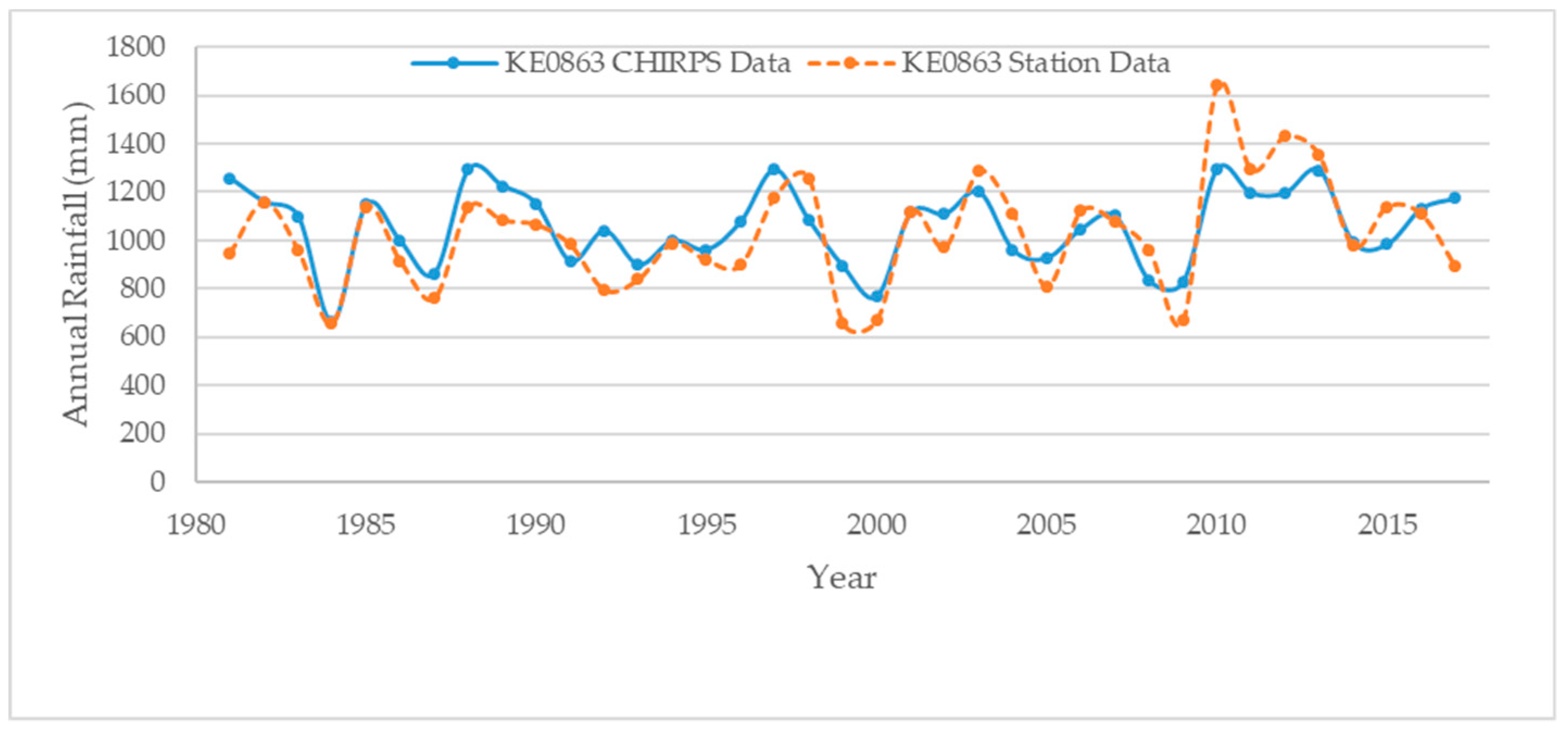
Figure 6 shows the results for a comparison between the CHIRPS gridded rainfall data and KE0863 station data at an annual scale for 1981 to 2017. The percentage bias (PBIAS) indicated an overestimation of the rainfall data at the station (2.4%), which is acceptable since it is within the range of ± 25). The Pearson correlation coefficient (r) value was 0.67, which is fulfills the requirement of r > 0.5 [
58]. The results agreed with Ayugi et al.’s study [
38], in which CHIRPS data overestimated precipitation in both a low-altitude, humid climate and in arid and semi-arid land (ASAL) for annual analysis. A high correlation was also seen when comparing the annual patterns of CHIRPS data with ground-based observation stations for all the regions, with the value of (r) being greater than 0.91. The mean annual rainfall was 1029 mm and 1059 mm for the observed data at the station and the gridded CHIRPS data, respectively. In general, the observed statistical results for the comparison between CHIRPS data and observed data at the station showed a high agreement, and therefore the gridded data were used for further analysis.
3.1.2. Standardized Precipitation Index (SPI) and Standardized Precipitation Standardized Precipitation Evaporation Index (SPEI)
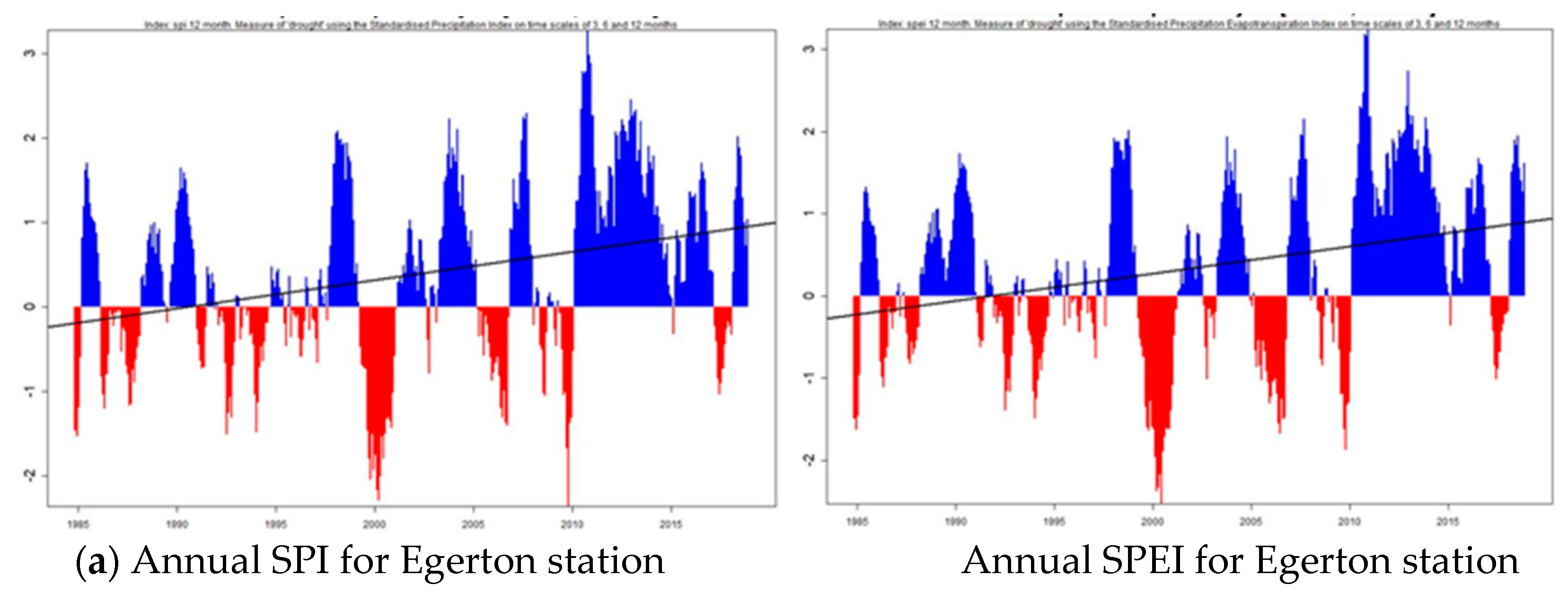
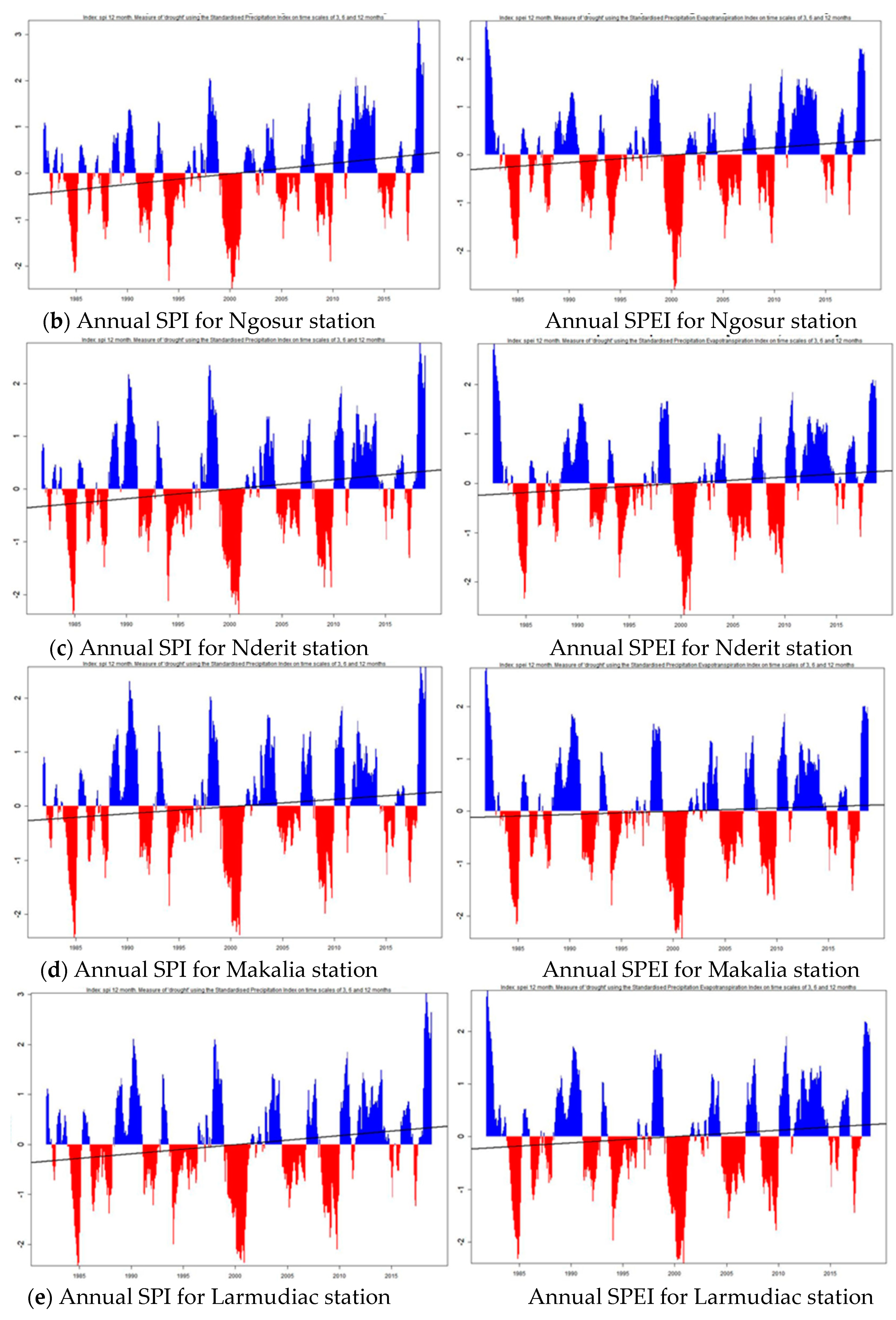
The results of both SPI and SPEI indices for the five subcatchments in Lake Nakuru Basin are as shown in
Figure 7a–e and summarized in
Table 5. The results in
Table 5 are from 1981 to 2018, with an emphasis on the 10-year period from 2009 to 2018. The results are very similar, with a higher frequency of wetter periods than drier periods being observed at Ngosur, Larmudiac, Makalia, and Nderit stations from 1981 to 2018. Egerton station (KE0863) recorded an equal distribution of wet and dry periods, with 50.00% positive anomalies and 50.00% negative anomalies. Ngosur station recorded 57.89% positive anomalies and 42.11% negative anomalies, while Nderit station recorded 55.26% wet periods and 44.74% dry periods. Larmudiac and Makalia stations experienced similar results, with 55.26% positive anomalies versus 44.74% negative anomalies. An analysis was also done for the last 10 years, which yielded similar recordings of the higher frequency of wet periods compared to dry periods. Egerton, Ngosur, Larmudiac, and Nderit stations recorded 70.00% wet periods and 30.00% dry periods, while Makalia station recorded 60.00% wet and 40.00% dry. The years 1984 and 2000 were seen as severely dry (SPI/SPEI < −2.00), while 2018 was observed to be severely wet (SPI/SPEI > 2.00) for the Ngosur, Nderit, Makalia, and Larmudiac subcatchments. The year 2010 was a severely wet year for Egerton University station. From the SPEI and SPI results shown in
Figure 7, 2010 to 2018 represented a period of wetter than normal rainfall and is the longest continuous wet period in the history of the data analyzed.
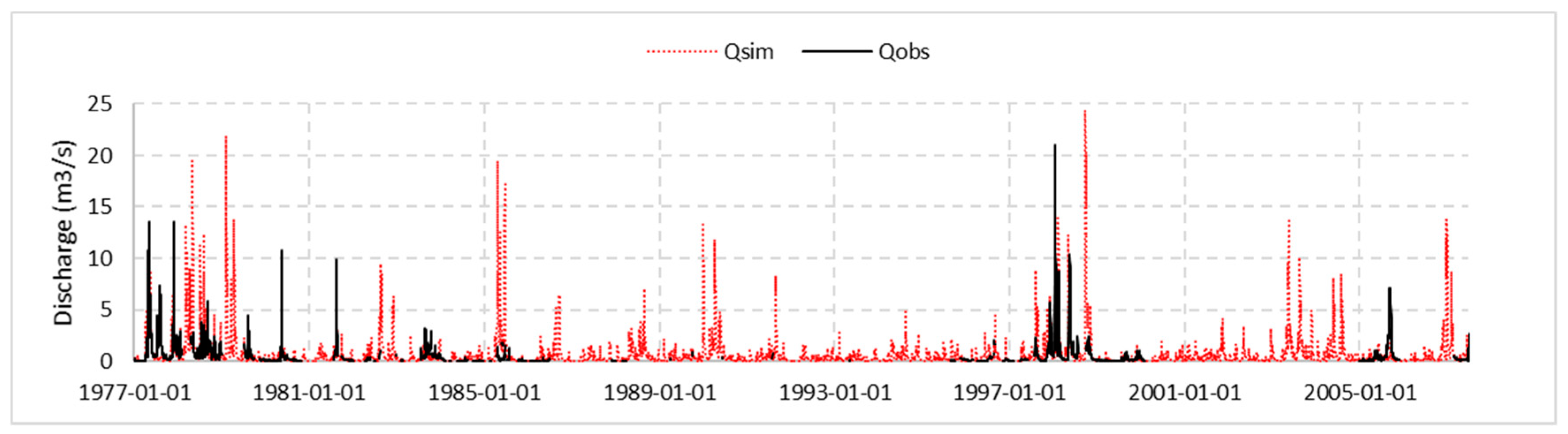
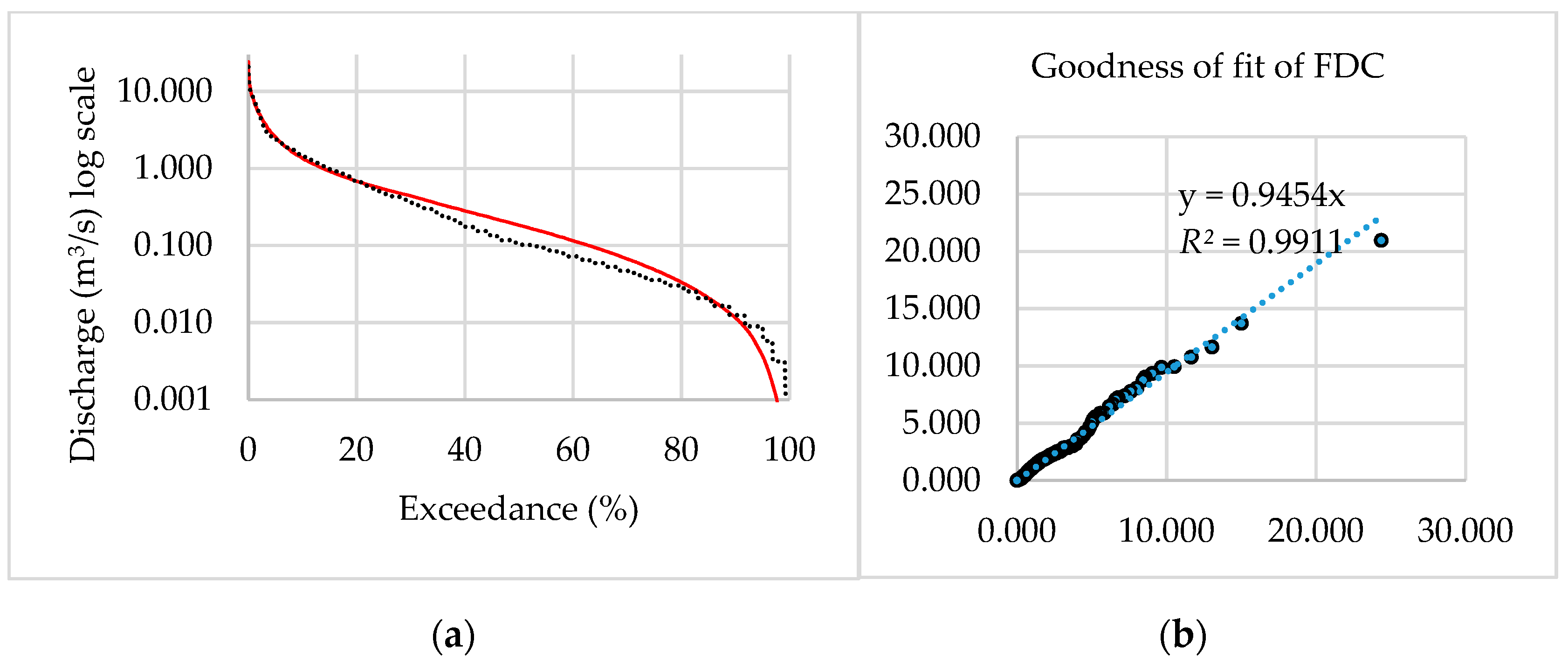
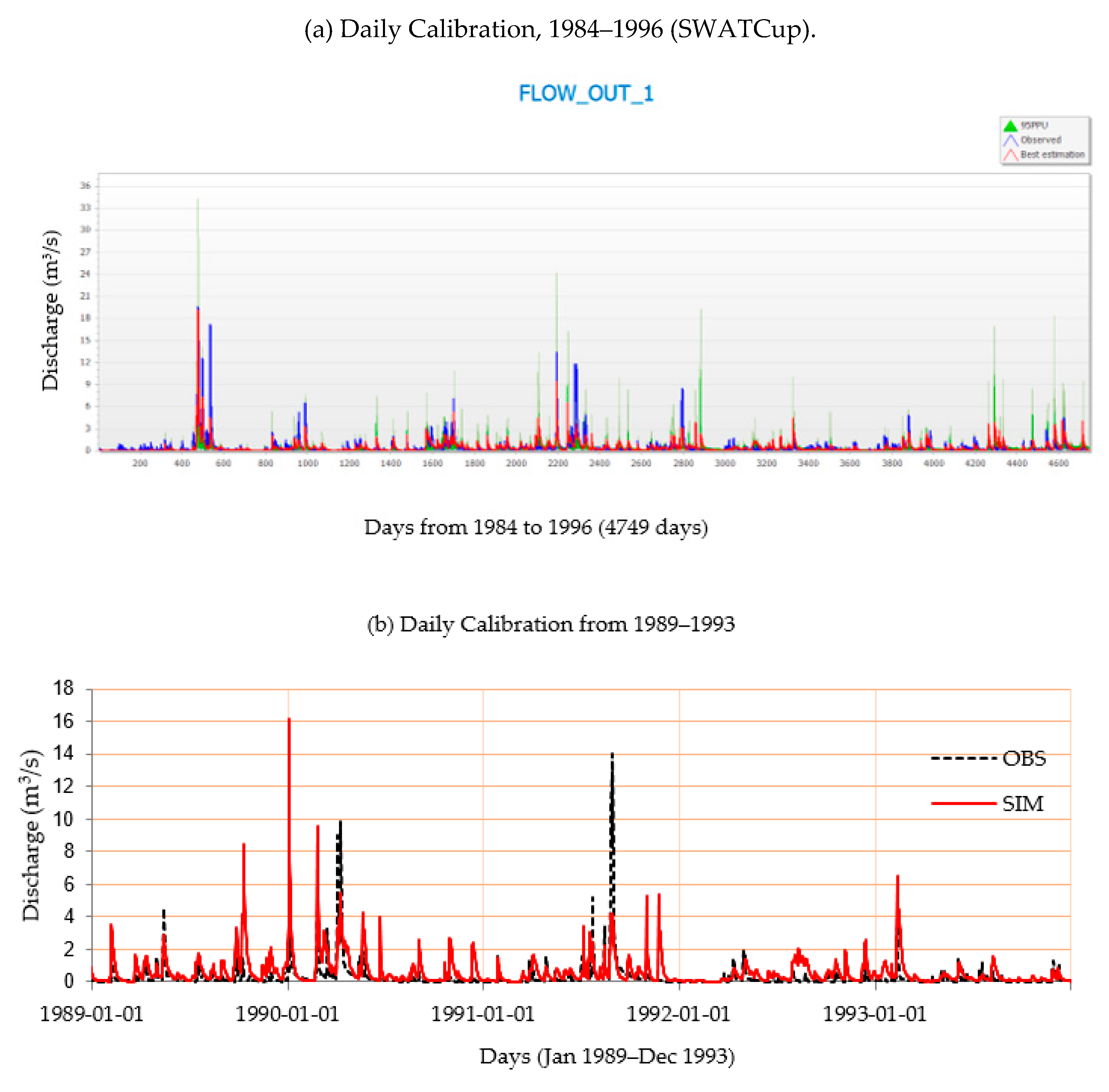
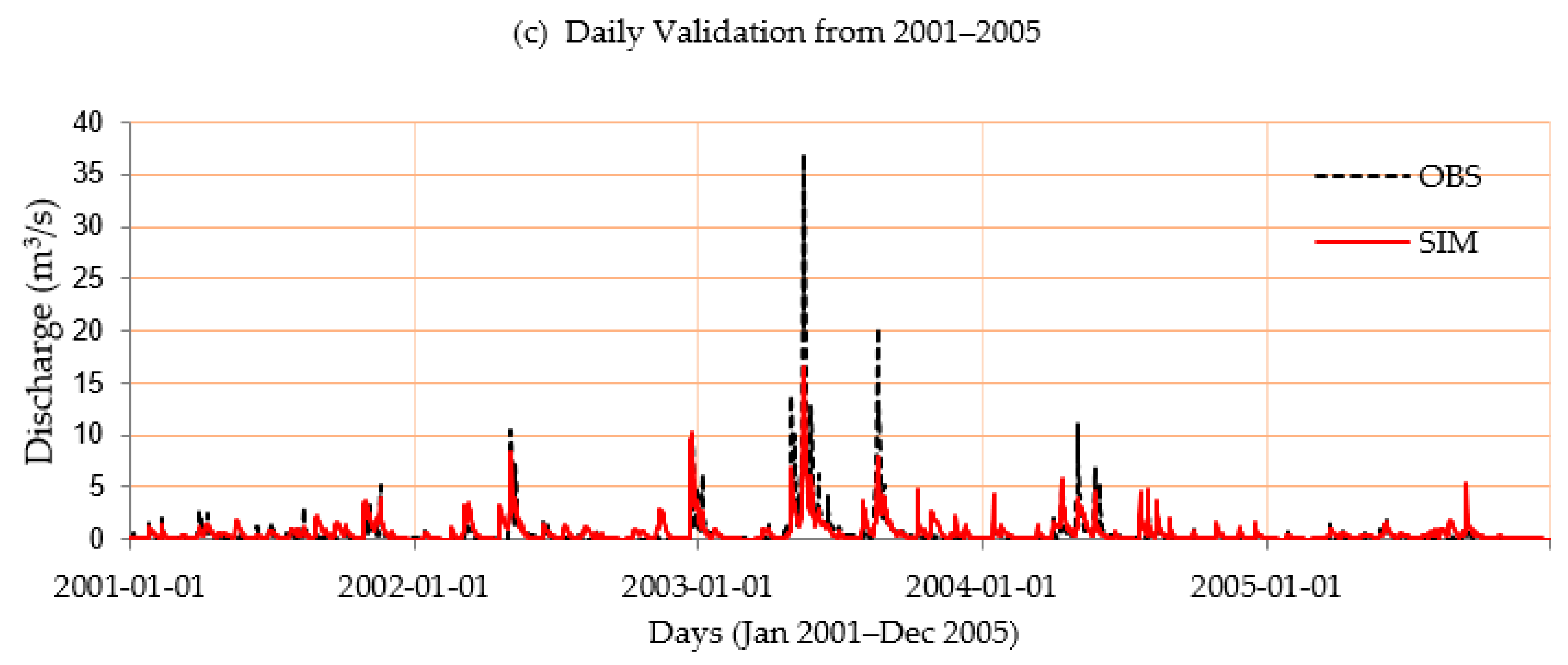
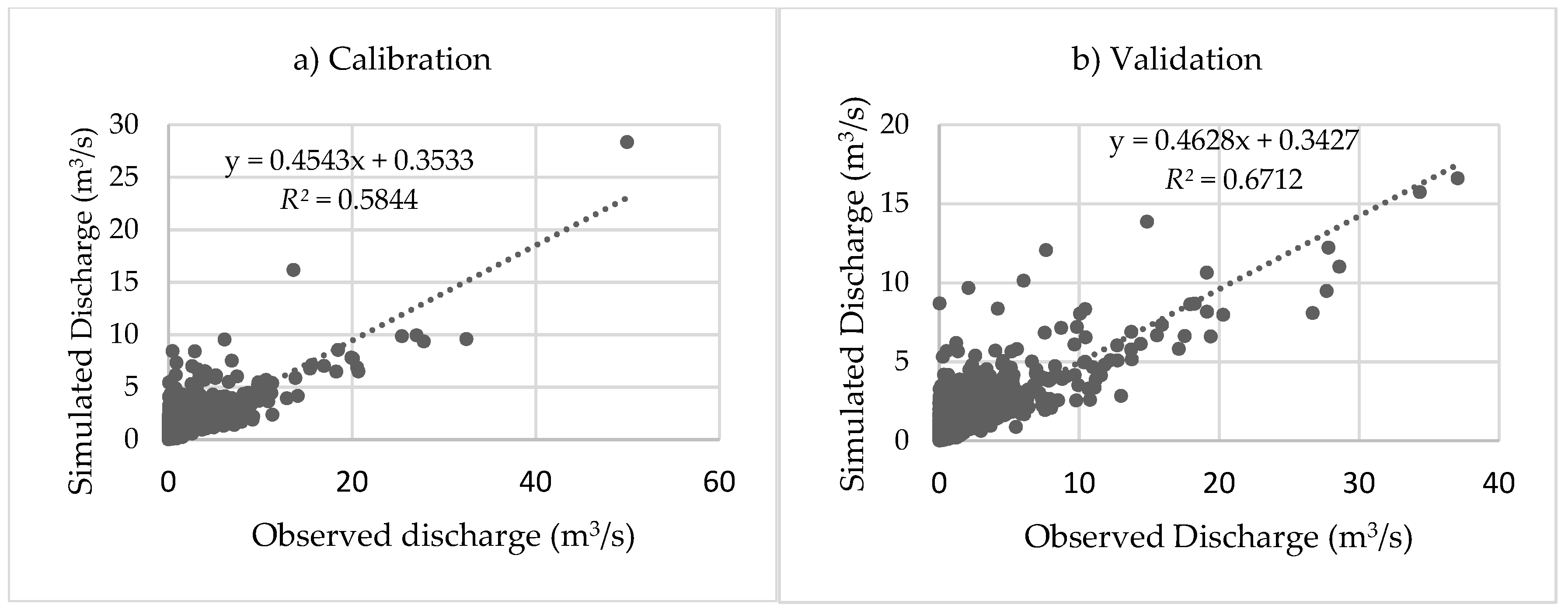
3.2. Model Performance
The model performance as shown in
Figure 8a–c was considered satisfactory for both calibration and validation period since the values of
fullfilled the requirement of
and NSE > 0.5 [
41,
52] The values of
R2 for the two periods indicated that there was a good correlation between the observed and simulated flow as shown in
Figure 9. The NSE and
R2 values were 0.58 for the calibration period and 0.52 and 0.67, respectively, for the validation period in the daily time series, as given in
Table 6.
The generated streamflow from each subcatchment was used for the calculations of the streamflow drought index (SDI).
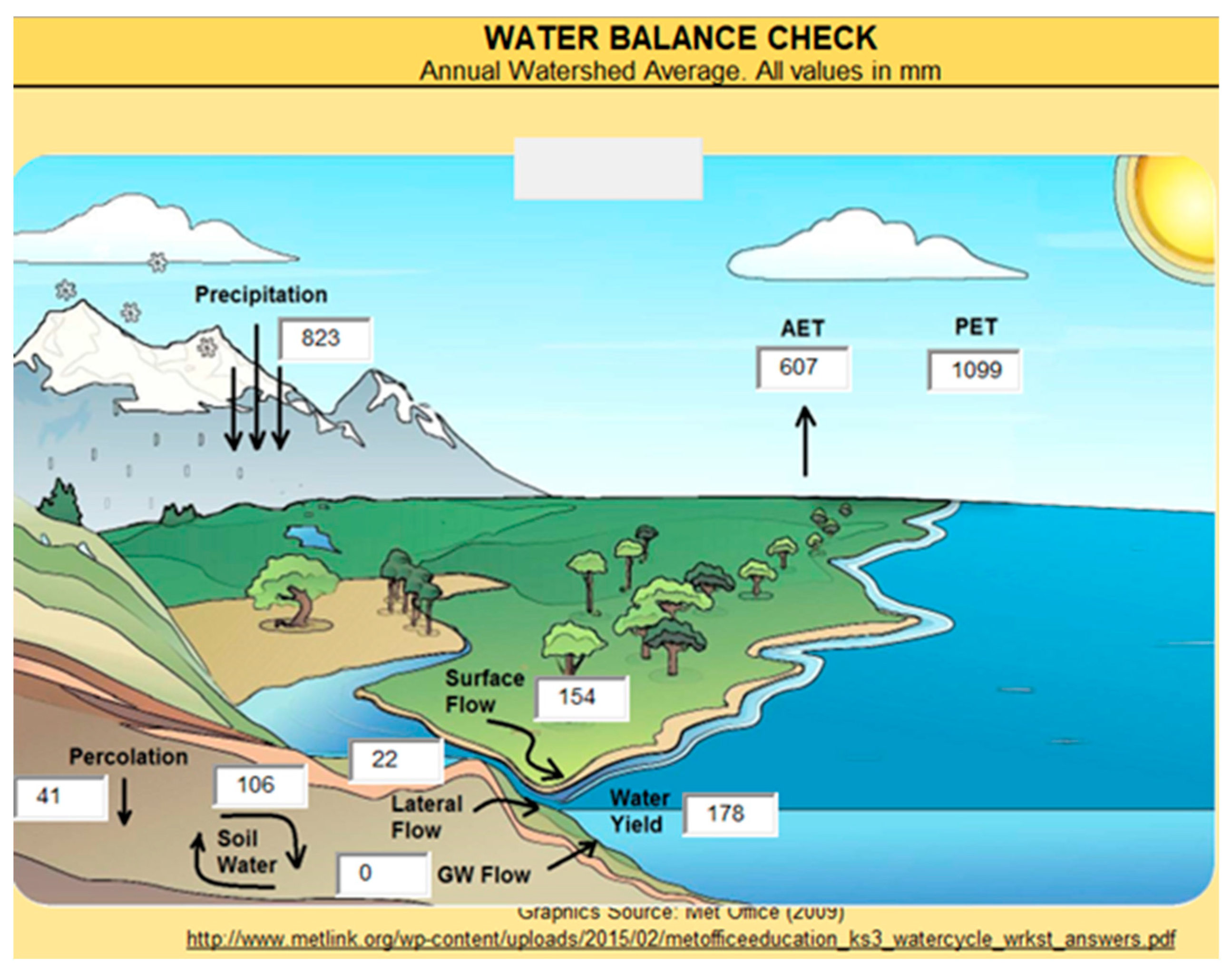
3.3. Long-Term Water Balance of Lake Nakuru Catchment from 1981 to 2018
Figure 10 represent the annual averages for the Lake Nakuru watershed for the daily simulation period, 1981 to 2018, carried out with SWAT model. Results show that actual evapotranspiration (ET) dominates the water balance, with a percentage of 73.75% of the average annual precipitation received in the watershed. The total water yield simulated by the SWAT model as the sum of surface runoff and the net contribution of groundwater and lateral flow was 21.62% of the average annual precipitation.
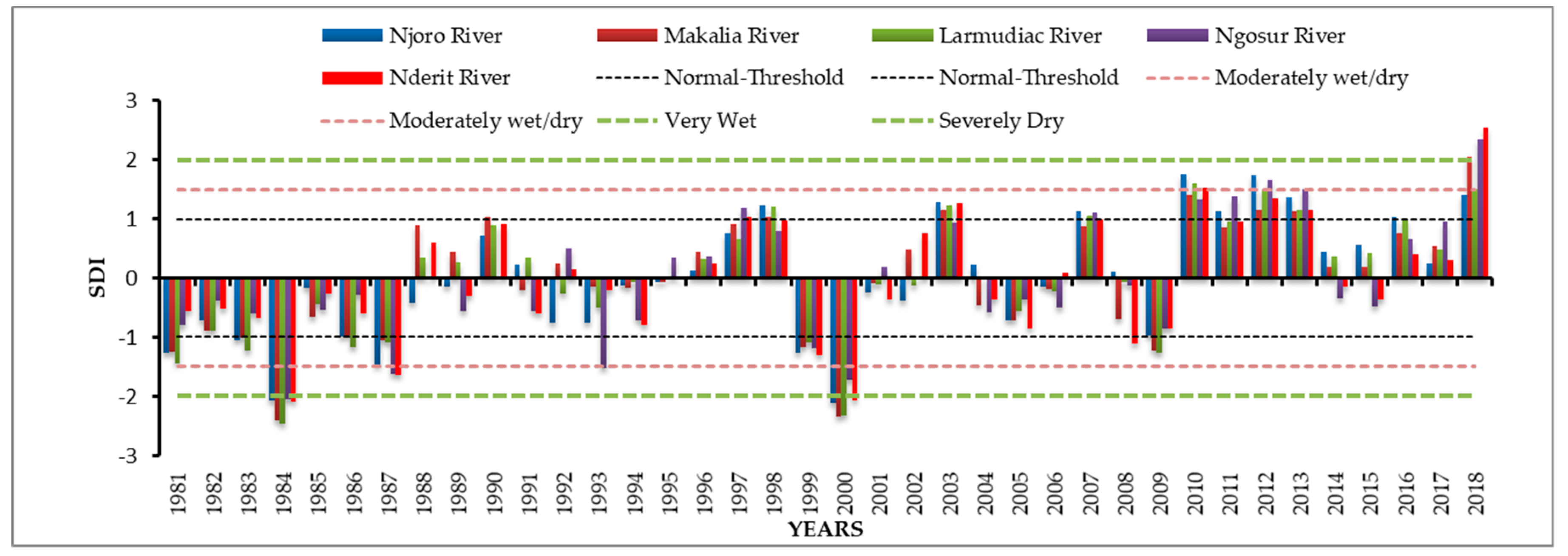
3.4. The Streamflow Drought Index (SDI)
The temporal variation of the 12-month SDI, implying a long-term drought, is shown in
Figure 11 from 1981 to 2018 for the five streams in the catchment.
Table 7 summarizes the frequency of dry years in comparison to wet years from 1981 to 2018 and emphasizes the 10-year results from 2009 to 2018. The results for Njoro River give 47.37% positive anomalies in comparison with 52.63% negative anomalies. Ngosur and Nderit Rivers have similar results, with 44.74% wet periods in comparison to 55.26% dry periods. Makalia River records an equal distribution of wet and dry periods at 50.00%, while Larmudiac River has a higher frequency of wet years (52.63%) than dry years (47.37%). The years 1984 and 2000 experienced the most severe long-term drought with SDI < −2.00. A prolonged dry period was experienced from 1981 to 1987, as indicated in
Figure 11. The period between 1988 and 1996 received streamflow at a normal threshold, which alternated between wet and dry periods except for 1993 for Ngosur River, which was a moderately dry year. The observations made from 2009 to 2018 show a higher frequency of wet periods compared to dry periods, with more than 60.00% positive anomalies.
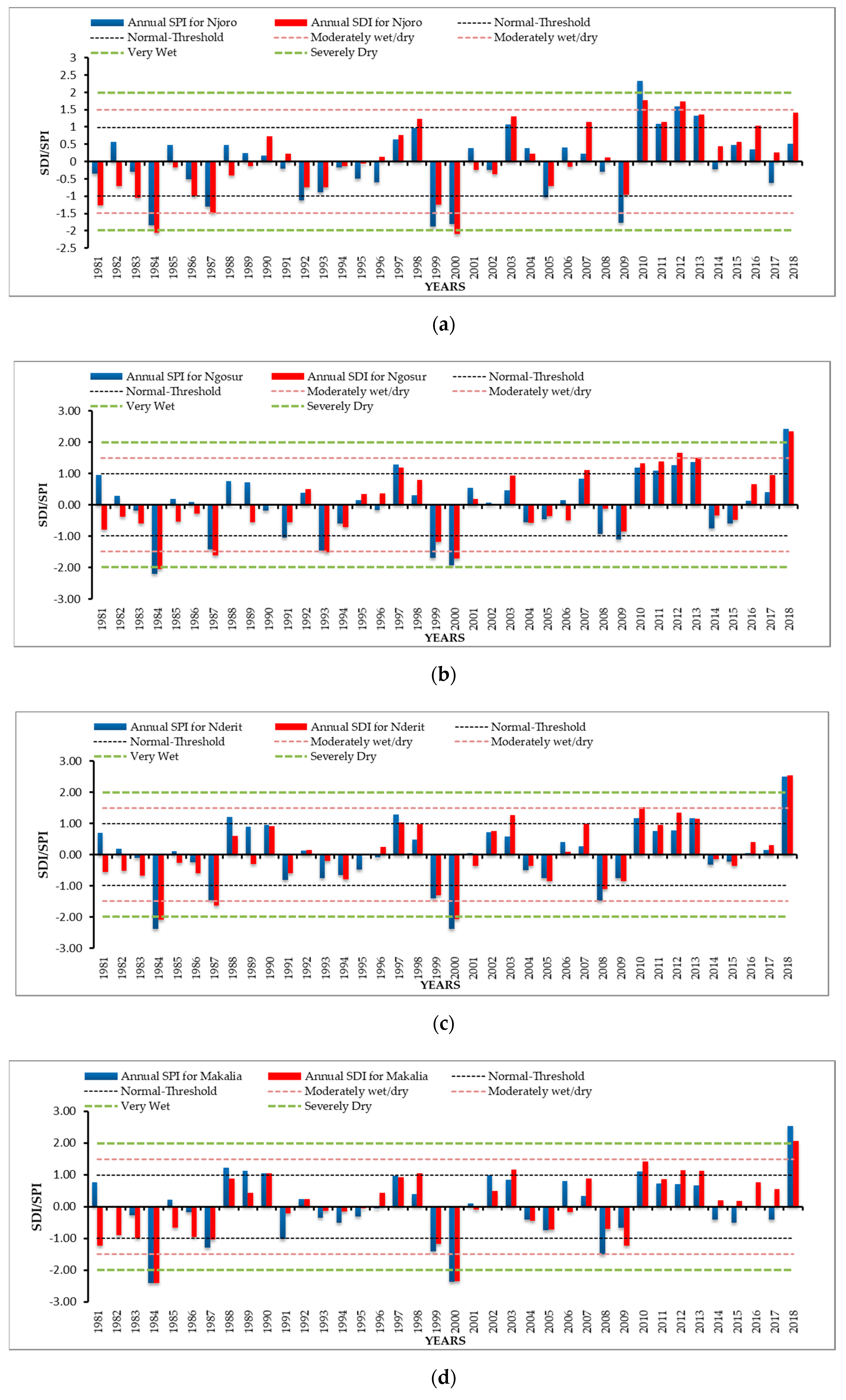
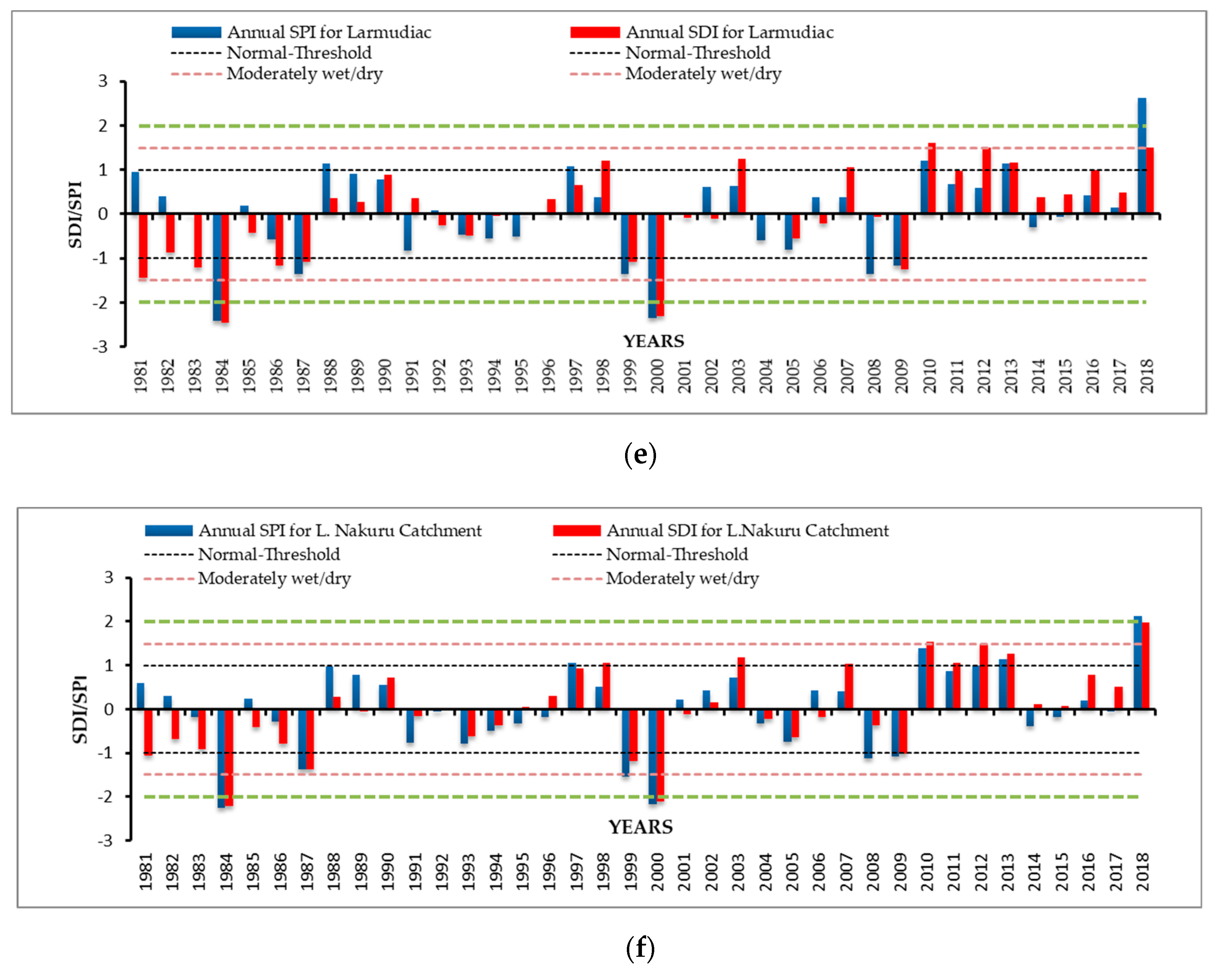
3.5. Comparison between 12-Month SPI and SDI at the Catchment Scale and in Individual Subcatchments
The results for the temporal variation of the SPI and SDI at the catchment scale and for the five individual subcatchments indicate that the drought events identified by the 12-month SPI are almost all identified by the 12-month SDI. There is thus a relationship between the hydrological drought indices and the meteorological indices.
The temporal variation for the 12-month SPI and SDI is shown in
Figure 12 and summarized in
Table 8. The period from 1981 to 2018 is subdivided into four sections for the analysis. A prolonged dry period is experienced from 1981 to 1987, with the SDI values for all subcatchments having 100.00% negative anomalies. Unlike Ngosur subcatchment, which observed 57.14% positive anomalies and 42.86% negative anomalies for SPI, the frequency of wet periods is less than 45.00% compared with the frequency for dry periods for Njoro, Larmudiac, Makalia, and Nderit subcatchments. For 1988 to 1996, the observations made for Ngosur and Nderit subcatchments are similar for both SPI and SDI, with the frequency of wet periods being 44.44% while that for dry periods was 55.56%. Njoro subcatchment observed 33.33% positive anomalies versus 66.67% negative anomalies for both SPI and SDI. An equal distribution of wet and dry periods was observed at 55.56% and 44.44%, respectively, for SPI and SDI for Larmudiac and Makalia subcatchments.
For the period between 1997 and 2009, an equal distribution of positive anomalies and negative anomalies was observed at 53.85% and 46.15%, respectively, for SPI and 46.15% and 53.85% for SDI for Njoro, Ngosur, and Nderit subcatchments. Larmudiac subcatchment observed 46.15% positive anomalies and 53.85% negative anomalies for SPI and 38.46% positive anomalies and 61.54% negative anomalies for SDI. Makalia subcatchment observed 53.85% and 46.15% positive and negative anomalies, respectively, for SPI, and a 38.46% and 61.54% frequency of wet and dry periods, respectively, for SDI.
The period 2010 to 2018 saw a higher frequency of wet periods compared to dry periods for all subcatchments, with Njoro, Larmudiac, and Makalia subcatchments having 100.00% positive anomalies for the SDI. Unlike Makalia subcatchment, which observed 66.67% positive anomalies and 33.33% negative anomalies for the SPI indices, the other four subcatchments observed a 77.78% frequency of wet periods and 22.22% frequency of dry periods. Nderit and Ngosur subcatchments recorded a higher frequency of wet periods compared with dry periods at 77.78% and 22.22%, respectively, for SDI. The years 1984 and 2004 experienced severe drought (SPI and SDI < −2), while 2010 was very wet for Njoro subcatchment (SPI and SDI > 2). The year 2018 was very wet (SPI and SDI > 2) for Makalia, Ngosur, Nderit, and Larmudiac subcatchments.
4. Conclusions
In this study, the temporal variability of rainfall and discharges into Lake Nakuru was analyzed using meteorological (SPI and SPEI) and hydrological (SDI) drought indices for a 38-year study period (1981–2018) and for a 10-year study period (2009–2018) for five subcatchments of Lake Nakuru. The major findings and conclusion were as follows:
(1) Gridded CHIRPS precipitation data showed high agreement with the observed data for Egerton station (KE0863) and were therefore used for the calculation of the meteorological drought indices (SPEI and SPI) for the four subcatchments without recorded data.
(2) The results showed that the SWAT model can be applied for the simulation of streamflow for the gauged and ungauged subcatchments for the study area, with satisfactory performance for both the calibration and the validation period. The results were used for the calculation of the hydrological drought index (SDI) for the study area.
(3) The results of temporal variation of the SPI and SDI at the catchment scale and for the five individual subcatchments indicate that there is a relationship between the hydrological drought indices and meteorological indices. The temporal variation for the 12-month SPI and SDI for all the subcatchments shows a higher frequency of prolonged dry periods from 1981 to 1996. A prolonged wet period was also experienced from 2010 to 2018. Severe drought was experienced in 1984 and 2000 while 2018 was a very wet year for the Larmudiac, Nderit, Ngosur, and Nderit subcatchments. The year 2010 was a very wet year for Njoro subcatchment.
(4) The results are similar to those obtained by Coppock et al. [
32]; in their study, the lake experienced prolonged drying and falling water levels from the mid-1980s through 1996, along with an associated increases in water salinity. According to the study, the lake dried up completely in 1995 and 1996, resulting in most birds disappearing and tourism being greatly diminished. From
Figure 12, its observed that the SPI and SDI indices for 1995 and 1996 are below the normal threshold (–0.5 < SPI/SDI < 0.5) and agree with the study. However, in 1997, a positive anomaly was observed for both the SPI and SDI indices (SPI/SDI > 0.5) for all the subcatchments, which could be a result of the El Niño-driven flooding in 1997 and 1998, during which the lake levels rebounded [
32]. The results of the SPI, SPEI, and SDI indices indicate that, from 2010 to 2018, there was a higher frequency of wet periods than dry periods, which could be why the lake has shown increasing levels since 2011, according to Onywere et al. [
33].
The results of the variability in rainfall and streamflow indices presented in this research provide a useful baseline for additional work on the impacts of climate change and climate variability on rainfall and stream flows for Lake Nakuru Basin. This will help with preparedness in planning for the infrastructure around the lake to avoid further losses caused by flooding.
In the future, it is recommended that research be conducted on the possible causes of the variability in Lake Nakuru’s water levels, which could be as a result of climate change, groundwater recharge, increased sedimentation, hydrological forcing, or tectonic uplifting of the Rift Valley floor. Coppock et al. [
32] calibrated a monthly water balance using available data for Lake Nakuru Basin from 1958 to 1976. The results indicated that rainfall was the largest source of water for the lake, followed by tributary inflows and then groundwater seepage. It is recommended that a lake water balance model be developed from 1980 to the present using the latest bathymetry survey to investigate whether hydrometeorological data can fully explain the variability in lake levels.