Projecting Wet Season Rainfall Extremes Using Regional Climate Models Ensemble and the Advanced Delta Change Model: Impact on the Streamflow Peaks in Mkurumudzi Catchment, Kenya
Abstract
1. Introduction
2. Materials and Methods
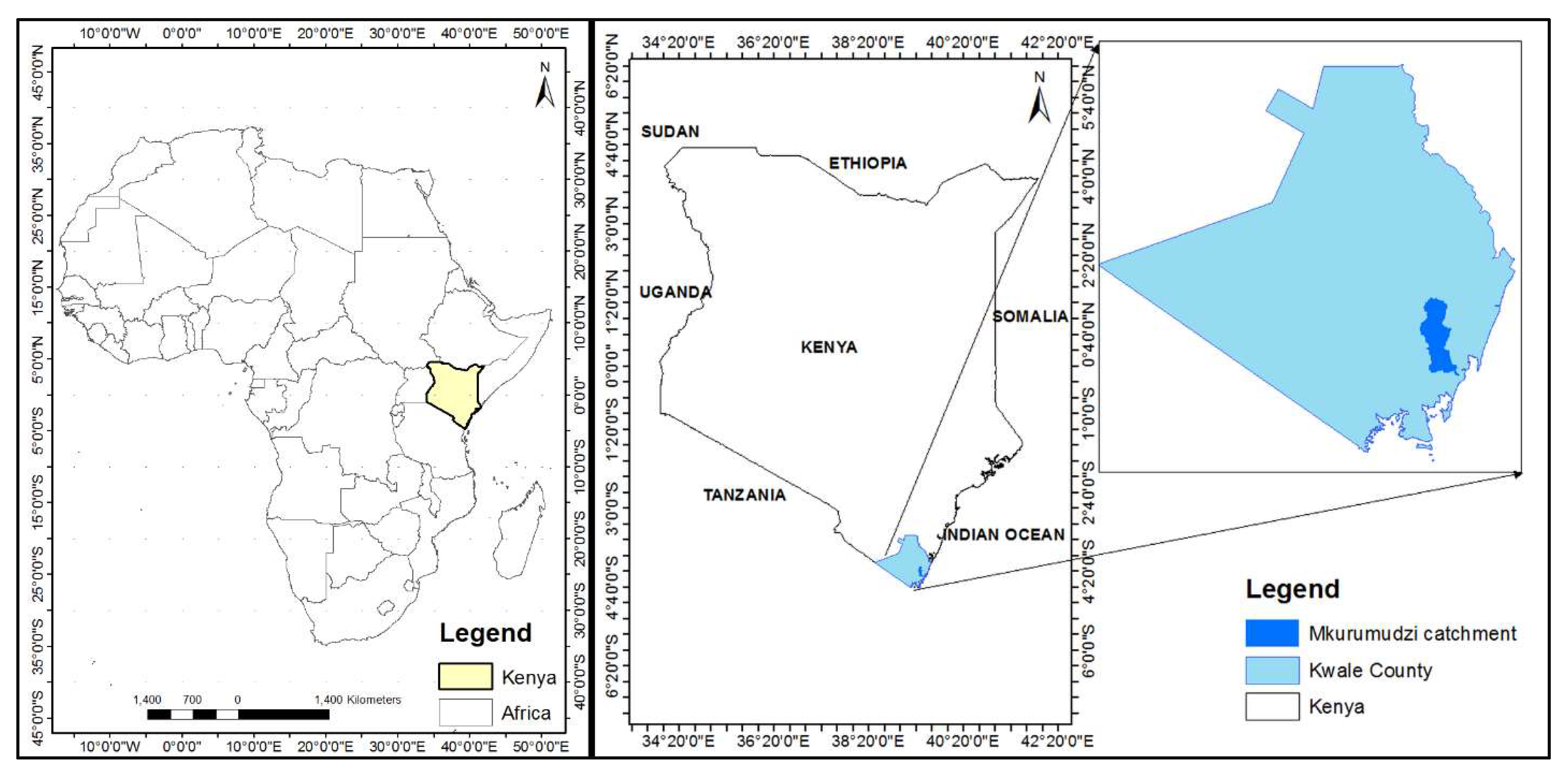
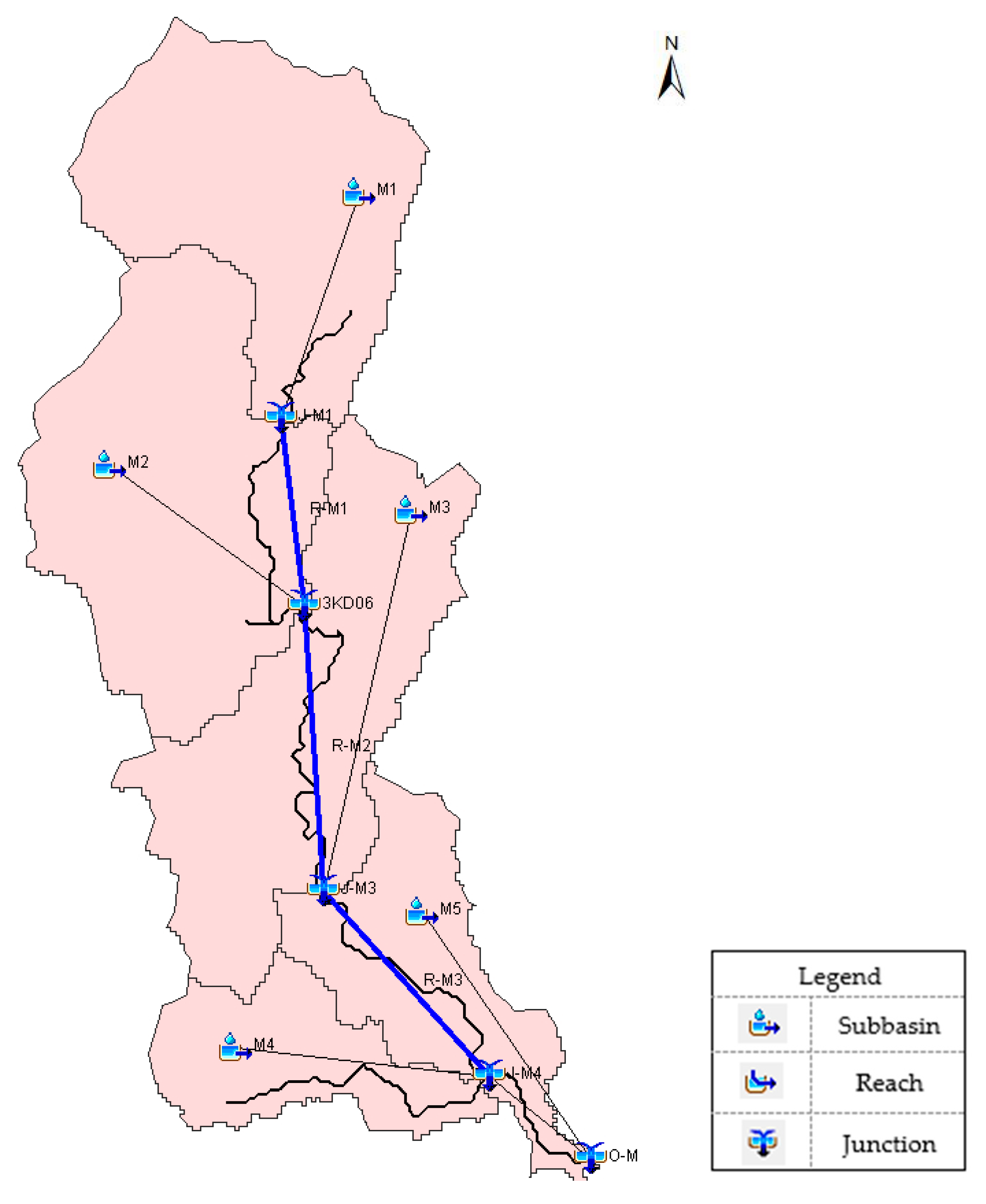
2.1. Study Area
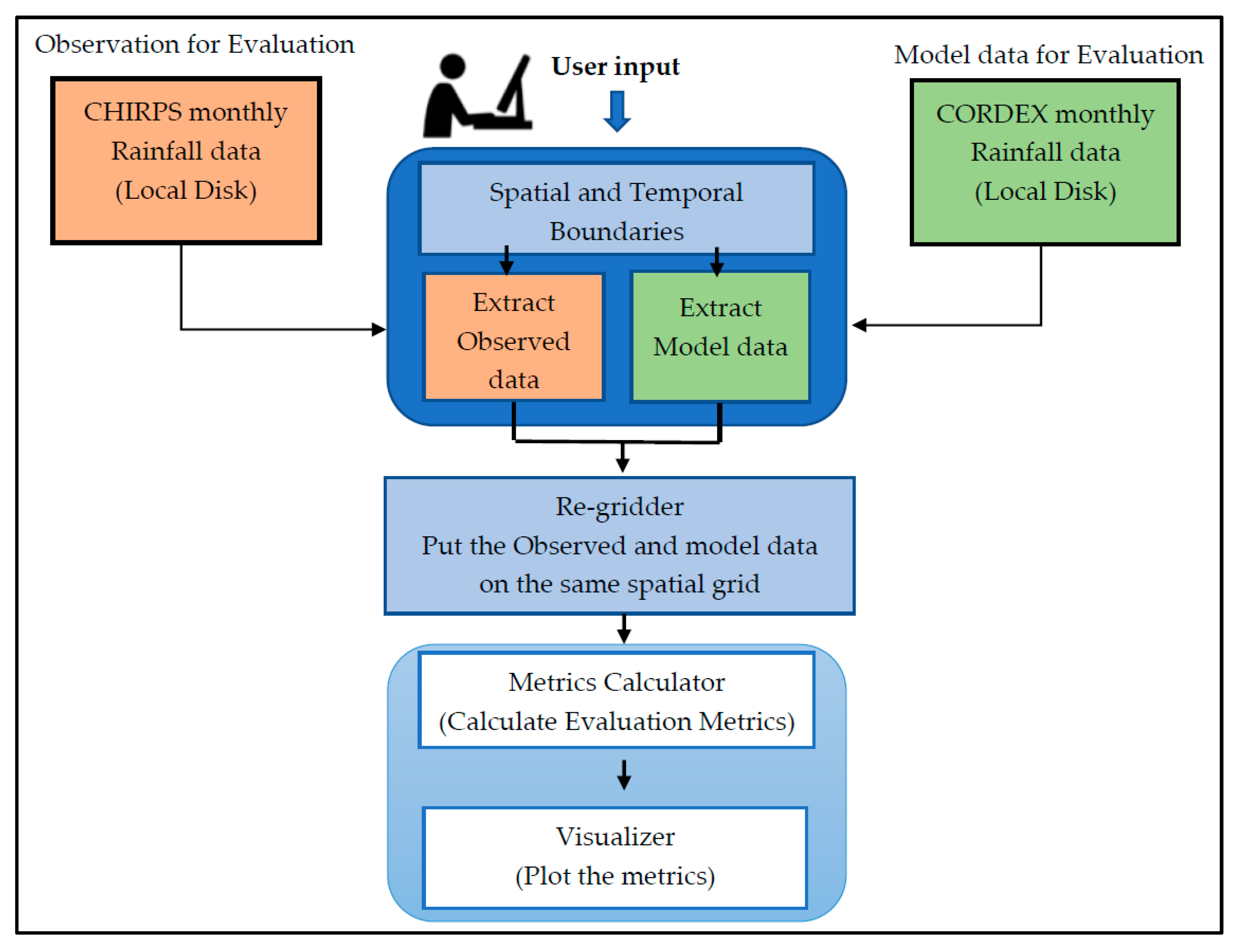
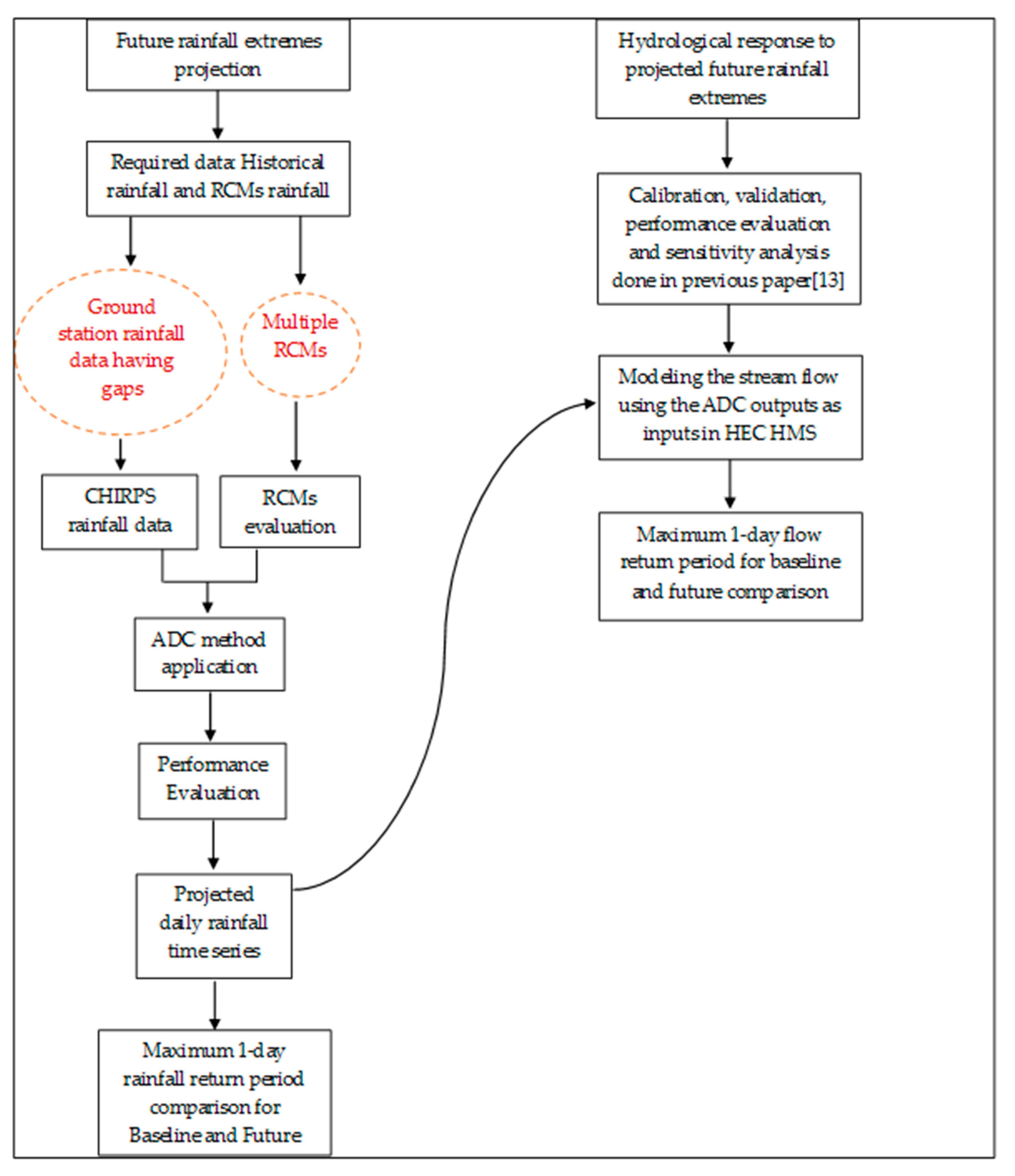
2.2. Flowchart of the Study
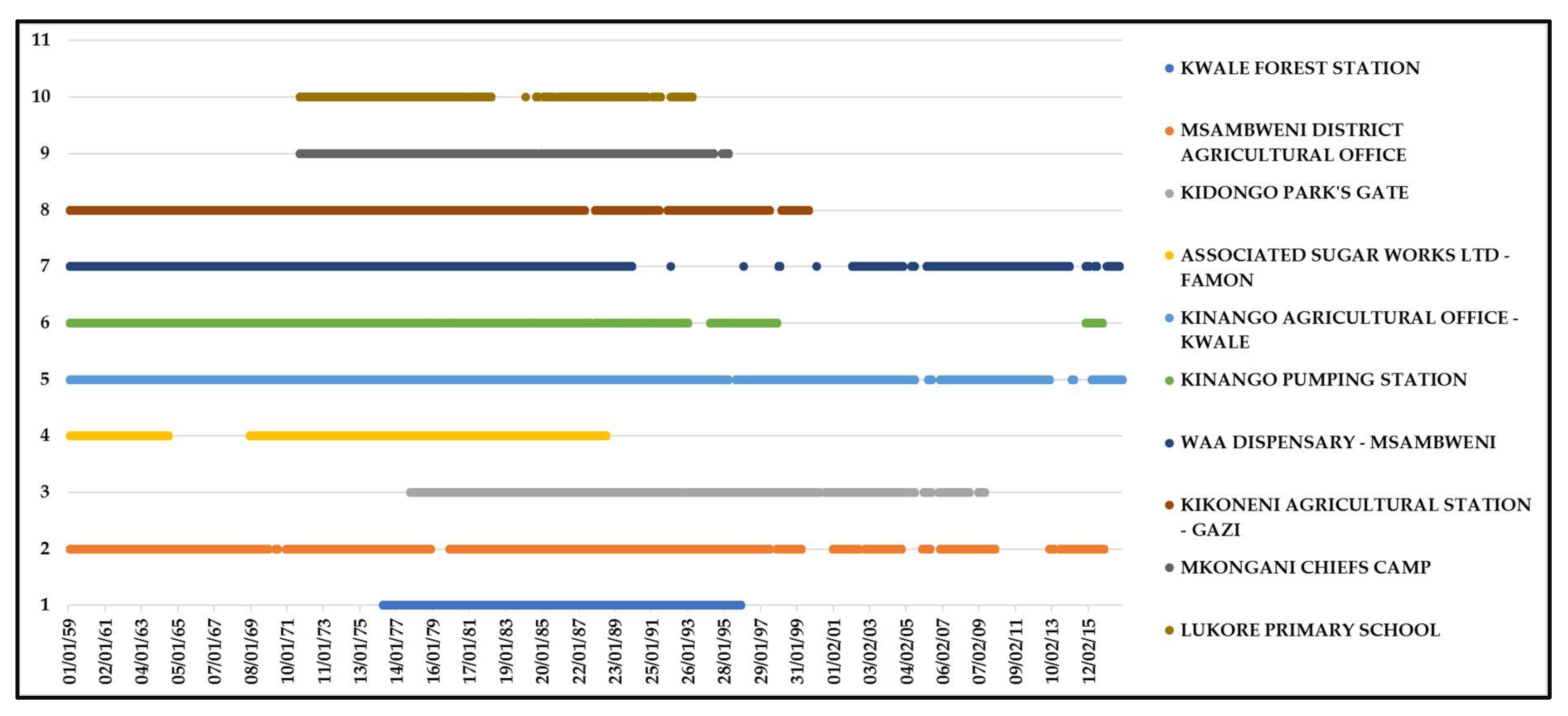
2.3. Available Rainfall Datasets
2.4. Evaluation Metrics
- (a)
- The coefficient of correlation (R2), which describes the percentage of the variance in observed data explained by the satellite. R2 ranges from 0 to 1, where values greater than 0.5 are considered acceptable [32,33].where Oi and Si are the observed and satellite rainfall at time I, respectively, and Ō and are the average observed and satellite rainfall during the evaluation period, respectively.
- (b)
- The dimensionless statistic: Index of agreement (d) was used and is given by:The index of agreement complements R2 by its ability to detect the additive and relative variations in the observed and simulated averages and variances. According to Willmott [32], varies between 0 (absolutely no agreement between the observed and the satellite rainfall) and 1 (perfect agreement).
- (c)
- The absolute error index represented by the RSR (RMSE standard deviation ratio) given by:
2.5. Projection of Future Rainfall Extremes Using the Advanced Delta Change Approach on Regional Climate Models Output
2.5.1. CORDEX Africa Rainfall Data
- -
- The pattern correlation ≥0.6.
- -
- the standard deviation ratio within the range of 1.00 ± 0.25.
2.5.2. Basin Model Setting-Up in HEC-HMS
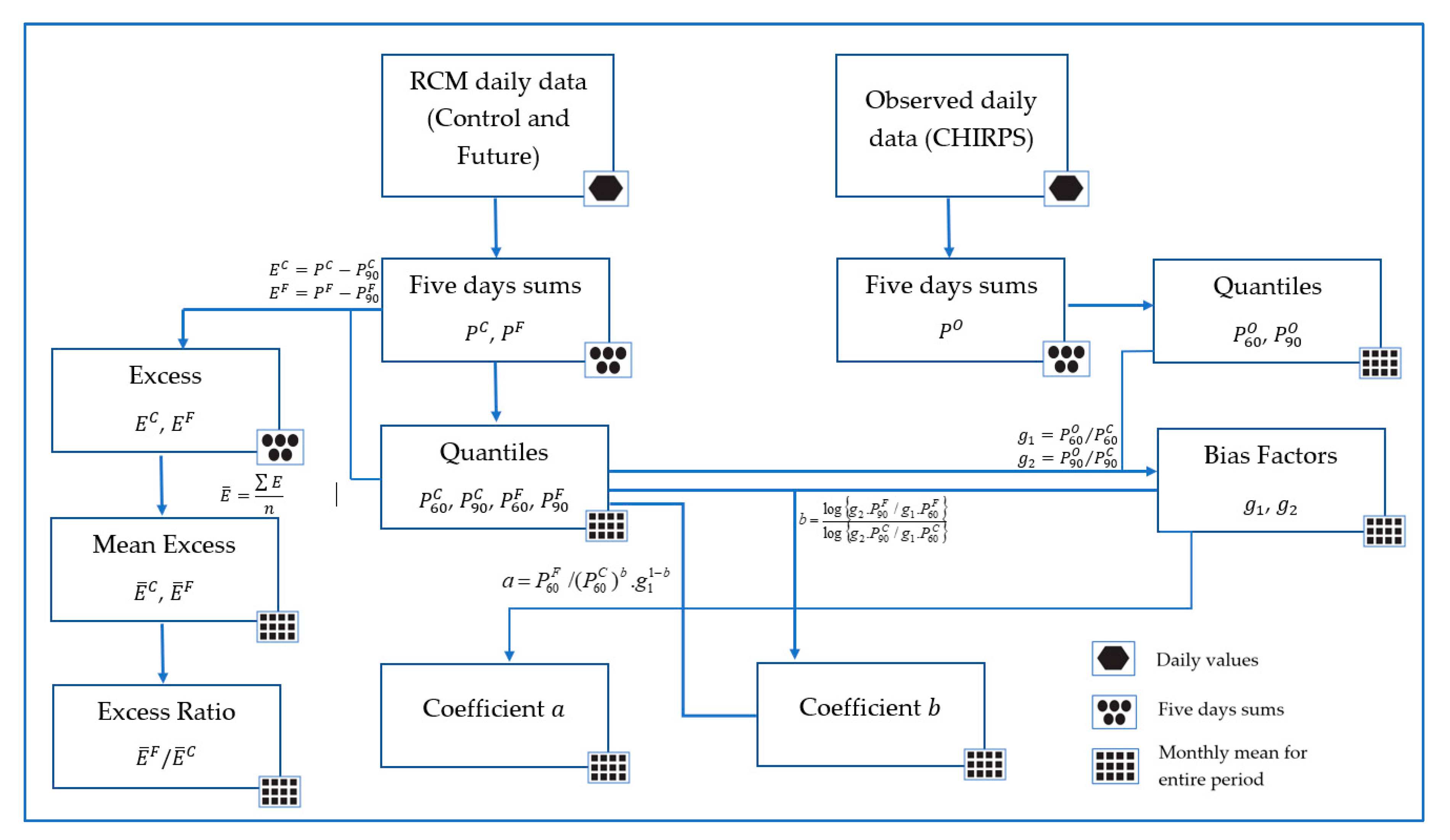
2.5.3. The Advanced Delta Change Approach
2.6. Best-Fit Probability Distribution and Return Period
2.6.1. Best-Fit Probability Distribution
2.6.2. Return Period of Rainfall and Streamflow
3. Results
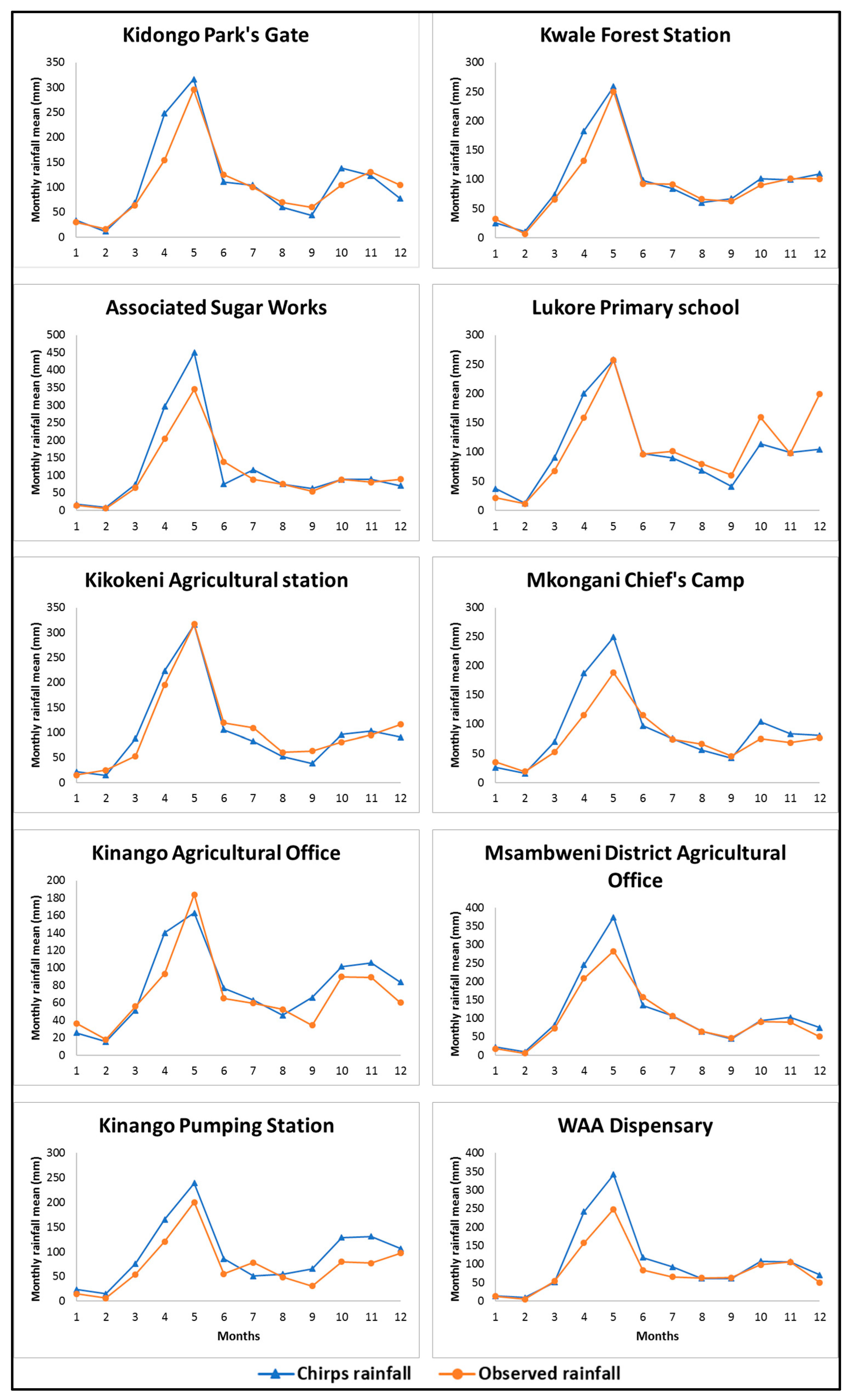
3.1. CHIRPS Datasets Accuracy Analysis
3.2. Projection of Future Rainfall Extremes Using the Advanced Delta Change Approach on Regional Climate Models Output
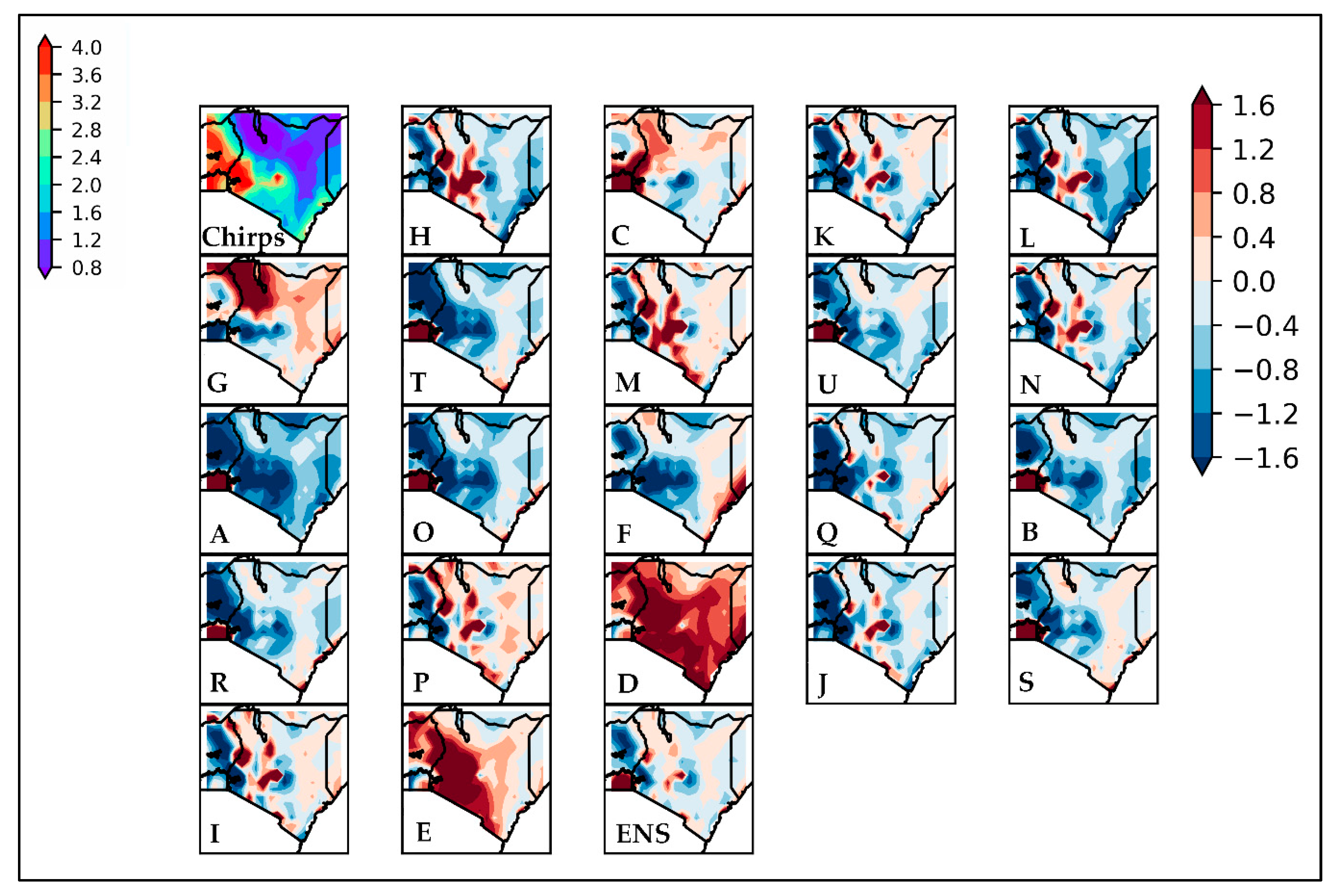
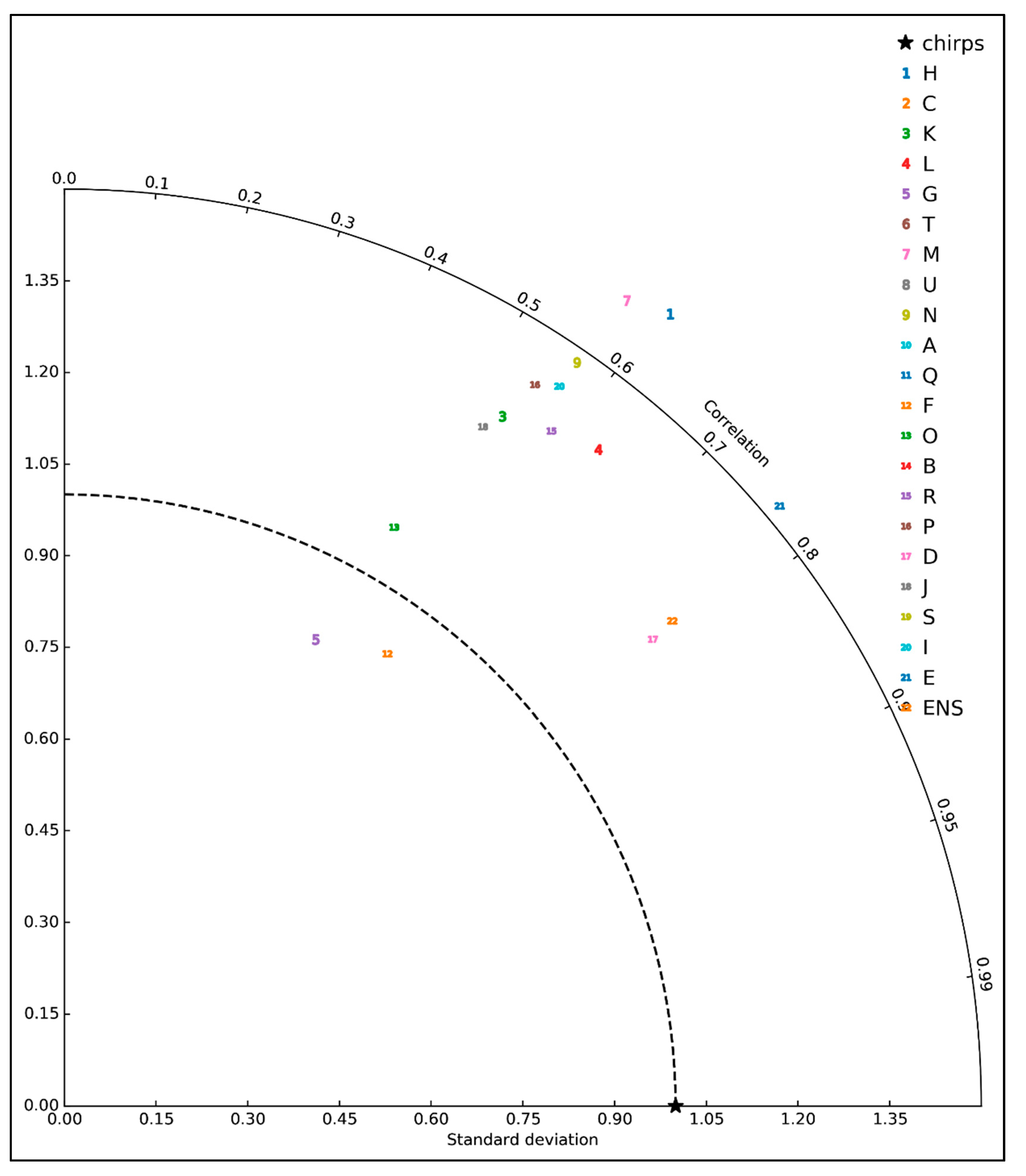
3.2.1. CORDEX Models Performance Evaluation and Selection
3.2.2. Validation of the Advance Delta Change Model
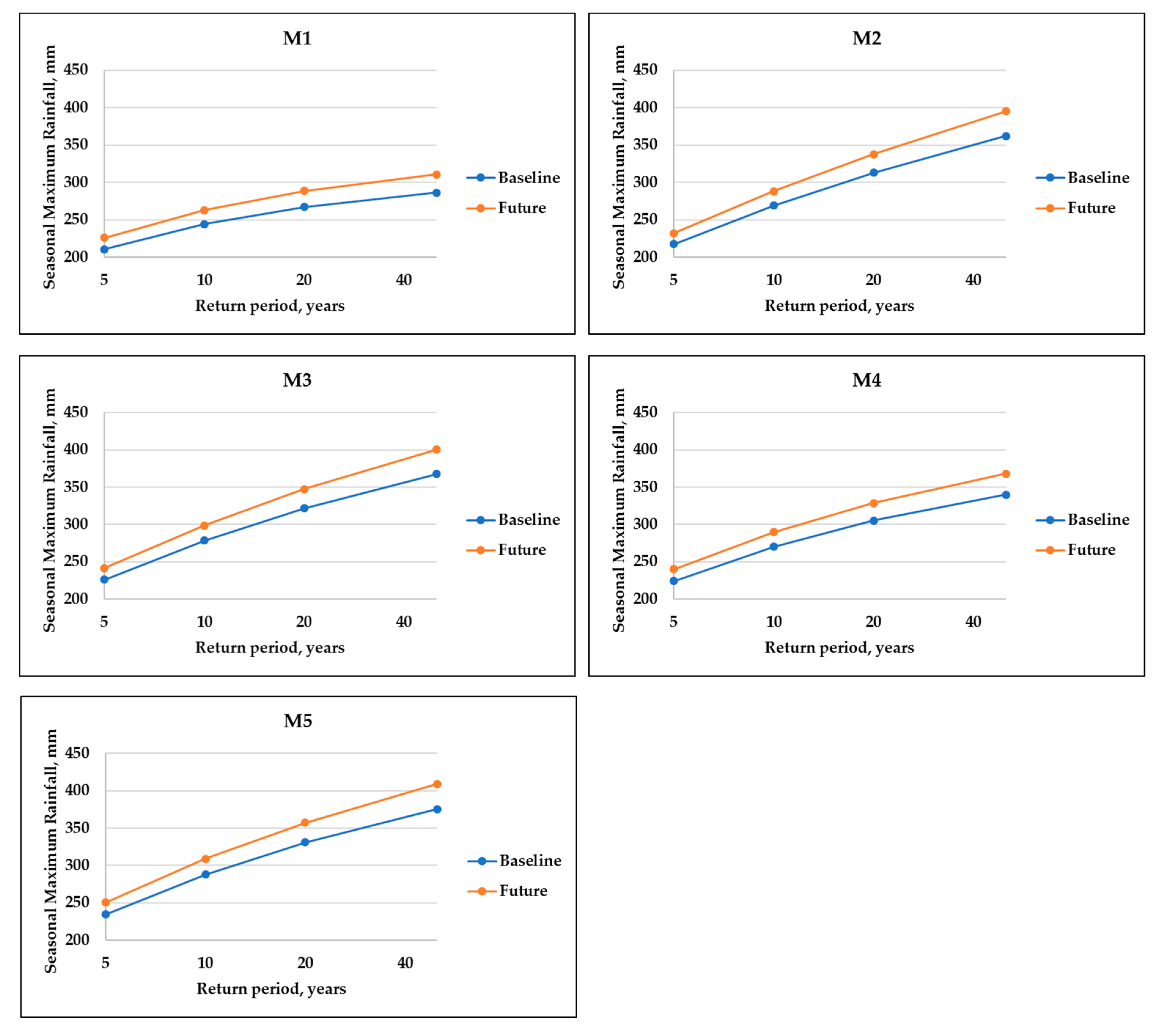
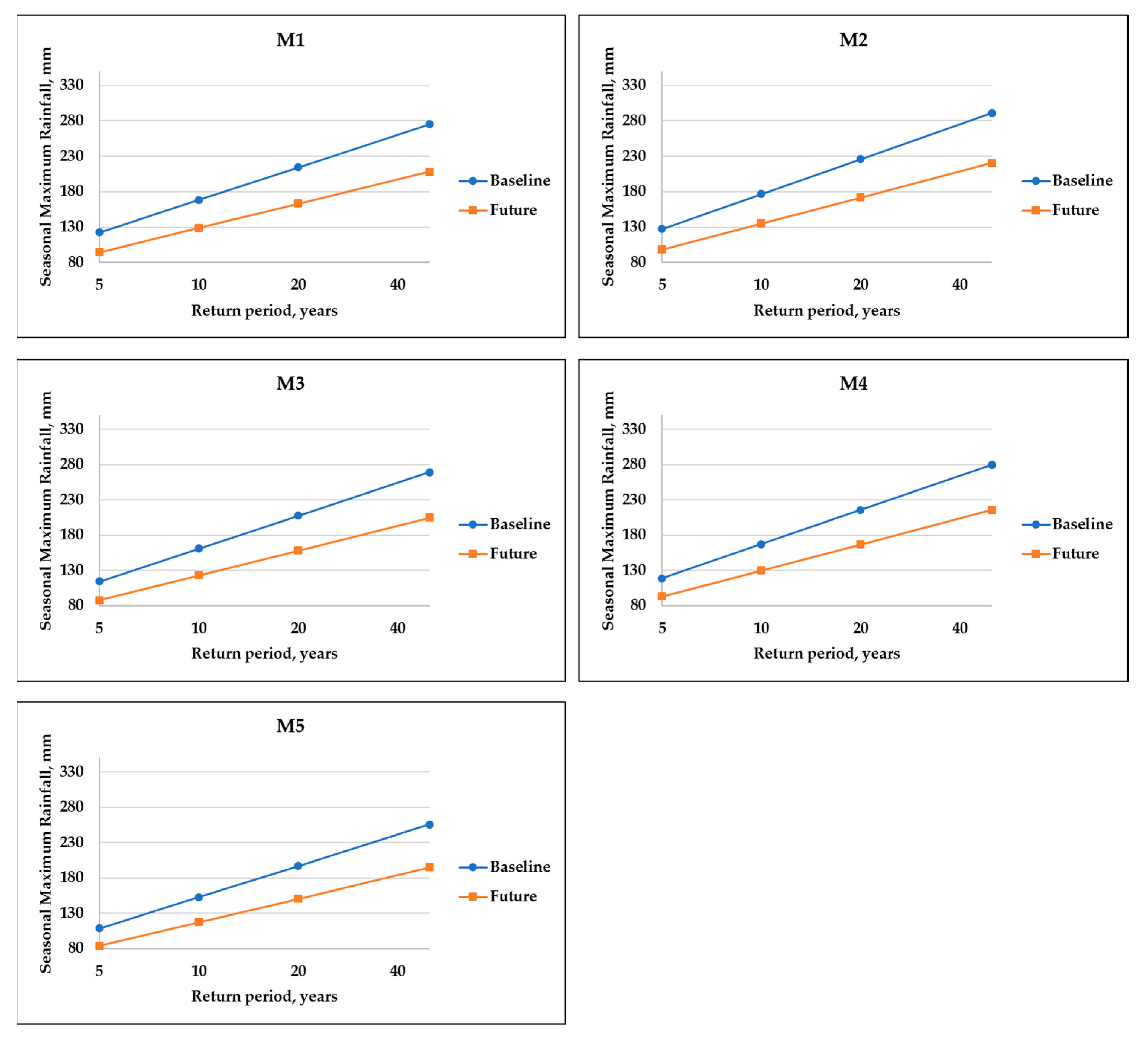
3.2.3. Quantiles Comparison under the Advanced Delta Approach
3.2.4. Best-Fit Probability Distributions for the Maximum One Day Rainfall in MAMJ and OND Seasons
3.2.5. Maximum One Day Rainfall Return Period before and after ADC
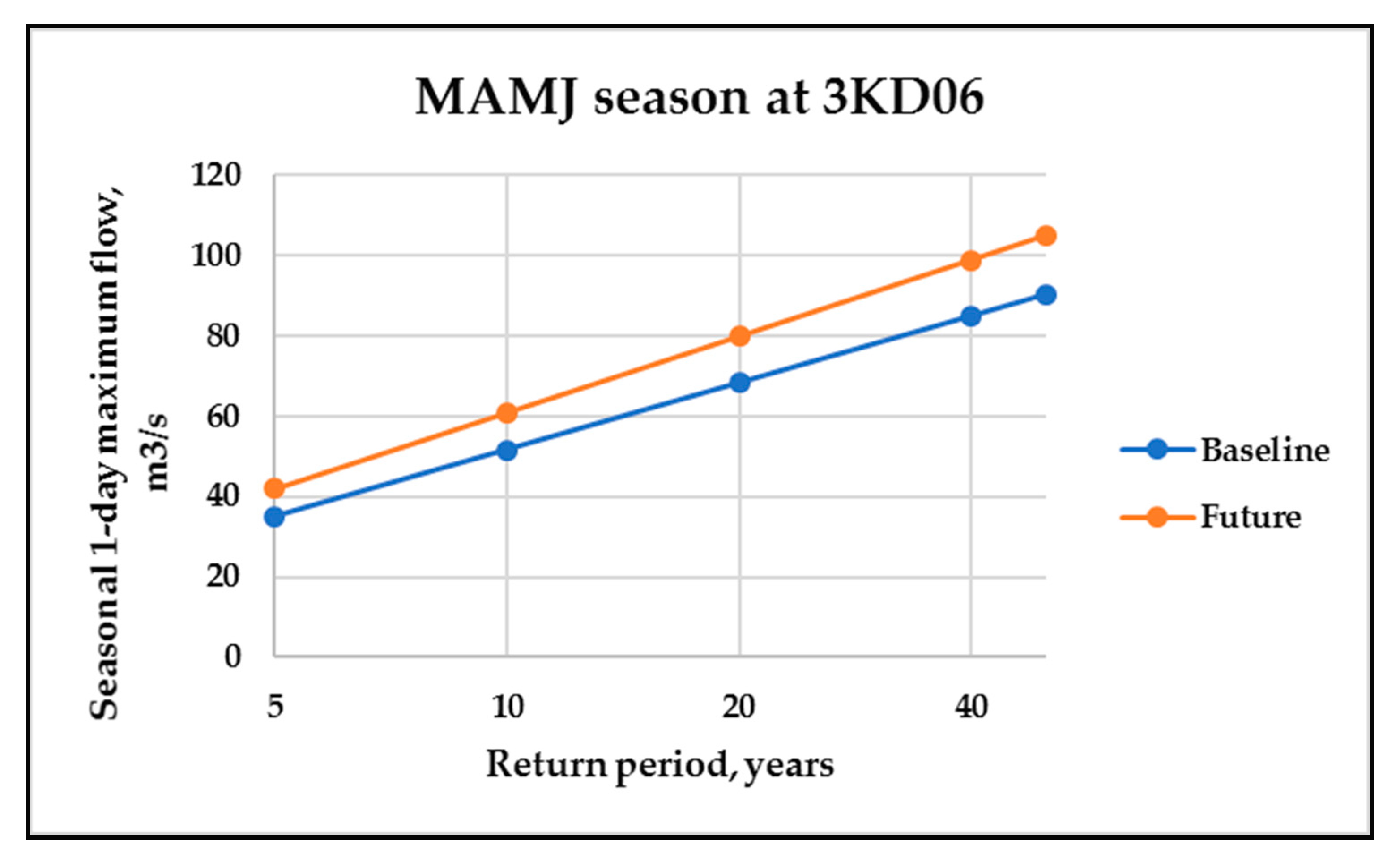
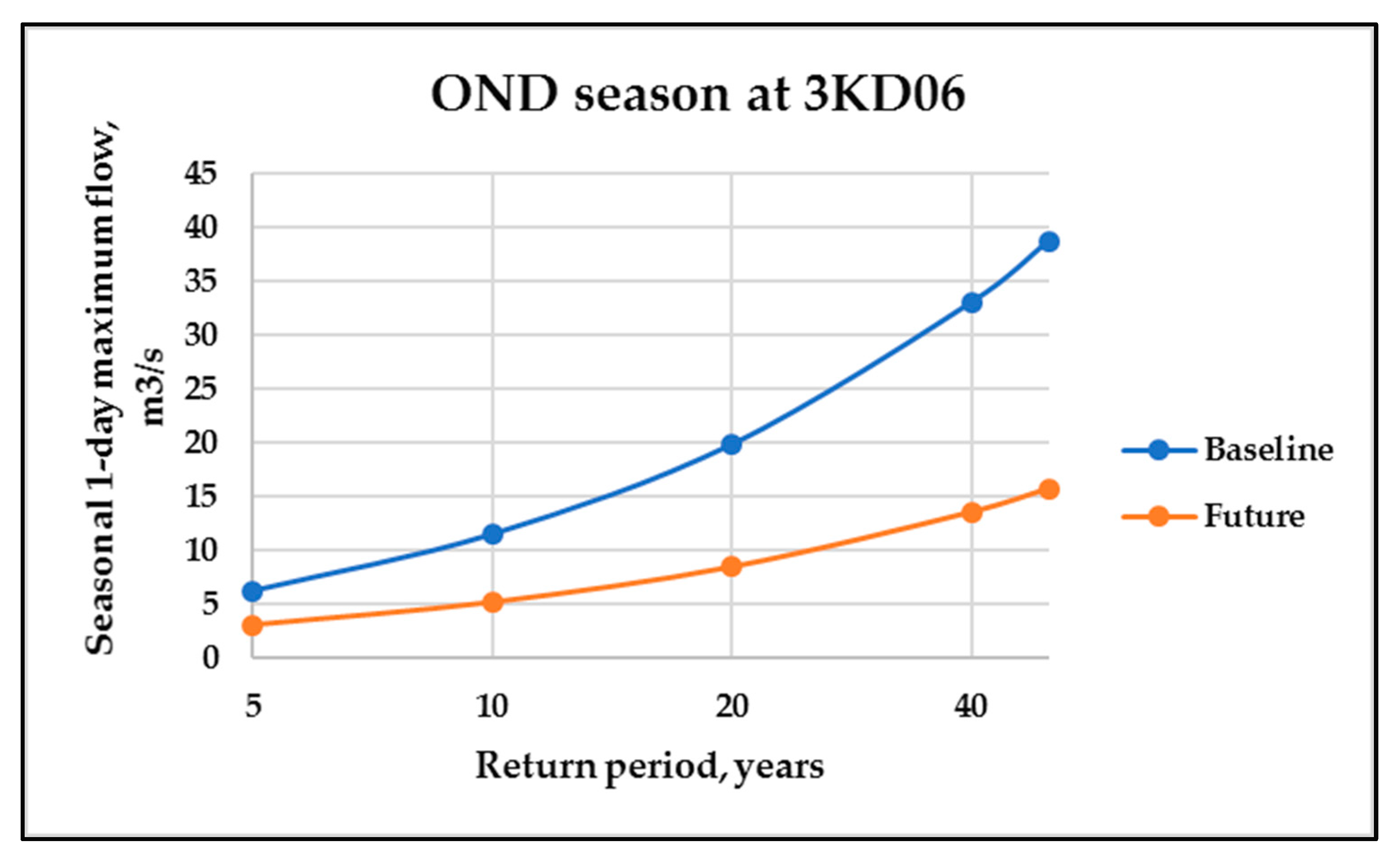
3.3. Hydrological Impact of the Projected Rainfall Extreme on the Gaging Station 3KD06 for the Period 2018–2041
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| n | Significance Level, α | |||
|---|---|---|---|---|
| 0.1 | 0.05 | 0.02 | 0.01 | |
| 1 | 0.95 | 0.975 | 0.99 | 0.995 |
| 2 | 0.77639 | 0.84189 | 0.9 | 0.92929 |
| 3 | 0.63604 | 0.7076 | 0.78456 | 0.829 |
| 4 | 0.56522 | 0.62394 | 0.68887 | 0.73424 |
| 5 | 0.50945 | 0.56328 | 0.62718 | 0.66853 |
| 6 | 0.46799 | 0.51926 | 0.57741 | 0.61661 |
| 7 | 0.43607 | 0.48342 | 0.53844 | 0.57581 |
| 8 | 0.40962 | 0.45427 | 0.50654 | 0.54179 |
| 9 | 0.38746 | 0.43001 | 0.4796 | 0.51332 |
| 10 | 0.36866 | 0.40925 | 0.45662 | 0.48893 |
| 11 | 0.35242 | 0.39122 | 0.4367 | 0.4677 |
| 12 | 0.33815 | 0.37543 | 0.41918 | 0.44905 |
| 13 | 0.32549 | 0.36143 | 0.40362 | 0.43247 |
| 14 | 0.31417 | 0.3489 | 0.3897 | 0.41762 |
| 15 | 0.30397 | 0.3376 | 0.37713 | 0.4042 |
| 16 | 0.29472 | 0.32733 | 0.36571 | 0.39201 |
| 17 | 0.28627 | 0.31796 | 0.35528 | 0.38086 |
| 18 | 0.27851 | 0.30936 | 0.34569 | 0.37062 |
| 19 | 0.27136 | 0.30143 | 0.33685 | 0.36117 |
| 20 | 0.26473 | 0.29408 | 0.32866 | 0.35241 |
| 21 | 0.25858 | 0.28724 | 0.32104 | 0.34427 |
| 22 | 0.25283 | 0.28087 | 0.31394 | 0.33666 |
| 23 | 0.24746 | 0.2749 | 0.30728 | 0.32954 |
| 24 | 0.24242 | 0.26931 | 0.30104 | 0.32286 |
| 25 | 0.23768 | 0.26404 | 0.29516 | 0.31657 |
| 26 | 0.2332 | 0.25907 | 0.28962 | 0.31064 |
| 27 | 0.22898 | 0.25438 | 0.28438 | 0.30502 |
| 28 | 0.22497 | 0.24993 | 0.27942 | 0.29971 |
| 29 | 0.22117 | 0.24571 | 0.27471 | 0.29466 |
| 30 | 0.21756 | 0.2417 | 0.27023 | 0.28987 |
Appendix B
References
- Boko, M.; Niang, I.; Nyong, A.; Al, E. Climate Change Adaptation and Vulnerability: Contribution of Working Group II to the IV Assessment Report of the IPCC Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Mason, S.J.; Waylen, P.R.; Mimmack, G.M.; Rajaratnam, B.; Harrison, J.M. Changes in extreme rainfall events in South Africa. Clim. Chang. 1999, 41, 249–257. [Google Scholar] [CrossRef]
- Fotso-nguemo, T.C.; Chamani, R.; Yepdo, Z.D.; Sonkoué, D.; Matsaguim, C.N.; Vondou, D.A.; Tanessong, R.S. Projected trends of extreme rainfall events from CMIP5 models over Central Africa. Atmos. Sci. Lett. 2018, 19, 1–8. [Google Scholar] [CrossRef]
- Ongoma, V.; Chen, H.; Omony, G.W. Variability of Extreme Weather Events over the Equatorial East Africa, a case study of Rainfall in Kenya and Uganda. Theor. Appl. Climatol. 2018, 131, 295–308. [Google Scholar] [CrossRef]
- Gebrechorkos, S.H.; Hülsmann, S.; Bernhofer, C. Changes in temperature and precipitation extremes in Ethiopia. Int. J. Climatol. 2018, 39, 18–30. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2014: Mitigation of Climate Change. Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Edenhofer, O., Pichs-Madruga, R., Sokona, Y., Farahani, E., Kadner, S., Seyboth, K., Adler, A., Baum, I., Brunner, S., Eickemeier, P., et al., Eds.; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Alotaibi, K.; Ghumman, A.R.; Haider, H.; Ghazaw, Y.M.; Shafiquzzama, M. Future Predictions of Rainfall and Temperature Using GCM and ANN for Arid Regions: A Case Study for the Qassim Region, Saudi Arabia. Water 2018, 10, 1260. [Google Scholar] [CrossRef]
- Pisnichenko, I.; Tarasova, T.A. Climate version of the ETA regional forecast model Evaluating. Theor. Appl. Climatol. 2007, 99, 255–272. [Google Scholar] [CrossRef][Green Version]
- Giorgi, F.; Mearns, L.O. Introduction to special section—Regional climate modeling revisited. J. Geophys. Res. 1999, 104, 6335–6352. [Google Scholar] [CrossRef]
- Pal, J.S.; Small, E.E.; Eltahir, E.A.B. Simulation of regional-scale water and energy budgets: Representation of subgrid cloud and precipitation processes within RegCM. J. Geophys. Res. 2000, 105, 579–594. [Google Scholar] [CrossRef]
- Marinucci, M.R.; Giorgi, F. A 2XCO2 climate change scenario over Europe generated using a limited area model nested in a general Circulation Model 1. Present-Day Seasonal Climate Simulation. J. Geophys. Res. Atmos. 1992, 97, 9989–10009. [Google Scholar] [CrossRef]
- USAID. A Review of Downscaling Methods for Climate Change Projections; United States Agency for International Development: Washington, DC, USA, 2014.
- Onyutha, C.; Tabari, H.; Rutkowska, A.; Nyeko-ogiramoi, P.; Willems, P. Comparison of different statistical downscaling methods for climate change rainfall projections over the Lake Victoria basin considering CMIP3 and CMIP5. J. Hydro-Environ. Res. 2016, 12, 31–45. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Verdin, A.; Rajagopalan, B.; Kleiber, W.; Podestá, G.; Bert, F. A conditional stochastic weather generator for seasonal to multi-decadal simulations. J. Hydrol. 2015, 556, 835–846. [Google Scholar] [CrossRef]
- Hay, L.E.; Wilby, R.L.; Leavesley, G.H. A Comparison of Delta Change and Downscaled GCM scenarios for three Mountainous Basins in the United States. J. Am. Water Resour. Assoc. 2000, 36, 387–397. [Google Scholar] [CrossRef]
- Graham, L.P.; Andréasson, J.; Carlsson, B. Assessing climate change impacts on hydrology from an ensemble of regional climate models, model scales and linking methods—A case on the Lule River basin. Clim. Chang. 2007, 81, 293–307. [Google Scholar] [CrossRef]
- Bordoy, R.; Burlando, P. Bias correction of regional climate model simulations in a region of complex orography. J. Appl. Meteorol. Climatol. 2013, 52, 82–101. [Google Scholar] [CrossRef]
- Leander, R.; Buishand, T.A. Resampling of regional climate model output for the simulation of extreme river flows. J. Hydrol. 2007, 332, 487–496. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Is bias correction of regional climate model (RCM) simulations possible for non-stationary conditions? Hydrol. Earth Syst. Sci. 2013, 17, 5061–5077. [Google Scholar] [CrossRef]
- Scharffenberg, W.A. Hydrologic Modeling System HEC-HMS—User’s Manual (ver. 4.0); USACE: Davis, CA, USA, 2013.
- Rehana, S.; Mujumdar, P.P. River water quality response under hypothetical climate change scenarios in Tunga-Bhadra river, India. Hydrol. Process. 2011, 25, 3373–3386. [Google Scholar] [CrossRef]
- Tefera, A.H. Application of water balance model simulation for water resource assessment in upper Blue Nile of North Ethiopia using HEC-HMS by GIS and remote sensing: Case of Beles river basin. Int. J. Hydrol. 2017, 1, 222–227. [Google Scholar] [CrossRef]
- Muli, N.M. Rainfall-Runoff Flood Modelling in Nairobi Urban Watershed. Master’s Thesis, Kenyatta University, Nairobi, Kenya, 2011. [Google Scholar]
- Bitew, G.T.; Mulugeta, A.B.; Miegel, K. Application of HEC-HMS Model for Flow Simulation in the Lake Tana Basin: The Case of Gilgel Abay Catchment, Upper Blue Nile Basin, Ethiopia. Hydrology 2019, 6, 1–17. [Google Scholar]
- Ouédraogo, W.A.A.; Raude, J.M.; Gathenya, M.J. Continuous Modeling of the Mkurumudzi River Catchment in Kenya Using the HEC-HMS Conceptual Model: Calibration, Validation, Model Performance Evaluation and Sensitivity Analysis. Hydrol. Sci. J. 2018, 5, 44. [Google Scholar] [CrossRef]
- Katuva, J.M. Water Allocation Assessment: A Study of Hydrological Simulation on Mkurumudzi River Basin. Ph.D. Thesis, University of Nairobi, Nairobi, Kenya, 2014. [Google Scholar]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The climate hazards infrared precipitation with stations—A new environmental record for monitoring extremes. Sci. Data 2015, 2, 1–21. [Google Scholar] [CrossRef]
- Yared, B.; Tsegaye, T.; Getachew, D.; Andualem, S. Evaluation of Satellite-Based Rainfall Estimates and Application to Monitor Meteorological Drought for the Upper Blue Nile Basin, Ethiopia. Remote Sens. 2017, 9, 669. [Google Scholar]
- Legates, D.R.; Mccabe, G.J. Evaluating the Use Of “Goodness-of-Fit” Measures in Hydrologic and Hydroclimatic Model Validation Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of Models. Phys. Geogr. 2013, 37–41. [Google Scholar] [CrossRef]
- Santhi, C.; Arnold, J.G.; Williams, J.R.; Dugas, W.A.; Srinivasan, R.; Hauck, L.M. Validation of the SWAT model on a large river basin with point and nonpoint sources. J. Am. Water Resour. Assoc. 2002, 37, 1169–1188. [Google Scholar] [CrossRef]
- Van Pelt, S.C.; Beersma, J.J.; Buishand, T.A.; van den Hurk, B.J.J.M.; Kabat, P. Future changes in extreme precipitation in the Rhine basin based on global and regional climate model simulations. Hydrol. Earth Syst. Sci. 2012, 16, 4517–4530. [Google Scholar] [CrossRef]
- Lee, H.; Goodman, A.; Mcgibbney, L.; Waliser, D.E.; Kim, J.; Loikith, P.C.; Gibson, P.B.; Massoud, E.C. Regional Climate Model Evaluation System powered by Apache Open Climate Workbench v1. 3.0: An enabling tool for facilitating regional climate studies. Geosci. Model Dev. 2018, 11, 4435–4449. [Google Scholar] [CrossRef]
- Waliser, D.E.; Kyo, L.; Goodman, A.; Wilson, B.; Loikith, P.; Gibson, P.B.; Massoud, E.C.; Zimdars, P.A. Tutorials Overview: Regional Climate Model Evaluation System. Available online: https://rcmes.jpl.nasa.gov/content/tutorials-overview (accessed on 31 January 2019).
- Riahi, K.; Grübler, A.; Nakicenovic, N. Scenarios of long-term socio-economic and environmental development under climate stabilization. Technol. Forecast. Soc. Chang. 2007, 74, 887–935. [Google Scholar] [CrossRef]
- Masui, T.; Matsumoto, K.; Hijioka, Y.; Kinoshita, T.; Nozawa, T.; Ishiwatari, S.; Kato, E.; Shukla, P.R.; Yamagata, Y.; Kainuma, M. An emission pathway to stabilize at 6 W/m2 of radiative forcing. Clim. Chang. Chang. 2011. [Google Scholar] [CrossRef]
- Thomson, A.M.; Calvin, K.V.; Smith, S.J.; Kyle, G.P.; Volke, A.; Patel, P.; Delgado-Arias, S.; Bond-Lamberty, B.; Wise, M.A.; Clarke, L.E. RCP4.5: A pathway for stabilization of radiative forcing by 2100. Clim. Chang. 2011, 109, 77. [Google Scholar] [CrossRef]
- Van Vuuren, D.P.; Stehfest, E.; Den Elzen, M.G.J.; Deetman, S.; Hof, A.; Isaac, M.; Klein Goldewijk, K.; Kram, T.; Mendoza Beltran, A.; Oostenrijk, R. RCP2.6: Exploring the possibility to keep global mean temperature change below 2 °C. Clim. Chang. 2011, 109, 95. [Google Scholar] [CrossRef]
- Feldman, A.D. Hydrologic modeling system HEC-HMS, Technical Reference Manual. Tech. Ref. Man. 2000, 145. [Google Scholar]
- Kraaijenbrink, P. Advanced Delta Change Method: Extension of an Application to CMIP5 GCMs; KNMI: De Bilt, The Netherlands, 2013. [Google Scholar]
- Markovic, R.D. Probability Functions of Best Fit to Distributions of Annual Precipitation and Runoff. In Colorado State University Hydrology Paper No. 8; Colorado State University: Fort Collins, CO, USA, 1965. [Google Scholar]
- Alam, A.A.; Emura, K.; Farnham, C.; Yuan, J. Best-Fit Probability Distributions and Return Periods for Maximum Monthly Rainfall in Bangladesh. Climate 2018, 6, 9. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Allis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments, 1st ed.; Cambridge University Press: Cambridge, UK, 1997; ISBN 978-0-521-43045-6. [Google Scholar]
- Conover, W.J. Practical Nonparametric Statistics, 3rd ed.; JohnWiley & Sons, Inc.: New York, NY, USA, 1999; ISBN 0471160687. [Google Scholar]
- O’Connor, P.D.T.; Kleyner, A. Appendix 3 Kolmogorov—Smirnov Tables. In Practical Reliability Engineering; John Wiley & Sons, Inc.: New York, NY, USA, 2012; pp. 455–456. [Google Scholar]
- Dinku, T.; Funk, C.; Peterson, P.; Maidment, R.; Tadesse, T.; Gadain, H.; Ceccato, P. Validation of the CHIRPS satellite rainfall estimates over eastern Africa. Q. J. R. Meteorol. Soc. 2018, 144, 292–312. [Google Scholar] [CrossRef]
- Kim, J.; Waliser, D.E.; Mattmann, C.A.; Goodale, C.E.; Hart, A.F.; Zimdars, P.A.; Crichton, D.J.; Jones, C.; Nikulin, G.; Hewitson, B.; et al. Evaluation of the CORDEX-Afrcia multi-RCM hindcast: Systematic model errors. Clim. Dyn. 2013, 42, 1189–1202. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Kisembe, J.; Favre, A.; Dosio, A.; Lennard, C.; Sabiiti, G.; Nimusiima, A. Evaluation of rainfall simulations over Uganda in CORDEX regional climate models. Theor. Appl. Climatol. 2018, 1–19. [Google Scholar] [CrossRef]

| No. | Performance Rating | R2 | d | RSR |
|---|---|---|---|---|
| 1 | Very Good | 0.75 to 1 | 0.90 to 1 | 0 to 0.50 |
| 2 | Good | 0.65 to 0.75 | 0.75 to 0.90 | 0.50 to 0.60 |
| 3 | Satisfactory | 0.50 to 0.65 | 0.50 to 0.75 | 0.60 to 0.70 |
| 4 | Unsatisfactory | <0.50 | <0.50 | >0.70 |
| RCMs | Institute | Driving GCMs | ID |
|---|---|---|---|
| CLMcom-CCLM4-8-17 | Climate Limited-area Modelling Community (CLM-Community), Germany | MOHC-HadGEM2-ES | A |
| MPI-M-MPI-ESM-LR | B | ||
| CNRM-CERFACS-CNRM-CM5 | C | ||
| UQAM-CRCM5 | Universite du Québec à Montréal, Canada | MPI-M-MPI-ESM-LR | D |
| CCCma-CanESM2 | E | ||
| KNMI-RACMO22T | Royal Netherlands Meteorological Institute, De Bilt, The Netherlands | MOHC-HadGEM2-ES | F |
| ICHEC-EC-EARTH | G | ||
| SMHI-RCA4 | Swedish Meteorological and Hydrological Institute, Rossby Centre | CCCma-CanESM2 | H |
| NOAA-GFDL-GFDL-ESM2M | I | ||
| NCC-NorESM1-M | J | ||
| CNRM-CERFACS-CNRM-CM5 | K | ||
| CSIRO-QCCCE-CSIRO-Mk3-6-0 | L | ||
| IPSL-IPSL-CM5A-MR | M | ||
| MIROC-MIROC5 | N | ||
| MOHC-HadGEM2-ES | O | ||
| MPI-M-MPI-ESM-LR | P | ||
| GERICS-REMO2009 | Helmholtz-Zentrum Geesthacht, Climate Service Center Germany, Alfred Wegener Institute, Helmholtz Centre for Polar and Marine Research, Germany | MOHC-HadGEM2-ES | Q |
| MPI-M-MPI-ESM-LR | R | ||
| NOAA-GFDL-GFDL-ESM2G | S | ||
| IPSL-IPSL-CM5A-LR | T | ||
| MIROC-MIROC5 | U |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Monthly scale | ||||||||||
| R2 | 0.64 | 0.79 | 0.81 | 0.76 | 0.77 | 0.56 | 0.58 | 0.67 | 0.73 | 0.68 |
| d | 0.84 | 0.91 | 0.86 | 0.89 | 0.93 | 0.81 | 0.89 | 0.87 | 0.88 | 0.88 |
| RSR | 0.49 | 0.50 | 0.92 | 1.01 | 0.49 | 0.74 | 0.57 | 0.62 | 0.56 | 0.55 |
| Annual scale | ||||||||||
| R2 | 0.62 | 0.61 | 0.29 | 0.88 | 0.7 | 0.18 | 0.77 | 0.77 | 0.72 | 0.77 |
| d | 0.86 | 0.84 | 0.54 | 0.94 | 0.89 | 0.55 | 0.92 | 0.9 | 0.8 | 0.83 |
| RSR | 0.69 | 0.77 | 0.99 | 0.42 | 0.56 | 1.17 | 0.52 | 0.59 | 0.91 | 0.82 |
| *Corresponding Stations’ Names | Kidongo Park’s Gate | Kwale Forest Station | Associated Sugar works | Lukore Primary school | Kikokeni Agricultural station | Mkongani Chief’s Camp | Kinango Agricultural Office | Msambweni Agricultural Office | Kinango Pumping station | WAA Dispensary |
| Rainfall Data Periods | Start Year–End Year |
|---|---|
| Observed period | 1982–1992 |
| Control period | 1982–1992 |
| Validation period | 2006–2016 |
| Observed period for validation | 2006–2016 |
| Stations | Statistics | P10 | P30 | P60 | P90 |
|---|---|---|---|---|---|
| M1 | RSR | 0.7 | 0.6 | 0.7 | 0.7 |
| R2 | 0.6 | 0.7 | 0.6 | 0.7 | |
| d | 0.9 | 0.9 | 0.9 | 0.9 | |
| M2 | RSR | 0.9 | 0.7 | 0.6 | 0.7 |
| R2 | 0.3 | 0.6 | 0.7 | 0.7 | |
| d | 0.7 | 0.9 | 0.9 | 0.9 | |
| M3 | RSR | 0.6 | 0.4 | 0.5 | 0.7 |
| R2 | 0.6 | 0.8 | 0.8 | 0.7 | |
| d | 0.9 | 1.0 | 0.9 | 0.9 | |
| M4 | RSR | 1.1 | 1.0 | 0.6 | 0.7 |
| R2 | 0.3 | 0.6 | 0.8 | 0.7 | |
| d | 0.7 | 0.8 | 0.9 | 0.9 | |
| M5 | RSR | 0.7 | 0.4 | 0.5 | 0.7 |
| R2 | 0.6 | 0.9 | 0.8 | 0.7 | |
| d | 0.9 | 1.0 | 1.0 | 0.9 |
| Ratio | Ratio | |||||
|---|---|---|---|---|---|---|
| Control Series (mm) | Future Series (mm) | Observed Series (mm) | Transformed Series (mm) | |||
| Months | (1982–2005) | (2018–2041) | (1982–2005) | (2018–2041) | ||
| January | 4.4 | 4.4 | 1.0 | 0.4 | 0.3 | 1.0 |
| February | 3.6 | 5.2 | 1.4 | 0.0 | 0.0 | 1.0 |
| March | 6.1 | 9.5 | 1.6 | 0.3 | 0.4 | 1.3 |
| April | 17.4 | 19.1 | 1.1 | 6.2 | 7.2 | 1.2 |
| May | 18.6 | 22.1 | 1.2 | 3.3 | 3.8 | 1.2 |
| June | 10.7 | 11.8 | 1.1 | 5.5 | 6.4 | 1.2 |
| July | 7.8 | 8.4 | 1.1 | 2.6 | 2.7 | 1.1 |
| Average | 9.8 | 11.5 | 1.2 | 2.6 | 3.0 | 1.1 |
| August | 7.6 | 6.9 | 0.9 | 0.9 | 0.8 | 0.8 |
| September | 9.3 | 7.0 | 0.8 | 0.5 | 0.4 | 0.7 |
| October | 15.1 | 11.5 | 0.8 | 0.6 | 0.4 | 0.8 |
| November | 16.1 | 12.4 | 0.8 | 2.4 | 2.0 | 0.8 |
| December | 8.0 | 6.0 | 0.7 | 0.2 | 0.2 | 0.9 |
| Average | 11.2 | 8.8 | 0.8 | 0.9 | 0.7 | 0.8 |
| Ratio | Ratio | |||||
|---|---|---|---|---|---|---|
| Control Series | Future Series | Observed Series | Transformed Series | |||
| Months | (1982–2005) | (2018–2041) | (1982–2005) | (2018–2041) | ||
| January | 12.8 | 12.7 | 1.0 | 10.5 | 12.6 | 1.2 |
| February | 11.4 | 16.8 | 1.5 | 6.7 | 10.0 | 1.5 |
| March | 18.6 | 23.3 | 1.3 | 30.1 | 36.5 | 1.2 |
| April | 38.6 | 40.9 | 1.1 | 85.7 | 93.6 | 1.1 |
| May | 40.4 | 45.1 | 1.1 | 149.1 | 161.4 | 1.1 |
| June | 27.5 | 28.4 | 1.0 | 44.4 | 47.6 | 1.1 |
| July | 18.7 | 20.0 | 1.1 | 35.2 | 32.3 | 0.9 |
| Average | 24.0 | 26.7 | 1.1 | 51.7 | 56.3 | 1.2 |
| August | 19.2 | 17.6 | 0.9 | 24.8 | 20.3 | 0.8 |
| September | 24.8 | 18.4 | 0.7 | 17.1 | 12.4 | 0.7 |
| October | 37.5 | 26.2 | 0.7 | 40.0 | 28.2 | 0.7 |
| November | 32.2 | 28.4 | 0.9 | 44.0 | 35.9 | 0.8 |
| December | 23.7 | 16.8 | 0.7 | 32.9 | 29.0 | 0.9 |
| Average | 27.4 | 21.5 | 0.8 | 31.8 | 25.2 | 0.8 |
| Seasons | Distributions | M1 | M2 | M3 | M4 | M5 | Average Dmax | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p-Value | p-Value | p-Value | p-value | p-Value | ||||||||
| MAMJ | LogNormal | 0.079 | 0.99 | 0.063 | 1.00 | 0.092 | 0.96 | 0.097 | 0.94 | 0.084 | 0.98 | 0.083 |
| Log Pearson III | 0.071 | 1.00 | 0.059 | 1.00 | 0.083 | 0.98 | 0.079 | 0.99 | 0.071 | 1.00 | 0.073 | |
| GEV-Max (L-moments) | 0.084 | 0.98 | 0.058 | 1.00 | 0.085 | 0.98 | 0.078 | 0.99 | 0.076 | 0.99 | 0.076 | |
| Pareto (L-moments) | 0.074 | 1.00 | 0.057 | 1.00 | 0.088 | 0.97 | 0.060 | 1.00 | 0.067 | 1.00 | 0.069 | |
| OND | Exponential (L-moments) | 0.072 | 1.00 | 0.067 | 1.00 | 0.075 | 0.99 | 0.089 | 0.97 | 0.093 | 0.96 | 0.079 |
| Log Pearson III | 0.081 | 0.99 | 0.084 | 0.98 | 0.084 | 0.98 | 0.093 | 0.96 | 0.100 | 0.93 | 0.09 | |
| Pareto (L-moments) | 0.072 | 1.00 | 0.067 | 1.00 | 0.077 | 0.99 | 0.088 | 0.97 | 0.097 | 0.95 | 0.080 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ouédraogo, W.A.A.; Gathenya, J.M.; Raude, J.M. Projecting Wet Season Rainfall Extremes Using Regional Climate Models Ensemble and the Advanced Delta Change Model: Impact on the Streamflow Peaks in Mkurumudzi Catchment, Kenya. Hydrology 2019, 6, 76. https://doi.org/10.3390/hydrology6030076
Ouédraogo WAA, Gathenya JM, Raude JM. Projecting Wet Season Rainfall Extremes Using Regional Climate Models Ensemble and the Advanced Delta Change Model: Impact on the Streamflow Peaks in Mkurumudzi Catchment, Kenya. Hydrology. 2019; 6(3):76. https://doi.org/10.3390/hydrology6030076
Chicago/Turabian StyleOuédraogo, Wendso Awa Agathe, John Mwangi Gathenya, and James Messo Raude. 2019. "Projecting Wet Season Rainfall Extremes Using Regional Climate Models Ensemble and the Advanced Delta Change Model: Impact on the Streamflow Peaks in Mkurumudzi Catchment, Kenya" Hydrology 6, no. 3: 76. https://doi.org/10.3390/hydrology6030076
APA StyleOuédraogo, W. A. A., Gathenya, J. M., & Raude, J. M. (2019). Projecting Wet Season Rainfall Extremes Using Regional Climate Models Ensemble and the Advanced Delta Change Model: Impact on the Streamflow Peaks in Mkurumudzi Catchment, Kenya. Hydrology, 6(3), 76. https://doi.org/10.3390/hydrology6030076





