How Surface Radiation on Forested Snowpack Changes across a Latitudinal Gradient
Abstract
1. Introduction
2. Materials and Methods
2.1. Radiation Calculations in FoRM
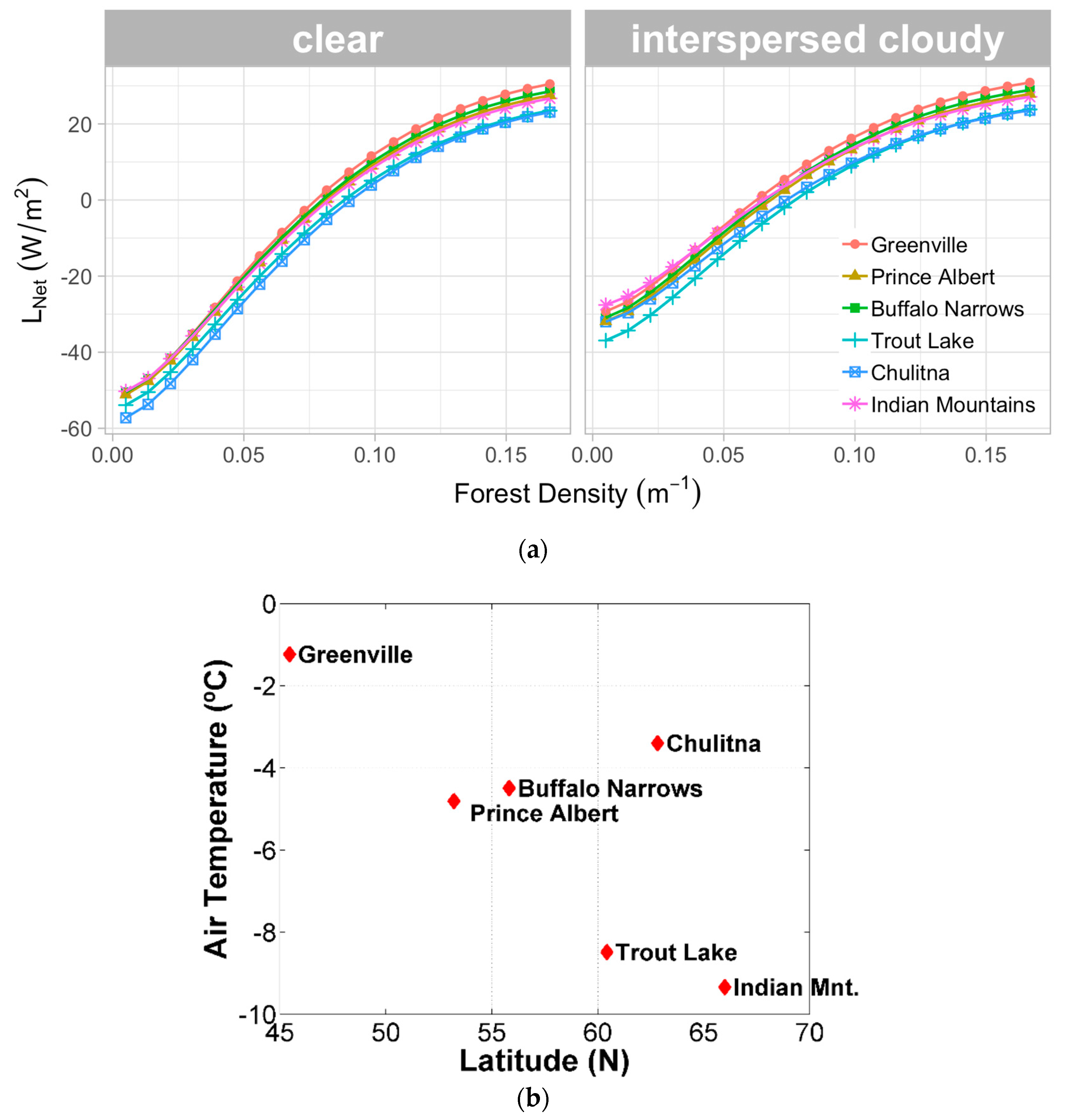
2.2. Study Areas
3. Results and Discussion
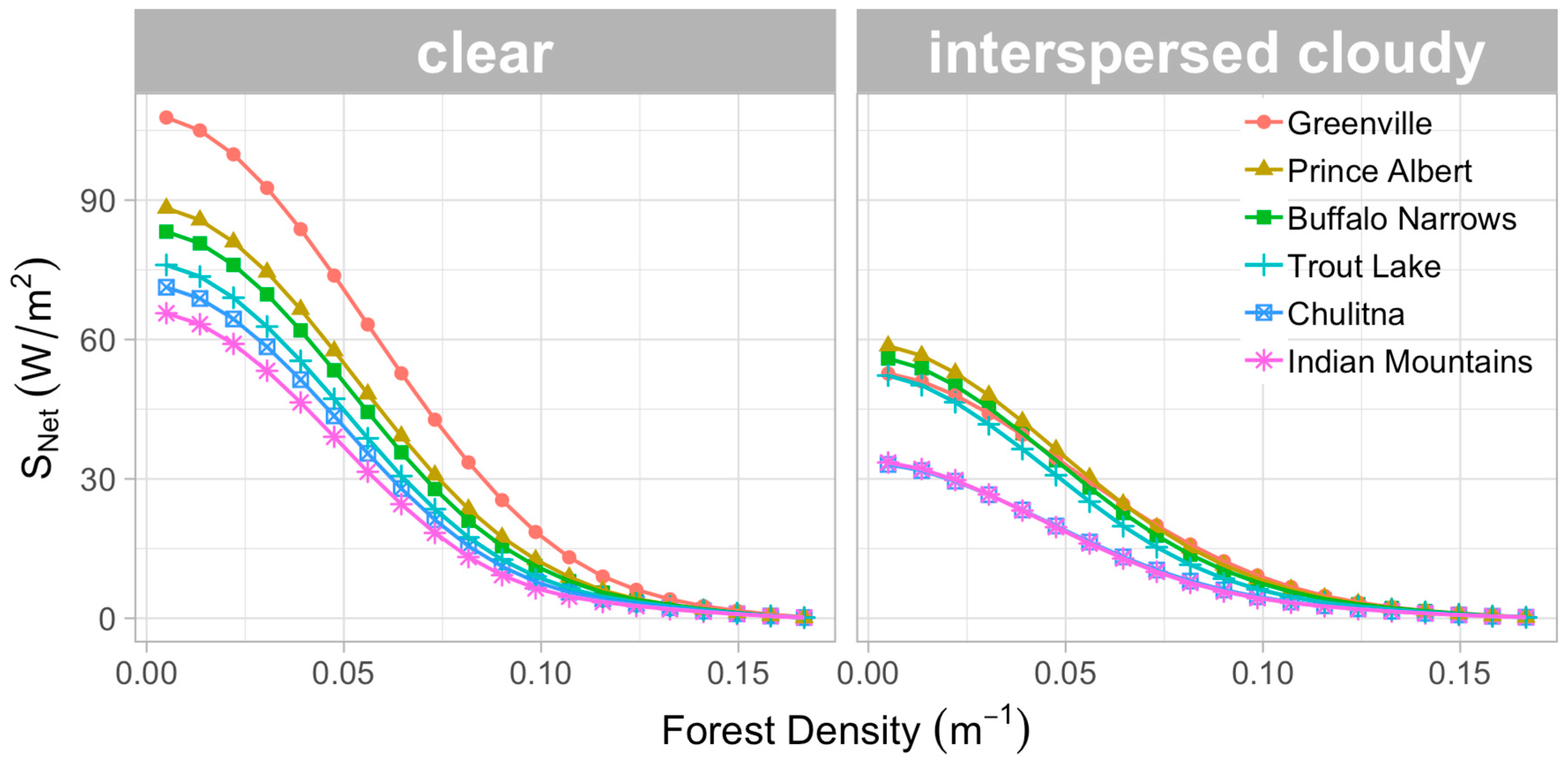
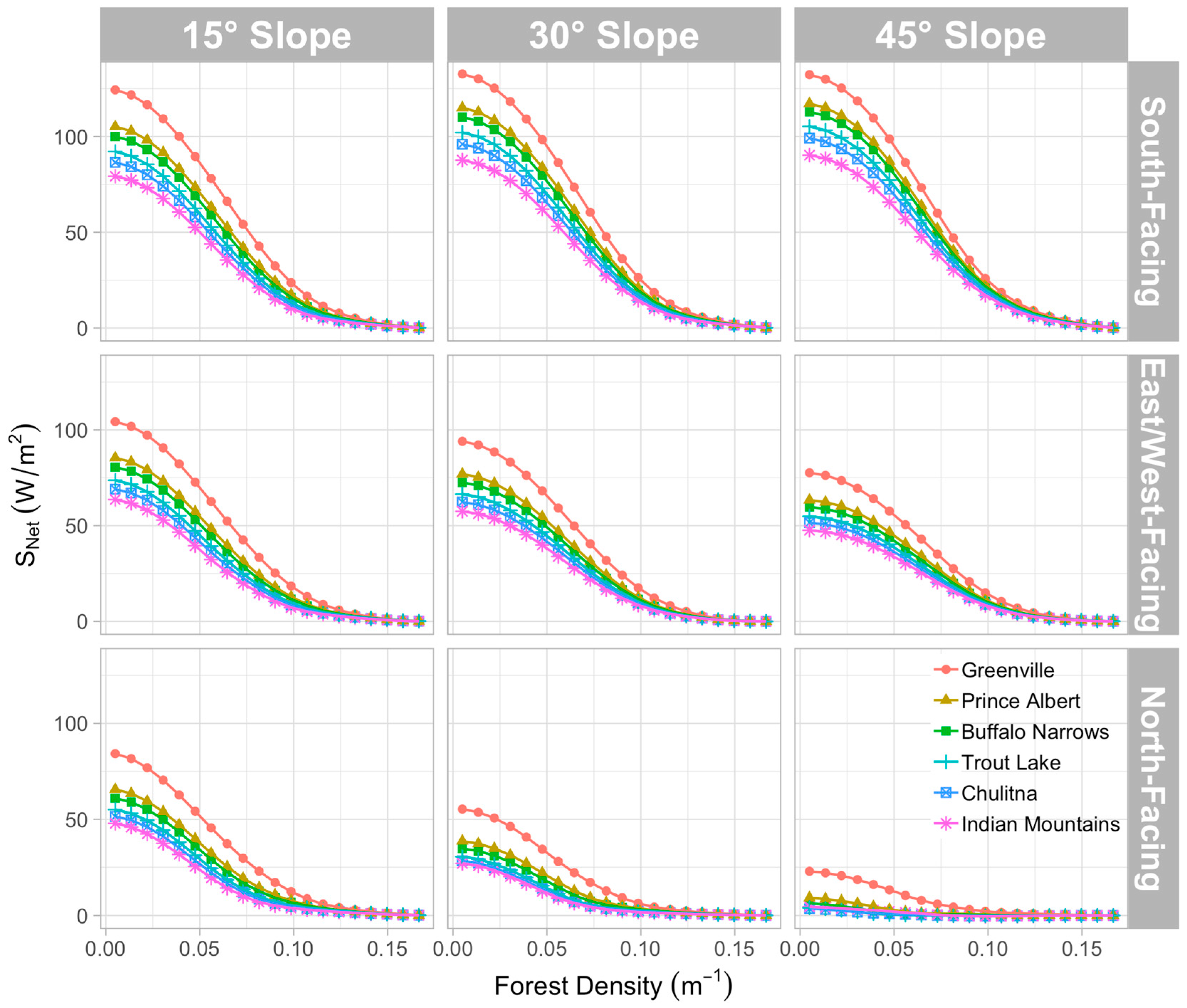
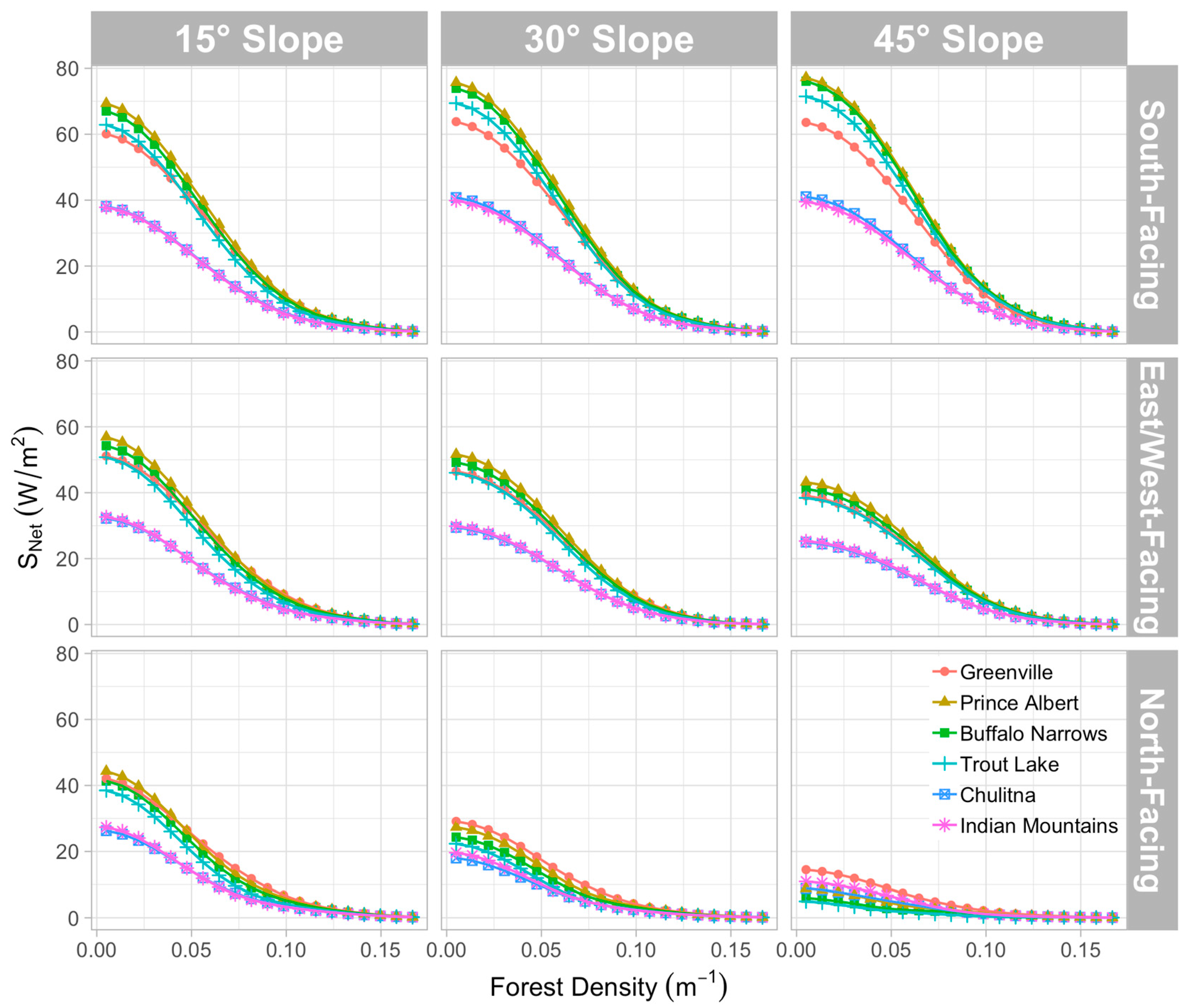
3.1. Effects of Latitudinal Location and Meteorological Characteristics on Net Shortwave Radiation Reaching the Forest Floor
3.1.1. On a Level Forest Floor
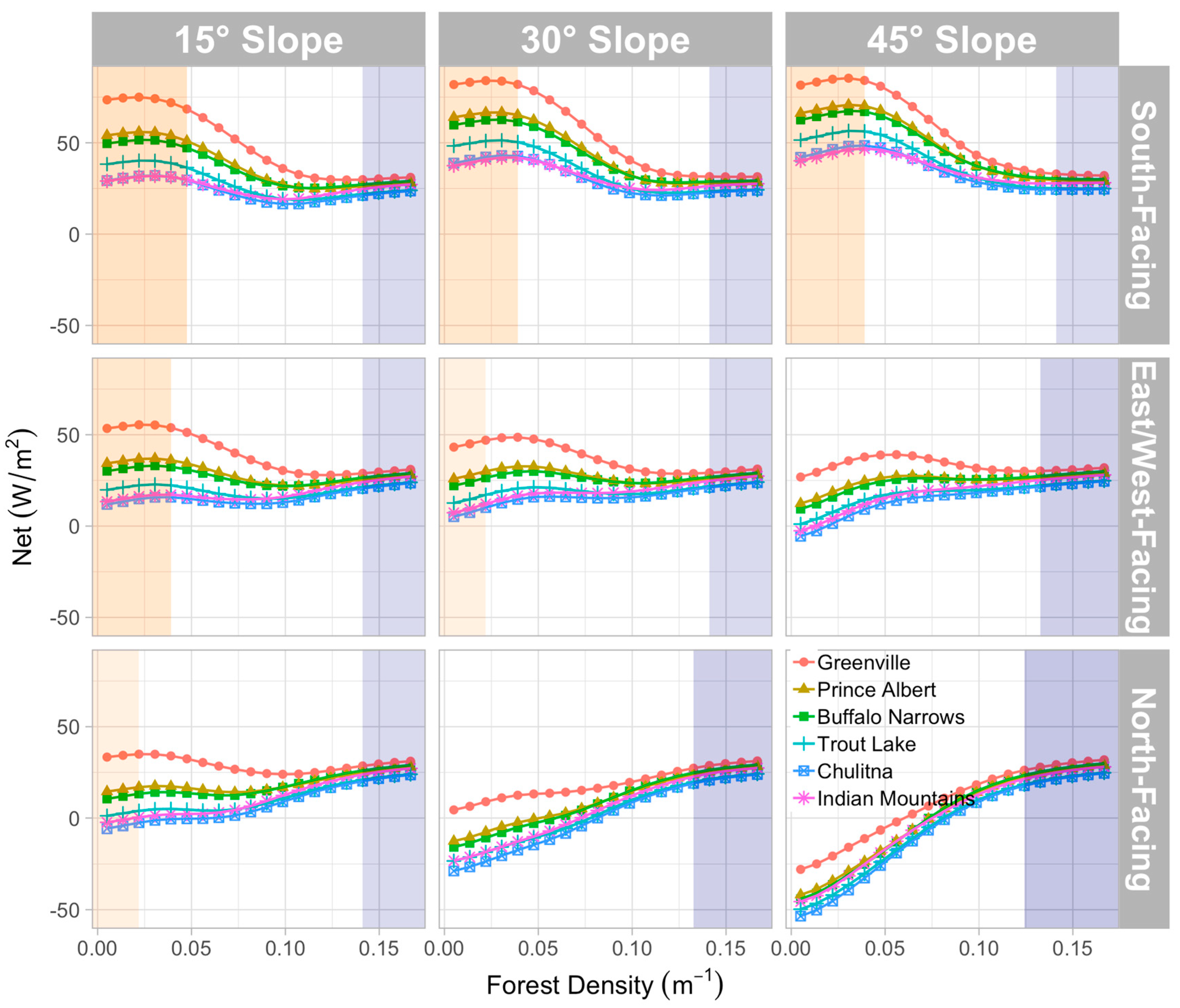
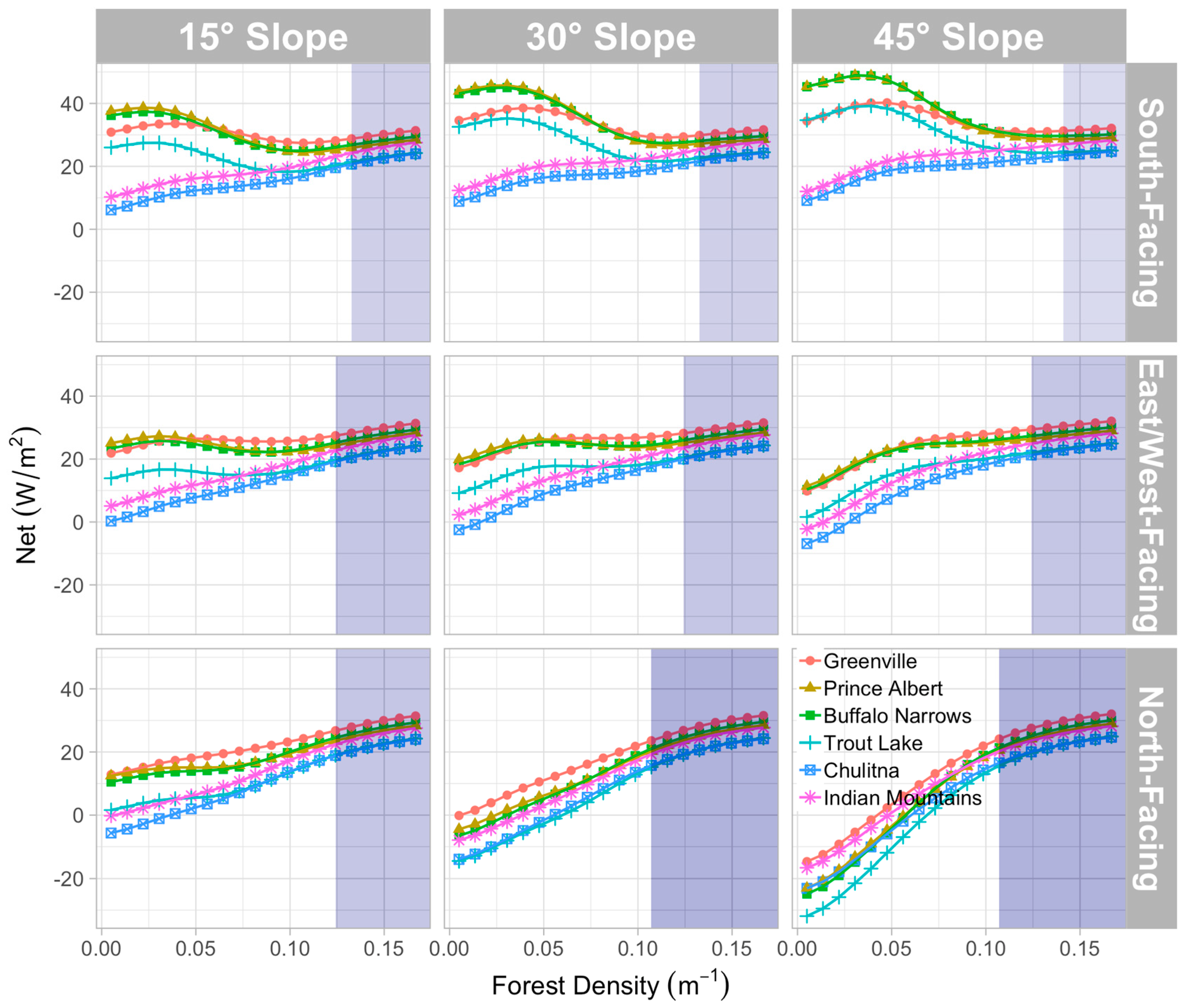
3.1.2. On a Sloping Forest Floor
3.2. Effects of Latitudinal Location and Meteorological Characteristics on Net Longwave Radiation Reaching the Forest Floor
3.2.1. On a Level Forest Floor
3.2.2. On a Sloping Forest Floor
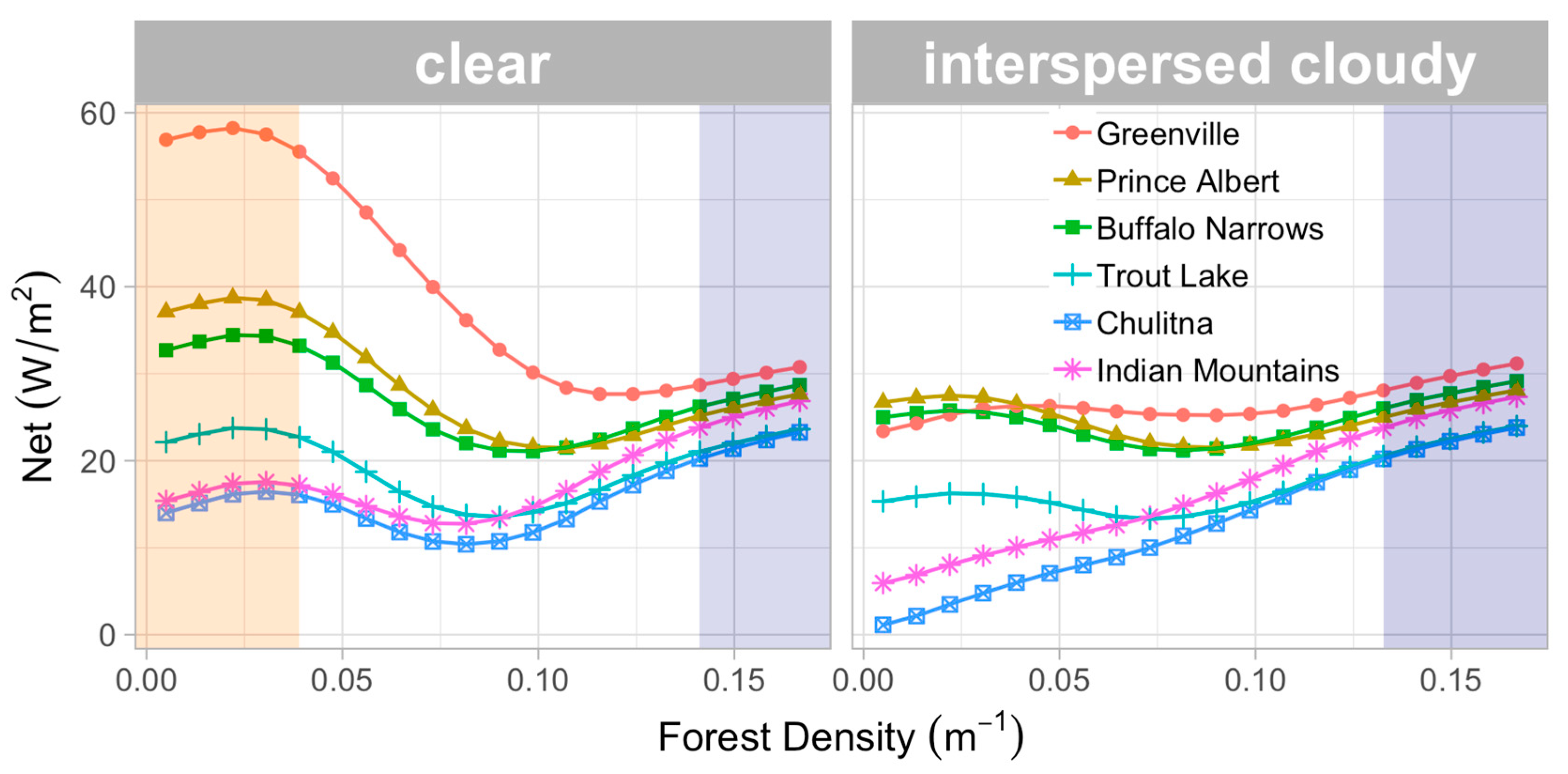
3.3. Net Radiation Variability
3.3.1. On a Level Forest Floor
3.3.2. On a Sloping Forest Floor
4. Conclusions
5. Data and Code Availability
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Bales, R.C.; Molotch, N.P.; Painter, T.H.; Dettinger, M.D.; Rice, R.; Dozier, J. Mountain hydrology of the western United States. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303. [Google Scholar] [CrossRef] [PubMed]
- Trujillo, E.; Molotch, N.P.; Goulden, M.L.; Kelly, A.E.; Bales, R.C. Elevation-dependent influence of snow accumulation on forest greening. Nat. Geosci. 2012, 5, 705. [Google Scholar] [CrossRef]
- Madani, K.; Lund, J.R. Estimated impacts of climate warming on California’s high-elevation hydropower. Clim. Chang. 2010, 102, 521–538. [Google Scholar] [CrossRef]
- Kumar, M.; Marks, D.; Dozier, J.; Reba, M.; Winstral, A. Evaluation of distributed hydrologic impacts of temperature-index and energy-based snow models. Adv. Water Resour. 2013, 56, 77–89. [Google Scholar] [CrossRef]
- Wang, R.; Kumar, M.; Marks, D. Anomalous trend in soil evaporation in a semi-arid, snow-dominated watershed. Adv. Water Resour. 2013, 57, 32–40. [Google Scholar] [CrossRef]
- Aguado, E. Radiation Balances of Melting Snow Covers at an Open Site in the Central Sierra-Nevada, California. Water Resour. Res. 1985, 21, 1649–1654. [Google Scholar] [CrossRef]
- Bohren, C.F.; Thorud, D.B. 2 Theoretical Models of Radiation Heat-Transfer between Forest Trees and Snowpacks. Agric. Meteorol. 1973, 11, 3–16. [Google Scholar] [CrossRef]
- Elder, K.; Dozier, J.; Michaelsen, J. Snow Accumulation and Distribution in an Alpine Watershed. Water Resour. Res. 1991, 27, 1541–1552. [Google Scholar] [CrossRef]
- Pomeroy, J.W.; Marks, D.; Link, T.; Ellis, C.; Hardy, J.; Rowlands, A.; Granger, R. The impact of coniferous forest temperature on incoming longwave radiation to melting snow. Hydrol. Process. 2009, 23, 2513–2525. [Google Scholar] [CrossRef]
- Sicart, J.E.; Pomeroy, J.W.; Essery, R.L.H.; Bewley, D. Incoming longwave radiation to melting snow: observations, sensitivity and estimation in northern environments. Hydrol. Process. 2006, 20, 3697–3708. [Google Scholar] [CrossRef]
- Price, A.G. Prediction of Snowmelt Rates in a Deciduous Forest. J. Hydrol. 1988, 101, 145–157. [Google Scholar] [CrossRef]
- Webster, C.; Rutter, N.; Zahner, F.; Jonas, T. Modeling subcanopy incoming longwave radiation to seasonal snow using air and tree trunk temperatures. J. Geophys. Res. Atmos. 2016, 121, 1220–1235. [Google Scholar] [CrossRef]
- Musselman, K.N.; Pomeroy, J.W.; Link, T.E. Variability in shortwave irradiance caused by forest gaps: Measurements, modelling, and implications for snow energetics. Agric. For. Meteorol. 2015, 207, 69–82. [Google Scholar] [CrossRef]
- Malle, J.; Rutter, N.; Mazzotti, G.; Jonas, T. Shading by trees and fractional snow cover control the sub-canopy radiation budget. J. Geophys. Res. Atmos. 2019, 124, 3195–3207. [Google Scholar] [CrossRef]
- Seyednasrollah, B.; Kumar, M.; Link, T.E. On the role of vegetation density on net snow cover radiation at the forest floor. J. Geophys. Res. Atmos. 2013, 118, 8359–8374. [Google Scholar] [CrossRef]
- Reifsnyder, W.E.; Lull, H.W. Radiant Energy in Relation to Forests; U.S. Department of Agriculture, Forest Service; U.S. Government Publishing Office: Washington, DC, USA, 1965; 111p.
- USACE. Snow Hydrology: Summary Report of the Snow Investigations; North Pacific Division, Corps of Engineers, U.S. Army: Portland, OR, USA, 1956; 437p.
- Seyednasrollah, B.; Kumar, M. Net radiation in a snow-covered discontinuous forest gap for a range of gap sizes and topographic configurations. J. Geophys. Res. Atmos. 2014, 119, 10323–10342. [Google Scholar] [CrossRef]
- Lundquist, J.D.; Dickerson-Lange, S.E.; Lutz, J.A.; Cristea, N.C. Lower forest density enhances snow retention in regions with warmer winters: A global framework developed from plot-scale observations and modeling. Water Resour. Res. 2013, 49, 6356–6370. [Google Scholar] [CrossRef]
- Seyednasrollah, B.; Kumar, M. Effects of tree morphometry on net snow cover radiation on forest floor for varying vegetation densities. J. Geophys. Res. Atmos. 2013, 118, 12508–12521. [Google Scholar] [CrossRef]
- Webster, C.; Rutter, N.; Jonas, T. Improving representation of canopy temperatures for modeling subcanopy incoming longwave radiation to the snow surface. J. Geophys. Res. Atmos. 2017, 122, 9154–9172. [Google Scholar] [CrossRef]
- Marthews, T.R.; Malhi, Y.; Iwata, H. Calculating downward longwave radiation under clear and cloudy conditions over a tropical lowland forest site: an evaluation of model schemes for hourly data. Theor. Appl. Climatol. 2012, 107, 461–477. [Google Scholar] [CrossRef]
- Seyednasrollah, B. FoRM: A physically based forest radiation model. Zenodo 2014. [Google Scholar] [CrossRef]
- Arbor Day Foundation (ADF). Tree Details—The Tree Guide at arborday.org. Available online: http://www.arborday.org/trees/treeGuide/TreeDetail.cfm?ID=39 (accessed on 7 January 2012).
- Lawler, R.R.; Link, T.E. Quantification of incoming all-wave radiation in discontinuous forest canopies with application to snowmelt prediction. Hydrol. Process. 2011, 25, 3322–3331. [Google Scholar] [CrossRef]
- Andreas, E.L. A New Method of Measuring the Snow-Surface Temperature. Cold Reg. Sci. Technol. 1986, 12, 139–156. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Vogel, C.A.; Hall, B. Seasonal variation of energy and water vapor exchange rates above and below a boreal jack pine forest canopy. J. Geophys. Res. Atmos. 1997, 102, 28939–28951. [Google Scholar] [CrossRef]
- Saugier, B.; Granier, A.; Pontailler, J.; Dufrene, E.; Baldocchi, D. Transpiration of a boreal pine forest measured by branch bag, sap flow and micrometeorological methods. Tree Physiol. 1997, 17, 511–519. [Google Scholar] [CrossRef]
- Warren, S.G. Optical-Properties of Snow. Rev. Geophys. 1982, 20, 67–89. [Google Scholar] [CrossRef]
- Dozier, J.; Warren, S.G. Effect of Viewing Angle on the Infrared Brightness Temperature of Snow. Water Resour. Res. 1982, 18, 1424–1434. [Google Scholar] [CrossRef]
- Prata, A.J. A new long-wave formula for estimating downward clear-sky radiation at the surface. Q. J. R. Meteor. Soc. 1996, 122, 1127–1151. [Google Scholar] [CrossRef]
- Kimball, B.A.; Idso, S.B.; Aase, J.K. A Model of Thermal-Radiation from Partly Cloudy and Overcast Skies. Water Resour. Res. 1982, 18, 931–936. [Google Scholar] [CrossRef]
- Flerchinger, G.; Xaio, W.; Marks, D.; Sauer, T.; Yu, Q. Comparison of algorithms for incoming atmospheric long-wave radiation. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Warren, S.G.; Wiscombe, W.J. A Model for the Spectral Albedo of Snow. II: Snow Containing Atmospheric Aerosols. J. Atmos. Sci. 1980, 37, 2734–2745. [Google Scholar] [CrossRef]
- Wiscombe, W.J.; Warren, S.G. A Model for the Spectral Albedo of Snow. I: Pure Snow. J. Atmos. Sci. 1980, 37, 2712–2733. [Google Scholar] [CrossRef]
- Melloh, R.A.; Hardy, J.P.; Bailey, R.N.; Hall, T.J. An efficient snow albedo model for the open and sub-canopy. Hydrol. Process. 2002, 16, 3571–3584. [Google Scholar] [CrossRef]
- Wang, Z.; Zeng, X.B. Evaluation of Snow Albedo in Land Models for Weather and Climate Studies. J. Appl. Meteorol. Clim. 2010, 49, 363–380. [Google Scholar] [CrossRef]
- Eck, T.F.; Deering, D.W. Canopy Albedo and Transmittance in a Boreal Forest. Remote Sens. Sci. Nineties 1990, 1–3, 883–886. [Google Scholar]
- Eck, T.F.; Deering, D.W. Canopy Albedo and Transmittance in a Spruce-Hemlock Forest in Mid-September. Agric. For. Meteorol. 1992, 59, 237–248. [Google Scholar] [CrossRef]
- Liu, B.Y.H.; Jordan, R.C. The Interrelationship and Characteristic Distribution of Direct, Diffuse and Total Solar Radiation. Sol. Energy 1960, 4, 1–19. [Google Scholar] [CrossRef]
- Monteith, J.L.; Unsworth, M.H. Principles of Environmental Physics, 3rd ed.; Elsevier: Amsterdam, The Netherlands; Boston, MA, USA, 2008; 418p. [Google Scholar]
- Campbell, G.S. Soil Physics with BASIC: Transport Models for Soil-Plant Systems; Elsevier: Amsterdam, The Netherlands; New York, NY, USA, 1985; 150p. [Google Scholar]
- Gryning, S.-E.; Batchvarova, E.; De Bruin, H. Energy balance of a sparse coniferous high-latitude forest under winter conditions. Bound Lay Meteorol. 2001, 99, 465–488. [Google Scholar] [CrossRef]
- Strong, W. Tree canopy effects on understory species abundance in high-latitude Populus tremuloides stands, Yukon, Canada. Community Ecol. 2011, 12, 89–98. [Google Scholar] [CrossRef]
- Ellis, C.; Pomeroy, J.; Essery, R.; Link, T. Effects of needleleaf forest cover on radiation and snowmelt dynamics in the Canadian Rocky Mountains. Can. J. For. Res. 2011, 41, 608–620. [Google Scholar] [CrossRef]
- Hardy, J.; Davis, R.; Jordan, R.; Li, X.; Woodcock, C.; Ni, W.; McKenzie, J. Snow ablation modeling at the stand scale in a boreal jack pine forest. J. Geophys. Res. Atmos. 1997, 102, 29397–29405. [Google Scholar] [CrossRef]
- Pomeroy, J.W.; Dion, K. Winter radiation extinction and reflection in a boreal pine canopy: Measurements and modelling. Hydrol. Process. 1996, 10, 1591–1608. [Google Scholar] [CrossRef]
- Koivusalo, H.; Kokkonen, T. Snow processes in a forest clearing and in a coniferous forest. J. Hydrol. 2002, 262, 145–164. [Google Scholar] [CrossRef]
- Hedstrom, N.; Pomeroy, J. Measurements and modelling of snow interception in the boreal forest. Hydrol. Process. 1998, 12, 1611–1625. [Google Scholar] [CrossRef]
- Essery, R.; Pomeroy, J.; Ellis, C.; Link, T. Modelling longwave radiation to snow beneath forest canopies using hemispherical photography or linear regression. Hydrol. Process. Int. J. 2008, 22, 2788–2800. [Google Scholar] [CrossRef]
- Molotch, N.P.; Barnard, D.M.; Burns, S.P.; Painter, T.H. Measuring spatiotemporal variation in snow optical grain size under a subalpine forest canopy using contact spectroscopy. Water Resour. Res. 2016, 52, 7513–7522. [Google Scholar] [CrossRef] [PubMed]
- Webster, C.; Rutter, N.; Zahner, F.; Jonas, T. Measurement of incoming radiation below forest canopies: A comparison of different radiometer configurations. J. Hydrometeorol. 2016, 17, 853–864. [Google Scholar] [CrossRef]
- Pretzsch, H. Canopy space filling and tree crown morphology in mixed-species stands compared with monocultures. For. Ecol. Manag. 2014, 327, 251–264. [Google Scholar] [CrossRef]
- Gratzer, G.; Darabant, A.; Chhetri, P.B.; Rai, P.B.; Eckmüllner, O. Interspecific variation in the response of growth, crown morphology, and survivorship to light of six tree species in the conifer belt of the Bhutan Himalayas. Can. J. For. Res. 2004, 34, 1093–1107. [Google Scholar] [CrossRef]
- Ford, K.R.; Ettinger, A.K.; Lundquist, J.D.; Raleigh, M.S.; Lambers, J.H.R. Spatial heterogeneity in ecologically important climate variables at coarse and fine scales in a high-snow mountain landscape. PLoS ONE 2013, 8, e65008. [Google Scholar] [CrossRef] [PubMed]
- Turnipseed, A.; Blanken, P.; Anderson, D.; Monson, R.K. Energy budget above a high-elevation subalpine forest in complex topography. Agric. For. Meteorol. 2002, 110, 177–201. [Google Scholar] [CrossRef]
- Seyednasrollah, B. solrad: To calculate solar radiation and related variables based on location, time and topographical conditions. Zenodo 2018. [Google Scholar] [CrossRef]
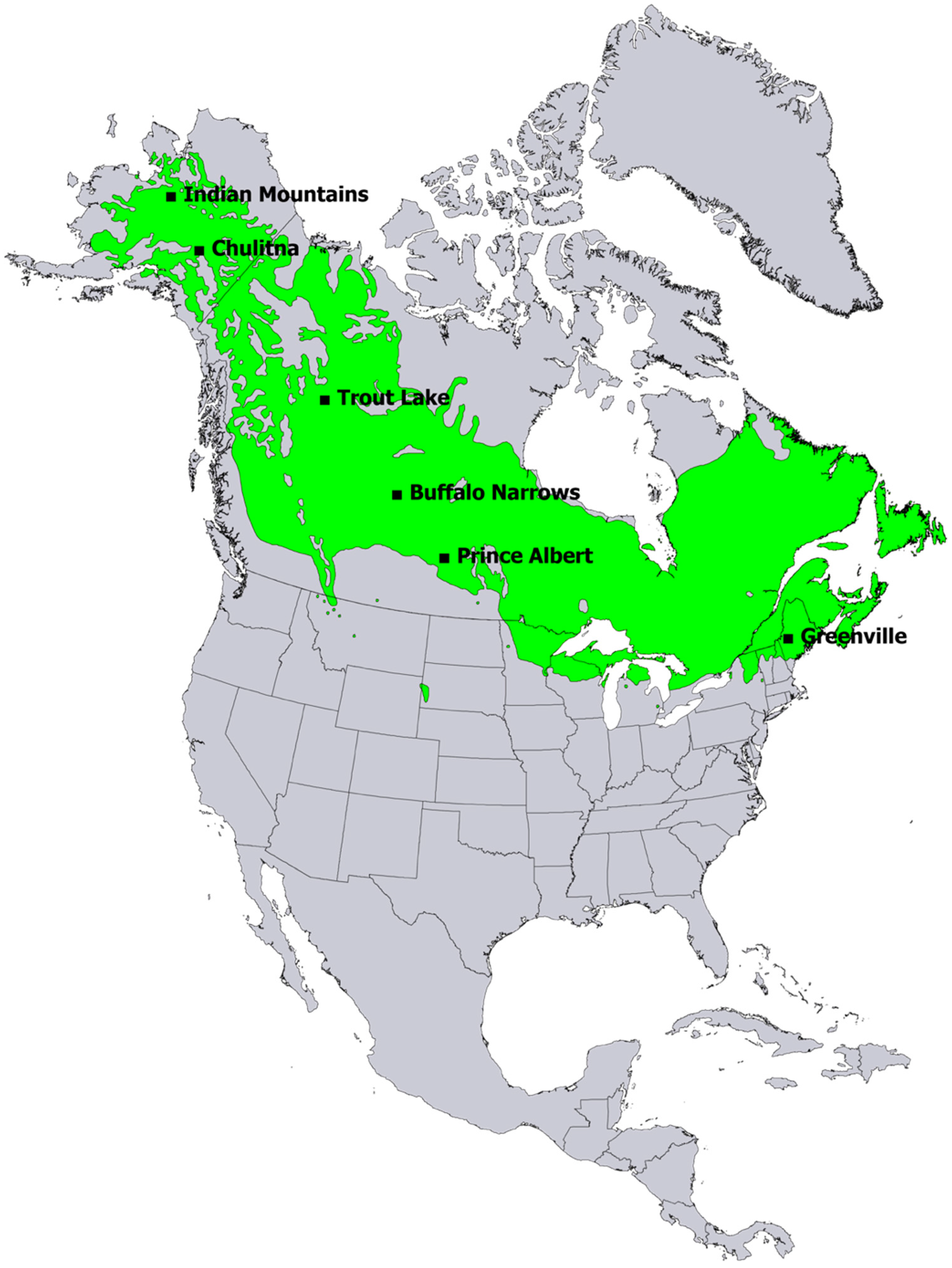
| Site | NCDC Code | Latitude (°N) | Longitude (°W) | Elevation (m) |
|---|---|---|---|---|
| Greenville, ME, USA | KGNR | 45.5 | 69.6 | 423 |
| Prince Albert, SK, Canada | CYPA | 53.2 | 105.7 | 428 |
| Buffalo Narrows, SK, Canada | CYVT | 55.8 | 108.4 | 440 |
| Trout Lake, BC, Canada | CWTE | 60.4 | 121.2 | 498 |
| Chulitna, AK, USA | PAEC | 62.8 | 149.9 | 411.5 |
| Indian Mountains, AK, USA | PAIM | 66.0 | 153.7 | 388.9 |
| Site | Observation Period | Seasonal Average Air Temperature (°C) | Seasonal Cloud Cover (%) |
|---|---|---|---|
| Greenville | 1982–2012 | −1.2 | 56 |
| Prince Albert | 1955–2012 | −4.8 | 53 |
| Buffalo Narrows | 1979–2012 | −4.5 | 53 |
| Trout Lake | 1994–2012 | −8.5 | 51 |
| Chulitna | 2006–2012 | −3.4 | 68 |
| Indian Mountains | 2005–2012 | −9.3 | 69 |
| Sky Condition | Site | ||||||
|---|---|---|---|---|---|---|---|
| Clear sky | Greenville | 0.12 | 27.7 | 0.02 | 58.2 | 56.9 | 30.8 |
| Prince Albert | 0.11 | 21.5 | 0.02 | 38.7 | 37.1 | 27.6 | |
| Buffalo Narrows | 0.1 | 21.1 | 0.02 | 34.4 | 32.7 | 28.7 | |
| Trout Lake | 0.09 | 13.6 | 0.02 | 23.8 | 22.1 | 23.6 | |
| Chulitna | 0.08 | 10.4 | 0.17 | 23.3 | 14 | 23.3 | |
| Indian Mountains | 0.08 | 12.7 | 0.17 | 26.9 | 15.4 | 26.9 | |
| Interspersed cloudy sky | Greenville | 0.01 | 23.4 | 0.17 | 31.2 | 23.4 | 31.2 |
| Prince Albert | 0.09 | 21.5 | 0.17 | 28.1 | 26.7 | 28.1 | |
| Buffalo Narrows | 0.08 | 21.2 | 0.17 | 29.1 | 25 | 29.1 | |
| Trout Lake | 0.07 | 13.3 | 0.17 | 24 | 15.3 | 24 | |
| Chulitna | 0.01 | 1.1 | 0.17 | 23.8 | 1.1 | 23.8 | |
| Indian Mountains | 0.01 | 5.9 | 0.17 | 27.3 | 5.9 | 27.3 |
| Sky Condition | Site | ||||||
|---|---|---|---|---|---|---|---|
| Clear sky | Greenville | 0.13 | 29.7 | 0.02 | 75 | 73.5 | 31.1 |
| Prince Albert | 0.12 | 24.8 | 0.02 | 55.9 | 54.1 | 28.1 | |
| Buffalo Narrows | 0.12 | 25.2 | 0.02 | 51.6 | 49.6 | 29.1 | |
| Trout Lake | 0.11 | 18.6 | 0.02 | 40.2 | 38.3 | 24 | |
| Chulitna | 0.11 | 16.5 | 0.03 | 32.1 | 29.3 | 23.6 | |
| Indian Mountains | 0.1 | 19.1 | 0.03 | 31.9 | 29.1 | 27.2 | |
| Interspersed cloudy sky | Greenville | 0.11 | 27.4 | 0.04 | 33.6 | 30.9 | 31.4 |
| Prince Albert | 0.11 | 24.5 | 0.02 | 38.7 | 37.5 | 28.4 | |
| Buffalo Narrows | 0.11 | 24.9 | 0.02 | 37.4 | 36.2 | 29.4 | |
| Trout Lake | 0.1 | 18.2 | 0.03 | 27.5 | 26 | 24.2 | |
| Chulitna | 0.01 | 6.1 | 0.17 | 24 | 6.1 | 24 | |
| Indian Mountains | 0.01 | 10.3 | 0.17 | 27.5 | 10.3 | 27.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seyednasrollah, B.; Kumar, M. How Surface Radiation on Forested Snowpack Changes across a Latitudinal Gradient. Hydrology 2019, 6, 62. https://doi.org/10.3390/hydrology6030062
Seyednasrollah B, Kumar M. How Surface Radiation on Forested Snowpack Changes across a Latitudinal Gradient. Hydrology. 2019; 6(3):62. https://doi.org/10.3390/hydrology6030062
Chicago/Turabian StyleSeyednasrollah, Bijan, and Mukesh Kumar. 2019. "How Surface Radiation on Forested Snowpack Changes across a Latitudinal Gradient" Hydrology 6, no. 3: 62. https://doi.org/10.3390/hydrology6030062
APA StyleSeyednasrollah, B., & Kumar, M. (2019). How Surface Radiation on Forested Snowpack Changes across a Latitudinal Gradient. Hydrology, 6(3), 62. https://doi.org/10.3390/hydrology6030062





