An Operational Method for Flood Directive Implementation in Ungauged Urban Areas
Abstract
1. Introduction
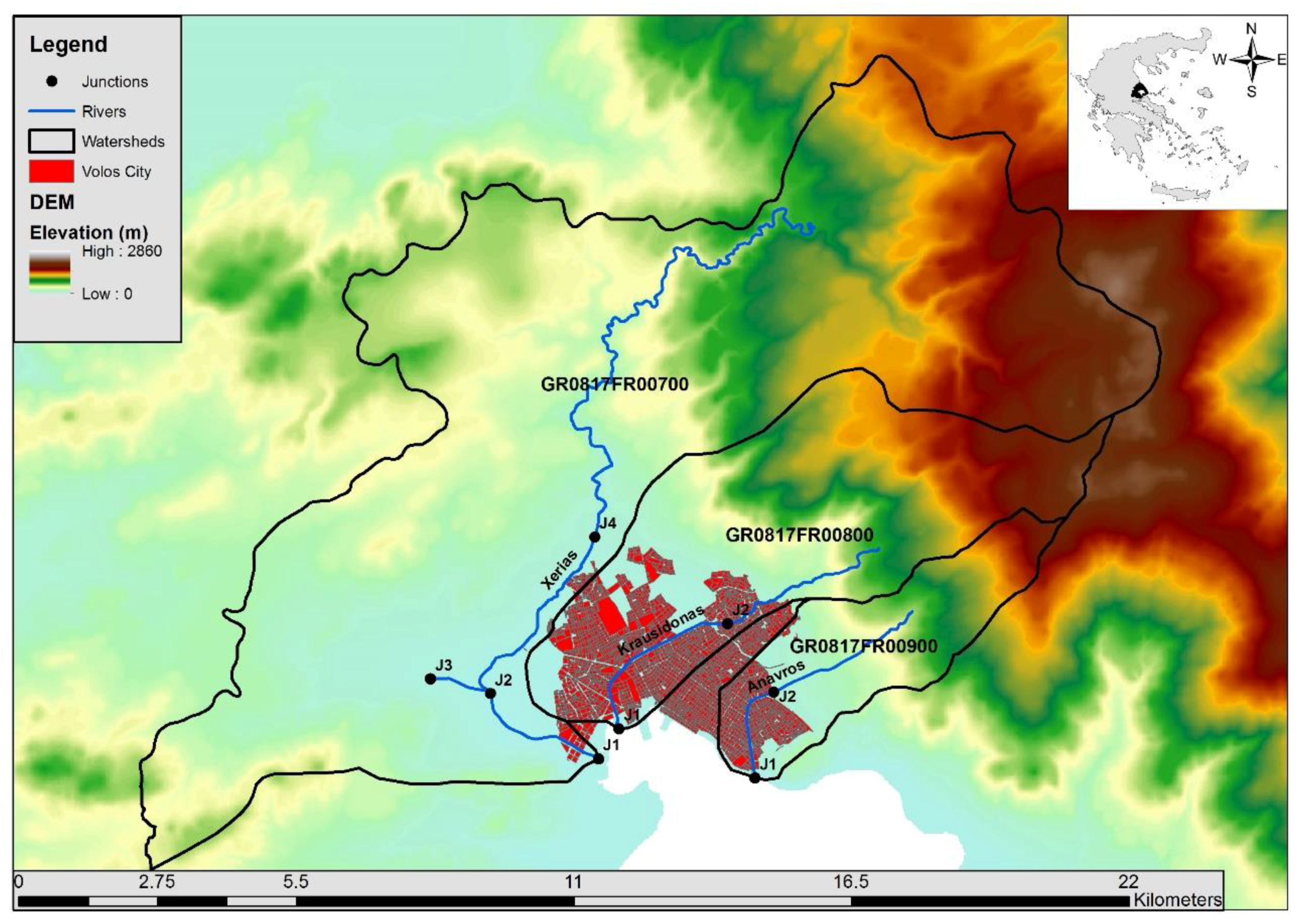
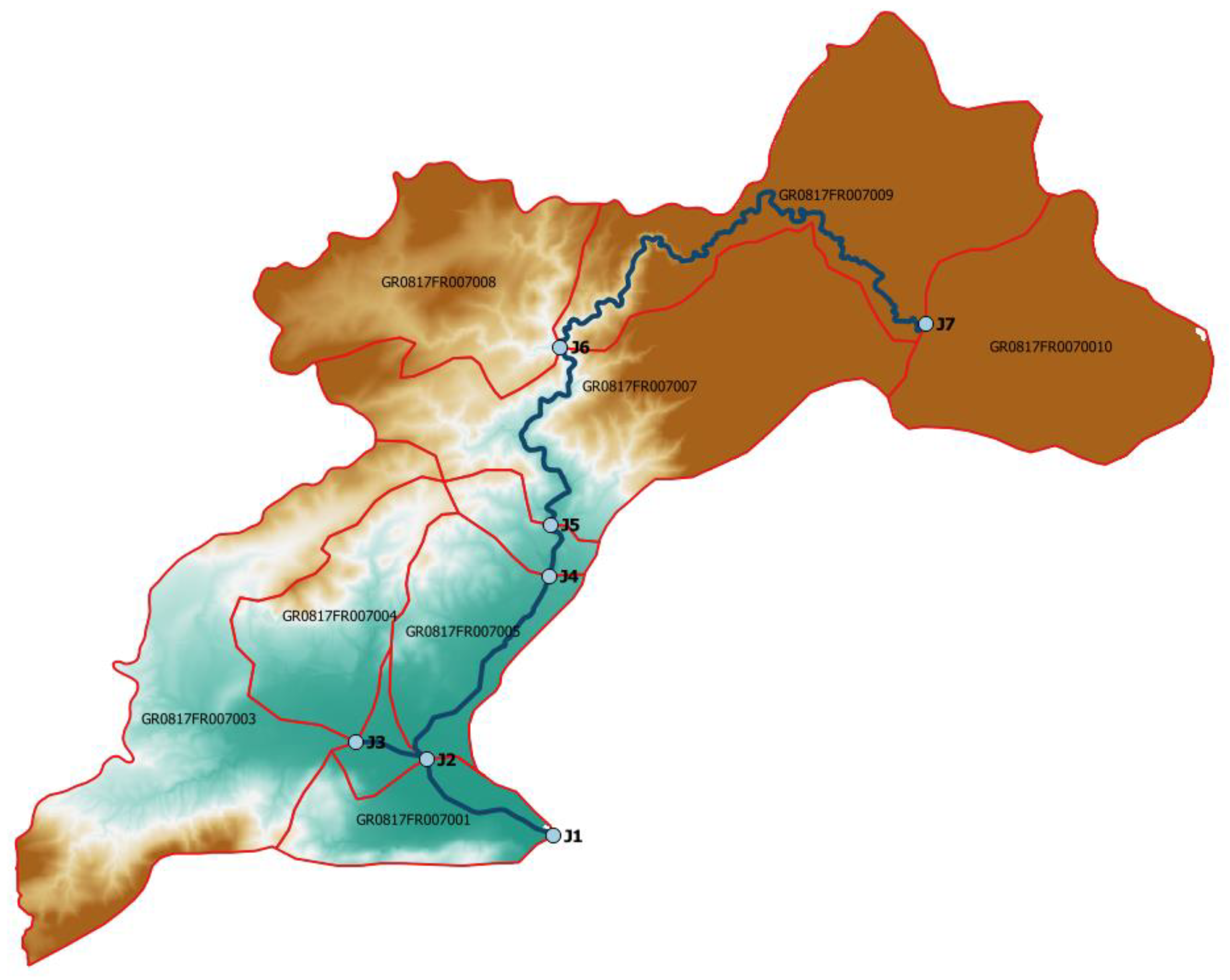
2. Study Area
3. Methodology
3.1. Overview of Flood Modelling Approach
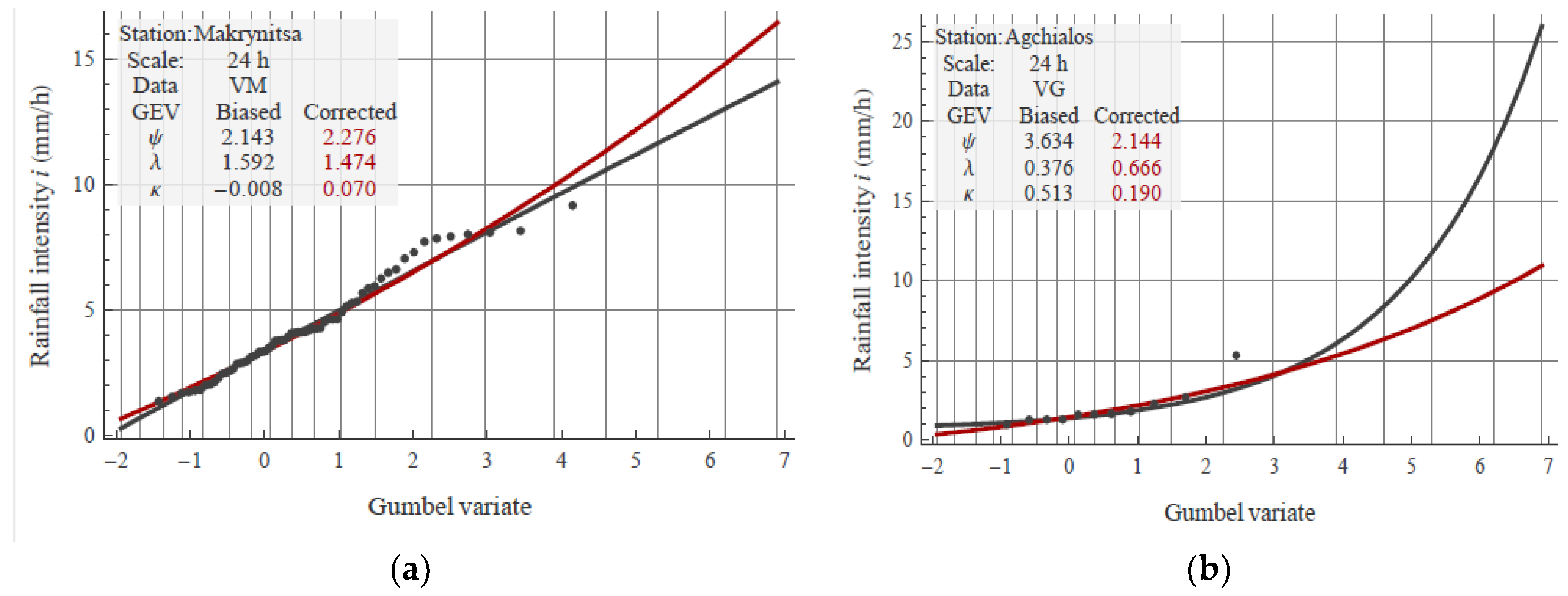
3.2. Design Rainfall
- Step 1:
- Global estimations of parameters η and θ were extracted on the basis of pluviographic data, by optimizing the fitting metric known as Kruskal-Wallis statistic [39] against the compound (unified) sample of extreme rainfall intensities for all available time scales.
- Step 2:
- At each station, the shape parameter κ is initially obtained by fitting the GEV model to the maximum 24 h data and estimating its parameters by the L-moments method [40,41]. Next, we employ the correction technique developed by [42], in order to adjust the biased estimations of κ, thus prohibiting both the use of too high values and the generation of negative values, which are unfeasible, since the maximum rainfall cannot be bounded. We remark that such inconsistencies are mainly due to sample uncertainties, which are induced due to the small size of the observed rainfall maxima, the existence of outliers as well as measurement errors.
- Step 3:
- Based on their point values of parameter κ, we employed a geographical classification of the stations to obtain regional values that are associated with climatic and topographic characteristics.
- Step 4:
- For given parameters κ, η and θ, we employed the L-moments method to estimate the scale and location parameters, λ′ and ψ′, at each station.
- Step 1:
- Using an appropriate generator of random numbers following the desirable distribution , we produce m synthetic samples = {, , …, }, where n is the length of the historical data.
- Step 2:
- From each synthetic sample xi we estimate its statistical characteristics and the corresponding sample parameters of , by applying the same procedure with the historical data (e.g., method of moments, L-moments, maximum likelihood, etc.).
- Step 3:
- For the desirable probability u, we generate m synthetic values using the inverse cumulative distribution function, i.e.:
- Step 4:
- We estimate the confidence limits (u) and (u), by computing the larger m (1 − γ)/2 and smaller m (1 + γ)/2 values of the sorted sample of (u).
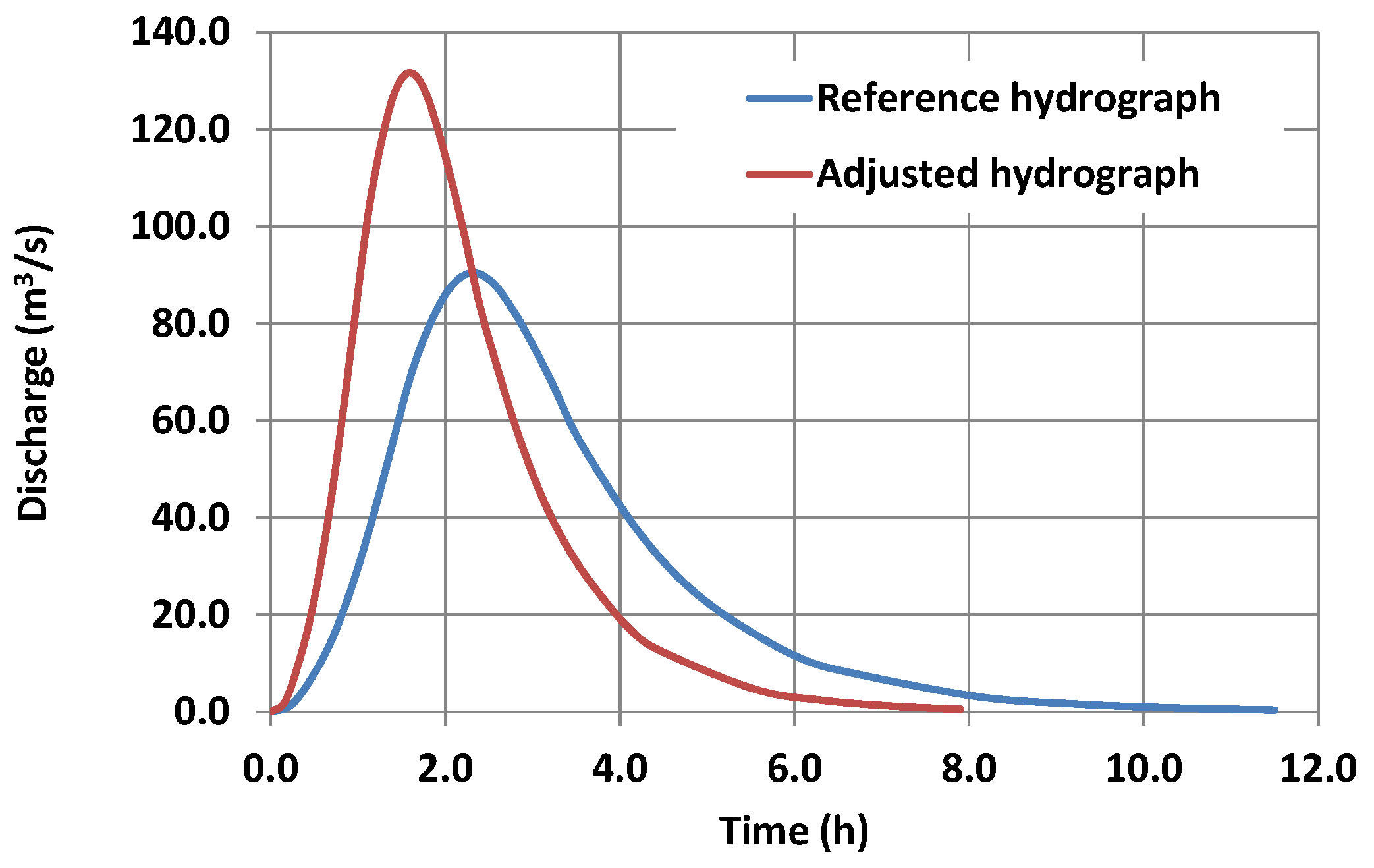
3.3. Hydrological Model Assumptions and Representation of Uncertainties
3.4. Hydraulic-Hydrodynamic Modelling
- Hydraulic structures close to erroneous DEM area.
- Hydraulic structures close to historical flood points.
- Hydraulic structures inside the Potential High Flood Risk Areas [34].
- Hydraulic structures close to recently recorded flood episodes.
- Hydraulic structures that accurate topographical data are absent.
- Hydraulic structures within main water bodies.
3.5. Hydraulic Simulation of Lower Course of Volos City Streams and Evaluation Procedure
4. Volos City: Application and Results of the Modelling Framework
4.1. Semi-Distributed Hydrological Modelling of Volos City Watersheds
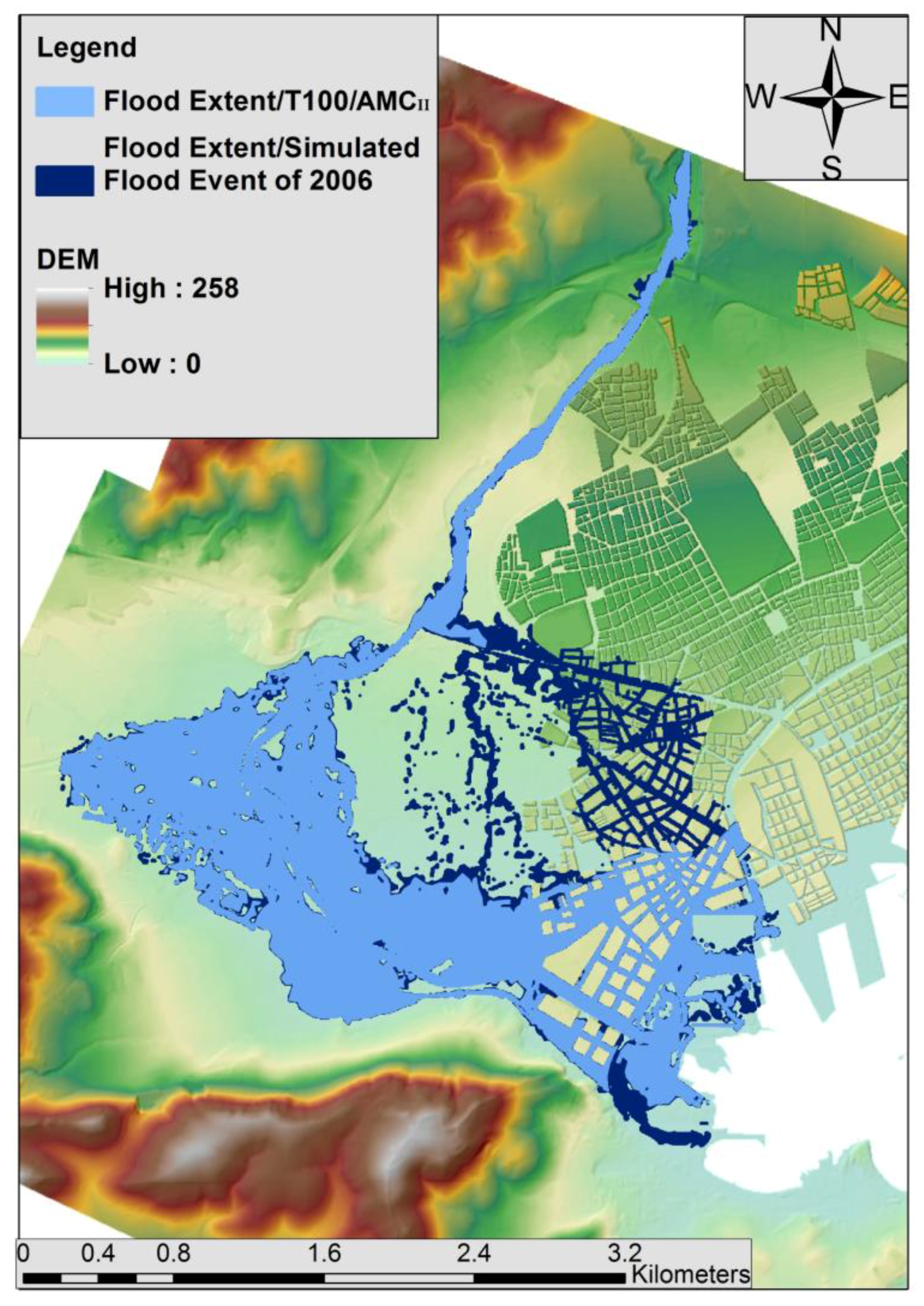
4.2. Hydraulic Modelling of Lower Course of Volos City Streams
5. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Tsakiris, G. Flood risk assessment: Concepts, modelling, applications. Nat. Hazards Earth Syst. Sci. 2014, 14, 1361–1369. [Google Scholar] [CrossRef]
- Hall, J.; Arheimer, B.; Borga, M.; Brázdil, R.; Claps, P.; Kiss, A.; Kjeldsen, T.R.; Kriauĉuniene, J.; Kundzewicz, Z.W.; Lang, M.; et al. Understanding flood regime changes in Europe: A state-of-the-art assessment. Hydrol. Earth Syst. Sci. 2014, 18, 2735–2772. [Google Scholar] [CrossRef]
- Kreibich, H.; Di Baldassarre, G.; Vorogushyn, S.; Aerts, J.C.J.H.; Apel, H.; Aronica, G.T.; Arnbjerg-nielsen, K.; Bouwer, L.M.; Bubeck, P.; Caloiero, T.; et al. Earth’s Future Special Section : Adaptation to flood risk : Results of international paired flood event studies. Earth’s Future 2017, 5, 953–965. [Google Scholar] [CrossRef]
- Diakakis, M.; Mavroulis, S.; Deligiannakis, G. Floods in Greece, a statistical and spatial approach. Nat. Hazards 2012, 62, 485–500. [Google Scholar] [CrossRef]
- Centre for Research on the Epidemiology of Disasters (CRED). Summarized Table of Natural Disasters in Greece from 1900 to 2017, EM-DAT: The CRED/OFDA International Disaster Database–www.emdat.be–Université Catholique de Louvain–Brussels–Belgium. Available online: http://www.emdat.be (accessed on 12 January 2018).
- Apel, H.; Thieken, A.H.; Merz, B.; Blöschl, G. Flood risk assessment and associated uncertainty. Nat. Hazards Earth Syst. Sci. 2004, 4, 295–308. [Google Scholar] [CrossRef]
- Aronica, G.; Bates, P.D.; Horritt, M.S. Assessing the uncertainty in distributed model predictions using observed binary pattern information within GLUE. Hydrol. Process. 2002, 16, 2001–2016. [Google Scholar] [CrossRef]
- Aronica, G.T.; Franza, F.; Bates, P.D.; Neal, J.C. Probabilistic evaluation of flood hazard in urban areas using Monte Carlo simulation. Hydrol. Process. 2012, 26, 3962–3972. [Google Scholar] [CrossRef]
- Dottori, F.; Di Baldassarre, G.; Todini, E. Detailed data is welcome, but with a pinch of salt: Accuracy, precision, and uncertainty in flood inundation modeling. Water Resour. Res. 2013, 49, 6079–6085. [Google Scholar] [CrossRef]
- Papaioannou, G.; Loukas, A.; Vasiliades, L.; Aronica, G.T. Flood inundation mapping sensitivity to riverine spatial resolution and modelling approach. Nat. Hazards 2016, 83, 117–132. [Google Scholar] [CrossRef]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.W.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Soil Conservation Service (SCS). National Engineering Handbook; Section 4, Hydrology (NEH-4); U.S. Department of Agriculture: Washington, DC, USA, 1972.
- Efstratiadis, A.; Koussis, A.D.; Koutsoyiannis, D.; Mamassis, N. Flood design recipes vs. reality: Can predictions for ungauged basins be trusted? Nat. Hazards Earth Syst. Sci. 2014, 14, 1417–1428. [Google Scholar] [CrossRef]
- Gr̈aler, B.; Van Den Berg, M.J.; Vandenberghe, S.; Petroselli, A.; Grimaldi, S.; De Baets, B.; Verhoest, N.E.C. Multivariate return periods in hydrology: A critical and practical review focusing on synthetic design hydrograph estimation. Hydrol. Earth Syst. Sci. 2013, 17, 1281–1296. [Google Scholar] [CrossRef]
- Horritt, M.S.; Di Baldassarre, G.; Bates, P.D.; Brath, A. Comparing the performance of a 2-D finite element and a 2-D finite volume model of floodplain inundation using airborne SAR imagery. Hydrol. Process. 2007, 21, 2745–2759. [Google Scholar] [CrossRef]
- Costabile, P.; Macchione, F. Enhancing river model set-up for 2-D dynamic flood modelling. Environ. Model. Softw. 2015, 67, 89–107. [Google Scholar] [CrossRef]
- Horritt, M.S.; Bates, P.D. Evaluation of 1D and 2D numerical models for predicting river flood inundation. J. Hydrol. 2002, 268, 87–99. [Google Scholar] [CrossRef]
- Merwade, V.; Cook, A.; Coonrod, J. GIS techniques for creating river terrain models for hydrodynamic modeling and flood inundation mapping. Environ. Model. Softw. 2008, 23, 1300–1311. [Google Scholar] [CrossRef]
- Hunter, N.M.; Bates, P.D.; Horritt, M.S.; Wilson, M.D. Simple spatially-distributed models for predicting flood inundation: A review. Geomorphology 2007, 90, 208–225. [Google Scholar] [CrossRef]
- Cook, A.; Merwade, V. Effect of topographic data, geometric configuration and modeling approach on flood inundation mapping. J. Hydrol. 2009, 377, 131–142. [Google Scholar] [CrossRef]
- Mohammed, J.R.; Qasim, J.M. Comparison of One-Dimensional HEC-RAS with Two-Dimensional ADH for Flow over Trapezoidal Profile Weirs. Casp. J. Appl. Sci. Res. 2012, 1, 1–32. [Google Scholar] [CrossRef]
- Néelz, S.; Pender, G.; Britain, G. Desktop Review of 2D Hydraulic Modelling Packages; DEFRA/Environment Agency: Bristol, UK, 2009; ISBN 9781849110792.
- Néelz, S.; Pender, G.; Wright, N.G. Benchmarking of 2D Hydraulic Modelling Packages; DEFRA/Environment Agency: Bristol, UK, 2010; ISBN 9781849111904.
- Néelz, S.; Pender, G. Benchmarking the Latest Generation of 2D Hydraulic Modelling Packages; DEFRA/Environment Agency: Bristol, UK, 2013; ISBN 9781849113069.
- Papaioannou, G.; Vasiliades, L.; Loukas, A.; Aronica, G.T. Probabilistic flood inundation mapping at ungauged streams due to roughness coefficient uncertainty in hydraulic modelling. Adv. Geosci. 2017, 44, 23–34. [Google Scholar] [CrossRef]
- Papaioannou, G.; Loukas, A.; Vasiliades, L.; Aronica, G.T. Sensitivity analysis of a probabilistic flood inundation mapping framework for ungauged catchments. Eur. Water 2017, 60, 9–16. [Google Scholar]
- Di Baldassarre, G.; Schumann, G.; Bates, P.D.; Freer, J.E.; Beven, K.J. Cartographie de zone inondable: Un examen critique d’approches déterministe et probabiliste. Hydrol. Sci. J. 2010, 55, 364–376. [Google Scholar] [CrossRef]
- Sarhadi, A.; Soltani, S.; Modarres, R. Probabilistic flood inundation mapping of ungauged rivers: Linking GIS techniques and frequency analysis. J. Hydrol. 2012, 458, 68–86. [Google Scholar] [CrossRef]
- Domeneghetti, A.; Vorogushyn, S.; Castellarin, A.; Merz, B.; Brath, A. Probabilistic flood hazard mapping: Effects of uncertain boundary conditions. Hydrol. Earth Syst. Sci. 2013, 17, 3127–3140. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Tegos, A.; Oikonomou, A.; Pagana, V.; Koukouvinos, A.; Mamassis, N.; Koutsoyiannis, D.; Efstratiadis, A. Comparative evaluation of 1D and quasi-2D hydraulic models based on benchmark and real-world applications for uncertainty assessment in flood mapping. J. Hydrol. 2016, 534, 478–492. [Google Scholar] [CrossRef]
- Bates, P.D.; Wilson, M.D.; Horritt, M.S.; Mason, D.C.; Holden, N.; Currie, A. Reach scale floodplain inundation dynamics observed using airborne synthetic aperture radar imagery: Data analysis and modelling. J. Hydrol. 2006, 328, 306–318. [Google Scholar] [CrossRef]
- Aggett, G.R.; Wilson, J.P. Creating and coupling a high-resolution DTM with a 1-D hydraulic model in a GIS for scenario-based assessment of avulsion hazard in a gravel-bed river. Geomorphology 2009, 113, 21–34. [Google Scholar] [CrossRef]
- Bates, P.D.; Horritt, M.S.; Aronica, G.; Beven, K. Bayesian updating of flood inundation likelihoods conditioned on flood extent data. Hydrol. Process. 2004, 18, 3347–3370. [Google Scholar] [CrossRef]
- Special Secretariat for Water, Ministry of Environment and Energy (SSW-MEE). Preliminary Assessment of the Flood Directive; Athens: Ministry of Environment and Energy; Available online: http://www.ypeka.gr/LinkClick.aspx?fileticket=T4DDG1hqQMY%3d&tabid=252&language=el-GR (accessed on 12 January 2018).
- Papaioannou, G.; Vasiliades, L.; Loukas, A. Multi-Criteria Analysis Framework for Potential Flood Prone Areas Mapping. Water Resour. Manag. 2015, 29, 399–418. [Google Scholar] [CrossRef]
- Harats, N.; Ziv, B.; Yair, Y.; Kotroni, V.; Dayan, U. Lightning and rain dynamic indices as predictors for flash floods events in the Mediterranean. Adv. Geosci. 2010, 53, 57–64. [Google Scholar] [CrossRef]
- Efstratiadis, A.; Papalexiou, S.M.; Markonis, I.; Mamassis, N. Ombrian curves. In Flood Risk Management Plan of River Basin District of Thessaly (GR08)–Phase A; Special Secretariat for Water, Ministry of Environment and Energy (SSW-MEE): Athens, Greece, 2016. [Google Scholar]
- Koutsoyiannis, D.; Kozonis, D.; Manetas, A. A mathematical framework for studying rainfall intensity-duration-frequency relationships. J. Hydrol. 1998, 206, 118–135. [Google Scholar] [CrossRef]
- Hirsch, R.M.; Helsel, D.R.; Cohn, T.A.; Gilroy, E.J. Statistical analysis of hydrological data. In Handbook of Hydrology; Maidment, D.R., Ed.; McGraw-Hill: New York, NY, USA, 1993. [Google Scholar]
- Hosking, J.R.M. L-Moments: Analysis and Estimation of Distributions Using Linear Combinations of Order Statistics. J. R. Stat. Soc. B 1990, 52, 105–124. [Google Scholar]
- Vogel, R.M.; Fennessey, N.M. L moment diagrams should replace product moment diagrams. Water Resour. Res. 1993, 29, 1745–1752. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; Koutsoyiannis, D. Battle of extreme value distributions : A global survey on extreme daily rainfall. Water Resour. Res. 2013, 49, 187–201. [Google Scholar] [CrossRef]
- Tyralis, H.; Koutsoyiannis, D.; Kozanis, S. An algorithm to construct Monte Carlo confidence intervals for an arbitrary function of probability distribution parameters. Comput. Stat. 2013, 28, 1501–1527. [Google Scholar] [CrossRef]
- Sutcliffe, J.V. Methods of Flood Estimation: A Guide to Flood Studies Report; Institute of Hydrology: Wallingford, UK, 1978; Volume 49. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: Singapore, 1988. [Google Scholar]
- Koutsoyiannis, D. A stochastic disaggregation method for design storm and flood synthesis. J. Hydrol. 1994, 156, 193–225. [Google Scholar] [CrossRef]
- National Regulator for Compulsory Specifications (NRCS). National Engineering Handbook: Part 630—Hydrology; NRCS: Washington, DC, USA, 2004. [Google Scholar]
- Michailidi, E.M.; Antoniadi, S.; Koukouvinos, A.; Bacchi, B.; Efstratiadis, A. Timing the time of concentration: Shedding light on a paradox. Hydrol. Sci. J. 2018, 63. [Google Scholar] [CrossRef]
- Grimaldi, S.; Petroselli, A.; Tauro, F.; Porfiri, M. Time of concentration: A paradox in modern hydrology. Hydrol. Sci. J. 2012, 57, 217–228. [Google Scholar] [CrossRef]
- Brunner, G. HEC-RAS River Analysis System: Hydraulic Reference Manual, Version 5.0. US Army Corps of Engineers–Hydrologic Engineering Center, 2016a; pp. 1–538. Available online: http://www.hec.usace.army.mil/software/hec-ras/documentation/HEC-RAS%205.0%20Reference%20Manual.pdf (accessed on 12 January 2018).
- Alfonso, L.; Mukolwe, M.M.; Di Baldassarre, G. Probabilistic Flood Maps to support decision-making: Mapping the Value of Information. Water Resour. Res. 2016, 52, 1026–1043. [Google Scholar] [CrossRef]
- Patel, D.P.; Ramirez, J.A.; Srivastava, P.K.; Bray, M.; Han, D. Assessment of flood inundation mapping of Surat city by coupled 1D/2D hydrodynamic modeling: A case application of the new HEC-RAS 5. Nat. Hazards 2017, 89, 93–130. [Google Scholar] [CrossRef]
- Vozinaki, A.E.K.; Morianou, G.G.; Alexakis, D.D.; Tsanis, I.K. Comparing 1D and combined 1D/2D hydraulic simulations using high-resolution topographic data: A case study of the Koiliaris basin, Greece. Hydrol. Sci. J. 2017, 62, 642–656. [Google Scholar] [CrossRef]
- Afshari, S.; Tavakoly, A.A.; Rajib, M.A.; Zheng, X.; Follum, M.L.; Omranian, E.; Fekete, B.M. Comparison of new generation low-complexity flood inundation mapping tools with a hydrodynamic model. J. Hydrol. 2018, 556, 539–556. [Google Scholar] [CrossRef]
- Brunner, G. Benchmarking of the HEC-RAS Two-Dimensional Hydraulic Modeling Capabilities. US Army Corps of Engineers—Hydrologic Engineering Center, 2016b; pp. 1–116. Available online: http://www.hec.usace.army.mil/software/hec-ras/documentation/RD-51_Benchmarking_2D.pdf (accessed on 12 January 2018).
- Tsubaki, R.; Fujita, I. Unstructured grid generation using LiDAR data for urban flood inundation modelling. Hydrol. Process. 2010, 24, 1404–1420. [Google Scholar] [CrossRef]
- Md Ali, A.; Solomatine, D.P.; Di Baldassarre, G. Assessing the impact of different sources of topographic data on 1-D hydraulic modelling of floods. Hydrol. Earth Syst. Sci. 2015, 19, 631–643. [Google Scholar] [CrossRef]
- Teng, J.; Vaze, J.; Dutta, D.; Marvanek, S. Rapid Inundation Modelling in Large Floodplains Using LiDAR DEM. Water Resour. Manag. 2015, 29, 2619–2636. [Google Scholar] [CrossRef]
- Bates, P.D.; De Roo, A.P.J. A simple raster-based model for flood inundation simulation. J. Hydrol. 2000, 236, 54–77. [Google Scholar] [CrossRef]
- Chow, W. Open-Channel Hydraulics, 1st ed.; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Hunter, N.M.; Bates, P.D.; Neelz, S.; Pender, G.; Villanueva, I.; Wright, N.G.; Liang, D.; Falconer, R.A.; Lin, B.; Waller, S.; et al. Benchmarking 2D hydraulic models for urban flooding. Proc. Inst. Civ. Eng. Water Manag. 2008, 161, 13–30. [Google Scholar] [CrossRef]
- Bellos, V. Ways for flood hazard mapping in urbanised environments : A short literature review. Water Util. 2012, 25–31. [Google Scholar]
- Schubert, J.E.; Sanders, B.F. Building treatments for urban flood inundation models and implications for predictive skill and modeling efficiency. Adv. Water Resour. 2012, 41, 49–64. [Google Scholar] [CrossRef]
- Bellos, V.; Tsakiris, G. Comparing Various Methods of Building Representation for 2D Flood Modelling In Built-Up Areas. Water Resour. Manag. 2015, 29, 379–397. [Google Scholar] [CrossRef]
- Brunner, G. HEC-RAS River Analysis System 2D Modeling User’s Manual. US Army Corps of Engineers—Hydrologic Engineering Center, 2016c; pp. 1–171. Available online: http://www.hec.usace.army.mil/software/hec-ras/documentation/HEC-RAS%205.0%202D%20Modeling%20Users%20Manual.pdf. (accessed on 12 January 2018).
- Horritt, M.S.; Bates, P.D. Predicting floodplain inundation: Raster-based modelling versus the finite-element approach. Hydrol. Process. 2001, 15, 825–842. [Google Scholar] [CrossRef]
- Alfieri, L.; Salamon, P.; Bianchi, A.; Neal, J.; Bates, P.; Feyen, L. Advances in pan-European flood hazard mapping. Hydrol. Process. 2014, 28, 4067–4077. [Google Scholar] [CrossRef]
- Jolliffe, I.T.; Stephenson, D.B. Forecast Verification; Wiley-Blackwell: Chichester, UK, 2012; ISBN 9780470660713. [Google Scholar]
- Koutsoyiannis, D.; Xanthopoulos, Th. Engineering Hydrology, 3rd ed.; National Technical University of Athens: Athens, Greece, 1999; p. 418. (In Greek) [Google Scholar]
- U.K. National Environmental Research Council (UK-NERC). Flood Studies Report; Institute of Hydrology: Wallingford, CT, USA, 1975.
| LABEL1 | LABEL2 | LABEL3 | Mannings n |
|---|---|---|---|
| 1 Artificial surfaces | 1.1 Urban fabric | 1.1.1 Continuous urban fabric | 0.013 |
| 1.1.2 Discontinuous urban fabric | |||
| 1.2 Industrial, commercial and transport units | 1.2.1 Industrial or commercial units | 0.013 | |
| 1.2.2 Road and rail networks and associated land | |||
| 1.2.3 Port areas | |||
| 1.2.4 Airports | |||
| 1.3 Mine, dump and construction sites | 1.3.1 Mineral extraction sites | 0.013 | |
| 1.3.2 Dump sites | |||
| 1.3.3 Construction sites | |||
| 1.4 Artificial, non-agricultural vegetated areas | 1.4.1 Green urban areas | 0.025 | |
| 1.4.2 Sport and leisure facilities | |||
| 2 Agricultural areas | 2.1 Arable land | 2.1.1 Non-irrigated arable land | 0.03 |
| 2.1.2 Permanently irrigated land | |||
| 2.1.3 Rice fields | |||
| 2.2 Permanent crops | 2.2.1 Vineyards | 0.08 | |
| 2.2.2 Fruit trees and berry plantations | |||
| 2.2.3 Olive groves | |||
| 2.3 Pastures | 2.3.1 Pastures | 0.035 | |
| 2.4 Heterogeneous agricultural areas | 2.4.1 Annual crops associated with permanent crops | 0.04 | |
| 2.4.2 Complex cultivation patterns | 0.04 | ||
| 2.4.3 Land principally occupied by agriculture, with significant areas of natural vegetation | 0.05 | ||
| 2.4.4 Agro-forestry areas | 0.06 | ||
| 3 Forest and semi natural areas | 3.1 Forests | 3.1.1 Broad-leaved forest | 0.1 |
| 3.1.2 Coniferous forest | |||
| 3.1.3 Mixed forest | |||
| 3.2 Scrub and/or herbaceous vegetation associations | 3.2.1 Natural grasslands | 0.04 | |
| 3.2.2 Moors and heathland | 0.05 | ||
| 3.2.3 Sclerophyllous vegetation | 0.05 | ||
| 3.2.4 Transitional woodland-shrub | 0.06 | ||
| 3.3 Open spaces with little or no vegetation | 3.3.1 Beaches, dunes, sands | 0.025 | |
| 3.3.2 Bare rocks | 0.035 | ||
| 3.3.3 Sparsely vegetated areas | 0.027 | ||
| 3.3.4 Burnt areas | 0.025 | ||
| 3.3.5 Glaciers and perpetual snow | 0.01 | ||
| 4 Wetlands | 4.1 Inland wetlands | 4.1.1 Inland marshes | 0.04 |
| 4.1.2 Peat bogs | |||
| 4.2 Maritime wetlands | 4.2.1 Salt marshes | 0.04 | |
| 4.2.2 Salines | |||
| 4.2.3 Intertidal flats | |||
| 5 Water bodies | 5.1 Inland waters | 5.1.1 Water courses | 0.05 |
| 5.1.2 Water bodies | |||
| 5.2 Marine waters | 5.2.1 Coastal lagoons | 0.07 | |
| 5.2.2 Estuaries | |||
| 5.2.3 Sea and ocean |
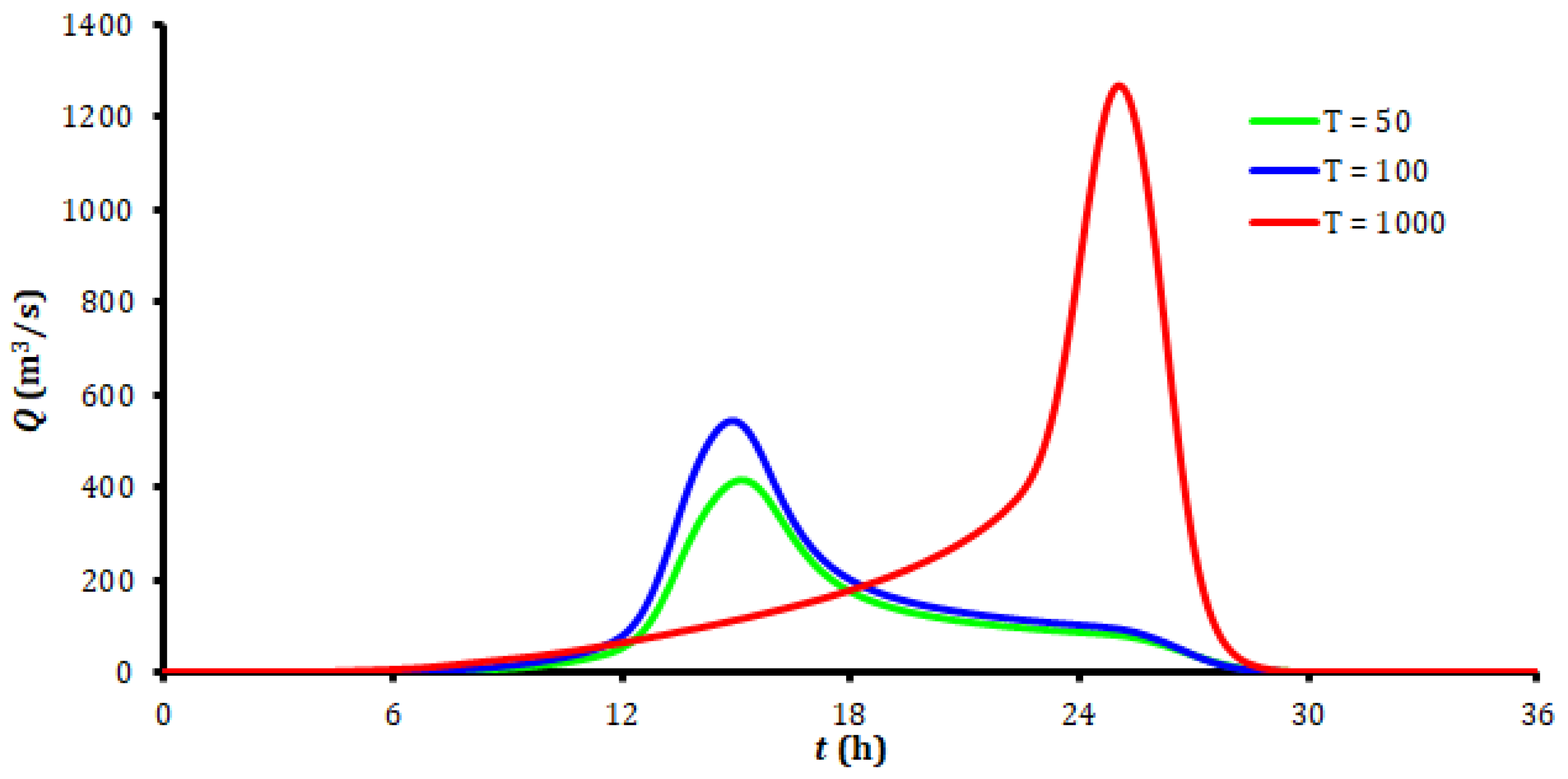
| Station | T = 50 Years | T = 100 Years | T = 1000 Years | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 20% low | IDF | 80% up | 20% low | IDF | 80% up | 20% low | IDF | 80% up | |
| Makrynitsa | 208.6 | 238.0 | 263.6 | 230.9 | 272.9 | 311.9 | 300.5 | 406.1 | 530.0 |
| Agchialos | 105.1 | 140.5 | 168.8 | 113.8 | 162.9 | 207.7 | 134.8 | 248.3 | 407.3 |
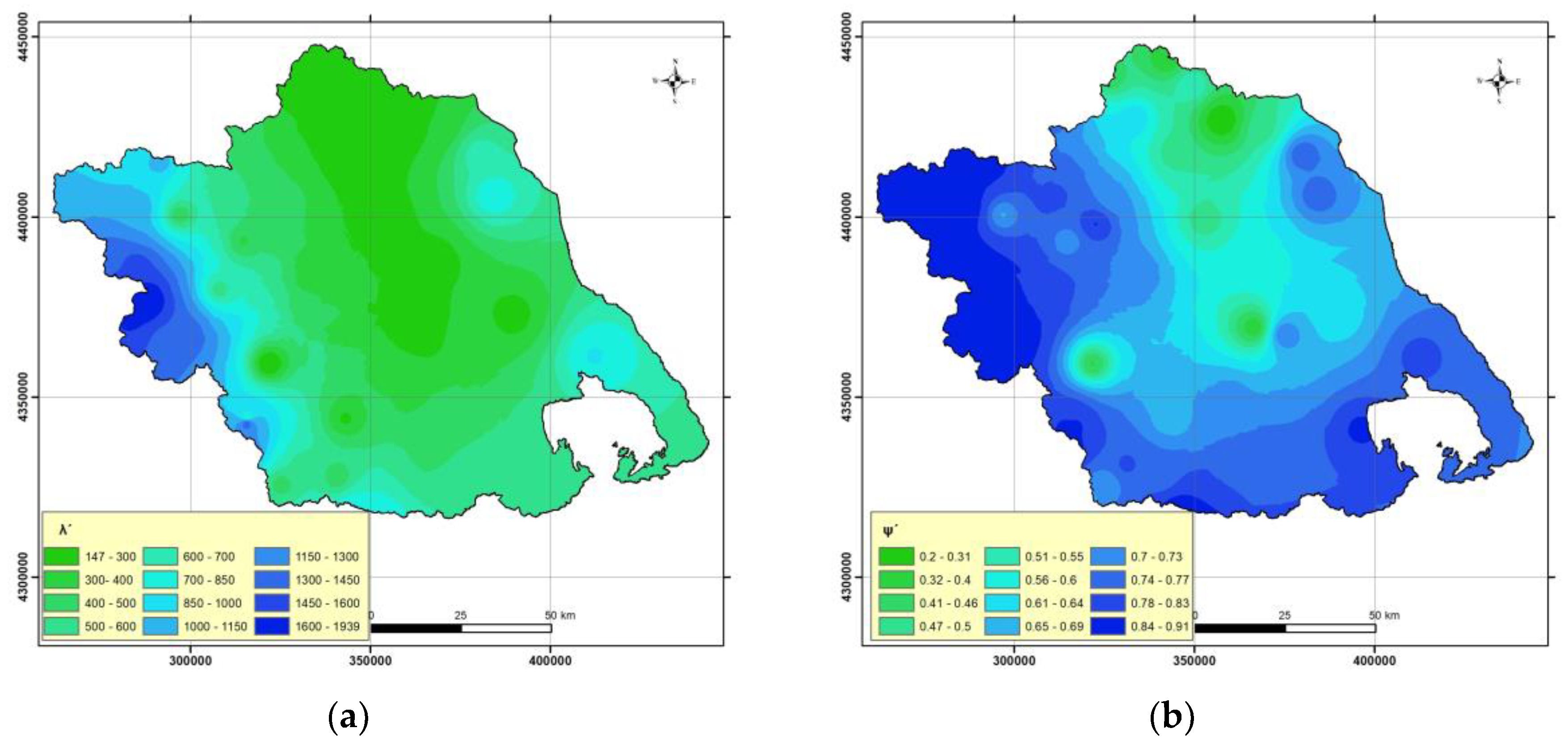
| id | A (km2) | zm (m) | zo (m) | Lmax (km) | λ′ | ψ′ | tc (h) | CNI | CNII | CNIII |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6.1 | 66.0 | 0.0 | 5.6 | 698.1 | 0.757 | 2.81 | 49.3 | 69.8 | 84.2 |
| 2 | 1.4 | 26.4 | 8.7 | 1.7 | 695.4 | 0.754 | 2.17 | 62.5 | 79.9 | 90.1 |
| 3 | 20.4 | 199.8 | 21.3 | 8.9 | 613.6 | 0.738 | 2.94 | 48.8 | 69.4 | 83.9 |
| 4 | 8.0 | 140.0 | 21.3 | 5.1 | 686.9 | 0.749 | 2.17 | 46.6 | 67.5 | 82.7 |
| 5 | 7.5 | 73.3 | 8.7 | 5.2 | 754.0 | 0.763 | 2.91 | 65.8 | 82.1 | 91.3 |
| 6 | 2.2 | 130.2 | 51.9 | 3.1 | 789.5 | 0.768 | 1.50 | 60.5 | 78.5 | 89.4 |
| 7 | 22.3 | 447.7 | 58.7 | 10.6 | 808.6 | 0.771 | 2.20 | 29.2 | 49.6 | 69.4 |
| 8 | 13.6 | 338.4 | 170.7 | 7.7 | 697.7 | 0.743 | 2.54 | 31.3 | 52.0 | 71.4 |
| 9 | 20.0 | 722.7 | 170.7 | 15.1 | 788.1 | 0.766 | 2.15 | 32.4 | 53.3 | 72.4 |
| 10 | 15.3 | 1236.7 | 800.1 | 7.0 | 825.0 | 0.775 | 1.57 | 49.3 | 69.8 | 84.2 |
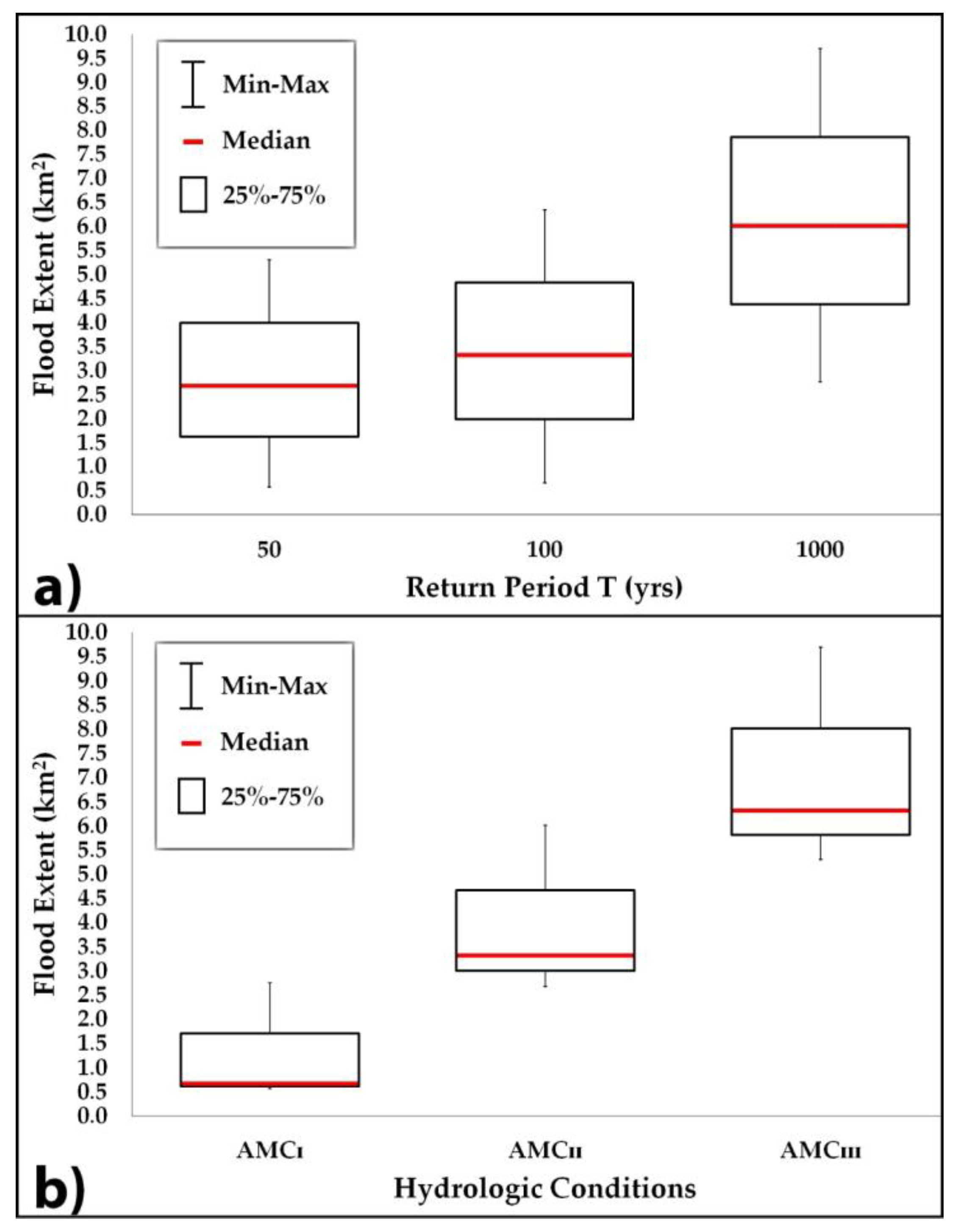
| Code | River Name | Hydrologic Conditions/Roughness Coefficient Conditions | Return Period (Years) | ||
|---|---|---|---|---|---|
| 50 | 100 | 1000 | |||
| GR0817FR00700 | Xerias | Dry (AMCI)/ −50% | 0.42 | 0.49 | 1.79 |
| Average (AMCII)/ Average | 2.15 | 2.63 | 4.84 | ||
| Wet (AMCIII)/ +50% | 3.69 | 4.49 | 6.33 | ||
| GR0817FR00800 | Krafsidonas | Dry (AMCI)/ −50% | 0.085 | 0.087 | 0.75 |
| Average (AMCII)/ Average | 0.34 | 0.45 | 0.99 | ||
| Wet (AMCIII)/ +50% | 0.93 | 1.34 | 2.91 | ||
| GR0817FR00900 | Anavros | Dry (AMCI)/ −50% | 0.068 | 0.081 | 0.21 |
| Average (AMCII)/ Average | 0.21 | 0.25 | 0.33 | ||
| Wet (AMCIII)/ +50% | 0.77 | 0.82 | 1.2 | ||
| Entire Volos city | Xerias & Krafsidonas & Anavros | Dry (AMCI)/ −50% | 0.57 | 0.66 | 2.76 |
| Average (AMCII)/ Average | 2.68 | 3.32 | 6.01 | ||
| Wet (AMCIII)/ +50% | 5.3 | 6.34 | 9.7 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papaioannou, G.; Efstratiadis, A.; Vasiliades, L.; Loukas, A.; Papalexiou, S.M.; Koukouvinos, A.; Tsoukalas, I.; Kossieris, P. An Operational Method for Flood Directive Implementation in Ungauged Urban Areas. Hydrology 2018, 5, 24. https://doi.org/10.3390/hydrology5020024
Papaioannou G, Efstratiadis A, Vasiliades L, Loukas A, Papalexiou SM, Koukouvinos A, Tsoukalas I, Kossieris P. An Operational Method for Flood Directive Implementation in Ungauged Urban Areas. Hydrology. 2018; 5(2):24. https://doi.org/10.3390/hydrology5020024
Chicago/Turabian StylePapaioannou, George, Andreas Efstratiadis, Lampros Vasiliades, Athanasios Loukas, Simon Michael Papalexiou, Antonios Koukouvinos, Ioannis Tsoukalas, and Panayiotis Kossieris. 2018. "An Operational Method for Flood Directive Implementation in Ungauged Urban Areas" Hydrology 5, no. 2: 24. https://doi.org/10.3390/hydrology5020024
APA StylePapaioannou, G., Efstratiadis, A., Vasiliades, L., Loukas, A., Papalexiou, S. M., Koukouvinos, A., Tsoukalas, I., & Kossieris, P. (2018). An Operational Method for Flood Directive Implementation in Ungauged Urban Areas. Hydrology, 5(2), 24. https://doi.org/10.3390/hydrology5020024









