Abstract
This study presents a comprehensive assessment of the variability and trends of the precipitation and temperature along with the trends in drought indices over the State of California. The non-parametric Mann–Kendall trend test is applied with a trend-free pre-whitening procedure in trend identification. A dataset containing 120-year (water years 1896–2015) monthly precipitation, average temperature, maximum temperature, minimum temperature and the Palmer Index for seven climatic regions of the state is used for this purpose. The results confirm previous work indicating that no clear trends are observed in precipitation, while a distinct warming trend is evident in temperature over the state. New findings of this study include: (1) in general, the variability of annual, winter (December–February) and spring (March–May) precipitation shows an increasing tendency, implying intensified frequency of the occurrence of dry or wet extremes; (2) on the annual scale and in the summer, statewide meteorological, hydrological and agricultural drought indices all have decreasing trends, indicating the more frequent occurrence of drought events; and (3) among seven regions, the South Coast Drainage region generally has the most significant warming trend, as well as the most significant declining trends in drought indices. Overall, these findings are highly meaningful from both theoretical and practical perspectives, in the context of providing critical information in developing prediction models and guiding water resources management practices, respectively.
1. Introduction
Understanding the variability and trends in hydroclimatic variables (including precipitation and temperature) and extreme events (including droughts) is of significant theoretical and practical importance. From a theoretical standpoint, this understanding sheds light on the (evolving) characteristics of these variables and lays the foundation in building improved predictive models to forecast their behavior in the future. From a practical viewpoint, this understanding can guide water resources management practices in terms of making adaptive plans and decisions, which is critical to dry areas, including the State of California, United States. As a top ten economy in the world and the home to over 38 million people, California’s development and growth have been largely relying on its ability to manage available water resources. In California, most of the population and farmlands is located in the southern half, while a majority of the precipitation falls in the northern mountain ranges. The state is also prone to drought with frequent drought events (most noticeably, 1929–1934, 1976–1977, 1987–1992, 2007–2009 and 2012–2015) recorded. The traditional water resources management means have been building water facilities, including storage and transfer projects, such the State Water Project (SWP) and the Central Valley Project (CVP), to redistribute water across different spatial and temporal scales. As the economy and population continue to grow, the demand for water is increasing inevitably. Increasing demand, in light of a changing climate, makes reliable water supply for the state unprecedentedly challenging. To address these challenges, the operations of existing water facilities need to be optimized to mitigate adverse impacts of hydroclimatic extremes (such as the extraordinary 2012–2015 drought) and to maximize the reliability of water supply. Foremost of this approach is to understand the historical variability and trends of hydroclimatic variables and the occurrence of extreme events (particularly drought from a water supply perspective) in the state. For instance, the initial water allocation decision of the SWP, which supplies water for approximately 25 million Californians for the next year, is typically made in late November or early December of the current year. The decision is often based on the projected wetness of the next year, as well as historical conditions in the record. The former is essentially a long-term forecast with large uncertainties. The latter thus plays a critical role in deciding the allocation quota. In this case, the social and economic value of good knowledge on the variability and trends of historical wetness conditions is tremendous.
Due to its importance, a large number of studies have been dedicated to investigating the variability and trends in hydroclimatic variables in numerous areas, including the State of California. These studies mostly used data at two spatial scales. The first one is the point scale. Historical measurements from individual observational gauges are examined [1,2,3,4,5,6]. The second one is the gridded scale, either converted from a point scale or through distributed models [7,8,9,10,11,12]. There are a few exceptions though, which employ the data at a regional scale [13,14,15], whilst water resource decisions and actions are generally operated at a local-to-regional scale. Most of these studies used datasets with a relatively short record period (less than a century). In addition, the linear regression approach was generally used in these studies in trend assessment. The trend detected by this method is largely impacted by the beginning and ending values of the targeted dataset. Despite that different datasets being investigated at different spatial scales, there is a strong consensus across these studies on a warming trend in temperature and no clear trend in precipitation over California. There have also been a number of studies on California drought, with particular interest on the most recent 2012–2015 drought [16,17,18,19,20,21,22,23,24,25,26]. These studies mostly focused on the causes of this drought, as well as its characteristics in a historical context. To our knowledge, no studies have been conducted to assess the trends of different types of drought at a regional scale over the state.
This study aims to present a comprehensive assessment of the variability and trends of the precipitation and temperature along with the trends in drought indices over California, extending beyond the earlier studies in terms of: (1) identifying potential trends in different types of drought at a regional scale; (2) using the longest available dataset through the instrumental record period since water year 1896; and (3) applying the widely-used non-parametric trend-free pre-whitening Mann–Kendall approach in trend analysis. This method addresses the serial correlation in the target time series and is less impacted by the beginning and ending values in comparison to the linear regression approach. This study should provide meaningful insights that drive better informed water resources management practices and support further research in predicting future hydroclimatic extremes.
2. Materials and Methods
2.1. Drought Indices
In general, drought is classified into four types: meteorological, hydrological, agricultural and socioeconomic [27,28]. The latter often stems from the first three and is normally represented in monetary form [29]. This study only considers the first three physically-based types of drought, which are typically characterized by deficits in precipitation, surface or subsurface water supplies, and soil moisture respectively. Drought severity is often quantified by a drought index, which normally measures the departure of an interested variable from its normal condition according to its historical distribution. Numerous drought indices have been developed in drought monitoring, assessment and prediction [29,30,31]. Of all these indices, the Palmer Index [32] was a landmark and has been widely applied since its inception [30,33,34,35,36,37,38]. The Palmer Index collectively refers to three indices: the Palmer Drought Severity Index (PDSI), the Palmer Hydrological Drought Index (PHDI) and the Palmer Z Index (Z Index), representing the severity of meteorological, hydrological and agricultural drought, respectively [30]. The PDSI is the most prominent index of meteorological drought in the United States [29,30]. The Z index is found more preferable than the widely-used Crop Moisture Index [39] in quantifying agricultural drought [40]. The PDSI, PHDI and Z indices are determined via a two-layer model which accounts for soil moisture gains (from precipitation) and losses (via evapotranspiration) [32]. They are dimensionless with positive (negative) values indicating abnormal wetness (dryness). This study assesses the trends in these three drought indices at different temporal and spatial scales across California.
2.2. Study Area and Dataset
This study focuses on seven climate divisions (Regions D1–D7, Figure 1) of the State of California defined by the United States National Climatic Data Center (NCDC) [41], as well as the whole state (Table 1). Monthly precipitation, temperature, PDSI, PHDI, Palmer’s Z Index of a 120-year period (water years 1896–2015) for these regions are obtained from the NCDC Climate Divisional Database (http://www.ncdc.noaa.gov/) for this study. Since 1931, monthly divisional precipitation and temperature data are determined as the equal-weighted average of observations from stations located within the boundary of the specific division. Prior to 1931, limited by the availability of station data, the divisional precipitation and temperature data are derived from corresponding statewide values published by the U.S. Department of Agriculture (USDA) via a linear regression method. The raw statewide values (prior to 1931) from the USDA are adjusted to achieve homogeneity with the post-1931 statewide values before being applied in deriving the divisional data. The drought indices are determined using the divisional precipitation and temperature data. For a detailed description of the methodology employed in developing the dataset, the readers are referred to [41].
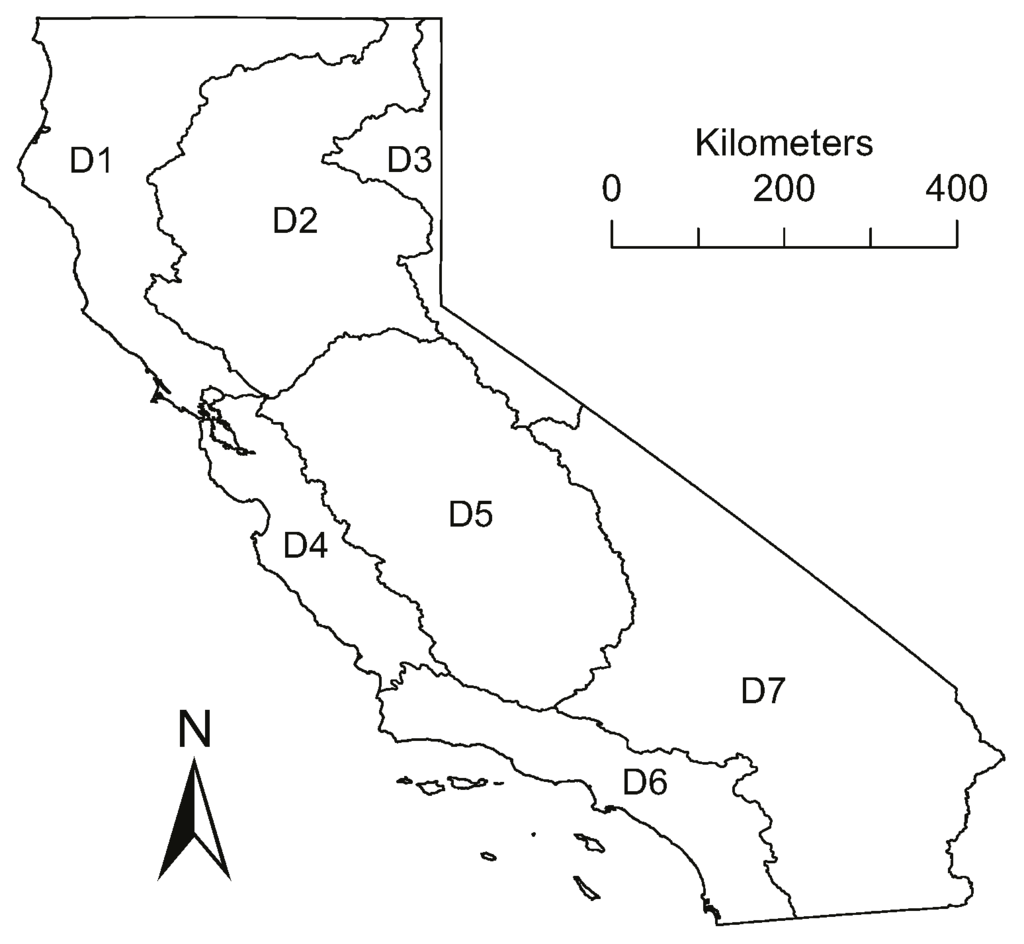
Figure 1.
Climatic divisions of the State of California.

Table 1.
Hydroclimatic characteristics of study regions. Precipitation and temperature values are corresponding long-term (water years 1896–2015) mean values. “N-A” denotes November–April.
These regions have contrasting hydroclimatic characteristics (Table 1, Figure 2). The region Southeast Desert Basin (D7) is the driest and warmest region, with annual precipitation and average temperature ranges from 42–357 mm and from 16.2–20.0 °C, respectively. The North Coast Drainage (D1) is the wettest region, of which the annual precipitation ranges from 519–2087 mm with a mean value of 1223 mm. On average, the state receives precipitation annually at an amount of 561 mm, of which 85% (477 mm) occurs in the wet season (November–April or N-A). The coolest region is the Northeast Interior Basin (D3), of which the mean annual temperature varies from −0.3–14.6 °C. In 82 years out of the 120-year period, the minimum annual temperature of this region was below zero. The long-term mean regional annual average temperature over the state ranges from 7.2–17.9 °C, with an average value of 14.2 °C. As for the regional maximum (minimum) temperature, the range is from 14.6–25.2 °C (−0.3–10.7 °C).
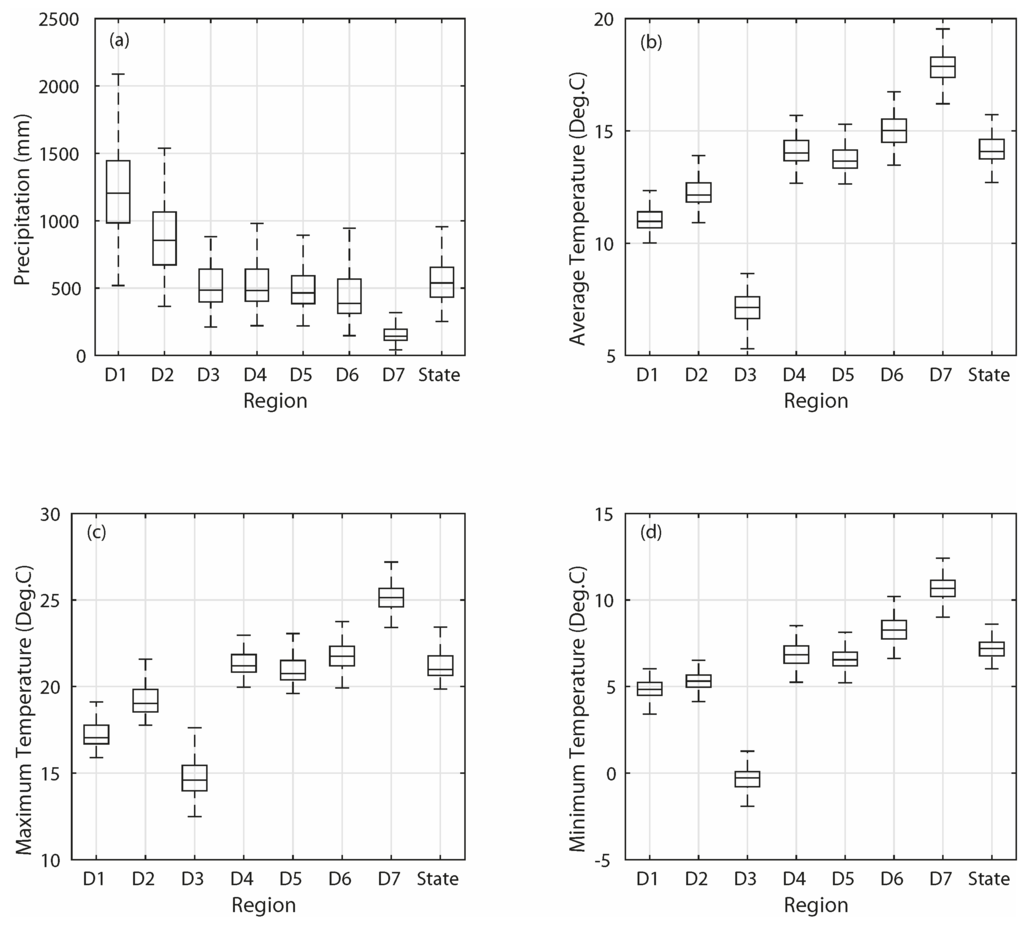
Figure 2.
Boxplots of the (a) annual precipitation, (b) annual average temperature, (c) annual maximum temperature and (d) annual minimum temperature of the study regions. The central mark on each box represents the median value; the edges of the boxes denote the 25th and 75th percentiles; the upper (lower) whisker is 1.5-times the interquartile range away from the top (bottom) of the box.
Despite the fact that these regions have very diverse hydroclimatic characteristics on the annual scale, they share some similarities on a finer monthly scale (Figure 3). Precipitation values of all regions show significant seasonality, with the majority amount occurring in the wet season from November–April. The percentage of wet season precipitation over the annual precipitation ranges from 74% (D7: Southeast Desert Basin) to 91% (D4 and D6: Central Coast Drainage and South Coast Drainage). Most of the regions receive the highest amount of precipitation in January, except for the South Coast Drainage (D6), where the precipitation in February is about 3% higher than its January counterpart. For the North Coast Drainage (D1), precipitation amounts in December and January are essentially identical. For the Southeast Desert Basin (D7), January and February observe almost a same amount of precipitation. Average temperature values also display strong seasonality, with low temperature in the winter (December–February) and high temperature in the summer (June–August). The lowest temperature always occurs in January. The highest temperature mostly appears in July, except for the South Coast Drainage (D6), of which the August temperature is slightly (0.9%) higher than its July temperature.
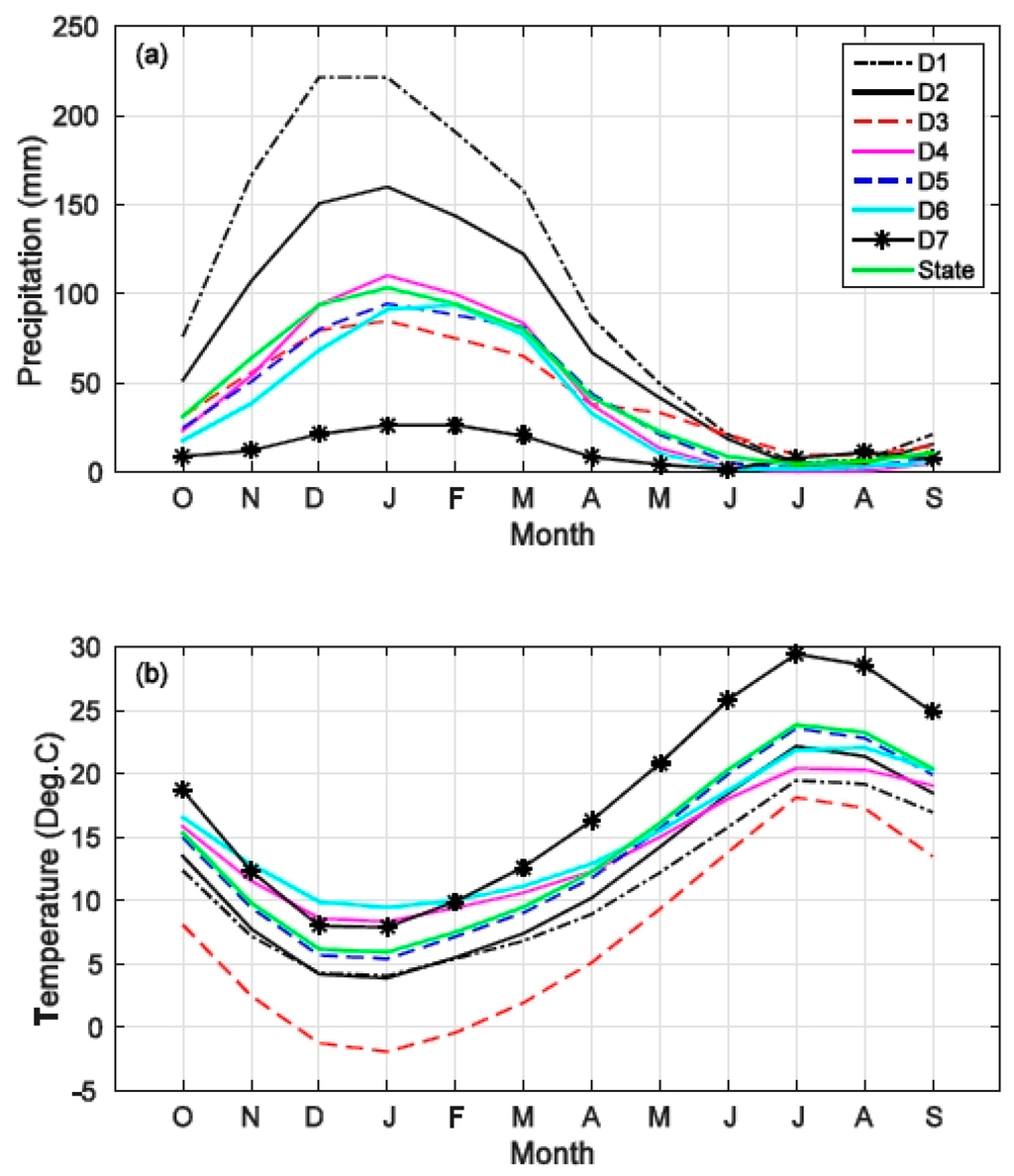
Figure 3.
(a) Mean monthly precipitation and (b) mean monthly average temperature of the study regions for October (O), November (N), December (D), January (J), February (F), March (M), April (A), May (M), June (J), July (J), August (A), and September (S).
Whereas sharing a similar pattern, the monthly values of precipitation (temperature) of these regions could be remarkably different. For instance, in January, the highest precipitation amount is 221 mm (D1: North Coast Drainage), almost nine times of the lowest regional amount 26 mm (D7: Southeast Desert Basin). The temperature in January ranges from −1.9 °C (D3: Northeast Interior Basin) to 9.5 °C (D6: South Coast Drainage), with a difference of 11.4 °C. The statewide precipitation and temperature of this month are 103 mm and 5.9 °C, respectively. It is also evident that the Northeast Interior Basin (D3) has consistently cooler monthly temperature than other regions across the year. In contrast, the Southeast Desert Basin (D7) has the highest regional monthly temperature from May–October.
On the seasonal scale, fall (September–November) precipitation accounts for 14% (D6) to 22% (D1) of annual precipitation (19% statewide); for winter, spring (March–May) and summer precipitation, the ranges are 46% (D3) to 58% (D4) (52% statewide), 21% (D7) to 29% (D5) (26% statewide), and 1% (D4) to 13% (D7) (3% statewide), respectively. Seasonal temperature in the Northeast Interior Basin (D3) is consistently the lowest among all regions, with values at 8.0 °C, −1.2 °C, 5.5 °C and 16.4 °C for fall, winter, spring and summer, respectively. In contrast, the temperature of the Southeast Desert Basin (D7) is the highest in fall (18.6 °C), spring (16.6 °C) and summer (28.0 °C). The South Coast Drainage (D6) has the highest winter temperature 9.8 °C (versus 8.6 °C of D7).
Overall, out of the seven regions (D1–D7), the North Coast Drainage (D1) and Sacramento Drainage (D2) receive higher than the statewide average precipitation (218% and 172% of the statewide average for D1 and D2, respectively). The percentage of average values for Northeast Interior Basin (D3), Central Coast Drainage (D4) and South Coast Drainage (D5) are about 90%. It is roughly 80% for the South Coast Drainage (D6) and 30% for the Southeast Desert Basin (D7). More than half of the annual precipitation falls in winter, while the summer observes about 3% of annual precipitation statewide. As for the temperature, the South Coast Drainage (D6) and the Southeast Desert Basin (D7) have higher than statewide average temperatures. The Central Coast Drainage (D4) and South Coast Drainage (D5) have slightly lower than average temperatures. The seasonal and annual average temperatures of the Northeast Interior Basin (D3) are the lowest among all regions.
2.3. Metrics
This study employs a parsimonious metric to represent variability: the ratio of the sub-period variance of a target variable (precipitation, temperature or Palmer Index in this study) over the period of record variance of the variable. A ratio above (below) one indicates that the target variable in the sub-period is more (less) variable than usual. This metrics has been extensively applied in assessing variability in hydro-climatic variables. For instance, [42,43] investigated streamflow variability in every 20-year sub-period within the record period for a large number of watershed in the western U.S. They used a jackknife procedure in verifying the significance of the variability in streamflow. They argued that a 20-year window provides enough sample size to develop reliable variances and persistence, although a longer period would be more desirable. The current study has a 120-year record of period (from water years 1896–2015). A 30-year window is applied to allow enough sample size (30) for variance calculation, as well as enough moving-window sub-periods (91) to capture potential decadal variability.
2.4. Trend Analysis
The Mann–Kendall test (MKT) [44,45] is a rank-based nonparametric approach widely used in assessing the significance of a trend in hydrologic data [46,47,48,49,50,51]. For an observed time series , where is the total number of observations, the MKT first calculates the sign (via the sign function ) of each possible pair of observations and assigns a value of 1, 0 or −1 if the difference is positive, zero or negative, respectively. The MKT statistic is calculated next as follows:
The test statistic is then determined by:
where is the variance of computed as .
The null hypothesis of no trend is rejected if , where is the probability of the standard normal distribution at a significance level of . A value of 0.05 for is applied in this study. The alternative hypothesis that a monotonic trend exists is favored under this condition. A positive (negative) value of indicates an upward (downward) trend.
This study employs the Theil–Sen approach (TSA) [52,53] to identify the slope of significant trends determined via the MKT. The TSA is a non-parametric procedure that can be used to determine the slope of the trend of a time series. It computes the slope as follows:
Serial correlation typically exists in hydroclimatic variables. The presence of positive serial correlation increases the probability of false rejection of the null hypothesis of no trends [54,55,56]. It is necessary to address the serial correlation to obtain more robust trend analysis results. This study employs a trend-free pre-whitening (TFPW) procedure [57,58] to deal with the serial correlation. The original time series (monthly divisional and statewide precipitation, temperature and drought indices of California in this study) with a significant trend is first de-trended. A lag-oneauto-regressive process is then removed from the de-trended time series to generate a new time series. The trend determined from the original time series is added to the new one, yielding a combined time series. The readers are referred to [57] for a detailed explanation on the TFPW procedure. In this study, the MKT is applied to the combined time series to determine the significance of a trend.
3. Results
3.1. Variability
Variability of precipitation, average temperature, maximum temperature and minimum temperature are investigated. The annual precipitation variability of each study region shares a similar pattern (Figure 4a). Before the early 1980s, the 30-year moving variances of all regions are generally less than their corresponding long-term variances (variability less than one). Since the early 1980s, annual precipitation variability increases (greater than one) across the state. The variability peaks in the late 1990s for most regions, except for regions South Coast Drainage (D6) and Southeast Desert Basin (D7). The peak variability of these two regions appears in 2007. On average, the wettest region (North Coast Drainage, D1) is the only region where the annual precipitation is more variable than usual. The median variability of this region is larger than one, whilst it is opposite for other regions. The driest region (Southeast Desert Basin, D7) has the largest variability range from 0.47 (1932) to 2.03 (2007). The variability time series of South Coast Drainage (D6) is highly correlated to that of the Southeast Desert Basin (D7), with a Spearman’s rank correlation value of 0.97. The variability time series of the Central Coast Drainage (D4) and San Joaquin Drainage (D5) also share the same amount of correlation. The correlation between annual precipitation over D6 and D7 (D4 and D5) is 0.89 (0.96).
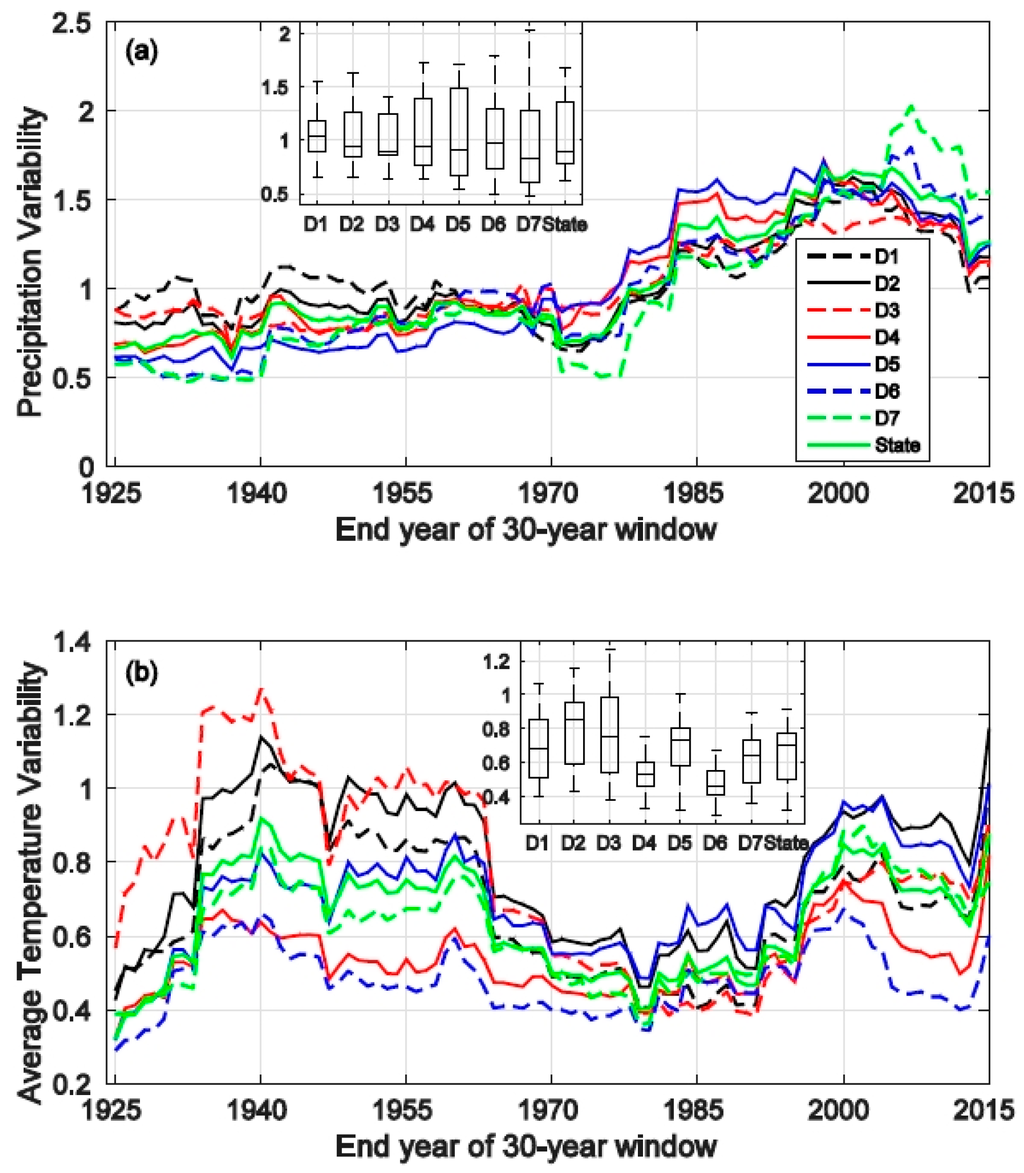
Figure 4.
Time series of the 30-year moving window of the (a) annual precipitation variability and (b) annual average temperature variability of the study regions. The insert diagram shows the boxplot of variability for each region. The description of boxplot features is provided in Figure 2’s caption.
Annual temperature variability generally exhibits a repeating increasing-decreasing pattern (Figure 4b). An increasing trend is observed till around 1940, followed by a decreasing trend till around 1980. Another increasing trend is apparent from 1980 to early 2000, followed by another decreasing trend till 2013. Except for the three regions in Northern California (D1–D3), the variability values in other regions (including statewide) are generally less than one, indicating that the long-term variances in these regions are larger than any 30-year sub-period variance. For those three northern regions, the median variability is also distinctly less than one. The coldest region (Northeast Interior Basin, D3) has the largest variability range from 0.38 (1991) to 1.27 (1940). The highest Spearman’s correlation (0.97) occurs between the North Coast Drainage (D1) and Sacramento Drainage (D2). The correlation between the annual average temperatures of these two regions is 0.93.
Annual maximum temperature variability (Figure 5a) has a general pattern similar to that of the annual average temperature variability. However, it is different in terms of the following: (1) the first increasing trend peaks earlier (in the middle 1930s rather than around 1940); and (2) the second increasing trend peaks later for all regions (in the middle to late 2000s rather than the early 2000s), except for Central Coast Drainage (D4) and South Coast Drainage (D6). The median variability of every region is considerably less than one, indicating that on average, the annual maximum temperature in a 30-year sub-period is less variable than usual. The highest Spearman’s correlation between regional variabilities is 0.95 (between regions North Coast Drainage and Sacramento Drainage). The correlation between annual maximum temperatures of these two regions is 0.92.
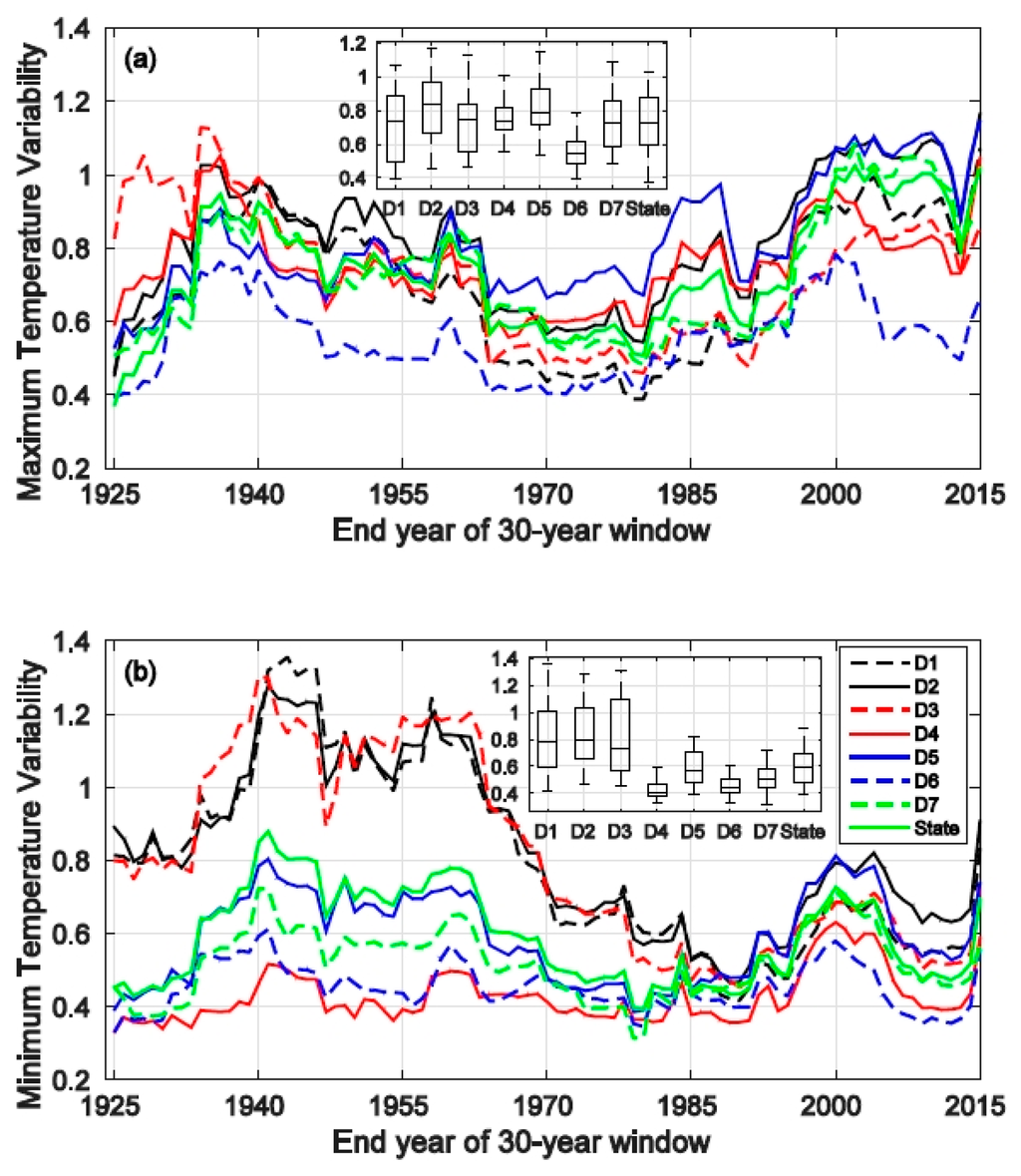
Figure 5.
Time series of the 30-year moving window of the (a) annual maximum temperature variability and (b) annual minimum temperature variability of different regions. The insert diagram shows the boxplot of variability for each region. The description of the boxplot features is provided in Figure 2’s caption.
Similar to the case of the annual average temperature, a repeating increasing-decreasing trend is observed in the annual minimum temperature variability (Figure 5b). In addition, the variabilities in the annual minimum temperature of the four southern regions (D4–D7) are consistently less than one. This shows that the annual minimum temperatures of those four regions are generally less variable than usual. Furthermore, the median variabilities of the three northern regions (D1–D3) are also less than one. It is also evident that the variabilities of these southern regions before 1984 are distinctly higher than those of the four northern regions. The correlations among these three regions (D1–D3) are consistently above 0.95.
In the annual average, maximum and minimum temperature, a sharp increase in the variability of 2015 (representing the 30-year window of 1986–2015) is consistent (Figure 4b and Figure 5). This is likely due to the fact that the temperature in 2015 is a record high and significantly higher than the long-term mean, as well as the 1986–2015 mean values (Table 2). The variance calculated with this extremely high value included is certainly larger than the case when this value is excluded.

Table 2.
Annual temperature of the water year 2015 versus the 1986–2015 mean and long-term mean values.
The overall variability pattern of winter precipitation (Figure 6a) mimics the pattern of the total annual precipitation (Figure 4a). This is not surprising, since a large portion (52% statewide) of the annual precipitation occurs in winter (Figure 3a). Similarly, the driest region (Southeast Desert Basin, D7) has the largest variability range (from 0.44–1.86). There is no clear trend in regional variabilities of summer precipitation (Figure 6c). This is likely due to the fact that summer precipitation generally derives from a small amount of storms and is thus highly variable from year to year. Additionally, it only accounts for a very small portion of the annual precipitation (3% statewide). The variability pattern of spring precipitation (Figure 6b) is generally similar to that of fall precipitation (Figure 6d), in spite of individual regional variabilities being largely different in the two cases. Overall, a general increasing trend is apparent. A sharp decrease in variability is observed after 2012. Most likely, this drop is caused by a lack of precipitation during the extraordinary 2012–2015 drought across the state. For instance, statewide spring precipitation in 2013, 2014 and 2015 accounts for only 47%, 83% and 49% of the 1986–2015 mean spring precipitation, respectively.
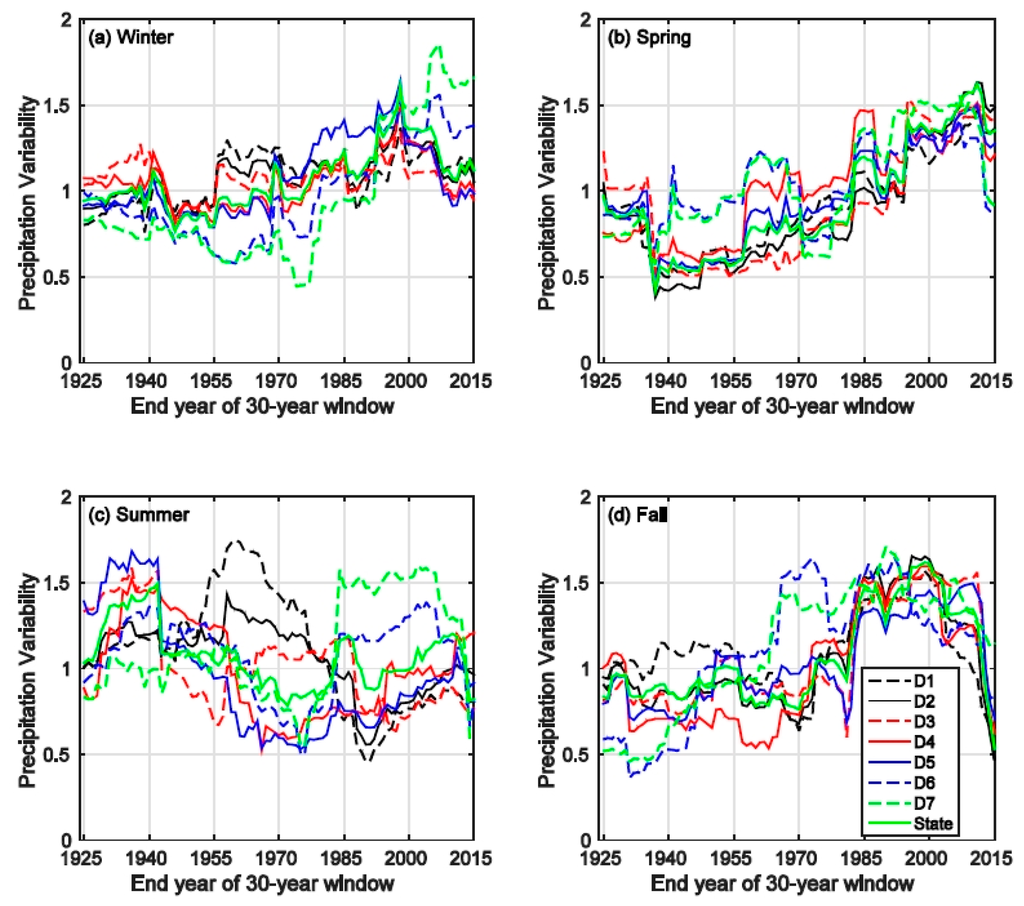
Figure 6.
Variability of the seasonal precipitation of different regions. (a) Winter; (b) Spring; (c) Summer; (d) Fall.
Winter, spring and fall temperature variabilities all exhibit cyclic patterns, while there is no evident pattern in summer temperature variability (Figure 7). The overall winter temperature variability peaks around the early 1960s for most regions and then starts declining till around 2013. After 1985, the variabilities are mostly less than one (Figure 7a). The general spring temperature variability first peaks in the late 1930s, followed by a declining trend till around 1985; after that, the variabilities for all regions start increasing till around 2004. A dip is observed after 2004 with the lowest variabilities occurring around 2008 (Figure 7b). The overall fall temperature variability first peaks at around 1940 for most regions and then declines till the late 1960s. It starts increasing again till 2001; after that, it becomes relatively stable (Figure 7d). In general, the variation range in winter (summer) is the largest (smallest). These cyclic patterns are also observed in the maximum temperature variability and minimum temperature variability (not shown) in winter, spring and fall. The only exception is that the minimum temperature variability exhibits no apparent pattern in fall. In summer, similarly, there are no evident patterns in the variabilities of maximum and minimum temperatures.
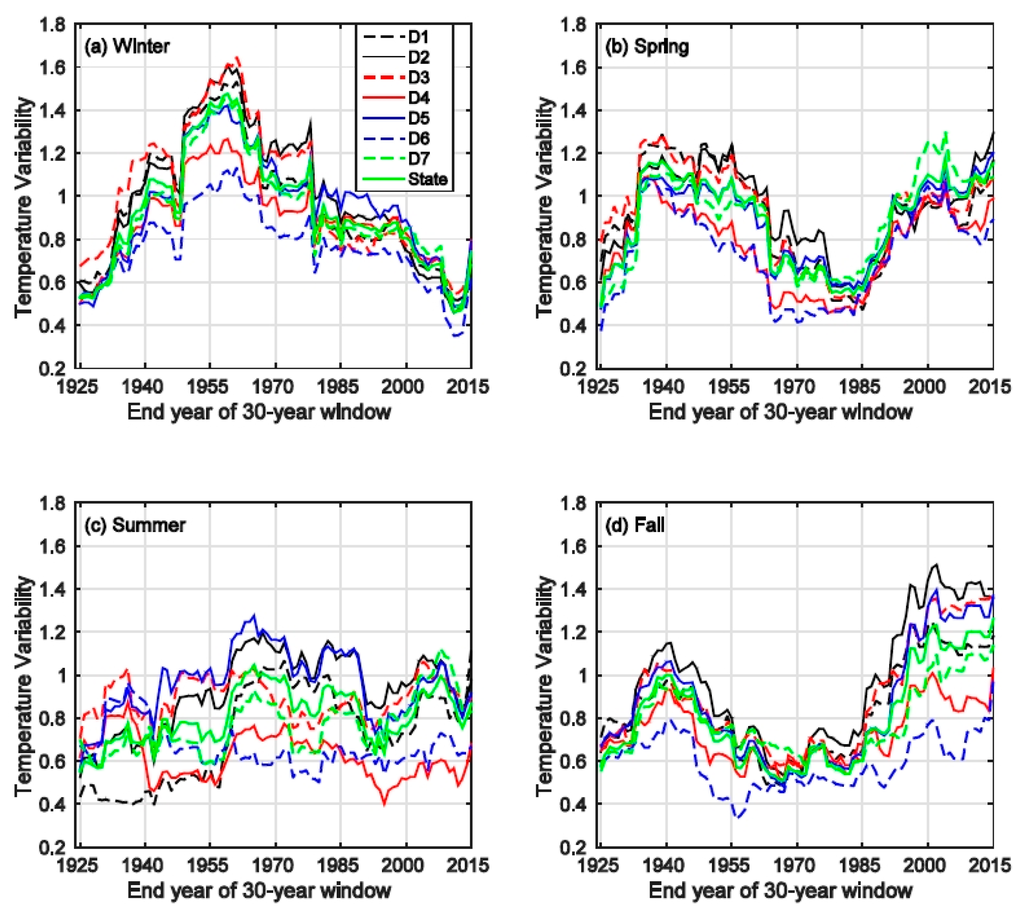
Figure 7.
Variability of the seasonal average temperature of different regions. (a) Winter; (b) Spring; (c) Summer; (d) Fall.
The variation range of precipitation variability differs among regions across different seasons (Figure 8a–d). The San Joaquin Drainage (D5) is the only one of which the median variability is less than one in all seasons. Statewide, the variability varies the most in spring (Figure 8b), with the upper bound (1.62) nearly four times of the lower bound (0.43). The median seasonal temperature variabilities of all regions are consistently less than one in all four seasons (Figure 8e–h). The South Coast Drainage (D6) is generally of the least variability among all regions followed by the Central Coast Drainage (D4), while regions including the Sacramento Drainage (D2), San Joaquin Drainage (D5) and Northeast Interior Basin (D3) typically have large variabilities. Statewide, the variability range in the winter is the largest (from 0.46–1.48).
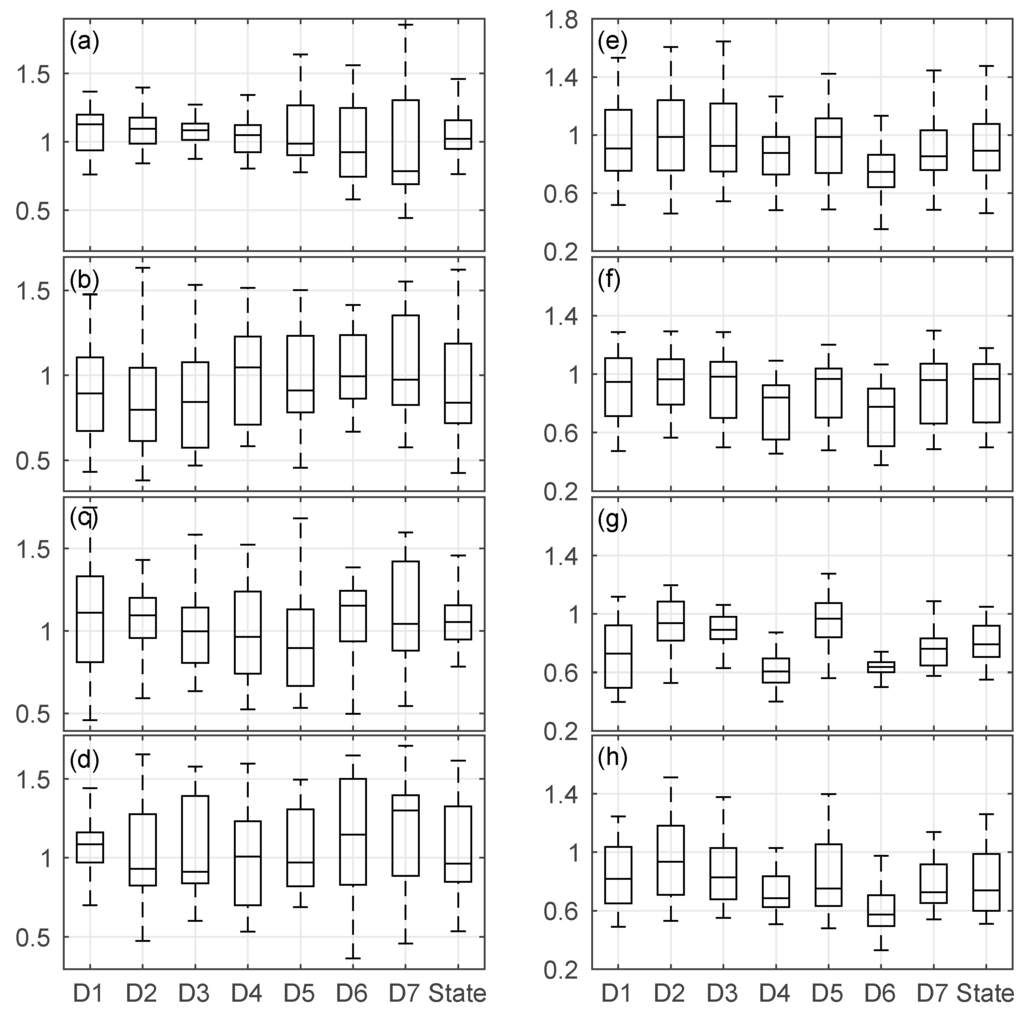
Figure 8.
Boxplot of precipitation variability (left column) (a–d) and average temperature variability (right column) (e–h) for winter, spring, summer and fall (Rows 1–4, respectively). The X-axis and Y-axis show the region name and variability values, respectively. The description of the boxplot features is provided in Figure 2’s caption.
3.2. Trend
There is no trend in annual precipitation in any region or statewide (Figure 9). An increasing trend is evident for the temperature over all regions. For annual average temperature (Tavg), trend slopes range from 0.07 °C/decade (Sacramento Drainage, D2) to 0.16 °C/decade (South Coast Drainage, D6); for annual maximum temperature (Tmax), the range is from 0.07 °C/decade (San Joaquin Drainage, D5) to 0.17 °C/decade (D6); for annual minimum temperature (Tmin), the slope varies from 0.05 °C/decade (D2) to 0.16 °C/decade (Central Coast Drainage, D4). The statewide increasing slopes for the annual average, maximum and minimum temperatures are roughly the same at 0.11 °C/decade. In contrast, a decreasing trend is apparent in drought indices for most regions, indicating intensified frequency of drought occurrence. Specifically, except for the two wettest regions (North Coast Drainage and Sacramento Drainage), other regions have declining trends with slopes ranging from −0.26/decade (D6) to −0.13/decade (Northeast Interior Basin, D3) in the meteorological drought index (PDSI); the range is from −0.26/decade (D6) to −0.12/decade (D5) for the hydrological drought index (PHDI). For the agricultural drought index (Z Index), a decreasing tendency is observed from D4–D7 ranging from −0.09/decade (D6) to −0.06/decade (D5). The statewide declining trend slopes for PDSI, PHDI and the Z Index are −0.14 /decade, −0.15 /decade and −0.06 /decade, respectively.
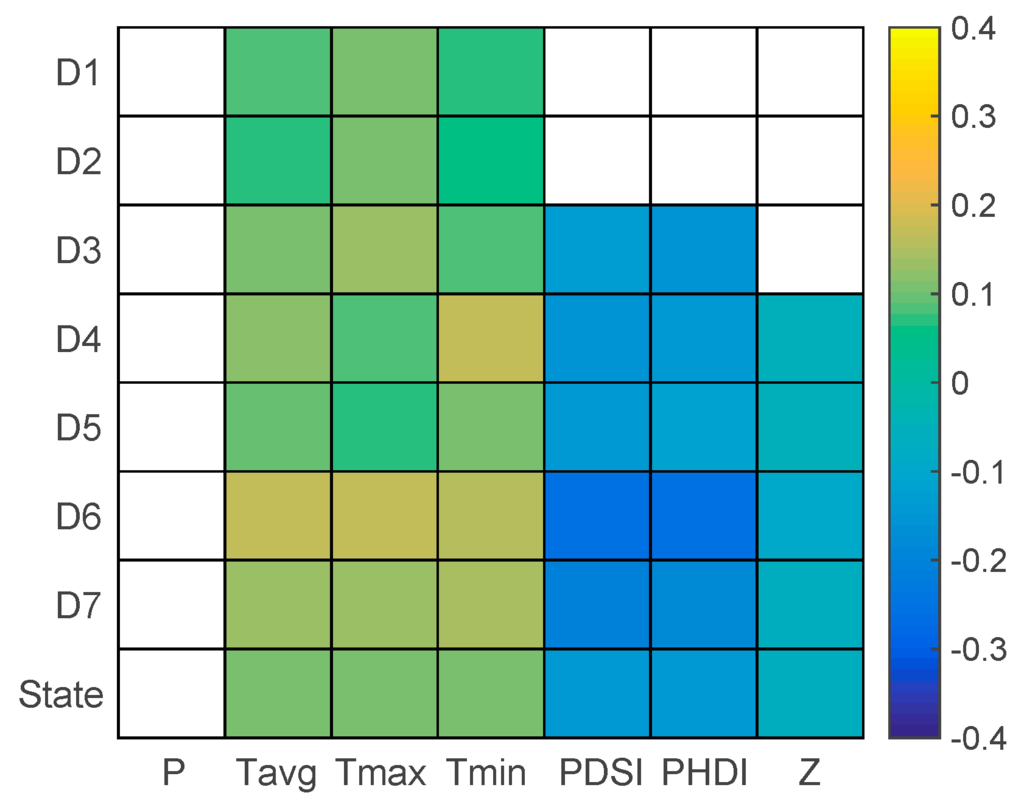
Figure 9.
Slope of significant trends of annual variables (per decade; the white color indicates no trends). Study variables and region names are shown in the X-axis and Y-axis, respectively. PDSI, Palmer Drought Severity Index; PHDI, Palmer Hydrological Drought Index.
On the seasonal scale, there is no trend in winter and fall precipitation (Figure 10). However, the region Southeast Deserts Basin (D7) tends to have a slightly decreasing trend (−0.1 cm/decade) in spring precipitation. The San Joaquin Drainage (D5) has a slightly increasing trend (0.04 cm/decade) in summer precipitation. The average temperature shows increasing trends across all four seasons, with the South Coast Drainage (D6) being the one with the most significant trend in every season. Statewide, the increasing trend slopes range from 0.10 °C/decade (winter) to 0.12 °C/decade (spring). The maximum temperature also exhibits an increasing trend except for the San Joaquin Drainage (D5) in summer. The South Coast Drainage (D6) has the most significant trend, except for the fall, when the Northeast Interior Basin (D3) region has a slightly higher trend slope. For minimum temperature, there is no significant trend for the Sacramento Drainage (D2) in winter and spring, neither for the North Coast Drainage (D1) in winter. In winter and fall, the Central Coast Drainage (D4) has the most significant trends; while in spring and summer, the South Coast Drainage (D6) has the most significant trends. The statewide trend is generally less significant in winter (with a slope of −0.08/decade) and spring (−0.1/decade) than in summer (−0.14/decade) and fall (−0.13/decade).
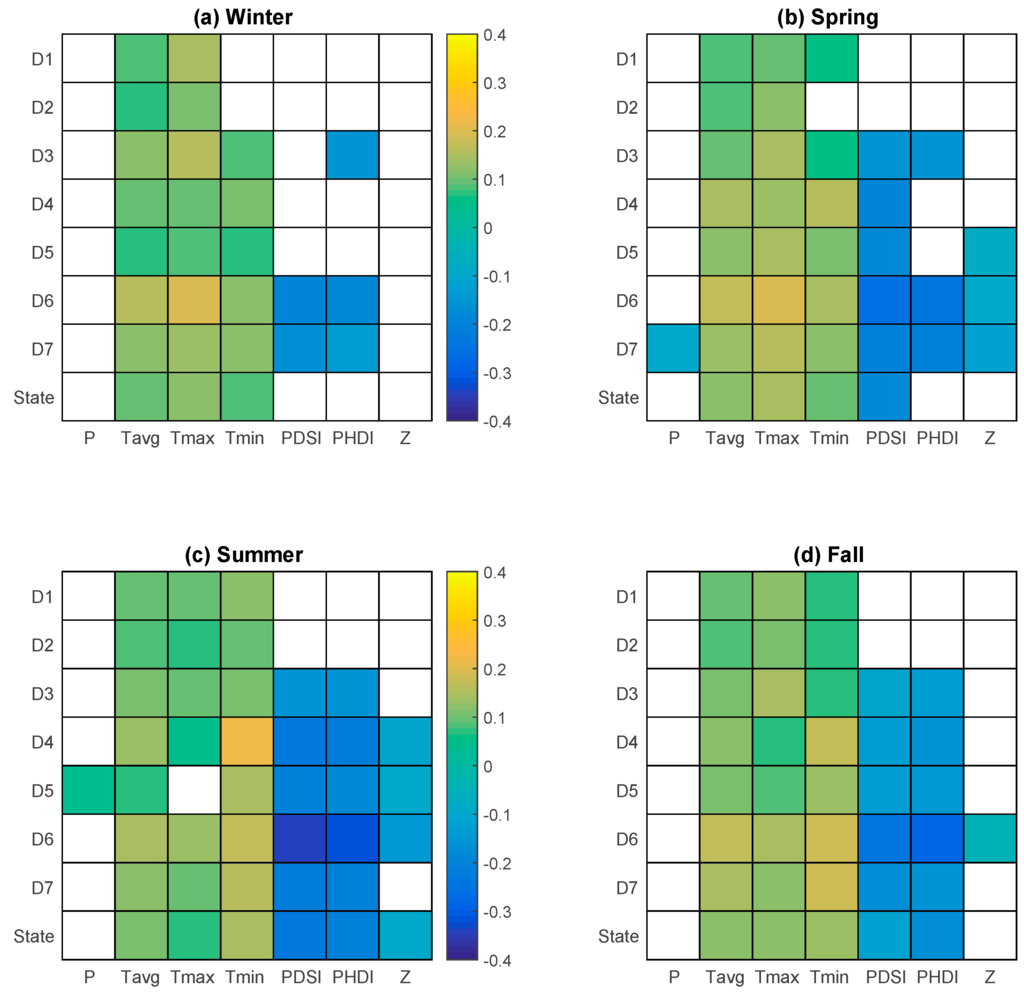
Figure 10.
Slope of the significant trends of seasonal variables (per decade; the white color indicates no trends). Study variables and region names are shown in the X-axis and Y-axis, respectively. (a) Winter; (b) Spring; (c) Summer; (d) Fall.
There are no trends in drought indices for the North Coast Drainage and Sacramento Drainage on the seasonal scale (Figure 10), which is consistent with that of the annual scale (Figure 9). There is no statewide trend in the Z Index in winter, spring and fall. There is no statewide trend for PHDI in winter and spring, either. In winter, no region exhibits a trend in the Z Index. Decreasing trends in PDSI and PHDI are observed for South Coast Drainage and Northeast Desert Basin (D6 and D7), with the former having slightly higher trends. The Northeast Interior Basin (D3) also shows a decreasing trend (−0.16/decade) in PHDI. In spring, those three regions (D3, D6 and D7) have significant declining trends in PHDI. The slopes of these trends are more significant than their counterparts in winter. Index PDSI show trends in all regions, except for the two wettest regions, with the highest trend slope in the South Coast Drainage (−0.26/decade) and the lowest slope in the Northeast Interior Basin (−0.15/decade). Relatively mild trends are observed for the Z Index from D5–D7 ranging from −0.11/decade to −0.09/decade. In summer, decreasing trends from D3–D7 are evident in PDSI and PHDI, with the South Coast Drainage (D6) having the most significant slopes for both indices (−0.34/decade and −0.32/decade, respectively). Slight trends are observed in the Z Index for regions D4–D6. The statewide trend slopes for three indices are −0.23/decade, −0.21/decade and −0.10/decade, respectively. In fall, the trend in the Z Index only exists in the South Coast Drainage (D6) with a slope of −0.05/decade. Regions D3–D7 also have significant trends in PDSI and PHDI. Region D6 again possesses the most significant trends, with slopes at −0.24/decade and −0.28/decade for PDSI and PHDI, respectively. The statewide trend slopes for these two indices in fall are −0.12/decade and −0.17/decade, respectively.
In addition to annual and seasonal scales, the trends of these variables are further investigated at the monthly scale. Precipitation shows no statistically significant trends in any month for any region. Temperature exhibits trends in multiple months for all regions (Figure 11). For temperature, May and September are the only two months where significant trends in all three temperature variables (average, maximum and minimum temperature) are observed across all regions. In May, except for Central Coast Drainage (D4), the trend slope in maximum temperature is the highest among three temperature variables, which is also the case in February and March. In September, for the three regions (D1–D3) in Northern California, the slope of the trend in maximum temperature is the largest; for the four regions (D4–D7) in Southern California, the trend slope in minimum temperature is the most significant, which is also the case statewide. In April, temperature trends are only observed in two coastal regions, D4 and D6. Those are also the only two regions where trends in minimum and average temperatures are observed for every month. In July and August, it is evident that the trend in minimum temperature is the most significant in three temperature variables across all regions. Statewide, in addition to April, there is no trend observed in December; for November, there is only a trend in the minimum temperature. The trend slope is consistently less than 0.2 °C/decade. The most apparent trends in all three variables appear in September. In summer and fall months (June–November), the trend in the minimum temperature is generally the most significant; in the winter and spring months, except for December and April, however, the trend in the maximum temperature is the most apparent among three temperature variables.
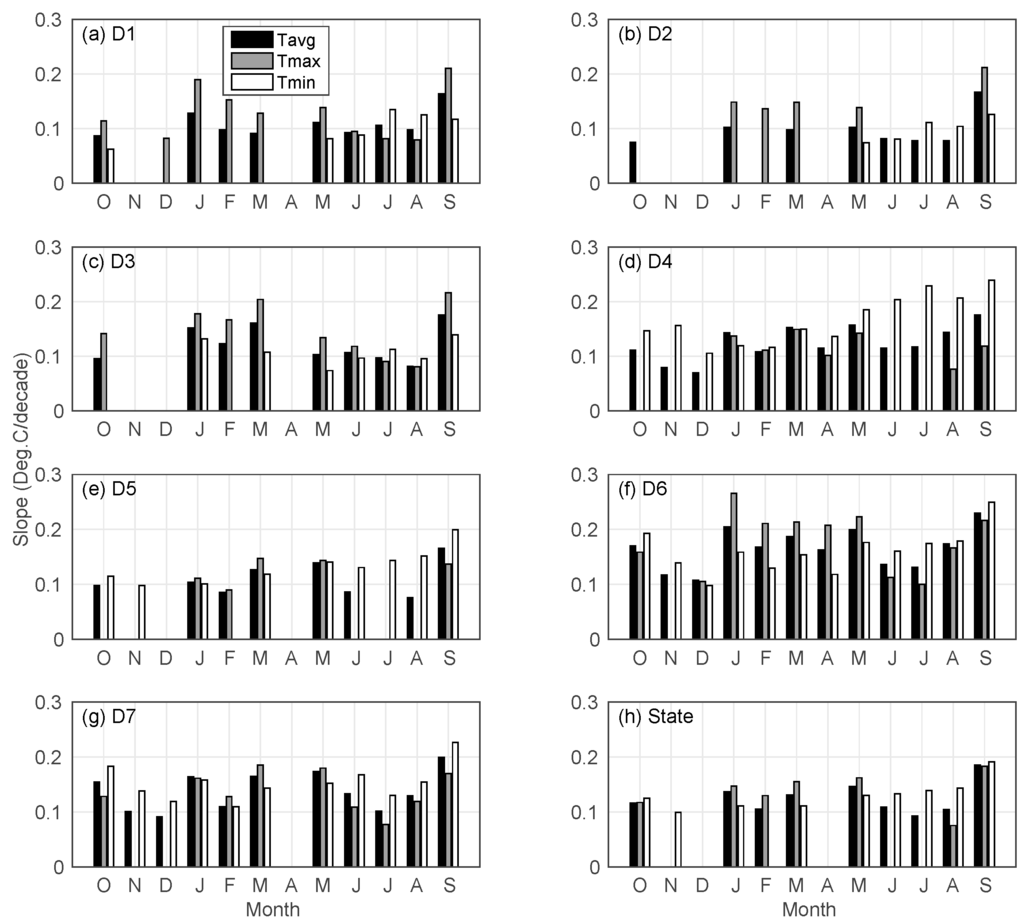
Figure 11.
Slope of significant trends of monthly temperature for regoins (a) North Coast Drainage (D1); (b) Sacramento Drainage (D2); (c) Northeast Interior Basin (D3); (d) Central Coast Drainage (D4); (e) San Joaquin Drainage (D5); (f) South Coast Drainage (D6); (g) Southeast Desert Basin (D7); (h) State from October (O) to September (S).
Drought indices show trends for most regions, except for the North Coast Drainage and Sacramento Drainage (Figure 12). These two regions are thus not presented. Regions including the Northeast Interior Basin (D3), Central Coast Drainage (D4) and San Joaquin Drainage (D5) see no trends in any of the drought indices in certain months (October–December for D3; November–February for D4 and D5) (Figure 12). For regions and months where trends are identified, the trends are consistently negative (declining). Most significant trends generally occur over the South Coast Drainage (D6). In contrast, the trends observed in the Northeast Interior Basin (D3) have relatively milder slopes (greater than −0.2/decade). Among three indices, the Z Index has the least frequent and least significant trend (characterized by a mild slope, should the trend exist). The trend in PDSI is the most significant in spring and summer months (March–August). Statewide, no trends are observed in winter months (December–February). However, declining trends exist for all three indices from May–September where the trend in the Z Index is normally the least significant. In September and October, the trend in PHDI is more significant than that of PDSI.
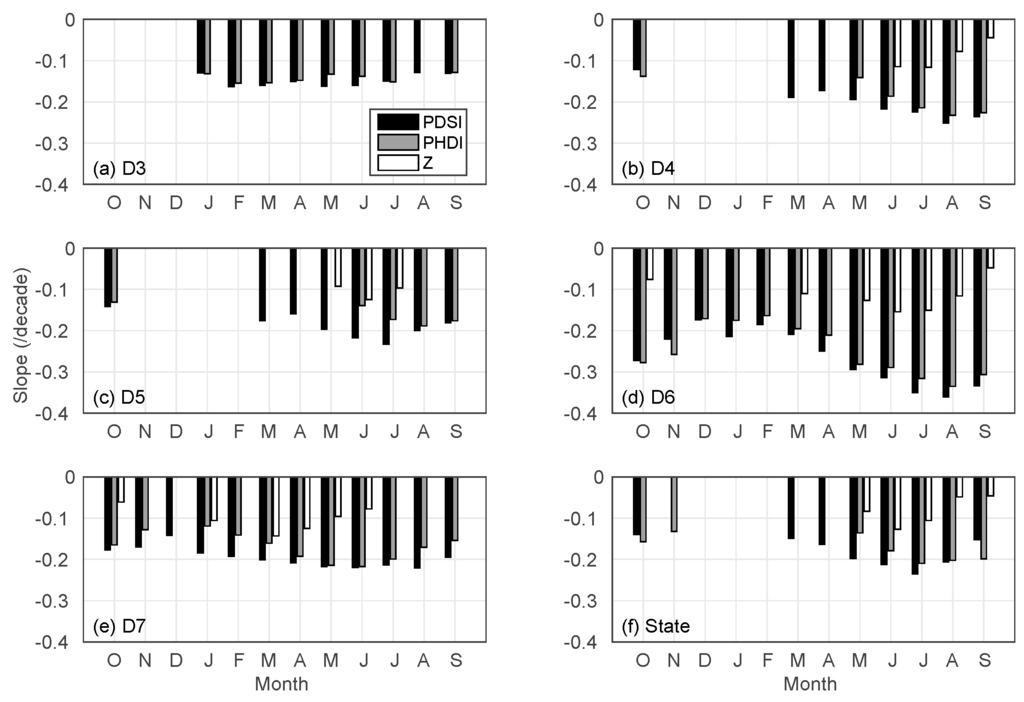
Figure 12.
Slope of significant trends of monthly drought indices. (a) Northeast Interior Basin (D3); (b) Central Coast Drainage (D4); (c) San Joaquin Drainage (D5); (d) South Coast Drainage (D6); (e) Southeast Desert Basin (D7); (f) State from October (O) to September (S).
4. Discussion
This study shows that annual, winter and spring precipitation variabilities generally increase throughout the record period across the state. This implies that precipitation extremes are being observed more frequently. The increasing occurrence of precipitation extremes is also projected till the end of this century [59,60,61,62,63]. For instance, [59] shows that wet extremes (dry extremes) are expected to become three (one and half to two) times more common over California by 2100. The work in [63] reports that drought and flooding events over the state are projected to increase by at least 50% in the same timeframe. They attribute these intensified extremes partly to strengthened El Niño-Southern Oscillation (ENSO) tele-connections. This is in line with the work of [64], which shows a dominant influence of the ENSO on wet season precipitation variability over the state (particularly the southern part). In spite of increasing variability, the current study further shows that the average amounts of annual and wet season precipitation remain almost the same. In addition, the current study identifies no trends in annual precipitation, winter precipitation and monthly precipitation in any region across the state. This finding is generally consistent with what is reported in previous studies [2,9]. Despite the high consensus of increasing precipitation extremes in the future, there is low consensus across the literature on how the precipitation mean and trends will evolve. The work in [65] indicates that by the end of this century, statewide annual mean precipitation could be 80%–100% of the historical average with major decreases in Central and Southern California. A different study [66] projects decreased precipitation in the winter and summer throughout the 21st century. Several other studies [60,67], however, notice large spatial differences in annual precipitation changes, including both increases and decreases. Projected precipitation trends vary largely depending on the models applied, the emissions scenarios investigated and the regions across the state [66,68,69,70,71,72].
While no significant trends in precipitation are observed in the record period, this study identifies increasing trends in average, maximum and minimum temperatures on both annual and seasonal scales nearly for all regions. Statewide, the increasing rate is about the same (0.11 °C/decade) for annual average, maximum and minimum temperatures. Specifically, the Southern Coast Drainage region generally has the most consistent (observed nearly every month) and significant (high increasing rate) warming trends at annual, seasonal and monthly scales. There is a strong consensus on the increasing trend in temperature across the state in the literature [5,7,8,9,13,14,73], though the specific increasing rates vary with different studies. Warming trends in temperature over the state are projected to continue throughout the 21st century [65,69,70,71,74,75,76]. The current work shows that, rather than an increasing trend, variability in temperature exhibits a decade-to multi-decade-long cyclic pattern on both annual and seasonal (except for summer) scales. This is probably linked to the leading patterns of sea surface variability, including the Pacific decadal variability (PDV) pattern. The work in [11] finds out that the PDV pattern plays a major role in determining the spatial and seasonal characteristics of both temperature and precipitation trends over the Unites States (including California). Despite this cyclic pattern in variability, extreme hot years (seasons) appear to occur more frequently, which is particularly evident since 2000. For instance, the year of 2015 is characterized with the highest annual, winter and fall statewide average temperatures in the 120-year record period (Table 3). Out of the hottest 10 years (with the highest statewide annual average temperatures), five years come from the last 15 years (2001–2015). For winter, spring, summer and fall temperatures, the corresponding numbers are four years, five years, six years and five years, respectively. The intensified occurrence frequency of extreme heat waves over the state is also observed in previous studies [5,9] and projected throughout the 21st century [61,69,77].

Table 3.
Top 10 years with highest statewide average temperatures.
Statewide, deceasing trends are evident in the drought indices investigated on the annual scale and in the summer. This reflects the increasing occurrence of annual and summer meteorological, hydrological and agricultural droughts. It is worth noting that no trends are observed in annual or summer precipitation. The decreasing trends in the meteorological drought index may be attributed to the increasing occurrence of (dry) precipitation extremes. In addition, no trends in these indices are detected in winter. This is expected, since winter is the wet season, when more than half of the annual precipitation occurs and when water demand is typically low. However, a decreasing trend in the meteorological drought index is observed in spring, indicating the more frequent occurrence of meteorological droughts in this season statewide. On the annual scale, the declining trend in the hydrological drought index is more significant than that of the meteorological drought index. This is likely due to the fact that snowmelt runoff is an important component of the streamflow. The increasing temperature possibility shifts the snowmelt runoff timing earlier and leads to a larger portion of precipitation falling as rainfall rather than snowfall [1,78,79,80,81], yielding the increased possibility of the occurrence of a hydrological drought, even though there is no deficit in precipitation. The study also shows that no trends are identified in the drought indices over the North Coast Drainage and the Sacramento Drainage on annual, seasonal and monthly scales. These are the two wettest regions of which the annual mean precipitation is markedly above the statewide average precipitation. The South Coast Drainage tends to have the most consistent and significant declining trends in these indices on annual, seasonal and monthly scales. Among the three indices, trends in the Z Index are generally the least frequent and least significant when compared to the other two drought indices. It should be pointed out that, despite its strength in combining both water supply (precipitation) and demand (potential evapotranspiration) into a single index, the Palmer Index may not work well in mountainous and snow-impacted basins [38,40,82,83,84], while large portions of California are mountainous areas. However, a detailed assessment of the skill and applicability of the Palmer Index in these areas is out the scope of the current study. For a comprehensive review on the strength and limitations of the Palmer Index, the readers are referred to [29,30].
5. Conclusions
This study conducts a detailed regional analysis of the characteristics of hydroclimatic variables and drought extremes in terms of variability and trends over California. The specific objective of this work is two-fold: (1) to assess the variability and trends of precipitation and temperature over the state; and (2) to detect potential trends of three physically-based types (meteorological, hydrological and agricultural) of drought over the state. A comprehensive dataset containing 120-year (water years 1896–2015) monthly precipitation, average temperature, maximum temperature, minimum temperature and the Palmer Index (including PDSI, PHDI and the Z Index) for seven climate regions of the state is used for this purpose. The Mann–Kendall test along with a trend-free pre-whitening procedure is employed in trend identification.
The results indicate that, at annual and seasonal scales, there are nearly no significant changes in mean precipitation, whilst an increasing trend is evident in average, maximum and minimum temperatures statewide and over each individual region. This finding is consistent with what was reported in previous work [2,5,9,14,73]. Specifically, this study shows that the statewide increasing rates for annual average, maximum and minimum temperatures are about the same (0.11 °C/decade) across the record period. On average, the warming trend over the South Coast Drainage is the most significant among all regions.
In a new finding, this study indicates that annual, winter and spring precipitation variabilities generally have an increasing tendency for every region. This implies the increasing frequency of precipitation extremes, which is also projected to occur throughout the 21st century with continuing warming expected [59,60,61,62,63]. The variabilities of annul and winter precipitation in the Northeast Desert Drainage vary in the widest ranges out of all seven regions.
Another new finding of this study is that no significant trends are detected in the three types of physically-based drought events over the two wettest regions of the state (North Coast Drainage and Sacramento Drainage) at annual, seasonal and monthly scales. For other regions, the South Coast Drainage tends to have the most significant declining trends in drought indices in general, indicating the most intensified frequency of the occurrence of drought events over this region. In summer, declining trends are observed in all three indices, highlighting the increased possibility of less than normal precipitation, streamflow and soil moisture in this season.
In spite of its advantageous properties and wide popularity among researchers, the Palmer Index applied in this study may not be the most appropriate choice for the snow impacted mountainous regions across the state. This is mostly due to the insufficient representation of the snow storage processes in the two-layer model used in deriving the Palmer Index. Nevertheless, this study focuses on the qualitative trend rather than the quantitative severity of drought. The specific values of drought indices have very marginal (if any) implications on the main findings of this study, as long as they are determined in the same manner. The alternatives of the Palmer Index, including the standardize precipitation (evapotranspiration) and runoff indices [85,86,87,88], are under evaluation and will be presented in our future work.
Overall, these findings are highly meaningful from both theoretical and practical perspectives. From a theoretical perspective, these findings provide critical information that can be adopted in enhancing and verifying forecast models that predict future hydroclimatic extremes. From a practical perspective, these findings have significant implications for water resource managers in making adaptive management plans, in the context of being better informed in deciding future water allocation quotas (based on identified variability and trends in historical conditions) and in determining reservoir releases before the summer when water demand is typically the highest (in light of the observed increasing frequency of drought occurrence during this season), among others.
Acknowledgments
The authors would like to thank two anonymous reviewers for their valuable comments that helped improve the quality of this study. The authors completed all aspects of this work on their own without any financial or in-kind support from any agencies. Any findings, opinions and conclusions expressed in this paper are solely the authors’ and do not reflect the views or opinions of their employer.
Author Contributions
The first author designed the study and produced the results. Both authors analyzed the results and wrote the paper together.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mote, P.W.; Hamlet, A.F.; Clark, M.P.; Lettenmaier, D.P. Declining mountain snowpack in western north america. Bull. Am. Meteorol. Soc. 2005, 86, 39–49. [Google Scholar] [CrossRef]
- Grundstein, A. Evaluation of climate change over the continental united states using a moisture index. Clim. Chang. 2009, 93, 103–115. [Google Scholar] [CrossRef]
- Pryor, S.; Howe, J.; Kunkel, K. How spatially coherent and statistically robust are temporal changes in extreme precipitation in the contiguous USA? Int. J. Climatol. 2009, 29, 31–45. [Google Scholar] [CrossRef]
- Grundstein, A.; Dowd, J. Trends in extreme apparent temperatures over the united states, 1949–2010. J. Appl. Meteorol. Clim. 2011, 50, 1650–1653. [Google Scholar] [CrossRef]
- Hoerling, M.P.; Dettinger, M.; Wolter, K.; Lukas, J.; Eischeid, J.; Nemani, R.; Liebmann, B.; Kunkel, K.E.; Kumar, A. Present weather and climate: Evolving conditions. In Assessment of Climate Change in the Southwest United States; Springer: Berlin, Germany, 2013; pp. 74–100. [Google Scholar]
- Schwartz, M.D.; Ault, T.R.; Betancourt, J.L. Spring onset variations and trends in the continental united states: Past and regional assessment using temperature-based indices. Int. J. Climatol. 2013, 33, 2917–2922. [Google Scholar] [CrossRef]
- Bonfils, C.; Duffy, P.B.; Santer, B.D.; Wigley, T.M.; Lobell, D.B.; Phillips, T.J.; Doutriaux, C. Identification of external influences on temperatures in california. Clim. Chang. 2008, 87, 43–55. [Google Scholar] [CrossRef]
- Bonfils, C.; Santer, B.D.; Pierce, D.W.; Hidalgo, H.G.; Bala, G.; Das, T.; Barnett, T.P.; Cayan, D.R.; Doutriaux, C.; Wood, A.W. Detection and attribution of temperature changes in the mountainous western united states. J. Clim. 2008, 21, 6404–6424. [Google Scholar] [CrossRef]
- Kunkel, K.; Stevens, L.; Stevens, S.; Sun, L.; Janssen, E.; Wuebbles, D.; Kruk, M.; Thomas, D.; Shulski, M.; Umphlett, N. Regional climate trends and scenarios for the us national climate assessment: Part 4. Climate of the us great plains. NOAA Tech. Rep. NESDIS 2013, 142, 91. [Google Scholar]
- Lavers, D.A.; Villarini, G. The contribution of atmospheric rivers to precipitation in europe and the united states. J. Hydrol. 2015, 522, 382–390. [Google Scholar] [CrossRef]
- Wang, H.; Schubert, S.; Suarez, M.; Chen, J.; Hoerling, M.; Kumar, A.; Pegion, P. Attribution of the seasonality and regionality in climate trends over the united states during 1950–2000. J. Clim. 2009, 22, 2571–2590. [Google Scholar] [CrossRef]
- Westby, R.M.; Lee, Y.-Y.; Black, R.X. Anomalous temperature regimes during the cool season: Long-term trends, low-frequency mode modulation, and representation in cmip5 simulations. J. Clim. 2013, 26, 9061–9076. [Google Scholar] [CrossRef]
- Cordero, E.C.; Kessomkiat, W.; Abatzoglou, J.; Mauget, S.A. The identification of distinct patterns in california temperature trends. Clim. Chang. 2011, 108, 357–382. [Google Scholar] [CrossRef]
- MacDonald, G.M. Water, climate change, and sustainability in the southwest. PNAS 2010, 107, 21256–21262. [Google Scholar] [CrossRef] [PubMed]
- McRoberts, D.B.; Nielsen-Gammon, J.W. A new homogenized climate division precipitation dataset for analysis of climate variability and climate change. J. Appl. Meteorol. Clim. 2011, 50, 1187–1199. [Google Scholar] [CrossRef]
- AghaKouchak, A.; Cheng, L.; Mazdiyasni, O.; Farahmand, A. Global warming and changes in risk of concurrent climate extremes: Insights from the 2014 california drought. Geophys. Res. Lett. 2014, 41, 8847–8852. [Google Scholar] [CrossRef]
- Cheng, L.; Hoerling, M.; AghaKouchak, A.; Livneh, B.; Quan, X.-W.; Eischeid, J. How has human-induced climate change affected california drought risk? J. Clim. 2016, 29, 111–120. [Google Scholar] [CrossRef]
- Hatchett, B.J.; Boyle, D.P.; Putnam, A.E.; Bassett, S.D. Placing the 2012–2015 california-nevada drought into a paleoclimatic context: Insights from walker lake, california-nevada, USA. Geophys. Res. Lett. 2015, 42, 8632–8640. [Google Scholar] [CrossRef]
- Mao, Y.; Nijssen, B.; Lettenmaier, D.P. Is climate change implicated in the 2013–2014 california drought? A hydrologic perspective. Geophys. Res. Lett. 2015, 42, 2805–2813. [Google Scholar] [CrossRef]
- Mehran, A.; Mazdiyasni, O.; AghaKouchak, A. A hybrid framework for assessing socioeconomic drought: Linking climate variability, local resilience, and demand. J. Geophys. Res. Atmos. 2015, 120, 7520–7533. [Google Scholar] [CrossRef]
- Robeson, S.M. Revisiting the recent california drought as an extreme value. Geophys. Res. Lett. 2015, 42, 6771–6779. [Google Scholar] [CrossRef]
- Seager, R.; Hoerling, M.; Schubert, S.; Wang, H.; Lyon, B.; Kumar, A.; Nakamura, J.; Henderson, N. Causes of the 2011–14 california drought. J. Clim. 2015, 28, 6997–7024. [Google Scholar] [CrossRef]
- Shukla, S.; Safeeq, M.; AghaKouchak, A.; Guan, K.; Funk, C. Temperature impacts on the water year 2014 drought in California. Geophys. Res. Lett. 2015, 42, 4384–4393. [Google Scholar] [CrossRef]
- Swain, D.L. A tale of two California droughts: Lessons amidst record warmth and dryness in a region of complex physical and human geography. Geophys. Res. Lett. 2015, 42, 9999–10003. [Google Scholar] [CrossRef]
- Griffin, D.; Anchukaitis, K.J. How unusual is the 2012–2014 california drought? Geophys. Res. Lett. 2014, 41, 9017–9023. [Google Scholar] [CrossRef]
- Williams, A.P.; Seager, R.; Abatzoglou, J.T.; Cook, B.I.; Smerdon, J.E.; Cook, E.R. Contribution of anthropogenic warming to california drought during 2012–2014. Geophys. Res. Lett. 2015, 42, 6819–6828. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Glantz, M.H. Understanding: The drought phenomenon: The role of definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef]
- American Mathematical Society. Policy statement: Meteorological drought. Bull. Am. Meteorol. Soc. 1997, 78, 847–849. [Google Scholar]
- Keyantash, J.; Dracup, J.A. The quantification of drought: An evaluation of drought indices. Bull. Am. Meteorol. Soc. 2002, 83, 1167–1180. [Google Scholar]
- Heim, R.R., Jr. A review of twentieth-century drought indices used in the united states. Bull. Am. Meteorol. Soc. 2002, 83, 1149–1165. [Google Scholar]
- Dai, A. Drought under global warming: A review. WIREs: Clim. Chang. 2011, 2, 45–65. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; US Department of Commerce, Weather Bureau: Washington, DC, USA, 1965; p. 58.
- Dai, A.; Trenberth, K.E.; Karl, T.R. Global variations in droughts and wet spells: 1900–1995. Geophys. Res. Lett. 1998, 25, 3367–3370. [Google Scholar] [CrossRef]
- Dai, A. Characteristics and trends in various forms of the palmer drought severity index during 1900–2008. J. Geophys. Res. Atmos. 2011. [Google Scholar] [CrossRef]
- Dai, A.; Trenberth, K.E.; Qian, T. A global dataset of palmer drought severity index for 1870–2002: Relationship with soil moisture and effects of surface warming. J. Hydrometeorol. 2004, 5, 1117–1130. [Google Scholar] [CrossRef]
- Kogan, F.N. Droughts of the late 1980s in the united states as derived from noaa polar-orbiting satellite data. Bull. Am. Meteorol. Soc. 1995, 76, 655–668. [Google Scholar] [CrossRef]
- Hu, Q.; Willson, G.D. Effects of temperature anomalies on the palmer drought severity index in the central united states. Int. J. Climatol. 2000, 1899–1911. [Google Scholar] [CrossRef]
- Haslinger, K.; Koffler, D.; Schöner, W.; Laaha, G. Exploring the link between meteorological drought and streamflow: Effects of climate-catchment interaction. Water Resour. Res. 2014, 50, 2468–2487. [Google Scholar] [CrossRef]
- Palmer, W.C. Keeping track of crop moisture conditions, nationwide: The new crop moisture index. Weatherwise 1968, 21, 156–161. [Google Scholar] [CrossRef]
- Karl, T.R. The sensitivity of the palmer drought severity index and palmer’s z-index to their calibration coefficients including potential evapotranspiration. J. Clim. Appl. Meteorol. 1986, 25, 77–86. [Google Scholar] [CrossRef]
- Guttman, N.B.; Quayle, R.G. A historical perspective of us climate divisions. Bull. Am. Meteorol. Soc. 1996, 77, 293–303. [Google Scholar] [CrossRef]
- Pagano, T.; Garen, D.; Sorooshian, S. Evaluation of official western us seasonal water supply outlooks, 1922–2002. J. Hydrometeorol. 2004, 5, 896–909. [Google Scholar] [CrossRef]
- Pagano, T.; Garen, D. A recent increase in western us streamflow variability and persistence. J. Hydrometeorol. 2005, 6, 173–179. [Google Scholar] [CrossRef]
- Mann, H. Non-parametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Charles Griffin: London, UK, 1975. [Google Scholar]
- Yue, S.; Pilon, P.; Cavadias, G. Power of the mann-kendall and spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Gautam, M.; Acharya, K. Streamflow trends in nepal. Hydrolog. Sci. J. 2012, 57, 344–357. [Google Scholar] [CrossRef]
- Kibria, K.N.; Ahiablame, L.; Hay, C.; Djira, G. Streamflow trends and responses to climate variability and land cover change in south dakota. Hydrology 2016. [Google Scholar] [CrossRef]
- Partal, T.; Kahya, E. Trend analysis in turkish precipitation data. Hydrol. Process. 2006, 20, 2011–2026. [Google Scholar] [CrossRef]
- Kahya, E.; Kalaycı, S. Trend analysis of streamflow in turkey. J. Hydrol. 2004, 289, 128–144. [Google Scholar] [CrossRef]
- Hamed, K.H. Trend detection in hydrologic data: The mann–kendall trend test under the scaling hypothesis. J. Hydrol. 2008, 349, 350–363. [Google Scholar] [CrossRef]
- Thiel, H. A rank-invariant method of linear and polynomial regression analysis, part 3. Nederl. Akad. Wetensch. Proc. 1950, 53, 1397–1412. [Google Scholar]
- Sen, P.K. Estimates of the regression coefficient based on kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Von Storch, H. Misuses of statistical analysis in climate research. In Analysis of Climate Variability; Springer: Berlin, Germany, 1995; pp. 11–26. [Google Scholar]
- Douglas, E.; Vogel, R.; Kroll, C. Trends in floods and low flows in the united states: Impact of spatial correlation. J. Hydrol. 2000, 240, 90–105. [Google Scholar] [CrossRef]
- Hamed, K.H.; Rao, A.R. A modified mann-kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Phinney, B. Canadian streamflow trend detection: Impacts of serial and cross-correlation. Hydrolog. Sci. J. 2003, 48, 51–63. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Berg, N.; Hall, A. Increased interannual precipitation extremes over california under climate change. J. Clim. 2015. [Google Scholar] [CrossRef]
- Das, T.; Dettinger, M.D.; Cayan, D.R.; Hidalgo, H.G. Potential increase in floods in california’s sierra nevada under future climate projections. Clim. Chang. 2011, 109, 71–94. [Google Scholar] [CrossRef]
- Tebaldi, C.; Hayhoe, K.; Arblaster, J.M.; Meehl, G.A. Going to the extremes. Clim. Chang. 2006, 79, 185–211. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, X. Downscaling and projection of winter extreme daily precipitation over north america. J. Clim. 2008, 21, 923–937. [Google Scholar] [CrossRef]
- Yoon, J.-H.; Wang, S.S.; Gillies, R.R.; Kravitz, B.; Hipps, L.; Rasch, P.J. Increasing water cycle extremes in California and in relation to enso cycle under global warming. Nat. Commun. 2015. [Google Scholar] [CrossRef] [PubMed]
- Fierro, A.O. Relationships between california rainfall variability and large-scale climate drivers. Int. J. Climatol. 2014, 34, 3626–3640. [Google Scholar] [CrossRef]
- Cayan, D.R.; Tyree, M.; Kunkel, K.E.; Castro, C.; Gershunov, A.; Barsugli, J.; Ray, A.J.; Overpeck, J.; Anderson, M.; Russell, J. Future climate: Projected average. In Assessment of Climate Change in the Southwest United States; Springer: Berlin, Germany, 2013; pp. 101–125. [Google Scholar]
- Seager, R.; Vecchi, G.A. Greenhouse warming and the 21st century hydroclimate of southwestern north america. PNAS 2010, 107, 21277–21282. [Google Scholar] [CrossRef] [PubMed]
- Hagemann, S.; Chen, C.; Clark, D.; Folwell, S.; Gosling, S.N.; Haddeland, I.; Hannasaki, N.; Heinke, J.; Ludwig, F.; Voss, F. Climate change impact on available water resources obtained using multiple global climate and hydrology models. Earth Syst. Dynam. 2013, 4, 129–144. [Google Scholar] [CrossRef]
- Maurer, E.P. Uncertainty in hydrologic impacts of climate change in the sierra nevada, california, under two emissions scenarios. Clim. Chang. 2007, 82, 309–325. [Google Scholar] [CrossRef]
- Cayan, D.R.; Maurer, E.P.; Dettinger, M.D.; Tyree, M.; Hayhoe, K. Climate change scenarios for the california region. Clim. Chang. 2008, 87, 21–42. [Google Scholar] [CrossRef]
- Gutzler, D.S.; Robbins, T.O. Climate variability and projected change in the western united states: Regional downscaling and drought statistics. Clim. Dynam. 2011, 37, 835–849. [Google Scholar] [CrossRef]
- Dettinger, M.D. Projections and downscaling of 21st century temperatures, precipitation, radiative fluxes and winds for the southwestern us, with focus on lake tahoe. Clim. Chang. 2013, 116, 17–33. [Google Scholar] [CrossRef]
- Liu, Y.; Goodrick, S.L.; Stanturf, J.A. Future us wildfire potential trends projected using a dynamically downscaled climate change scenario. Forest Ecol. Manag. 2013, 294, 120–135. [Google Scholar] [CrossRef]
- Walsh, J.; Wuebbles, D.; Hayhoe, K.; Kossin, J.; Kunkel, K.; Stephens, G.; Thorne, P.; Vose, R.; Wehner, M.; Willis, J. Chapter 2: Our changing climate. In Climate Change Impacts in the United States: The Third National Climate Assessment; Melillo, J.M., Richmond, T.C., Yohe, G.W., Eds.; US Global Change Research Program: Washington, DC, USA, 2014; pp. 19–67. [Google Scholar]
- Elguindi, N.; Grundstein, A. An integrated approach to assessing 21st century climate change over the contiguous us using the narccap rcm output. Clim. Chang. 2013, 117, 809–827. [Google Scholar] [CrossRef]
- Ashfaq, M.; Bowling, L.C.; Cherkauer, K.; Pal, J.S.; Diffenbaugh, N.S. Influence of climate model biases and daily-scale temperature and precipitation events on hydrological impacts assessment: A case study of the united states. J. Geophys. Res. Atmos. 2010. [Google Scholar] [CrossRef]
- Scherer, M.; Diffenbaugh, N.S. Transient twenty-first century changes in daily-scale temperature extremes in the united states. Clim. Dynam. 2014, 42, 1383–1404. [Google Scholar] [CrossRef]
- Gershunov, A.; Guirguis, K. California heat waves in the present and future. Geophys. Res. Lett. 2012. [Google Scholar] [CrossRef]
- Cayan, D.R.; Dettinger, M.D.; Kammerdiener, S.A.; Caprio, J.M.; Peterson, D.H. Changes in the onset of spring in the western united states. Bull. Am. Meteorol. Soc. 2001, 82, 399–415. [Google Scholar] [CrossRef]
- Stewart, I.T.; Cayan, D.R.; Dettinger, M.D. Changes in snowmelt runoff timing in western north america under abusiness as usual’climate change scenario. Clim. Chang. 2004, 62, 217–232. [Google Scholar] [CrossRef]
- McCabe, G.J.; Clark, M.P. Trends and variability in snowmelt runoff in the western united states. J. Hydrometeorol. 2005, 6, 476–482. [Google Scholar] [CrossRef]
- Regonda, S.K.; Rajagopalan, B.; Clark, M.; Pitlick, J. Seasonal cycle shifts in hydroclimatology over the western united states. J. Clim. 2005, 18, 372–384. [Google Scholar] [CrossRef]
- Alley, W.M. The palmer drought severity index: Limitations and assumptions. J. Clim. Appl. Meteorol. 1984, 23, 1100–1109. [Google Scholar] [CrossRef]
- Akinremi, O.; McGinn, S.; Barr, A. Evaluation of the palmer drought index on the canadian prairies. J. Clim. 1996, 9, 897–905. [Google Scholar] [CrossRef]
- Weber, L.; Kkemdirim, L. Palmer’s drought indices revisited. Geogr. Ann. A. 1998, 80, 153–172. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–183.
- Farahmand, A.; AghaKouchak, A. A generalized framework for deriving nonparametric standardized drought indicators. Adv. Water Resour. 2015, 76, 140–145. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).