Hydrological Evaluation of TRMM Rainfall over the Upper Senegal River Basin
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data and Tools
2.2.1. Data
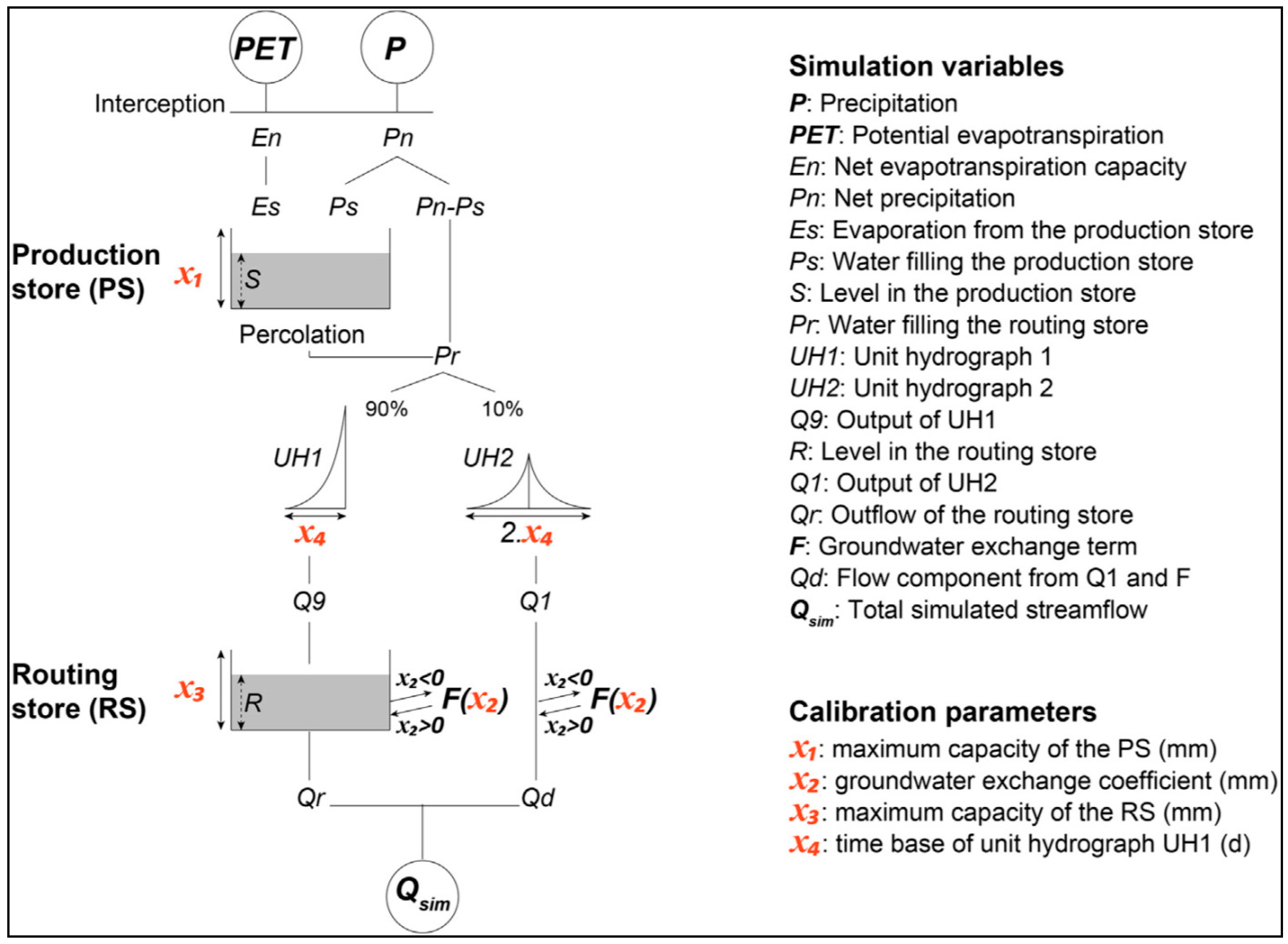
2.2.2. GR4J Hydrological Model
2.3. Methods
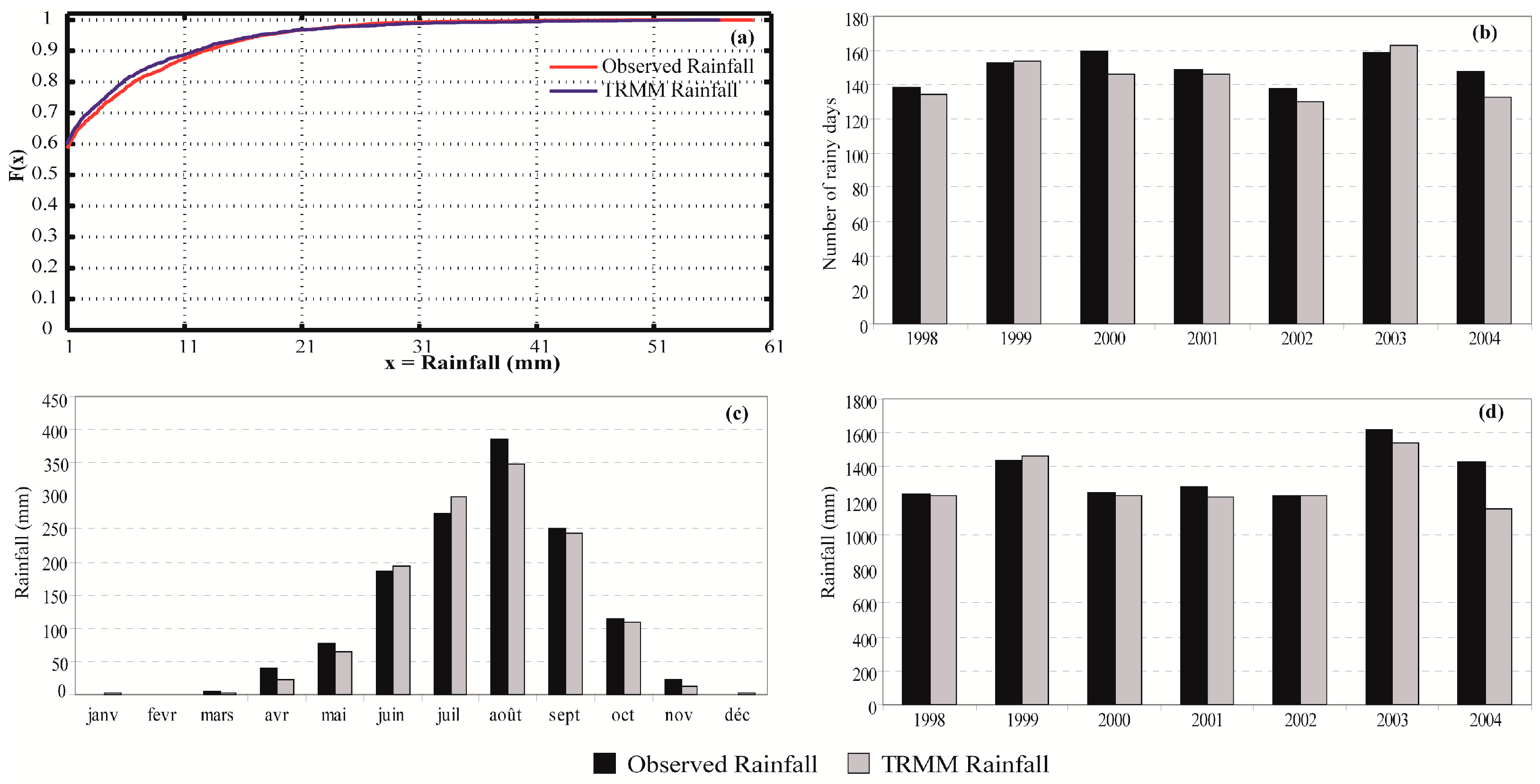
2.3.1. Evaluation of TRMM Rainfalls Data
2.3.2. Calibration and Validation of GR4J Model
2.3.3. Simulation of Daily Flows with Observed and TRMM Rainfalls
2.3.4. Comparison of Observed and Calculated Flows Rates with Observed and TRMM Rainfalls
3. Results
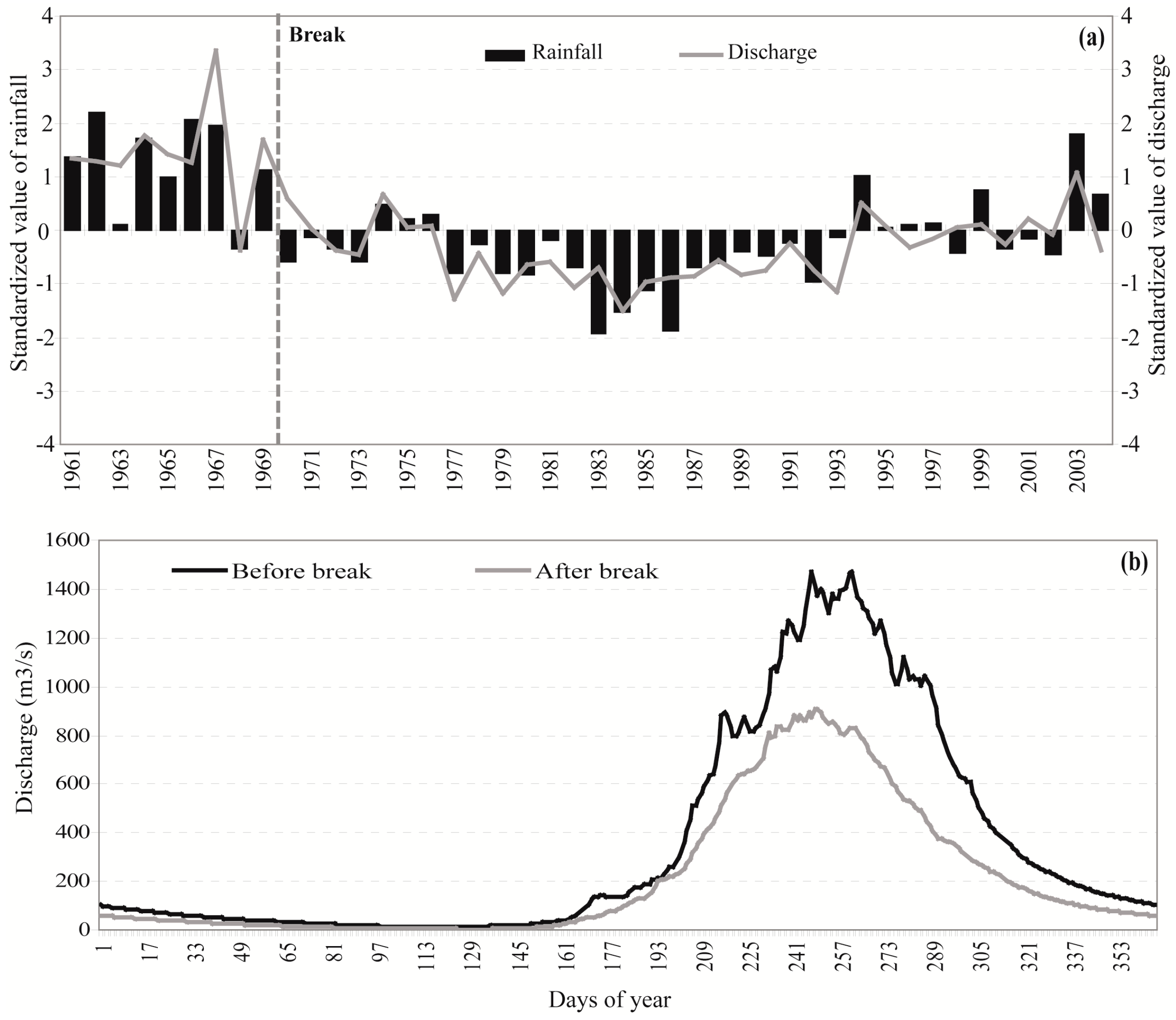
3.1. Evaluation of TRMM Data
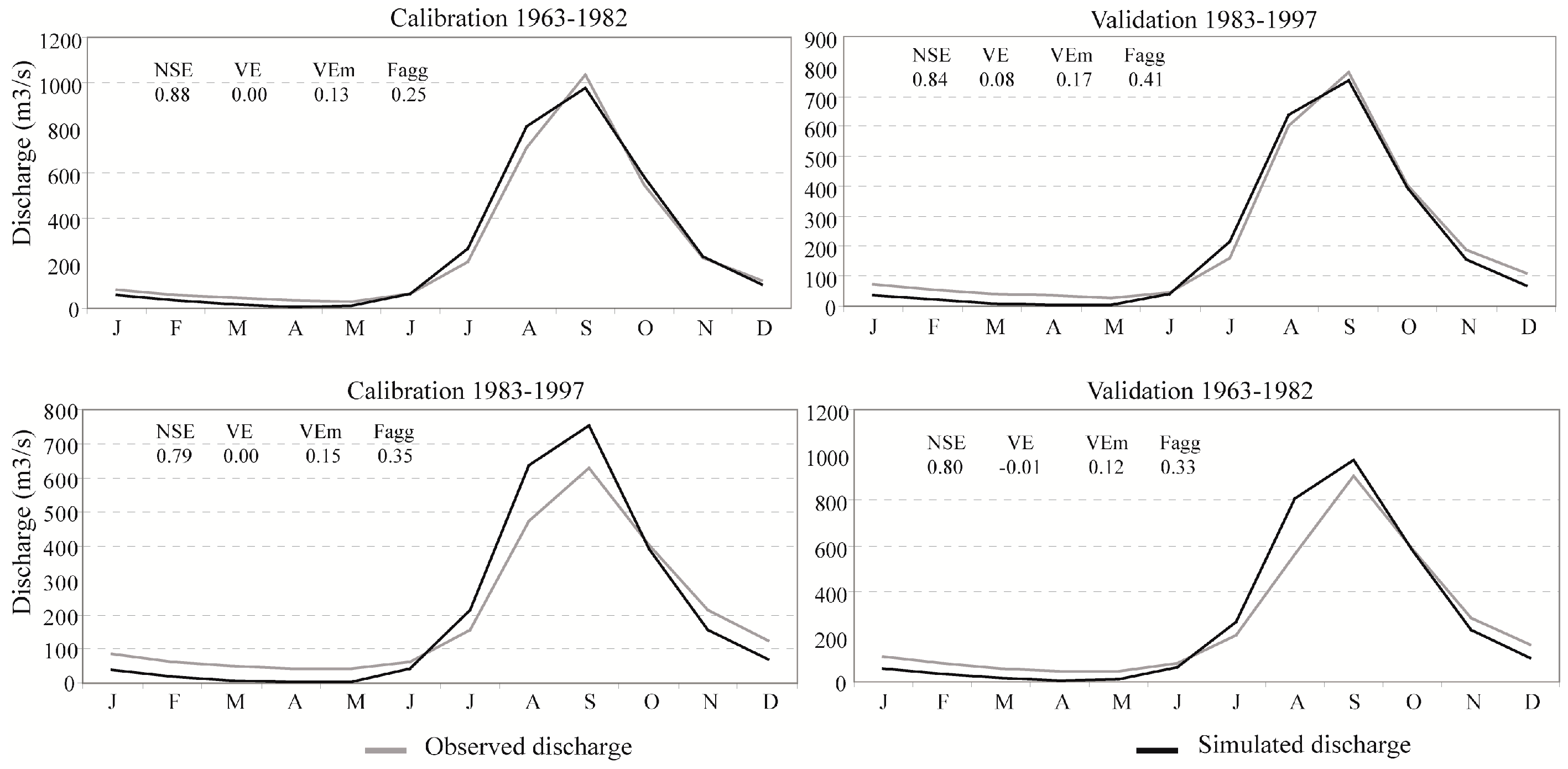
3.2. Efficiency of the Model GR4J on Calibration-Validation
3.3. Comparison of Simulated Daily Flows with Observed and TRMM Rainfalls
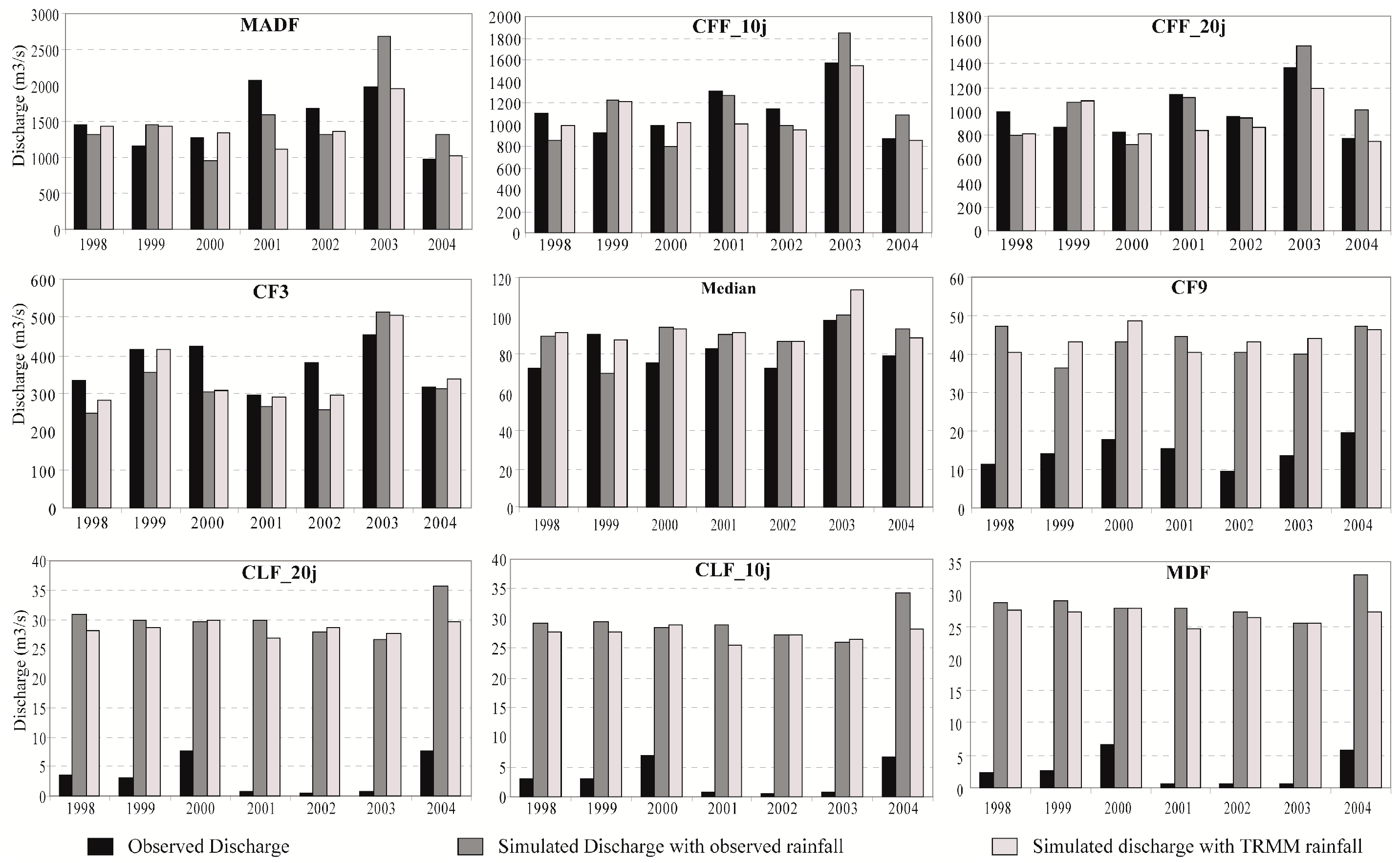
3.4. Comparison of Observed and Calculated Characteristics Flow Rates with Observed and TRMM Rainfalls
4. Conclusions and Discussion
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| TRMM | Tropical Rainfall Measuring Mission |
| PERSIANN | Precipitation Estimation from Remotely-Sensed Information using Artificial Neural Networks |
| RT | Real Time |
| CMORPH | Climate Prediction Center Morphing method |
| GSMaP | Global Satellite Mapping of Precipitation |
| GCPC-1DD | Global Precipitation Climatology Project One Degree Daily estimate |
| RFE2 | African Rainfall Estimate |
| EPSAT | Estimation des Precipitation par SATellite |
| AMMA-CATCH | African Monsoon Multidisciplinary Analysis-Couplage Atmosphere Tropicale Cycle Hydrologique |
| CPC/FEWS | Climate Prediction Center/ Famine Early Warning System |
| GR4J | Modèle du Génie Rural (Agricultural Engineering Model) à 4 paramètres Journalier (4 Daily parameters) |
| GR2M | Modèle du Génie Rural (Agricultural Engineering Model) à 2 paramètres Mensuel (2 Monthly parameters) |
| NASA | National Aeronautics and Space Administration |
| OMVS | Organisation pour la Mise en Valeur du fleuve Sénégal (Organization for the Development of the Senegal River) |
References
- Carbonnel, J.P.; Hubert, P. Sur la sécheresse au Sahel d’Afrique de l’Ouest. Une rupture climatique dans les séries pluviométriques du Burkina-Faso (ex Haute-Volta). C.R. Acad. Sci., t. 301; Série II n°13; Paris, France, 1985; pp. 941–944. (In French) [Google Scholar]
- Nicholson, S.E. The spatial coherence of African rainfall anomalies: Interhemispheric teleconnections. J. Clim. Appl. Meteor. 1986, 25, 1365–1381. [Google Scholar] [CrossRef]
- Hubert, P.; Carbonnel, J.P.; Chaouche, A. Segmentation des séries hydrométéorologiques; application à des séries de précipitations et de débits de l’Afrique de l’Ouest. J. Hydrol. 1988, 110, 349–367. (In French) [Google Scholar] [CrossRef]
- Olivry, J.C.; Bricquet, J.P.; Bamba, F.; Diarra, M. Le régime hydrologique du Niger supérieur et le déficit des deux dernières décennies. Available online: http://horizon.documentation.ird.fr/exldoc/pleins_textes/doc34–06/41211.pdf (accessed on 27 January 2016). (In French)
- Servat, E.; Paturel, J.E.; Lubes-Niel, H.; Kouamé, B.; Masson, J.M.; Travaglio, M.; Marieu, B. De différents aspects de la variabilité de la pluviométrie en Afrique de l’Ouest et Centra lenon sahélienne. Rev. Sci. l’Eau 1999, 12, 363–387. (In French) [Google Scholar] [CrossRef]
- Paturel, J.E.; Servat, E.; Delattre, M.O.; Lubès-Niel, H. Analyse de séries pluviométriques de longue durée en Afrique de l’Ouest et Centrale non sahélienne dans un contexte de variabilité climatique. Hydrol. Sci. J. 1998, 43, 937–946. (In French) [Google Scholar] [CrossRef]
- Nicholson, S.E.; Some, B.; Kone, B. An Analysis of Recent Rainfall Conditions in West Africa, Including the Rainy Seasons of the 1997 El Niño and the 1998 La Niña Years. J. Clim. 2000, 13, 2628–2640. [Google Scholar] [CrossRef]
- Mahé, G.; Paturel, J.E. 1896–2006 Sahelian annual rainfall variability and runoff increase of Sahelian Rivers. C.R. Geosci. 2009, 341, 538–546. [Google Scholar] [CrossRef]
- Hubert, P.; Bader, J.C.; Bendjoudi, H. Un siècle de débits annuels du fleuve Sénégal. J. Sci. Hydrol. 2007, 52, 68–73. (In French) [Google Scholar] [CrossRef]
- Abrate, T.; Hubert, P.; Sighomnou, D. A study on hydrological series of the Niger River. Hydrol. Sci. J. 2013, 58, 271–279. [Google Scholar] [CrossRef]
- FAOSTAT. FAO Statistical Service. United Nations Food and Agriculture Organization, 2012. Available online: http://faostat.fao.org/site/291/default.aspx (accessed on 25 January2015).
- Charnay, B. Pour une gestion intégrée des ressources en eau sur un territoire de montagne. Le cas du bassin versant du Giffre (Haute-Savoie). Thèse de Doctorat, Géographie présentée à l’Université de Savoie (E.D. SISEO), France, 2010. Available online: https://tel.archives-ouvertes.fr/tel-00472979/ (accessed on 30 March 2016). [Google Scholar]
- Global Water Partnership; International Network of Basin Organization. A Handbook for Integrated Water Resources Management in Basins; Elanders: Stockholm, Sweden, 2009; p. 112. [Google Scholar]
- Lasserre, F.; Dexcroix, L. La gestion intégrée des ressources en eau par bassin: Au-delà de la rhétorique. In Eaux et Territoires: Tensions, Coopérations et Géopolitique de l’eau; Harmattan: Paris, France, 2003; pp. 221–239. (In French) [Google Scholar]
- Bodian, A.; Dezetter, A.; Dacosta, H. Rainfall-Runoff Modelling of Water Resources in the Upper Senegal River Basin. Int. J. Water Resour. Dev. 2015. [Google Scholar] [CrossRef]
- Ardoin-Bardin, S. Variabilité hydro-climatique et impacts sur les ressources en eau de grands bassins hydrographiques en zone soudano-sahélien. Thèse de doctorat, Université de Montpellier II, Montpellier, Hérault, France, 2004. [Google Scholar]
- Dezetter, A.; Paturel, J.-E.; Ruelland, D.; Ardoin-Bardin, S.; Ferry, L.; Mahé, G.; Dieulin, C.; Servat, E. Modélisation semi-spatialisée des ressources en eau du fleuve Niger à Koulikoro. Prise en compte des variabilités spatio-temporelles. In Proceedings of the 13th IWRA World Water Congress, Montpelier, France, 1–4 September 2008; Available online: www.iwra.org/congress/2008/resource/authors/ abs728_ article.pdf (accessed on 12 December 2014). (In French)
- Ardoin-Bardin, S.; Dezetter, A.; Servat, E.; Paturel, J.E.; Mahé, G.; Niel, H.; Dieulin, C. Using general circulation model outputs to assess impacts of climate change on runoff for large hydrological catchments in West Africa. Hydrol. Sci. J. 2009, 54, 77–89. (In French) [Google Scholar] [CrossRef]
- Cornelissen, T.; Diekkrüger, B.; Giertz, S. A comparison of hydrological models for assessing the impact of land use and climate change on discharge in a tropical catchment. J. Hydrol. 2013, 498, 221–236. [Google Scholar] [CrossRef]
- Bop, M.; Amadou, A.; Seidou, O.; Kébé, C.M.F.; Ndione, J.A.; Sambou, S.; Sanda, I.S. Modeling the Hydrological Dynamic of the Breeding Water Bodies in Barkedji’s Zone. J. Water Resour. Prot. 2014, 6, 741–755. [Google Scholar] [CrossRef]
- Angelina, A.; Gado, D.A.; Seidou, O.; Seidou, S.I.; Ketvara, S. Changes to flow regime on the Niger River at Koulikoro under a changing climate. Hydrol. Sci. J. 2014. [Google Scholar] [CrossRef]
- Panthou, G.; Vischel, T.; Lebel, T. Recent trends in the regime of extreme rainfall in the Central Sahel. Int. J. Clim. 2014. [Google Scholar] [CrossRef]
- Bodian, A.; Ndiaye, O.; Dacosta, H. Evolution des caractéristiques des pluies journalières dans le bassin versant du fleuve Sénégal: Avant et après rupture. J. des Sci. Hydrol. 2016. (In French) [Google Scholar] [CrossRef]
- Nicholson, S.E.; Some, B.; McCollum, J.; Nelkin, E.; Klotter, D.; Berte, Y.; Diallo, B.M.; Gaye, I.; Kpabeba, G.; Ndiaye, O.; et al. Validation of TRMM and other rainfall estimates with a high-density gauge dataset for West Africa. Part II: Validation of TRMM Rainfall Products. J. Appl. Meteor. 2003, 42, 1355–1368. [Google Scholar] [CrossRef]
- Hughes, D.A. An evaluation of the potential use of satellite rainfall data for input to water resource estimation models in southern Africa. In Climate Variability and Change-Hydrological Impacts, Proceedings of the Fifth FRIEND World Conference, Havana, Cuba, 27 November–1 December 2006.
- Stisen, S.; Jensen, K.H.; Sandholt, I.; Grimes, D.I.F. A remote sensing driven distributed hydrological model of the Senegal River basin. J. Hydrol. 2008, 354, 131–148. [Google Scholar] [CrossRef]
- Dezetter, A.; Fabre, J.; Ruelland, D.; Servat, E. Selecting an optimal climatic dataset for integrated modelling of the Ebro hydrosystem. In Hydrology in a Changing World: Environmental and Human Dimensions Proceedings of FRIEND-Water; IAHS Press: Montpellier, France, 2014. [Google Scholar]
- Thiemig, V.; Rojas, R.; Bigiarini, M.Z.; de Roo, A. Hydrological evaluation of satellite-based rainfall estimates over the Volta and Baro-Akobo Basin. J. Hydrol. 2013, 499, 324–338. [Google Scholar] [CrossRef]
- Chen, C.; Yu, Z.; Li, L.; Yang, C. Adaptability Evaluation of TRMM Satellite Rainfall and Its Application in the Dongjiang River Basin. Procedia Environ. Sci. 2011, 10 Part A, 396–402. [Google Scholar] [CrossRef]
- Ali, A.; Lebel, T.; Amani, A. Estimation of rainfall in the Sahel. Part 1: Error function. J. Appl. Meteorol. 2005, 44, 1691–1706. [Google Scholar] [CrossRef]
- Ali, A.; Amani, A.; Diedhiou, A.; Lebel, T. Estimation of rainfall in the Sahel. Part 2: Evaluation of rain gauge networks in the CILSS countries and objective intercomparison of rainfall products. J. Appl. Meteorol. 2005, 44, 1707–1722. [Google Scholar] [CrossRef]
- Su, F.; Hong, Y.; Lettenmaier, D.P. Evaluation of TRMM Multisatellite Precipitation Analysis (TMPA) and Its Utility in Hydrologic Prediction in the La Plata Basin. J. Hydrometeorolog. 2007. [Google Scholar] [CrossRef]
- Roca, R.; Chambon, P.; Jobard, I.; Kirstetter, P.E.; Gosset, M.; Bergès, J.C. Comparing Satellite and Surface Rainfall Products over West Africa at Meteorologically Relevant Scales during the AMMA campaign using error estimates. J. Appl. Meteorol. Climatol. 2010, 49, 715–731. [Google Scholar] [CrossRef]
- Almazroui, M. Calibration of TRMM rainfall climatology over Saudi Arabia during 1998–2009. Atmos. Res. 2011, 99, 400–414. [Google Scholar] [CrossRef]
- Jobard, I.; Chopin, F.; Bergès, J.C.; Roca, R. An intercomparison of 10-day precipitation satellite products during West African monsoon. Int. J. Remote Sens. 2001, 32. [Google Scholar] [CrossRef]
- Kisrtetter, P.E.; Viltard, N.; Gosset, M. An error model for instantaneous satellite rainfall estimates: Evaluation of BRAIN-TMI over West Africa. Q. J. R. Meteorol. Soc. 2012, 139, 894–911. [Google Scholar] [CrossRef]
- Kacimi, S.; Viltard, N.; Kisrtetter, P.E. A new methodology for rain identification from passive microwave data in Tropics using neuronal networks. Q. J. R. Meteorol. Soc. 2013, 139, 919–922. [Google Scholar] [CrossRef]
- Thiemig, V.; Rojas, R.; Zambrano-Bigiarini, M.; Levizzani, V.; De Roo, A. Validation of Satellite-Based Precipitation Products over Sparsely Gauged African River Basins. J. Hydrom. 2012, 13, 1760–1783. [Google Scholar] [CrossRef]
- Gosset, M.; Viarre, J.; Quantin, G.; Alcoba, M. Evaluation of several rainfall products used for hydrological applications over West Africa using two high-resolution gauge networks. Q. J. R. Meteorol. Soc. 2013, 139, 923–940. [Google Scholar] [CrossRef]
- Diem, J.E.; Hartter, J.; Ryan, S.J.; Palace, M.W. Validation of Satellite Rainfall Products for Western Uganda. J. Hydrom. 2014, 15, 2030–2038. [Google Scholar] [CrossRef]
- Roca, R.; Bergès, J.C.; Brogniez, H.; Capderou, M.; Chambon, P.; Chomette, O.; Cloché, S.; Fiolleau, T.; Jobard, I.; Lémond, J.; et al. On the Water and energy cycle in the Tropics. C. R. Geosci. 2010. [Google Scholar] [CrossRef]
- Casse, C.; Gosset, M.; Peugeot, C.; Pedinotti, V.; Boone, A.; Tanimoun, B.A.; Decharme, B. Potential of satellite rainfall products to predict Niger River flood events in Niamey. Atmos. Res. 2015, 163, 162–176. [Google Scholar] [CrossRef]
- Stisen, S.; Sandholt, I. Evaluation of remote-sensing-based rainfall products through predictive capability in hydrological runoff modeling. Hydrol. Process. 2010, 24, 879–891. [Google Scholar] [CrossRef]
- Bader, J.C.; Lamagat, J.P.; Guiguen, N. Gestion du barrage de Manantali sur le fleuve Sénégal: Analyse quantitative d’un conflit d’objectifs. Hydrol. Sci. J. 2003, 48, 525–538. [Google Scholar] [CrossRef]
- Amoussou, E.; Tramblay, Y.; Totin, H.S.V.; Mahé, G.; Camberlin, P. Dynamique et modélisation des crues dans le bassin du Mono à Nangbéto (Togo/Bénin). Hydrol. Sci. J. 2014. (In French) [Google Scholar] [CrossRef]
- Le Lay, M. Modélisation hydrologique dans un contexte de variabilité hydro-climatique. Une approche comparative pour l’étude du cycle hydrologique à méso-échelle au Bénin. Thèse de Doctorat, Institut National Polytechnique de Grenoble, Laboratoire d’études des Transferts en Hydrologie et Environnement, Grenoble, France, 2006. [Google Scholar]
- Bodian, A.; Dezetter, A.; Dacosta, H. Apport de la modélisation hydrologique pour la connaissance de la ressource en eau: Application au haut bassin du fleuve Sénégal. Climatologie 2012, 9, 109–125. (In French) [Google Scholar]
- Bodian, A.; Dacosta, H.; Dezetter, A. Analyse des débits de crues et d’étiages dans le bassin versant du fleuve Sénégal en amont du barrage de Manantali. Revue du LACEEDE «Climat et développement» 2013, 15, 46–56. (In French) [Google Scholar]
- CSE. Etude d’impacts des feux de brousses sur l’eau, les sols et la végétation dans la partie guinéenne du bassin du fleuve Sénégal. OMVS Report, Dakar, 2006. (In French) [Google Scholar]
- Kane, H.; Diallo, A. Etude portant sur l’évaluation de l’état de l’environnement des ressources naturelles et des ressources en eau dans la partie guinéenne du bassin du fleuve Sénégal, en se servant du système d’indicateurs de l’Observatoire de l’environnement de l’OMVS. OMVS Report, Dakar, 2005. (In French) [Google Scholar]
- Rochette, C. Lebassin du Fleuve Sénégal. Monographies Hydrologiques. Edition Orstom; Office de la recherche scientifique et technique outre-mer: Paris, France, 1974. (In French) [Google Scholar]
- Farr, T.G.; Kobrick, M. Shuttle Radar Topography Mission produces a wealth of data. Amer. Geophys. Union Eos. 2000, 81, 583–585. [Google Scholar] [CrossRef]
- Werner, M. Shuttle Radar Topography Mission (SRTM), Mission overview. J. Telecom. (Frequenz) 2001, 55, 75–79. [Google Scholar] [CrossRef]
- Dione, O. Evolution Climatique Récente et Dynamique Fluviale dans les Hauts Bassins des Fleuves Sénégal et Gambie. Thèse de doctorat, Université Lyon 3 Jean Moulin, Lyon, France, 1996. [Google Scholar]
- Bodian, A.; Dacosta, H.; Dezetter, A. Caractérisation spatio-temporelle du régime pluviométrique du haut bassin du fleuve Sénégal dans un contexte de variabilité climatique. Physio-Géo. 2011, V, 116–133. (In French) [Google Scholar] [CrossRef]
- Daily TRMM and Others Rainfall Estimate (3B42 V7 derived) V7. Available online: http://catalog.data.gov/dataset/daily-trmm-and-others-rainfall-estimate-3b42-v7-derived-v7 (accessed on 5 March 2014).
- Schneider, U. The Global Precipitation Climatology Project 5GPCP) Combined Precipitation Dataset. Bull. Am. Meteorol. Soc. 1995, 78, 5–20. [Google Scholar]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrom. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Moazami, S.; Golian, S.; Kavianpour, M.R.; Hong, Y. Comparison of PERSIANN and V7 TRMM Multi-satellite Precipitation Analysis (TMPA) products with rain gauge data over Iran. Int. J. Remote Sens. 2013, 34, 8156–8171. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andreassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Collet, L. Capacité à satisfaire la demande en eau sous contraintes climatique et anthropique sur un bassin versant méditerranéen. Thèse de doctorat, Université de MontpellierII:Montpellier, Hérault, France, 2013. [Google Scholar]
- Oudin, L.; Hervieu, F.; Michel, C.; Perrin, C.; Andréassian, V.; Anctil, F.; Loumagne, C. Which potential evapotranspiration input for a lumped rainfall–runoff model? Part 2—towards a simple and efficient potential evapotranspiration model for rainfall–runoff modelling. J. Hydrol. 2005, 303, 290–306. [Google Scholar] [CrossRef]
- Fabre, J.; Ruelland, D.; Dezetter, A.; Grouillet, B. Simulating past changes in the balance between water demand and availability and assessing their main drivers at the river basin scale. Hydrol. Earth Syst. Sci. 2015. [Google Scholar] [CrossRef]
- Ben Khediri, W.; Drogue, G. Quel est l’impact de l’échantillonnage spatial des précipitations et de l’évapotranspiration potentielle sur le pouvoir prédictif d’un modèle hydrologique empirique? Available online: http://lodel.irevues.inist.fr/climatologie/index.php?id=1095 (accessed on 11 April 2016). (In French)
- Collischonn, B.; Collischonn, W.; Tucci, C.E.M. Daily hydrological modeling in the Amazon basin using TRMM rainfall estimates. J. Hydrol. 2008, 360, 207–216. [Google Scholar] [CrossRef]
- Kouassi, A.M.; N’guessan Bi, T.M.; Kouame, K.F.; Kouame, K.A.; Okeringri, J.C.; Biemi, J. Application de la méthode des simulations croisées à l’analyse des tendances dans la relation pluie-débit à partir du modèle GR2M: Cas du basin versant du N’zi-Bandama (Côte d’Ivoire). C.R. Géosci. 2012, 344, 288–296. (In French) [Google Scholar] [CrossRef]
- Ruelland, D.; Ardoin-Bardin, S.; Collet, L.; Roucou, P. Simulating future trends in hydrological regime of a large Sudano-Sahelian catchment under climate change. J. Hydrol. 2012, 424–425, 207–216. [Google Scholar] [CrossRef]
- Rosenbrock, H.H. An automatic method for finding the greatest or least value of a function. Comput. J. 1960, 3, 175–184. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R.A. Simplex method for function minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models. Part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Lin, J.-Y.; Cheng, C.-T.; Chau, K.-W. Using support vector machines for long-term discharge prediction. Hydrol. Sci. J. 2006, 51, 599–612. [Google Scholar] [CrossRef]
- Santhi, C.; Arnold, J.-G.; Williams, J.-R.; Dugas, W.-A.; Srinivasan, R.; Hauck, L.M. Validation of the swat model on a large river basin with point and nonpoint sources. J. Am. Water Res. Assoc. 2001, 37, 1169–1188. [Google Scholar] [CrossRef]
- Wang, W.-C.; Chau, K.-W.; Cheng, C.-T.; Qiu, L. A comparison of performance of several artificial intelligence methods for forecasting monthly discharge time series. J. Hydrol. 2009, 347, 294–306. [Google Scholar]
- Legates, D.-R.; McCabe, G.-J. Evaluating the use of “goodness-of-fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Moriasi, D.-N.; Arnold, J.-G.; Van Liew, M.-W.; Bingner, R.-L.; Harmel, R.-D.; Veith, T.-L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Hingray, B.; Picouet, C.; Musy, A. Hydrologie 2, une science pour l’ingénieur; Presses Polytechniques et Universitaire Romande (PPUR): Lausanne, Suisse, 2009; p. 600. (In French) [Google Scholar]
- Vauchel, P. Hydraccess: Base de Données Hydrométriques Sous Access 2000; IRD: Dakar, Senegal, 2000. (In French) [Google Scholar]
- Mahé, G. Variabilité pluie-débit en Afrique de l’Ouest et Centrale au 20ème siècle : changements hydro-climatiques, occupation du sol et modélisation hydrologique; Université de Montpellier II: Montpellier, France, 2006; p. 160. (In French) [Google Scholar]
- Diallo, I. Caractérisation du cycle de l’eau dans le système de mousson de l’Afrique de l’Ouest et son évolution dans un contexte de changement climatique. Thèse de doctorat, Université Cheikh Anta Diop, Dakar, Senegal, 2015. [Google Scholar]
- Pushpalatha, R.; Perrin, C.; Le Moine, N.; Mathevet, T.; Andréassian, V. A downward structural sensitivity analysis of hydrological models to improve low-flow simulation. J. Hydrol. 2011, 411, 66–76. [Google Scholar] [CrossRef]
- Pushpalatha, R.; Perrin, C.; Le Moine, N.; Andréassian, V. A review of efficiency criteria suitable for evaluating low-flow simulations. J. Hydrol. 2012, 420–421, 171–182. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Pulido-Velazquez, D.; Sahuquillo, A.; Andreu, J.; Pulido-Velazquez, M. An efficient conceptual model to simulate water body-aquifer interaction in Conjunctive Use Management Model. Water Resour. Res. 2007. [Google Scholar] [CrossRef]
- Pulido-Velazquez, D.; Sahuquillo, A.; Andreu, J. A conceptual-numerical model to simulate hydraulic head in aquifers that are hydraulically connected to surface water bodies. Hydrol. Process. 2012, 26, 1435–1448. [Google Scholar] [CrossRef]
- Wu, C.L.; Chau, K.W.; Li, Y.S. Methods to improve neural network performance in daily flows prediction. J. Hydrol. 2009, 372, 80–93. [Google Scholar] [CrossRef]
- Chen, X.-Y.; Chau, K.-W.; Busari, A.O. A comparative study of population-based optimization algorithms for downstream river flow forecasting by a hybrid neural network model. Engin. Appl. Artif. Intell. 2015, 46, 258–268. [Google Scholar]
- Chau, K.-W.; Wu, C.-L. A Hybrid Model Coupled with Singular Spectrum Analysis for Daily Rainfall Prediction. J. Hydroinformat. 2010, 12, 458–473. [Google Scholar]
- Wang, W.-C.; Chau, K.-W.; Xu, D.-M.; Chen, X.-Y. Improving forecasting accuracy of annual runoff time series using ARIMA based on EEMD decomposition. Water Resour. Manag. 2015, 29, 2655–2675. [Google Scholar] [CrossRef]
- Li, Z.; Yang, D.; Gao, B.; Jiao, Y.; Hong, Y.; Xu, T. Multiscale Hydrologic Applications of the Latest Satellite Precipitation Products in the Yangtze River Basin using a Distributed Hydrologic Model. J. Hydrometeorol. 2015. [Google Scholar] [CrossRef]
- Anagnostou, E.N.; Maggioni, V.; Nikolopoulos, E.I.; Meskele, T.; Hossain, F.; Papadopoulos, A. Benchmarking High-Resolution Global Satellite Rainfall Products to Radar and Rain-Gauge Rainfall Estimates. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1667–1683. [Google Scholar] [CrossRef]
- Yilmaz, K.K.; Hogue, T.S.; Hsu, K.; Sorooshian, S.; Gupta, H.V.; Wagener, T. Intercomparison of rain gauge, radar, and satellite-based precipitation estimates with emphasis on hydrologic forecasting. J. Hydrom. 2005, 6, 497–517. [Google Scholar] [CrossRef]
- Yong, B.; Hong, Y.; Ren, L.L.; Gourley, J.J.; Huffman, G.J.; Chen, X.; Wang, W.; Khan, S.I. Assessment of evolving TRMM-based multisatellite real-time precipitation estimation methods and their impacts on hydrologic prediction in a high latitude basin. J. Geophys. Res. 2012, 117, D09108. [Google Scholar] [CrossRef]
- Capdevila, A.S.; Valdes, J.B.; Stakhiv, E.Z. Water Management Applications for Satellite Precipitation Products: Synthesis and Recommendations. J. Am. Water Resour. Assoc. (JAWRA) 2014, 50, 509–525. [Google Scholar] [CrossRef]
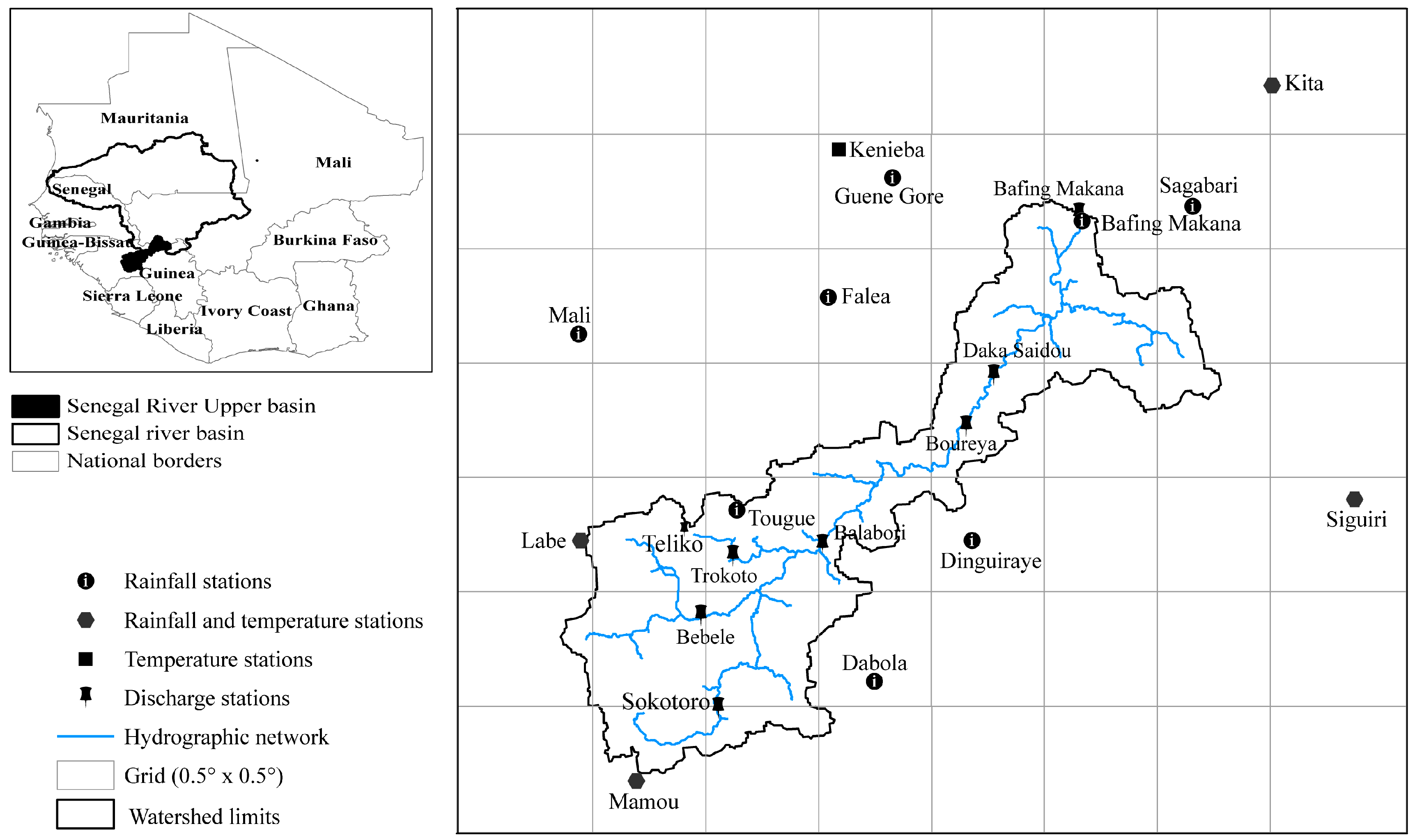

| Stations | Elevation (m) | Start of Record | End of Record | % Gaps | Mean Annual Rainfall (mm) |
|---|---|---|---|---|---|
| Bafing Makana | 239 | 1 January 1963 | 1 September 1997 | 37.5 | 1190 |
| Dabola | 438 | 1 January 1933 | 1 October 2001 | 14.6 | 1514 |
| Dinguiraye | 490 | 16 January 1922 | 16 December 2005 | 43.7 | 1375 |
| Faléa | 455 | 1 March 1956 | 31 December 2003 | 30.4 | 1433 |
| Labé | 1025 | 16 January 1923 | 16 December 2006 | 0.7 | 1626 |
| Mali | 1464 | 16 January 1931 | 16 December 2005 | 26.2 | 1625 |
| Mamou | 782 | 2 January 1921 | 31 December 2008 | 1.9 | 1881 |
| Siguiri | 362 | 2 January 1922 | 30 June 2007 | 1.7 | 1272 |
| Tougué | 86 | 16 January 1923 | 16 August 2004 | 22.3 | 1559 |
| Kita | 328 | 1 January 1931 | 30 September 2009 | 1.5 | 1007 |
| Guene-Gore | 240 | 1 May 1956 | 31 December 2002 | 26.8 | 1246 |
| Sagabari | 332 | 1 July 1959 | 1 September 1997 | 18.8 | 1151 |
| Stations | Elevation (m) | Start of Record | End of Record | % Gaps | Mean Annual Temperature (°C) |
|---|---|---|---|---|---|
| Labé | 1025 | 5 January 1939 | 31 December 2004 | 2.2 | 22 |
| Mamou | 782 | 1 January 1924 | 31 December 2006 | 2.4 | 23 |
| Siguiri | 362 | 1 August 1943 | 28 January 2005 | 5.6 | 27 |
| Kita | 328 | 1 January 1950 | 31 December 2008 | 2.3 | 28 |
| Kénéba | 136 | 1 January 1950 | 31 December 2004 | 4.1 | 29 |
| Criterion | Formula | Scale | Ideal Value |
|---|---|---|---|
| 0 | |||
| 1 | |||
| 0 | |||
| 0 |
| Acronym | Description |
|---|---|
| MADF | MAximum Daily Flow |
| CFF_10d | Characteristic Flood Flow on a 10-day period |
| CFF_20d | Characteristic Flood Flow on a 20-day period |
| CF3 | Characteristic Flow exceeded 3 months in the year |
| Median | Flows exceeded six months in the year |
| CF9 | Characteristic Flow exceeded 9 months in the year |
| CLF_20d | Characteristic Low Flow on a 20-day period |
| CLF_10d | Characteristic Low Flow on a 10-day period |
| MDF | Minimum Daily Flow |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bodian, A.; Dezetter, A.; Deme, A.; Diop, L. Hydrological Evaluation of TRMM Rainfall over the Upper Senegal River Basin. Hydrology 2016, 3, 15. https://doi.org/10.3390/hydrology3020015
Bodian A, Dezetter A, Deme A, Diop L. Hydrological Evaluation of TRMM Rainfall over the Upper Senegal River Basin. Hydrology. 2016; 3(2):15. https://doi.org/10.3390/hydrology3020015
Chicago/Turabian StyleBodian, Ansoumana, Alain Dezetter, Abdoulaye Deme, and Lamine Diop. 2016. "Hydrological Evaluation of TRMM Rainfall over the Upper Senegal River Basin" Hydrology 3, no. 2: 15. https://doi.org/10.3390/hydrology3020015
APA StyleBodian, A., Dezetter, A., Deme, A., & Diop, L. (2016). Hydrological Evaluation of TRMM Rainfall over the Upper Senegal River Basin. Hydrology, 3(2), 15. https://doi.org/10.3390/hydrology3020015








