Evapotranspiration Partitioning in Selected Subtropical Fruit Tree Orchards Based on Sentinel 2 Data Using a Light Gradient-Boosting Machine (LightGBM) Learning Model in Malelane, South Africa
Abstract
1. Introduction
- (1)
- Evaluate the feasibility and accuracy of Bayesian-optimized LightGBM for modelling and in grapefruit, litchi, and mango orchards;
- (2)
- Use the modelled and to partition orchard water use and thereby close the knowledge gap on beneficial versus non-beneficial water consumption, informing best irrigation practices in semi-arid environments.
2. Materials and Methods
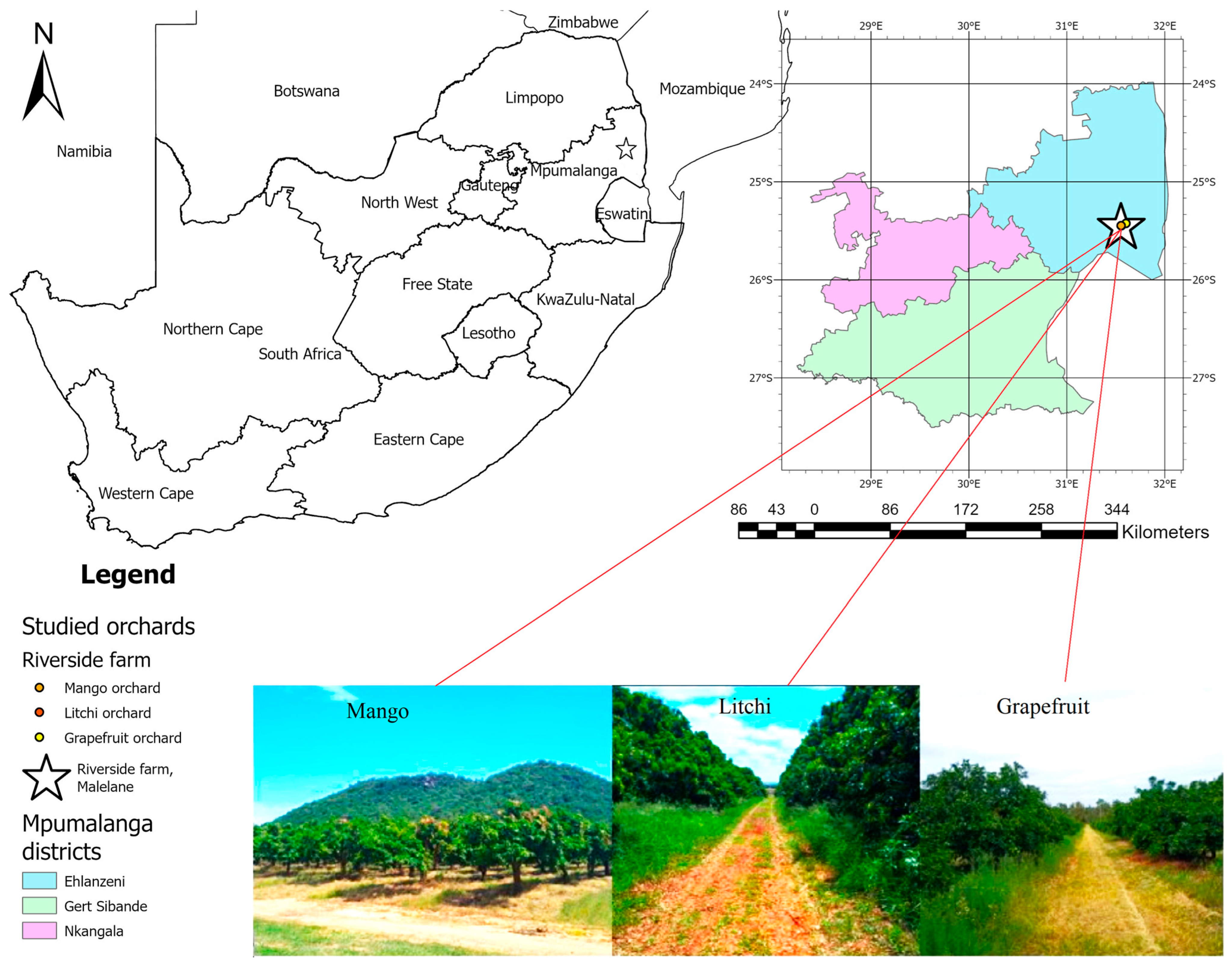
2.1. Study Site and Plant Material
2.2. Data Collection
2.2.1. Microclimate Measurements
2.2.2. Normalized Difference Vegetation Index ()
2.2.3. Leaf Area Index
2.2.4. Transpiration Measurements
2.2.5. Evapotranspiration Measurements
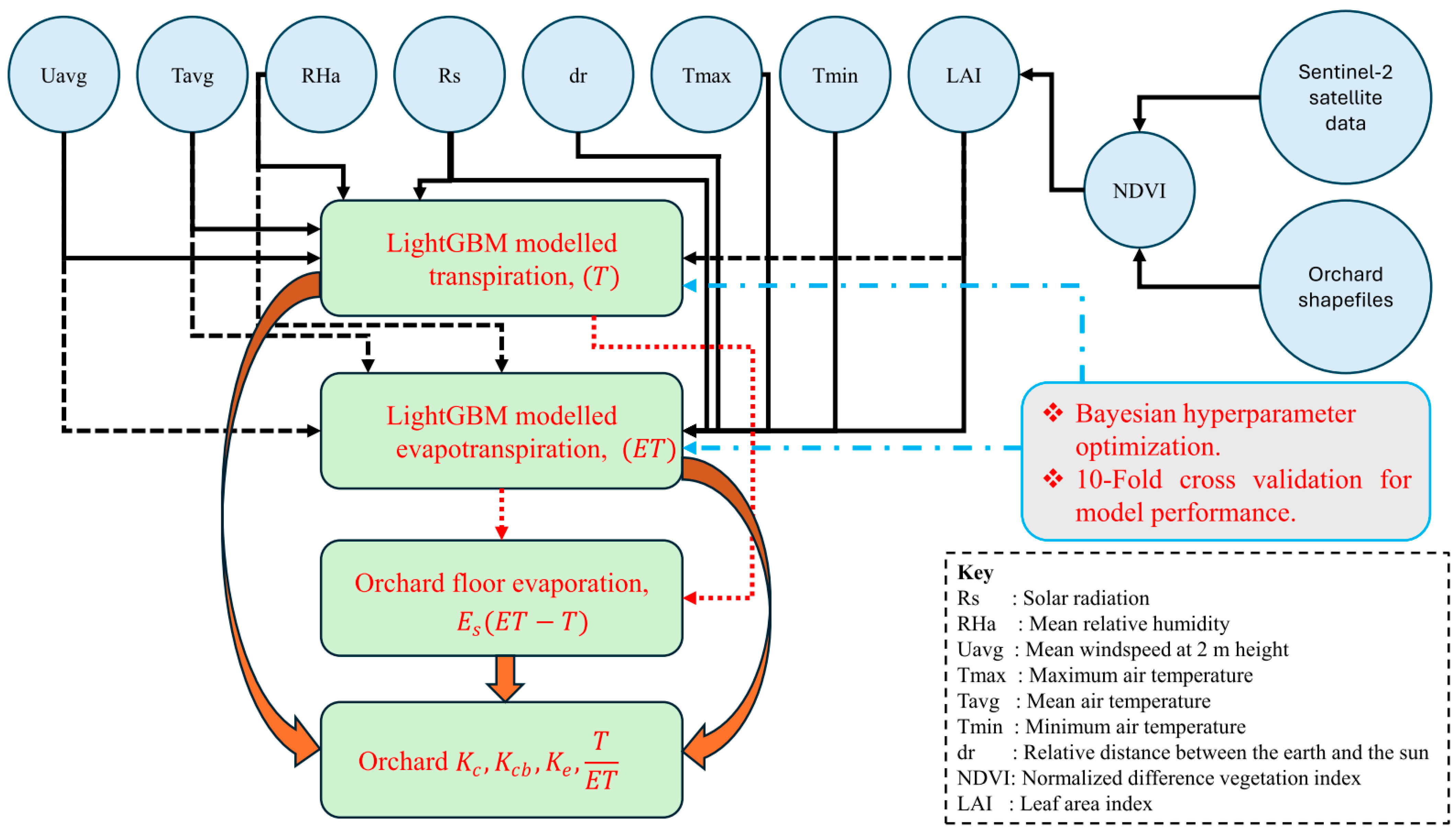
2.3. Models’ Description
2.4. Models’ Validation and Evaluation Metrics
2.4.1. Cross-Validation and Independent Validation
2.4.2. Validation Metrics
2.4.3. LightGBM Model Interpretability Analysis
3. Results
3.1. Microclimate
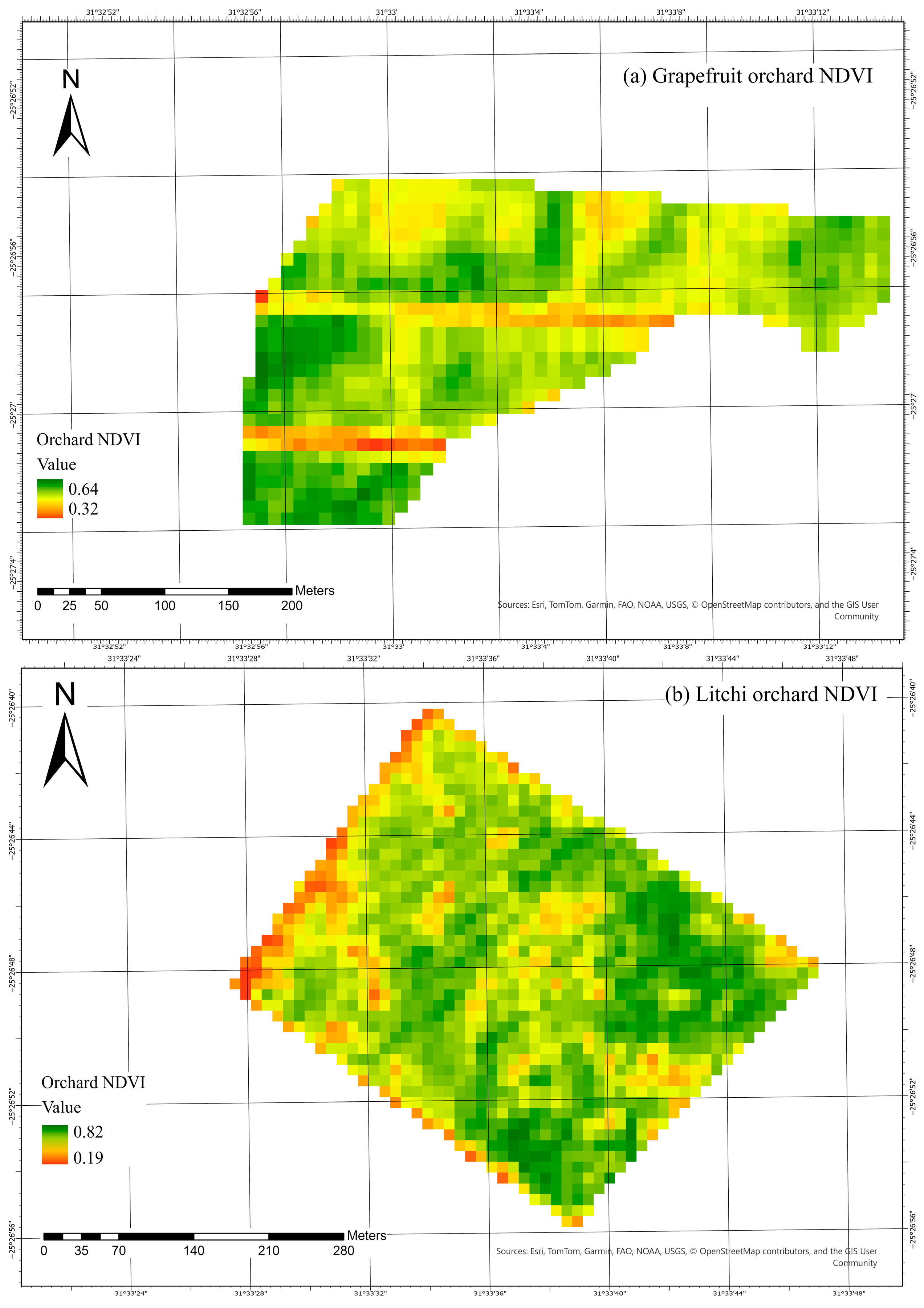
3.2. Orchard Leaf Area Index ()
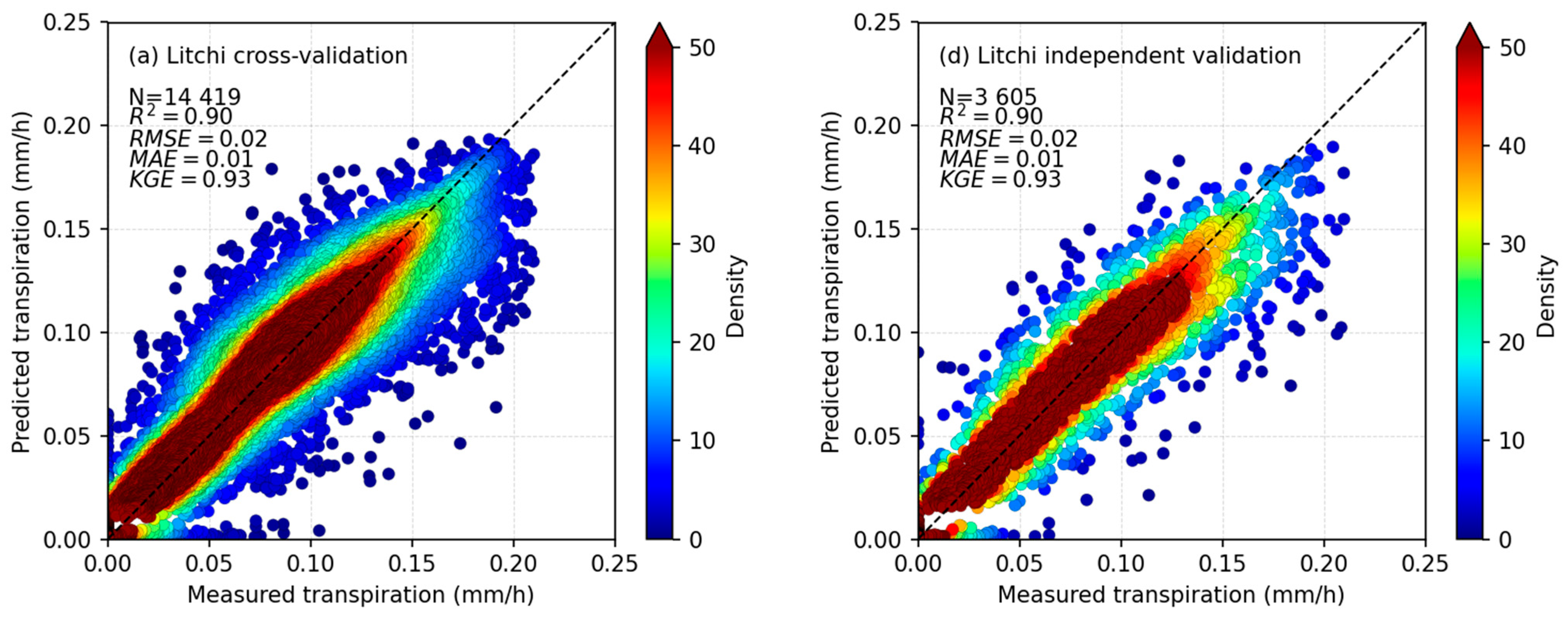
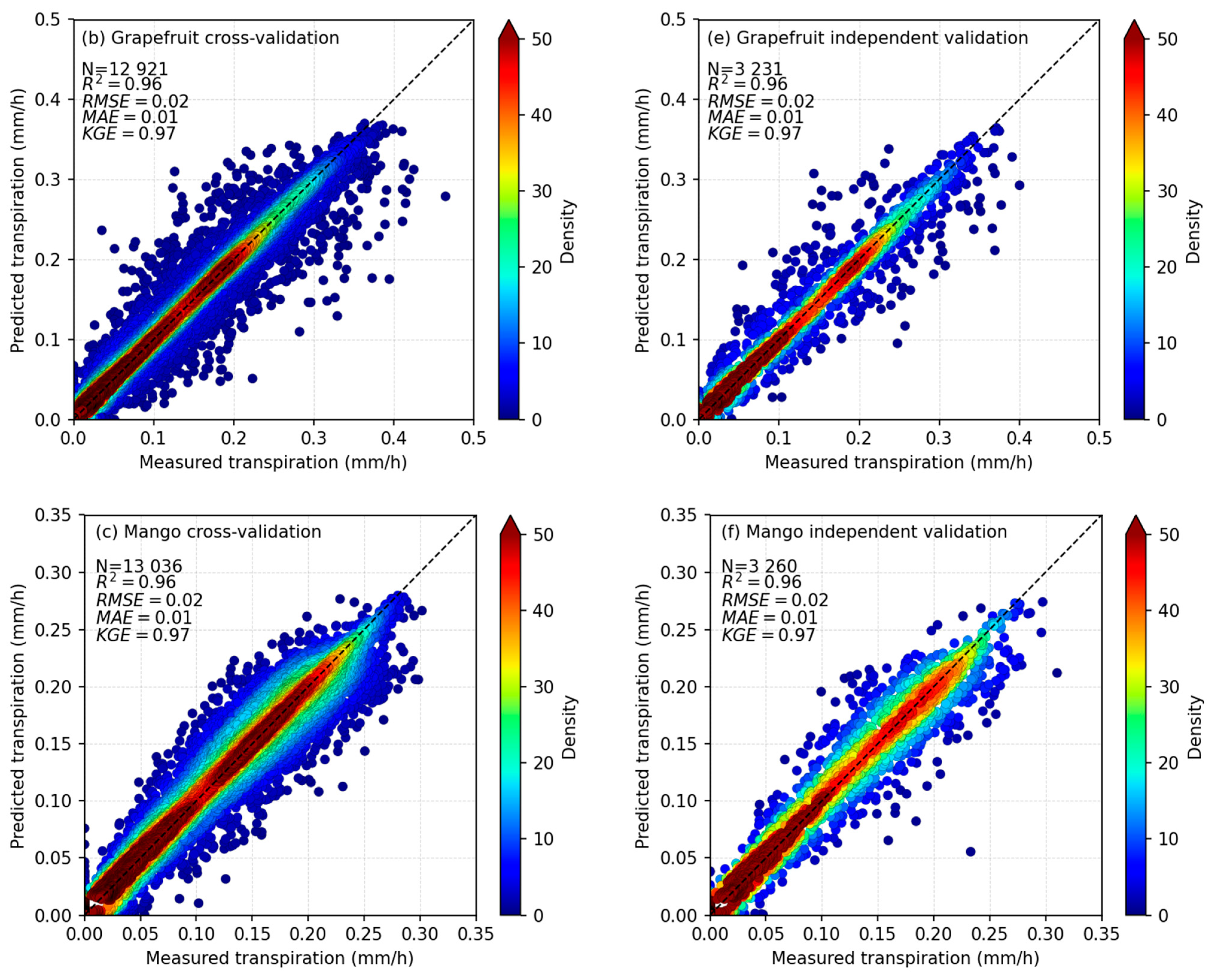
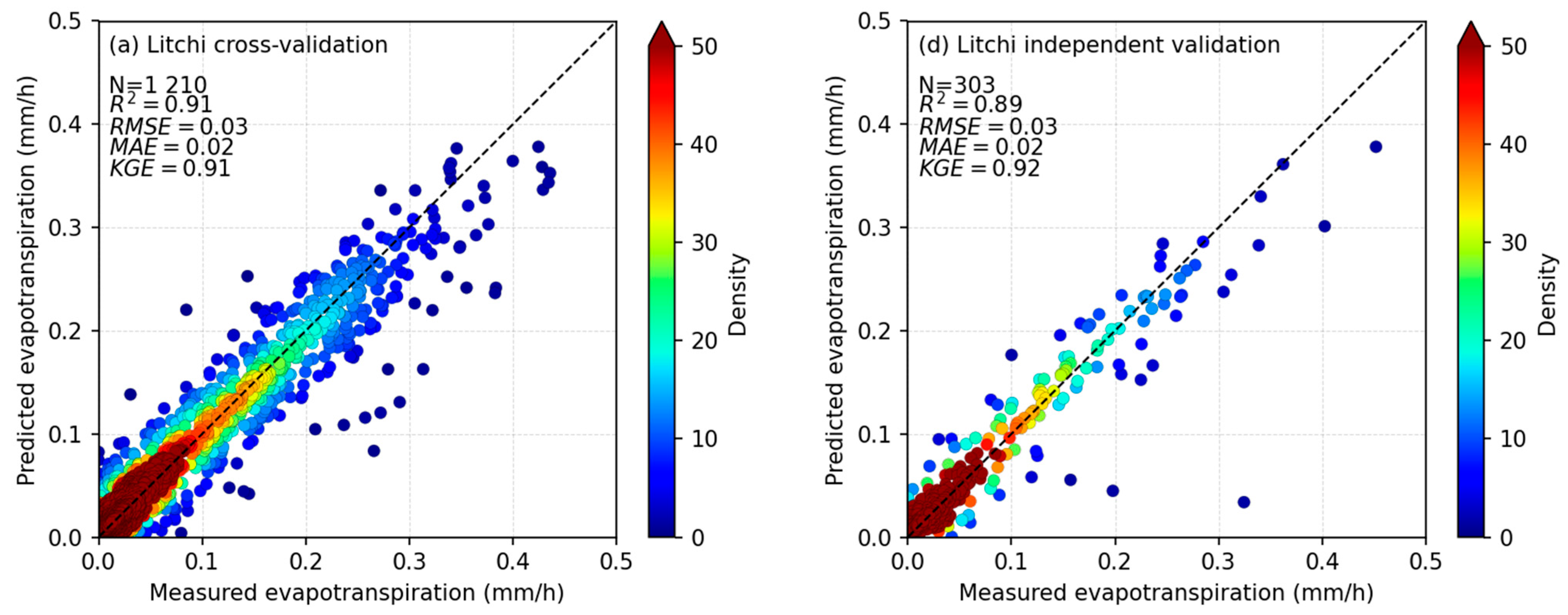
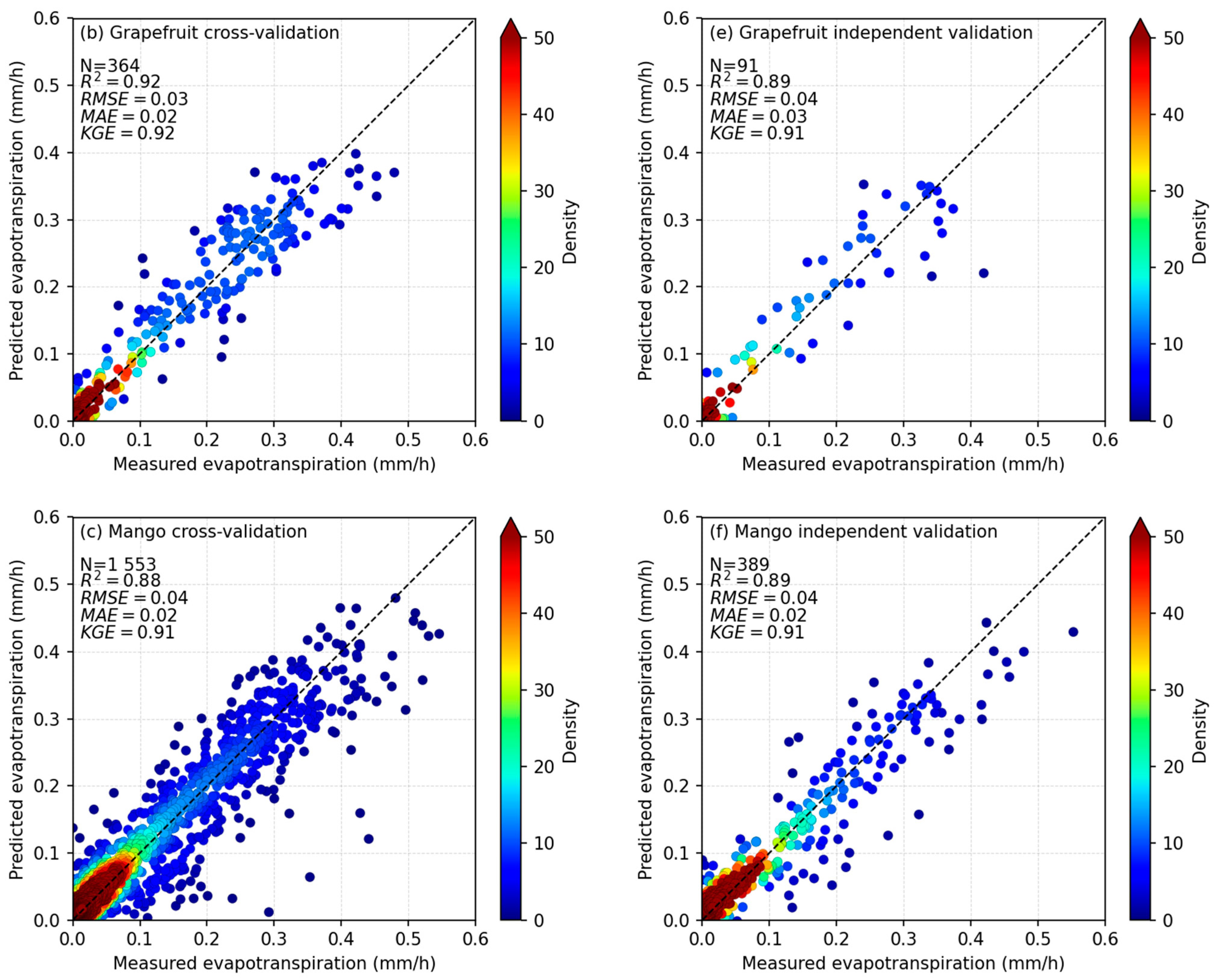
3.3. Transpiration and Evapotranspiration Models Accuracy
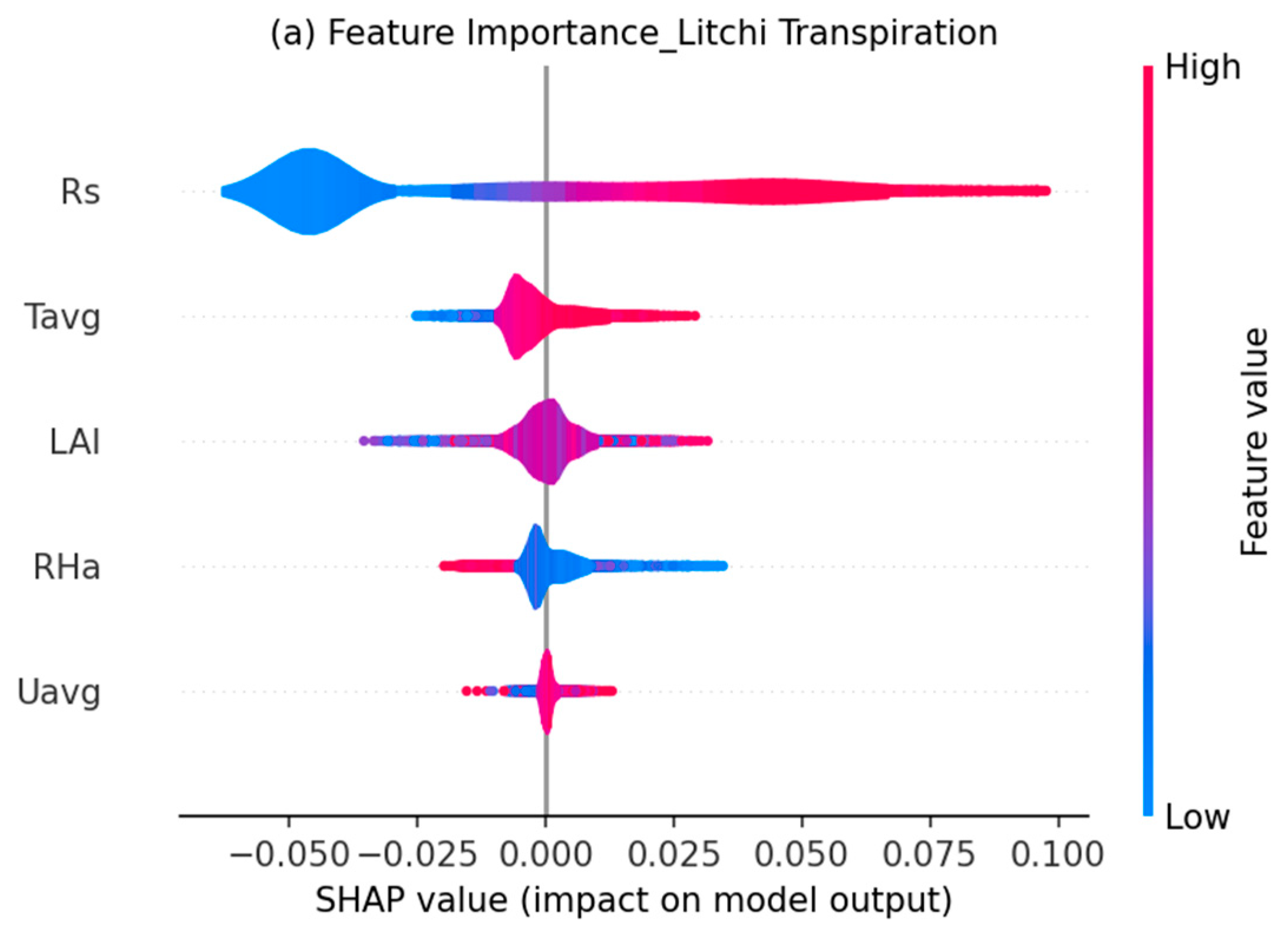
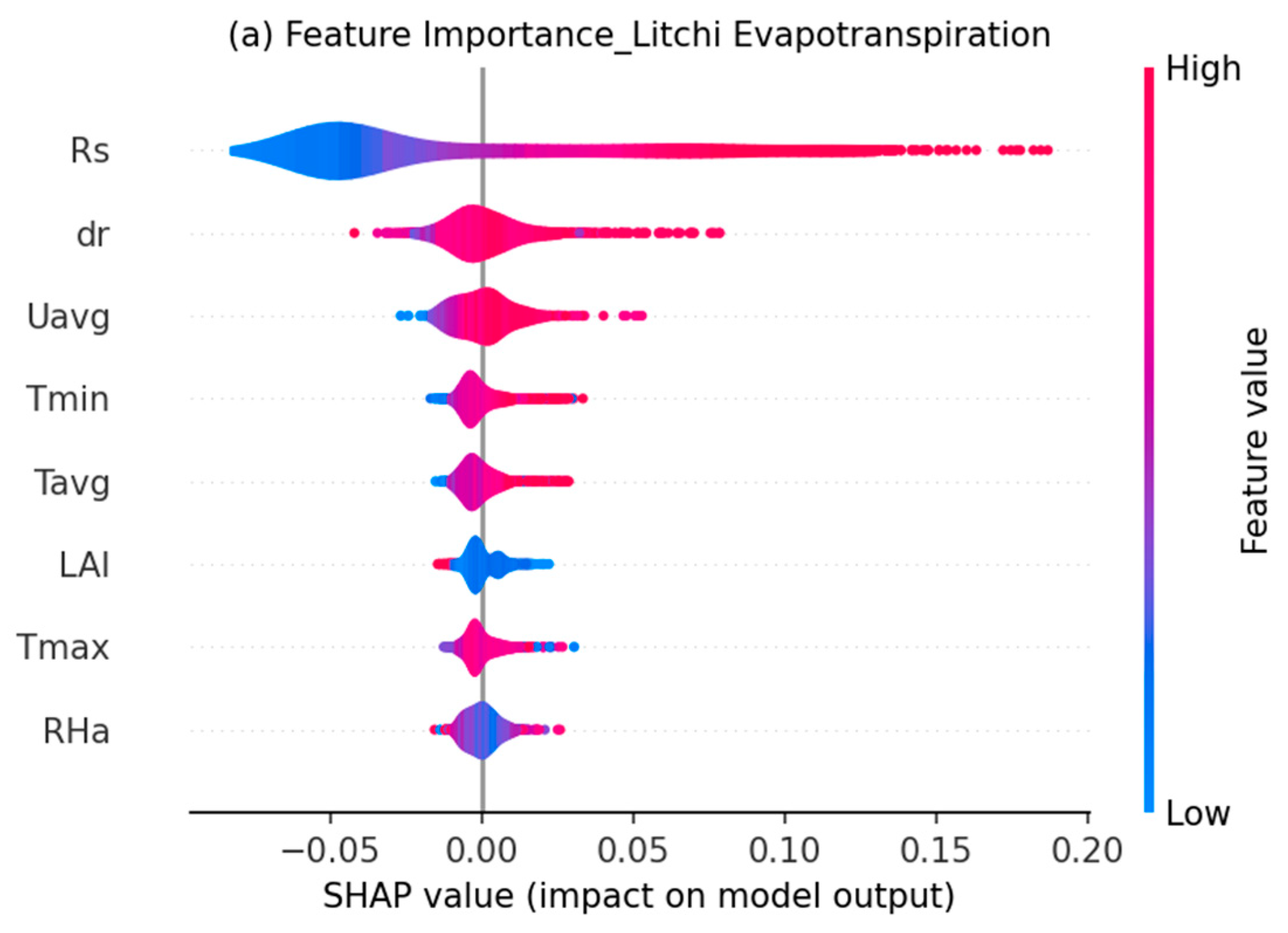
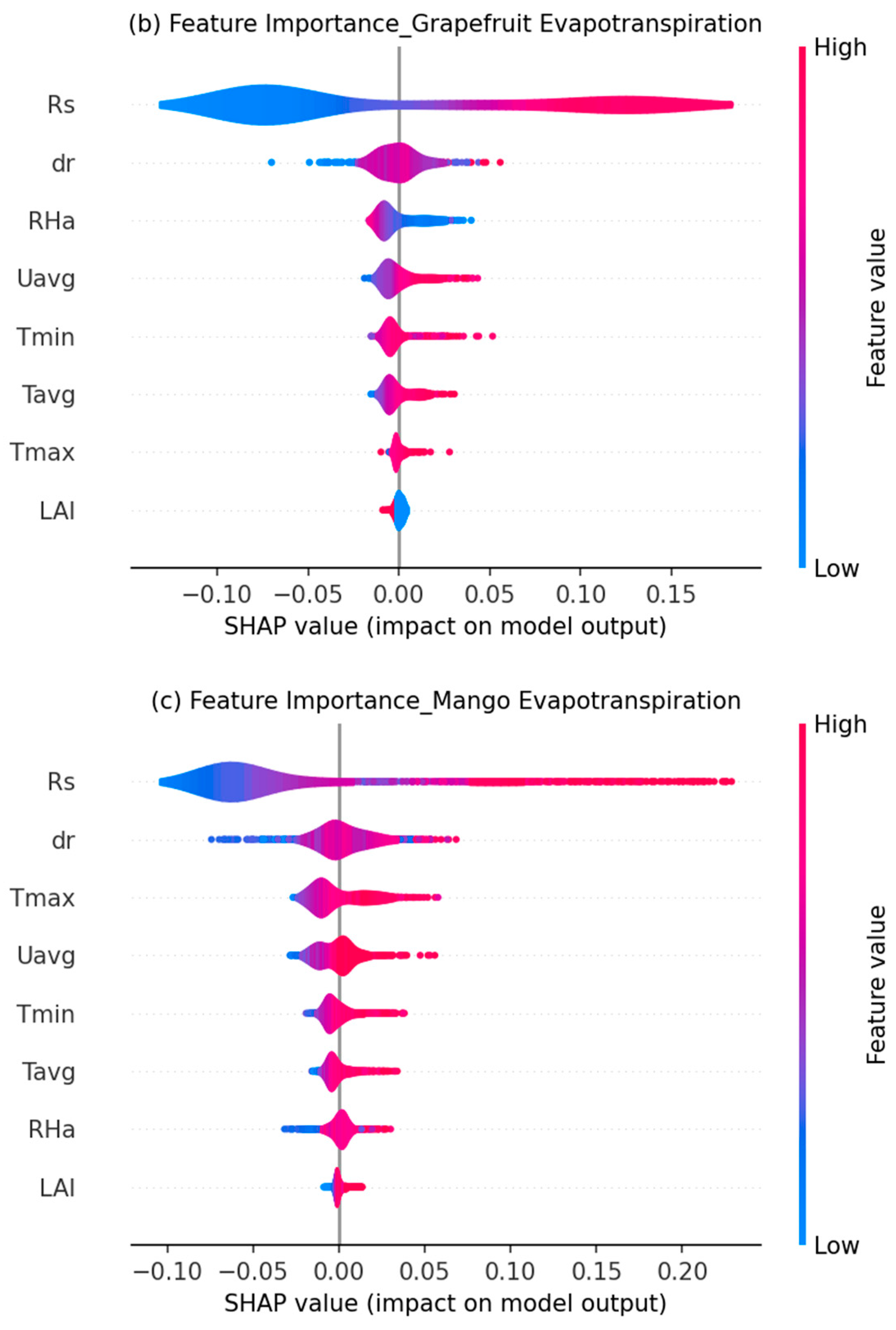
3.4. LightGBM Learning Model Interpretability
3.5. Orchard Evapotranspiration Partitioning Dynamics
3.5.1. Orchard , and
3.5.2. Crop Coefficient, Basal Coefficient, and Soil-Evaporation Coefficient
3.5.3. Partitioning
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Y.; Liu, X.; Zhang, X.; Gu, X.; Yu, L.; Cai, H.; Peng, X. Using Solar-Induced Chlorophyll Fluorescence to Predict Winter Wheat Actual Evapotranspiration through Machine Learning and Deep Learning Methods. Agric. Water Manag. 2025, 309, 109322. [Google Scholar] [CrossRef]
- Tabari, H.; Kisi, O.; Ezani, A.; Hosseinzadeh Talaee, P. SVM, ANFIS, Regression and Climate Based Models for Reference Evapotranspiration Modeling Using Limited Climatic Data in a Semi-Arid Highland Environment. J. Hydrol. 2012, 444–445, 78–89. [Google Scholar] [CrossRef]
- Aytek, A. Co-Active Neurofuzzy Inference System for Evapotranspiration Modeling. Soft Comput. 2009, 13, 691–700. [Google Scholar] [CrossRef]
- Kool, D.; Agam, N.; Lazarovitch, N.; Heitman, J.L.; Sauer, T.J.; Ben-Gal, A. A Review of Approaches for Evapotranspiration Partitioning. Agric. For. Meteorol. 2014, 184, 56–70. [Google Scholar] [CrossRef]
- Shukla, S.; Jaber, F.H.; Goswami, D.; Srivastava, S. Evapotranspiration Losses for Pepper under Plastic Mulch and Shallow Water Table Conditions. Irrig. Sci. 2013, 31, 523–536. [Google Scholar] [CrossRef]
- Achite, M.; Jehanzaib, M.; Sattari, M.T.; Toubal, A.K.; Elshaboury, N.; Wałęga, A.; Krakauer, N.; Yoo, J.-Y.; Kim, T.-W. Modern Techniques to Modeling Reference Evapotranspiration in a Semiarid Area Based on ANN and GEP Models. Water 2022, 14, 1210. [Google Scholar] [CrossRef]
- Khan, M.S.; Baik, J.; Choi, M. A Physical-Based Two-Source Evapotranspiration Model with Monin–Obukhov Similarity Theory. GIsci. Remote Sens. 2021, 58, 88–119. [Google Scholar] [CrossRef]
- Kang, M.; Cho, S.; Kim, S.-J.; Kim, E.; Kang, M. Deviations in Evapotranspiration Measurements between Enclosed-and Open-Path Eddy Covariance Systems. Hydrol. Sci. J. 2025, 70, 1011–1019. [Google Scholar] [CrossRef]
- Baldocchi, D.D.; Hincks, B.B.; Meyers, T.P. Measuring Biosphere-Atmosphere Exchanges of Biologically Related Gases with Micrometeorological Methods. Ecology 1988, 69, 1331–1340. [Google Scholar] [CrossRef]
- Aubinet, M.; Vesala, T.; Papale, D. (Eds.) Eddy Covariance; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating Soil Moisture—Climate Interactions in a Changing Climate: A Review. Earth Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Olivier, F.; Singels, A. The Effect of Crop Residue Layers on Evapotranspiration, Growth and Yield of Irrigated Sugarcane†. Water SA 2012, 38, 77–86. [Google Scholar] [CrossRef]
- Ren, Z.; Che, T.; Xu, F.; Zhang, Y.; Tan, J.; Wang, J.; Wang, W. Validation of Remotely Sensed Evapotranspiration Products Using Optical–Microwave Scintillometer Flux Measurements Over the Heterogeneous Surfaces. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 5687–5703. [Google Scholar] [CrossRef]
- Bowen, I.S. The Ratio of Heat Losses by Conduction and by Evaporation from Any Water Surface. Phys. Rev. 1926, 27, 779–787. [Google Scholar] [CrossRef]
- Grantz, D.A.; Meinzer, F.C. Regulation of Transpiration in Field-Grown Sugarcane: Evaluation of the Stomatal Response to Humidity with the Bowen Ratio Technique. Agric. For. Meteorol. 1991, 53, 169–183. [Google Scholar] [CrossRef]
- Qiu, R.; Katul, G.G.; Zhang, L.; Qin, S.; Jiang, X. The Effects of Changing Environments, Abiotic Stresses, and Management Practices on Cropland Evapotranspiration: A Review. Rev. Geophys. 2025, 63, e2024RG000858. [Google Scholar] [CrossRef]
- Gokool, S.; Chetty, K.T.; Jewitt, G.P.W.; Heeralal, A. Estimating Total Evaporation at the Field Scale Using the SEBS Model and Data Infilling Procedures. Water SA 2016, 42, 673. [Google Scholar] [CrossRef][Green Version]
- Garofalo, S.P.; Ardito, F.; Sanitate, N.; De Carolis, G.; Ruggieri, S.; Giannico, V.; Rana, G.; Ferrara, R.M. Robustness of Actual Evapotranspiration Predicted by Random Forest Model Integrating Remote Sensing and Meteorological Information: Case of Watermelon (Citrullus lanatus, (Thunb.) Matsum. & Nakai, 1916). Water 2025, 17, 323. [Google Scholar] [CrossRef]
- Callejas-Rodelas, J.Á.; Knohl, A.; van Ramshorst, J.; Mammarella, I.; Markwitz, C. Comparison between Lower-Cost and Conventional Eddy Covariance Setups for CO2 and Evapotranspiration Measurements above Monocropping and Agroforestry Systems. Agric. For. Meteorol. 2024, 354, 110086. [Google Scholar] [CrossRef]
- Li, Z.-L.; Tang, R.; Wan, Z.; Bi, Y.; Zhou, C.; Tang, B.; Yan, G.; Zhang, X. A Review of Current Methodologies for Regional Evapotranspiration Estimation from Remotely Sensed Data. Sensors 2009, 9, 3801–3853. [Google Scholar] [CrossRef]
- Mashabatu, M.; Motsei, N.; Jovanovic, N.; Nhamo, L. A Validation of FruitLook Data Using Eddy Covariance in a Fully Mature and High-Density Japanese Plum Orchard in the Western Cape, South Africa. Water 2025, 17, 324. [Google Scholar] [CrossRef]
- Yu, H.; Cao, C.; Zhang, Q.; Bao, Y. Construction of an Evapotranspiration Model and Analysis of Spatiotemporal Variation in Xilin River Basin, China. PLoS ONE 2021, 16, e0256981. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Yu, G.; Zhou, Y.; Sun, X.; Li, Y.; Shi, P.; Wang, Y.; Song, X.; Zheng, Z.; Zhang, L.; et al. Partitioning of Evapotranspiration and Its Controls in Four Grassland Ecosystems: Application of a Two-Source Model. Agric. For. Meteorol. 2009, 149, 1410–1420. [Google Scholar] [CrossRef]
- Hu, X.; Shi, L.; Lin, G.; Lin, L. Comparison of Physical-Based, Data-Driven and Hybrid Modeling Approaches for Evapotranspiration Estimation. J. Hydrol. 2021, 601, 126592. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and Environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar] [PubMed]
- Lhomme, J.-P.; Chehbouni, A. Comments on Dual-Source Vegetation–Atmosphere Transfer Models. Agric. For. Meteorol. 1999, 94, 269–273. [Google Scholar] [CrossRef]
- Zhuang, Q.; Wang, H.; Xu, Y. Comparison of Remote Sensing Based Multi-Source ET Models over Cropland in a Semi-Humid Region of China. Atmosphere 2020, 11, 325. [Google Scholar] [CrossRef]
- Ntshidi, Z.; Dzikiti, S.; Mazvimavi, D.; Mobe, N.T. Contribution of Understorey Vegetation to Evapotranspiration Partitioning in Apple Orchards under Mediterranean Climatic Conditions in South Africa. Agric. Water Manag. 2021, 245, 106627. [Google Scholar] [CrossRef]
- Bastidas-Obando, E.; Bastiaanssen, W.G.M.; Jarmain, C. Estimation of Transpiration Fluxes from Rainfed and Irrigated Sugarcane in South Africa Using a Canopy Resistance and Crop Coefficient Model. Agric. Water Manag. 2017, 181, 94–107. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Gurney, R.J. The Theoretical Relationship between Foliage Temperature and Canopy Resistance in Sparse Crops. Q. J. R. Meteorol. Soc. 1990, 116, 497–519. [Google Scholar] [CrossRef]
- Shuttleworth, W.J.; Wallace, J.S. Evaporation from Sparse Crops-an Energy Combination Theory. Q. J. R. Meteorol. Soc. 1985, 111, 839–855. [Google Scholar] [CrossRef]
- Gao, R.; Torres-Rua, A.F.; Nieto, H.; Zahn, E.; Hipps, L.; Kustas, W.P.; Alsina, M.M.; Bambach, N.; Castro, S.J.; Prueger, J.H.; et al. ET Partitioning Assessment Using the TSEB Model and SUAS Information across California Central Valley Vineyards. Remote Sens. 2023, 15, 756. [Google Scholar] [CrossRef]
- Gao, R.; Torres-Rua, A.F.; Aboutalebi, M.; White, W.A.; Anderson, M.; Kustas, W.P.; Agam, N.; Alsina, M.M.; Alfieri, J.; Hipps, L.; et al. LAI Estimation across California Vineyards Using SUAS Multi-Seasonal Multi-Spectral, Thermal, and Elevation Information and Machine Learning. Irrig. Sci. 2022, 40, 731–759. [Google Scholar] [CrossRef]
- Kaya, Y.; Polat, N. A Linear Approach for Wheat Yield Prediction by Using Different Spectral Vegetation Indices. Int. J. Eng. Geosci. 2023, 8, 52–62. [Google Scholar] [CrossRef]
- Moran, M.S.; Scott, R.L.; Keefer, T.O.; Emmerich, W.E.; Hernandez, M.; Nearing, G.S.; Paige, G.B.; Cosh, M.H.; O’Neill, P.E. Partitioning Evapotranspiration in Semiarid Grassland and Shrubland Ecosystems Using Time Series of Soil Surface Temperature. Agric. For. Meteorol. 2009, 149, 59–72. [Google Scholar] [CrossRef]
- Dzikiti, S.; Lotter, D.; Mpandeli, S.; Nhamo, L. Assessing the Energy and Water Balance Dynamics of Rain-Fed Rooibos Tea Crops (Aspalathus linearis) under Changing Mediterranean Climatic Conditions. Agric. Water Manag. 2022, 274, 107944. [Google Scholar] [CrossRef]
- Agam, N.; Evett, S.R.; Tolk, J.A.; Kustas, W.P.; Colaizzi, P.D.; Alfieri, J.G.; McKee, L.G.; Copeland, K.S.; Howell, T.A.; Chávez, J.L. Evaporative Loss from Irrigated Interrows in a Highly Advective Semi-Arid Agricultural Area. Adv. Water Resour. 2012, 50, 20–30. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, S.; Wang, J.; Zeng, R.; Zhang, S.; Bai, Y.; Zhang, J. Evapotranspiration Partitioning for Croplands Based on Eddy Covariance Measurements and Machine Learning Models. Agronomy 2025, 15, 512. [Google Scholar] [CrossRef]
- Dzikiti, S.; Gush, M.B.; Taylor, N.J.; Volschenk, T.; Midgley, S.; Lötze, E.; Schmeisser, M.; Doko, Q. Measurement and Modelling of Water Use by High Yielding Apple Orchards and Orchards of Different Age Groups in the Winter Rainfall Areas of South Africa. Acta Hortic. 2017, 1150, 31–38. [Google Scholar] [CrossRef]
- Ortega-Farias, S.; Lopéz-Olivari, R.; Poblete-Echeverría, C.; Zuñiga, M. Evaluation of a Two-Layer Model and Sap Flow to Estimate Olive Transpiration. Acta Hortic. 2012, 951, 147–152. [Google Scholar] [CrossRef]
- Fernández, J.E.; Diaz-Espejo, A.; Hernandez-Santana, V.; Cuevas, M.V. Does Precision Irrigation Help to Reduce Water Consumption in Agriculture? Acta Hortic. 2019, 1253, 199–206. [Google Scholar] [CrossRef]
- Rafi, Z.; Merlin, O.; Le Dantec, V.; Khabba, S.; Mordelet, P.; Er-Raki, S.; Amazirh, A.; Olivera-Guerra, L.; Ait Hssaine, B.; Simonneaux, V.; et al. Partitioning Evapotranspiration of a Drip-Irrigated Wheat Crop: Inter-Comparing Eddy Covariance-, Sap Flow-, Lysimeter- and FAO-Based Methods. Agric. For. Meteorol. 2019, 265, 310–326. [Google Scholar] [CrossRef]
- Bao, Y.; Liu, T.; Duan, L.; Tong, X.; Zhang, L.; Singh, V.P.; Lei, H.; Wang, G. Comparison of an Improved Penman-Monteith Model and SWH Model for Estimating Evapotranspiration in a Meadow Wetland in a Semiarid Region. Sci. Total Environ. 2021, 795, 148736. [Google Scholar] [CrossRef]
- Gassmann, M.I.; Tonti, N.E.; Burek, A.; Pérez, C.F. Estimation of Evapotranspiration of a Salt Marsh in Southern South America with Coupled Penman-Monteith and Surface Resistance Models. Agric. For. Meteorol. 2019, 266–267, 109–118. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, P.; Tansey, K.; Liu, J.; Delaney, B.; Quan, W. An Interpretable Approach Combining Shapley Additive Explanations and LightGBM Based on Data Augmentation for Improving Wheat Yield Estimates. Comput. Electron. Agric. 2025, 229, 109758. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Ebtehaj, I.; Bonakdari, H.; Deo, R.C.; Danandeh Mehr, A.; Mohtar, W.H.M.W.; Diop, L.; El-shafie, A.; Singh, V.P. Novel Approach for Streamflow Forecasting Using a Hybrid ANFIS-FFA Model. J. Hydrol. 2017, 554, 263–276. [Google Scholar] [CrossRef]
- Khosravi, K.; Farooque, A.A.; Naghibi, A.; Heddam, S.; Sharafati, A.; Hatamiafkoueieh, J.; Abolfathi, S. Enhancing Pan Evaporation Predictions: Accuracy and Uncertainty in Hybrid Machine Learning Models. Ecol. Inform. 2025, 85, 102933. [Google Scholar] [CrossRef]
- Colliot, O. (Ed.) Machine Learning for Brain Disorders; Springer: New York, NY, USA, 2023; Volume 97. [Google Scholar] [CrossRef]
- Zhao, Y.; Dong, H.; Huang, W.; He, S.; Zhang, C. Seamless Terrestrial Evapotranspiration Estimation by Machine Learning Models across the Contiguous United States. Ecol. Indic. 2024, 165, 112203. [Google Scholar] [CrossRef]
- Amani, S.; Shafizadeh-Moghadam, H.; Morid, S. Integrating Sentinel-2 and Sentinel-3 for Actual Evapotranspiration Estimation across Diverse Climate Zones Using the Sen-ET Plugin and Machine Learning Models. Earth Sci. Inform. 2025, 18, 338. [Google Scholar] [CrossRef]
- Hussain, J.; Fu, X.; Chen, J.; Ali, N.; Iqbal, S.M.; Hussain, W.; Hussain, A.; Saleem, A. Estimation of Rock Strength Parameters from Petrological Contents Using Tree-Based Machine Learning Techniques. AI Civ. Eng. 2025, 4, 4. [Google Scholar] [CrossRef]
- Castillo-Girones, S.; Munera, S.; Martínez-Sober, M.; Blasco, J.; Cubero, S.; Gómez-Sanchis, J. Artificial Neural Networks in Agriculture, the Core of Artificial Intelligence: What, When, and Why. Comput. Electron. Agric. 2025, 230, 109938. [Google Scholar] [CrossRef]
- Li, M.; Hall, T.; MacHugh, D.E.; Chen, L.; Garrick, D.; Wang, L.; Zhao, F. KPRR: A Novel Machine Learning Approach for Effectively Capturing Nonadditive Effects in Genomic Prediction. Brief Bioinform. 2024, 26, bbae683. [Google Scholar] [CrossRef] [PubMed]
- Grinsztajn, L.; Edouard, O.; Gaël, V. Why Do Tree-Based Models Still Outperform Deep Learning on Typical Tabular Data? Adv. Neural Inf. Process. Syst. 2022, 35, 507–520. [Google Scholar]
- Rahmati, O.; Falah, F.; Naghibi, S.A.; Biggs, T.; Soltani, M.; Deo, R.C.; Cerdà, A.; Mohammadi, F.; Tien Bui, D. Land Subsidence Modelling Using Tree-Based Machine Learning Algorithms. Sci. Total Environ. 2019, 672, 239–252. [Google Scholar] [CrossRef]
- Pal, S.; Das, P.; Sarda, R. Exploring Inconsistent and Susceptible Reservoir Storage Areas Using Frequency and Rule-Based Decision Tree Approach. Environ. Dev. 2025, 54, 101146. [Google Scholar] [CrossRef]
- Wei, F.; Dong, Y.; Wu, N.; Li, F.; Lu, H. Assessing the Temporal Stability of Snail-Climate Relationships since the Last Glacial Maximum: Insights from Boosted Regression Trees and LOESS Models. Palaeogeogr. Palaeoclim. Palaeoecol. 2025, 662, 112771. [Google Scholar] [CrossRef]
- de Paz, E.G.G.; Vaquera-Huerta, H.; Albores-Velasco, F.J.; Bauer-Mengelberg, J.R.; Romero-Padilla, J.M. Convex Partition: A Bayesian Regression Tree for Black-Box Optimisation. Pattern Recognit. Lett. 2025; in press. [Google Scholar] [CrossRef]
- Kouloumpris, E.; Vlahavas, I. Markowitz Random Forest: Weighting Classification and Regression Trees with Modern Portfolio Theory. Neurocomputing 2025, 620, 129191. [Google Scholar] [CrossRef]
- Li, L.; Chen, S.; Yang, C.; Meng, F.; Sigrimis, N. Prediction of Plant Transpiration from Environmental Parameters and Relative Leaf Area Index Using the Random Forest Regression Algorithm. J. Clean Prod. 2020, 261, 121136. [Google Scholar] [CrossRef]
- Teshome, F.T.; Bayabil, H.K.; Schaffer, B.; Ampatzidis, Y.; Hoogenboom, G.; Singh, A. Simulating Soil Hydrologic Dynamics Using Crop Growth and Machine Learning Models. Comput. Electron. Agric. 2024, 224, 109186. [Google Scholar] [CrossRef]
- EL Bilali, A.; Hadri, A.; Taleb, A.; Tanarhte, M.; EL Khalki, E.M.; Kharrou, M.H. A Novel Hybrid Modeling Approach Based on Empirical Methods, PSO, XGBoost, and Multiple GCMs for Forecasting Long-Term Reference Evapotranspiration in a Data Scarce-Area. Comput. Electron. Agric. 2025, 232, 110106. [Google Scholar] [CrossRef]
- Zhang, H.; Li, W.; Wang, G.; Song, F.; Wen, Z.; Zhang, H.; Tong, L.; Kang, S. Predicting Stomatal Conductance of Chili Peppers Using TPE-Optimized LightGBM and SHAP Feature Analysis Based on UAVs’ Hyperspectral, Thermal Infrared Imagery, and Meteorological Data. Comput. Electron. Agric. 2025, 231, 110036. [Google Scholar] [CrossRef]
- Wei, C.; Li, Z.; Zhu, D.; Xu, T.; Liang, Z.; Liu, Y.; Zhao, N. Regulation of the Physicochemical Properties of Nutrient Solution in Hydroponic System Based on the CatBoost Model. Comput. Electron. Agric. 2025, 229, 109729. [Google Scholar] [CrossRef]
- Shang, K.; Yao, Y.; Di, Z.; Jia, K.; Zhang, X.; Fisher, J.B.; Chen, J.; Guo, X.; Yang, J.; Yu, R.; et al. Coupling Physical Constraints with Machine Learning for Satellite-Derived Evapotranspiration of the Tibetan Plateau. Remote Sens. Environ. 2023, 289, 113519. [Google Scholar] [CrossRef]
- Hailegnaw, N.S.; Awoke, G.W.; Santos, A.D.C.; Schaffer, B.; Vargas, A.I.; Souza, E.R.D.; Bayabil, H.K. Assessing Salinity-Induced Impacts on Plant Transpiration through Machine Learning: From Model Development to Deployment. Model. Earth Syst. Environ. 2025, 11, 173. [Google Scholar] [CrossRef]
- Fan, J.; Ma, X.; Wu, L.; Zhang, F.; Yu, X.; Zeng, W. Light Gradient Boosting Machine: An Efficient Soft Computing Model for Estimating Daily Reference Evapotranspiration with Local and External Meteorological Data. Agric. Water Manag. 2019, 225, 105758. [Google Scholar] [CrossRef]
- Feliciano, D.; Smith, P.; Mabhaudhi, T. Climate Change Exacerbates Inequalities between Small-Scale and Large-Scale Farmers in South Africa’s Fruit Export Market. Reg Environ. Change 2025, 25, 28. [Google Scholar] [CrossRef]
- Nel, G.P.; Dangare, P.; Kleinert, A.; Dzikiti, S. Estimating Crop Coefficients and Water Use of a Full-Bearing Mango Orchard in North-Eastern South Africa Using the Fraction of Vegetation Cover and a Dual Source Evapotranspiration Model. Sci. Hortic. 2024, 336, 113388. [Google Scholar] [CrossRef]
- Dangare, P.; Nel, G.P.; Sawunyama, T.; Cronje, P.J.R.; Dzikiti, S. Measurement and Modelling of Water Use by Litchi (Litchi sinensis) Orchards under Subtropical Conditions. Acta Hortic. 2024, 1409, 167–174. [Google Scholar] [CrossRef]
- Li, M.; Wang, P.; Tansey, K.; Sun, Y.; Guo, F.; Zhou, J. Improved Field-Scale Drought Monitoring Using MODIS and Sentinel-2 Data for Vegetation Temperature Condition Index Generation through a Fusion Framework. Comput. Electron. Agric. 2025, 234, 110256. [Google Scholar] [CrossRef]
- Sprintsin, M.; Karnieli, A.; Berliner, P.; Rotenberg, E.; Yakir, D.; Cohen, S. The Effect of Spatial Resolution on the Accuracy of Leaf Area Index Estimation for a Forest Planted in the Desert Transition Zone. Remote Sens. Environ. 2007, 109, 416–428. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. Source Approach for Estimating Soil and Vegetation Energy Fluxes in Observations of Directional Radiometric Surface Temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Gao, L.; Wang, X.; Johnson, B.A.; Tian, Q.; Wang, Y.; Verrelst, J.; Mu, X.; Gu, X. Remote Sensing Algorithms for Estimation of Fractional Vegetation Cover Using Pure Vegetation Index Values: A Review. ISPRS J. Photogramm. Remote Sens. 2020, 159, 364–377. [Google Scholar] [CrossRef]
- Li, X.; Yang, P.; Ren, S.; Li, Y.; Liu, H.; Du, J.; Li, P.; Wang, C.; Ren, L. Modeling Cherry Orchard Evapotranspiration Based on an Improved Dual-Source Model. Agric. Water Manag. 2010, 98, 12–18. [Google Scholar] [CrossRef]
- Burgess, S.S.O.; Adams, M.A.; Turner, N.C.; Beverly, C.R.; Ong, C.K.; Khan, A.A.H.; Bleby, T.M. An Improved Heat Pulse Method to Measure Low and Reverse Rates of Sap Flow in Woody Plants. Tree Physiol. 2001, 21, 589–598. [Google Scholar] [CrossRef]
- Dzikiti, S.; Volschenk, T.; Midgley, S.J.E.; Lötze, E.; Taylor, N.J.; Gush, M.B.; Ntshidi, Z.; Zirebwa, S.F.; Doko, Q.; Schmeisser, M.; et al. Estimating the Water Requirements of High Yielding and Young Apple Orchards in the Winter Rainfall Areas of South Africa Using a Dual Source Evapotranspiration Model. Agric. Water Manag. 2018, 208, 152–162. [Google Scholar] [CrossRef]
- Lopez-Bernal, A.; Alcantara, E.; Testi, L.; Villalobos, F.J. Spatial Sap Flow and Xylem Anatomical Characteristics in Olive Trees under Different Irrigation Regimes. Tree Physiol. 2010, 30, 1536–1544. [Google Scholar] [CrossRef] [PubMed]
- Wullschleger, S.D.; King, A.W. Radial Variation in Sap Velocity as a Function of Stem Diameter and Sapwood Thickness in Yellow-Poplar Trees. Tree Physiol. 2000, 20, 511–518. [Google Scholar] [CrossRef]
- Swanson, R.H.; Whitfield, D.W.A. A Numerical Analysis of Heat Pulse Velocity Theory and Practice. J. Exp. Bot. 1981, 32, 221–239. [Google Scholar] [CrossRef]
- Dzikiti, S.; Ntshidi, Z.; Le Maitre, D.C.; Bugan, R.D.H.; Mazvimavi, D.; Schachtschneider, K.; Jovanovic, N.Z.; Pienaar, H.H. Assessing Water Use by Prosopis Invasions and Vachellia Karroo Trees: Implications for Groundwater Recovery Following Alien Plant Removal in an Arid Catchment in South Africa. For. Ecol. Manag. 2017, 398, 153–163. [Google Scholar] [CrossRef]
- Singh, N.K.; Nagahara, M. LightGBM-, SHAP-, and Correlation-Matrix-Heatmap-Based Approaches for Analyzing Household Energy Data: Towards Electricity Self-Sufficient Houses. Energies 2024, 17, 4518. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, T. Application of Improved LightGBM Model in Blood Glucose Prediction. Appl. Sci. 2020, 10, 3227. [Google Scholar] [CrossRef]
- Abbassi, B.; Cheng, L.-Z. Curvilinear Lineament Extraction: Bayesian Optimization of Principal Component Wavelet Analysis and Hysteresis Thresholding. Comput. Geosci. 2025, 194, 105768. [Google Scholar] [CrossRef]
- Cihan, P. Bayesian Hyperparameter Optimization of Machine Learning Models for Predicting Biomass Gasification Gases. Appl. Sci. 2025, 15, 1018. [Google Scholar] [CrossRef]
- Soares, R.C.; Silva, J.C.; de Lucena, J.A.; Filho, A.C.L.; de Souza Ramos, J.G.G.; Brito, A.V. Integration of Bayesian Optimization into Hyperparameter Tuning of the Particle Swarm Optimization Algorithm to Enhance Neural Networks in Bearing Failure Classification. Measurement 2025, 242, 115829. [Google Scholar] [CrossRef]
- Chen, H.; Cheng, Y.; Du, T.; Wu, X.; Cao, Y.; Liu, Y. Enhancing the Performance of Recycled Aggregate Green Concrete via a Bayesian Optimization Light Gradient Boosting Machine and the Nondominated Sorting Genetic Algorithm-III. Constr. Build Mater. 2025, 458, 139527. [Google Scholar] [CrossRef]
- Chatterjee, S.; Baath, G.S.; Sapkota, B.R.; Flynn, K.C.; Smith, D.R. Enhancing LAI Estimation Using Multispectral Imagery and Machine Learning: A Comparison between Reflectance-Based and Vegetation Indices-Based Approaches. Comput. Electron. Agric. 2025, 230, 109790. [Google Scholar] [CrossRef]
- Liao, W.; Chen, Z.; Li, P.; Tan, J.; Li, H.; Zhao, C. Enhanced Battery Health Monitoring in Electric Vehicles: A Novel Hybrid HBA-HGBR Model. J. Energy Storage 2025, 110, 115316. [Google Scholar] [CrossRef]
- Karunasingha, D.S.K. Root Mean Square Error or Mean Absolute Error? Use Their Ratio as Well. Inf. Sci. 2022, 585, 609–629. [Google Scholar] [CrossRef]
- Liu, X.; Tang, Z.; Wei, J. Multi-Layer Perceptron Model Integrating Multi-Head Attention and Gating Mechanism for Global Navigation Satellite System Positioning Error Estimation. Remote Sens. 2025, 17, 301. [Google Scholar] [CrossRef]
- Ahmed, Y.; Akter, T.; Prima, M.; Dutta, K.R.; Mukut, S.; Ahsan, M.; Rahman, M.M.; Mohammad Ziaul Hyder, M.K. Advanced Ciprofloxacin Quantification: A Machine Learning and Metaheuristic Approach Using Ultrasensitive Chitosan-Gold Nanoparticle Based Electrochemical Sensor. J. Environ. Chem. Eng. 2025, 13, 115094. [Google Scholar] [CrossRef]
- Mohammadi, B.; Chen, M.; Nikoo, M.R.; Al-Maktoumi, A.; Yu, Y.; Yu, R. Enhancing Daily Runoff Prediction: A Hybrid Model Combining GR6J-CemaNeige with Wavelet-Based Gradient Boosting Technique. J. Hydrol. 2025, 657, 133114. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the Mean Squared Error and NSE Performance Criteria: Implications for Improving Hydrological Modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Barzegar, R.; Adamowski, J.; Moghaddam, A.A. Application of Wavelet-Artificial Intelligence Hybrid Models for Water Quality Prediction: A Case Study in Aji-Chay River, Iran. Stoch. Environ. Res. Risk Assess. 2016, 30, 1797–1819. [Google Scholar] [CrossRef]
- Alhakeem, Z.M.; Jebur, Y.M.; Henedy, S.N.; Imran, H.; Bernardo, L.F.A.; Hussein, H.M. Prediction of Ecofriendly Concrete Compressive Strength Using Gradient Boosting Regression Tree Combined with GridSearchCV Hyperparameter-Optimization Techniques. Materials 2022, 15, 7432. [Google Scholar] [CrossRef] [PubMed]
- Duarte, F.S.L.G.; Rios, R.A.; Hruschka, E.R.; de Mello, R.F. Decomposing Time Series into Deterministic and Stochastic Influences: A Survey. Digit. Signal Process. 2019, 95, 102582. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, A.; Li, J.; Nguyen, P.; Analui, B.; Hsu, K.; Sorooshian, S. Improve Streamflow Simulations by Combining Machine Learning Pre-Processing and Post-Processing. J. Hydrol. 2025, 655, 132904. [Google Scholar] [CrossRef]
- Huang, C.; Ma, L.; Li, X. Applying the LightGBM Model and SHAP Interpretation to Understand the Urban Land Price Index and Its Influencing Factors in China. Appl. Econ. Lett. 2024, 1–5. [Google Scholar] [CrossRef]
- Nohara, Y.; Matsumoto, K.; Soejima, H.; Nakashima, N. Explanation of Machine Learning Models Using Shapley Additive Explanation and Application for Real Data in Hospital. Comput. Methods Programs Biomed. 2022, 214, 106584. [Google Scholar] [CrossRef]
- Cubitt, R.; Roth, A.E. The Shapley Value: Essays in Honor of Lloyd S. Shapley. Econ. J. 1991, 101, 644. [Google Scholar] [CrossRef]
- Lipovetsky, S.; Conklin, M. Analysis of Regression in Game Theory Approach. Appl. Stoch. Models Bus. Ind. 2001, 17, 319–330. [Google Scholar] [CrossRef]
- Hossen, M.A.; Hasan, M.M.; Ahmed, Y.; Aziz, A.A.; Yaacof, N.; Leong, K.H. Experimental and AI-Driven Enhancements in Gas-Phase Photocatalytic CO2 Conversion over Synthesized Highly Ordered Anodic TiO2 Nanotubes. Energy Convers. Manag. 2025, 327, 119544. [Google Scholar] [CrossRef]
- Stoy, P.C.; El-Madany, T.S.; Fisher, J.B.; Gentine, P.; Gerken, T.; Good, S.P.; Klosterhalfen, A.; Liu, S.; Miralles, D.G.; Perez-Priego, O.; et al. Reviews and Syntheses: Turning the Challenges of Partitioning Ecosystem Evaporation and Transpiration into Opportunities. Biogeosciences 2019, 16, 3747–3775. [Google Scholar] [CrossRef]
- Kisi, O. Modeling Reference Evapotranspiration Using Three Different Heuristic Regression Approaches. Agric. Water Manag. 2016, 169, 162–172. [Google Scholar] [CrossRef]
- Perera, K.C.; Western, A.W.; Nawarathna, B.; George, B. Forecasting Daily Reference Evapotranspiration for Australia Using Numerical Weather Prediction Outputs. Agric. For. Meteorol. 2014, 194, 50–63. [Google Scholar] [CrossRef]
- Fan, J.; Yue, W.; Wu, L.; Zhang, F.; Cai, H.; Wang, X.; Lu, X.; Xiang, Y. Evaluation of SVM, ELM and Four Tree-Based Ensemble Models for Predicting Daily Reference Evapotranspiration Using Limited Meteorological Data in Different Climates of China. Agric. For. Meteorol. 2018, 263, 225–241. [Google Scholar] [CrossRef]
- Granata, F. Evapotranspiration Evaluation Models Based on Machine Learning Algorithms—A Comparative Study. Agric. Water Manag. 2019, 217, 303–315. [Google Scholar] [CrossRef]
- Walls, S.; Binns, A.D.; Levison, J.; MacRitchie, S. Prediction of Actual Evapotranspiration by Artificial Neural Network Models Using Data from a Bowen Ratio Energy Balance Station. Neural Comput. Appl. 2020, 32, 14001–14018. [Google Scholar] [CrossRef]
- Liu, J.; Meng, X.; Ma, Y.; Liu, X. Introduce Canopy Temperature to Evaluate Actual Evapotranspiration of Green Peppers Using Optimized ENN Models. J. Hydrol. 2020, 590, 125437. [Google Scholar] [CrossRef]
- Pagano, A.; Amato, F.; Ippolito, M.; De Caro, D.; Croce, D.; Motisi, A.; Provenzano, G.; Tinnirello, I. Machine Learning Models to Predict Daily Actual Evapotranspiration of Citrus Orchards under Regulated Deficit Irrigation. Ecol. Inform. 2023, 76, 102133. [Google Scholar] [CrossRef]
- Menzel, C.; Oosthuizen, J.; Roe, D.; Doogan, V. Water Deficits at Anthesis Reduce CO2 Assimilation and Yield of Lychee (Litchi Chinensis Sonn.) Trees. Tree Physiol. 1995, 15, 611–617. [Google Scholar] [CrossRef]
- Zhao, M.; Liu, Y.; Konings, A.G. Evapotranspiration Frequently Increases during Droughts. Nat. Clim. Change 2022, 12, 1024–1030. [Google Scholar] [CrossRef]
- Ünlu, M.; Kanber, R.; Koc, D.L.; Özekici, B.; Kekec, U.; Yesiloglu, T.; Ortas, İ.; Ünlu, F.; Kapur, B.; Tekin, S.; et al. Irrigation Scheduling of Grapefruit Trees in a Mediterranean Environment throughout Evaluation of Plant Water Status and Evapotranspiration. Turk. J. Agric. For. 2014, 38, 908–915. [Google Scholar] [CrossRef]
- de Azevedo, P.V.; da Silva, B.B.; da Silva, V.P.R. Water Requirements of Irrigated Mango Orchards in Northeast Brazil. Agric. Water Manag. 2003, 58, 241–254. [Google Scholar] [CrossRef]
- Abou Ali, A.; Bouchaou, L.; Er-Raki, S.; Hssaissoune, M.; Brouziyne, Y.; Ezzahar, J.; Khabba, S.; Chakir, A.; Labbaci, A.; Chehbouni, A. Assessment of Crop Evapotranspiration and Deep Percolation in a Commercial Irrigated Citrus Orchard under Semi-Arid Climate: Combined Eddy-Covariance Measurement and Soil Water Balance-Based Approach. Agric. Water Manag. 2023, 275, 107997. [Google Scholar] [CrossRef]
- Paredes, P.; Petry, M.T.; Oliveira, C.M.; Montoya, F.; López-Urrea, R.; Pereira, L.S. Single and Basal Crop Coefficients for Estimation of Water Requirements of Subtropical and Tropical Orchards and Plantations with Consideration of Fraction of Ground Cover, Height, and Training System. Irrig. Sci. 2024, 42, 1059–1097. [Google Scholar] [CrossRef]
- Gush, M.B.; Taylor, N.J. The Water Use of Selected Fruit Tree Orchards: Technical Report on Measurements and Modelling; WRC Report No. 1770/2/14; Water Research Commission (WRC): Pretoria, South Africa, 2014; Volume 2, pp. 1–285. [Google Scholar]
- Dzikiti, S.; Dangare, P.; Nel, G.P.; Masanganise, J.N.; Kapangaziwiri, E.; Kleinert, A.; Cronje, P.J.; Midgley, S.J.E.; Raath, P.; Mashimbye, E.Z.; et al. Developing A Decision Support System for Water Use and Water-Use Efficiency Of Irrigated Crops in The Inkomati-Usuthu Water Management Area; Water Research Commission (WRC) Report No. 3129/1/24; Water Research Commission (WRC): Pretoria, South Africa, 2024. [Google Scholar]
- Lobit, P.; Mpandeli, N.S.; Annandale, J.G.; Jovanovic, N.Z.; du Sautoy, N. Validation of the Soil Evaporation Subroutine of the SWB-2D Model in a Hedgerow Peach Orchard. S. Afr. J. Plant Soil 2004, 21, 220–229. [Google Scholar] [CrossRef]
- Ntshidi, Z.; Dzikiti, S.; Mazvimavi, D.; Mobe, N.T. Effect of Different Irrigation Systems on Water Use Partitioning and Plant Water Relations of Apple Trees Growing on Deep Sandy Soils in the Mediterranean Climatic Conditions, South Africa. Sci. Hortic. 2023, 317, 112066. [Google Scholar] [CrossRef]


| Crop Type | Cultivar | Rootstock | Age (yrs) | Orchard Size (ha) | Number of Plants per Hectare | Tree Height (m) | Irrigation System |
|---|---|---|---|---|---|---|---|
| Grapefruit | Star Ruby | C35/5×5B | 14 | 6.25 | 476 | 2.90 | Microsprinkler |
| Litchi | Mauritius | Mauritius | 53 | 13.10 | 70 | 6.30 | Microsprinkler |
| Mango | Tommy Atkins | - | 39 | 9.50 | 303 | 4.70 | Microsprinkler |
| Grapefruit | Litchi | Mango | |
|---|---|---|---|
| Minimum | 0.32 | 0.19 | 0.30 |
| Maximum | 0.64 | 0.82 | 0.80 |
| Mean | 0.53 | 0.59 | 0.63 |
| Standard deviation | 0.04 | 0.11 | 0.06 |
| Orchard | Evapotranspiration Measurement Campaign Period |
|---|---|
| Grapefruit | 6–9 December 2022; 7–21 March 2023 |
| Litchi | 16–31 July 2022; 20 September 2022–18 October 2022; 14 November 2022–1 December 2022 |
| Mango | 3–28 March 2022; 11 April 2022–30 May 2022; 26 June 2022–3 July 2022 |
| Date (m/yy) | Rs (MJ/m2/d) | Tx (°C) | Tn (°C) | RH (%) | Rain (mm) | Uavg (m/s) | ETo (mm) | Grapefruit LAI (m2/m2) | Litchi LAI (m2/m2) | Mango LAI (m2/m2) |
|---|---|---|---|---|---|---|---|---|---|---|
| Oct-21 | 15.5 | 41.0 | 9.7 | 65.5 | 28.7 | 1.1 | 120.7 | 1.5 | 2.1 | 3.1 |
| Nov-21 | 17.5 | 39.1 | 13.0 | 73.1 | 137.7 | 1.2 | 125.0 | 3.2 | 5.3 | 3.1 |
| Dec-21 | 17.5 | 39.1 | 16.3 | 78.1 | 138.4 | 1.0 | 128.7 | 3.0 | 4.7 | 3.1 |
| Jan-22 | 18.8 | 35.1 | 18.3 | 79.7 | 203.2 | 1.1 | 133.2 | 2.8 | 4.2 | 3.2 |
| Feb-22 | 21.0 | 39.4 | 18.4 | 72.3 | 4.8 | 1.2 | 138.0 | 2.6 | 3.8 | 3.2 |
| Mar-22 | 16.8 | 38.3 | 16.3 | 73.4 | 84.6 | 1.1 | 120.8 | 2.1 | 3.5 | 4.3 |
| Apr-22 | 13.9 | 37.4 | 12.1 | 74.1 | 69.3 | 1.2 | 92.2 | 3.1 | 4.7 | 4.7 |
| May-22 | 12.3 | 33.0 | 10.8 | 76.0 | 113.0 | 1.1 | 77.0 | 3.1 | 4.3 | 4.3 |
| Jun-22 | 12.2 | 28.2 | 7.0 | 68.4 | 5.8 | 1.4 | 71.1 | 4.3 | 4.8 | 4.4 |
| Jul-22 | 12.9 | 30.4 | 7.9 | 70.0 | 4.3 | 1.2 | 77.5 | 2.2 | 3.9 | 3.7 |
| Aug-22 | 15.1 | 34.4 | 7.7 | 62.9 | 3.8 | 1.3 | 100.0 | 1.6 | 2.6 | 2.3 |
| Sep-22 | 16.6 | 38.6 | 9.3 | 60.6 | 31.0 | 1.3 | 121.1 | 1.6 | 2.2 | 2.9 |
| Oct-22 | 16.5 | 43.0 | 16.2 | 67.8 | 0.8 | 1.4 | 134.9 | 2.0 | 2.4 | 3.1 |
| Nov-22 | 17.4 | 37.6 | 14.7 | 73.8 | 37.1 | 1.3 | 125.9 | 2.4 | 2.6 | 3.3 |
| Dec-22 | 18.2 | 39.8 | 15.4 | 74.0 | 81.3 | 1.3 | 139.6 | 3.0 | 2.7 | 3.5 |
| Jan-23 | 20.5 | 39.8 | 16.1 | 71.7 | 62.2 | 1.3 | 155.3 | 3.7 | 3.2 | 3.0 |
| Feb-23 | 15.9 | 34.5 | 15.6 | 79.4 | 461.4 | 1.2 | 108.0 | 3.0 | 3.4 | 3.1 |
| Mar-23 | 18.7 | 36.9 | 15.2 | 75.8 | 8.9 | 1.1 | 129.2 | 2.5 | 3.8 | 3.3 |
| Apr-23 | 15.6 | 38.4 | 14.8 | 71.3 | 30.2 | 1.0 | 102.4 | 1.6 | 3.1 | 2.6 |
| May-23 | 11.6 | 34.1 | 11.7 | 77.1 | 63.2 | 1.0 | 74.0 | 2.8 | 4.4 | 2.3 |
| Jun-23 | 12.7 | 29.4 | 10.8 | 64.0 | 2.0 | 1.2 | 72.3 | 2.5 | 3.2 | 2.0 |
| Jul-23 | 12.0 | 31.5 | 8.5 | 63.9 | 47.8 | 1.3 | 77.7 | 1.6 | 3.3 | 2.1 |
| Aug-23 | 18.0 | 32.3 | 7.9 | 63.1 | 0 | 1.4 | 107.0 | 1.7 | 3.0 | 2.2 |
| Sept-23 | 19.1 | 39.1 | 10.0 | 59.6 | 47.9 | 1.5 | 133.0 | 1.5 | 2.2 | 2.1 |
| Parameter Name | Litchi T | Litchi ET | Grapefruit T | Grapefruit ET | Mango T | Mango ET |
|---|---|---|---|---|---|---|
| n_estimators | 851 | 997 | 718 | 871 | 483 | 583 |
| max_depth | 27 | 17 | 46 | 24 | 44 | 26 |
| learning_rate | 0.0101 | 0.1050 | 0.2369 | 0.1015 | 0.07270 | 0.07622 |
| num_leaves | 92 | 225 | 183 | 182 | 40 | 99 |
| lambda_l1 | 1.671 × 10−4 | 0.09843 | 0.4712 | 1.415 × 10−6 | 0.1132 | 0.2037 |
| lambda_l2 | 1.814 | 5.002 × 10−8 | 0.1677 | 1.171 × 10−3 | 1.969 × 10−5 | 2.231 × 10−5 |
| bagging_fraction | 0.8848 | 0.4272 | 0.9850 | 0.6667 | 0.9701 | 0.6694 |
| bagging_freq | 2 | 2 | 5 | 2 | 6 | 5 |
| feature_fraction | 0.9234 | 0.5967 | 0.9625 | 0.7356 | 0.9794 | 0.7260 |
| max_bin | 47 | 215 | 64 | 170 | 173 | 108 |
| min_child_samples | 87 | 86 | 76 | 28 | 50 | 100 |
| min_samples_leaf | 3 | 1 | 5 | 2 | 6 | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dangare, P.; Mashimbye, Z.E.; Cronje, P.J.R.; Masanganise, J.N.; Gokool, S.; Ntshidi, Z.; Naiken, V.; Sawunyama, T.; Dzikiti, S. Evapotranspiration Partitioning in Selected Subtropical Fruit Tree Orchards Based on Sentinel 2 Data Using a Light Gradient-Boosting Machine (LightGBM) Learning Model in Malelane, South Africa. Hydrology 2025, 12, 189. https://doi.org/10.3390/hydrology12070189
Dangare P, Mashimbye ZE, Cronje PJR, Masanganise JN, Gokool S, Ntshidi Z, Naiken V, Sawunyama T, Dzikiti S. Evapotranspiration Partitioning in Selected Subtropical Fruit Tree Orchards Based on Sentinel 2 Data Using a Light Gradient-Boosting Machine (LightGBM) Learning Model in Malelane, South Africa. Hydrology. 2025; 12(7):189. https://doi.org/10.3390/hydrology12070189
Chicago/Turabian StyleDangare, Prince, Zama E. Mashimbye, Paul J. R. Cronje, Joseph N. Masanganise, Shaeden Gokool, Zanele Ntshidi, Vivek Naiken, Tendai Sawunyama, and Sebinasi Dzikiti. 2025. "Evapotranspiration Partitioning in Selected Subtropical Fruit Tree Orchards Based on Sentinel 2 Data Using a Light Gradient-Boosting Machine (LightGBM) Learning Model in Malelane, South Africa" Hydrology 12, no. 7: 189. https://doi.org/10.3390/hydrology12070189
APA StyleDangare, P., Mashimbye, Z. E., Cronje, P. J. R., Masanganise, J. N., Gokool, S., Ntshidi, Z., Naiken, V., Sawunyama, T., & Dzikiti, S. (2025). Evapotranspiration Partitioning in Selected Subtropical Fruit Tree Orchards Based on Sentinel 2 Data Using a Light Gradient-Boosting Machine (LightGBM) Learning Model in Malelane, South Africa. Hydrology, 12(7), 189. https://doi.org/10.3390/hydrology12070189







