Uncertainty in Kinetic Energy Models for Rainfall Erosivity Estimation in Semi-Arid Regions
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Rainfall Data Collection
2.3. Kinetic Energy Models-KE and Erosivity Index-EI30
- KE is the kinetic energy of rainfall (MJ ha−1),
- I is the average rainfall intensity (mm h−1),
- R is the rainfall height (mm).
- KEr is the kinetic energy of rainfall (MJ ha−1 mm−1);
- Ir is the rainfall intensity during the adopted time interval (mm h−1).
- EI30 is the rainfall erosivity index (MJ ha−1 mm h−1),
- I30 is the maximum rainfall intensity over 30 min during the event (mm h−1).
2.4. Statistical Analysis
3. Results and Discussion
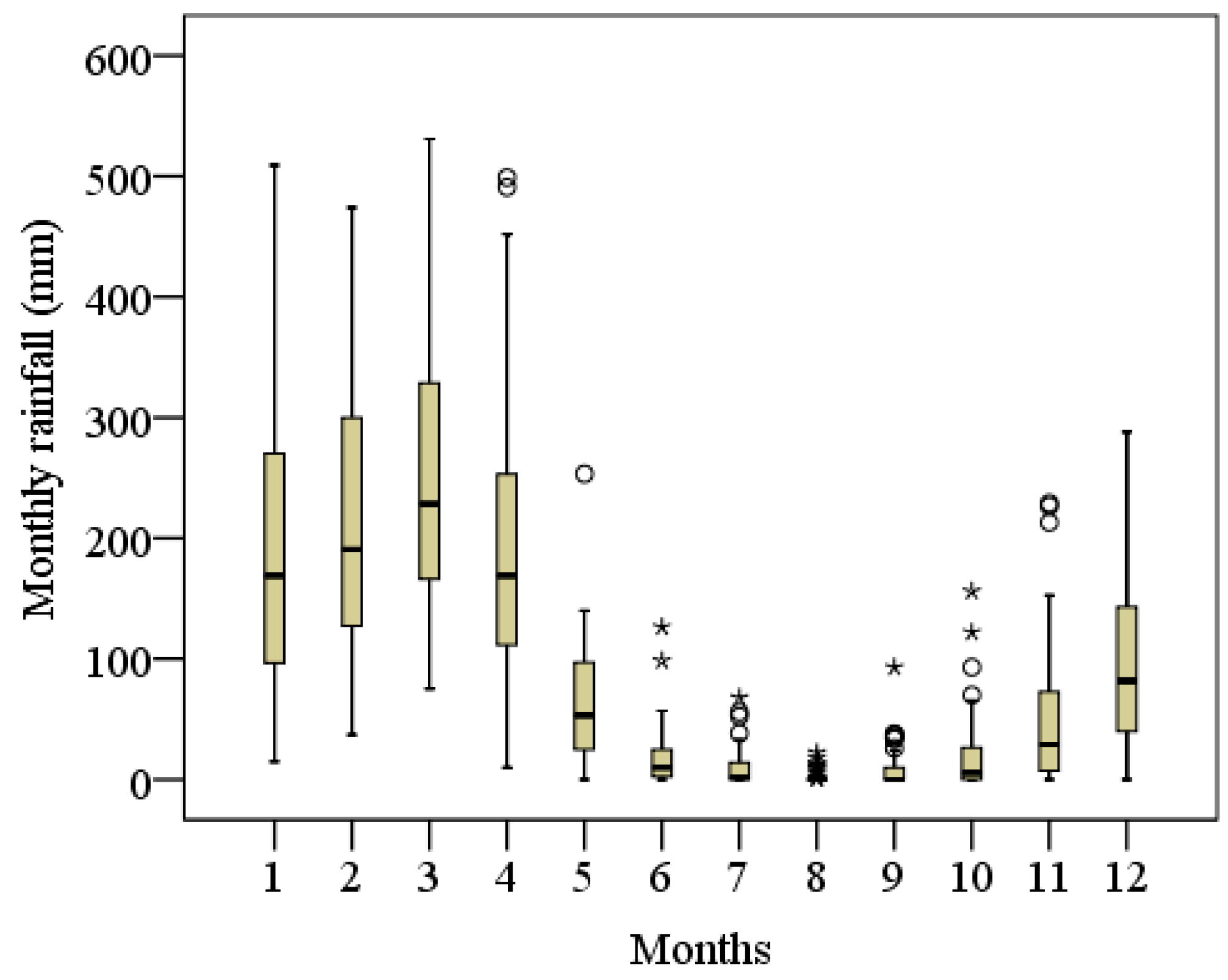
3.1. Rainfall Event Characteristics
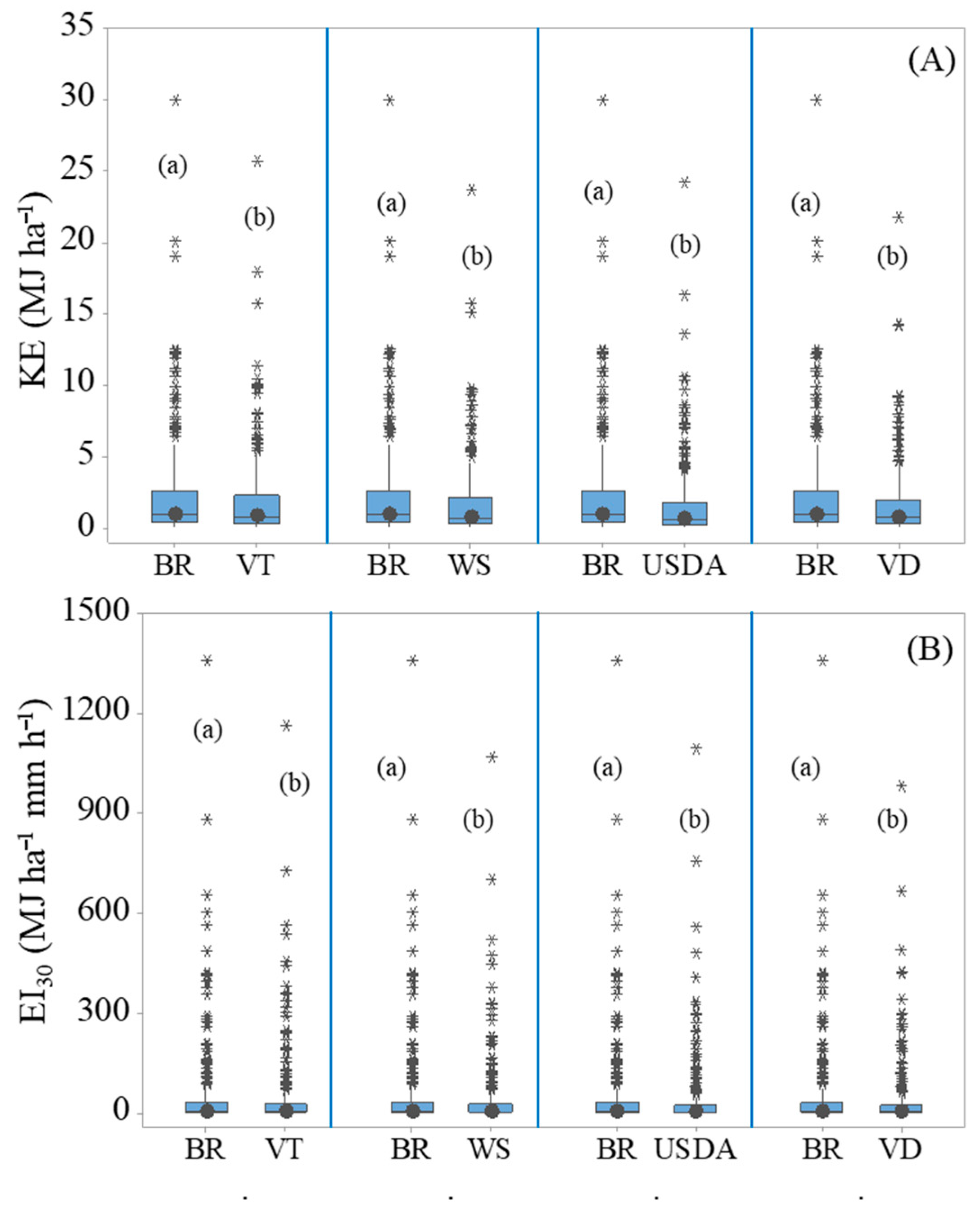
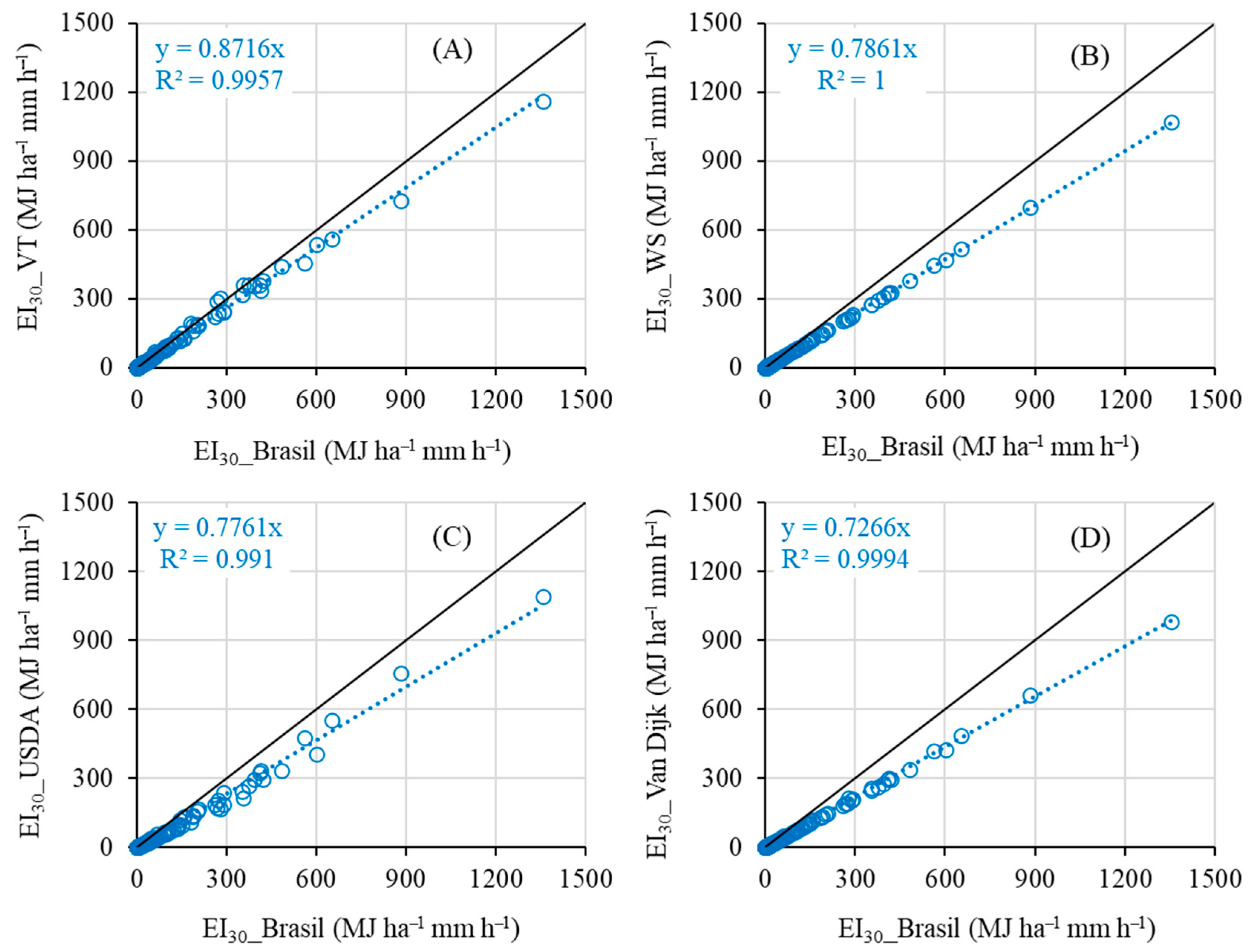
3.2. Kinetic Energy Models-KE and Erosivity Index-EI30
3.3. Erosive Events
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Campos, D.A.; Andrade, E.M.; Castanho, A.D.; Feitosa, R.C.; Palácio, H.Q. Biomass dynamics in a fragment of Brazilian tropical forest (Caatinga) over consecutive dry years. Appl. Sci. 2020, 10, 7813. [Google Scholar] [CrossRef]
- Brasil, J.B.; Guerreiro, M.S.; Andrade, E.M.; Palácio, H.A.Q.; Medeiros, P.H.A.; Ribeiro Filho, J.C. Minimum Rainfall Inter-Event Time to Separate Rainfall Events in a Low Latitude Semi-Arid Environment. Sustainability 2022, 14, 1721. [Google Scholar] [CrossRef]
- Soares, N.S.; Costa, C.A.G.; Carneiro de Lima, J.B.; Francke, T.; de Araújo, J.C. Method for identification of hydrological seasons in the semi-arid Caatinga biome, Brazil. Hydrol. Sci. J. 2024, 69, 309–320. [Google Scholar] [CrossRef]
- Guerreiro, M.S.; Andrade, E.M.; Sousa, M.M.M.; Brasil, J.B.; Palácio, H.A.Q. Contribution of Non-Rainfall Water Input to Surface Soil Moisture in a Tropical Dry Forest. Hydrology 2022, 9, 102. [Google Scholar] [CrossRef]
- Brasil, J.B.; Andrade, E.M.; Palácio, H.A.Q.; Fernández-Raga, M.; Ribeiro Filho, J.C.; Medeiros, P.H.A.; Guerreiro, M.S. Canopy Effects on Rainfall Partition and Throughfall Drop Size Distribution in a Tropical Dry Forest. Atmosphere 2022, 13, 1126. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Meusburger, K.; Yu, B.; Klik, A.; Jae Lim, K.; Yang, J.E.; Ni, J.; Miao, C.; Chattopadhyay, N.; et al. Global rainfall erosivity assessment based on high-temporal resolution rainfall records. Sci. Rep. 2017, 7, 4175. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Matthews, F.; Liakos, L.; Bezak, N.; Diodato, N.; Ballabio, C. Global rainfall erosivity projections for 2050 and 2070. J. Hydrol. 2022, 610, 127865. [Google Scholar] [CrossRef]
- Santos, W.P.; Avanzi, J.C.; Viola, M.R.; Chou, S.C.; Acuña-Guzman, S.F.; Pontes, L.M.; Curi, N. Projections of rainfall erosivity in climate change scenarios for the largest watershed within Brazilian territory. Catena 2022, 213, 106225. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhu, D.; Wu, Z.; Cao, Z. Extreme rainfall erosivity: Research advances and future perspectives. Sci. Total Environ. 2024, 917, 170425. [Google Scholar] [CrossRef]
- Brasil, J.B.; Andrade, E.M.; Guerreiro, M.S.; Palácio, H.A.Q.; Ribeiro Filho, J.C.; Fernández-Raga, M.; Medeiros, P.H.A. Measurement and modelling of kinetic energy and erosivity of rainfall and throughfall in a tropical semiarid region. J. Hydrol. 2024, 644, 132088. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses: A Guide to Conservation Planning (No. 537); Department of Agriculture, Science and Education Administration: Washington, DC, USA, 1978. [Google Scholar]
- Brychta, J.; Podhrázská, J.; Šťastná, M. Review of methods of spatio-temporal evaluation of rainfall erosivity and their correct application. Catena 2022, 217, 106454. [Google Scholar] [CrossRef]
- Wang, L.; Li, Y.; Gan, Y.; Zhao, L.; Qin, W.; Ding, L. Rainfall erosivity index for monitoring global soil erosion. Catena 2024, 234, 107593. [Google Scholar] [CrossRef]
- Medeiros, P.H.A.; de Araújo, J.C. Temporal variability of rainfall in a semiarid environment in Brazil and its effect on sediment transport processes. J. Soils Sediments 2014, 14, 1216–1223. [Google Scholar] [CrossRef]
- Teixeira, D.B.S.; Cecílio, R.A.; Moreira, M.C.; Pires, G.F.; Fernandes Filho, E.I. Recent advancements in rainfall erosivity assessment in Brazil: A review. Catena 2022, 219, 106572. [Google Scholar] [CrossRef]
- Yamaura, Y.; Yamada, Y.; Matsuura, T.; Tamai, K.; Taki, H.; Sato, T.; Hashimoto, S.; Murakami, W.; Toda, K.; Saito, H.; et al. Modeling impacts of broad-scale plantation forestry on ecosystem services in the past 60 years and for the future. Ecosyst. Serv. 2021, 49, 101271. [Google Scholar] [CrossRef]
- Van Dijk, A.I.J.M.; Bruijnzeel, L.A.; Rosewell, C.J. Rainfall intensity–kinetic energy relationships: A critical literature appraisal. J. Hydrol. 2002, 261, 1–23. [Google Scholar] [CrossRef]
- USDA-Agricultural Research Service. Science Documentation Revised Universal Soil Loss Equation Version 2. 2013. Available online: https://www.ars.usda.gov/ (accessed on 2 September 2024).
- Jiang, Y.; Gao, J.; Yang, L.; Wu, S.; Dai, E. The interactive effects of elevation, precipitation and lithology on karst rainfall and runoff erosivity. Catena 2021, 207, 105588. [Google Scholar] [CrossRef]
- Nearing, M.A.; Yin, S.Q.; Borrelli, P.; Polyakov, V.O. Rainfall erosivity: An historical review. Catena 2017, 157, 357–362. [Google Scholar] [CrossRef]
- Sampaio, M.R.L.; Barboza, E.N.; Crisostomo, N.C.; Bezerra Neto, F.d.C.; Silva, D.H.d.; Felizardo, R.d.O.; Pinto, N.A. Estudo comportamental da precipitação pluviométrica no município de Crato-Ceará, no período entre 1974–2009. Rev. Bras. De Gestão Ambient. 2019, 13, 27–33. Available online: https://www.gvaa.com.br/revista/index.php/RBGA/article/view/7729 (accessed on 2 September 2024).
- Foster, G.R.; McCool, D.K.; Renard, K.G.; Moldenhauer, W.C. Conversion of the universal soil loss equation to SI metric units. J. Soil Water Conserv. 1981, 36, 355–359. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Camargo, A.D.; Sentelhas, P.C. Avaliação do desempenho de diferentes métodos de estimativa da evapotranspiração potencial no Estado de São Paulo, Brasil. Rev. Bras. De Agrometeorol. 1997, 5, 89–97. [Google Scholar]
- da Costa, S.A.T.; de Souza, L.S.B.; de Assunção Montenegro, A.A.; de Souza, C.A.A.; de Morais, J.E.F.; de Carvalho Lopes, D.; Neto, A.J.S.; de Souza Santos, J.P.A.; Jardim, A.M.D.R.F.; Alves, C.P.; et al. Calibration and validation of the AquaCrop model for forage cactus production systems under different management interventions in the semi-arid region of Brazil. Phys. Chem. Earth Parts A/B/C 2024, 136, 103716. [Google Scholar] [CrossRef]
- Carvalho, T.; Brosinsky, A.; Foerster, S.; Teixeira, A.; Medeiros, P. Reservoir sediment characterisation by diffuse reflectance spectroscopy in a semiarid region to support sediment reuse for soil fertilization. J. Soils Sediments 2022, 22, 2557–2577. [Google Scholar] [CrossRef]
- Nanko, K.; Tanaka, N.; Leuchner, M.; Levia, D.F. Throughfall Erosivity in Relation to Drop Size and Crown Position: A Case Study from a Teak Plantation in Thailand. In Forest-Water Interactions; Levia, D.F., Carlyle-Moses, D.E., Iida, S., Michalzik, B., Nanko, K., Tischer, A., Eds.; Ecological Studies; Springer: Cham, Switzerland, 2020; Volume 240. [Google Scholar] [CrossRef]
- Santos, J.C.N.; Andrade, E.M.; Medeiros, P.H.A.; Palácio, H.A.Q.; Araújo, J.R. Sediment delivery ratio in a small semi-arid watershed under conditions of low connectivity1. Rev. Ciência Agronômica 2017, 48, 49–58. [Google Scholar] [CrossRef]
- Gupta, S.; Borrelli, P.; Panagos, P.; Alewell, C. An advanced global soil erodibility (K) assessment including the effects of saturated hydraulic conductivity. Sci. Total Environ. 2024, 908, 168249. [Google Scholar] [CrossRef]


| Variables | N° of Events | Mean | StDev | Minimum | Q1 | Q2 Median | Q3 | Maximum |
|---|---|---|---|---|---|---|---|---|
| R | 283 | 9.92 | 13.29 | 0.40 | 2.00 | 5.20 | 12.20 | 107.80 |
| D | 3.91 | 4.03 | 0.08 | 1.08 | 2.75 | 5.17 | 23.75 | |
| I | 4.38 | 6.89 | 0.21 | 0.96 | 2.27 | 4.89 | 81.60 | |
| I30 | 9.24 | 10.96 | 0.40 | 2.00 | 4.40 | 12.00 | 53.60 | |
| KE_Brasil | 2.22 | 3.43 | 0.05 | 0.32 | 0.92 | 2.61 | 29.99 | |
| EI30_Brasil | 50.91 | 136.58 | 0.02 | 0.63 | 4.09 | 32.84 | 1355.68 |
| Methods | Indexes | Error | |||||
|---|---|---|---|---|---|---|---|
| Nash | d | C | Performance | RMSE | ME | ||
| Brasil × VT | 0.97 | 0.99 | 0.99 | optimal | 0.59 | 0.29 | |
| KE | Brasil × WS | 0.93 | 0.98 | 0.98 | optimal | 0.89 | 0.50 |
| Brasil × USDA | 0.89 | 0.96 | 0.96 | optimal | 1.14 | 0.68 | |
| Brasil × Van Dijk | 0.89 | 0.96 | 0.96 | optimal | 1.12 | 0.56 | |
| EI30 | Brasil × VT | 0.98 | 0.99 | 0.99 | optimal | 20.46 | 5.85 |
| Brasil × WS | 0.95 | 0.98 | 0.98 | optimal | 31.14 | 11.08 | |
| Brasil × USDA | 0.94 | 0.98 | 0.98 | optimal | 34.31 | 13.67 | |
| Brasil × Van Dijk | 0.91 | 0.97 | 0.97 | optimal | 39.88 | 13.81 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brasil, J.B.; Meireles, A.C.M.; Oliveira, C.W.; de Menezes, S.M.; Arraes, F.D.D.; Guerreiro, M.S. Uncertainty in Kinetic Energy Models for Rainfall Erosivity Estimation in Semi-Arid Regions. Hydrology 2025, 12, 181. https://doi.org/10.3390/hydrology12070181
Brasil JB, Meireles ACM, Oliveira CW, de Menezes SM, Arraes FDD, Guerreiro MS. Uncertainty in Kinetic Energy Models for Rainfall Erosivity Estimation in Semi-Arid Regions. Hydrology. 2025; 12(7):181. https://doi.org/10.3390/hydrology12070181
Chicago/Turabian StyleBrasil, José Bandeira, Ana Célia Maia Meireles, Carlos Wagner Oliveira, Sirleide Maria de Menezes, Francisco Dirceu Duarte Arraes, and Maria Simas Guerreiro. 2025. "Uncertainty in Kinetic Energy Models for Rainfall Erosivity Estimation in Semi-Arid Regions" Hydrology 12, no. 7: 181. https://doi.org/10.3390/hydrology12070181
APA StyleBrasil, J. B., Meireles, A. C. M., Oliveira, C. W., de Menezes, S. M., Arraes, F. D. D., & Guerreiro, M. S. (2025). Uncertainty in Kinetic Energy Models for Rainfall Erosivity Estimation in Semi-Arid Regions. Hydrology, 12(7), 181. https://doi.org/10.3390/hydrology12070181







