Abstract
Streamflow is one of the most important variables in hydrology, but it is difficult to measure continuously. As a result, nearly all streamflow time series are estimated from rating curves that define a mathematical relationship between streamflow and some easy-to-measure proxy like water surface elevation (stage). Despite the existence of automated methods, most rating curves are still fit manually, which can be time-consuming and subjective. Although several automated methods exist, they vary greatly in performance because of the non-convex nature of the problem. In this work, we develop a parameterization of the segmented power law that works reliably with minimal data, which could serve operationally or as a benchmark for evaluating other methods. The model, along with test data and tutorials, is available as an open-source Python package called ratingcurve. The implementation uses a modern probabilistic machine-learning framework, which is relatively easy to modify so that others can improve upon it.
1. Introduction
Streamflow time series are widely used in hydrologic research, water resource management, engineering design, and flood forecasting, but they are difficult to measure directly. In nearly all time-series applications, streamflow is estimated from rating curves or “ratings” that describe the relation between streamflow and an easy-to-measure proxy, like stage. The shape of the rating is specific to each streamgage and is governed by channel conditions at or downstream from the gage, referred to as controls. Section controls, like natural riffles or artificial weirs, occur downstream from the gage, whereas channel controls, like the geometry of the banks, represent conditions along the entire stream reach (the upstream and downstream vicinity of the gage). Regardless of the type, the behavior of each control is often well-approximated with standard hydraulic equations that take the general form of a power law with an offset parameter
where q is the discharge (streamflow); h is the height of the water above some datum (stage); is the stage of zero flow (the offset parameter); is the hydraulic head; b is the slope of the rating curve when plotted in log-log space; and C is a scale factor equal to the discharge when the head is equal to one [1]. When multiple controls are present, the rating curve is divided into segments with one power law corresponding to each control resulting in a multi-segment or compound rating.
Although automated methods exist, most ratings are still fit manually using a graphical method of plotting stage and discharge in log–log space. With the appropriate location parameter, each control can be fit to a straight-line segment in log space [1,2]. Variants of this method have been used for decades, first with pencil and log paper and now with computer-aided software. However, the fitting process is still done manually by adjusting parameters to achieve an acceptable fit.
Single-segment ratings are easily fit by automated methods [3], but compound ratings are more challenging because their solution is non-convex or multimodal [4]. As a result, optimization algorithms can become stuck in local optima and fail to converge to the global optimum. General function approximators, such as natural splines [5] or neural networks, are sometimes able to avoid these calibration issues; however, their generality comes at the cost of requiring more data to constrain their greater flexibility and prevent overfitting. In contrast, power-law rating models are based on the hydraulic equations governing uniform open-channel flow, like the Manning Equation [6]. Due to that physical basis, power laws are potentially more robust than other generic curve-fitting functions, requiring less data to achieve the same fit and being less prone to overfitting.
Several models for fitting rating curves already exist. Some, like power laws, are physics-based in that their structure corresponds to the governing hydraulic equations [7,8]; some are more data-driven with more flexible structures like splines [5] or local regression [9]; and some are a hybrid of the two [10]. Each style of parameterization comes with tradeoffs: physics-based parameterizations require less data but may be non-convex, which makes them challenging to fit, whereas data-driven approaches are easier to fit but require more data (e.g., [5]). However, different algorithms may achieve different tradeoffs in this regard, and it is not obvious which approach is best. Existing physically-based parameterizations tend to use Bayesian sampling algorithms as opposed to optimization [11] and incorporate priors (to constrain the solution domain), both of which can help with non-convex fitting problems. Examples of priors include constraining the exponent b to be around 5/3, constraining the number of rating segments, or constraining the transitions between segments around a particular stage. Being Bayesian, these algorithms inherently estimate uncertainty in the fitted parameters and discharge, which is important for many applications. However, many of these physically-based parameterizations differ in their exact formulation, which, because of their non-convex nature, can greatly affect their performance.
In this paper, we develop a parameterization approximating the classic segmented power law used in most manual methods. Our implementation distinguishes itself by:
- Estimating the optimal locations of breakpoints, as well as the number of segments;
- Accounting for uncertainty in the measurements and the rating model;
- Fitting with minimal data;
- Using similar assumptions to current operational methods;
- Using a community-developed probabilistic programming library;
- Having an easy-to-use Python package with documentation, tutorials, and test datasets.
Together, these qualities make our implementation well-suited for operational use and could make it a standard against which to benchmark new and existing methods.
2. Parameterization
Our parameterization of the rating curve uses a segmented power law, similar to classic manual methods [1,2], as well as some automated methods [7,8]. However, these methods differ in their parameterizations, which can greatly affect their performance because of the non-convex nature of the optimization. As a result, some methods may require substantially more data or constraints to achieve an acceptable fit. For example, the Reitan and Petersen-Øverleir [7] parameterization slices the channel cross-section horizontally to form each segment, such that segments stack one on top of the other. Once the stage rises beyond the range of a particular control, that control is “drowned out” and flow through that segment ceases to increase with stage. The Le Coz et al. [8] parameterization can slice the cross-section horizontally or vertically but differs in that the segments are summed after transforming them back to their original scale, whereas Reitan and Petersen-Øverleir [7] sum the segments in log.
The ratingcurve package implements several parameterizations, but after testing, one seemed especially reliable and simple, which we adopted as our benchmark method, that of slicing the channel cross-section vertically into control segments (so controls never drown out) and summing them in log, which is somewhat like a ReLU (rectified linear unit) neural network with hydraulic controls as neurons. This parameterization, which is denoted in matrix and vector notation (i.e., bold upper (lower) case variables are matrices (vectors) and unbolded variables are scalars), is given by
where is vector of n stage observations; are the m unknown segment breakpoints; the first of which is the stage of zero flow (i.e., h when ); max is the element-wise maximum, which returns a matrix; is a vector of m offsets with the first value being 0 and the rest being 1, which ensures that additional segments never subtract discharge ( and are broadcast to matrices); are discharge measurements corresponding to each h measurement; a is a bias parameter equal to , the scale factor; is the slope of the log-transformed segment; are cumulative are the slopes adjustments of each log-transformed segment (so the slope of the mth segment is ); is a scalar giving the residual error; and is the uncertainty in each discharge observation (optional). Operations combining matrices and vectors use standard broadcasting rules. For example, when subtracting a length-m vector from a matrix, the vector is repeated n times to match the dimensions of the matrix.
The default priors and settings are documented in the ratingcurve package; in general, they do not need to be modified. In addition to selecting the number of segments, the user can specify a prior distribution on the breakpoints. The default assumes the breakpoints are monotonically ordered and uniformly distributed across the range of the data, . Alternatively, the user can specify approximate locations for each breakpoint and their uncertainty as normal distributions.
Uncertainty in the discharge observations is typically reported as a standard error (SE) or relative standard error (RSE, where ). For convenience, we convert that standard error to a geometric error as . For small uncertainties, the difference between the RSE and geometric error is negligible, and for large uncertainties, it is not known which error model is more accurate. Like Reitan and Petersen-Øverleir [7], we assume is normally distributed with mean zero and variance , . That simplification can create unaccounted heteroscedasticity [12] but generally yields a reasonable estimate for the rating and its uncertainty.
3. Calibration
The algorithm uses PyMC [13], an open-source Python library for Bayesian statistical modeling and probabilistic machine learning. Using PyMC, the core model can be expressed in several lines of code, making it easier to extend or modify, like changing the priors, the parameterization of the rating curve, or the inference algorithm to achieve different tradeoffs of speed and accuracy. This paper demonstrates two inference algorithms: Automatic Differentiation Variational Inference (ADVI) [14] and Hamiltonian Monte Carlo with the No-U-Turn Sampler (NUTS) [15]. ADVI is a Bayesian optimization algorithm, whereas NUTS is a Markov chain Monte Carlo (MCMC) sampling algorithm. In general, MCMC sampling is slower than optimization but better for non-convex problems [11].
4. Usage
The Data availability section provides links to the Python package and source code repository, which includes additional documentation and tutorials. Here, we demonstrate the most basic usage, with additional examples provided in Appendix A. Given observations of discharge (q), stage (h), and, optionally, the standard error of the discharge observations (e), a two-segment rating is fit with
- rating = PowerLawRating(segments=2)
- rating.fit(q, h, e, method="advi")
- rating.plot()
- and produces a plot like Figure 1.
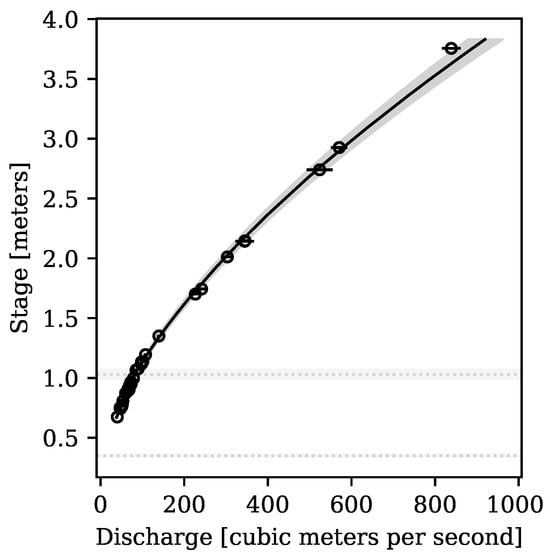 Figure 1. Two-segment rating curve, with 95-percent prediction interval, for the Green River near Jensen, Utah (U.S. Geological Survey streamgage 09261000); generated by rating.plot() and fit using ADVI. The circles with error bars show the discharge observations and their uncertainty. Horizontal dotted lines show the segment breakpoints and their 95-percent prediction intervals.
Figure 1. Two-segment rating curve, with 95-percent prediction interval, for the Green River near Jensen, Utah (U.S. Geological Survey streamgage 09261000); generated by rating.plot() and fit using ADVI. The circles with error bars show the discharge observations and their uncertainty. Horizontal dotted lines show the segment breakpoints and their 95-percent prediction intervals.
A rating curve fit can also be exported as a table for use by other applications, as illustrated in Table 1. In addition to the mean discharge for each stage, the table gives the median and geometric standard error (GSE), which measures the dispersion of a log-normal distribution,
where is a vector containing p samples from the modeled posterior distribution for discharge at a given value of stage. The GSE is then multiplied and divided by the median to estimate prediction intervals [16].

Table 1.
Rating table generated by rating.table(). Units are feet (ft) and cubic feet per second (ft3 s−1); geometric standard error (GSE) is a unitless factor.
5. Benchmarking Results
We compared the performance of our segmented power law against a log-transformed natural spline and the generalized power law model with constant variance (GPLM) [10] using a simulated three-segment rating curve. The spline is an example of a simple data-driven model, whereas the GPLM is a hybrid of data-driven and physics-based approaches.
All of the models use log transformations, which helps with heteroscedasticity, and can approximate complex functions like a multi-segment rating curve [5]. Unlike the spline, the power laws have a physical basis: their parameters can have physical interpretations, like the stage of zero flow, and their structure is similar to standard hydraulic equations, like the formulas of Manning and Chézy [10]. However, segmented power laws are also notoriously difficult to calibrate [5,7], and the model performance depends, in large part, on the parameterization as well as its priors. If the calibration challenges are overcome, physics-based models should yield high-quality fits with fewer observations [7]. Conceptually, the segmented power law optimization searches for ways to transform the observations such that each rating segment can be approximated by a straight line in log space. Therefore, an optimal parameterization requires only two observations per rating segment. Our power-law parameterization achieves that criterion, fitting three segments with six observations.
Each model was benchmarked against observations generated from a simulated a three-segment rating curve. The simulated cross section consists of a control section resembling an obtuse angled weir, a rectangular main channel, and a floodplain. Figure 2 shows a side-by-side comparison of each model fit with 6, 12, 24, and 48 randomly selected stage-discharge observations. For best accuracy, the curves were fit using MCMC algorithms (in the case of our power law and the spline, we used NUTS). In the fits to our segmented power law and the spline, we also specified that the power law had three segments and that the spline had eight degrees of freedom, the same as the power law (one bias, three offsets, three slopes, and one uncertainty). Otherwise, default settings were used.
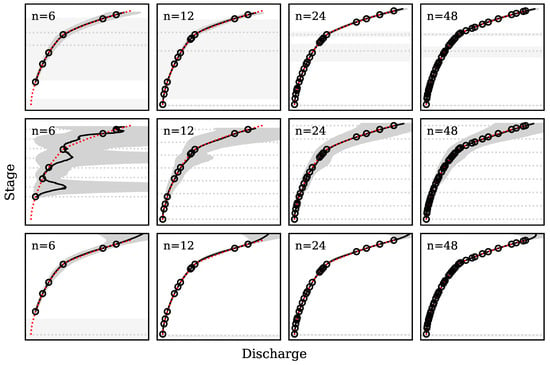
Figure 2.
Our segmented-power law model (top), a natural spline (middle), and generalized power law model [10] (bottom) fit with different numbers of observations (n). The dashed red line is the true rating curve and the circles are the simulated observations. Horizontal dotted lines show segment breakpoints, knot locations, and stage of zero flow for the models, respectively. The shaded regions depict 95-percent prediction intervals for the rating and breakpoints.
Relative to our segmented power law, the natural spline fit 5–20× faster but yielded poorer fits, particularly when (Figure 2). Reducing the degrees of freedom might improve performance when but also sacrifices flexibility when .
In general, the accuracy of data-driven approaches is highly dependent on the availability of data. For example, Coxon et al. [9] recommend a minimum of 20 stage-discharge measurements for their data-driven approach. Taken over the lifetime of a streamgage, 20 measurements may be manageable. However, ratings shift through time from erosion, deposition, vegetation growth, debris/ice jams, etc. [17,18], and it may be impracticable to collect 20 measurements between each shift. Furthermore, when applied to historical data, it is impossible to collect additional observations. In either case, a physical parameterization may be necessary to achieve an acceptable fit from limited data.
By comparison, the power law yielded a good fit with six observations—two fewer than the number of model parameters. Our intent is not to disparage all splines—both parameterizations are technically splines. Rather, we wanted to demonstrate a classic tradeoff between being ease-of-fit and accuracy, which is a characteristic of data-driven and physical approaches.
This paper focuses on one parameterization of the classic multi-segment power law, but others might achieve better tradeoffs of speed and accuracy for certain situations. For example, our comparison uses NUTS, which is accurate but slow. With six observations, NUTS fit the three-segment power law in around 10 min. With 48 observations, NUTS completed in 1 min; a 10× speedup. In general, stronger priors, more observations, or fewer segments would reduce that time. By comparison, ADVI generally achieved a NUTS-like fit in several seconds, but it occasionally failed to converge on the optimum solution.
A better parameterization might yield better convergence with a faster inference algorithm. More work could be done in this regard, but our current version seems fast and reliable enough for operational use and could serve as a benchmark for testing other methods. For example, on the same simulated test, the GPLM and segmented power law yielded similar fits, but the GPLM was substantially faster than NUTS. Notably, neither our model nor the GPLM address shifts in the rating curve through time or hysteresis. Such limitations could, in theory, be addressed, and any such effort will depend, in part, on building from a good starting parameterization.
6. Conclusions
Despite the existence of automated methods, most stage-discharge rating curves are still fit manually. Although the governing hydraulic equations are relatively simple and well-understood, they are notoriously difficult to solve for multiple controls. Among the automated methods, no parameterization has emerged as the standard, and functionally equivalent parameterizations may vary greatly in performance. In the best case, a segmented power law can fit a stage-discharge rating with two observations per rating segment. Our parameterization achieves that, fitting a three-segment rating with six observations. Furthermore, our relatively simple parameterization, use of a community-developed probabilistic programming library, and packaging provide a benchmark for operationalizing automated methods that could promote more widespread use, testing, and refinement by the hydrologic community.
Author Contributions
T.O.H.: Conceptualization, Methodology, Software, Writing—Original Draft; K.J.D.: Software, Writing—Review and Editing; T.A.K.: Conceptualization, Project Administration, Writing—Review and Editing; and T.M.O.: Conceptualization, Writing—Review and Editing; and M.B.Y.: Conceptualization, Writing—Review and Editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The latest version of ratingcurve is available at GitHub (https://github.com/thodson-usgs/ratingcurve, accessed on 21 December 2023), as well as code.usgs.gov (accessed on 21 December 2023) [19] Packaged versions are available via PyPI and conda-forge. A link to the official release of the version used in this paper will appear here in due course. The GPLM model is implemented in the bdrc R package [10].
Acknowledgments
Any opinions, findings, conclusions, or recommendations expressed in this material do not necessarily reflect the views of the NSF. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.
Conflicts of Interest
Authors T.O.H., K.J.D., T.A.K., and T.M.O. are employed by the U.S. Geological Survey. Author M.B.Y. is employed by Environment and Climate Change Canada.
Abbreviations
The following abbreviations are used in this manuscript:
| ADVI | Automatic Differentiation Variational Inference |
| MCMC | Markov chain Monte Carlo |
| NUTS | No-U-Turn Sampler |
| USGS | United States Geological Survey |
Appendix A. Additional Examples
This appendix shows rating curves fit to example datasets collected by USGS or taken from other studies [10,20], all of which are included in the ratingcurve package (Table A1 and Figure A1). The examples have one to three segments, some have uncertainty in the discharge observations, and some do not. The Green River and Three-Segment Simulated datasets were also used in the main text. For the Three-Segment Simulated dataset, ADVI and NUTS sometimes yielded different breakpoints. Visual inspection of the plot gives a good indication of whether ADVI converged to the optimal solution. In such cases, the user may try refitting with ADVI or use NUTS. Adjusting the initialization could help to mitigate this problem, but this occasionally introduced other undesirable effects, so the current version uses a simple initialization.

Table A1.
Test datasets included in the ratingcurve package.
Table A1.
Test datasets included in the ratingcurve package.
| Dataset | Data Source |
|---|---|
| Chalk Creek, USA | USGS streamgage 10131000 |
| Colorado River, USA | USGS streamgage 09185600 |
| Green River, USA | USGS streamgage 09261000 |
| Provo River, USA | USGS streamgage 10154200 |
| Three-Segment Simulated | This study |
| Mahurangi River, New Zealand | Kiang et al. [20] |
| Nordura River, Iceland | Hrafnkelsson et al. [10] |
| Skajalfandafljot River, Iceland | Hrafnkelsson et al. [10] |
| Isére River, France | Kiang et al. [20] |
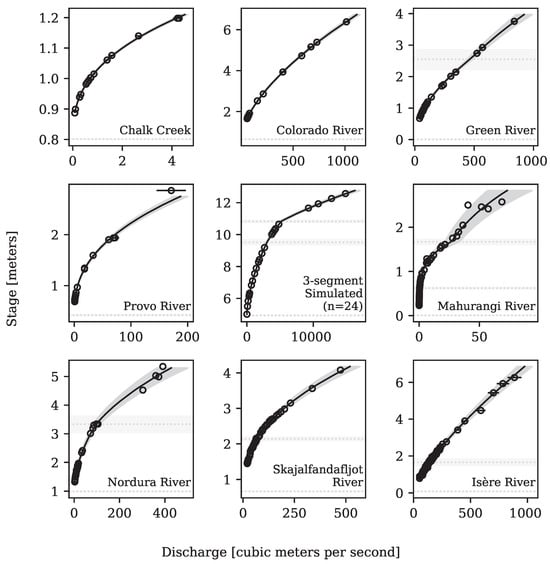
Figure A1.
Example datasets fit with our segmented power law using default priors and ADVI. The circles with error bars show the observations and their uncertainty. Circles without error bars are observations without uncertainty information. Horizontal dotted lines show the segment breakpoints and their prediction intervals.
References
- ISO 18320:2020; Hydrometry–Measurement of Liquid Flow in Open Channels—Determination of the Stage-Discharge Relationship. International Organization for Standardization: Geneva, Switzerland, 2020.
- Kennedy, E.J. Discharge Ratings at Gaging Stations, U.S. Geological Survey Techniques of Water-Resources Investigations, Book 3, Chapter A10; U.S. Geological Survey: Reston, VA, USA, 1984.
- Venetis, C. A note on the estimation of the parameters in logarithmic stage-discharge relationships with estimates of their error. Int. Assoc. Sci. Hydrol. Bull. 1970, 15, 105–111. [Google Scholar] [CrossRef]
- Reitan, T.; Petersen-Øverleir, A. Existence of the frequentistic estimate for power-law regression with a location parameter, with applications for making discharge rating curves. Stoch. Environ. Res. Risk Assess. 2006, 20, 445–453. [Google Scholar] [CrossRef]
- Fenton, J.D. On the generation of stream rating curves. J. Hydrol. 2018, 564, 748–757. [Google Scholar] [CrossRef]
- Manning, R. On the flow of water in open channels and pipes. Trans. Inst. Civ. Eng. Irel. 1891, 20, 179–207. [Google Scholar]
- Reitan, T.; Petersen-Øverleir, A. Bayesian methods for estimating multi-segment discharge rating curves. Stoch. Environ. Res. Risk Assess. 2008, 23, 627–642. [Google Scholar] [CrossRef]
- Le Coz, J.; Renard, B.; Bonnifait, L.; Branger, F.; Le Boursicaud, R. Combining hydraulic knowledge and uncertain gaugings in the estimation of hydrometric rating curves: A Bayesian approach. J. Hydrol. 2014, 509, 573–587. [Google Scholar] [CrossRef]
- Coxon, G.; Freer, J.; Westerberg, I.K.; Wagener, T.; Woods, R.; Smith, P.J. A novel framework for discharge uncertainty quantification applied to 500 UK gauging stations. Water Resour. Res. 2015, 51, 5531–5546. [Google Scholar] [CrossRef] [PubMed]
- Hrafnkelsson, B.; Sigurdarson, H.; Rögnvaldsson, S.; Örn Jansson, A.; Vias, R.D.; Gardarsson, S.M. Generalization of the power-law rating curve using hydrodynamic theory and Bayesian hierarchical modeling. Environmetrics 2021, 33, e2711. [Google Scholar] [CrossRef]
- Ma, Y.A.; Chen, Y.; Jin, C.; Flammarion, N.; Jordan, M.I. Sampling can be faster than optimization. Proc. Natl. Acad. Sci. USA 2019, 116, 20881–20885. [Google Scholar] [CrossRef] [PubMed]
- Petersen-Øverleir, A. Accounting for heteroscedasticity in rating curve estimates. J. Hydrol. 2004, 292, 173–181. [Google Scholar] [CrossRef]
- Salvatier, J.; Wiecki, T.V.; Fonnesbeck, C. Probabilistic programming in Python using PyMC3. PeerJ Comput. Sci. 2016, 2, e55. [Google Scholar] [CrossRef]
- Kucukelbir, A.; Tran, D.; Ranganath, R.; Gelman, A.; Blei, D.M. Automatic differentiation variational inference. J. Mach. Learn. Res. 2017, 18, 1–45. [Google Scholar]
- Hoffman, M.D.; Gelman, A. The No-U-Turn Sampler: Adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 2014, 15, 1593–1623. [Google Scholar]
- Limpert, E.; Stahel, W.A.; Abbt, M. Log-normal distributions across the sciences: Keys and clues. BioScience 2001, 51, 341. [Google Scholar] [CrossRef]
- Herschy, R.W.; Herschy, R. Streamflow Measurement, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar] [CrossRef]
- Mansanarez, V.; Renard, B.; Coz, J.L.; Lang, M.; Darienzo, M. Shift Happens! Adjusting Stage-Discharge Rating Curves to Morphological Changes at Known Times. Water Resour. Res. 2019, 55, 2876–2899. [Google Scholar] [CrossRef]
- Hodson, T.O.; Doore, K.J. Ratingcurve: A Python Package for Fitting Streamflow Ratting Curves; U.S. Geological Survey: Reston, VA, USA, 2024. [CrossRef]
- Kiang, J.E.; Gazoorian, C.; McMillan, H.; Coxon, G.; Le Coz, J.; Westerberg, I.K.; Belleville, A.; Sevrez, D.; Sikorska, A.E.; Petersen-Øverleir, A.; et al. A Comparison of Methods for Streamflow Uncertainty Estimation. Water Resour. Res. 2018, 54, 7149–7176. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).