Evapotranspiration Estimation with the Budyko Framework for Canadian Watersheds
Abstract
1. Introduction
2. Methodology
2.1. Budyko Model and Fu’s Equation
2.2. Attribution Analysis
3. Study Area and Data
3.1. Study Area
3.2. Data Collection
4. Results and Discussion
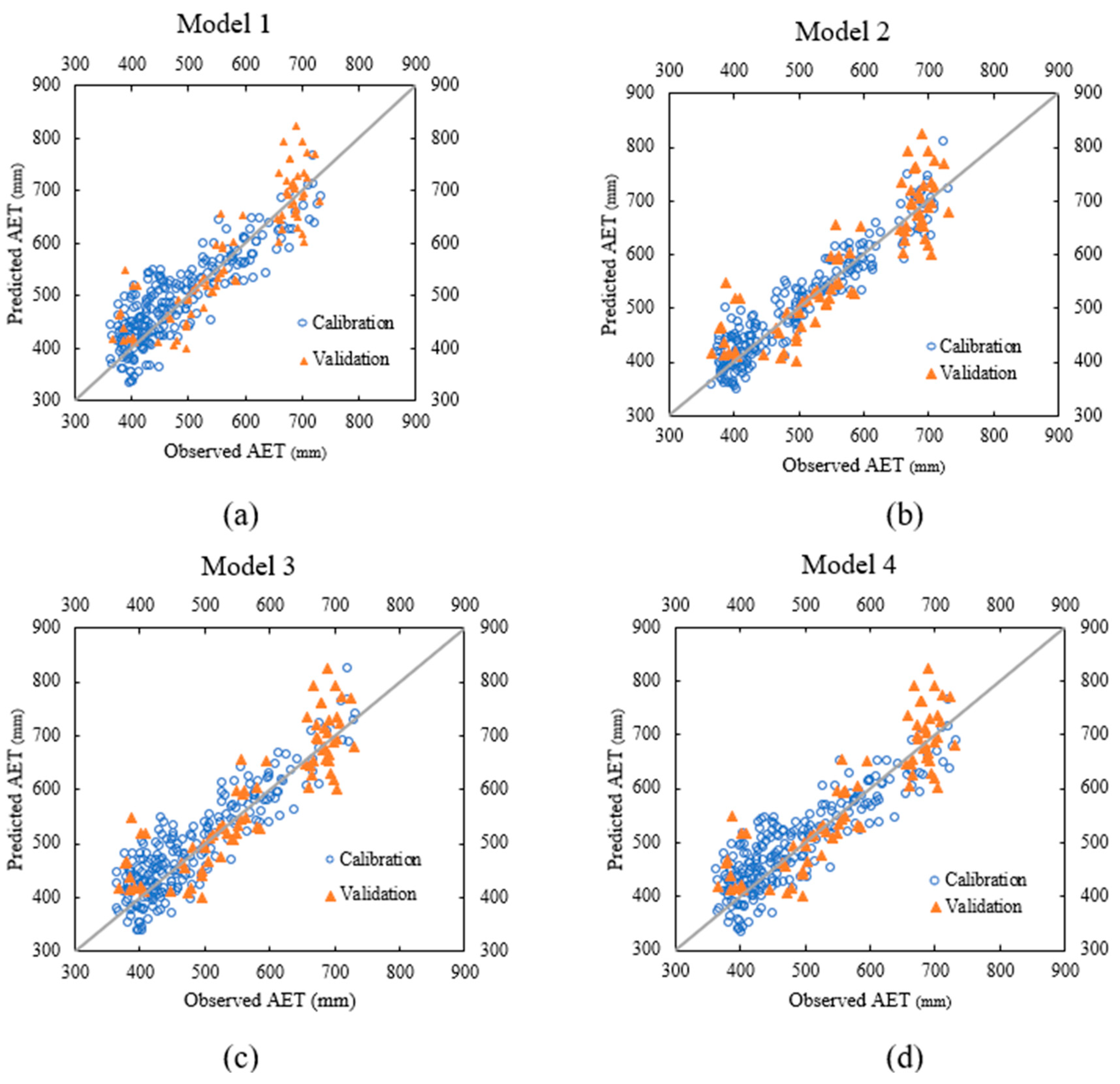
4.1. Calibration of ω
4.2. Empirical Estimation of ω
4.3. Climate and Vegetation Contributions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gao, X.; Sun, M.; Zhao, Q.; Wu, P.; Zhao, X.; Pan, W.; Wang, Y. Actual ET modelling based on the Budyko framework and the sustainability of vegetation water use in the loess plateau. Sci. Total Environ. 2017, 579, 1550–1559. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.-Y.; Chiu, C.-C.; Chen, C.-J.; Lin, C.-Y.; Shiah, F.-K. Assessing future availability of water resources in Taiwan based on the Budyko framework. Ecol. Indic. 2023, 146, 109808. [Google Scholar] [CrossRef]
- Van der Velde, Y.; Vercauteren, N.; Jaramillo, F.; Dekker, S.C.; Destouni, G.; Lyon, S.W. Exploring hydroclimatic change disparity via the Budyko framework. Hydrol. Process. 2014, 28, 4110–4118. [Google Scholar] [CrossRef]
- Kuczera, G. Improved parameter inference in catchment models: 1. Evaluating parameter uncertainty. Water Resour. Res. 1983, 19, 1151–1162. [Google Scholar] [CrossRef]
- Schultz, G.A. Remote sensing in hydrology. J. Hydrol. 1988, 100, 239–265. [Google Scholar] [CrossRef]
- Kite, G.W.; Pietroniro, A. Remote sensing applications in hydrological modelling. Hydrol. Sci. J. 1996, 41, 563–591. [Google Scholar] [CrossRef]
- Schmugge, T.J.; Kustas, W.P.; Ritchie, J.C.; Jackson, T.J.; Rango, A. Remote sensing in hydrology. Adv. Water Resour. 2002, 25, 1367–1385. [Google Scholar] [CrossRef]
- Capolongo, D.; Refice, A.; Bocchiola, D.; D’addabbo, A.; Vouvalidis, K.; Soncini, A.; Zingaro, M.; Bovenga, F.; Stamatopoulos, L. Coupling multitemporal remote sensing with geomorphology and hydrological modeling for post flood recovery in the Strymonas dammed river basin (Greece). Sci. Total Environ. 2019, 651, 1958–1968. [Google Scholar] [CrossRef]
- Han, P.; Long, D.; Han, Z.; Du, M.; Dai, L.; Hao, X. Improved understanding of snowmelt runoff from the headwaters of China’s Yangtze River using remotely sensed snow products and hydrological modeling. Remote Sens. Environ. 2019, 224, 44–59. [Google Scholar] [CrossRef]
- Meresa, H. Modelling of river flow in ungauged catchment using remote sensing data: Application of the empirical (SCS-CN), artificial neural network (ANN) and hydrological model (HEC-HMS). Model. Earth Syst. Environ. 2019, 5, 257–273. [Google Scholar] [CrossRef]
- Huang, Q.; Qin, G.; Zhang, Y.; Tang, Q.; Liu, C.; Xia, J.; Chiew, F.H.S.; Post, D. Using remote sensing data-based hydrological model calibrations for predicting runoff in ungauged or poorly gauged catchments. Water Resour. Res. 2020, 56, e2020WR028205. [Google Scholar] [CrossRef]
- Xiong, J.; Abhishek Xu, L.; Chandanpurkar, H.A.; Famiglietti, J.S.; Zhang, C.; Ghiggi, G.; Guo, S.; Pan, Y.; Vishwakarma, B.D. ET-WB: Water-balance-based estimations of terrestrial evaporation over global land and major global basins. Earth Syst. Sci. Data 2023, 15, 4571–4597. [Google Scholar] [CrossRef]
- Qiu, H.; Niu, J.; Phanikumar, M.S. Quantifying the space--time variability of water balance components in an agricultural basin using a process-based hydrologic model and the Budyko framework. Sci. Total Environ. 2019, 676, 176–189. [Google Scholar] [CrossRef] [PubMed]
- Rango, A.; Shalaby, A.I. Operational applications of remote sensing in hydrology: Success, prospects and problems. Hydrol. Sci. J. 1998, 43, 947–968. [Google Scholar] [CrossRef]
- Abera, W.; Tamene, L.; Abegaz, A.; Solomon, D. Understanding climate and land surface changes impact on water resources using Budyko framework and remote sensing data in Ethiopia. J. Arid. Environ. 2019, 167, 56–64. [Google Scholar] [CrossRef]
- Greve, P.; Burek, P.; Wada, Y. Using the Budyko framework for calibrating a global hydrological model. Water Resour. Res. 2020, 56, e2019WR026280. [Google Scholar] [CrossRef]
- Li, D.; Pan, M.; Cong, Z.; Zhang, L.; Wood, E. Vegetation control on water and energy balance within the Budyko framework. Water Resour. Res. 2013, 49, 969–976. [Google Scholar] [CrossRef]
- Ning, T.; Li, Z.; Liu, W. Vegetation dynamics and climate seasonality jointly control the interannual catchment water balance in the Loess Plateau under the Budyko framework. Hydrol. Earth Syst. Sci. 2017, 21, 1515–1526. [Google Scholar] [CrossRef]
- Yu, Y.; Zhou, Y.; Xiao, W.; Ruan, B.; Lu, F.; Hou, B.; Wang, Y.; Cui, H. Impacts of climate and vegetation on actual evapotranspiration in typical arid mountainous regions using a Budyko-based framework. Hydrol. Res. 2021, 52, 212–228. [Google Scholar] [CrossRef]
- Zhang, L.; Potter, N.; Hickel, K.; Zhang, Y.; Shao, Q. Water balance modeling over variable time scales based on the Budyko framework--Model development and testing. J. Hydrol. 2008, 360, 117–131. [Google Scholar] [CrossRef]
- Donohue, R.J.; Roderick, M.L.; McVicar, T.R. Roots, storms and soil pores: Incorporating key ecohydrological processes into Budyko’s hydrological model. J. Hydrol. 2012, 436, 35–50. [Google Scholar] [CrossRef]
- Roderick, M.L.; Farquhar, G.D. A simple framework for relating variations in runoff to variations in climatic conditions and catchment properties. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Dakhlaoui, H.; Ruelland, D.; Tramblay, Y.; Bargaoui, Z. Evaluating the robustness of conceptual rainfall-runoff models under climate variability in northern Tunisia. J. Hydrol. 2017, 550, 201–217. [Google Scholar] [CrossRef]
- Xu, X.; Liu, W.; Scanlon, B.R.; Zhang, L.; Pan, M. Local and global factors controlling water-energy balances within the Budyko framework. Geophys. Res. Lett. 2013, 40, 6123–6129. [Google Scholar] [CrossRef]
- Booty, W.; Lam, D.; Bowen, G.; Resler, O.; Leon, L. Modelling changes in stream water quality due to climate change in a southern Ontario watershed. Can. Water Resour. J. 2005, 30, 211–226. [Google Scholar] [CrossRef]
- Darbandsari, P.; Coulibaly, P. Inter-comparison of lumped hydrological models in data-scarce watersheds using different precipitation forcing data sets: Case study of Northern Ontario, Canada. J. Hydrol. Reg. Stud. 2020, 31, 100730. [Google Scholar] [CrossRef]
- Grillakis, M.G.; Koutroulis, A.G.; Tsanis, I.K. Climate change impact on the hydrology of Spencer Creek watershed in Southern Ontario, Canada. J. Hydrol. 2011, 409, 1–19. [Google Scholar] [CrossRef]
- Jyrkama, M.I.; Sykes, J.F. The impact of climate change on spatially varying groundwater recharge in the grand river watershed (Ontario). J. Hydrol. 2007, 338, 237–250. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, W.; Leon, L.; Wong, I.; McCrimmon, C.; Dove, A.; Fong, P. Hydrologic modeling and evaluation of Best Management Practice scenarios for the Grand River watershed in Southern Ontario. J. Great Lakes Res. 2016, 42, 1289–1301. [Google Scholar] [CrossRef]
- Rahman, M.; Bolisetti, T.; Balachandar, R. Hydrologic modelling to assess the climate change impacts in a Southern Ontario watershed. Can. J. Civ. Eng. 2012, 39, 91–103. [Google Scholar] [CrossRef]
- Fu, B.P. On the calculation of the evaporation from land surface. Sci. Atmos. Sin 1981, 5, 23–31. [Google Scholar]
- Bertola, M.; Viglione, A.; Vorogushyn, S.; Lun, D.; Merz, B.; Blschl, G. Do small and large floods have the same drivers of change? A regional attribution analysis in Europe. Hydrol. Earth Syst. Sci. 2021, 25, 1347–1364. [Google Scholar] [CrossRef]
- Hu, J.; Ma, J.; Nie, C.; Xue, L.; Zhang, Y.; Ni, F.; Deng, Y.; Liu, J.; Zhou, D.; Li, L.; et al. Attribution Analysis of Runoff change in Min-tuo River Basin based on SWAT model simulations, china. Sci. Rep. 2020, 10, 2900. [Google Scholar] [CrossRef] [PubMed]
- Philip, S.Y.; Kew, S.F.; Van Oldenborgh, G.J.; Anslow, F.S.; Seneviratne, S.I.; Vautard, R.; Coumou, D.; Ebi, K.L.; Arrighi, J.; Singh, R.; et al. Rapid attribution analysis of the extraordinary heatwave on the Pacific Coast of the US and Canada June 2021. Earth Syst. Dyn. 2021, 13, 1689–2022. [Google Scholar] [CrossRef]
- Xu, J.; Gao, X.; Yang, Z.; Xu, T. Trend and attribution analysis of runoff changes in the Weihe River basin in the last 50 years. Water 2021, 14, 47. [Google Scholar] [CrossRef]
- Zhou, S.; Yu, B.; Huang, Y.; Wang, G. The complementary relationship and generation of the Budyko functions. Geophys. Res. Lett. 2015, 42, 1781–1790. [Google Scholar] [CrossRef]
- Zhou, S.; Yu, B.; Zhang, L.; Huang, Y.; Pan, M.; Wang, G. A new method to partition climate and catchment effect on the mean annual runoff based on the B udyko complementary relationship. Water Resour. Res. 2016, 52, 7163–7177. [Google Scholar] [CrossRef]
- Yang, H.; Krantzberg, G.; Dong, X.; Hu, X. Environmental outcomes of climate migration and local governance: An empirical study of Ontario. Int. J. Clim. Change Strateg. Manag. 2023; ahead-of-print. [Google Scholar]
- Koppa, A.; Alam, S.; Miralles, D.G.; Gebremichael, M. Budyko-based long-term water and energy balance closure in global watersheds from earth observations. Water Resour. Res. 2021, 57, e2020WR028658. [Google Scholar] [CrossRef]
- Xu, X.; Li, X.; He, C.; Tia, W.; Tian, J. Development of a simple Budyko-based framework for the simulation and attribution of ET variability in dry regions. J. Hydrol. 2022, 610, 127955. [Google Scholar] [CrossRef]
- Acker, J.G.; Leptoukh, G. Online Analysis Enhances Use of NASA Earth Science Data. Trans. Am. Geophys. Union 2017, 88, 14–17. [Google Scholar] [CrossRef]
- Zhou, P.; Li, C.; Li, Z.; Cai, Y. Assessing uncertainty propagation in hybrid models for daily streamflow simulation based on arbitrary polynomial chaos expansion. Adv. Water Resour. 2022, 160, 104110. [Google Scholar] [CrossRef]
- Aminikhanghahi, S.; Cook, D.J. A survey of methods for time series change point detection. Knowl. Inf. Syst. 2017, 51, 339–367. [Google Scholar] [CrossRef] [PubMed]
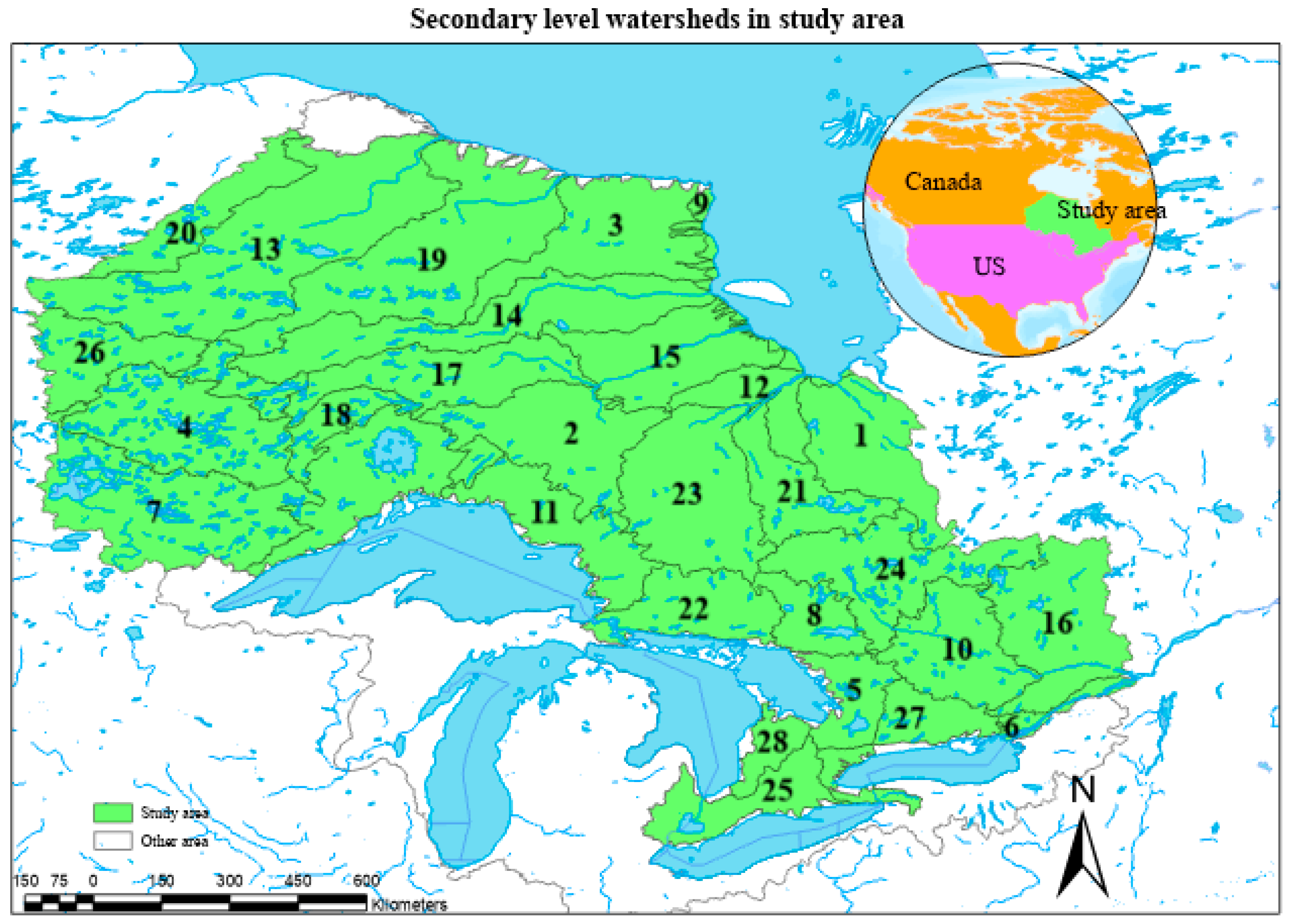

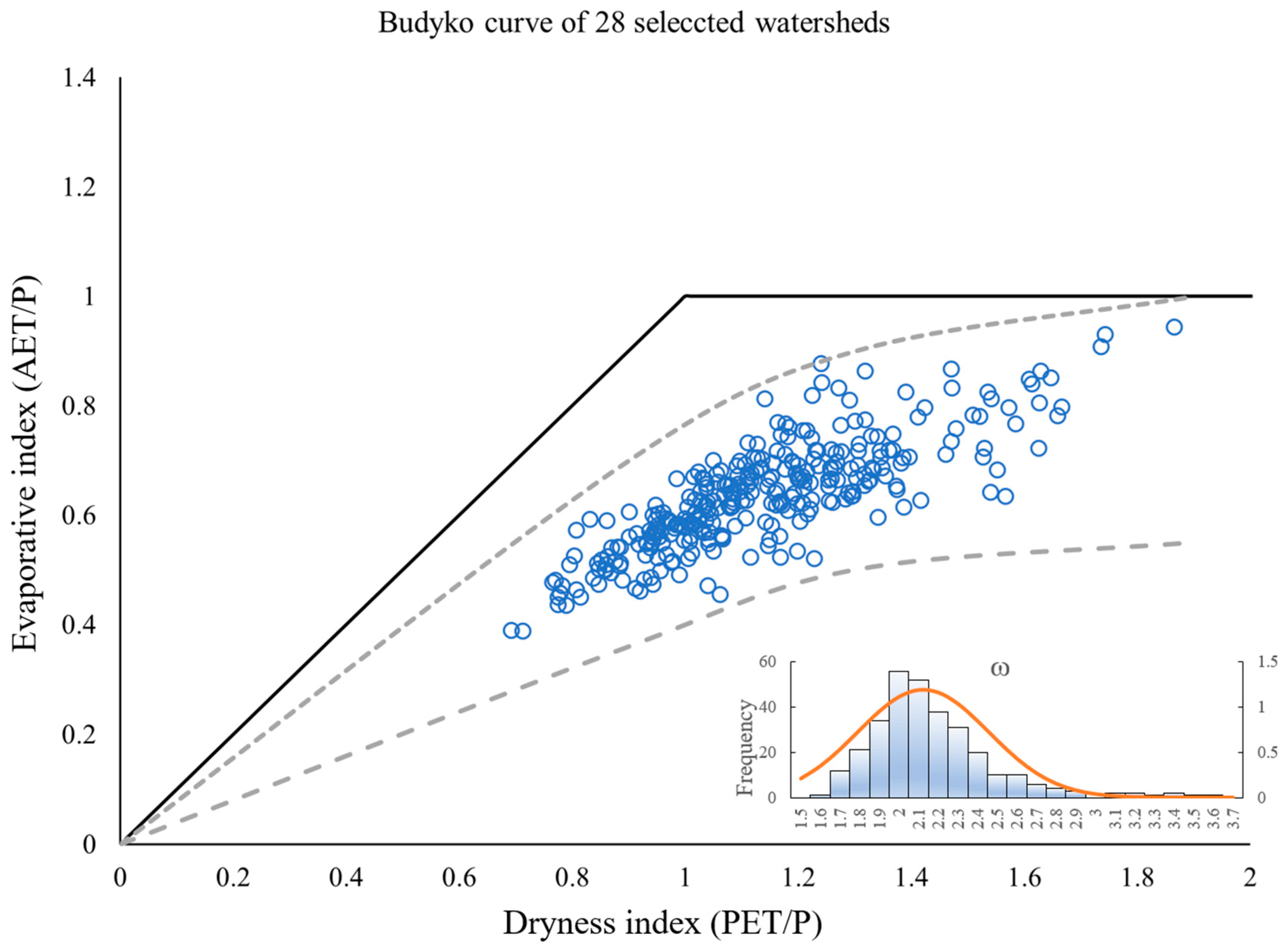
| Watershed Number | Watershed Name | Watershed Area (km2) | Latitude (Degree) | Longitude (Degree) | Slope | Elevation (m) |
|---|---|---|---|---|---|---|
| 1 | Harricanaw River-Coast | 42,700 | 49.84 | −79.12 | 0.25 | 214.3 |
| 2 | Kenogami River | 48,400 | 50.12 | −85.29 | 0.24 | 255.3 |
| 3 | Ekwan River-Coast | 44,500 | 54.04 | −84.29 | 0.14 | 86.0 |
| 4 | English River and Nelson River | 64,600 | 50.76 | −92.08 | 0.37 | 399.8 |
| 5 | Eastern Georgian Bay | 19,800 | 44.96 | −79.49 | 0.54 | 309.3 |
| 6 | Upper St.Lawrence River | 7400 | 44.76 | −75.42 | 0.24 | 80.6 |
| 7 | Winnipeg River | 74,300 | 48.72 | −93.04 | 0.34 | 397.5 |
| 8 | Wanipitai River and French River | 19,600 | 46.55 | −80.26 | 0.57 | 306.7 |
| 9 | Western James Bay Shoreline | 7700 | 53.16 | −81.84 | 0.05 | 10.2 |
| 10 | Central Ottawa River | 40,600 | 45.92 | −77.42 | 0.88 | 316.1 |
| 11 | Northeastern Lake Superior | 36,100 | 48.98 | −86.02 | 0.85 | 385.6 |
| 12 | Moose River | 18,100 | 50.77 | −81.33 | 0.11 | 104.9 |
| 13 | Severn River | 100,000 | 53.9 | −91.04 | 0.13 | 218.4 |
| 14 | Attawapiskat River-Coast | 57,200 | 52.38 | −86.75 | 0.11 | 189.3 |
| 15 | Lower Albany River-Coast | 40,200 | 51.72 | −83.17 | 0.07 | 80.4 |
| 16 | Lower Ottawa River | 55,000 | 46.45 | −75.43 | 0.98 | 295.1 |
| 17 | Upper Albany River | 39,200 | 51.34 | −87.48 | 0.16 | 248.6 |
| 18 | Northwestern Lake Superior | 14,000 | 49.85 | −89.34 | 0.55 | 393.6 |
| 19 | Winisk River-Coast | 4400 | 53.77 | −87.84 | 0.11 | 151.5 |
| 20 | Hayes River | 76,300 | 54.53 | −92.23 | 0.16 | 202.0 |
| 21 | Abitibi River | 22,900 | 49.07 | −80.54 | 0.29 | 258.2 |
| 22 | Northern Lake Huron | 32,800 | 46.74 | −82.6 | 0.72 | 374.6 |
| 23 | Missinaibi River and Mattagami River | 60,300 | 48.98 | −82.6 | 0.29 | 286.7 |
| 24 | Upper Ottawa River | 50,600 | 47.5 | −78.73 | 0.62 | 336.3 |
| 25 | Northern Lake Erie | 28,700 | 42.94 | −81.7 | 0.2 | 257.3 |
| 26 | Eastern Lake Winnipeg | 27,000 | 51.72 | −94.32 | 0.21 | 353.6 |
| 27 | Northern Lake Ontario and Niagara River | 25,500 | 44.21 | −78.38 | 0.54 | 266.8 |
| 28 | Eastern Lake Huron | 10,800 | 43.97 | −81.11 | 0.33 | 278.9 |
| Data | Length | Temporal Resolution | Spatial Resolution |
|---|---|---|---|
| Precipitation | 2010 to 2020 | daily | 10 km by 10 km |
| AET | 2010 to 2020 | annually | 500 m by 500 m |
| PET | 2010 to 2020 | annually | 500 m by 500 m |
| NDVI | 2010 to 2020 | monthly | 1000 m by 1000 m |
| Model | Calibration | Validation | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NSE | RMSE (mm) | MAE (mm) | MBE (mm) | MAPE (%) | d | NSE | RMSE (mm) | MAE (mm) | MBE (mm) | MAPE (%) | d | |
| 1 | 0.75 | 46.4 | 37.3 | 9.51 | 8.06 | 0.93 | 0.73 | 56.8 | 45.3 | −1.16 | 8.33 | 0.91 |
| 2 | 0.90 | 32.4 | 25.2 | 5.07 | 5.23 | 0.97 | 0.65 | 66.7 | 54.4 | 10.50 | 10.80 | 0.90 |
| 3 | 0.79 | 43.2 | 35.2 | 10.00 | 7.66 | 0.95 | 0.74 | 55.5 | 42.7 | 9.27 | 7.89 | 0.94 |
| 4 | 0.76 | 45.9 | 36.8 | 9.40 | 7.96 | 0.93 | 0.74 | 55.8 | 44.8 | 0.77 | 8.23 | 0.91 |
| ID | Change from 2010 Through 2015 to 2016 to 2020 | ||||
|---|---|---|---|---|---|
| ΔAET (mm) | ΔPET (mm) | ΔP (mm) | ΔM | ΔS | |
| 1 | −6.63 | −60.04 | 4.83 | 0.01 | −0.05 |
| 2 | 1.78 | −41.44 | −58.36 | 0.01 | −0.16 |
| 3 | −15.21 | −52.02 | −21.14 | 0.01 | 0.49 |
| 4 | 0.16 | −33.22 | −31.48 | −0.02 | 0.47 |
| 5 | −8.02 | −58.74 | −27.39 | −0.01 | 0.13 |
| 6 | −10.43 | −49.26 | −2.36 | −0.01 | 0.03 |
| 7 | −13.03 | −30.87 | −13.11 | 0 | 0.19 |
| 8 | −4.39 | −66.37 | −34.65 | −0.01 | −0.14 |
| 9 | −15.54 | −44.41 | −29.76 | 0 | 0.39 |
| 10 | −4.56 | −55.44 | 49.29 | 0 | 0.06 |
| 11 | −7.8 | −52.58 | 56.72 | 0 | −0.06 |
| 12 | −4.81 | −58.21 | −33.17 | 0.02 | −0.1 |
| 13 | −4.8 | −25.73 | 23.98 | 0.01 | 0.36 |
| 14 | −0.6 | −57.9 | 9.01 | 0.01 | 0.16 |
| 15 | −6.54 | −56.15 | −85.88 | 0.02 | −0.07 |
| 16 | −6.07 | −50.98 | 86.42 | 0.01 | −0.25 |
| 17 | 4.92 | −54.58 | −45.91 | 0 | −0.12 |
| 18 | −4.4 | −50.02 | −10.46 | −0.01 | −0.3 |
| 19 | −5.98 | −55.1 | 50.41 | 0.01 | 0.46 |
| 20 | −7.23 | −18.21 | 20.57 | 0.01 | 0.27 |
| 21 | −2.67 | −53.38 | 13.74 | 0.02 | −0.15 |
| 22 | −8.05 | −59.25 | 78.74 | −0.01 | −0.37 |
| 23 | −2.88 | −43.83 | 42.85 | 0.01 | −0.22 |
| 24 | −3.82 | −58.9 | 1.6 | 0.01 | −0.23 |
| 25 | 9.34 | −44.89 | −43.01 | 0.01 | 0.02 |
| 26 | −8.8 | −24.45 | −57.53 | −0.01 | 0.32 |
| 27 | −5.52 | −52.53 | 19.5 | 0 | 0.09 |
| 28 | −3.38 | −52.69 | −15.06 | 0.01 | 0.01 |
| ID | C P (mm) | C PET (mm) | C ω (mm) | C M_Model 2 (mm) | C S_Model 2 (mm) | C M_Model 4 (mm) | C S_Model 4 (mm) |
|---|---|---|---|---|---|---|---|
| 1 | 1.29 | −17.8 | 2.49 | 2.92 | −0.43 | 2.94 | −0.46 |
| 2 | −18.61 | −10.92 | 25.56 | * | * | * | * |
| 3 | −6.55 | −17.49 | 18.15 | 3.83 | 14.32 | 5.06 | 13.09 |
| 4 | −11.88 | −6.91 | 18.99 | * | * | * | * |
| 5 | −9.58 | −17.16 | 19.27 | 52.4 | −33.12 | 84.52 | −65.25 |
| 6 | −0.79 | −15.37 | 7.14 | 9.45 | −2.3 | 9.81 | −2.66 |
| 7 | −5.95 | −6.16 | −10.9 | 1.99 | −12.89 | 1.65 | −12.55 |
| 8 | −10.91 | −19.04 | 12.75 | 8.86 | 3.89 | 8.17 | 4.58 |
| 9 | −11.13 | −14.95 | 14.96 | 2.88 | 12.08 | 3.76 | 11.21 |
| 10 | 16.84 | −15.63 | −4.54 | 2.64 | −7.18 | 1.65 | −6.19 |
| 11 | 14.92 | −16.31 | −13.93 | −34.87 | 20.94 | −62.06 | 48.13 |
| 12 | −10.01 | −16.03 | 12.09 | 16.76 | −4.68 | 16.98 | −4.89 |
| 13 | 9.97 | −5.33 | −13.58 | −3.54 | −10.04 | −3.84 | −9.74 |
| 14 | 3.07 | −13.55 | 4.07 | 2.49 | 1.57 | 2.56 | 1.5 |
| 15 | −26.28 | −15.48 | 31.82 | 37.72 | −5.9 | 36.93 | −5.11 |
| 16 | 24.21 | −16.02 | −14.67 | 41.13 | −55.8 | 19.56 | −34.23 |
| 17 | −16.44 | −12.44 | 24.55 | 4.87 | 19.68 | 4.7 | 19.85 |
| 18 | −4.17 | −11.38 | 8.93 | 3.12 | 5.81 | 2.84 | 6.09 |
| 19 | 17.85 | −13.57 | −7.7 | −2.74 | −4.96 | −3.1 | −4.59 |
| 20 | 10.56 | −3.49 | −12.68 | −5.62 | −7.06 | −5.92 | −6.76 |
| 21 | 4.64 | −14.62 | −7.68 | −11.41 | 3.73 | −12.39 | 4.71 |
| 22 | 23.25 | −17.64 | −34.02 | −10.28 | −23.74 | −8.45 | −25.56 |
| 23 | 13.99 | −11.97 | −28.28 | 35.93 | −64.21 | 22.27 | −50.55 |
| 24 | 0.46 | −17.29 | 8.99 | −67.37 | 76.35 | −20.43 | 29.42 |
| 25 | −17.23 | −11.08 | 19.77 | 17.62 | 2.15 | 17.62 | 2.16 |
| 26 | −19.84 | −4.61 | 15.9 | −17.58 | 33.48 | −14.79 | 30.69 |
| 27 | 7.6 | −14.07 | 0.19 | −0.61 | 0.8 | −0.31 | 0.5 |
| 28 | −5.59 | −15.77 | −2.02 | −1.96 | −0.06 | −1.95 | −0.07 |
| ID | RC P (%) | RC PET (%) | RC M_Model 2 (%) | RC S_Model 2 (%) | RC M_Model 4 (%) | RC S_Model 4 (%) |
|---|---|---|---|---|---|---|
| 1 | −0.2 | 2.69 | −0.44 | 0.07 | −0.44 | 0.07 |
| 2 | −10.47 | −6.15 | * | * | * | * |
| 3 | 0.43 | 1.15 | −0.33 | −0.86 | −0.33 | −0.86 |
| 4 | −72.86 | −42.36 | * | * | * | * |
| 5 | 1.19 | 2.14 | −10.54 | 8.13 | −10.54 | 8.13 |
| 6 | 0.08 | 1.47 | −0.94 | 0.26 | −0.94 | 0.26 |
| 7 | 0.46 | 0.47 | −0.13 | 0.96 | −0.13 | 0.96 |
| 8 | 2.48 | 4.33 | −1.86 | −1.04 | −1.86 | −1.04 |
| 9 | 0.72 | 0.96 | −0.24 | −0.72 | −0.24 | −0.72 |
| 10 | −3.69 | 3.42 | −0.36 | 1.36 | −0.36 | 1.36 |
| 11 | −1.91 | 2.09 | 7.95 | −6.17 | 7.95 | −6.17 |
| 12 | 2.08 | 3.33 | −3.53 | 1.02 | −3.53 | 1.02 |
| 13 | −2.08 | 1.11 | 0.8 | 2.03 | 0.8 | 2.03 |
| 14 | −5.14 | 22.71 | −4.29 | −2.52 | −4.29 | −2.52 |
| 15 | 4.02 | 2.37 | −5.65 | 0.78 | −5.65 | 0.78 |
| 16 | −3.99 | 2.64 | −3.22 | 5.64 | −3.22 | 5.64 |
| 17 | −3.34 | −2.53 | 0.96 | 4.03 | 0.96 | 4.03 |
| 18 | 0.95 | 2.59 | −0.65 | −1.39 | −0.65 | −1.39 |
| 19 | −2.98 | 2.27 | 0.52 | 0.77 | 0.52 | 0.77 |
| 20 | −1.46 | 0.48 | 0.82 | 0.94 | 0.82 | 0.94 |
| 21 | −1.74 | 5.47 | 4.64 | −1.76 | 4.64 | −1.76 |
| 22 | −2.89 | 2.19 | 1.05 | 3.17 | 1.05 | 3.17 |
| 23 | −4.86 | 4.16 | −7.74 | 17.56 | −7.74 | 17.56 |
| 24 | −0.12 | 4.53 | 5.35 | −7.71 | 5.35 | −7.71 |
| 25 | −1.84 | −1.19 | 1.89 | 0.23 | 1.89 | 0.23 |
| 26 | 2.25 | 0.52 | 1.68 | −3.49 | 1.68 | −3.49 |
| 27 | −1.38 | 2.55 | 0.06 | −0.09 | 0.06 | −0.09 |
| 28 | 1.65 | 4.67 | 0.58 | 0.02 | 0.58 | 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Z.; Li, Z.; Baetz, B. Evapotranspiration Estimation with the Budyko Framework for Canadian Watersheds. Hydrology 2024, 11, 191. https://doi.org/10.3390/hydrology11110191
Yan Z, Li Z, Baetz B. Evapotranspiration Estimation with the Budyko Framework for Canadian Watersheds. Hydrology. 2024; 11(11):191. https://doi.org/10.3390/hydrology11110191
Chicago/Turabian StyleYan, Zehao, Zhong Li, and Brian Baetz. 2024. "Evapotranspiration Estimation with the Budyko Framework for Canadian Watersheds" Hydrology 11, no. 11: 191. https://doi.org/10.3390/hydrology11110191
APA StyleYan, Z., Li, Z., & Baetz, B. (2024). Evapotranspiration Estimation with the Budyko Framework for Canadian Watersheds. Hydrology, 11(11), 191. https://doi.org/10.3390/hydrology11110191







