Investigating Uncertainty of Future Predictions of Temperature and Precipitation in The Kerman Plain under Climate Change Impacts
Abstract
:1. Introduction
2. Materials and Methods
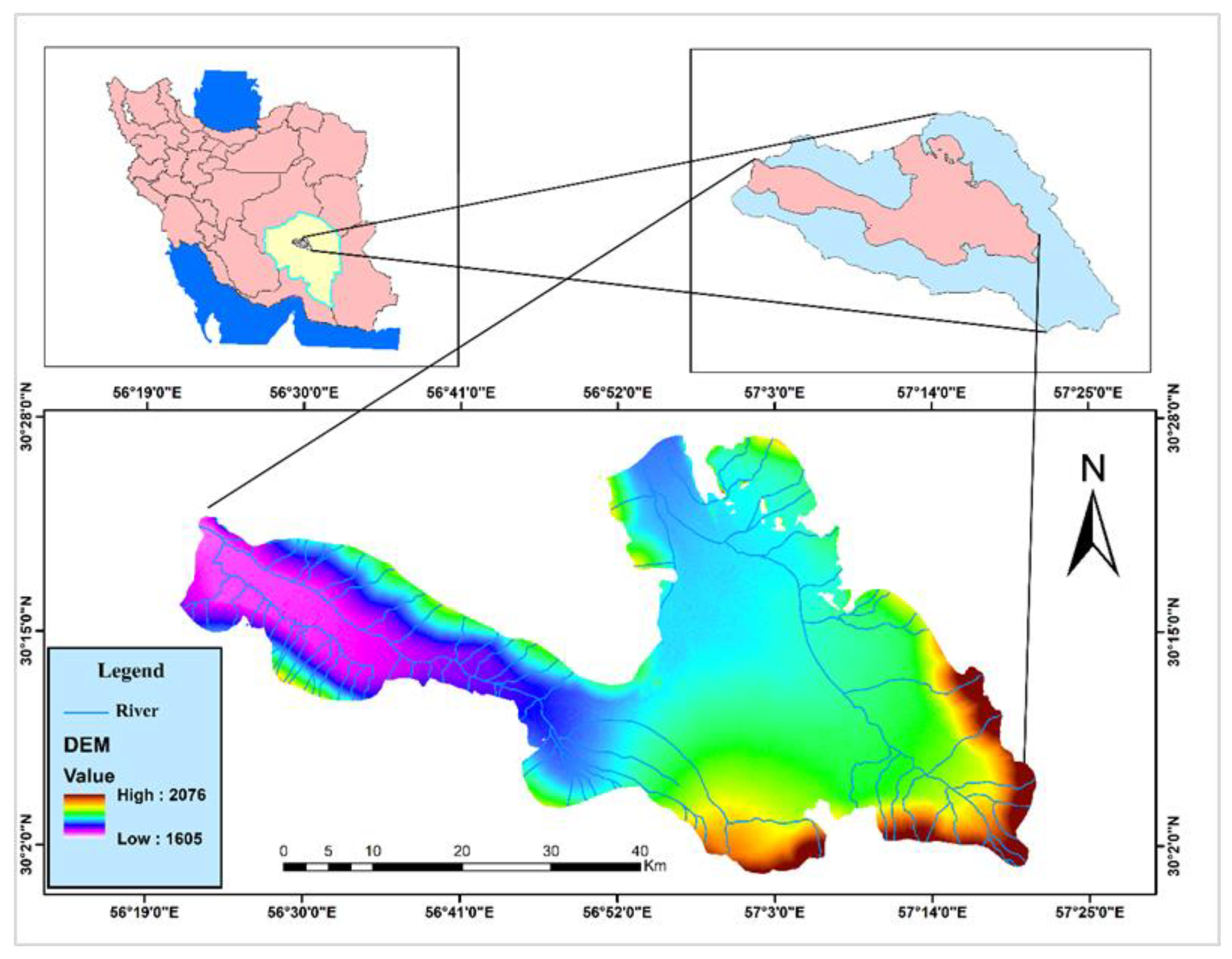
2.1. Study Area
2.2. Global Climate Model
Downscaling
2.3. Trend Analysis Method
2.4. Sequential Mann–Kendall Test
2.5. Uncertainty Analysis
3. Results
3.1. Annual Changes in Precipitation
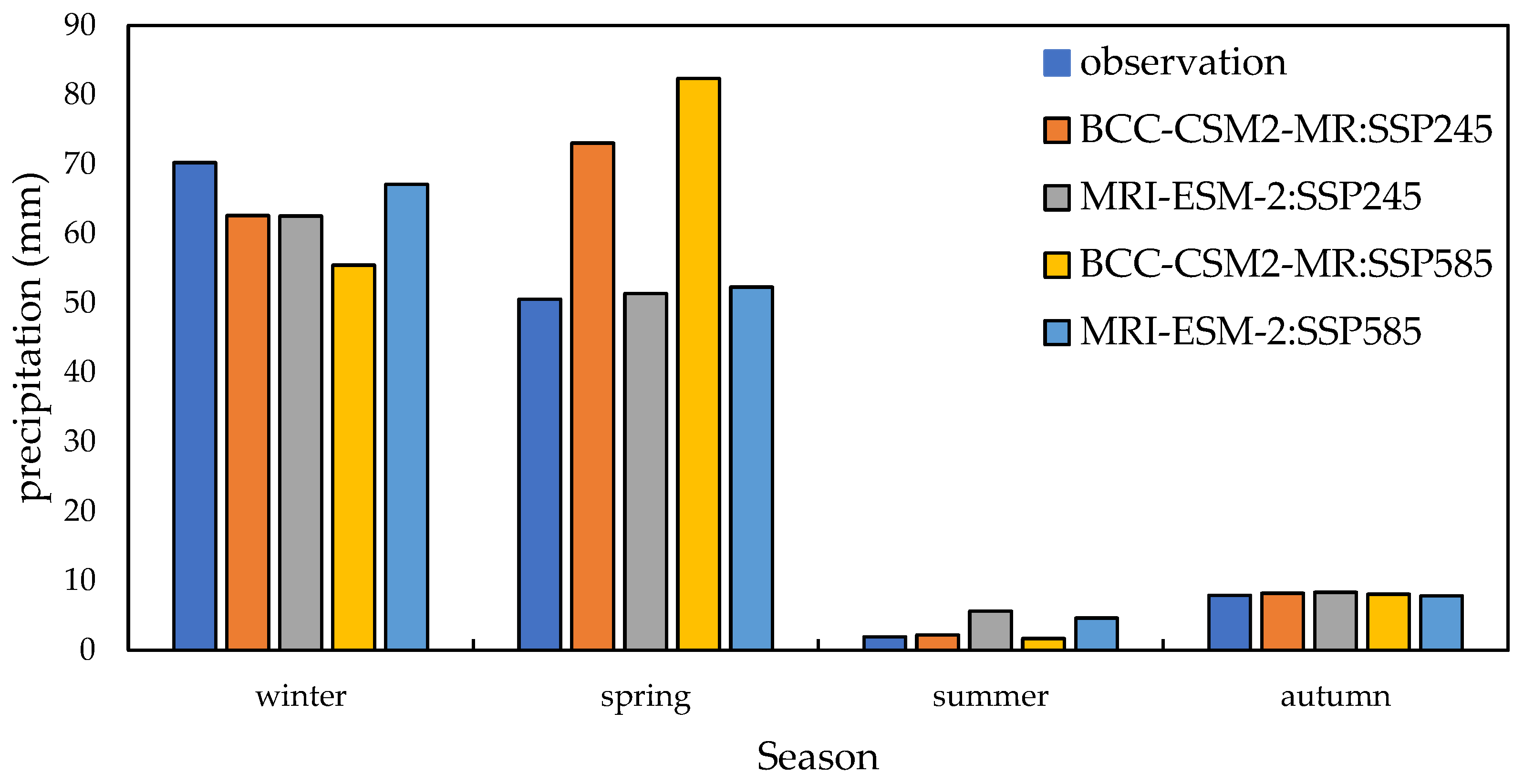
3.2. Seasonal Changes in Precipitation
3.3. Annual Changes in Temperature
3.4. Trends in Annual Precipitation Changes
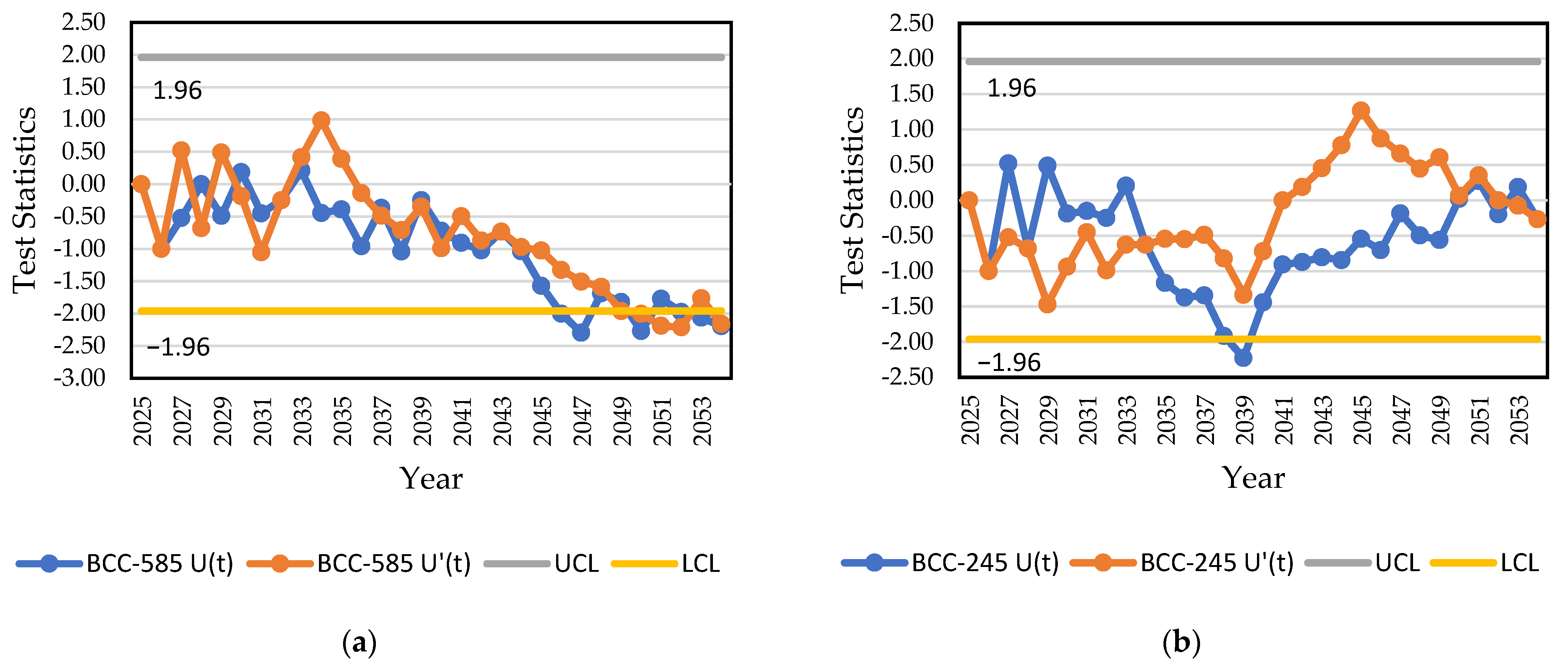
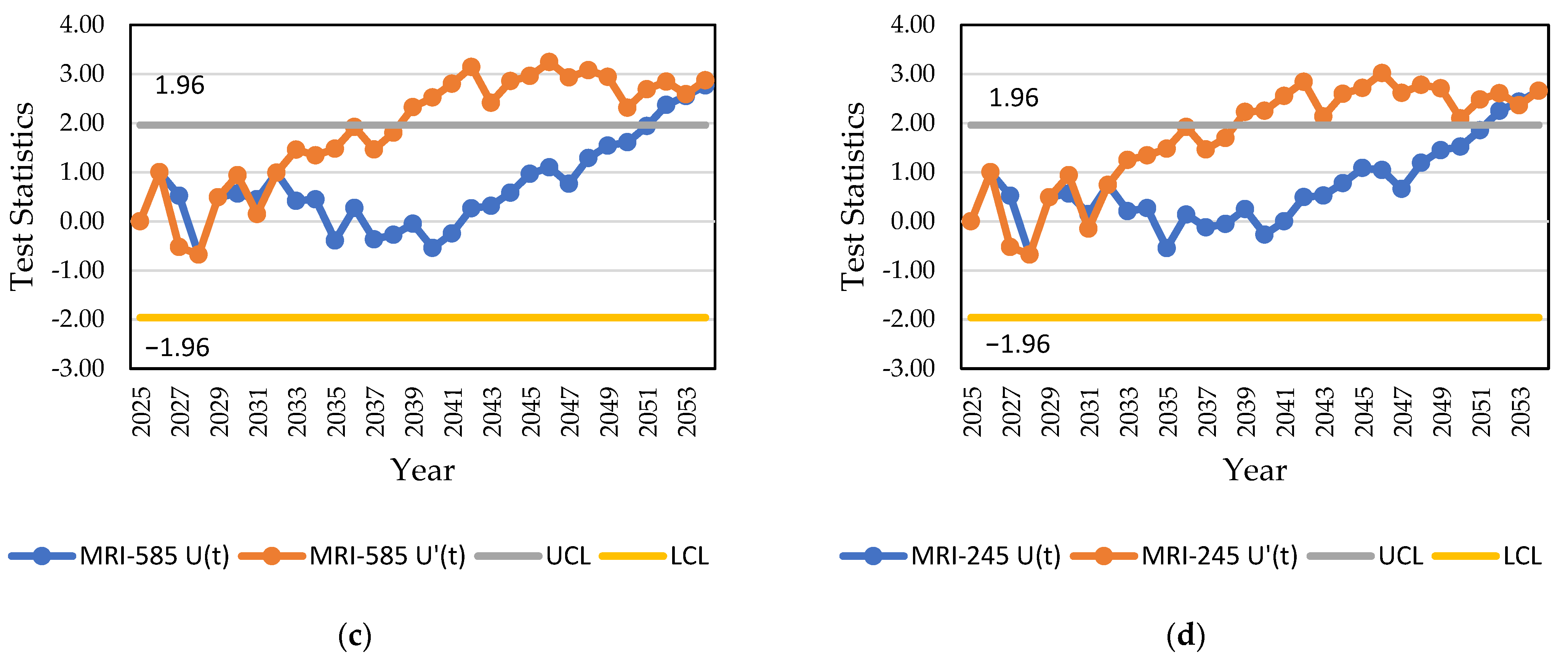
3.5. Assessment of the Uncertainty of Temperature and Precipitation Predictions
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Goyal, R.; Gaur, M.K. The Implications of Climate Change on Water Resources of Rajasthan, in Hydro-Meteorological Extremes and Disasters; Springer: Berlin/Heidelberg, Germany, 2022; pp. 265–278. [Google Scholar] [CrossRef]
- Stocker, T. Climate Change 2013: The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Wang, B.; Kim, H.-J.; Kikuchi, K.; Kitoh, A. Diagnostic metrics for evaluation of annual and diurnal cycles. Clim. Dyn. 2010, 37, 941–955. [Google Scholar] [CrossRef]
- Pachauri, R.K.; Allen, M.R.; Barros, V.R.; Broome, J.; Cramer, W.; Christ, R.; Church, J.A.; Clarke, L.; Dahe, Q.; Dasgupta, P.; et al. Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge UK; New York, NY, USA; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- Zahabiyoun, B.; Goodarzi, M.R.; Bavani, A.R.M.; Azamathulla, H.M. Assessment of Climate Change Impact on the Gharesou River Basin Using SWAT Hydrological Model. CLEAN Soil Air Water 2013, 41, 601–609. [Google Scholar] [CrossRef]
- Mitchell, T.D. Pattern Scaling: An Examination of the Accuracy of the Technique for Describing Future Climates. Clim. Chang. 2003, 60, 217–242. [Google Scholar] [CrossRef]
- Carter, T.; Hulme, M.; Lal, M. General Guidelines on the Use of Scenario Data for Climate Impact and Adaptation Assessment; Finnish Environmental Institute: Helsinki, Finland, 2007. [Google Scholar]
- Gupta, V.; Singh, V.; Jain, M.K. Assessment of precipitation extremes in India during the 21st century under SSP1-1.9 mitigation scenarios of CMIP6 GCMs. J. Hydrol. 2020, 590, 125422. [Google Scholar] [CrossRef]
- Katz, R. Techniques for estimating uncertainty in climate change scenarios and impact studies. Clim. Res. 2002, 20, 167–185. [Google Scholar] [CrossRef]
- Thai, H.; Mentré, F.; Holford, N.H.; Veyrat-Follet, C.; Comets, E. A comparison of bootstrap approaches for estimating uncertainty of parameters in linear mixed-effects models. Pharm. Stat. 2013, 12, 129–140. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Analysis of changes in meteorological variables using Mann-Kendall and Sen’s slope estimator statistical tests in Serbia. Glob. Planet. Chang. 2013, 100, 172–182. [Google Scholar] [CrossRef]
- Fatehifar, A.; Goodarzi, M.R.; Hedesh, S.S.M.; Dastjerdi, P.S. Assessing watershed hydrological response to climate change based on signature indices. J. Water Clim. Chang. 2021, 12, 2579–2593. [Google Scholar] [CrossRef]
- Singh, D.; Gupta, R.D.; Jain, S.K. Assessment of impact of climate change on water resources in a hilly river basin. Arab. J. Geosci. 2015, 8, 10625–10646. [Google Scholar] [CrossRef]
- Rahman, A.U.; Dawood, M. Spatio-statistical analysis of temperature fluctuation using Mann–Kendall and Sen’s slope approach. Clim. Dyn. 2017, 48, 783–797. [Google Scholar] [CrossRef]
- Alamgir, M.; Khan, N.; Shahid, S.; Yaseen, Z.M.; Dewan, A.; Hassan, Q.; Rasheed, B. Evaluating severity–area–frequency (SAF) of seasonal droughts in Bangladesh under climate change scenarios. Stoch. Environ. Res. Risk Assess. 2020, 34, 447–464. [Google Scholar] [CrossRef]
- Alam, S.; Ali, M.; Rahaman, A.Z.; Islam, Z. Multi-model ensemble projection of mean and extreme streamflow of Brahmaputra River Basin under the impact of climate change. J. Water Clim. Chang. 2021, 12, 2026–2044. [Google Scholar] [CrossRef]
- Goodarzi, M.R.; Abedi, M.J.; Pour, M.H. Climate change and trend analysis of precipitation and temperature: A case study of Gilan, Iran. In Current Directions in Water Scarcity Research; Elsevier: Amsterdam, The Netherlands, 2022; pp. 561–587. [Google Scholar] [CrossRef]
- Zeybekoğlu, U. Temperature series analysis of the Hirfanli Dam Basin with the Mann-Kendall and Sequential Mann-Kendall tests. Turk. J. Eng. 2023, 7, 306–313. [Google Scholar] [CrossRef]
- Goodarzi, M.R.; Mohtar, R.H.; Piryaei, R.; Fatehifar, A.; Niazkar, M. Urban WEF Nexus: An Approach for the Use of Internal Resources under Climate Change. Hydrology 2022, 9, 176. [Google Scholar] [CrossRef]
- Niazkar, M.; Goodarzi, M.R.; Fatehifar, A.; Abedi, M.J. Machine learning-based downscaling: Application of multi-gene genetic programming for downscaling daily temperature at Dogonbadan, Iran, under CMIP6 scenarios. Theor. Appl. Clim. 2023, 151, 153–168. [Google Scholar] [CrossRef]
- Zarrin, A.; Dadashi-Rodbari, A.; Salehabadi, N. Projected temperature anomalies and trends in different climate zones in Iran based on CMIP6. Iran Geophys. J. 2021, 15, 35–54. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Wilby, R.; Dawson, C.; Barrow, E. SDSM—A decision support tool for the assessment of regional climate change impacts. Environ. Model. Softw. 2002, 17, 145–157. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; Trajkovic, S.; Zounemat-Kermani, M.; Li, B.; Kisi, O. Daily streamflow prediction using optimally pruned extreme learning machine. J. Hydrol. 2019, 577, 123981. [Google Scholar] [CrossRef]
- Rajabi, A.; Sedghi, H.; Eslamian, S.S.; Musavi, H. Comparison of Lars-WG and SDSM downscaling models in Kermanshah (Iran). Ecol. Environ. Conserv. 2010, 16, 1–7. [Google Scholar]
- Semenov, M.A.; Barrow, E.M.; Lars-Wg, A. A Stochastic Weather Generator for Use in Climate Impact Studies; User Manual: Hertfordshire, UK, 2002. [Google Scholar]
- Bihrat, Ö.; Bayazit, M. The power of statistical tests for trend detection. Turk. J. Eng. Environ. Sci. 2003, 27, 247–251. [Google Scholar]
- Takeuchi, K.; Xu, Z.; Ishidiaira, H. Monitoring trend step changes in precipitation in Japanese precipitation. J. Hydrol. 2003, 279, 144–150. [Google Scholar]
- Hırca, T.; Türkkan, G.E.; Niazkar, M. Applications of innovative polygonal trend analyses to precipitation series of Eastern Black Sea Basin, Turkey. Theor. Appl. Clim. 2021, 147, 651–667. [Google Scholar] [CrossRef]
- Nashwan, M.S.; Shahid, S. Spatial distribution of unidirectional trends in climate and weather extremes in Nile river basin. Theor. Appl. Clim. 2019, 137, 1181–1199. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; Wang, X.; Nawaz, N.; Khan, N. Spatiotemporal changes in aridity of Pakistan during 1901–2016. Hydrol. Earth Syst. Sci. 2019, 23, 3081–3096. [Google Scholar] [CrossRef]
- Pohlert, T. Non-Parametric Trend Tests and Change-Point Detection. 2018. Available online: https://cran.r-project.org/web/packages/trend/trend.pdf (accessed on 15 July 2023).
- Niazkar, M.; Piraei, R.; Türkkan, G.E.; Hırca, T.; Gangi, F.; Afzali, S.H. Drought analysis using innovative trend analysis and machine learning models for Eastern Black Sea Basin. Theor. Appl. Clim. 2023, 1–20. [Google Scholar] [CrossRef]
- Lee, J.M.; Kwon, E.H.; Woo, N.C. Natural and Human-Induced Drivers of Groundwater Sustainability: A Case Study of the Mangyeong River Basin in Korea. Sustainability 2019, 11, 1486. [Google Scholar] [CrossRef]
- Gilbert, R.O. Statistical Methods for Environmental Pollution Monitoring; John Wiley & Sons: Hoboken, NJ, USA, 1987. [Google Scholar]
- Gumus, V.; Yenigun, K. Evaluation of Lower Firat Basin streamflow by trend analysis. In Proceedings of the 7th International Advances in Civil Engineering Conference, Istanbul, Turkey, 10–13 October 2006. [Google Scholar] [CrossRef]
- Gouvea, L.F.; Ara, A.; Gigante, R.L.; Spatti, R.A.; Louzada, F. Bootstrap resampling as a tool for calculating uncertainty measurement. Braz. Appl. Sci. Rev. 2020, 4, 901–912. [Google Scholar] [CrossRef]
- Lubke, G.H.; Campbell, I.; McArtor, D.; Miller, P.; Luningham, J.; van den Berg, S.M. Assessing Model Selection Uncertainty Using a Bootstrap Approach: An Update. Struct. Equ. Model. Multidiscip. J. 2016, 24, 230–245. [Google Scholar] [CrossRef]
- Nakhaei, M.; Ghazban, F.; Nakhaei, P.; Gheibi, M.; Wacławek, S.; Ahmadi, M. Successive-Station Streamflow Prediction and Precipitation Uncertainty Analysis in the Zarrineh River Basin Using a Machine Learning Technique. Water 2023, 15, 999. [Google Scholar] [CrossRef]
- Mesbahzadeh, T.; Miglietta, M.M.; Mirakbari, M.; Sardoo, F.S.; Abdolhoseini, M. Joint Modeling of Precipitation and Temperature Using Copula Theory for Current and Future Prediction under Climate Change Scenarios in Arid Lands (Case Study, Kerman Province, Iran). Adv. Meteorol. 2019, 2019, 6848049. [Google Scholar] [CrossRef]

| Source ID | Source Type | Variant Label | Institution Code | Developing Country | Publication Year | Nominal Resolution | Resolution Accuracy (Grade) |
|---|---|---|---|---|---|---|---|
| BCC-CSM2-MR | AOGCM | r1i1p1 | BCC | China | 2017 | 100 km | 1.12° × 1.12° |
| MRI-ESM-2 | AOGCM | r1i1p1 | CCCma | Japan | 2019 | 100 km | 1.12° × 1.12° |
| Station Name | Annual Average Precipitation in the Observation Period (1985 to 2014) (mm) | GCM Model | Climate Scenario | Annual Average Precipitation in the Future (2025 to 2054) (mm) | Future Precipitation Changes Compared to the Base Period (mm) | The Percentage of Future Precipitation Changes Compared to the Base Period |
|---|---|---|---|---|---|---|
| Kerman plain | 130.62 | BCC-CSM2-MR | SSP245 | 146.04 | 15.42 | 11.8 |
| SSP585 | 147.54 | 16.92 | 12.95 | |||
| MRI-ESM-2 | SSP245 | 127.86 | −2.76 | −2.11 | ||
| SSP585 | 131.86 | 1.24 | 0.94 |
| Station Name | Annual Minimum Temperature during the Observation Period (1985 to 2014) (°C) | GCM Model | Climate Scenario | Annual Minimum Temperature in the Future (2025 to 2054) (°C) | Future Temperature Changes Compared to the Base Period (°C) |
|---|---|---|---|---|---|
| Kerman plain | 7.38 | BCC-CSM2-MR | SSP245 | 8.59 | 1.21 |
| SSP585 | 8.73 | 1.35 | |||
| MRI-ESM-2 | SSP245 | 7.95 | 0.57 | ||
| SSP585 | 8.46 | 1.08 |
| Station Name | Annual Maximum Temperature during the Observation Period (1985 to 2014) (°C) | GCM Model | Climate Scenario | Annual Maximum Temperature in the Future (2025 to 2054) (°C) | Future Temperature Changes Compared to the Base Period (°C) |
|---|---|---|---|---|---|
| Kerman plain | 25.27 | BCC-CSM2-MR | SSP245 | 26.97 | 1.7 |
| SSP585 | 27.07 | 1.82 | |||
| MRI-ESM-2 | SSP245 | 25.86 | 0.62 | ||
| SSP585 | 26.48 | 1.21 |
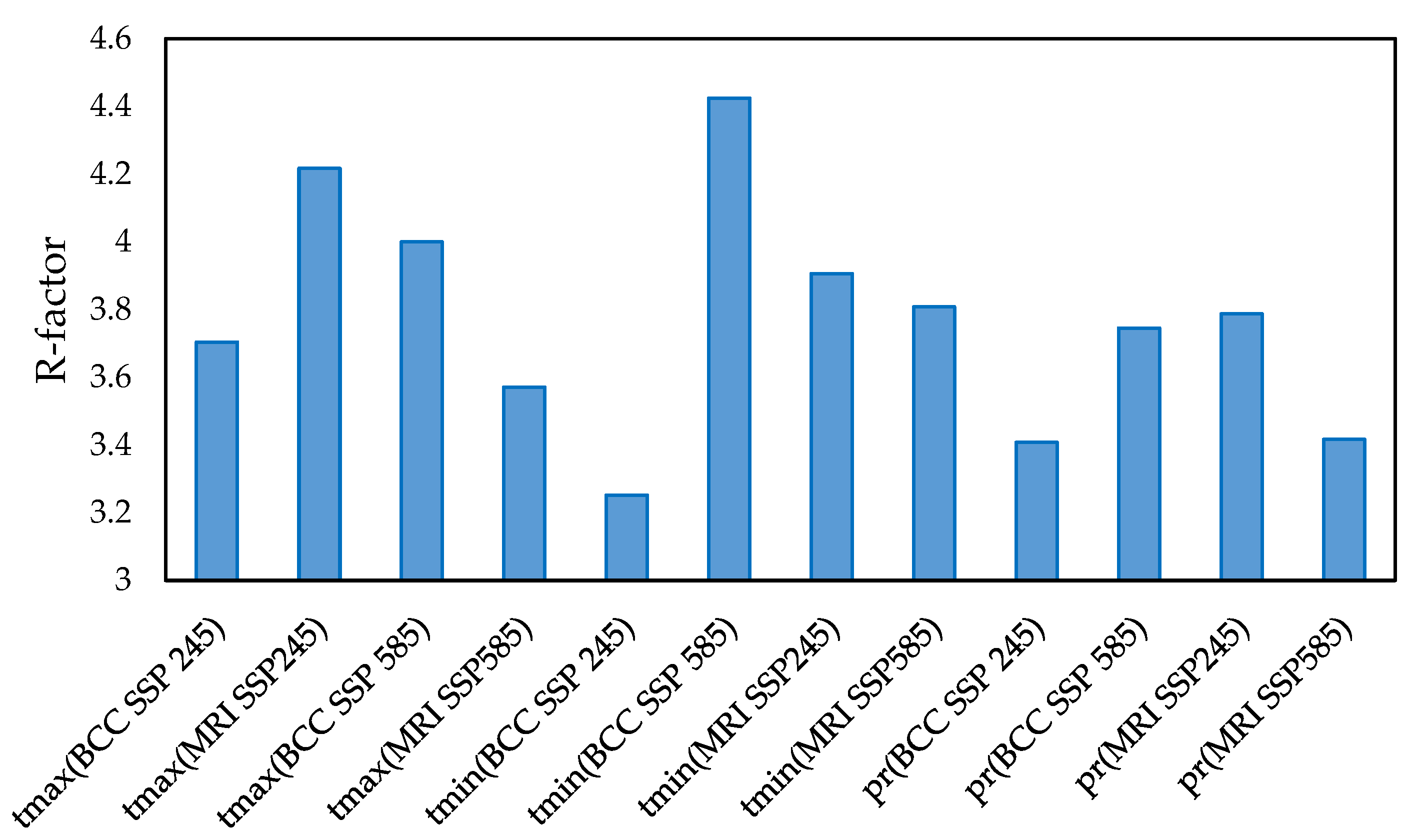
| Climatic Parameter | Mean | Median | Standard Deviation | 2.5% | 97.5% | R-Factor |
|---|---|---|---|---|---|---|
| Tmax (BCC-SSP245) | 28.78 | 28.8 | 0.162 | 28.5 | 29.1 | 3.70 |
| Tmin (BCC-SSP245) | 9.5 | 9.5 | 0.123 | 9.3 | 9.7 | 3.25 |
| Tmin (BCC-SSP585) | 9.53 | 9.5 | 0.113 | 9.3 | 9.8 | 4.42 |
| Tmax (BCC-SSP585) | 28.67 | 28.67 | 0.175 | 28.3 | 29 | 4 |
| Tmin (MRI-SSP245) | 8.47 | 8.47 | 0.128 | 8.2 | 8.7 | 3.90 |
| Tmax (MRI-SSP245) | 26.87 | 26.78 | 0.166 | 26.4 | 27.1 | 4.21 |
| Tmin (MRI-SSP585) | 8.94 | 8.94 | 0.1313 | 8.7 | 9.2 | 3.80 |
| Tmax (MRI-SSP585) | 27.32 | 27.32 | 0.168 | 27 | 27.6 | 3.57 |
| Pr (BCC-SSP245) | 132.32 | 126.8 | 18.78 | 109 | 173 | 3.41 |
| Pr (BCC-SSP585) | 144.48 | 145.2 | 10.76 | 126.7 | 167 | 3.74 |
| Pr (MRI-SSP245) | 123.989 | 118.65 | 11.09 | 105.9 | 147.9 | 3.78 |
| Pr (MRI-SSP585) | 128.91 | 123.95 | 11.97 | 110.1 | 151 | 3.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goodarzi, M.R.; Heydaripour, M.; Jamali, V.; Sabaghzadeh, M.; Niazkar, M. Investigating Uncertainty of Future Predictions of Temperature and Precipitation in The Kerman Plain under Climate Change Impacts. Hydrology 2024, 11, 2. https://doi.org/10.3390/hydrology11010002
Goodarzi MR, Heydaripour M, Jamali V, Sabaghzadeh M, Niazkar M. Investigating Uncertainty of Future Predictions of Temperature and Precipitation in The Kerman Plain under Climate Change Impacts. Hydrology. 2024; 11(1):2. https://doi.org/10.3390/hydrology11010002
Chicago/Turabian StyleGoodarzi, Mohammad Reza, Mahnaz Heydaripour, Vahid Jamali, Maryam Sabaghzadeh, and Majid Niazkar. 2024. "Investigating Uncertainty of Future Predictions of Temperature and Precipitation in The Kerman Plain under Climate Change Impacts" Hydrology 11, no. 1: 2. https://doi.org/10.3390/hydrology11010002
APA StyleGoodarzi, M. R., Heydaripour, M., Jamali, V., Sabaghzadeh, M., & Niazkar, M. (2024). Investigating Uncertainty of Future Predictions of Temperature and Precipitation in The Kerman Plain under Climate Change Impacts. Hydrology, 11(1), 2. https://doi.org/10.3390/hydrology11010002






