Evaluation of BOLAM Fine Grid Weather Forecasts with Emphasis on Hydrological Applications

Abstract

The evaluation of weather forecast accuracy is of major interest in decision making in almost every sector of the economy and in civil protection. To this, a detailed assessment of Bologna Limited-Area Model (BOLAM) seven days fine grid 3 h predictions is made for precipitation, air temperature, relative humidity, and wind speed over a large lowland agricultural area of a Mediterranean-type climate, characterized by hot summers and rainy moderate winters (plain of Arta, NW Greece). Timeseries that cover a four-year period (2016–2019) from seven agro-meteorological stations located at the study area are used to run a range of contingency and accuracy measures as well as Taylor diagrams, and the results are thoroughly discussed. The overall results showed that the model failed to comply with the precipitation regime throughout the study area, while the results were mediocre for wind speed. Considering relative humidity, the results revealed acceptable performance and good correlation between the model output and the observed values, for the early days of forecast. Only in air temperature, the forecasts exhibited very good performance. Discussion is made on the ability of the model to predict major rainfall events and to estimate water budget components as rainfall and reference evapotranspiration. The need for skilled weather forecasts from improved versions of the examined model that may incorporate post-processing techniques to improve predictions or from other forecasting services is underlined.

1. Introduction

Accurate weather forecasting by means of robust weather prediction models is critical for several industries and for civil protection agencies. Farmers rely on weather to grow crops, industries such as transportation and construction need to plan for potential disruptions, such as road closures and delays, and civil protection agencies need critical information that can help them prepare for and respond to natural disasters and other emergencies.

Numerical weather prediction tries to foresee weather at evolution of time and involves the integration of hydrodynamics to numerical methods with specified initial conditions. The verification of those weather forecast models is an essential part of any forecasting system and obviously is the subject of many studies.

In this context, López López et al. [1] asserted that the Ensemble Prediction Systems (EPS) have good reliability over study areas in Mexico for thresholds of 5–20 mm of rain accumulated in 24 h and manage to adequately represent the mean and 95 percentile of rain accumulated in 6 h for a forecast horizon of 90 h. On the other hand, Apicella et al. [2] concluded that precipitation forecasts are affected by relatively high uncertainties, due to the inherent unpredictable nature of precipitation, which is particularly evident over the Italian territory that they studied. Further, Shahrban et al. [3] found that there are only a few studies in Australia that have assessed the forecast of precipitation and, by using rain radar observations for verification, concluded that the forecast skill of the Australian Community Climate Earth-System Simulator (ACCESS) needed significant improvement for hydrological modelling applications.

Clark and Hay [4] examined 40 years of 8-day atmospheric forecasts over the contiguous USA from the National Centers for Environmental Prediction (NCEP) for predictions of streamflow using daily precipitation along with maximum and minimum temperature and found the biases in the NCEP forecasts to be quite extreme. In many regions, systematic precipitation biases exceed 100% of the mean, with temperature biases exceeding 3 °C. In another study, the long-term verification of the German Weather Service models showed that they are fairly successful in discriminating between cases of rain and of no rain [5]. The Eta Weather Forecast Model was evaluated over Central Africa by Tanessong et al. [6] and found quite good temperature predictions but not good simulations for precipitation. Pinson and Hagedorn [7], indicated generally good quality of ensemble forecasts of ECMWF (European Centre for Medium-Range Weather Forecasts) for wind speed, verified by 731 stations over Europe. Regional Atmospheric Modeling System (RAMS) was evaluated by Tiriolo et al. [8], with a root mean square error of approximately 2–3 K for temperature and 12–16% for relative humidity. The verification has been performed against surface SYNOPtic observation (SYNOP) stations over southern Italy. Liu et al. [9], found out that numerical models, which have been used for forecasting services in northwestern China, have not been extensively evaluated, and thus they evaluated forecast performance for four meteorological models during summer over that area. Their study showed that the RMSE of the forecast temperature at 2 m for each model was consistent with daily variations, the RMSE of the forecast zonal and meridional wind speeds at 10 m for each model was high during daytime and low at night and no model had forecast skills for small-scale high-intensity precipitation but they did have high forecast skills for large-scale precipitation. Varlas et al. [10] evaluated the precipitation forecasts produced from WRFARW model (Advanced Weather Research and Forecasting) for a 4-year period (September 2015–August 2019) using measurements from 24 meteorological stations. The results of the statistical evaluation indicated that the use of the hydrometeorological modelling system provides skillful precipitation and water level forecasts.

Considering the Bologna Limited-Area Model (BOLAM), Koussis et al. [11] verified the precipitation forecasts for eight cases with widespread precipitation over Greece during fall and winter 2000–2001. Values of 24 h accumulated precipitation were compared against observations from the Greek synoptic surface network. Bias and mean absolute error values revealed that BOLAM overpredicts the low to medium precipitation amounts and underpredicts the high precipitation amounts. An one-year evaluation of BOLAM for temperature, wind and precipitation in Cyprus was presented by Savvidou et al. [12]. The findings showed that the model underestimated temperature in general and the wind speed in the coastal areas. Considering precipitation, the results were satisfactory for the smaller thresholds while declining for the larger. A comparison between the outputs of two versions of BOLAM for a flood event that took place in Rome at 2008 [13]. The results suggested that the upgraded model provided a more realistic representation of the cyclone warm sector even if no evidence was found that the model upgrade was able to reduce the forecasting error about the position and the shape of the cyclone.

In this study we attempt a comprehensive assessment of the accuracy and reliability of BOLAM’s seven days fine grid predictions for precipitation, air temperature, relative humidity and wind speed over the plain of Arta, located at northwestern Greece for a four-year period (15 January 2016–22 December 2019). Using data from seven stations located at the study area along with a range of evaluation metrics and hydrological applications, we attempt to reveal the forecast’s effectiveness to provide insights into its usefulness and inform future forecasting efforts.

2. Materials and Methods

2.1. Study Area

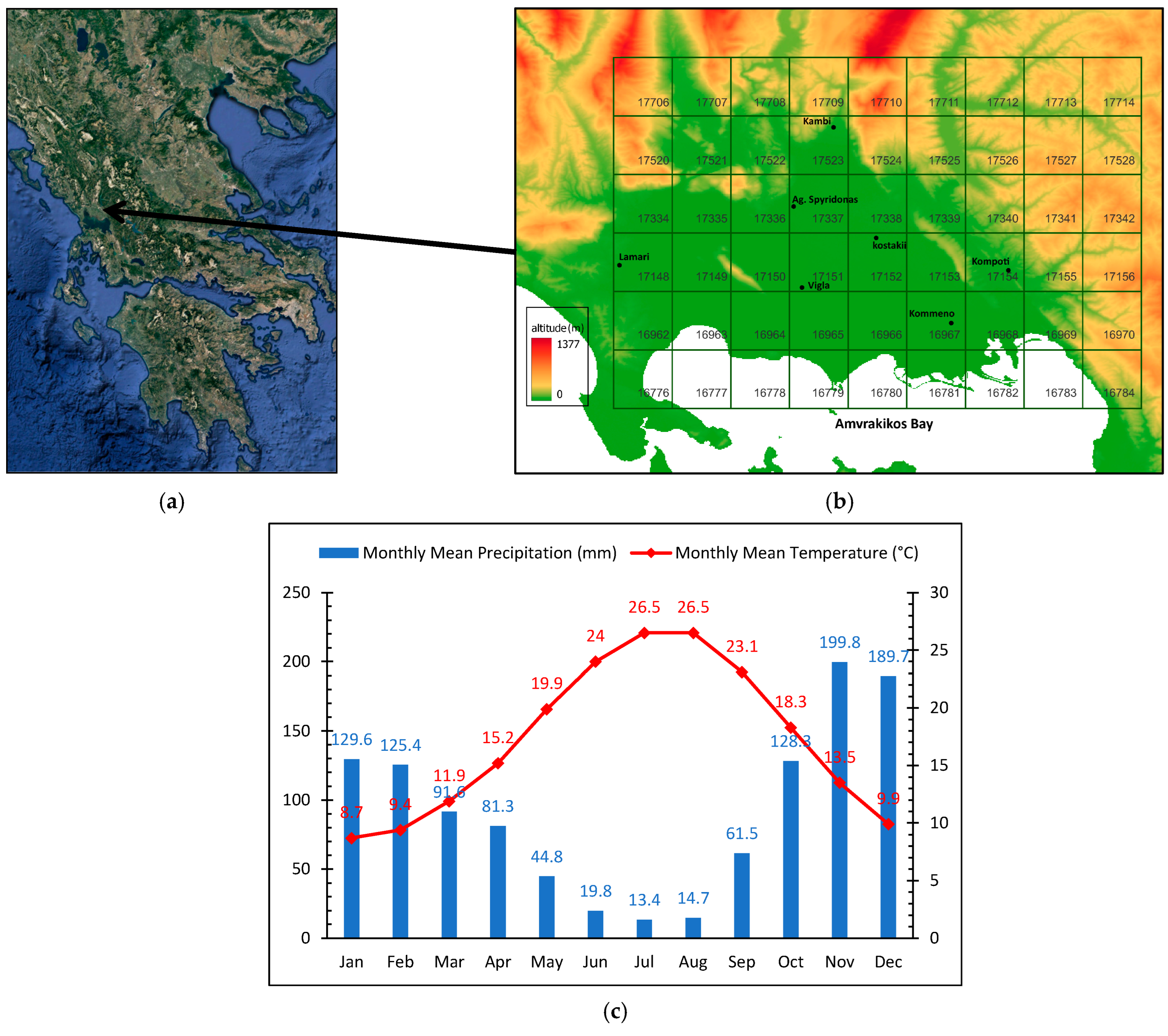
The plain of Arta (Figure 1a) lies at the northwestern part of Greece, in the Region of Epirus, and has a total area of approximately 45,000 ha. The prevailing crops in the plain consist of citrus, olive, and kiwifruit trees, along with some arable crops. Olive is the most important crop in terms of surface area at a regional level with approximately 5500 ha of cultivated land of which 30% is irrigated [14]. The plain is bordered by mountains on the north and east and by the sea at the south and west. The climate of Arta’s plain is of Mediterranean type, characterized by hot summers and rainy moderate winters, following the atmospheric circulation regime of the northeastern part of the Mediterranean region [15,16]. The annual precipitation is 1100 mm and the average temperature is 17.2 °C (Figure 1c), concentrated mainly during winter months, rendering irrigation a necessity during summer [17]. Two large rivers (Arachthos and Louros) traverse the plain, functioning as the main surface water resources.

2.2. Forecast Data

In the framework of the IRMA project which was funded by the European Territorial Cooperation Programme (ETCP) GREECE-ITALY 2007–2013, the National Observatory of Athens (NOA) delivered forecast data to the University of Ioannina for almost four years (15 January 2016–22 December 2019) [18], to be integrated into a platform for estimating near-real-time crop water requirements and irrigation forecasts across the study area [19]. The forecasts were available early each day, for the current (Day 0) and six days ahead (Day 1 to Day 6), in the form of a text file that contained all the information from Grid 2 of BOLAM model [20,21].

BOLAM performs one-way nested simulations, using two nested grid domains: (a) a coarse grid consisting of 135 × 110 points with a 0.21 degrees horizontal grid interval (approximately 23 km) centered at 41° N latitude and 15° E longitude, covering the area of the Eastern Mediterranean, and (b) a fine grid consisting of 140 × 128 points with a 0.06 degrees horizontal grid interval (approximately 6.5 km) centered at 38° N latitude and 24° E longitude (approximately the position of Athens). The fine grid covers the Greek peninsula with its maritime areas expanding from the Ionian Sea in the west up to the Turkish coasts in the east [21].

Figure 1b presents the 9 × 6 square grid with cell size of 4.33 km, created from the 54 points provided by NOA, with 0.05 degrees grid increment. Each grid cell is named after the BOLAM grid point identifier. For each point, the basic meteorological parameters, i.e., precipitation (mm), air temperature (°C), relative humidity (%), wind speed at 10 m (bf), wind direction (degrees) and air pressure (hPa) were provided in 3 h steps from 15 January 2016–22 December 2019.

In the context of the present study, the seven days forecasts of precipitation, air temperature, relative humidity and wind speed were evaluated.

Table 1. NOA’s 3 h-forecast data details.

Forecast Day	Range	Number of Timesteps
Day 0	03:00–21:00 UTC	7
Day 1	00:00–21:00 UTC	8
Day 2	00:00–21:00 UTC	8
Day 3	00:00–21:00 UTC	8
Day 4	00:00–21:00 UTC	8
Day 5	00:00–21:00 UTC	8
Day 6	00:00 UTC	1

presents the range and number of 3 h records for each day of forecast.

2.3. Agro-Meteorological Stations Network

The forecasts were verified against meteorological data acquired from 7 stations located at the study area for the same time span. These stations belong to a larger network which currently counts 18 telemetric agro-meteorological stations installed across the Epirus water district by the University of Ioannina. This network is part of the Open Hydrosystem Information Network (Openhi.net) which is a national large-scale infrastructure for collecting, processing and storing data on the surface waters of Greece, serving applied, research and operational needs [22].

All stations were installed and maintained according to WMO [23] and FAO guidelines [24] and they have modular design to support different types of sensors. Each station is equipped with sensors to record in 10 min intervals (UTC + 02:00) the following parameters:

• Precipitation (mm) (Model Rain-O-Matic, Pronamic ApS, Skjern, Denmark, accuracy ±2%, resolution 0.20 mm),
• Air temperature (°C) (Model EE08, E + E Elektronik GmbH, Engerwitzdorf, Austria, accuracy ±0.2 °C, measuring range −40 to 80 °C),
• Air relative humidity (%) (Model EE08, E + E Elektronik GmbH, Engerwitzdorf, Austria, accuracy ±2%, measuring range 0 to 100%),
• Solar radiation (W m⁻²) (Model PYR, MeterGroup Inc, Pullman, Washington, DC, USA, accuracy ±5%, measuring range 0 to 1750 W m⁻²),
• Wind speed at 3 m height (m s⁻¹) (Model 4.3515.51.000, Thies GmbH & Co., Göttingen Germany, accuracy ±0.5 m s⁻¹ or ±5% of measured value, resolution 0.4 m wind run, measuring range 0.9 to 40 m s⁻¹), and
• Wind direction (as degrees from North) (Model NRG 200P, NRGSystems Inc., Hinesburg, Vermont, USA, measuring range Direction-360°, resolution approx. 0.5°, sensitivity approx. 1 m s⁻¹).

Data are transmitted by UHF or GPRS (model A753 addWAVE, Adcon Telemetry GmbH, Vienna, Austria) to the communications center (model A850, Adcon Telemetry GmbH, Vienna, Austria) and are freely provided in near real time by the Openhi.net online timeseries database: https://system.openhi.net (accessed on 31 July 2023).

The measurements of each station were compared to the forecast values of the matching grid cell according to its location. This was chosen on purpose, since further manipulation of the forecast data by means of interpolation would result in alteration of the actual forecast data (Figure 1b).

Table 2. Agro-meteorological stations information and the corresponding BOLAM grid cell identifiers.

BOLAM ID	Station Name/ URL (accessed on 31 July 2023)	Longitude (Degrees)	Latitude (Degrees)	Altitude (m)
16967	Kommeno/ system.openhi.net/stations/1406/	21.012	39.051	10
17148	Lamari/ system.openhi.net/stations/1428/	20.731	39.099	6
17151	Vigla/ system.openhi.net/stations/1405/	20.885	39.079	0
17152	Kostakii/ system.openhi.net/stations/1402/	20.947	39.122	10
17154	Kompoti/ system.openhi.net/stations/1407/	21.061	39.095	15
17337	Agios Spyridonas/ system.openhi.net/stations/1403/	20.876	39.149	10
17523	Kambi/ system.openhi.net/stations/1404/	20.913	39.216	20

presents the stations information along with the corresponding BOLAM grid cell identifiers, in ascending order.

2.4. Timeseries Preprocessing

Firstly, the historical data time zone was shifted from Eastern European Time (EET) to Coordinated Universal Time (UTC) to match the forecasts. Additionally, non-valid values were discarded and records with missing values were omitted through a range check procedure. Additionally, the historical data timeseries had 10 min step, so they were aggregated using the Hydrognomon software (https://hydrognomon.openmeteo.org (accessed on 31 July 2023)) to 3 h timestep. Hydrognomon is a free software tool for the processing of hydrological data. Available processing techniques include time step aggregation and regularization, interpolation, regression analysis and infilling of missing values, consistency tests, data filtering, graphical and tabular visualization of timeseries [25].

Additionally, wind speed was measured at 3 m height above the ground, so logarithmic transformation to the height of 10 m took place according to Equation (1) [23,26]:

$$\frac{u_{10}}{u_3}=\frac{\mathrm{l}\mathrm{n}\left(10/z_0\right)}{\mathrm{l}\mathrm{n}\left(3/z_0\right)}$$

(1)

where u₃ and u₁₀ are the wind speed values (m s⁻¹) at 3 and 10 m height, correspondingly and z₀ is the aerodynamic roughness length, which for low crops is considered equal to 0.1 m [23]. Subsequently, the wind speed data were converted to the Beaufort scale in order to be comparable with the forecasts [27].

To perform the evaluation, the timestamps of forecasts and observations needed to be matched. This was accomplished using Matlab, resulting in pairs of observations—forecasts from Day 0 to Day 6. Thus, for each station and for each meteorological variable, seven forecast–observation files were created so that the evaluation could be performed. Consequently, approximately 1,700,000 forecast–observation pairs in 196 files were generated for evaluation.

2.5. Evaluation Criteria

The forecasts’ quality was assessed by applying accuracy measures along with Taylor diagrams for all variables, combined with contingency measures for precipitation. Below follows a short description of the above-mentioned criteria.

2.5.1. Accuracy Measures—Taylor diagram

All forecasted variables, i.e., precipitation, air temperature, relative humidity and wind speed, were evaluated by several accuracy measures such as the mean bias error (MBE), the mean absolute error (MAE), the root mean square error (RMSE) and the Nash–Sutcliffe Efficiency (EF), as reported in Malamos and Koutsoyiannis [28]:

$$\mathrm{M}\mathrm{B}\mathrm{E}=\frac{1}{n} \sum _{i=1}^n(f_i-o_i)$$

(2)

$$\mathrm{M}\mathrm{A}\mathrm{E}=\frac{1}{n} \sum _{i=1}^n\left|f_i-o_i\right|$$

(3)

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}={\left[\frac{1}{n}{ \sum _{i=1}^n(f_i-o_i)}^2\right]}^{1/2}$$

(4)

$$\mathrm{E}\mathrm{F}=1-\frac{\sum _{i=1}^n{(f_i-o_i)}^2}{\sum _{i=1}^n{(\overline{o}-o_i)}^2}$$

(5)

where $n$ is the number of forecasts/observations, $o_i$ is the ith observation, $f_i$ is the ith forecast, $\overline{o}$ is the observations average while $\overline{f}$ is the forecasts average.

Apart from the above presented measures we also implemented the Taylor diagram [29] that provides a way of plotting three statistics on a two-dimensional diagram that indicates the proximity of the forecast to the observed values. The statistics needed to create a Taylor diagram are: (i) the correlation coefficient, r, (ii) the centered pattern root mean square difference, RMSD, and (iii) the standard deviation of forecasts and observations, ${\sigma }_f$ and ${\sigma }_o$, respectively. These statistics assist to determine how much of the overall RMSD in patterns is attributable to a difference in variance and how much is due to poor pattern correlation [29].

The equation providing the aforementioned RMSD statistic, following the above presented notation, is [29]:

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{D}={\left[\frac{1}{n}\sum _{i=1}^n{\left[\left(f_i-\overline{f}\right)-(o_i-\overline{o})\right]}^2\right]}^{1/2}$$

(6)

Each forecast day is plotted on a polar style diagram with the Obs point representing the observation. The radial distances from the origin to the points are proportional to timeseries standard deviations and the azimuthal positions give the correlation coefficient between observation and forecast timeseries. The RMSD between forecast and observation timeseries is proportional to their distance apart, in the same units as the standard deviation [29].

The Taylor diagram has been used in various studies related to the evaluation of climate forecasts and simulations. Lorenzo et al. [30], used it to evaluate irradiance forecasts while Phakula et al. [31] also used it to evaluate maximum and minimum temperature forecasts over South Africa. Similarly, Salih et al. [32] used the Taylor diagram to determine the effectiveness of simulating precipitation over Tensfit Basin in Morocco.

Taylor diagrams were created for all the variables, i.e., precipitation, air temperature, relative humidity and wind speed. In particular for precipitation, since the case “no rain” in both forecasts and observations was not considered for contingency evaluation, they are not considered either for creating Taylor diagrams.

2.5.2. Contingency Measures

The evaluation of precipitation forecasts included contingency measures which are not quantitative indicators of a weather event forecast. The forecast is valued by the fact that the event happened or not, versus whether it was predicted or not. These cases are designated as a, b, c and d, according to

Table 3. Contingency table.

		Event Observed
		Yes	No
Event Forecast	Yes	a	b
	No	c	d

.

Based on the above, the following statistics can be calculated [33]:

Frequency bias:

$$FBIAS=\frac{a+b}{a+c}$$

(7)

Probability of detection:

$$PoD=\frac{a}{a+c}$$

(8)

Success rate:

$$SR=\frac{\alpha }{a+b}$$

(9)

Critical success index:

$$CSI=\frac{a}{a+b+c}$$

(10)

The frequency bias, FBIAS, is simply the ratio of the number of “yes” forecasts to the number of “yes” observations. Unbiased forecasts exhibit FBIAS = 1, indicating that the event was forecasted the same number of times that it was observed. Note that FBIAS provides no information about the correspondence between the individual forecasts and observations of the events on particular occasions, so that Equation (7) is not an accuracy measure. FBIAS greater than 1 indicates that the event was forecasted more often than observed. Conversely, FBIAS less than one indicates that the event was forecasted less often than observed.

Probability of detection (PoD) is the ratio of correct forecasts to the number of times this event occurred. The optimum value is 1, when all the events have been forecasted.

Success rate (SR) is the ratio of correct predictions to the number of all predictions. The optimum value is 1, which means all predictions were correct.

Critical success index (CSI) is the number of correct “yes” forecasts divided by the total number of occasions on which that event was forecast and/or observed. The CSI is used when the event to be forecast (as the “yes” event) occurs substantially less frequently than the nonoccurrence (the “no” event), such as precipitation [33]. The optimum is 1, when the forecast model is always successful.

The above presented measures were applied using various thresholds of precipitation such as: 0.2 mm, 1 mm, 3 mm, 5 mm, 10 mm and 20 mm. Each case was studied considering precipitation forecast or event with mm of precipitation equal to or greater than the threshold, thus the 0.2 mm threshold means that all recorded events were considered. These thresholds were adopted to provide a thorough evaluation of the precipitation occurrence since the smaller provided forecast value was 0.1 mm while the agro-meteorological stations had resolution of 0.2 mm. The other five thresholds, i.e., 1, 3, 5, 10 and 20 mm were chosen based on literature [2,11,20].

3. Results and Discussion

Table 4. Three-hour average and standard deviation of air temperature, air relative humidity and precipitation station data, per cell of the forecast grid.

BOLAM Cell—Station	Air Temperature (°C)		Rel. Humidity (%)		Precipitation (mm)
	$\overline{\mathit{o}}$	σo	$\overline{\mathit{o}}$	σo	$\overline{\mathit{o}}$	σo
16967—Kommeno	16.6	8.1	84.8	19.4	2.0	5.1
17148—Lamari	17.5	7.9	74.3	19.8	2.3	4.9
17151—Vigla	17.0	7.9	83.1	19.3	2.1	5.1
17152—Kostakii	17.3	8.4	80.5	21.2	2.3	4.8
17154—Kompoti	16.6	8.7	82.0	20.6	2.5	5.7
17337—Agios Spyridonas	16.9	8.3	80.1	21.2	1.9	4.6
17523—Kampi	17.7	8.6	74.8	22.3	2.3	5.0

presents the 3 h average and standard deviation of the stations recorded data for air temperature, air relative humidity and precipitation for the examined BOLAM grid cells. It is obvious that the statistical characteristics of the data are similar but the magnitude of differences between them justifies the need of dense stations network for tracing their variability. In the case of precipitation, the standard deviation is greater than the average in all cases, implying highly non-normally distributed data with increased frequency of high values.

3.1. Precipitation Forecast Evaluation

As stated earlier, the precipitation forecasts evaluation comprises from contingency measures, Taylor diagrams and accuracy measures for each of the seven days of forecast, i.e., Day 0 to Day 6, as presented below. Particularly for each day, the calculated contingency measures for the different rain thresholds, i.e., 0.2 mm, 1 mm, 3 mm, 5 mm, 10 mm and 20 mm are presented. As stated earlier, the 0.2 mm threshold represents all recorded precipitation events.

3.1.1. Frequency Bias

Figure 2a–g presents the frequency bias of BOLAM precipitation forecasts for Day 0 to Day 6, against the optimum value of 1 that is depicted with a dashed line.

The similarity of the FBIAS pattern between the different days of forecast, with FBIAS consistency falling below the optimal value FBIAS = 1 with increasing precipitation thresholds is evident. The best performance of the forecast model is observed in the case of the 0.2 mm threshold which is the case of all predicted precipitation events that can be measured, but the predictive capacity of the model decreases towards the last day of forecast. FBIAS tends to get values smaller than 1, i.e., the event was forecasted less often than observed, when the precipitation threshold increases to 3 mm and more. In particular for precipitation events greater or equal to 20 mm, the forecasts fail to portray the actual precipitation events of this magnitude.

Considering the spatial variation of FBIAS, the forecasts of the stations located to the north, near the mountains (BOLAM grid cells: 17337 and 17523), presented larger values of FBIAS than the rest, signifying that the model forecasted more rainfall events than those observed. This attribute could be explained by the local orography effects that can influence rainfall patterns by causing upward movement of moist air, leading to enhanced precipitation on windward slopes and rain shadow effects on the leeward side of mountains.

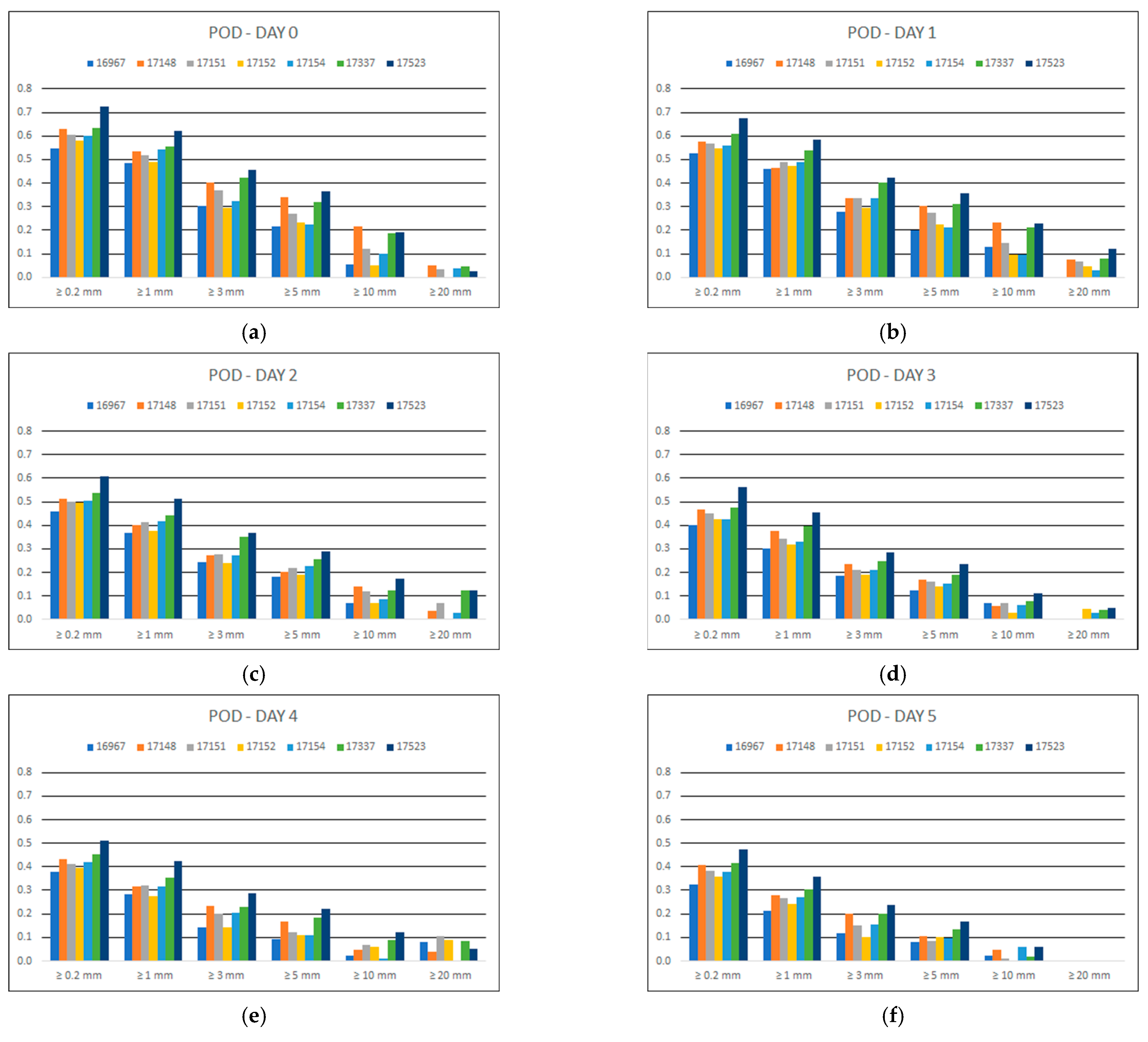
3.1.2. Probability of Detection

Figure 3 portrays the probability of detection (PoD) of BOLAM precipitation forecasts per grid cell with a station, for each forecast day and for each rain threshold.

It appears that there is a decrease in the PoD values by increasing rain thresholds, i.e., the model’s failure to predict precipitation events as the thresholds increase. Additionally, considering the days ahead increase, there is a gradual decrease in PoD values between consecutive days. It is impressive that from Day 5 onwards, the model failed to predict any event larger than 20 mm.

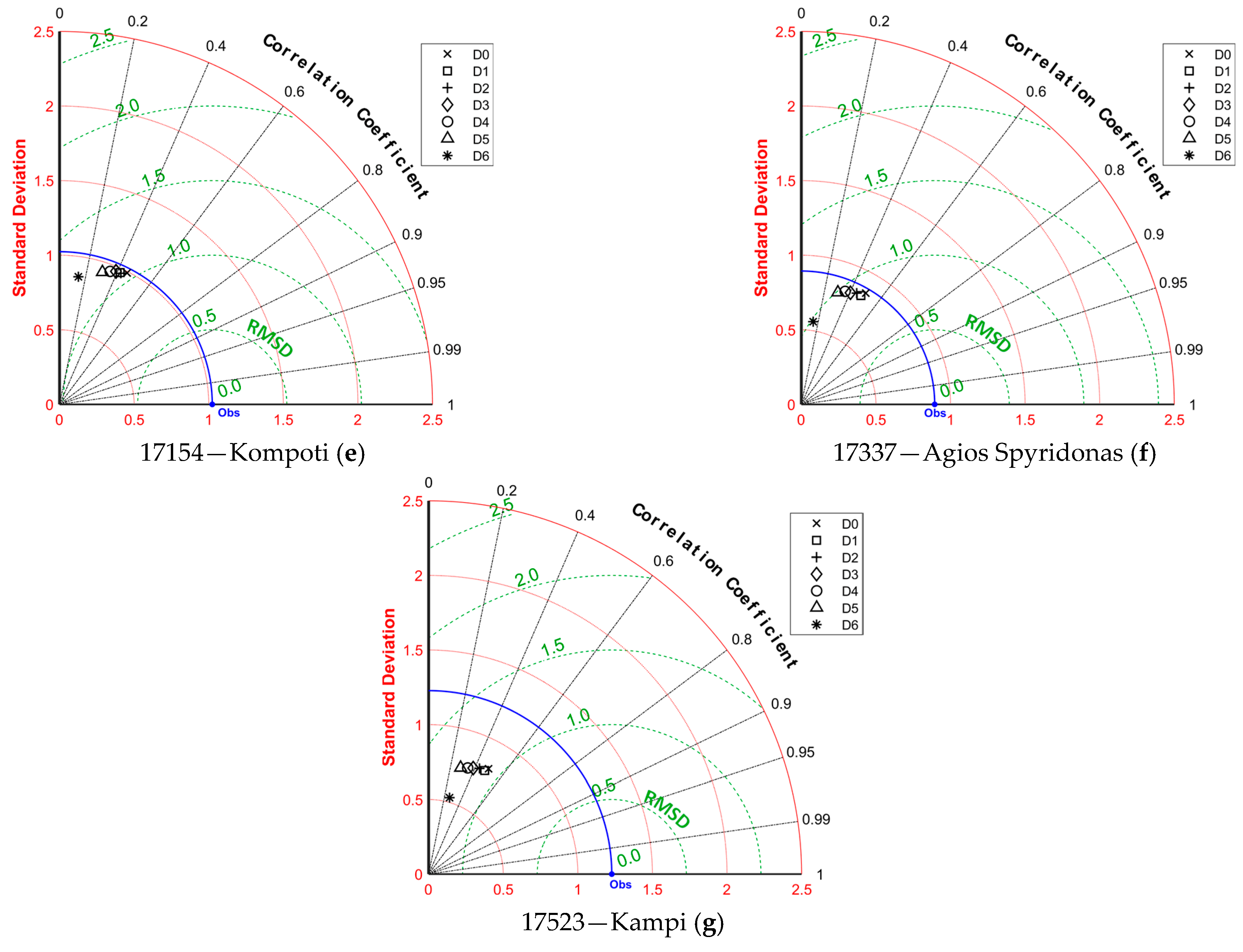
As for the spatial variation of PoD, the forecasts of the northernmost station (BOLAM grid cell: 17523) presented the larger values of PoD.

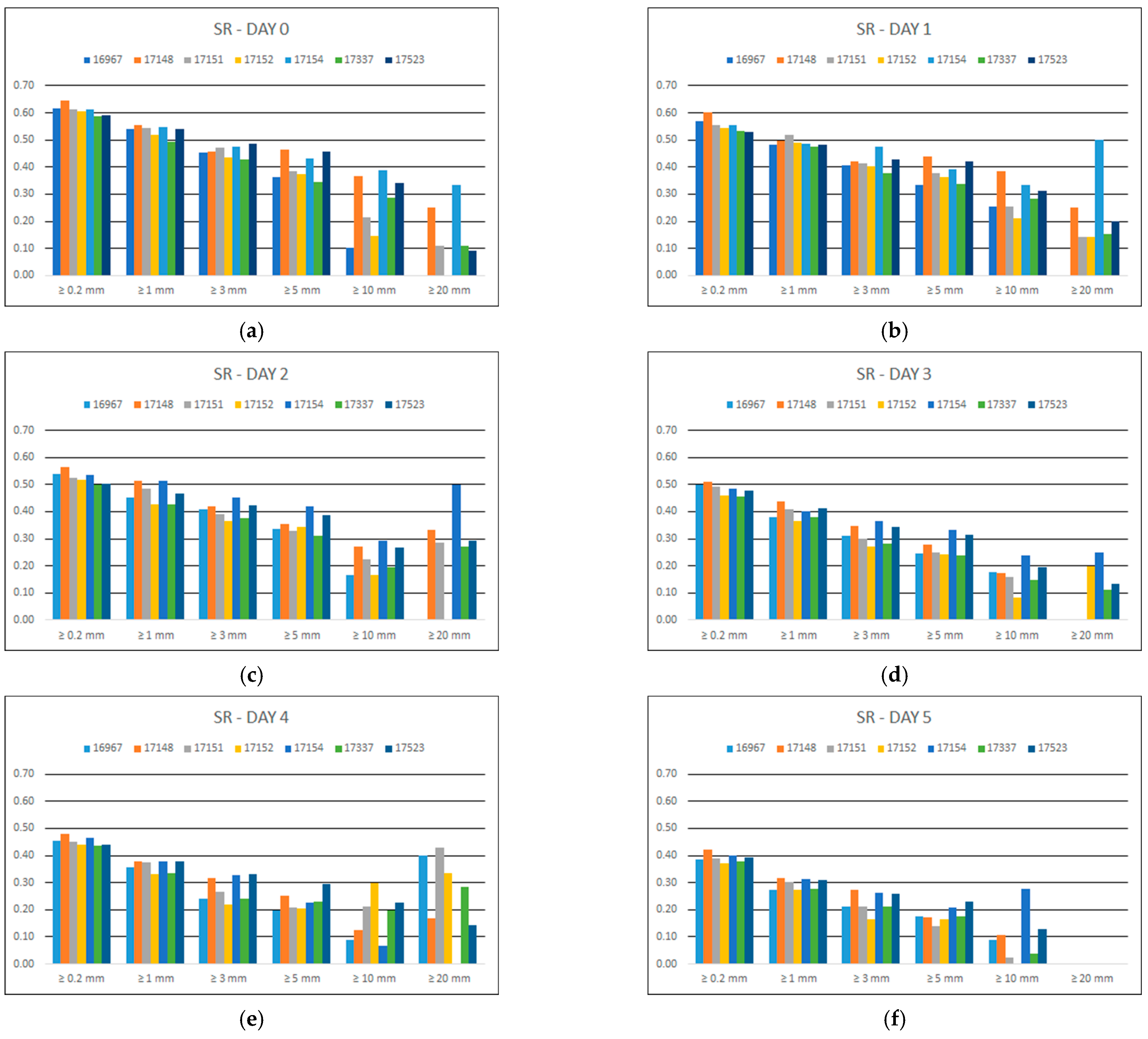
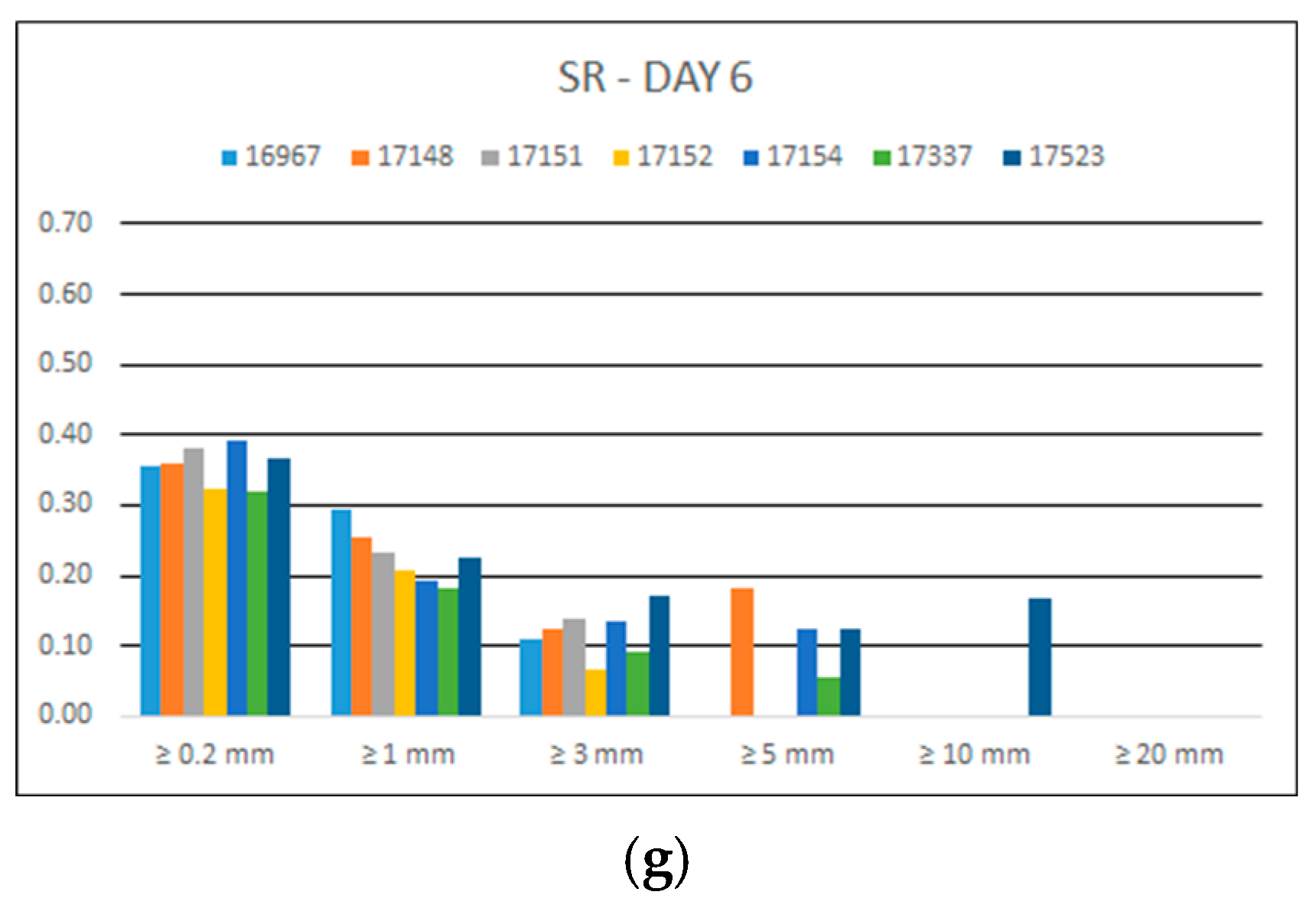
3.1.3. Success Rate

Figure 4 represents the success rate (SR) of precipitation forecasts per BOLAM grid cell with a station for each forecast day and for each rain threshold.

It is obvious that the larger values of SR accounted for the 0.2 mm threshold in all cases. There is gradual decrease in SR for thresholds greater than 0.2 mm. As days ahead increase, there is a gradual decrease in SR values between consecutive days; and beyond Day 3, the success rate of the forecasts is smaller than 0.5. As previously, from Day 5 onwards, the model presented SR = 0 for events larger than 20 mm; this signifies a total failure of prediction of high rainfall depths.

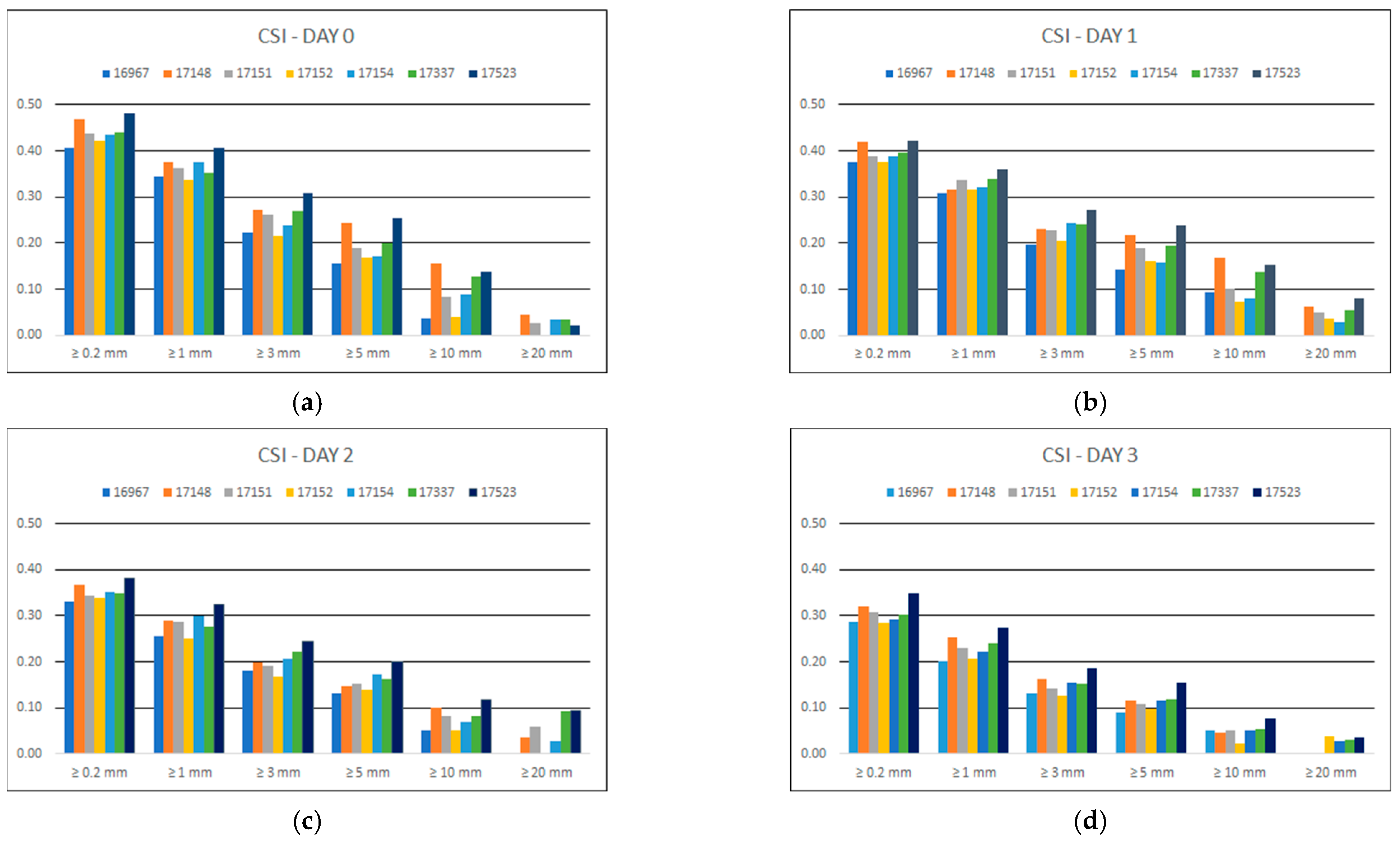
3.1.4. Critical Success Index

Figure 5 depicts the critical success index (CSI) of precipitation forecasts per BOLAM grid cell with a station for each forecast day and for each rain threshold.

For all days of forecast the overall performance is poor since the best CSI score is less than 0.5 for Day 0, meaning that less than half of the forecasted precipitation events were correctly predicted. As the rain threshold increases above 1 mm, there is an obvious decrease in the CSI. As the days ahead increase, the CSI values decrease similarly to the previously presented metrics, concluding to values for Day 5 less than 0.05 for events greater than 10 mm and zero for events greater than 20 mm. For Day 6, the model presented CSI = 0 for events larger than 10 mm apart from the case of northernmost station located at grid cell 17523. Overall, the larger CSI values were found at grid cell 17523 (station: Kambi) while the worst at cell 17152 (station: Kostakii), similarly with the case of PoD.

3.1.5. Accuracy Measures

Table 5. Accuracy measures for 3 h precipitation forecasts.

16967—Kommeno					17148—Lamari
	MBE	MAE	RMSE	EF		MBE	MAE	RMSE	EF
Day 0	−0.7	2.3	5.8	−0.20	Day 0	−0.5	2.5	4.8	0.04
Day 1	−0.6	2.3	5.3	−0.09	Day 1	−0.6	2.5	4.8	0.03
Day 2	−0.9	2.3	5.3	−0.07	Day 2	−0.8	2.5	5	−0.08
Day 3	−0.8	2.5	5.4	−0.12	Day 3	−0.8	2.6	5.4	−0.32
Day 4	−0.9	2.5	5.5	−0.15	Day 4	−0.7	2.7	5.3	−0.26
Day 5	−0.9	2.4	5.5	−0.24	Day 5	−0.7	2.7	5.4	−0.32
Day 6	−1.3	2.6	5.3	−0.26	Day 6	−1.2	3	5.6	−0.37
17151—Vigla					17152—Kostakii
	MBE	MAE	RMSE	EF		MBE	MAE	RMSE	EF
Day 0	−0.6	2.6	6	−0.21	Day 0	−0.8	2.6	5.7	−0.19
Day 1	−0.4	2.5	6.1	−0.41	Day 1	−0.8	2.6	5.6	−0.35
Day 2	−0.7	2.4	5.4	−0.11	Day 2	−1.0	2.6	5.2	−0.18
Day 3	−0.7	2.5	5.4	−0.13	Day 3	−1.0	2.7	5.3	−0.22
Day 4	−0.7	2.5	5.4	−0.13	Day 4	−1.0	2.7	5.3	−0.27
Day 5	−0.7	2.6	5.7	−0.33	Day 5	−1.0	2.7	5.4	−0.36
Day 6	−0.8	2.4	4.8	−0.35	Day 6	−0.9	2.5	4.6	−0.40
17154—Kompoti					17337—Agios Spyridonas
	MBE	MAE	RMSE	EF		MBE	MAE	RMSE	EF
Day 0	−1.0	2.6	5.7	−0.04	Day 0	−0.2	2.4	5.4	−0.22
Day 1	−1.0	2.6	5.6	0.01	Day 1	0	2.4	6	−0.69
Day 2	−1.2	2.6	5.7	0	Day 2	−0.3	2.3	4.9	−0.12
Day 3	−1.3	2.8	6	−0.13	Day 3	−0.3	2.4	5	−0.21
Day 4	−1.2	2.9	6.1	−0.18	Day 4	−0.4	2.4	4.9	−0.17
Day 5	−1.1	2.8	6	−0.20	Day 5	−0.3	2.5	5.3	−0.40
Day 6	−2.1	3.7	7.8	−0.21	Day 6	−0.5	2.5	4.9	−0.35
17523—Kampi
	MBE	MAE	RMSE	EF
Day 0	−0.3	2.6	5.3	−0.07
Day 1	−0.1	2.6	5.7	−0.28
Day 2	−0.4	2.7	5.3	−0.09
Day 3	−0.4	2.8	5.5	−0.20
Day 4	−0.5	2.8	5.2	−0.12
Day 5	−0.4	2.8	5.5	−0.32
Day 6	−0.7	3.2	6.2	−0.27

depicts the outcome of the accuracy measures used for the evaluation of the 3 h precipitation forecasts. The poor quality of the predicted values is evident since the EF criterion is negative or very close to zero in almost every forecast day and grid cell. Even the best performance, for Day 0 and Day 1 at cell 17148—Lamari is low as the EF values are 0.04 and 0.03, respectively. According to literature [34], since EF is less than zero the model-predicted values are worse than simply using the observed mean. Additionally, the MBE is negative in all cases, indicating a tendency to underestimate precipitation. Considering the rest of the metrics, they present similar variation in all cases.

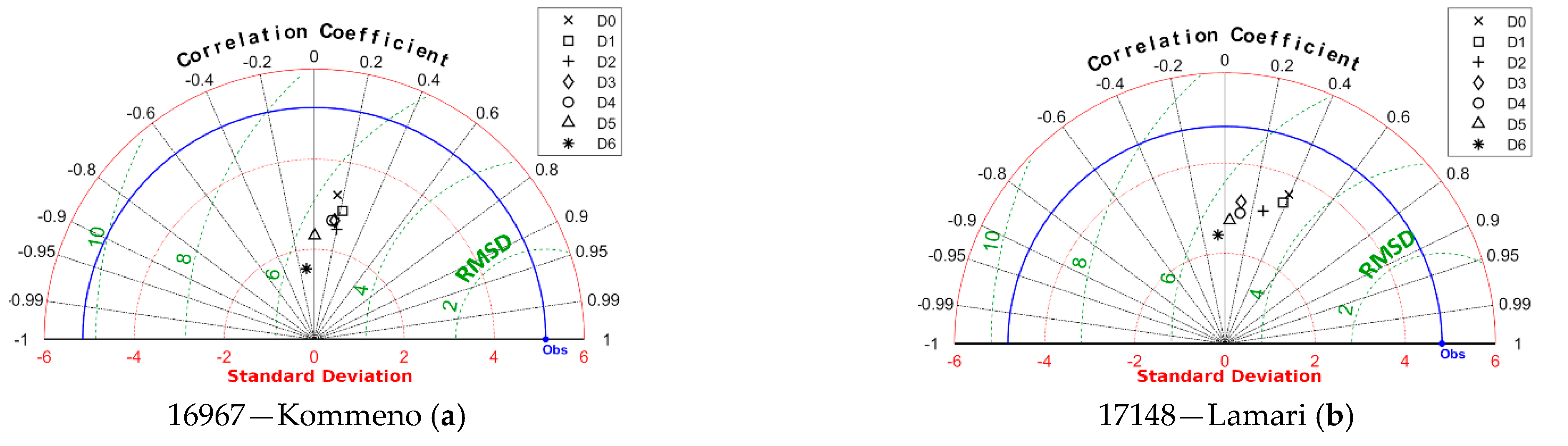
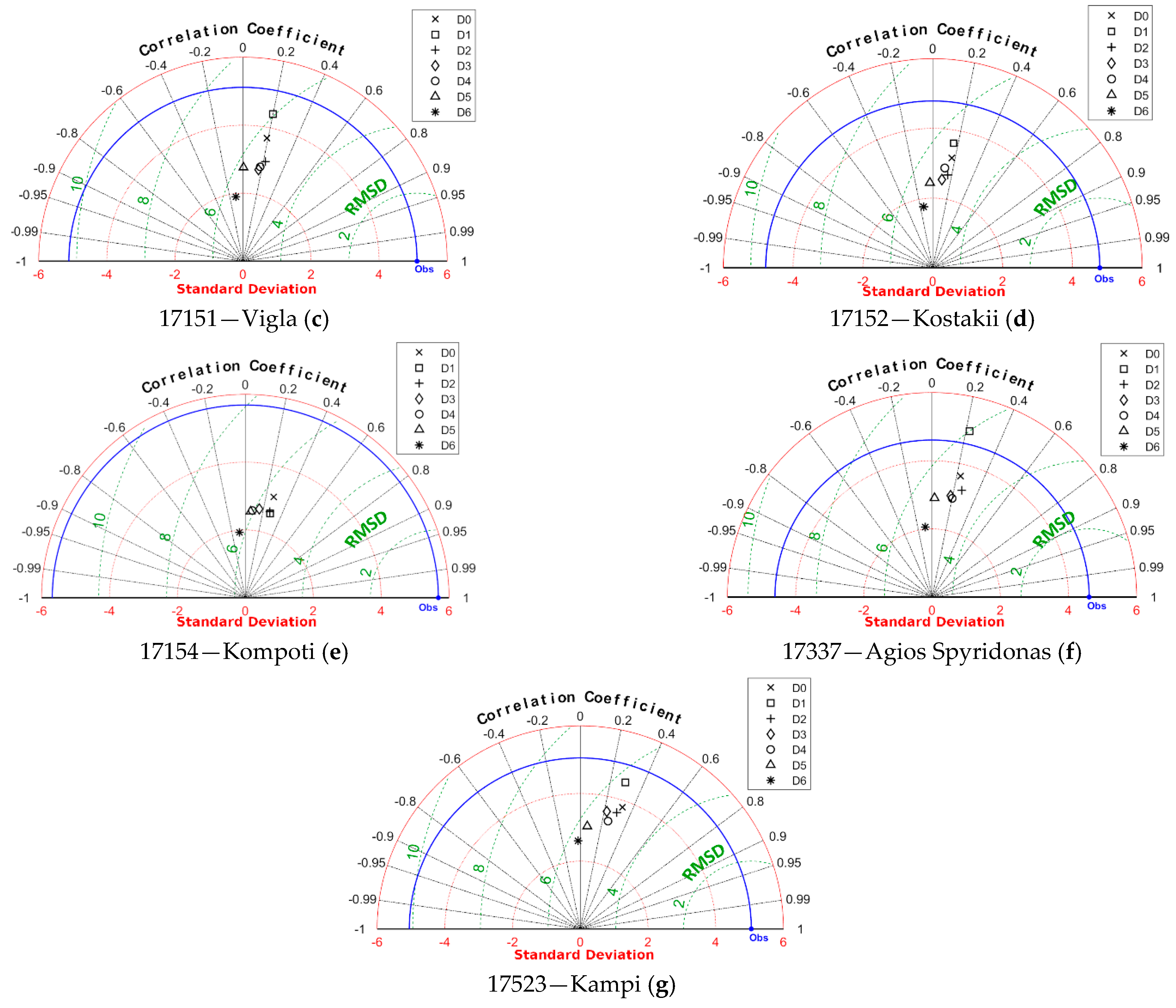
3.1.6. Taylor Diagrams

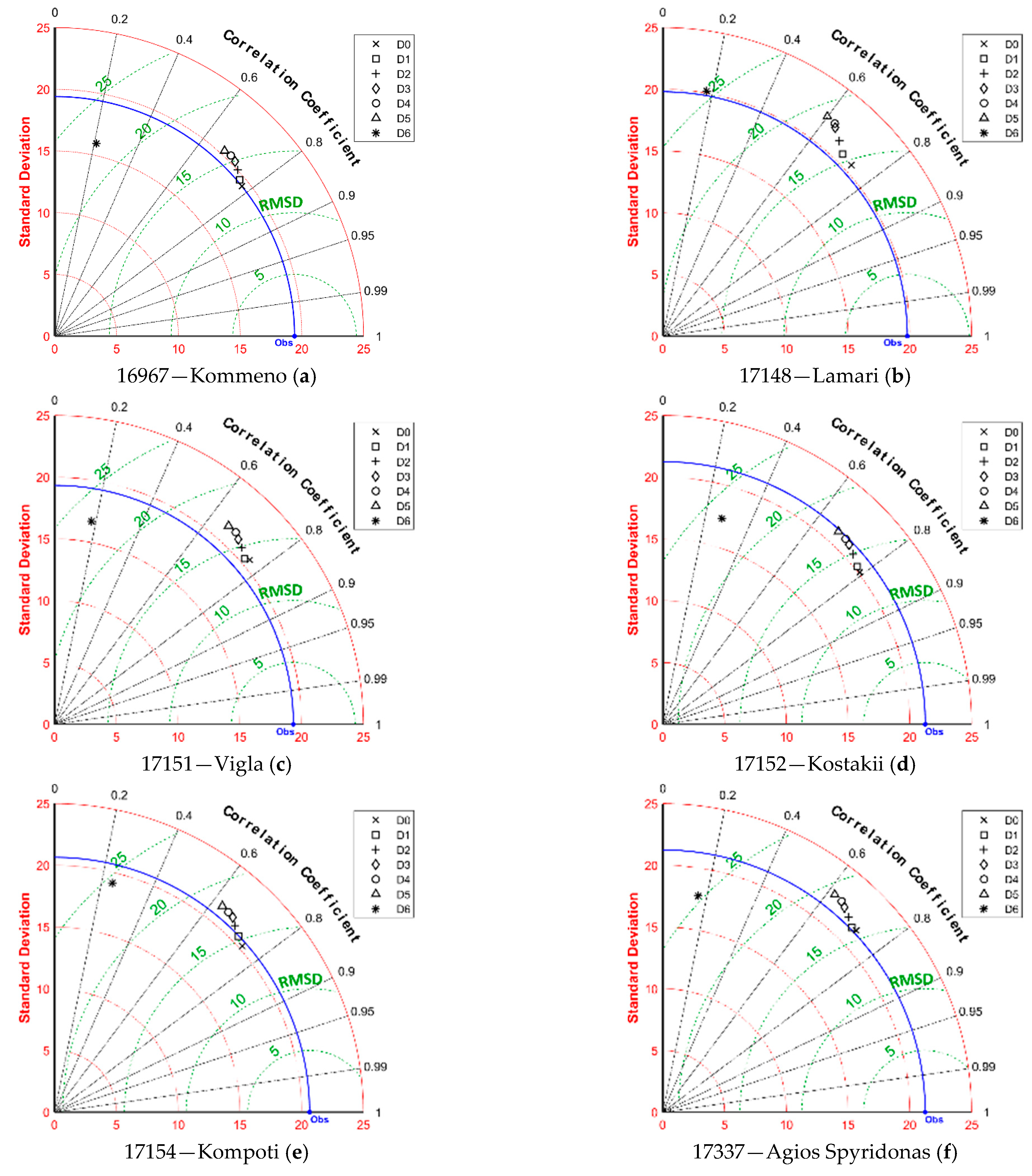
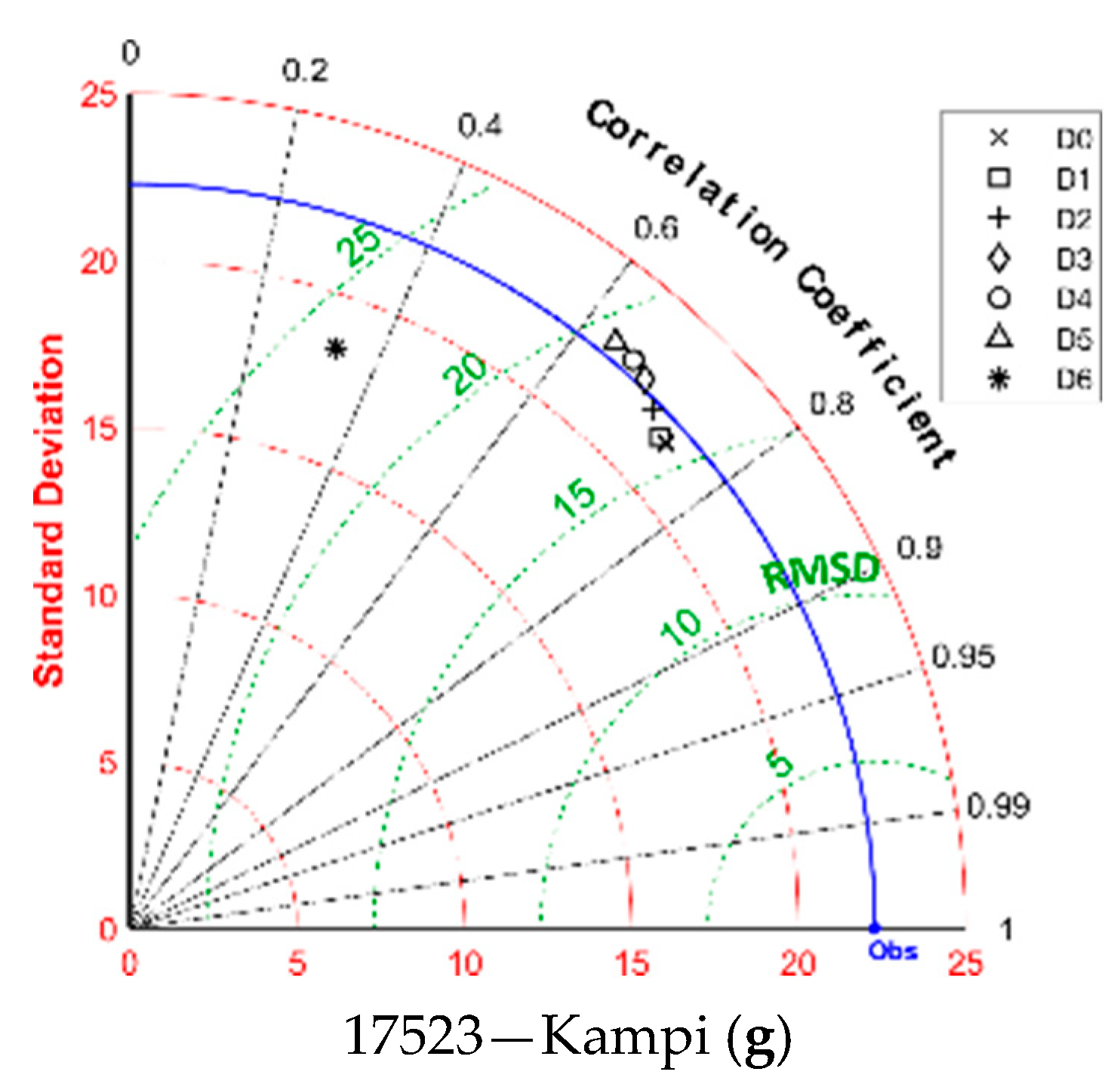
Taylor diagrams were also created for the quantitative evaluation of precipitation forecasts, which are presented in Figure 6. Each of the diagrams presents the proximity of the forecasts to the observed values of the agro-meteorological stations located inside the corresponding BOLAM grid cell for each of the seven days ahead.

At the stations’ cells, the correlation coefficient, r, ranges from 0 to 0.4 for Day 0 to Day 5, respectively, while negative values are encountered for Day 6. The standard deviation is strongly underestimated in all cases and is far from the observed value. This means that the variability of the precipitation regime was not correctly attributed. In particular, large precipitation depths were underestimated, while smaller precipitation depths were overestimated. Considering the RMSD criterion, this varies for 4 mm to 6 mm in all stations’ cells.

3.1.7. Air Temperature Evaluation

Table 6. Accuracy measures for air temperature forecasts.

16967—Kommeno					17148—Lamari
Day	MBE	MAE	RMSE	EF	Day	MBE	MAE	RMSE	EF
Day 0	−0.2	1.7	2.2	0.93	Day 0	−0.6	1.8	2.2	0.92
Day 1	0.1	1.9	2.3	0.92	Day 1	−0.3	1.9	2.3	0.91
Day 2	0.1	1.9	2.4	0.91	Day 2	−0.2	2.0	2.4	0.91
Day 3	0.2	2.0	2.5	0.90	Day 3	−0.2	2.1	2.6	0.90
Day 4	0.2	2.1	2.7	0.89	Day 4	−0.1	2.1	2.7	0.89
Day 5	0.2	2.2	2.8	0.88	Day 5	−0.1	2.3	2.8	0.87
Day 6	1.7	2.8	3.4	0.69	Day 6	1.3	2.7	3.2	0.71
17151—Vigla					17152—Kostakii
Day	MBE	MAE	RMSE	EF	Day	MBE	MAE	RMSE	EF
Day 0	−0.3	1.4	1.7	0.95	Day 0	−0.8	1.7	2.1	0.94
Day 1	−0.2	1.4	1.8	0.95	Day 1	−0.6	1.7	2.1	0.94
Day 2	−0.1	1.5	2.0	0.94	Day 2	−0.5	1.8	2.2	0.93
Day 3	−0.1	1.7	2.1	0.93	Day 3	−0.5	1.8	2.3	0.92
Day 4	0.0	1.8	2.2	0.92	Day 4	−0.4	1.9	2.4	0.92
Day 5	0.0	1.9	2.4	0.91	Day 5	−0.4	2.1	2.6	0.90
Day 6	0.6	2.0	2.6	0.81	Day 6	0.6	2.1	2.7	0.81
17154—Kompoti					17337—Agios Spyridonas
Day	MBE	MAE	RMSE	EF	Day	MBE	MAE	RMSE	EF
Day 0	−0.7	2.2	2.6	0.91	Day 0	−0.7	1.9	2.4	0.92
Day 1	−0.4	2.2	2.7	0.91	Day 1	−0.5	1.9	2.4	0.92
Day 2	−0.3	2.3	2.7	0.90	Day 2	−0.4	2.0	2.5	0.91
Day 3	−0.2	2.3	2.9	0.89	Day 3	−0.3	2.1	2.7	0.90
Day 4	−0.2	2.4	2.9	0.88	Day 4	−0.3	2.2	2.8	0.89
Day 5	−0.2	2.5	3.1	0.87	Day 5	−0.2	2.3	2.9	0.88
Day 6	1.7	2.8	3.4	0.67	Day 6	0.9	2.6	3.2	0.72
17523—Kampi
Day	MBE	MAE	RMSE	EF
Day 0	−2.5	2.9	3.4	0.85
Day 1	−2.2	2.7	3.3	0.85
Day 2	−2.1	2.7	3.3	0.85
Day 3	−2.0	2.7	3.3	0.85
Day 4	−2.0	2.7	3.4	0.84
Day 5	−1.9	2.8	3.5	0.83
Day 6	−0.7	2.3	3.1	0.76

presents the accuracy measures for the air temperature forecasts. It’s obvious that the model exhibits notable performance up to Day 5 for all grid cells apart from 17523. The forecast’s performance decreases in Day 6, though remaining acceptable and reasonable.

Considering grid cell 17523, that refers to the Kampi station, the decrease in the forecast’s performance is considerable. A plausible explanation could be the fact that is the furthest from the sea, near the mountains (Figure 1b), thus affected by the orography. Furthermore, it exhibits similar statistical characteristics as presented in the following Taylor diagrams (Figure 7g).

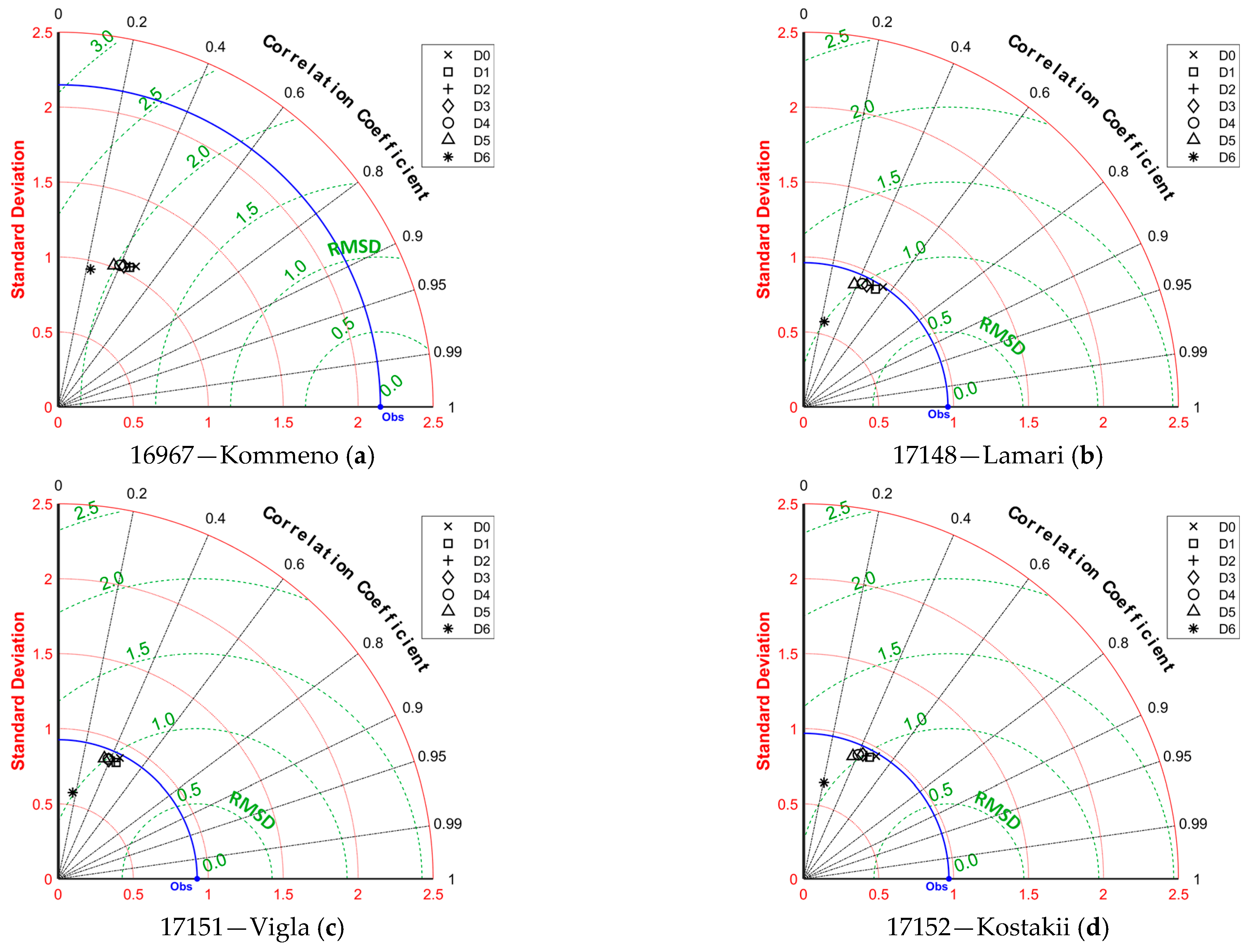
The Taylor diagrams created for the evaluation of air temperature forecasts are shown in Figure 7. Day 0 to Day 5 forecasts exhibit standard deviations close to the observations, meaning that the temperature forecasts do not significantly underestimate high temperatures nor overestimate the smaller ones. The correlation coefficient, r, is close to 0.95 and the RMSD ranges from 2 °C to 2.5 °C proving that the temperature forecasts respect the actual temperature variability. Even Day 6 forecasts present a correlation coefficient close to 0.9, with standard deviation of approximately 2 °C smaller than the observed and RMSD ranging from 3 °C to 4 °C.

3.1.8. Relative Humidity Evaluation

Table 7. Accuracy measures for relative humidity.

16967—Kommeno					17148—Lamari
Day	MBE	MAE	RMSE	EF	Day	MBE	MAE	RMSE	EF
Day 0	−12.2	14.3	17.8	0.19	Day 0	−4.8	11.4	15.3	0.39
Day 1	−11.0	13.2	17.4	0.20	Day 1	−4.3	11.9	16.2	0.33
Day 2	−11.4	13.9	18.3	0.12	Day 2	−5.0	12.9	17.5	0.22
Day 3	−11.9	14.5	19.1	0.03	Day 3	−5.5	13.8	18.7	0.11
Day 4	−12.3	15.1	19.8	−0.04	Day 4	−5.8	14.1	19.1	0.07
Day 5	−12.3	15.5	20.2	−0.09	Day 5	−5.7	14.7	19.8	0.00
Day 6	−15.0	16.0	22.0	−5.69	Day 6	−14.2	19.1	25.6	−4.07
17151—Vigla					17152—Kostakii
Day	MBE	MAE	RMSE	EF	Day	MBE	MAE	RMSE	EF
Day 0	−11.3	14.1	17.9	0.17	Day 0	−9.2	12.7	16.3	0.43
Day 1	−10.3	13.2	17.4	0.19	Day 1	−8.1	12.0	16.1	0.43
Day 2	−10.7	13.9	18.3	0.10	Day 2	−8.6	12.8	17.2	0.34
Day 3	−11.1	14.5	19.2	0.02	Day 3	−9.0	13.5	18.2	0.27
Day 4	−11.5	15.1	19.9	−0.06	Day 4	−9.5	14.2	18.9	0.21
Day 5	−11.5	15.6	20.5	−0.12	Day 5	−9.5	14.8	19.6	0.15
Day 6	−14.8	16.9	23.0	−5.18	Day 6	−15.0	17.2	23.1	−4.07
17154—Kompoti					17337—Agios Spyridonas
Day	MBE	MAE	RMSE	EF	Day	MBE	MAE	RMSE	EF
Day 0	−11.5	14.4	18.7	0.21	Day 0	−9.2	14.0	18.3	0.27
Day 1	−10.9	14.1	18.8	0.17	Day 1	−8.8	13.6	18.3	0.26
Day 2	−11.5	14.9	19.9	0.07	Day 2	−9.3	14.5	19.4	0.17
Day 3	−11.9	15.6	20.7	−0.01	Day 3	−9.7	15.2	20.3	0.08
Day 4	−12.4	16.2	21.4	−0.08	Day 4	−10.1	15.7	20.9	0.03
Day 5	−12.5	16.6	22.0	−0.14	Day 5	−10.1	16.3	21.6	−0.03
Day 6	−19.5	20.4	27.0	−12.61	Day 6	−15.8	19.0	25.3	−3.46
17523—Kampi
Day	MBE	MAE	RMSE	EF
Day 0	−3.5	12.2	16.2	0.47
Day 1	−3.3	12.2	16.4	0.46
Day 2	−4.0	12.9	17.4	0.39
Day 3	−4.6	13.7	18.4	0.32
Day 4	−4.7	14.3	19.1	0.27
Day 5	−4.8	14.8	19.8	0.21
Day 6	−11.4	16.8	22.6	−1.25

presents the accuracy measures for the relative humidity forecasts. It is apparent that the forecasts underestimate the relative humidity in all cases, especially for those stations which are nearest to the sea, i.e., Kommeno, Vigla and Kompoti. The best performance, in terms of the largest EF values along with the smallest MBE, MAE, RMSE values, were achieved at the Kampi station, which is the furthest from the sea, located in the northern side of the study area (Figure 1b), contrasting the air temperature evaluation and depicting the spatial heterogeneity in soil–atmosphere interactions.

Additionally, the best scores were achieved at Day 0 and Day 1, with acceptable values of the EF criterion, especially for three stations, i.e., Lamari, Kostakii and Kampi, while all indices are declining for the subsequent days. In many cases, the EF criterion is negative portraying the poor quality of the predicted values, making use of the observed mean preferable to the model-predicted values. The Day 6 forecasts systematically present the worst scores among the other forecasts.

Furthermore, the corresponding Taylor diagrams were created for the evaluation of relative humidity forecasts which are shown in Figure 8. The declining performance is obvious as the days ahead increase, with Day 6 failing to catch on the other forecasts with an r less than 0.4 in all cases and standard deviations far from the observed values. On the other hand, the standard deviation of the forecasts for Day 0 to Day 5 are close to the that of the observation. The correlation coefficient, r, ranges from 0.6 to 0.8, gradually declining from Day 0 to Day 5, revealing good correlation between the model output and the observed values. The RMSD ranges from 13.5% to 20% in accordance with the r variation.

3.1.9. Wind Speed Evaluation

Table 8. Accuracy measures for wind speed.

16967—Kommeno					17148—Lamari
Day	MBE	MAE	RMSE	EF	Day	MBE	MAE	RMSE	EF
Day 0	−0.7	1.5	2.0	0.14	Day 0	0.4	0.8	1.0	−0.07
Day 1	−0.6	1.4	2.0	0.14	Day 1	0.4	0.8	1.0	−0.10
Day 2	−0.6	1.4	2.0	0.13	Day 2	0.4	0.8	1.1	−0.16
Day 3	−0.6	1.5	2.0	0.10	Day 3	0.4	0.8	1.1	−0.21
Day 4	−0.6	1.5	2.1	0.08	Day 4	0.4	0.8	1.1	−0.25
Day 5	−0.6	1.5	2.1	0.04	Day 5	0.4	0.9	1.1	−0.28
Day 6	0.5	1.0	1.4	−0.53	Day 6	0.8	0.9	1.1	−2.25
17151—Vigla					17152—Kostakii
Day	MBE	MAE	RMSE	EF	Day	MBE	MAE	RMSE	EF
Day 0	0.4	0.8	1.0	−0.22	Day 0	0.3	0.8	1.0	−0.06
Day 1	0.5	0.8	1.1	−0.29	Day 1	0.4	0.8	1.0	−0.16
Day 2	0.5	0.8	1.1	−0.31	Day 2	0.4	0.8	1.1	−0.19
Day 3	0.5	0.9	1.1	−0.37	Day 3	0.4	0.8	1.1	−0.23
Day 4	0.5	0.9	1.1	−0.39	Day 4	0.4	0.8	1.1	−0.26
Day 5	0.5	0.9	1.1	−0.45	Day 5	0.4	0.8	1.1	−0.28
Day 6	0.9	1.0	1.1	−6.15	Day 6	0.8	0.9	1.1	−3.50
17154—Kompoti					17337—Agios Spyridonas
Day	MBE	MAE	RMSE	EF	Day	MBE	MAE	RMSE	EF
Day 0	0.4	0.8	1.1	−0.15	Day 0	0.5	0.8	1.0	−0.24
Day 1	0.4	0.9	1.2	−0.28	Day 1	0.5	0.8	1.0	−0.33
Day 2	0.4	0.9	1.2	−0.27	Day 2	0.5	0.8	1.1	−0.41
Day 3	0.4	0.9	1.2	−0.31	Day 3	0.5	0.9	1.1	−0.46
Day 4	0.4	0.9	1.2	−0.37	Day 4	0.5	0.9	1.1	−0.51
Day 5	0.4	0.9	1.2	−0.42	Day 5	0.5	0.9	1.1	−0.56
Day 6	1.0	1.1	1.3	−7.88	Day 6	1.0	1.0	1.2	−4.38
17523—Kampi
Day	MBE	MAE	RMSE	EF
Day 0	−0.1	0.8	1.1	0.21
Day 1	0.0	0.8	1.1	0.20
Day 2	0.0	0.9	1.1	0.15
Day 3	0.0	0.9	1.2	0.09
Day 4	0.0	0.9	1.2	0.05
Day 5	−0.1	0.9	1.2	−0.02
Day 6	0.6	0.9	1.1	−0.35

and Figure 9 present the accuracy measures and the Taylor diagrams for the wind speed forecasts, respectively. The declining performance is obvious as the days ahead increase, with Day 6 failing to catch on the other forecasts. The poor quality of the predicted values is apparent since the EF criterion achieved small or even negative values while the mean absolute error reached up to 1.5 Beaufort.

Additionally, low values of the correlation coefficient were encountered, ranging from 0.14 (Day 6 at 17337—Agios Spyridonas) to 0.55 (Day 0 at 17148—Lamari). Positive values of MBE reveal the tendency to overestimate the wind speed, except for cells 16967 (Kommeno) and 17523 (Kampi).

In the case of cell 16967, the wind speed was underestimated with negative MBE values and RMSE around 2 Beaufort, except for Day 6. The standard deviation was also underestimated denoting that the variability of the wind regime was not correctly attributed. This behavior may be attributed to the prevailing conditions caused by the station’s proximity to the sea.

Similar to the relative humidity evaluation, the best scores were encountered at cell 17523 (Kampi) the furthest from the sea, located near the mountains (Figure 1b), obviously affected by the orography. Interesting is the fact that the air temperature forecasts were inversely affected, as previously presented.

3.2. Assessment on Hydrological Applications

3.2.1. Forecasting Major Rainfall Events

Forecasting major rainfall events is essential for water resources management since it allows authorities to prepare and plan for potential emergencies, such as flooding, landslides or even dam failures, which can cause significant damage and loss of life. By having early warning systems in place, communities can be evacuated or take necessary precautions to mitigate the impact of heavy rainfall events. This information can be used to plan and implement appropriate measures to prevent or mitigate damage. The accuracy and effectiveness of forecasting models have a significant impact on the safety and well-being of communities. So, investigation of their quality in the study area can contribute to the appropriate actions and measures needed at events such as those.

We selected the two most characteristic cases, in terms of magnitude, that the model was unsuccessful in predicting the actual major events throughout the studied period. The first refers to the failed/underestimated prediction of a major event, while the second reports a false alarm about another major event. The validation took place against data from five stations since the sixth was not operational at that time and the rain gauge of the seventh was out of commission.

On 22 October 2016 between 00:00 and 03:00 UTC, a major rainfall caused flooding in the plain of Arta. The recorded rainfall ranged from 65.4 to 137.4 mm in a three-hour period, which, according to the methodology presented by Iliopoulou et al. [35], corresponded to return periods that span from ~15 years for 65.4 mm/3 h (17523—Kampi) to ~300 years for 137.4 mm/3 h (16967—Kommeno).

Table 9. Three-hour forecasts and aggregated observations (mm) before and after the major rainfall event that occurred on 22 October 2016.

	16967—Kommeno
Timestamp (UTC)	Day 1	Day 2	Day 3	Day 4	Day 5	Obs
22/10/2016 0:00	6.4	17.5	11.1	17.6	0.0	8.1
22/10/2016 3:00	8.1	8.1	19	21.2	0.0	137.4
22/10/2016 6:00	10.4	19.5	9.4	8.7	0.0	3.9
Total	24.9	45.1	39.5	47.5	0.0	149.4
	17151—Vigla
Timestamp UTC	Day 1	Day 2	Day 3	Day 4	Day 5	Obs
22/10/2016 0:00	6.3	13.4	15.2	30.1	0.3	28
22/10/2016 3:00	7	8.1	17.5	15.5	0.2	108
22/10/2016 6:00	6.1	10.5	5.8	4.8	0.0	2.4
Total	19.4	32	38.5	50.4	0.5	138.4
	17152—Kostakii
Timestamp UTC	Day 1	Day 2	Day 3	Day 4	Day 5	Obs
22/10/2016 0:00	8.2	17.4	13.7	26.7	0.1	12
22/10/2016 3:00	9.4	9.7	20.7	26.2	0.0	94.6
22/10/2016 6:00	9.6	18.7	12.3	7.4	0.0	1.4
Total	27.2	45.8	46.7	60.3	0.1	108
	17337—Agios Spyridonas
Timestamp UTC	Day 1	Day 2	Day 3	Day 4	Day 5	Obs
22/10/2016 0:00	15.8	21.6	16.6	30.4	0.1	6.2
22/10/2016 3:00	13.7	22.1	23.3	15.4	0.1	99.4
22/10/2016 6:00	6.8	17.1	7.9	7.3	0.0	0.6
Total	36.3	60.8	47.8	53.1	0.2	106.2
	17523—Kampi
Timestamp UTC	Day 1	Day 2	Day 3	Day 4	Day 5	Obs
22/10/2016 0:00	15.5	25.5	21.3	33.5	0.2	6.2
22/10/2016 3:00	15.3	26.2	27.3	14.7	0.1	65.4
22/10/2016 6:00	4.1	13.3	7.3	7.1	0.0	1.2
Total	34.9	65	55.9	55.3	0.3	72.8

presents the BOLAM model’s 3 h forecasts versus the stations’ records for the specified period, as well as the corresponding totals. In all cases, the model failed to predict the major rain event during its occurrence but also for 3 h before and after. An interesting find is that the Day 1 forecast underestimated the event more than those of the other days ahead, which, on the other hand, is consistent to the findings of the contingency analysis presented earlier (Figure 2, Figure 3, Figure 4 and Figure 5).

Secondly, on 28 November 2016 between 00:00 and 06:00 UTC, the BOLAM’s Day 1 forecast forecasted a major rainfall event, which, according to the methodology presented by Iliopoulou et al. [35], corresponded to return periods that range from ~15 years for 85.2 mm/9 h (16967—Kommeno) to ~1100 years for 244.2 mm/9 h (17337—Agios Spyridonas).

Table 10. Three-hour forecasts and aggregated observations (mm) for the unsuccessful major rain event forecasting on 28 November 2016.

	16967—Kommeno
Timestamp UTC	Day 1	Day 2	Day 3	Day 4	Day 5	Obs
28/11/2016 0:00	16.3	4.4	1.1	0	0	0.0
28/11/2016 3:00	15.3	5.2	0.5	0.3	0.1	0.0
28/11/2016 6:00	53.6	8.1	0.1	0.5	0.3	0.0
Total	85.2	17.7	1.7	0.8	0.4	0.0
	17151—Vigla
Timestamp UTC	Day 1	Day 2	Day 3	Day 4	Day 5	Obs
28/11/2016 0:00	110.6	6.3	0.5	0.6	0.4	0.0
28/11/2016 3:00	71.9	8.6	0.2	0.7	0.8	0.0
28/11/2016 6:00	21.1	10.5	0.1	0.7	3.1	0.0
Total	203.6	25.4	0.8	2	4.3	0.0
	17152—Kostakii
Timestamp UTC	Day 1	Day 2	Day 3	Day 4	Day 5	Obs
28/11/2016 0:00	87	6.3	1.1	0.3	0.1	0.0
28/11/2016 3:00	51.5	8.7	0.5	0.4	0.5	0.0
28/11/2016 6:00	39.5	9.7	0.1	0.6	1.8	0.0
Total	178	24.7	1.7	1.3	2.4	0.0
	17337—Agios Spyridonas
Timestamp UTC	Day 1	Day 2	Day 3	Day 4	Day 5	Obs
28/11/2016 0:00	92	9.7	0.9	0.5	0.4	0.0
28/11/2016 3:00	143.5	11.2	0.3	0.8	1.9	0.0
28/11/2016 6:00	8.7	10.3	0.2	1.2	4.9	0.0
Total	244.2	31.2	1.4	2.5	7.2	0.0
	17523—Kampi
Timestamp UTC	Day 1	Day 2	Day 3	Day 4	Day 5	Obs
28/11/2016 0:00	50.9	15.5	1	0.6	0.2	0.0
28/11/2016 3:00	119.1	16.8	0.5	1.1	3.4	0.0
28/11/2016 6:00	1.7	11	0.4	2.2	6.4	0.0
Total	171.7	43.3	1.9	3.9	10	0.0

presents the BOLAM model’s 3 h forecasts versus the stations’ records for 28 November 2016, as well as the sum of rainfall for forecasts and the recorded data. It is impressive that no rainfall was recorded during this period, according to all stations, demonstrating the poor performance of the forecast model. Furthermore, these large quantities affected the 2016 sum of Day 1’s rainfall forecasts, as we present in the following section.

3.2.2. Estimating Water Budget Components: Precipitation and Evapotranspiration

Meteorological data are involved in several topics of hydrology, such as identifying potential flood risks or estimating evapotranspiration as a major part of the water balance concerning the amount of water needed for irrigation. However, collecting meteorological data is time-consuming, expensive and in some cases impossible. While meteorological data require sophisticated equipment and complex data processing techniques, weather forecasts can be accessed from a range of sources, including online weather services and mobile applications. This ease of access and analysis makes weather forecasts appear as convenient alternatives and poses the question whether scientists can, given the circumstances, rely on weather forecasts to quickly gather information on weather instead of seeking meteorological data.

In this context, we present a comparison between the mean annual/monthly precipitation and the mean annual/monthly evapotranspiration of the study area as they were calculated using the provided 3 h forecasts of precipitation and temperature at each cell containing a station, against those calculated using the actual data, aggregated in daily scale. The evaluation refers to forecasts of Day 1 to 5 since those of Day 0 and Day 6 did not include eight 3 h records per day (Table 1).

According to

Table 11. Mean annual precipitation based on forecasts against observations (mm).

Year	Day 1	Day 2	Day 3	Day 4	Day 5	Observation
2016	1289	1027	954	901	877	1229
2017	774	737	767	724	704	1039
2018	939	904	818	762	742	1156
2019	960	727	735	816	835	1379

the annual difference between the observations and the forecasted precipitation, ranges from −651 mm for Day 2 of 2019 to 61 mm for Day 1 of 2016. The latter is the only case of overestimation, and was explained in the previous section, where it is shown that a large amount of precipitation was predicted for the 28 November 2016 but never occurred. It is obvious that the best performance among all days of forecast is that of Day 1, and the worst is that of Day 5, as expected.

The observed four-year average is 1200 mm yielding an average difference of 357 mm between forecasts and observations, i.e., a 30% underestimation.

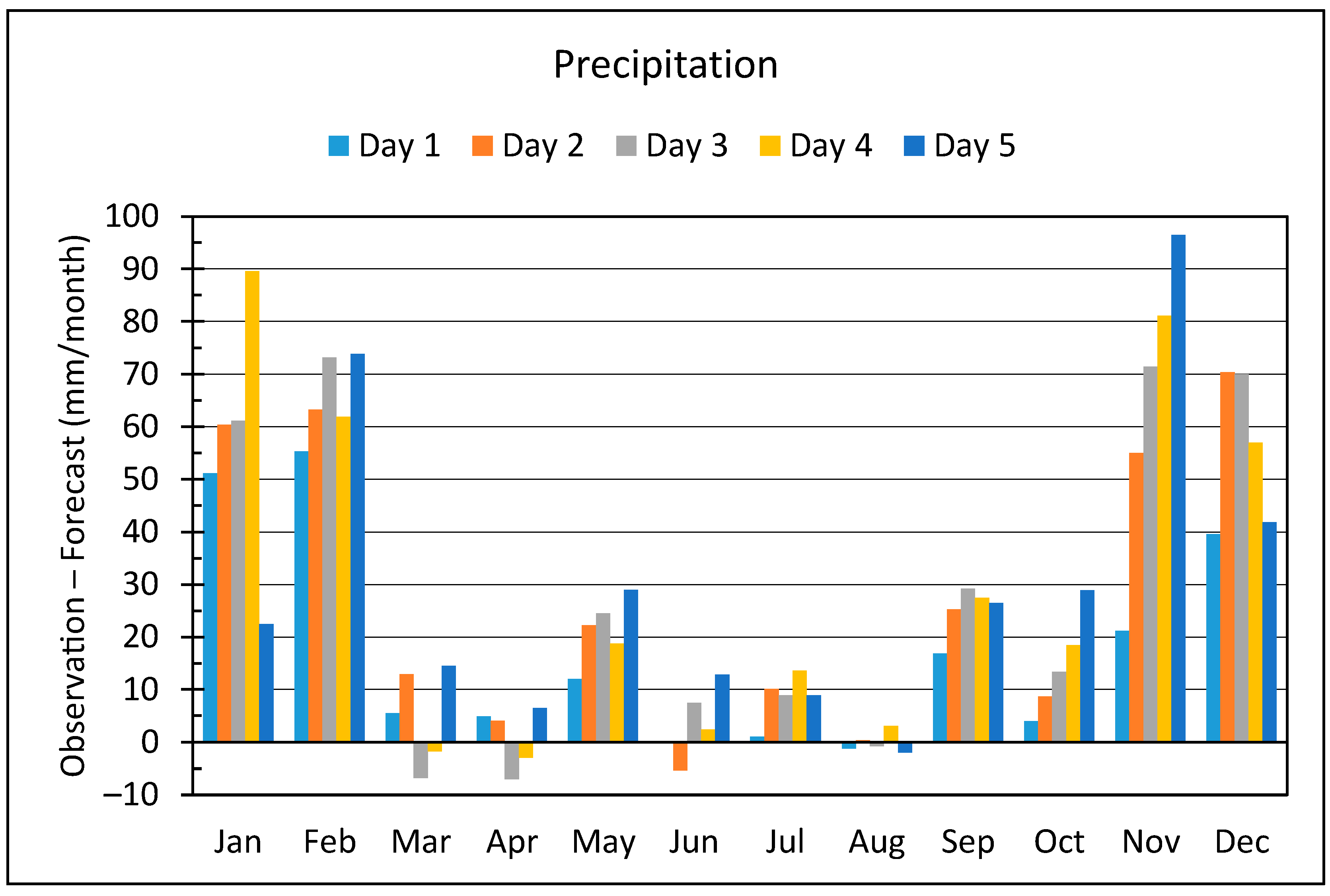
Considering the monthly average difference between precipitation data and forecasts for the four years (Figure 10), the underestimation throughout the year is evident, though intensifying from November to February, i.e., the rainy season, reaching up to 96.5 mm per month for Day 5 on November.

Based on the above analysis, it is obvious that the deviations between precipitation data and forecasts along with their seasonal distribution, do not support the use of precipitation forecasts instead of measurements.

Considering the case of reference evapotranspiration, since the forecast data missed information concerning solar radiation or any other applicable information, we implemented the Hargreaves-Samani equation [36]. It estimates the reference evapotranspiration, ET_o (mm d⁻¹) at daily scale using only air temperature data (°C) as:

$${\mathrm{E}\mathrm{T}}_{\mathrm{o}}=0.0023·{0.408·R}_a·\left(T_{mean}+17.8\right){·\left(T_{maximum}-T_{minimum}\right)}^{0.5}$$

(11)

where R_a is the extraterrestrial radiation (MJ m⁻² d⁻¹). This method has received considerable attention since it can produce satisfactory results compared to the FAO Penman-Monteith equation as an alternative in the case of limited data availability [24], and it considered accurate enough for hydrological purposes [37,38,39,40].

According to

Table 12. Mean annual ET_o based on forecasts against observations (mm).

Year	Day 1	Day 2	Day 3	Day 4	Day 5	Observation
2016	1049	1062	1060	1064	1087	1217
2017	1092	1102	1118	1118	1130	1283
2018	1084	1093	1100	1101	1114	1254
2019	1081	1098	1103	1105	1127	1258

, the annual difference between the observations and the forecasted ET_o, ranges from −130 mm for Day 5 of 2016 to −190 mm for Day 1 of 2017. Additionally, the observed four-year average is 1253 mm yielding an average difference of 158 mm between forecasts and observations, i.e., 13%.

An interesting find, contrasting the preceding evaluation of the temperature forecasts, is that the ET_o values that were calculated based on the Day 5’s forecasts, were closer to the observed ones, instead those of Day 1. An explanation is that the differences between the maximum and minimum air temperature of the Day 5 forecasts are closer to the actual data, which is supported by the MBE values presented at Table 6.

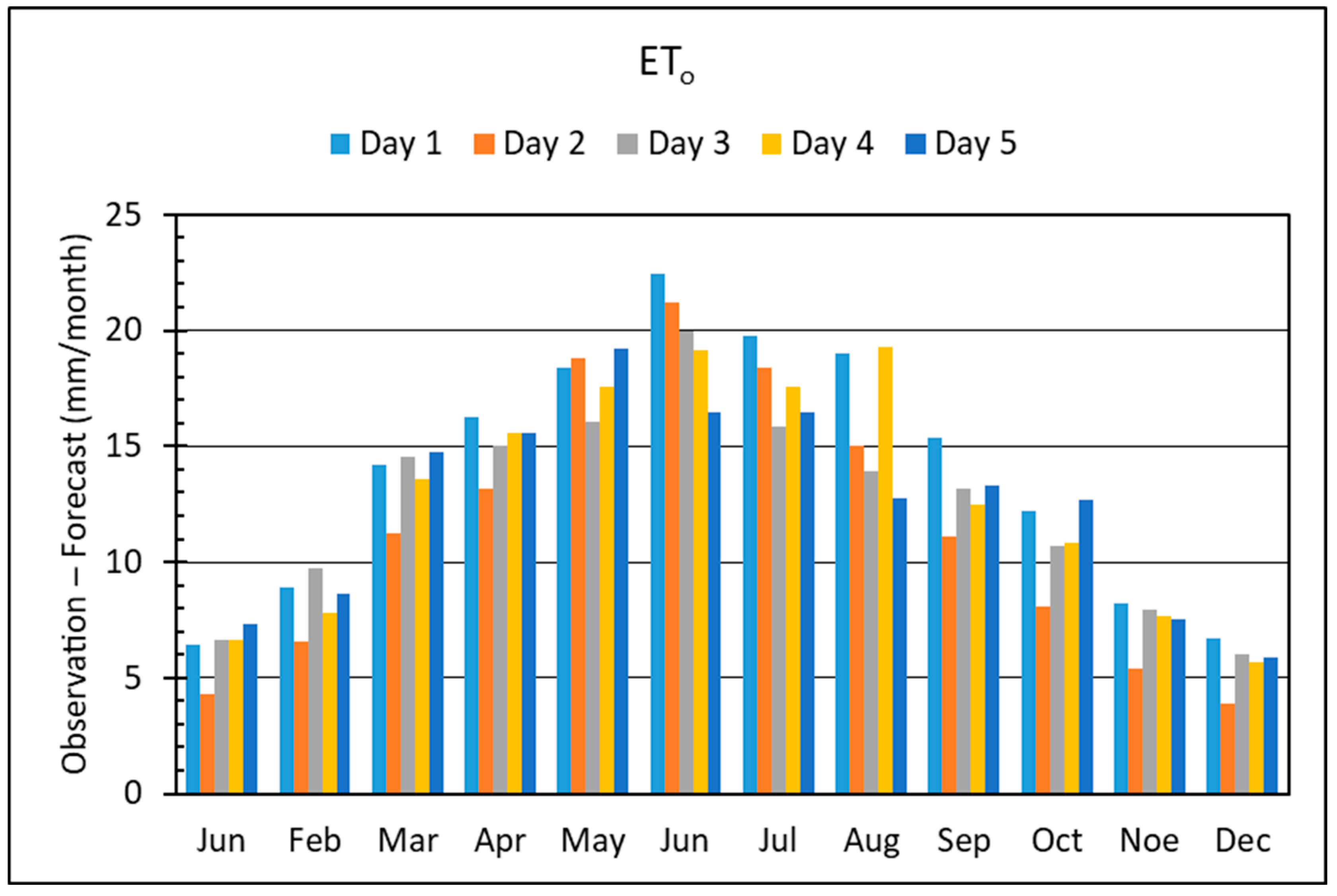
Figure 11 presents the monthly average difference between ET_o data and forecasts for the four years, portraying an apparent underestimation of forecast based ET_o. This deviation increases during the warm-dry period of the year, i.e., April to August, reaching up to 22.4 mm per month for Day 1 on June, doubting the suitability of the ET_o forecasts in accurate estimation of the irrigation needs. However, based on the above findings, the temperature forecasts may serve as a compromise to annual, or monthly in some cases, ET_o estimation in the absence of temperature data.

4. Conclusions

We presented the evaluation of the NOA’s BOLAM model forecasts across a rainy study area, i.e., the plain of Arta, against the measurements of seven agro-meteorological stations for the period from 15 January 2016 to 22 December 2019. The provided forecasts comprised from seven days of 3 h gridded data for precipitation, air temperature, relative humidity and wind speed and they were compared to those of the stations contained at each corresponding grid cell. After the initial timeseries preprocessing, the evaluation dataset was comprised from approximately 1,700,000 forecast–observation pairs. Several evaluation criteria were applied, such as contingency measures, Taylor diagrams and accuracy measures.

The need for spatial analysis of the involved parameters variability was established with noticeable differences between the grided forecasts and the corresponding agro-meteorological stations, indicating the need for a dense multipoint analysis across the study area. This was evident in the case of the grid cell referring to the station located at the northern side of the study area, far from the sea, which achieved the best scores for relative humidity and wind speed but exhibited the worst performance for air temperature.

For the case of precipitation, all criteria exposed that the 3 h forecasts failed to comply with the precipitation regime throughout the study area. All the large precipitation depths were underestimated, while from the fifth day of forecast onwards, the model failed to predict any event larger than 20 mm per 3 h, as presented. Furthermore, the Nash–Sutcliffe Efficiency criterion was negative or very close to zero in almost every forecast day and grid cell.

On the other hand, air temperature forecasts exhibit notable performance up to Day 5 for almost all grid cells. The forecast’s performance exhibits a decrease in Day 6 though remaining acceptable and reasonable. However, the temperature forecasts do not underestimate high temperatures nor overestimate the smaller ones with high correlation coefficients. These prove that the temperature forecasts respect the actual temperature variability (mostly the annual and daily cycles) and they are reliable.

Considering relative humidity, the forecasts underestimated the relative humidity in all cases, especially for those stations adjacent to the sea depicting the spatial heterogeneity in soil–atmosphere interactions. The best scores were achieved at Day 0 and Day 1 while for the subsequent days all performance indices declined, with Day 6 failing to catch on the other forecasts. The Nash–Sutcliffe Efficiency criterion achieved acceptable values at Day 0 and Day 1 at three stations, but for the rest of the forecast range, the performance declined, making use of the observed mean preferable to the model-predicted values.

As for the wind speed forecasting, the findings portrayed the BOLAM’s poor performance, since the model presented small or even negative values of the Nash–Sutcliffe Efficiency criterion along with low values of the correlation coefficient. Additionally, the wind speed was overestimated in all cases aside from the station located close to the sea where strong underestimation was noted.

The evaluation of forecasting major rainfall events revealed that the model was unsuccessful in predicting the actual events. In the first case, there was a failed prediction of an actual major rainfall event while the second reported a false alarm about a major event that never occurred.

Further analysis included the comparison between forecasted and observed estimates of mean annual/monthly precipitation and mean annual/monthly reference evapotranspiration across the study area. The deviations between precipitation data and forecasts along with their seasonal distribution, showed that the use of rainfall forecasts failed to approximate the observations. The temperature based ET_o estimations proved that the temperature forecasts may underestimate ET_o, but they may serve as a compromise to estimate ET_o at annual scale in the absence of actual temperature data. However, this deviation increases during the warm-dry period of the year, doubting the suitability of forecasts in accurate estimation of the ET_o in monthly scale.

Undoubtedly the evaluation of a forecast is a critical step in determining its effectiveness and its usefulness in informing decision-making processes. This paper provided a comprehensive assessment of the accuracy and reliability of the BOLAM’s seven days fine grid 3 h forecasts for the plain of Arta at northwestern Greece against observed data. Even if the findings support only the quantitative forecasting of temperature and in some cases the relative humidity, evident is the need for skilled weather forecasts from improved versions of the examined model that may incorporate post-processing techniques to improve predictions or from other forecasting services.