Abstract
Accurate precipitation estimation remains a challenge, though it is fundamental for most hydrological analyses. In this regard, this study aims to achieve two objectives. Firstly, we evaluate the performance of two precipitation products from the Integrated Multi-satellitE Retrievals for Global Precipitation Measurement (GPM-IMERG) for Sicily, Italy, from 2016 to 2020 by a set of categorical indicators and statistical indices. Analyses indicate the favorable performance of daily estimates, while half-hourly estimates exhibited poorer performance, revealing larger discrepancies between satellite and ground-based measurements at sub-hourly timescales. Secondly, we propose four multi-source merged models within Artificial Neural Network (ANN) and Multivariant Linear Regression (MLR) blending frameworks to seek potential improvement by exploiting different combinations of Soil Moisture (SM) measurements from the Soil Moisture Active Passive (SMAP) mission and atmospheric factor of Precipitable Water Vapor (PWV) estimations, from the Advanced Microwave Scanning Radiometer-2 (AMSR2). Spatial distribution maps of some diagnostic indices used to quantitatively evaluate the quality of models reveal the best performance of ANNs over the entire domain. Assessing variable sensitivity reveals the importance of IMERG satellite precipitation and PWV in non-linear models such as ANNs, which outperform the MLR modeling framework and individual IMERG products.
1. Introduction
The precise estimation of precipitation perhaps plays the most significant role in water-related studies [1] and in many hydrologic modeling and forecasting applications. For many years, the most reliable source of rainfall measurements has been represented by ground rain gauge networks [2,3], which have the great advantage of high accuracy in monitoring precipitation, even if measurements refer to a small area around the instrument. Rain gauge networks, on the other hand, are usually poorly distributed in plateaus, mountains, deserts, and other areas, and may not even be present in uninhabited areas, creating gaps in the data [2,3].
Currently, satellite-retrieved and atmospheric reanalysis precipitation are increasingly used in an attempt to bridge the spatiotemporal gaps of in-situ rain gauge networks, although estimation errors still limit their practical applications [4]. Among these products, the Integrated MultisatellitE Retrievals from Global Precipitation Measurement (GPM) constellation (IMERG; [5]) is widely used. Many studies have been devoted to validating and improving IMERG data with respect to ground-based data. Some of these studies have evaluated IMERG data on a global scale (e.g., [6]), while others have focused on some specific areas of the globe such as Europe [7,8,9], vast territories throughout Asia [10,11,12,13,14,15], and America [16,17,18,19]. Their investigations suggest the promising use of IMERG to estimate spatiotemporal variability of rainfall across diverse rainfall patterns, climates, and geographical characteristics; nonetheless, they highlight the importance of regional calibration to improve IMERG reliability. In a comprehensive global review, [20] identified the lack of studies evaluating sub-daily scales for the latest version (V06) release of IMERG as an issue that should be addressed more, particularly for Europe, for which satellite precipitation products have been investigated less than those for Asian and American territories.
With reference to the Mediterranean basin, the area has been always subjected to high uncertainty in rainfall estimations due to its unique topography and complex climate [21]. According to the literature, the discrepancy between satellite and ground measurements in this area is higher in regions characterized by a complex morphology and influenced by land–sea transitions, especially when the finer temporal resolutions are considered [22,23,24]. Additionally, the Mediterranean region is one of the most vulnerable areas of the globe to the effects of climate change [25,26,27], which makes rainfall estimation from satellites difficult since the climate today is exposed to more frequent and severe extreme events, particularly at finer temporal resolutions (e.g., hourly and sub-hourly) [28], that the complexity becomes more evident than those modeled in the past [25,28,29,30,31,32,33].
Precipitation estimation over sub-hourly time scales plays a critical role for many sectors impacted by natural phenomena. Nevertheless, only a few studies have focused on evaluating satellite products with rain-gauge measurements at fine scales [20]. However, half-hourly rainfall estimates of IMERG are available to the public, and there are selected studies evaluating hourly and sub-hourly IMERG data. Some of these studies include an evaluation of IMERG V06 at an hourly scale over Canada [34], at 1, 6, and 24 h scales by [35] over Brazil, and at 1 and 3 h scales by [36]. Although these studies highlight the potential of IMERG at sub-hourly scales, they also suggest that there is still room for further improvement in product accuracy at fine sub-daily scales for practical aims. Impacts of temporal resolution on space-based precipitation estimates over Southern Italy are similarly construed to a few. To give an example, [37] set a 10-day threshold for stable performances of satellite estimates in terms of categorical indicators and statistical metrics, whereas [38] discovered a reasonable performance in remote-sensing estimates above a 6 h temporal resolution. Most recently, daily and 6 h data from IMERG V04, [22] suggested that the performance of GPM satellite data is primarily driven by temporal aggregation rather than orography.
Following these evaluations, many researchers have attempted to reduce the uncertainties involved in Satellite Rainfall Estimates (SRE) using different methods such as the mean correction factor method [39], quantile mapping [40], and the Bayesian approach [41]. However, these methods are often associated with various limitations and, for this reason, are often replaced by more advanced methods [42,43]. In some cases, the blending of ancillary variables to enhance precipitation estimates has been implemented to overcome these limitations [44]. These merging techniques have proven to be effective in improving the accuracy of precipitation estimates from satellites [45,46]. For instance, some authors blended SRE along with the topography and physical characteristics of a region through a linear parametric model [47], while others took advantage of atmospheric variables, specifically Precipitable Water Vapor (PWV), which is suggested to be highly interconnected to precipitation [48]. The authors of [4] improved rainfall estimates through a fusion of weather radars, satellite estimates, soil moisture data, and terrain elevations within two distinct model frameworks: Artificial Neural Network (ANN) and Geographically Weighted Regression (GWR). The authors of [49] blended four multisource precipitation estimates, including IMERG, CMORPH (CPC MORPHing technique), Climate Hazards Group Infrared Precipitation with station data (CHIRPS), and the Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks by Dynamic Infrared–Rain Rate (PERSIANN-PDIR), with PWV and land surface temperature.
Various strategies for combining satellite-based and ancillary data have been widely used to improve space-based estimates, including linear regression as the most common method with desirable outcomes [50,51]. In addition to scientific techniques, Machine Learning (ML) techniques, such as ANNs, have been increasingly applied in rainfall studies due to their ability to extract a non-linear relationship between independent and dependent variables, without the need for predefined relationships; this has led to a significant improvement compared to traditional blending methods [46,49,52,53,54,55]. A summary of selected literature reviews in this field is reported in Table 1.
In this study, we develop a methodology to correct high-resolution satellite precipitation estimations over the Mediterranean island of Sicily, Italy, through blending atmospheric characteristics and land surface factors. The methodology is a two-phase process. During the first phase, the latest version of individual IMERG (V06) precipitation estimations, at a relatively high temporal resolution (i.e., half-hourly) and daily scale, is validated against observed data provided by the rain gauge network of the Agrometeorological Information Service of Sicily (Servizio Informativo Agrometeorologico Siciliano—SIAS) for the period 2016–2020. Upon gaining a deep insight into the satellite performance over the region, the second phase concentrates on enhancing the accuracy of space-based precipitation estimations through blending IMERG with ancillary data that describe interactions with atmospheric content and land surface properties. In this regard, two techniques are applied, namely, Multivariant Linear Regression (MLR) and ANN. Given that Surface Soil Moisture (SSM) retrievals are strongly associated with rainfall depth [56,57], successful blending approaches by [49,55] have inspired this study to include soil moisture in precipitation estimation models as a potential ancillary variable.
We believe that the framework developed within the study may offer a promising solution for generating more reliable inputs in hydrological studies, such as those aimed at assessing flow regime alteration [58], particularly in complex terrain areas that are prone to extreme events, such as the Mediterranean region. Moreover, its potential benefits could be extended to the catchment and regional scales, contributing to improving studies on hydrogeological risk assessment.
The manuscript is organized as follows. Section 2 describes the study area, dataset, and merging methods. The results are presented and discussed in Section 3. Section 4 concludes the paper.

Table 1.
Summary of selected literature for review.
Table 1.
Summary of selected literature for review.
| Author | Framework, Material, and Approach | Study Area Study Period | Result(s) |
|---|---|---|---|
| Moazemi et al., 2021 [34] | Evaluating different IMERG precipitation products with hourly resolution | Canada 2014–2018 |
|
| Caracciolo et al., 2018 [22] | Examining the performance of IMERG-v06 SPEs over Mediterranean islands of Italy | Italy 2015–2016 |
|
| Brocca et al., 2013 [57] | SM2RAIN approach to space precipitation estimates based on soil moisture data from ASCAT | South Europe 2008–2011 |
|
| Wehbe et al., 2020 [4] | Two fusion approaches based on ANN and GWR to merge satellite precipitation estimates, weather radars, and soil moisture | UAE 2015–2018 |
|
| Beykahmadi et al., 2021 [48] | Improving the accuracy of daily and 6-hourly SPEs of IMERG through PWV and land surface elevation | Iran 2015–2017 |
|
| Nosratpour et al., 2022 [49] | Fusion model based on the integration of CMORPH, PDIR, CHIRPS, IMERG, PWV, and LST through MLR and ANN | Iran 2017–2021 |
|
| Zhao et al., 2022 [59] | Integrate multi-source precipitation products (APHRODITE, ERA5, CHIRPS) with environmental factors (vegetation and soil moisture) through a ML model | China 1987–2017 |
|
2. Materials and Methods
2.1. Study Area
Sicily is the largest island in the Mediterranean Sea and is located at the southern end of Italy, between latitudes 36° N and 39° N and longitudes 12° E and 16° E (Figure 1). It is separated from the Italian Peninsula by the Strait of Messina and bordered by the Ionian Sea (eastward), the Tyrrhenian Sea (northward), and the Channel of Sicily (southward), which separates Sicily from Africa (Figure 1). The island covers an area of approximately 25,700 km2, with orography ranging from 0 to 3320 m a.s.l. at the volcano Etna (Figure 1). The climate there is typical of that in Mediterranean regions. Because of its geographic position and morphology, Sicily is characterized by significant spatiotemporal variability in precipitation; the mean annual precipitation ranges between approximately 360 mm in the southeastern part of the island and approximately 1900 mm in the northeastern part of the island [60], with summers (i.e., from June through August) typically dry, with little or no rain, and the highest amount of rainfall occurring during the winter months [61,62].
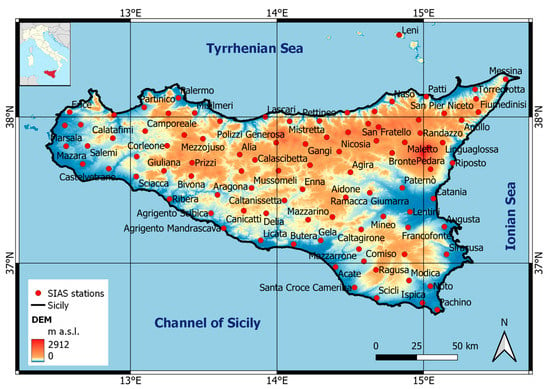
Figure 1.
Digital Elevation Model (DEM) of Sicily and location of SIAS rain gauge stations.
Figure 1 shows the Digital Elevation Model (DEM) of Sicily and its location in the Mediterranean Sea (see inset in Figure 1). DEM has a 20 × 20 m resolution and is provided by the Italian National Geoportal (http://www.pcn.minambiente.it/mattm/en/; accessed on 15 January 2023).
2.2. Datasets
2.2.1. Precipitation Data: Ground and Satellite Observations
In this study, ground-based and satellite precipitation measurements were used. Ground-based data were provided by the SIAS, which manages a network of approximately 100 tipping bucket rain gauges distributed over the entire island (Figure 1) that collect data with a temporal resolution of 10 min and a rain resolution of 0.2 mm. For the comparison with the IMERG data, the original data were aggregated at both half-hourly and daily scales. For daily data, a wet day (or rainy day) was defined as a day in which a minimum rainfall of 1 mm/day occurred. In addition, an inter-event time was fixed equal to 1 h, which separated one rain event from the next [63,64].
Satellite data were obtained from IMERG, which is a unified algorithm that provides multi-satellite precipitation products to the U.S. GPM team. The current version of the dataset is the V06, with 0.1° spatial resolution (i.e., approximately 10 × 10 km at the latitudes of Sicily) and 30 min temporal resolution (GPM_3IMERGHH) [44]. This was used to obtain the dataset of the GPM Level 3 IMERG “Final” at the daily scale at the same spatial resolution (GPM_3IMERGDF).
IMERG combines retrievals from Passive Microwave (PMW) and Microwave-calibrated Infrared (IR) to produce a quasi-global (60° S–60° N) precipitation product based only on satellite data. Raw data are processed and then gridded and merged with IR data to provide global, homogeneous precipitation measurements [65]. IMERG has three types of products based on latency and the processing method applied to observations: early (IMERG-E), late (IMERG-L), and final (IMERG-F). While early and late products are available 3 and 12 h after the observations, respectively, the final version is released 3.5 months later. An advantage of IMERG-F is the additional levels of data processing that are not considered in the first two products. The gridded data are available from mid-March 2014 to the present. The products used in this study were GPM_3IMERGHH-06 and GPM_3IMERGDF-06, corresponding to half-hourly and daily temporal resolutions, respectively.
For both the ground-based and satellite precipitation, data within the period of 2016 to 2020 were considered. Table 2 reports the main characteristics of the SIAS and IMERG rainfall datasets.

Table 2.
Overview of the high-resolution ground and satellite-based products used in this study.
2.2.2. Ancillary Data: Precipitable Water Vapor and Soil Moisture
In addition to precipitation data, some ancillary data coming from remote sensing measurements, namely, the precipitable water vapor and the soil moisture, were considered in this study.
The amount of vertically accumulated water vapor in the atmosphere is defined as the amount of water per unit area. Here, the Precipitable Water vapor over Land product (GCOM-W PWL Research Product—kg/m2) was retrieved at the daily scale and on a spatial resolution of approximately 10 km from the Japan Aerospace Exploration Agency (JAXA) portal of Advanced Microwave Scanning Radiometer-2 (AMSR2), which was launched aboard the Global Change Observation Mission 1st-Water (GCOM-W1) satellite. Data were acquired in HDF format for the period 2016–2020 via ftp service through https://www.eorc.jaxa.jp/AMSR/index_en.html (accessed on 5 April 2023). AMSR2 provides data on global precipitation, ocean wind speed, water vapor, sea ice concentration, brightness, temperature, and soil moisture with the purpose of analyzing variations in water circulation [66]. Estimations of vertically integrated columns of water vapor over land are conducted using polarization differences of 18 and 23 GHz channels, respectively.
Data on soil moisture remotely sensed were obtained from the SMAP satellite available through the National Snow and Ice Data Center (NSIDC) (https://nsidc.org/data/spl3smp_e/versions/3 accessed on 5 April 2023). Soil moisture estimates using SMAP’s passive microwave radiometer have been proven to outperform other satellite soil moisture datasets when compared to in-situ soil moisture data. Since 2015, the SMAP-L3E (Enhanced SMAP data from Level 3 of processing) dataset has been available at the spatial resolution of 9 × 9 km on a daily scale for free. Although the spatial resolution of the product is roughly close to 10 km, which is the common spatial resolution of all datasets, we implemented a bilinear interpolation method to rescale and adjust the product’s spatial resolution. The SM data in the topmost layer were evaluated and discarded if the soil temperature was below 273 °K (~0 °C). The investigated period was again from 2016 to 2020.
A summary of detailed information regarding the two ancillary datasets used in this study is listed in Table 2.
2.3. Methodology
With the growing volume and complexity of data, traditional statistical methods are often inadequate to handle very large datasets. Concerning this matter, data mining techniques have proven to be an essential part of the data analysis process. By leveraging a variety of methods, including machine learning and statistical modeling, data mining enables analysts to identify relationships within large, different, and independent variables. In the context of meteorology and climatology, data mining techniques have shown promising results in enhancing the accuracy and reliability of precipitation estimates, as discussed in the previous section. This technology is used for descriptive and predictive purposes, where the last one is mainly the core of meteorology and atmospheric science. In this study, both purposes have two distinct phases. Phase 1 evaluates and compares daily and half-hourly rainfall estimates in terms of some statistical and categorical indices that are discussed in Section 3.2. Thereafter, the effects of the variables originating from different sources, such as atmosphere or land, on precipitation estimations are examined by two methods (i.e., MLR and ANN) in phase 2, which are briefly discussed in the following section.
Machine learning models require both training (calibration) and testing (validation) procedures to ensure that they are accurate, reliable, and generalizable. While it is necessary that the training data is representative of the entire dataset, there is currently no precise mathematical guideline to determine the minimum size required for these subsets. Despite this, the present study followed suggestions from the literature and randomly assigned 75% of the dataset for training and the remaining subset for assessment.
2.3.1. Multivariant Linear Regression Model
Linear regression is heavily used in atmospheric science to decrease the complexity of relationships among variables and extract the level of their association. In this study, two MLR models were proposed to improve rainfall estimates by merging rainfall remote estimations with PWV and SM. Before applying the procedure to the data, each dataset was standardized using its mean and standard deviation [67] to ensure that all variables contributed at a common scale.
Following studies by [52,53,59], which used water vapor in the atmosphere and soil moisture as ancillary variables, this study merged two models based on an MLR framework, as defined below:
where denotes the value of precipitation estimated by the i-th linear integration model (i = 1, 2), Z is the variable associated with its subscript, and ci are the coefficients of the model variables. Equations (1) and (2) will be hereafter referred to as MLR1 and MLR2, respectively. MLR1 aims to mathematically interconnect the amount of IMERG precipitation estimates, , to the amount of water vapor in the atmosphere, , which can potentially be converted into rain. MLR2 performs similarly to MLR1, including the amount of water received by soil in terms of rain at the very first layer, , as well. The coefficients for the proposed models were calculated using the Harmony Search (HS) algorithm, which is a meta-heuristic and self-learning algorithm that has recently been developed [63,64,65,66,67].
The HS algorithm is an optimization technique that combines existing harmonies to generate new ones using three hyperparameters: Pitch Adjustment Rate (PAR), Harmony Memory Considering Rate (HMCR), and BandWidth (BW). The initial population of harmonies is followed by the generation of new harmonies by means of a random combination of elements from the existing population. Harmonies that provide a higher level of fitting replace the previous ones until a stopping criterion is met. Optimal hyperparameter values have been recommended based on experiments, including BW = 0.1, PAR = 0.1, HMCR = 0.7, and a maximum number of iterations equal to 1500. The HS algorithm has been implemented in MATLAB and further information can be found in [63,64,65,66,67]. Figure 2a shows a flowchart of the HS algorithm used in this study.
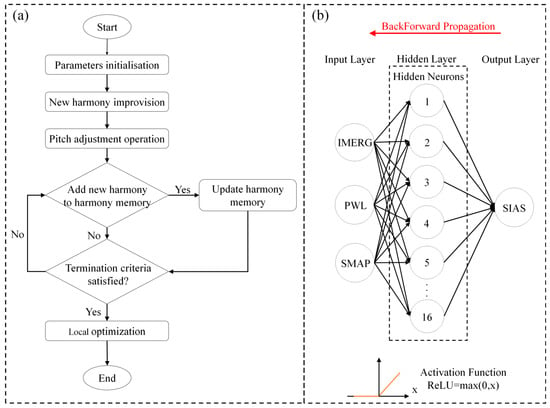
Figure 2.
(a) Harmony search algorithm flowchart; (b) Schematic diagram of neural network architecture, input data, hidden layer, neurons, activation function, and output prediction.
2.3.2. Artificial Neural Networks
Artificial Neural Networks (ANNs) have been developed as generalizations of mathematical models of biological nervous systems [68] and today are used as useful alternatives to traditional statistical modeling techniques in many scientific disciplines.
The architecture of an ANN typically consists of three main types of layers: an input layer, which contains the independent variables, an output layer, which produces the desired output or dependent variable, and one or more hidden layers, which contain neurons that apply activation functions to compute complex relationships between the input and output layers.
The input layer receives the raw input data, while the output layer produces the final output or prediction. The hidden layers are instead responsible for transforming the input data into a format that is better suited for predicting the desired output. Each neuron in a hidden layer applies an activation function to the weighted sum of its inputs, which introduces nonlinearity into the network and allows it to model complex relationships between the input and output variables. Overall, the architecture of an ANN with its input, output, and hidden layers, along with the activation functions used in the hidden layers, play a crucial role in determining the network’s ability to learn from data and, therefore, its performance. A schematic architecture of the neural network used in this work is illustrated in Figure 2b.
This study used a Multilayer Perceptron model with the backpropagation algorithm network; a growing number of papers in the atmospheric literature have demonstrated that MLP provides robust estimates within a fast, simple yet powerful algorithm [4,46,69] that is particularly suitable for mimicking what happens in the atmosphere. Indeed, unlike traditional statistical techniques, the MLP makes no prior assumptions concerning the data distribution and can model highly non-linear functions. Therefore, it has become an attractive alternative to numerical models, particularly in dynamic systems, including those studied by atmospheric science [70].
The MLP used in this study is defined as follows:
where l0 represents the input layer, li represents the i-th hidden layer, Wi is the weight matrix of the i-th layer, and f is the transfer function of the Nl-layered neural network. Output(Z) is the desired ANN output from the initial input layer, Z. As for the MLP case, two integrated ANN models were defined to estimate rainfall as below:
where represents the precipitation estimated from merging initial input layers j, as defined in vectors (7) and (8).
An ANN was trained using the backpropagation algorithm or backward propagation of errors, which is a generalized extension of the Least Mean Squared rule [71]. It works by propagating the error from the output layer back through the network, adjusting the weights of the connections between neurons in order to minimize the difference between the predicted output and the target output. The objective function used to train the MLP is defined as below:
where Pobs(i) and PModel(i) indicate the i-th observed and estimated precipitation, respectively. Applying the backpropagation error algorithm to developed models, the number of layers and neurons was computed by a trial-and-error procedure during the calibration process. Table 3 provides an overview of the details of the parameters and ANN configuration network.

Table 3.
Overview of selected configuration and parameter values for the proposed ANN models.
2.3.3. Performance Analyses
The performances of 3IMERGHH and 3IMERGDF products were evaluated against SIAS ground observations using a pixel-to-pixel comparison. To achieve this, ground station data were interpolated using the Inverse Distance Weighting (IDW) technique to create a raster with a spatial resolution of 10 km, which is the same as that for the IMERG products. In addition to the individual IMERG products, the performances of the MLR and ANN merged models were also evaluated.
Several diagnostic indices were used to quantitatively evaluate the quality of the models and products by quantifying the error within the satellite data and models using ground observations as a reference. These indices included the Pearson Correlation Coefficient (CC), which measures the linear correlation between two datasets, Relative Bias (RBias), which indicates the systematic bias of datasets, Root Mean Square Error (RMSE), which measures the average error magnitude weighting it towards larger errors, Nash-Sutcliffe Efficiency (NSE), which is used to assess the predictive skill of hydrological models, and Willmott Index (WIA), which is used to evaluate the accuracy of model estimations.
In addition to statistical metrics, categorical metrics including Probability Of Detection (POD), Critical Success Index (CSI), and False Alarm Ratio (FAR) were used to analyze the detection capability of the satellite products or simulated models [72] by setting the cut-off value to the 5th percentile of the resampled SIAS rainfall empirical distribution in each grid cell and considering rainfall events exceeding 1 mm per day. Using a contingency table, POD deals with the question of what fraction of the observed events was correctly estimated. FAR represents events identified by the simulation but not confirmed by observations, while CSI describes the overall skill of the simulation relative to reference observations [73]. Table 4 summarizes the statistical and categorical metrics used for the evaluation of individual IMERG products and merged models, where is the observed gauge data of order i, is the estimated data of order i, is the average of dataset, Hits are the days when both satellites and stations recorded the event as rainy, FalseAlarm are the days when satellites recorded rain but the gauges did not, and Misses are the days when satellites did not register rain but the gauges did.

Table 4.
Summary of statistical/categorical indices used to evaluate the satellite precipitation products and the performance of the MLR and ANN models. Bold values indicate a perfect agreement between satellite (or modeled) data and reference data (i.e., SIAS data).
3. Results and Discussion
3.1. Evaluation across Temporal Scales
This section presents the assessment of individual IMERG products with ground reference data, reported in Table 5. Starting with half-hourly data, it is worth noting that this is the first time that this IMERG product has been evaluated against ground-based data at this relatively high temporal resolution over the largest island of the Mediterranean Sea. Over the entire period here investigated (2016–2020), CC = 0.22 along with RMSE = 0.86 mm was achieved, thus denoting a weak correlation between satellite products and observed data. Moreover, negative values of RBias (−1.1) and NSE (−0.4) suggested an underestimation and unsatisfactory estimates for rainfall, respectively, at the half-hourly scale. With reference to categorical indices, a POD with an average value of 0.66 depicted an acceptable detection power of estimate on rainfall/non-rainfall events at such a resolution. This was followed by an adequate value of CSI, equal to 0.64, which indicated that the half-hourly data performed satisfactorily in distinguishing correct warned events out of all warnings issued and unwarned events. Moreover, IMERG half-hourly data provided many false rainfall events occurrences, as reported by FAR equal to 0.41. Whenever the FAR and POD are both relatively high, it is safe to assume that over-warnings occurred [74]. It is noteworthy that the results at this time scale are in accordance with those of previous studies on hourly IMERG precipitation estimates for Sicily [22].

Table 5.
Summary of the spatially averaged evaluation metrics at half-hourly and daily time scales for Sicily.
As expected, switching to daily data improved the performance in terms of both statistical and categorical indices compared to those obtained with half-hourly data. For instance, on average, CC equal to 0.63 indicated a stronger correlation with SIAS measurements compared to half-hourly data. Considering RBias, daily estimations showed a positive value, thus indicating an overestimation of ground-based data. As expected, errors within satellite estimates were larger in terms of RMSE at the daily scale than at the half-hourly scale, with values of 3.3 mm and 0.86 mm, respectively. This was mainly because the daily scale retrieval averaged out some of the short-term variability (including half-hourly estimates) and could be more robust to noise and errors, but it could also result in the loss of important information or a cumulation of errors within sub-daily retrievals. In contrast, the higher temporal resolution of the half-hourly scale captured more short-term variability in rainfall, but this also made the estimates more sensitive to noise and errors in the data, as well as to errors in the processing algorithms. On the other hand, NSE had a notable improvement from negative values to 0.34, indicating preferable estimations and better-matched ground measurements. Considering categorical indices, daily estimates generally exhibited less error in detecting precipitation compared to half-hourly ones, with decreasing FAR values and increasing values of POD and CSI. In this case, it is noteworthy that the results agree with those previously found over the same region by [22]. As these results have been previously proven by many authors [34,75,76,77] across the world and, more specifically, by [22] for Sicily, such an analysis confirms that an aggregating time scale has a significantly positive impact on satellite estimates.
In conclusion, the poor sub-hourly metrics and still improvable daily performances here obtained reveal the need for IMERG products to be corrected with ground observations across regions with complex terrain or improved with other methods such as the blending techniques discussed in Section 3.2.
3.2. Fusion Models Performance Analysis
3.2.1. Primary Results
This section presents the results obtained from applying two blending techniques. As previously mentioned, the main goal of such techniques is to improve the performance of IMERG precipitation estimates by optimally combining them with ancillary datasets that represent atmospheric and land surface characteristics. Half-hourly IMERG data show poor performance for the study area, as discussed in Section 3.1, and, therefore, there is a critical need to improve precipitation estimates at sub-daily/hourly time scales; however, the improvement techniques presented here were applied only to daily scale precipitation. This is mainly because the spatial and temporal resolutions of the ancillary data used here (SM and PWV) were lower than those of the IMERG data; in this case, the only temporal scale that matches with all ancillary data is the daily one.
With reference to the application of the Harmony Search algorithm, the coefficients of integrated multi-linear variant models (Equations (1) and (2)) were determined and are represented in Table 6.

Table 6.
Summary of the coefficients related to the calibration of MLR models.
According to [78], the importance of the predictor variables depends on the weights of the coefficients within a linear regression. In this case, as expected, IMERG had the heaviest weight among all datasets, while PWV had a stronger impact than SM on the regression procedure, unlike the results obtained by [79] for the Iberian Peninsula.
Figure 3 contains the spatial mean of the temporally averaged values for statistic and categoric metrics for daily rainfall events for the period 2016–2020. To facilitate visual comparison, all metrics were transformed into a scale that ranged between 0 and 1, with 1 representing the ideal value. Thus, a larger area on the spider plot indicates better model performance. This was also applied to RBias, which was converted to normalized bias (hereafter referred to as NBias) simply dividing by the total sample size.
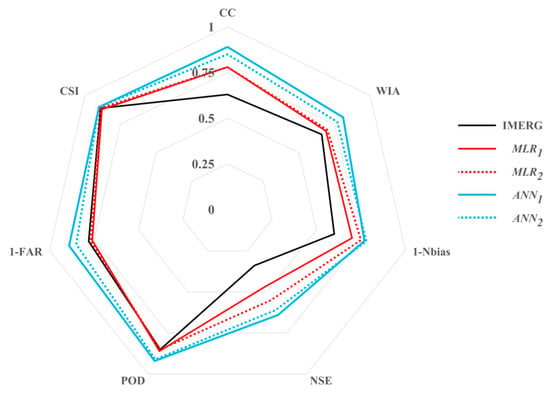
Figure 3.
Spider plot showing the results of the general comparison of satellite precipitation estimates and the MLR and ANN models with observed data from SIAS rain gauge networks.
As the evaluation metrics reported in Figure 3 suggest, ANN2 outperformed other models and the individual IMERG product. More generally, CC indicated a very high degree of agreement with reference to precipitation when passing from individual IMERG estimates to merged models, as shown in Figure 3. The values of NSE of the merged models imply an overall modest improvement compared to individual satellite products. Indeed, ranging from 0.55 to 0.64, NSE fell within the ideal range commonly defined for a model [80] and showed satisfactory estimates of merged models. Comparing the two methods of blending data, i.e., ANN and MLR, the use of ANNs led to a decrease in the magnitude of errors, as demonstrated by the highest values of WIA (0.81) and 1-NBias (0.77), indicating less overestimated data. MLR1 produced a marginal improvement in the wetness index anomaly (WIA) to 0.70 compared to IMERG’s WIA of 0.66. Conversely, MLR2′s total increase in WIA of 0.3 was even less than the improvement attained by MLR1. This adverse performance of MLR2 compared to MLR1 may have been due to a nonlinear relation between rainfall and ancillary variables that made the WIA unsuitable to describe such a relationship. In addition, except for MLR1 and MLR2, a general slight improvement was achieved in terms of POD and FAR when compared to IMERG estimates; higher values were reached for ANN2 (i.e., 7% and 11%, respectively), which was recognized as the best estimator among all. From one point of view, improvements in categorical indicators were less considerable compared to improvements in statistical indices. This was a clear sign that improvements due to the blending techniques used were mainly reflected in estimations of rainfall intensity, volume, and overall trends rather than in the detection ability.
3.2.2. Spatial Analysis
To further evaluate the performance of the merged models for the study region, Figure 4 and Figure 5 show the spatial distribution of selected statistical and categorical metrics, respectively, for Sicily for the period 2016–2020. Metrics were calculated using equations previously defined in Section 2.3, considering daily values as estimated from IMERG products and measured by the SIAS network.
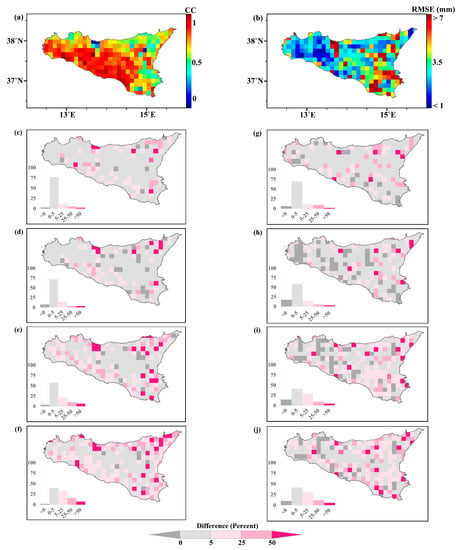
Figure 4.
Comparison of IMERG data and model estimates. Panels on the first row (a,b) show the spatial distribution of CC and RMSE for IMERG individual products with reference to SIAS data, while the subsequent panels (c–j) illustrate the relative deviations of each blending model’s estimates from the IMERG data. The relative frequency function (percentage) of pixels falling within different classes is displayed inside each panel.
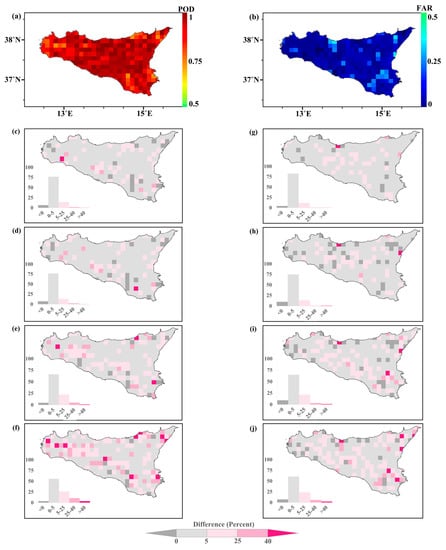
Figure 5.
Same as Figure 4 but for categorical metrics (i.e., POD and FAR). Scale bars are modified to the ranges where the POD and FAR fell, i.e., 0.5–1 and 0–0.5, respectively. Panels on the first row (a,b) show the spatial distribution of POD and FAR for IMERG individual products with reference to SIAS data, while the subsequent panels (c–j) illustrate the relative deviations of each blending model’s estimates from the IMERG data. The relative frequency function (percentage) of pixels falling within different classes is displayed inside each panel.
With reference to Figure 4 and Figure 5, the first row (panels a and b) shows the spatial distribution of the CC and RMSE calculated using IMERG daily estimations and SIAS reference data. To better highlight improvements due to the application of blending models and their possible spatial patterns, rows 2 through 5 (including panels c to j) instead show the percentage variation between the metrics obtained from the estimates of the blending model and the IMERG product, here used as a term of comparison, for each pixel. The difference was calculated using the following formula: [(Model Value − IMERG Value)/IMERG Value] × 100.
Figure 4a,b depict the spatial distribution of the CC for IMERG, revealing that a vast majority of pixels exhibited good agreement with SIAS measurements (e.g., orange to red pixels), particularly in the central and southern regions. On the contrary, regions with complex orography on the east and northeast sides and the coastlines on the north and east sides of the island show less significant correlations. The spatial distribution of errors, as demonstrated by the RMSE map in Figure 4b, follows a similar pattern, with an average RMSE below 3.5 mm observed across the left-half side of the island, but increasing to over 7 mm in the south-eastern corner. This distinct spatial pattern of error distribution is aligned with patterns previously detected by [22,37]. Expectedly, CC and RMSE spatial distribution maps by IMERG V06 for 2016–2020 were quite similar to those of version 03 by [22] in 2015–2016 for Sicily. The worst performances along the coastlines are likely due to the weakness of the IMERG retrieval techniques in distinguishing the different radiative characteristics of hydrometeors over the land and ocean [14,25].
The spatial maps of differences depicted in Figure 4 reveal that all the blending models successfully improved precipitation estimations in terms of statistical metrics. Specifically, the MLR models improved the CC, especially on the east side and in the southern regions, despite some negative results indicated by dark grey pixels in Figure 4. Greater improvements were reached with the ANN models. Specifically, the ANN2 model improved pixels with previously weak values of CC that were not improved by the MLR models. The ANN models showed an increase in the level of agreement across the island, characterized by a pattern that included a 5–25% improvement along the coastline. Over 25% of the increase in agreement was concentrated in the eastern corners of the island, where the highest values of disagreement were observed. Conversely, there were either zero or minimal changes in the central parts of the island, where the level of agreement was already high. This improvement pattern was further accentuated by the use of the model ANN2.
Regarding the RMSE, the relative frequency function indicated that the number of pixels with worsened rainfall estimations decreased from MLRs to ANNs. Most pixels in MLR1 exhibited negligible changes or remained unchanged, while the number of pixels with reduced RMSE increased in MLR2, even though this was compensated by many worsened estimations, especially in the west corner of the island, where the accuracy of remote sensing instruments was adversely affected by complex oceanic streams. Consequently, no significant spatial improvements in RMSE were observed in MLR1 or MLR2. However, as for the CC, ANNs not only followed a pattern of error reduction along the coastline of a 5–25% reduction in RMSE but also demonstrated a significant increase in the frequency of pixels that were improved by over 50% on the frequency function, with a concentration of pixels improved by over 25% on the right-half side of the island. Furthermore, in addition to the aforementioned improvement pattern, there was a reduction of over 50% in the high values of RMSE observed in a few individual pixels scattered throughout the island. Taken together, these findings suggest that the ANN models, specifically ANN2, yielded notable improvements in estimating precipitation patterns across the island, with an ability to capture the complex spatial variability of precipitation.
The findings from the analysis of the two categorical indices, POD and FAR, are presented in Figure 5a,b along with the deviation spatial maps of the proposed models (Figure 5c–j). The maps of POD and FAR illustrate the ability of IMERG to effectively distinguish daily rainfall events from non-rainfall events at various locations with a 95% probability of detection above the threshold of 1 mm. Overall, IMERG showed promising detection ability, with values approaching perfection for both POD and FAR, which is aligned with the spatiotemporally averaged values for IMERG reported in Figure 3 (POD = 0.85, FAR = 0.22). Nevertheless, some errors persisted, particularly in the three corners of the island. The spatial maps of categorical indices are aligned with the results of IMERG V03 by [22] and the Tropical Rainfall Measuring Mission (TRMM) Multisatellite Precipitation Analysis (TMPA) product by [37] for the region, as well as the spatial maps of CC and RMSE. Most pixels remained unchanged or experienced less than 5% improvement with all models, particularly MLRs. Conversely, ANN models, particularly ANN2, effectively improved detection capability in the poorly detected regions on the east and west corners, as demonstrated by the increase in dark pink pixels, while also substantially reducing the number of worsened pixels. Overall, the ANN2 blending model was the most effective approach for improving detection in pixels that were frequently associated with inaccurate detections.
Examining in detail the major inconsistencies and errors between the gauge measurements, IMERG daily products, and daily estimations corrected by applying blending models, it is possible to notice worse performances over the eastern region, which is poorly gauged (especially in the southeast corner) and characterized by high intensity and depth of rainfall [28] and diverse mechanisms of precipitation (i.e., orographic rather than cyclonic) that can be challenging to estimate accurately due to interactions with complex orography causing large spatial variations [81,82,83].
A distinct spatial pattern of errors was observed repeatedly for Sicily when using TMPA product by [37], as well as with different old versions of IMERG products by [22], which was also identified in the present study using the latest version of an IMERG individual product. Hopefully, this pattern of errors was efficiently detected and addressed by the ANN models to obtain a more consistent spatial map of evaluation metrics. This additionally demonstrates the ANN2 model’s capability of integrating the response of soil moisture and precipitable water vapor of the atmosphere into the precipitation correction process more effectively than the MLR process.
3.2.3. Seasonality Analysis
To further diagnose the models’ inter-comparison, Figure 6 illustrates the spatially averaged monthly time series of rainfall records from SIAS, along with generated estimates by IMERG, MLR, and ANN, for the period 2016–2020.
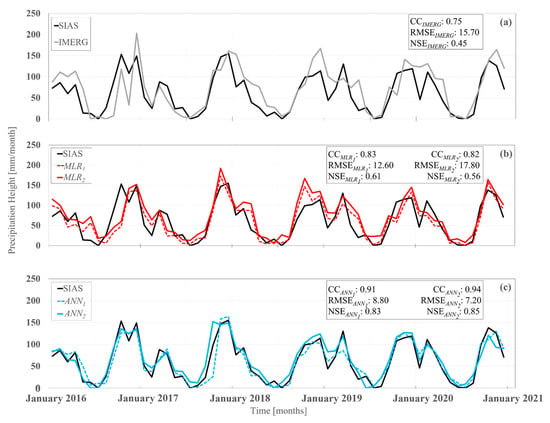
Figure 6.
Monthly average rainfall series from 2016 to 2020 for SIAS (black line) compared to IMERG (grey line) in panel (a), generated MLR models (solid and dashed red lines) in panel (b), and generated ANN models (solid and dashed blue lines) in panel (c).
As shown in Figure 6, all rainfall products generally showed high agreement with the recorded rainfall pattern of the region, with wet autumn and spring seasons and dry summers. Considering NBias in Figure 3, a tendency towards overestimation was visible within all series, particularly during the wet seasons, which was significantly reduced by the ANN models. Generally, the blending models, particularly the ANNs, resulted in substantial increases in agreement with ground records compared to the individual IMERG product.
From Figure 6, a strong agreement between MLR1 and SIAS records (CC = 0.83) at the monthly scale can be observed. After incorporating the SM variable into MLR2, a relative improvement compared to IMERG individual estimations was observed. However, it was outweighed by an increase in RMSE and a decrease in NSE values from 12.6 to 17.8 mm and from 0.61 to 0.56, respectively, when compared to MLR1. This indicated that either SM was highly correlated with the PWV, leading to redundant information being included in the model, or a simple linear model was not able to extract the relationships among variables, which ANN models do efficiently.
ANN models provided a time series close to the reference data, as shown by the NSE over 0.83 and CC over 0.91, with the magnitude of errors almost halved from 15.7 mm in IMERG to 7.2 mm in the ANN2 model. After the analysis of the wet and dry seasons, the merged models appeared to be more consistent with SIAS measurements during dry months. Conversely, estimations showed more deviation from the reference data in wet seasons, mostly with reference to winter peaks, when the average depth of rainfall exceeded 100 mm rainfall. Comparing ANN2 and ANN1 for some wet months (e.g., October and December 2018, March and December 2019, and January and October 2020, to name a few), it is possible to observe that the SM variable contributed to improving the accuracy of precipitation estimates in wet months, as expected. On the other hand, in dry months, only negligible improvements were observed. Among all blending models, once again, ANN2 appeared to be more aligned with the SIAS ground data and outperformed other models in terms of seasonality agreement.
3.2.4. Sensitivity Analysis
When blending independent variables to improve rainfall estimates, it is important to assess the sensitivity of the results to each input ancillary variable. One common approach is to perform a sensitivity analysis by systematically removing one variable at a time from a model that includes all variables and quantifying the impact of that change on the accuracy of the estimations. The sensitivity of a model to the removal of individual input variables can be measured by computing the increase in the Mean Squared Error (MSE) of the model after the variable is removed while keeping the other input variables constant. The larger the increase in MSE, the more sensitive the model is to the removal of the variable, thus indicating the importance of that variable for the model performance.
The variable importance methodology first introduced by [78] helps to recognize influential variables and the relative contribution of each in improving the capability of a model in reproducing precipitation. The first step in such an analysis is to fit a model to a dataset using a chosen set of input variables. The baseline MSE of the model is then calculated using the chosen set of input variables. For each input variable, the variable is removed from the model, and the model is refitted to the data using the remaining variables. The new MSE for the model with the variable removed is then calculated. The percentage increase in MSE for each variable, hereafter named %IncMSE, was calculated by taking the difference between the baseline MSE and the new MSE after removing the variable and dividing the result by the baseline MSE. The input variables were then ranked based on their %IncMSE values, with larger values indicating greater importance. The results obtained by applying the variable importance test for the three explanatory variables (i.e., SM, PWV, and IMERG products) are presented in Figure 7.
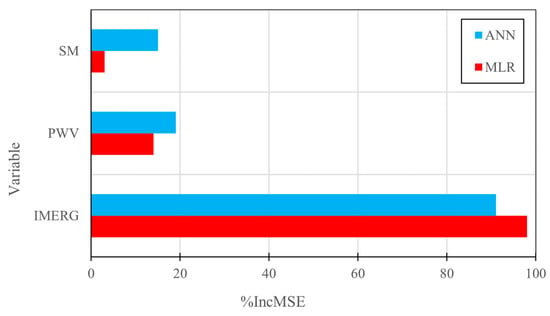
Figure 7.
Variable importance plot for IMERG, PWV, and SM: %IncMSE is the percentage increase in mean square error.
As expected, IMERG satellite precipitation was ranked as the most important estimator variable, showing its strong impact in model estimations by producing the highest values of %IncMSE, i.e., 91% and 98% for MLR and ANN, respectively. Moreover, PWV was ranked as the next most significant variable by showing high %IncMSE, i.e., 14% and 19% for MLR and ANN, respectively. This meant that when including the PWV variable in the blending models, the mean square error between reference records and generated models decreased by an average of 14–19%. Comparing the values of WIA in Figure 3 for IMERG (0.69) to those of MLR1 (0.69) and ANN1 (0.77) suggested similar improvements in terms of reducing the magnitude of errors. Moreover, as previously observed in Figure 3, SM played a minor role in MLR by slightly improving the performance of the model. Here, the removal of the SM variable also caused negligible changes, with the lowest value of %IncMSE (i.e., 3%) observed in MLR2. This supports our previous observations that SM did not contribute to a considerable improvement within the linear regression blending model. Conversely, in a non-linear model such as ANN, the removal of the SM variable led to an increase in error, with a %IncMSE equal to approximately 15% observed in ANN2. This finding is consistent with our previous observations from Figure 3, where the inclusion of SM and PWV within the ANN model led to a decrease in WIA from 0.70 to 0.69. These corroborate the findings reported in Section 3.2.1, which suggested that the ANN model outperformed the MLR model in accurately reconstructing precipitation estimates through the merging of IMERG products with PWV and SM variables.
4. Conclusions
Accurate and reliable precipitation data are a crucial input variable used in many hydrologic and hydraulic modeling frameworks, particularly in the context of climate change-induced sustainability and risk management policies. This study explored, for the first time in Sicily, the performance of half-hourly rainfall estimates and daily IMERG estimates in reproducing observed precipitation for the period 2016–2020. While the daily IMERG estimates provided satisfactory results for the investigated region, the half-hourly assessment revealed potential weaknesses, such as an inability to accurately distinguish between rainfall and non-rainfall events or represent precise values for rainfall depth.
Four merging models were developed within a multivariant regression and a neural network framework. To evaluate the improvement in detection power due to the application of the merged models, different statistical (i.e., CC, NBias, and RMSE) and categorical (i.e., POD, FAR, and CSI) indicators were used. The results show that exploiting SM and PWV data for the assessment of daily precipitation leads to improvements in the estimation of precipitation provided by IMERG products. Furthermore, the artificial neural networks and multiple linear regression fusion techniques improved the accuracy compared to the original IMERG product. Consistent with the findings reported by [4], who reported the failure of linear regression approaches in capturing the intricate and spatiotemporal nonlinear relationships between precipitation and other land/atmospheric variables compared with ANN approaches, this study showed significant improvements in precipitation estimation when using neural network models to merge SM and PWV with IMERG data compared to multivariant linear regression models. As the sensitivity analysis suggested, SM and PWV contributed efficiently and almost equally to enhancing rainfall estimates within an ANN framework. Despite the considerable improvement due to the blending models, a minority of errors still existed, especially in the west and northwest regions where the rainfall depth and intensity were both high.
In conclusion, the suggested ANN-based correction framework offers a promising solution for generating more reliable inputs in hydrological studies, particularly in complex terrain areas that are prone to extreme events such as the Mediterranean region. Its potential benefits extend to various scales, including catchment-level assessments and macro- and regional-level evaluations, which can contribute to water-related risk reduction efforts. To further refine the physically based ANN representation, it might be worthwhile to incorporate additional interconnected variables from the surface or atmosphere, such as land surface temperature, humidity, and wind, in future research.
Author Contributions
Conceptualization, research methodology, data curation, analysis, code scripting, original manuscript composition, reviewing and editing, and validation of data, N.B.; conceptualization, research methodology, interpretation and analysis of data, reviewing and editing, A.F.; conceptualization, research methodology, interpretation and analysis of data, reviewing and editing, L.V.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The ground measurement dataset related to this article was provided by the regional agency SIAS (Servizio Informativo Agrometeorologico Siciliano) through a formal request (http://www.sias.regione.sicilia.it/ accessed on 5 April 2023). The publicly available satellite datasets of IMERG, PWV, and SM can be found at the following respective locations: https://gpm.nasa.gov/data/directory, https://www.eorc.jaxa.jp/AMSR/index_en.html, and https://nsidc.org/data/spl3smp_e/versions/3 accessed on 5 April 2023.
Acknowledgments
We would like to express our gratitude for the opportunity to conduct this research and for the resources provided by the University of Palermo.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kucera, P.A.; Ebert, E.E.; Turk, F.J.; Levizzani, V.; Kirschbaum, D.; Tapiador, F.J.; Loew, A.; Borsche, M. Precipitation from space: Advancing Earth system science. Bull. Am. Meteorol. Soc. 2013, 94, 365–375. [Google Scholar] [CrossRef]
- Luo, X.; Wu, W.; He, D.; Li, Y.; Ji, X. Hydrological simulation using TRMM and CHIRPS precipitation estimates in the lower Lancang-Mekong river basin. Chin. Geogr. Sci. 2019, 29, 13–25. [Google Scholar] [CrossRef]
- Tian, F.; Hou, S.; Yang, L.; Hu, H.; Hou, A. How does the evaluation of the GPM IMERG rainfall product depend on gauge density and rainfall intensity? J. Hydrometeorol. 2018, 19, 339–349. [Google Scholar] [CrossRef]
- Wehbe, Y.; Temimi, M.; Adler, R.F. Enhancing precipitation estimates through the fusion of weather radar, satellite retrievals, and surface parameters. Remote Sens. 2020, 12, 1342. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Braithwaite, D.; Hsu, K.; Joyce, R.; Xie, P.; Yoo, S.-H. NASA global precipitation measurement (GPM) integrated multi-satellite retrievals for GPM (IMERG). Algorithm Theor. Basis Doc. Version 2015, 4. [Google Scholar]
- Smith, T.M.; Arkin, P.A.; Bates, J.J.; Huffman, G.J. Estimating bias of satellite-based precipitation estimates. J. Hydrometeorol. 2006, 7, 841–856. [Google Scholar] [CrossRef]
- Navarro, A.; García-Ortega, E.; Merino, A.; Sánchez, J.L.; Kummerow, C.; Tapiador, F.J. Assessment of IMERG precipitation estimates over Europe. Remote Sens. 2019, 11, 2470. [Google Scholar] [CrossRef]
- Lockhoff, M.; Zolina, O.; Simmer, C.; Schulz, J. Representation of precipitation characteristics and extremes in regional reanalyses and satellite-and gauge-based estimates over western and central Europe. J. Hydrometeorol. 2019, 20, 1123–1145. [Google Scholar] [CrossRef]
- Islam, M.A.; Yu, B.; Cartwright, N. Assessment and comparison of five satellite precipitation products in Australia. J. Hydrol. 2020, 590, 125474. [Google Scholar] [CrossRef]
- Jiang, L.; Bauer-Gottwein, P. How do GPM IMERG precipitation estimates perform as hydrological model forcing? Evaluation for 300 catchments across Mainland China. J. Hydrol. 2019, 572, 486–500. [Google Scholar] [CrossRef]
- Tang, G.; Ma, Y.; Long, D.; Zhong, L.; Hong, Y. Evaluation of GPM Day-1 IMERG and TMPA Version-7 legacy products over Mainland China at multiple spatiotemporal scales. J. Hydrol. 2016, 533, 152–167. [Google Scholar] [CrossRef]
- Prakash, S.; Mitra, A.K.; AghaKouchak, A.; Liu, Z.; Norouzi, H.; Pai, D. A preliminary assessment of GPM-based multi-satellite precipitation estimates over a monsoon dominated region. J. Hydrol. 2018, 556, 865–876. [Google Scholar] [CrossRef]
- Mahmoud, M.T.; Hamouda, M.A.; Mohamed, M.M. Spatiotemporal evaluation of the GPM satellite precipitation products over the United Arab Emirates. Atmos. Res. 2019, 219, 200–212. [Google Scholar] [CrossRef]
- Xin, Y.; Yang, Y.; Chen, X.; Yue, X.; Liu, Y.; Yin, C. Evaluation of IMERG and ERA5 precipitation products over the Mongolian Plateau. Sci. Rep. 2022, 12, 21776. [Google Scholar] [CrossRef]
- Tan, M.L.; Duan, Z. Assessment of GPM and TRMM precipitation products over Singapore. Remote Sens. 2017, 9, 720. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, L.-F.; Bras, R.L. Evaluation of the quality of precipitation products: A case study using WRF and IMERG data over the central United States. J. Hydrometeorol. 2018, 19, 2007–2020. [Google Scholar] [CrossRef]
- Sungmin, O.; Kirstetter, P.E. Evaluation of diurnal variation of GPM IMERG-derived summer precipitation over the contiguous US using MRMS data. Q. J. R. Meteorol. Soc. 2018, 144, 270–281. [Google Scholar]
- Wen, Y.; Behrangi, A.; Lambrigtsen, B.; Kirstetter, P.-E. Evaluation and uncertainty estimation of the latest radar and satellite snowfall products using SNOTEL measurements over mountainous regions in western United States. Remote Sens. 2016, 8, 904. [Google Scholar] [CrossRef]
- Gebregiorgis, A.S.; Kirstetter, P.E.; Hong, Y.E.; Gourley, J.J.; Huffman, G.J.; Petersen, W.A.; Xue, X.; Schwaller, M.R. To what extent is the day 1 GPM IMERG satellite precipitation estimate improved as compared to TRMM TMPA-RT? J. Geophys. Res. Atmos. 2018, 123, 1694–1707. [Google Scholar] [CrossRef]
- Pradhan, R.K.; Markonis, Y.; Godoy, M.R.V.; Villalba-Pradas, A.; Andreadis, K.M.; Nikolopoulos, E.I.; Papalexiou, S.M.; Rahim, A.; Tapiador, F.J.; Hanel, M. Review of GPM IMERG performance: A global perspective. Remote Sens. Environ. 2022, 268, 112754. [Google Scholar] [CrossRef]
- Rebora, N.; Molini, L.; Casella, E.; Comellas, A.; Fiori, E.; Pignone, F.; Siccardi, F.; Silvestro, F.; Tanelli, S.; Parodi, A. Extreme rainfall in the Mediterranean: What can we learn from observations? J. Hydrometeorol. 2013, 14, 906–922. [Google Scholar] [CrossRef]
- Caracciolo, D.; Francipane, A.; Viola, F.; Noto, L.V.; Deidda, R. Performances of GPM satellite precipitation over the two major Mediterranean islands. Atmos. Res. 2018, 213, 309–322. [Google Scholar] [CrossRef]
- Hisam, E.; Mehr, A.D.; Alganci, U.; Seker, D.Z. Comprehensive evaluation of Satellite-Based and reanalysis precipitation products over the Mediterranean region in Turkey. Adv. Space Res. 2022, 71, 3005–3021. [Google Scholar] [CrossRef]
- Retalis, A.; Katsanos, D.; Michaelides, S.; Tymvios, F. Evaluation of high-resolution satellite precipitation data over the Mediterranean Region. In Precipitation Science; Elsevier: Amsterdam, The Netherlands, 2022; pp. 159–175. [Google Scholar]
- Noto, L.V.; Cipolla, G.; Francipane, A.; Pumo, D. Climate change in the mediterranean basin (part I): Induced alterations on climate forcings and hydrological processes. Water Resour. Manag. 2023, 37, 2287–2305. [Google Scholar] [CrossRef]
- Orth, R.; Zscheischler, J.; Seneviratne, S.I. Record dry summer in 2015 challenges precipitation projections in Central Europe. Sci. Rep. 2016, 6, 28334. [Google Scholar] [CrossRef] [PubMed]
- Shukla, P.R.; Skea, J.; Calvo Buendia, E.; Masson-Delmotte, V.; Pörtner, H.O.; Roberts, D.; Zhai, P.; Slade, R.; Connors, S.; Van Diemen, R. IPCC, 2019: Climate Change and Land: An IPCC special report on climate change, desertification, land degradation, sustainable land management, food security, and greenhouse gas fluxes in terrestrial ecosystems. 2019, in press. Available online: https://spiral.imperial.ac.uk/handle/10044/1/76618 (accessed on 6 April 2023).
- Treppiedi, D.; Cipolla, G.; Francipane, A.; Noto, L. Detecting precipitation trend using a multiscale approach based on quantile regression over a Mediterranean area. Int. J. Climatol. 2021, 41, 5938–5955. [Google Scholar] [CrossRef]
- Nanni, P.; Peres, D.J.; Musumeci, R.E.; Cancelliere, A. Worry about Climate Change and Urban Flooding Risk Preparedness in Southern Italy: A Survey in the Simeto River Valley (Sicily, Italy). Resources 2021, 10, 25. [Google Scholar] [CrossRef]
- Aronica, G.; Brigandí, G.; Morey, N. Flash floods and debris flow in the city area of Messina, north-east part of Sicily, Italy in October 2009: The case of the Giampilieri catchment. Nat. Hazards Earth Syst. Sci. 2012, 12, 1295–1309. [Google Scholar] [CrossRef]
- Arnone, E.; Pumo, D.; Viola, F.; Noto, L.; La Loggia, G. Rainfall statistics changes in Sicily. Hydrol. Earth Syst. Sci. 2013, 17, 2449–2458. [Google Scholar] [CrossRef]
- Diodato, N. Climatic fluctuations in southern Italy since the 17th century: Reconstruction with precipitation records at Benevento. Clim. Chang. 2007, 80, 411–431. [Google Scholar] [CrossRef]
- Noto, L.; Cipolla, G.; Pumo, D.; Francipane, A. Climate Change in the Mediterranean Basin (Part II): A Review of Challenges and Uncertainties in Climate Change Modeling and Impact Analyses. Water Resour. Manag. 2023, 37, 2307–2323. [Google Scholar] [CrossRef]
- Moazami, S.; Najafi, M. A comprehensive evaluation of GPM-IMERG V06 and MRMS with hourly ground-based precipitation observations across Canada. J. Hydrol. 2021, 594, 125929. [Google Scholar] [CrossRef]
- Freitas, E.D.S.; Coelho, V.H.R.; Xuan, Y.; de CD Melo, D.; Gadelha, A.N.; Santos, E.A.; Galvão, C.D.O.; Ramos Filho, G.M.; Barbosa, L.R.; Huffman, G.J. The performance of the IMERG satellite-based product in identifying sub-daily rainfall events and their properties. J. Hydrol. 2020, 589, 125128. [Google Scholar] [CrossRef]
- Manz, B.; Páez-Bimos, S.; Horna, N.; Buytaert, W.; Ochoa-Tocachi, B.; Lavado-Casimiro, W.; Willems, B. Comparative ground validation of IMERG and TMPA at variable spatiotemporal scales in the tropical Andes. J. Hydrometeorol. 2017, 18, 2469–2489. [Google Scholar] [CrossRef]
- Lo Conti, F.; Hsu, K.-L.; Noto, L.V.; Sorooshian, S. Evaluation and comparison of satellite precipitation estimates with reference to a local area in the Mediterranean Sea. Atmos. Res. 2014, 138, 189–204. [Google Scholar] [CrossRef]
- Chiaravalloti, F.; Brocca, L.; Procopio, A.; Massari, C.; Gabriele, S. Assessment of GPM and SM2RAIN-ASCAT rainfall products over complex terrain in southern Italy. Atmos. Res. 2018, 206, 64–74. [Google Scholar] [CrossRef]
- Shah, R.D.; Mishra, V. Development of an experimental near-real-time drought monitor for India. J. Hydrometeorol. 2015, 16, 327–345. [Google Scholar] [CrossRef]
- Ringard, J.; Seyler, F.; Linguet, L. A quantile mapping bias correction method based on hydroclimatic classification of the Guiana shield. Sensors 2017, 17, 1413. [Google Scholar] [CrossRef]
- Tian, Y.; Peters-Lidard, C.D.; Eylander, J.B. Real-time bias reduction for satellite-based precipitation estimates. J. Hydrometeorol. 2010, 11, 1275–1285. [Google Scholar] [CrossRef]
- Ajaaj, A.A.; Mishra, A.; Khan, A.A. Comparison of BIAS correction techniques for GPCC rainfall data in semi-arid climate. Stoch. Environ. Res. Risk Assess. 2016, 30, 1659–1675. [Google Scholar] [CrossRef]
- Chen, J.; Brissette, F.P.; Chaumont, D.; Braun, M. Finding appropriate bias correction methods in downscaling precipitation for hydrologic impact studies over North America. Water Resour. Res. 2013, 49, 4187–4205. [Google Scholar] [CrossRef]
- Chappell, A.; Renzullo, L.J.; Raupach, T.H.; Haylock, M. Evaluating geostatistical methods of blending satellite and gauge data to estimate near real-time daily rainfall for Australia. J. Hydrol. 2013, 493, 105–114. [Google Scholar] [CrossRef]
- Xu, L.; Chen, N.; Moradkhani, H.; Zhang, X.; Hu, C. Improving global monthly and daily precipitation estimation by fusing gauge observations, remote sensing, and reanalysis data sets. Water Resour. Res. 2020, 56, e2019WR026444. [Google Scholar] [CrossRef]
- Zhang, L.; Li, X.; Zheng, D.; Zhang, K.; Ma, Q.; Zhao, Y.; Ge, Y. Merging multiple satellite-based precipitation products and gauge observations using a novel double machine learning approach. J. Hydrol. 2021, 594, 125969. [Google Scholar] [CrossRef]
- Yin, Z.-Y.; Zhang, X.; Liu, X.; Colella, M.; Chen, X. An assessment of the biases of satellite rainfall estimates over the Tibetan Plateau and correction methods based on topographic analysis. J. Hydrometeorol. 2008, 9, 301–326. [Google Scholar] [CrossRef]
- Beyk Ahmadi, N.; Rahimzadegan, M. Improving the accuracy of global precipitation measurement integrated multi-satellite retrievals (GPM IMERG) using atmosphere precipitable water and altitude in climatic regions of Iran. Int. J. Remote Sens. 2021, 42, 2759–2781. [Google Scholar] [CrossRef]
- Nosratpour, R.; Rahimzadegan, M.; Beikahmadi, N. Introducing a merged precipitation satellite model using satellite precipitation products, land surface temperature, and precipitable water vapor. Geocarto Int. 2022, 37, 11782–11812. [Google Scholar] [CrossRef]
- Sharifi, E.; Saghafian, B.; Steinacker, R. Downscaling satellite precipitation estimates with multiple linear regression, artificial neural networks, and spline interpolation techniques. J. Geophys. Res. Atmos. 2019, 124, 789–805. [Google Scholar] [CrossRef]
- Alexakis, D.; Tsanis, I. Comparison of multiple linear regression and artificial neural network models for downscaling TRMM precipitation products using MODIS data. Environ. Earth Sci. 2016, 75, 1077. [Google Scholar] [CrossRef]
- Kayri, M.; Kayri, I.; Gencoglu, M.T. The performance comparison of Multiple Linear Regression, Random Forest and Artificial Neural Network by using photovoltaic and atmospheric data. In Proceedings of the 2017 14th International Conference on Engineering of Modern Electric Systems (EMES), Oradea, Romania, 1–2 June 2017; pp. 1–4. [Google Scholar]
- Nandakumar, S.; Valarmathi, R.; Juliet, P.S.; Brindha, G. Artificial Neural Network for Rainfall Analysis Using Deep Learning Techniques. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2021; p. 042022. [Google Scholar]
- Folino, G.; Guarascio, M.; Chiaravalloti, F.; Gabriele, S. A Deep Learning based architecture for rainfall estimation integrating heterogeneous data sources. In Proceedings of the 2019 International Joint Conference on Neural Networks (IJCNN), Budapest, Hungary, 14–19 July 2019; pp. 1–8. [Google Scholar]
- Noto, L.; Beikahmadi, N.; Pumo, D.; Francipane, A. An Artificial Intelligence–Based Blending of Satellite products across Mediterranean Island of Sicily, Italy using GPM-IMERG V06 Final Run. In Proceedings of the Copernicus Meetings, Bonn, Germany, 5–9 September 2022. [Google Scholar]
- Brocca, L.; Ciabatta, L.; Massari, C.; Moramarco, T.; Hahn, S.; Hasenauer, S.; Kidd, R.; Dorigo, W.; Wagner, W.; Levizzani, V. Soil as a natural rain gauge: Estimating global rainfall from satellite soil moisture data. J. Geophys. Res. Atmos. 2014, 119, 5128–5141. [Google Scholar] [CrossRef]
- Brocca, L.; Moramarco, T.; Melone, F.; Wagner, W. A new method for rainfall estimation through soil moisture observations. Geophys. Res. Lett. 2013, 40, 853–858. [Google Scholar] [CrossRef]
- Pumo, D.; Francipane, A.; Cannarozzo, M.; Antinoro, C.; Noto, L.V. Monthly hydrological indicators to assess possible alterations on rivers’ flow regime. Water Resour. Manag. 2018, 32, 3687–3706. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, K.; Dong, N.; Wang, H. Optimally integrating multi-source products for improving long series precipitation precision by using machine learning methods. J. Hydrol. 2022, 609, 127707. [Google Scholar] [CrossRef]
- Di Piazza, A.; Lo Conti, F.; Noto, L.V.; Viola, F.; La Loggia, G. Comparative analysis of different techniques for spatial interpolation of rainfall data to create a serially complete monthly time series of precipitation for Sicily, Italy. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 396–408. [Google Scholar] [CrossRef]
- Francipane, A.; Cipolla, G.; Maltese, A.; La Loggia, G.; Noto, L. Using very high resolution (VHR) imagery within a GEOBIA framework for gully mapping: An application to the Calhoun Critical Zone Observatory. J. Hydroinform. 2020, 22, 219–234. [Google Scholar] [CrossRef]
- Forestieri, A.; Lo Conti, F.; Blenkinsop, S.; Cannarozzo, M.; Fowler, H.J.; Noto, L.V. Regional frequency analysis of extreme rainfall in Sicily (Italy). Int. J. Climatol. 2018, 38, e698–e716. [Google Scholar] [CrossRef]
- Yang, X.-S. Harmony search as a metaheuristic algorithm. In Music-Inspired Harmony Search Algorithm; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–14. [Google Scholar]
- Chen, J.; Pan, Q.-K.; Li, J.-Q. Harmony search algorithm with dynamic control parameters. Appl. Math. Comput. 2012, 219, 592–604. [Google Scholar] [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Mahdavi, M.; Fesanghary, M.; Damangir, E. An improved harmony search algorithm for solving optimization problems. Appl. Math. Comput. 2007, 188, 1567–1579. [Google Scholar] [CrossRef]
- Manjarres, D.; Landa-Torres, I.; Gil-Lopez, S.; Del Ser, J.; Bilbao, M.N.; Salcedo-Sanz, S.; Geem, Z.W. A survey on applications of the harmony search algorithm. Eng. Appl. Artif. Intell. 2013, 26, 1818–1831. [Google Scholar] [CrossRef]
- Hassoun, M.H. Fundamentals of Artificial Neural Networks; MIT Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Chen, H.; Chandrasekar, V.; Cifelli, R.; Xie, P. A machine learning system for precipitation estimation using satellite and ground radar network observations. IEEE Trans. Geosci. Remote Sens. 2019, 58, 982–994. [Google Scholar] [CrossRef]
- Zhang, Q.-J.; Gupta, K.C.; Devabhaktuni, V.K. Artificial neural networks for RF and microwave design-from theory to practice. IEEE Trans. Microw. Theory Tech. 2003, 51, 1339–1350. [Google Scholar] [CrossRef]
- Du, K.-L.; Swamy, M.N. Neural Networks and Statistical Learning; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Sharifi, E.; Steinacker, R.; Saghafian, B. Assessment of GPM-IMERG and other precipitation products against gauge data under different topographic and climatic conditions in Iran: Preliminary results. Remote Sens. 2016, 8, 135. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2011; Volume 100. [Google Scholar]
- Schaefer, J.T. The critical success index as an indicator of warning skill. Weather Forecast. 1990, 5, 570–575. [Google Scholar] [CrossRef]
- Khodadoust Siuki, S.; Saghafian, B.; Moazami, S. Comprehensive evaluation of 3-hourly TRMM and half-hourly GPM-IMERG satellite precipitation products. Int. J. Remote Sens. 2017, 38, 558–571. [Google Scholar] [CrossRef]
- Yang, M.; Liu, G.; Chen, T.; Chen, Y.; Xia, C. Evaluation of GPM IMERG precipitation products with the point rain gauge records over Sichuan, China. Atmos. Res. 2020, 246, 105101. [Google Scholar] [CrossRef]
- Xu, S.; Shen, Y.; Niu, Z. Evaluation of the IMERG version 05B precipitation product and comparison with IMERG version 04A over mainland China at hourly and daily scales. Adv. Space Res. 2019, 63, 2387–2398. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Bhuiyan, M.A.E.; Nikolopoulos, E.I.; Anagnostou, E.N.; Quintana-Seguí, P.; Barella-Ortiz, A. A nonparametric statistical technique for combining global precipitation datasets: Development and hydrological evaluation over the Iberian Peninsula. Hydrol. Earth Syst. Sci. 2018, 22, 1371–1389. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Rojas, Y.; Minder, J.R.; Campbell, L.S.; Massmann, A.; Garreaud, R. Assessment of GPM IMERG satellite precipitation estimation and its dependence on microphysical rain regimes over the mountains of south-central Chile. Atmos. Res. 2021, 253, 105454. [Google Scholar] [CrossRef]
- Adhikari, A.; Behrangi, A. Assessment of satellite precipitation products in relation with orographic enhancement over the western United States. Earth Space Sci. 2022, 9, e2021EA001906. [Google Scholar] [CrossRef]
- Roe, G.H. Orographic precipitation. Annu. Rev. Earth Planet. Sci. 2005, 33, 645–671. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).