Next Article in Journal
Cultural Heritage in the Light of Flood Hazard: The Case of the “Ancient” Olympia, Greece
Previous Article in Journal
Probabilistic Approach to Tank Design in Rainwater Harvesting Systems
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Hydrology
Volume 10
Issue 3
10.3390/hydrology10030060
hydrology-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Reconstruction of Recharge and Discharge Pattern in the Polder Drainage Canal Network

by
Gordon Gilja
1,*,
Neven Kuspilić
1,
Martina Lacko
1 and
Davor Romić
2
1
Department of Hydroscience and Engineering, Faculty of Civil Engineering, University of Zagreb, Fra Andrije Kacica Miosica 26, 10000 Zagreb, Croatia
2
Department of Soil Amelioration, Faculty of Agriculture, University of Zagreb, Svetosimunska 25, 10000 Zagreb, Croatia
*
Author to whom correspondence should be addressed.
Hydrology 2023, 10(3), 60; https://doi.org/10.3390/hydrology10030060
Submission received: 7 February 2023 / Accepted: 24 February 2023 / Published: 28 February 2023
Browse Figures
Versions Notes

Abstract

:
Rainfed agriculture is dependent on rainfall and runoff patterns, especially in lowland areas that rely on pumping operation to remove excess water from the drainage network. Polder areas are extremely vulnerable to saltwater intrusion and subsequent soil salinization driven by rising sea levels and accelerated by climate change. The aim of this paper is to reconstruct the recharge and discharge pattern in the Vidrice polder, a drainage canal network within the Neretva River Delta agroecosystem used to collect the surface and subsurface runoff from the agricultural land and saltwater infiltration through the aquifer. Water regime data are collected over an 18-month period of real-time monitoring at 15 min intervals on three stations along the primary drainage canal and one station at the secondary canal. Analysis of water level flashiness in the Vidrice polder using the Richards-Baker flashiness index (R-Bindex) indicates that daily pumping of water infiltrated in the canal network is sub-optimal: discharge fluctuates significantly more than recharge, by 46% on average, resulting in unnecessary lowering of the water level in the drainage network. The results show that the correlation between the intensive rainfall events (>10 mm/day) and the recharge rates can be used to modify the daily pumping operation and maintain high freshwater levels in the canal network to increase the resistance to infiltration and reduce saltwater intrusion into the polder.

1. Introduction

The flow zones in tidal confluences are in continuous transition and repetitive tidal cycle, influencing hydrodynamics, sediment transport, morphological changes, and water/soil salinity [1]. The advantages of intertidal zones, such as large variety of habitats, high land productivity, and accessibility, attract diverse users who compete for the available resources, increasing environmental pressures [2]. These pressures are even more emphasized when the intertidal zone overlaps with the river confluence, affecting the associated riparian zones. Such riparian zones are suitable for agricultural production due to high soil fertility and easy access to freshwater for irrigation [3]. On the other hand, if the cultivated land is located in a polder, it is more vulnerable to rising sea level and flooding, which shifts the focus to single crops and reduces productivity [4]. Potential impacts of global climate change include changes in precipitation and runoff patterns, streamflow and flooding, as well as sea water levels, making polders especially exposed to extreme weather events [5]. In southern Croatia the significant increase in the mean air temperature of 1 °C since 1961 was observed, accompanied by increased sea surface salinity [6], with regional climate models predicting further temperature increase in the range between 0.5 °C and 3.5 °C [7]. Agriculture requires steady and safe freshwater resources to maintain an agricultural ecosystem, which is often challenged by extensive water use or unsustainable abstraction. According to the Common Agricultural Policy, sustainable water management is essential for sustainable agricultural systems in the EU through achieving social, environmental, and economic objectives (enabling safe, healthy, and sustainable food production, at the same time protecting natural resources, enhancing biodiversity, and reducing the impact of climate change and providing a source of stable and fair income).
The water level regime of coastal aquifers is primarily influenced by tides and rainfall [8], especially for sandy aquifers [9]. Prajapati et al. [10] studied groundwater level variation following extreme rainfall on a monthly timescale over 2 years using data from 18 gauging stations and found a strong positive correlation between rainfall and groundwater levels. Reduced rainfall patterns influenced by climate change is the leading cause of drought [11], which has become a major issue for rain-fed agricultural areas over the last decades [12]. To achieve safe agricultural production that is resilient to climate change, stakeholders balance between the agriculture yield and ecosystem functions, by using hydraulic structures to control the water regime, most of which need to be maintained or replaced to adapt to new conditions [13]. Aging infrastructure, combined with population growth and climate change, poses significant risk to agriculture [14], as the structures are often high energy consumers [15] and introduce additional environmental risks [16]. These challenges can be addressed by improving the maintenance of water-related infrastructure, including the addition of monitoring and remote-control functionality. Monitoring and remote-control solutions development will be driven by new technologies based on sensors that provide real-time data for continuous monitoring and automated decision making supported by the Internet of Things (IoT) that connects various devices in a network. Although relatively new, Industry 4.0 is already considered an integral part of agricultural management, enabling significant improvements and increasing efficiency in both agricultural practice and irrigation [17]. The use of IoT enables the integration of real-time monitoring data from multiple sensors with a decision support system, for example, assessment of crop performance [18], controlling water quality [19], warning notifications about potentially unfavorable crop condition [20], track soil salinization [21], automated operation of irrigation systems [22], etc., while reducing costs [23].
One of the locations with ageing infrastructure and under significant water stress due to soil salinization is the Neretva River Delta (NRD), a polder constructed in the late 19th century on the largest river confluence in Croatia (Figure 1). The NRD is suitable for agriculture due to the mild Mediterranean climate, providing favorable conditions for crop cultivation. Average monthly temperatures during winter are above freezing temperatures, with an average temperature of 7.4 °C. Agricultural production in the NRD faces challenges related to irrigation imposed by the Neretva River flow regime characterized by the prolonged periods of low flows during summer [24] allowing saltwater intrusion into the delta [25], including the polder area [26], resulting in soil salination and reduction of agricultural yields. Surface water monitoring in the NRD has shown that both surface- and groundwater are highly saline [27].
Over the past century, global mean sea level has risen 21 cm [28], with climate change scenarios predicting an additional rise in the 21st century spanning from 28 cm to 1.02 m, depending on the emissions scenario [29], exposing coastal areas to additional risks of flooding and salinization and requiring revision of the existing management plans. The management plan for any complex environment, such as deltas, must be based on a monitoring system, which usually combines an ecohydrological information system with a decision support system [30]. Parts of the NRD have been monitored in the past under various research projects, each focused on specific interests, e.g., water quality monitoring [31], hydrogeology [32], soil salinization [12], groundwater salinization [33], salt wedge intrusion into the Neretva River [34], etc. The concept of the project “Advanced monitoring of soil salinization risk in the Neretva Delta agroecosystem” (DELTASAL) [35] is to improve reliability of data acquired by monitoring through development of an advanced system for monitoring, forecasting, and reporting of water and soil conditions in the NRD agroecosystem, mainly used for agriculture. Data collected within the monitoring are continuous real-time measurements of surface water and groundwater regimes, as well as water quality measurements, encompassing processes in the soil and water across different scales.
The reliability of any monitoring depends on the input data quality, mandating filtered, accurate data upon which operation and management plans can be established to control the water regime. Precipitation data, namely its intensity, duration, and frequency, is base input for drainage or irrigation systems design and operation [36]. Precipitation surplus or deficit, compared to water demand in a reference timeframe, must be either drained or abstracted from adjacent freshwater sources to sustain agricultural production. The aim of this paper is to reconstruct the recharge and discharge pattern in the drainage canal network of the Vidrice polder from the measured surface water fluctuations. The drainage canal network is used to collect surface and subsurface runoff from the agricultural land and saltwater infiltration through the aquifer, and pumping it out of the system. Currently, the water from the canal network is used for irrigation, which therefore means that the system needs to be operating in optimal conditions to serve as a freshwater reservoir. The input data for analysis are real-time surface water level and flow velocity data collected on the multi-point grid of hydrostations distributed along the primary drainage canal, and one placed on the secondary canal.

2. Materials and Methods

2.1. Study Area

The Neretva River is a trans-boundary river, with 90% of its 215 km long course in Bosnia and Herzegovina and wide alluvial delta in the Adriatic Sea, mainly used for agricultural production. The hydrological regime of the Neretva River can be generally divided into two characteristic periods: a high flow season from October to April and a low flow period from May to September. The flow rate varies between 40 m3/s and 1800 m3/s with a long-term average of 355 m3/s. The flow regime is influenced by the hydro power plants built upstream—they have reduced the natural flow variations, prolonged the low flows duration and flow rate, and reduced the intensity of winter floods [9]. When the Neretva River flow rate is less than 100 m3/s, water level in the NRD is under the influence of tidal oscillations [37], creating favorable conditions for saltwater intrusion into the groundwater and soil salinization. Research of Deković and Vranješ [37] analyzed the response of deep and shallow piezometers to tidal oscillations and rainfall events. They concluded that shallow piezometers respond instantly to the rainfall, as well as pumping. Deep piezometers are also shown to respond to tidal oscillations, indicating high potential for soil salinization. Average hydraulic conductivity of the rhizosphere sandy layer was obtained experimentally as 1.84 × 10−4 m/s. At higher flow rates, up to 180 m3/s, the water level is not affected by tides, but saltwater intrusion is present up to 20 km into the Neretva River. Saltwater intrusion does not occur at high flows > 500 m3/s [26]. Over the years, several solutions have been presented to reduce saltwater intrusion, most of them focused on the hydraulic structures that prevent inflow from the sea during low flows [38,39].
The present climate of the NRD is Mediterranean with significant differences in rainfall patterns throughout the year. The average annual rainfall is 1309 mm, of which 66% occurred during the winter period and only 13% during summer, with minimum rainfall in July (36 mm on average) [40]. Analyzing the short-term precipitation data recorded by the Croatian Meteorological and Hydrological Service for the period from 2014 until 2022, a constant reduction of rainfall is observed, ~20% in comparison to the long-term average. The summer season (June–August) is the dry season, with total monthly precipitation not exceeding 100 mm in the recent period. During the other three seasons, total monthly precipitation exceeded 100 mm on more than 10 occasions during this period, while during autumn and winter total monthly precipitation also exceeded 100 mm on 5 and 4 occasion, respectively. When the period since the start of the DELTASAL project, in early 2020, to the present is analyzed, it can be observed that rainfall during this period has significantly reduced during summer and spring, with total monthly rainfall not exceeding 75 mm and 90 mm, respectively. Rainfall is expected to reduce during summer in the future as well, which will impose more water related stress on the saltwater regime in the NRD and impede agricultural production in the area.

2.2. Drainage Canal Network

In the second part of the 20th century land reclamation works were initiated on flood defense system (building of the embankment along the shoreline) and drainage (construction of pumping stations to drain excess water) to facilitate agricultural production. Today, the initial concept of the NRD amelioration system has been abandoned and the drainage system is additionally used as a source of freshwater for irrigation. Saltwater intrusion is present in the entire NRD, which is reflected in the irrigation water quality and subsequently on the agricultural production of citruses that are salt-sensitive horticultural crops. Under the UNFCCC Convention this area is one of the most vulnerable areas in Croatia. The NRD amelioration system is divided into several smaller sub-systems, each consisting of a drainage channel network ending at the pumping station, from where the water is pumped to the Neretva River reach flowing to the sea. The system is further divided into smaller sub-systems, one of which is the Vidrice polder, spanning 641.04 ha (Figure 2). This pilot location is specific due to its biodiversity—water network within the delta consists of a surface irrigation and drainage canal network, a karst aquifer dominated by the tidal regime but also replenished by the freshwater from the upstream river flow, and affected by brackish water from several small karst springs. The Vidrice polder is drained by a canal network consisting of one primary drainage canal O-II (9.4 km long) and 9 secondary canals (20.64 km in total). The primary canal is up to 5 m deep and up to 30 m wide, with straight layout ending at the pumping station that has 3 installed pumps with an installed power of 420 kW and a total capacity of up to 7.5 m3/s, depending on the water levels. The pumping station is used to drain the excess water and maintain the water level below the rhizosphere. According to the Flood Risk Management Plan, the pumping regime is defined as follows: maximum water level in the primary canal is −1.2 m above sea level (masl), minimum water level is −3.5 masl, and corresponding water levels in the intake basin of −1.5 masl and −3.0 masl. The pump outlet is designed as a syphon and operable for water levels in the recipient between 1.7 masl and −0.3 masl. The pumping station operates cyclically during the night, between 10 PM and 7 AM., with exceptions on days with excessive rainfall. The entire area is a polder with an elevation between −0.50 masl and +1.90 masl, which allows for seawater intrusion into the drainage canal network.

2.3. Surface Water Monitoring

The surface water monitoring setup consists of 4 stations—three of them (PC1, PC2, and PC3) are located on the primary canal O-II, with their respective positions reflecting the main inflow points from the secondary canals, and one is located on the secondary canal (SC), a characteristic canal adjacent to the arable plots (Figure 3a). The monitoring stations are commercially available HydroStations manufactured by Geolux (https://www.geolux-radars.com/ (accessed on 7 February 2023)). The HydroStations are equipped with the LX-80 Radar Level Sensor (resolution 0.5 mm, accuracy +/−2 mm), the RSS-2-300 W surface velocity radar (range 0.02 m/s to 15 m/s, resolution 0.001 m/s, accuracy 1%), and the SmartObserver Datalogger for real-time data transmission, all powered by the solar panel (Figure 3b). All measurements are collected and synchronized at 15 min intervals and transmitted in real-time to the cloud-based interface for remote access. The monitoring system is part of the modular monitoring automated continuous water quality monitoring systems (ACMS)—i.e., it can be upgraded to enable both ground and surface water parameters to be monitored (water level, temperature, EC, etc.). HydroStations were installed in November 2020 and have been in continuous operation since. Data is stored in the normalized database that allows data transfer and retrieval using each instrument supplier’s protocol. The database can be accessed and data retrieved by stakeholders publicly through an online portal [41].
Water level data from four installed monitoring stations in the Vidrice polder were collected during the period from 18 November 2020 to 10 June 2022, encompassing more than one full hydrological year. The raw water level dataset varied between 54,056 and 54,503 values, depending on the observed station (Table 1), which included some erroneous data—duplicate data entries, missing values, and outliers. In order to format the data into the required 15 min intervals and complete the time-series, a preliminary analysis of the data had to be performed. Firstly, the excess data were truncated based on duplicate entries and multiple entries within the interval. Secondly, outlier data were filtered out using the phase-threshold method [42] routinely used for high-frequency turbulence data. Finally, missing and filtered data were substituted with polynomial interpolation method to complete the time-series with 15 min intervals for the observed period, or closest value in case it was reliable and collected within the tolerance of ±5 min from the reference timestamp of the 15 min interval. As a result, a time-series of 54,672 water level data values at the 15 min interval for the observed period was derived and used as input to the outlier filtering method.
In addition to real-time water level data obtained from the monitoring stations, an automatic Pinova Meteo agriculture weather station is installed at the location of SC station that measures a number of weather-related parameters, such as precipitation, air temperature and humidity, wind speed, and global radiation at 10 min intervals. The location of the weather station was selected as the most appropriate, as it is located in the study area. In order to maintain groundwater at an optimal level to support agricultural production under the dynamics of saltwater–freshwater exchange, seasonal influences on saltwater intrusion should be considered. Therefore, a preliminary analysis of water level fluctuations at the four monitoring stations was conducted based on the four meteorological seasons—summer, autumn, winter, and spring season. The summer season, according to the observation data, extends from June through August and is predominantly described as a consistently dry period without precipitation. The most important season for the analysis due to the amount of significant rainfall events, also referred to as the rainy season, is the spring and autumn period. The spring season covers the period that can be described as a period of average precipitation and, according to the observation data, lasts from March through May. The autumn season spans from September through November, while the winter season spans from December through February. Since temperatures in the area do not allow for long periods of snow cover, precipitation during winter consists mostly of rainfall, making it similar to autumn. Rainy and spring seasons are represented twice in the dataset, according to the available record that ends just at the start of summer. The preliminary analysis of the observed data consists of determining the range of water level data for each period at monitoring stations PC1, PC2, PC3, and SC. Further seasonal analysis of water levels and discharges on a daily scale was performed for PC1, identified as a representative station for further analysis since it is closest to the pumping station, and therefore reflects the total discharge and water level fluctuation affecting the pumping regime.

2.4. Data Processing

Data processing was done in 4 steps: (1) explanatory data analysis for the entire time-series, (2) identify daily pattern of the available dataset, (3) correlate characteristic events with rainfall pattern, and (4) discuss potential optimization of the flow regime based on the obtained results. Explanatory data analysis was conducted for the high and low peaks of the water level time-series. The water levels are cyclical, with percolating water recharging the canal system during the day and pumps discharging the system during the night. This diurnal cycle has two peaks: high peak late in the day and low peak just before dawn. The time-series was decomposed into daily patterns to obtain the two peak values for each day, low peak in the morning (tlow,i) after pumping has stopped and high peak in the afternoon (thigh,i) after recharge. Peak distribution was analyzed using boxplots to obtain basic statistical values and calculate the distribution of the data across different characteristic seasons. Based on the results of the explanatory data analysis, difference in the water regime across seasons was estimated and confirmed based on the existence of different patterns, depending on the rainfall. After the initial analysis defined different seasonal patterns, the analysis was downscaled to daily data. For each season, daily cycle was identified for each day, calculating main variables that supplement peak data: time difference between the two peaks within the single day (∆t) and corresponding recharging and discharging rate. Water level gradient during recharging/discharging and corresponding flow rate are calculated as follows:
S R , i = Δ H i Δ t i = H h i g h , i − H l o w , i t h i g h , i − t l o w , i × 100 ,
S D , i = Δ H i Δ t i = H h i g h , i − H l o w , i + 1 t l o w , i + 1 − t h i g h , i × 100 ,
Q R , i = Δ V i Δ t i = V h i g h , i − V l o w , i t h i g h , i − t l o w , i ,
Q D , i = Δ V i Δ t i = V h i g h , i − V l o w , i + 1 t l o w , i + 1 − t h i g h , i ,
where: i = single day in the time series; SR,i = recharging water level gradient [cm/h]; SD,i = discharging water level gradient [cm/h]; QR,i = recharging flow rate [m3/s]; QD,i = discharging flow rate [m3/s]; ∆Hi = absolute water level difference between high and low peak [m]; Hhigh,i = water level corresponding to the high peak [masl]; Hlow,i = water level corresponding to the low peak [masl]; Hlow,i+1 = water level corresponding to the low peak of the following day [masl]; ∆ti = time elapsed between high and low peak occurrence [h] or [s]; thigh,i = high peak time of the occurrence [h]; tlow,i = low peak time of the occurrence [h]; tlow,i+1 = low peak time of the occurrence during the following day [h]; ∆Vi = volume of the water in the canal network calculated from the hypsometric curve [m3]; Vhigh,i = volume of the water in the canal network at the high peak [m3]; Vlow,i = volume of the water in the canal network at the low peak [m3]; Vlow,i+1 = volume of the water in the canal network at the low peak for the following day [m3].
These values were used to determine the base water regime during the dry summer periods, i.e., baseflow recharge and detect changes in comparison to increased surface and subsurface runoff induced by precipitation during the rainy season. Following the determination of the baseflow water regime characteristics, the characteristic events were correlated with all precipitation events across different seasons. Correlation was separately conducted for different time lags following the rainfall, different averaging of recharge and discharge, and divided across the rainy season. The variability of the flow between recharge and discharge across all seasons was quantified using the Richards-Baker Flashiness Index (R-Bindex) [43], reflecting the rate of magnitude of oscillations in daily flows. The R-Bindex is a dimensionless index calculated as follows:
R − B i n d e x = ∑ i = 1 n Q i − Q i − 1 ∑ i = 1 n Q i ,
where: R-Bindex = Richards-Baker Flashiness Index [/]; i = single day in the time series; Qi = average daily flow rate [m3/s]; n = number of days in the series.
When flow rate does not change between consecutive days, i.e., flow is constant, the R-Bindex value is zero, while R-Bindex values increase with severity of changes in the flow.

3. Results

The daily maximum and minimum water level data depending on the season were analyzed at the monitoring stations (PC1, PC2, PC3, SC) in the Vidrice polder using a boxplot (Figure 4). All analyzed stations show similar results in terms of seasonal behavior of maximum and minimum water levels, which is to be expected since they are all part of the enclosed drainage canal system with distributed groundwater recharge, and limited potential of flood wave propagation along the primary canal. In that sense, it is observed that variation of water levels for both high and low daily peaks have similar distribution of quartiles for all stations. The median for low peaks ranges from −2.71 masl to −2.63 masl for the primary canal, and −2.64 masl for the secondary canal. The interquartile range of low peaks ranges from 0.30 m to 0.33 m for the primary canal, and 0.23 m for the secondary canal. A similar trend is observed for high peaks: the median along the primary canal ranges from −2.25 masl to −2.40 masl and −2.35 masl for the secondary canal. The interquartile range of low peaks ranges from 0.26 m to 0.29 m for the primary canal, and 0.26 m for the secondary canal. The largest interquartile range, and overall variation, is observed for the rainy season, while the smallest is observed for the summer season, as expected. The interquartile difference of interquartile range between low and high peaks is negligible for all seasons, while the total range is higher for low peaks that are controlled by pumping, suggesting that the target minimum value is arbitrary and probably relies on perceived volume needed to accumulate recharge expected by the forecasted rainfall. From this analysis it can be concluded that in the canal network there is no significant propagation of flood waves, and the water regime can be analyzed using the data from a single station in the network, in this case PC1 which is located at the outlet of the system.
Based on the boxplot results and negligible differences between fluctuations of high and low peaks across all stations, PC1 was selected as representative for further analysis because of its location closest to the drainage system outlet, representing full flow in the drainage canal system. In addition to analysis of high and low peaks and dynamics throughout the observation period, the time-series observed at PC1 was divided into a series of measurement data to represent daily water fluctuations (Figure 5a–d), which are currently regulated by a pumping station that operates during the night in a cyclic regime. The median daily results for the observation period show similarities for the spring and summer season operations, which generally begin at 10 PM and end at 7 AM the following day (Figure 5e). However, the results for spring and winter show a shift in the pumping station operations by one hour earlier, starting from 9 PM, increasing the total pumping time to alleviate additional recharge resulting from the excessive rainfall.
The Vidrice polder recharge rates were calculated using Equation (3) for daily intervals to determine baseflow recharge during the dry period and correlate additional recharge following the rainfall events. It can be seen that the span of the recharge is from 0.5 m3/s to 6.5 m3/s, corresponding to the pump station capacity (Table 2). Average daily recharge rates for the Vidrice polder are highest during autumn, followed by winter, spring, and summer in descending order. Results show that recharge is the highest when water level in the canal network is kept at the lowest level (Figure 5e), when excess pumping increases the hydraulic head between the sea water level and the water level in canal network. Results are summarized in the table below.
The average daily recharge rate is 1.2 m3/s, and does not differ significantly for different season, as is the case for the minimum daily recharge rate. Significant differences can be seen for maximum daily recharge rates, which are highest during autumn and winter and lowest during spring and summer, influenced by the intensive rainfall events (Figure 6). The average and maximum water level fluctuations (Table 2) do not correspond with the recharge: maximum pump capacity is not used to achieve maximum water level reduction, indicating that pumps are urgently started when water level rises abruptly, disrupting the standard regime of operation. The following figure (Figure 6) shows time-series data for recharge and corresponding discharge calculated using Equation (4).

4. Discussion

When daily recharge and discharge data are presented as a scatterplot (Figure 7), no visible pattern explaining the pumping regime depending on the recharge can be observed. Correlation was calculated using the least squares method and evaluated at the 95% confidence level. The overall correlation between recharge and discharge is moderate (R2 = 0.44), indicating that correlation exists between the inflow and pumping regime, but there is no apparent trend that the pumping operation is synchronized with the inflow in the system. If regression lines are calculated for recharge/discharge data pairs divided according to the seasons (Figure 7), a similar pattern can be observed—strongest highest correlation for the autumn (R2 = 0.57), and weakest for the summer season (R2 = 0.10). Correlation results for all seasons are significant at the 95% confidence level, with p-values of 3.4 × 10−20, 3.1 × 10−23, 4.3 × 10−14, and 1.3 × 10−3, for autumn, winter, spring, and summer season, respectively. Spring season exhibits lower correlation (R2 = 0.27) than the autumn and winter season (R2 = 0.43). Lack of correlation between the anticipated recharge and corresponding discharge can be confirmed by isolating only dry period data (precipitation < 1 mm/day), where correlation is weak (R2 = 0.26), indicating that during the dry period constant inflow pumping operation is arbitrary, focusing on the water level lowering without taking into account the potential recharge. The same is observed during summer when precipitation is extremely low and recharge/discharge correlation has a different trend than for the rainy season (Figure 7), resulting from predefined cyclic operation adapted only to groundwater inflow. If data is further divided based on the precipitation intensity to light precipitation (<10 mm/day) and heavy precipitation (>10 mm/day), it is observed that pumps have the capacity to adapt to intensive rainfall events to prevent flooding once the operator notices the increased trend of recharge—correlation is increasing precipitation intensity (R2 = 0.50 for light and R2 = 0.63 for heavy precipitation). A similar observation was made by Yu et al. [44], demonstrating fast exchange of solutes between groundwater and surface water in polders, driven by the infiltration in dry periods when excess water is pumped out of the polder.
Since the cost of pump operation and maintenance is the largest expense in the drainage network [45], the cost-effectiveness of day to day operation is key for reducing costs. Many studies have focused on reducing cost by utilizing the time-scheduling operating strategies during low-cost energy tariff [46,47]. In order to sustain time-scheduled operation, an initial investment in the water level and meteorological stations is required, as well es establishment of prognostic models and decision-making procedures. Model predictive control (MPC) has shown applicable for control of different water-related systems due to its capability for dealing with model-based predictions, such as precipitation forecasts or tidal motion. Aydin et al. [48] used a nonlinear MPC to maintain the water level in the polder within ±5 cm of the set threshold for salinity control. Aydin et al. [49] also deployed MPC to control the salinity in polders in real-time by means of flushing operations and saline groundwater exfiltration. Horváth et al. [50] used MPC to keep water levels in the Dutch polder within the safety limits with a bandwidth of 20 cm, while saving 80% of the electricity costs. Although the model-based predictions have shown applicable, there is still room for their improvement, since the modelling of the groundwater component in the polder is shown to have discrepancies in comparison with measured data [51].
Analysis of the water level flashiness using the R-Bindex also demonstrates that pump operation can be optimized because the R-Bindex is constantly higher for discharge than for recharge for all seasons (Table 3). While the R-Bindex is relatively low for both recharge and discharge, reflecting the cyclic water regime behavior, it is higher for discharge up to 105% for spring in comparison to the corresponding recharge. The R-Bindex for recharge is calculated as 0.08, 0.17, 0.23, 0.24, and 0.21 for summer, spring, winter, autumn, and overall, respectively. The R-Bindex for discharge is calculated as 0.10, 0.32, 0.34, 0.35, and 0.31 for summer, winter, autumn, spring, and overall, respectively. Similarly, standard deviation of discharge is significantly higher for discharge than for recharge, up to 256% for spring. Higher R-Bindex and standard deviation values indicate that the discharging trend is fluctuating significantly more than recharging, reducing its efficiency.
Further analysis is conducted on the dependence of flow rate fluctuations during the recharge phase, and the rainfall is used to investigate if rainfall events could have significant influence on the water level dynamics in the Vidrice polder. Since the runoff area is small and the time of concentration is short, topographic conditions allow for fast surface runoff. When the dependence of recharge to intensive rainfall (p > 10 mm/day) is analyzed, it is observed that weak to moderate correlation exist between the two variables (Figure 8). Calculated R2 values are 0.25, 0.36, and 0.45 for autumn, spring, and winter season, respectively. The calculated correlation is lower than the one between discharge and recharge (Figure 7), which is expected since the amount of available precipitation data is low in comparison to daily flow data. Additionally, neither of the correlation results showed to be significant at the 95% confidence level, with p-values of 0.104, 0.146, and 0.0675 for autumn, winter, and spring season. Since the analysis is done for the relatively short time-period, the low amount of data is affecting the statistical analysis and emphasizes the importance of long-term data acquisition in order to obtain relevant and reliable dataset.
Nevertheless, the moderate correlation between rainfall and recharge provides the basis to implement a proactive approach to pumping, forecasting the potential recharge and adjusting the pumping capacity accordingly as an alternative to a reactive approach focusing on pumping the excess water once it has already reached the canal network. A proactive approach would allow evacuation of minimal water volumes to sustain higher base water levels in the system, reducing saltwater intrusion and at the same time accumulating freshwater resources suitable for irrigation.
To demonstrate discrepancy in pump operation, several rainfall events of the same intensities have been singled out that have occurred for different conditions of water level lowering in canals (Figure 9). The rainfall events are independent of each other, as well as from other rainfall events, p > 10 mm, in order to be comparable and exclude the effect of soil saturation following previous rainfall. Five events have been selected for 25 mm < p < 50 mm. It can be seen that rainfall of this intensity is not the primary generator of recharge since the recharge rate is inversely related to rainfall (R2 = 0.99), and positively to lowering of the water levels. For this limited subset it can be seen that groundwater recharge contributes more than surface runoff, and therefore imposes a high risk of surface water salinization. To reduce salinization, freshwater inflow must be retained in the canals, which can only be done through optimization of the pumping operation, by reducing the water level only to remove excess infiltration and accommodate immediate rainfall.
Groundwater infiltration and salinization of the surface water can be reduced by keeping high water levels in canals. Since the area is small, surface runoff is rapid and systems should be emptied only prior to extreme rainfall events that pose a flooding hazard. In all other scenarios, the water level should be kept at a high level that reduces pumping requirements since groundwater infiltration is reduced, and the pumping head is lower, in turn reducing both required discharge and net pump head. This would reduce both the cost of operation and water salinization of the polder, having positive effects on overall agricultural production. Based on the continuous water level and rainfall monitoring within the catchment, the direct runoff can be calculated and used to support optimization of the pumping regime in pump-controlled polders. Yan et al. [52] used the WALRUS simulator to successfully prove that water levels in canals can be retained higher than groundwater during the rainy season and completely eliminate groundwater infiltration. They showed that one of the effects of such regulation is decreased phosphorus export to watercourses downstream [53]. Benefits of water retention in the drainage canal network can also be in reducing water salinity, which is especially important if water is used for irrigation, as well as reduced flooding downstream.
The current pumping regime cannot be considered optimal, as it follows pre-defined dynamics without taking into account seasonal influences on saltwater intrusion. Since the water level in the drainage canal network is lower than the groundwater level, it could be stipulated that pumping drains freshwater from the soil replenished occasionally by the rainfall, and thus allowing the daily tides to penetrate further into the polder. The time of concentration, or system response to rainfall, is important to consider in forecasting the recharge. R2 values for correlation of rainfall events occurring on the same day with recharge and water level fluctuations are 0.24 and 0.29, respectively. If a shift of one day is introduced into the same correlation, the R2 values for recharge remain the same (0.23), while R2 values for water level fluctuation decreases to 0.15. This discrepancy in correlation strength when a day-shift is introduced can be explained as over-pumping following the rainfall event, which in turn reduces the water level in the canal network, allowing for larger fluctuations: water level recharge fluctuation during periods without precipitation is 32 cm, on average, while it increases to 44 cm for no precipitation days that follow the days with rainfall > 10 mm/day. Results of the water regime analyses presented in this paper show that surface water monitoring must be established to provide data for water management within the polder to keep the groundwater at optimal levels to support agricultural production under the dynamics of saltwater–freshwater exchange.

5. Conclusions

This paper analyzed the current surface water regime in the pump-controlled Vidrice polder, where the pumping regime is predefined and severe salinization is present. Analysis of the hydrological regime of the Vidrice polder shows that required daily pumping of the water infiltrated in the canal network is sub-optimal, affecting the groundwater level needed to support agricultural production under the threat of saltwater intrusion. During the dry season, base inflow in the canal network does not fluctuate significantly, and recharge depends only on the available hydraulic head between the polder and the Adriatic Sea. High and rapid inflows into the canal network result from intensive rainfall events (p > 10 mm/day), which have a short time of concentration, and can be used to correlate total precipitation with average recharge. Although such correlation is relatively weak, it indicates that daily pumping operation can be modified to anticipate high recharges and manage the water regime in the network to accommodate the required volume of rainfall. Currently, excess water is pumped from the network following the rainfall event, in turn reducing the resistance to groundwater infiltration of the seawater, which contributes to soil salinization in the area. The correlation between rainfall and recharge provides the basis to implement a proactive approach to pumping, by forecasting the potential recharge and adjusting the pumping capacity accordingly. Based on the outcomes of the DELTASAL project, the pumping operation can be optimized to maintain high freshwater levels in the canal network and reduce the water levels according to expected inflow after rainfall to increase the resistance to infiltration, reduce saltwater intrusion, and sustain agricultural production.

Author Contributions

Conceptualization, G.G. and N.K.; methodology, G.G.; software, G.G. and M.L.; validation, M.L.; formal analysis, G.G. and N.K.; investigation, G.G. and N.K.; resources, N.K. and D.R.; data curation, M.L.; writing—original draft preparation, G.G.; writing—review and editing, G.G., N.K. and D.R.; visualization, G.G. and M.L.; supervision, N.K.; project administration, D.R.; funding acquisition, D.R. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the European Regional Development Fund through the project “Advanced agroecosystem monitoring system at risk of salinization and contamination” (DELTASAL) (KK.05.1.1.02.0011.) and by the Environmental Protection and Energy Efficiency Fund of the Republic of Croatia.

Institutional Review Board Statement

Not applicable.

Data Availability Statement

All data are presented in the main text.

Acknowledgments

This work was supported in part by the Croatian Science Foundation under the project R3PEAT (UIP-2019-04-4046) and “Young Researchers’ Career Development Project—Training New Doctoral Students” (DOK-2020-01-5354).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Bilal, A.; Xie, Q.; Zhai, Y. Flow, Sediment, and Morpho-Dynamics of River Confluence in Tidal and Non-Tidal Environments. J. Mar. Sci. Eng. 2020, 8, 591. [Google Scholar] [CrossRef]
  2. Nordlund, L.M.; de la Torre-Castro, M.; Erlandsson, J.; Conand, C.; Muthiga, N.; Jiddawi, N.; Gullström, M. Intertidal Zone Management in the Western Indian Ocean: Assessing Current Status and Future Possibilities Using Expert Opinions. AMBIO 2014, 43, 1006–1019. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  3. Osawa, T.; Mitsuhashi, H.; Ushimaru, A. River confluences enhance riparian plant species diversity. Plant Ecol. 2010, 209, 95–108. [Google Scholar] [CrossRef]
  4. Kumer Saha, C.; Alam, M. Popularizing farm machinery in the polder zones of Bangladesh. Polder Tidings 2021, 3, 10–11. [Google Scholar]
  5. Eden, J.M.; Kew, S.F.; Bellprat, O.; Lenderink, G.; Manola, I.; Omrani, H.; van Oldenborgh, G.J. Extreme precipitation in the Netherlands: An event attribution case study. Weather Clim. Extrem. 2018, 21, 90–101. [Google Scholar] [CrossRef]
  6. CHANGE WE CARE. Adaptation/Management Plan for Neretva River Delta. Climate cHallenges on coAstal and traNsitional chanGing arEas: WEaving a Cross-Adriatic Response; European Union: Maastricht, The Netherlands, 2021. [Google Scholar]
  7. Gajić-Čapka, M.; Güttler, I.; Cindrić, K.; Branković, Č. Observed and simulated climate and climate change in the lower Neretva river basin. J. Water Clim. Chang. 2018, 9, 124–136. [Google Scholar] [CrossRef]
  8. Vallejos, A.; Sola, F.; Pulido-Bosch, A. Processes Influencing Groundwater Level and the Freshwater-Saltwater Interface in a Coastal Aquifer. Water Resour. Manag. 2015, 29, 679–697. [Google Scholar] [CrossRef]
  9. Vranješ, M.; Prskalo; Džeba, T. Hydrology and hydrogeology of the Neretva and Trebišnjica basins, overview of the construction of part of the HE system-upper horizons. e-ZBORNIK Electron. Collect. Pap. Fac. Civ. Eng. 2013, 5, 1–13. [Google Scholar]
  10. Prajapati, R.; Upadhyay, S.; Talchabhadel, R.; Thapa, B.R.; Ertis, B.; Silwal, P.; Davids, J.C. Investigating the nexus of groundwater levels, rainfall and land-use in the Kathmandu Valley, Nepal. Groundw. Sustain. Dev. 2021, 14, 100584. [Google Scholar] [CrossRef]
  11. Wang, S.; Zhang, Q.; Wang, J.; Liu, Y.; Zhang, Y. Relationship between Drought and Precipitation Heterogeneity: An Analysis across Rain-Fed Agricultural Regions in Eastern Gansu, China. Atmosphere 2021, 12, 1274. [Google Scholar] [CrossRef]
  12. Lovrinović, I.; Bergamasco, A.; Srzić, V.; Cavallina, C.; Holjević, D.; Donnici, S.; Erceg, J.; Zaggia, L.; Tosi, L. Groundwater Monitoring Systems to Understand Sea Water Intrusion Dynamics in the Mediterranean: The Neretva Valley and the Southern Venice Coastal Aquifers Case Studies. Water 2021, 13, 561. [Google Scholar] [CrossRef]
  13. Šimunić, I.; Likso, T.; Orlović-Leko, P.; Ciglenečki, I.; Bubalo Kovačić, M.; Gilja, G.; Mustać, I. The influence of combined drainage on the stability of agricultural production in condition of climate change. Reliab. Theory Appl. 2022, 17, 82–87. [Google Scholar] [CrossRef]
  14. Mazibuko, N.; Antwil, M.; Rubhara, T. Agricultural infrastructure as the driver of emerging farmers’ income in South Africa. A stochastic frontier approach. Agron. Colomb. 2020, 38, 261–271. [Google Scholar] [CrossRef]
  15. Cosgrove, W.J.; Loucks, D.P. Water management: Current and future challenges and research directions. Water Resour. Res. 2015, 51, 4823–4839. [Google Scholar] [CrossRef] [Green Version]
  16. Nowak, B.; Ptak, M.; Bartczak, J.; Sojka, M. Hydraulic Structures as a Key Component of Sustainable Water Management at the Catchment Scale—Case Study of the Rgilewka River (Central Poland). Buildings 2022, 12, 675. [Google Scholar] [CrossRef]
  17. Bekić, D.; Halkijević, I.; Gilja, G.; Lončar, G.; Potočki, K.; Carević, D. Examples of trends in water management systems under influence of modern technologies. Građevinar 2019, 71, 833–842. [Google Scholar] [CrossRef]
  18. Jayaraman, P.P.; Yavari, A.; Georgakopoulos, D.; Morshed, A.; Zaslavsky, A. Internet of Things Platform for Smart Farming: Experiences and Lessons Learnt. Sensors 2016, 16, 1884. [Google Scholar] [CrossRef]
  19. AlMetwally, S.A.H.; Hassan, M.K.; Mourad, M.H. Real Time Internet of Things (IoT) Based Water Quality Management System. Procedia CIRP 2020, 91, 478–485. [Google Scholar] [CrossRef]
  20. dos Santos, U.J.L.; Pessin, G.; da Costa, C.A.; da Rosa Righi, R. AgriPrediction: A proactive internet of things model to anticipate problems and improve production in agricultural crops. Comput. Electron. Agric. 2019, 161, 202–213. [Google Scholar] [CrossRef]
  21. Gorji, T.; Sertel, E.; Tanik, A. Monitoring soil salinity via remote sensing technology under data scarce conditions: A case study from Turkey. Ecol. Indic. 2017, 74, 384–391. [Google Scholar] [CrossRef]
  22. Borah, S.; Kumar, R.; Mukherjee, S. Low-cost IoT framework for irrigation monitoring and control. Int. J. Intell. Unmanned Syst. 2020, 9, 63–79. [Google Scholar] [CrossRef]
  23. Morais, R.; Silva, N.; Mendes, J.; Adão, T.; Pádua, L.; López-Riquelme, J.A.; Pavón-Pulido, N.; Sousa, J.J.; Peres, E. mySense: A comprehensive data management environment to improve precision agriculture practices. Comput. Electron. Agric. 2019, 162, 882–894. [Google Scholar] [CrossRef]
  24. Vranješ, M.; Romić, D. Construction of the barrier in the Neretva River. In Proceedings of the 5th Croatian Water Conference with International Participation: Croatian Waters Facing the Challenge of Climate Changes, Opatija, Croatia, 18–21 May 2011. [Google Scholar]
  25. Krvavica, N.; Gotovac, H.; Lončar, G. Salt-wedge dynamics in microtidal Neretva River estuary. Reg. Stud. Mar. Sci. 2021, 43, 101713. [Google Scholar] [CrossRef]
  26. Ljubenkov, I.; Vranješ, M. Numerical model of stratified flow—Case study of the Neretva riverbed salination. Građevinar 2012, 64, 101–112. [Google Scholar] [CrossRef]
  27. Romić, D.; Zovko, M.; Romić, M.; Ondrašek, G.; Salopek, Z. Quality aspects of the surface water used for irrigation in the Neretva Delta (Croatia). J. Water Land Dev. 2008, 12, 59–70. [Google Scholar] [CrossRef] [Green Version]
  28. Palmer, M.D.; Domingues, C.M.; Slangen, A.B.A.; Dias, F.B. An ensemble approach to quantify global mean sea-level rise over the 20th century from tide gauge reconstructions. Environ. Res. Lett. 2021, 16, 044043. [Google Scholar] [CrossRef]
  29. Fox-Kemper, B.; Hewitt, H.T.; Xiao, C.; Aðalgeirsdóttir, G.; Drijfhout, S.S.; Edwards, T.L.; Golledge, N.R.; Hemer, M.; Kopp, R.E.; Krinner, G.; et al. Ocean, cryosphere, and sea level change. In Climate Change 2021: The Physical Science Basis. Contribution of Working Group I to the Sixth Assessment Report to the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
  30. Margeta, J.; Fistanić, I. System management and monitoring at the Neretva river basin. Građevinar 2000, 52, 331–338. [Google Scholar]
  31. Romić, D.; Castrignanò, A.; Romić, M.; Buttafuoco, G.; Bubalo Kovačić, M.; Ondrašek, G.; Zovko, M. Modelling spatial and temporal variability of water quality from different monitoring stations using mixed effects model theory. Sci. Total Environ. 2020, 704, 135875. [Google Scholar] [CrossRef]
  32. Srzić, V.; Lovrinović, I.; Racetin, I.; Pletikosić, F. Hydrogeological Characterization of Coastal Aquifer on the Basis of Observed Sea Level and Groundwater Level Fluctuations: Neretva Valley Aquifer, Croatia. Water 2020, 12, 348. [Google Scholar] [CrossRef] [Green Version]
  33. Lovrinović, I.; Srzić, V.; Matić, I.; Brkić, M. Combined Multilevel Monitoring and Wavelet Transform Analysis Approach for the Inspection of Ground and Surface Water Dynamics in Shallow Coastal Aquifer. Water 2022, 14, 656. [Google Scholar] [CrossRef]
  34. Krvavica, N.; Ružić, I. Assessment of sea-level rise impacts on salt-wedge intrusion in idealized and Neretva River Estuary. Estuar. Coast. Shelf Sci. 2020, 234, 106638. [Google Scholar] [CrossRef] [Green Version]
  35. Gilja, G.; Kuspilić, N.; Romić, D.; Zovko, M.; Harasti, A. Advanced monitoring of soil salinization risk in the Neretva Delta agroecosystem. In Proceedings of the EGU General Assembly 2021, Wien, Austria, 19–30 April 2021. [Google Scholar] [CrossRef]
  36. Sung, J.H.; Baek, D.; Ryu, Y.; Seo, S.B.; Seong, K.-W. Effects of Hydro-Meteorological Factors on Streamflow Withdrawal for Irrigation in Yeongsan River Basin. Sustainability 2021, 13, 4969. [Google Scholar] [CrossRef]
  37. Deković, J. Interpretacija Mjerenja na Području Opuzen-Ušće i Vidrice iz 2014. Godine. Ph.D. Thesis, University of Split, Split, Croatia, 2015. [Google Scholar]
  38. Holjević, D. Zaštita od zaslanjivanja voda i tla u dolini Neretve. Hrvat. Vodoprivr. 2020, 230, 50–54. [Google Scholar]
  39. Samokovlija Dragičević, J. Irrigation problems in lower reaches of Neretva. Građevinar 2008, 60, 373–378. [Google Scholar]
  40. Gajić-Čapka, M. Oborina na širem dubrovačkom području. Hrvat. Vode 2010, 18, 305–312. [Google Scholar]
  41. Reljić, M.; Romić, M.; Romić, D.; Gilja, G.; Mornar, V.; Ondrasek, G.; Bubalo Kovačić, M.; Zovko, M. Advanced Continuous Moni-toring System—Tools for Water Resource Management and Decision Support System in Salt Affected Delta. Agriculture 2023, 13, 369. [Google Scholar] [CrossRef]
  42. Goring, D.; Nikora, V. Despiking Acoustic Doppler Velocimeter Data. J. Hydraul. Eng. 2002, 128, 117–126. [Google Scholar] [CrossRef] [Green Version]
  43. Baker, D.B.; Richards, R.P.; Loftus, T.T.; Kramer, J.W. A New Flashiness Index: Characteristics And Applications To Midwestern Rivers And Streams. JAWRA J. Am. Water Resour. Assoc. 2004, 40, 503–522. [Google Scholar] [CrossRef]
  44. Yu, L.; Rozemeijer, J.; van Breukelen, B.M.; Ouboter, M.; van der Vlugt, C.; Broers, H.P. Groundwater impacts on surface water quality and nutrient loads in lowland polder catchments: Monitoring the greater Amsterdam area. Hydrol. Earth Syst. Sci. 2018, 22, 487–508. [Google Scholar] [CrossRef] [Green Version]
  45. Bastiene, N.; Saulys, V. Maintanance peculiarities of polder systems in Lithuania during the last decade. In Proceedings of the International Scientific Conference: Research for Rural Development 2007, Jelgava, Latvia, 16–18 May 2007. [Google Scholar]
  46. Blinco, L.J.; Simpson, A.R.; Lambert, M.F.; Marchi, A. Comparison of Pumping Regimes for Water Distribution Systems to Minimize Cost and Greenhouse Gases. J. Water Resour. Plan. Manag. 2016, 142, 04016010. [Google Scholar] [CrossRef] [Green Version]
  47. Napierała, M. A Study on Improving Economy Efficiency of Pumping Stations Based on Tariff Changes. Energies 2022, 15, 799. [Google Scholar] [CrossRef]
  48. Aydin, B.E.; Oude Essink, G.H.P.; Delsman, J.R.; van de Giesen, N.; Abraham, E. Nonlinear model predictive control of salinity and water level in polder networks: Case study of Lissertocht catchment. Agric. Water Manag. 2022, 264, 107502. [Google Scholar] [CrossRef]
  49. Aydin, B.E.; Rutten, M.; Oude Essink, G.H.P.; Delsman, J. Polder Flushing: Model Predictive Control of Flushing Operations to Effective and Real Time Control of Salinity in Polders. Procedia Eng. 2016, 154, 94–98. [Google Scholar] [CrossRef] [Green Version]
  50. Horváth, K.; van Esch, B.; Vreeken, T.; Piovesan, T.; Talsma, J.; Pothof, I. Potential of model predictive control of a polder water system including pumps, weirs and gates. J. Process Control 2022, 119, 128–140. [Google Scholar] [CrossRef]
  51. O’Kane, J.P.; Migliori, L. The Hydrology and Hydraulics of a Pumped Polder in North Kerry. In Proceedings of the 2004 Irish National Hydrology Conference, London, UK, 10 November 2004. [Google Scholar]
  52. Yan, R.; Gao, J.; Huang, J. WALRUS-paddy model for simulating the hydrological processes of lowland polders with paddy fields and pumping stations. Agric. Water Manag. 2016, 169, 148–161. [Google Scholar] [CrossRef]
  53. Yan, R.; Li, L.; Gao, J. Modelling the regulation effects of lowland polder with pumping station on hydrological processes and phosphorus loads. Sci. Total Environ. 2018, 637–638, 200–207. [Google Scholar] [CrossRef]
Hydrology 10 00060 g001 550
Figure 1. Overview map of the polders in the ameliorated area in the lower NRD (magenta—national border, cyan—individual polders).
Figure 1. Overview map of the polders in the ameliorated area in the lower NRD (magenta—national border, cyan—individual polders).
Hydrology 10 00060 g001
Hydrology 10 00060 g002 550
Figure 2. Layout of the drainage canal network in the Vidrice polder with names of individual canals.
Figure 2. Layout of the drainage canal network in the Vidrice polder with names of individual canals.
Hydrology 10 00060 g002
Hydrology 10 00060 g003 550
Figure 3. Location of the surface water regime monitoring stations PC1, PC2, PC3, and SC (a); photo of the monitoring station at the PC1 (b).
Figure 3. Location of the surface water regime monitoring stations PC1, PC2, PC3, and SC (a); photo of the monitoring station at the PC1 (b).
Hydrology 10 00060 g003
Hydrology 10 00060 g004 550
Figure 4. Boxplot of water level fluctuations at PC1, PC2, PC3, and SC (a) and water level fluctuations at PC1 across seasons (b). Data is separately presented for low peaks and high peaks, from left to right for each station and season, respectively. Symbol “x” marks mean value, strikethrough marks median value, and circles represent potential outliers.
Figure 4. Boxplot of water level fluctuations at PC1, PC2, PC3, and SC (a) and water level fluctuations at PC1 across seasons (b). Data is separately presented for low peaks and high peaks, from left to right for each station and season, respectively. Symbol “x” marks mean value, strikethrough marks median value, and circles represent potential outliers.
Hydrology 10 00060 g004
Hydrology 10 00060 g005a 550Hydrology 10 00060 g005b 550
Figure 5. Daily water level regime at PC1 for spring (a), autumn (b), summer (c), and winter (d) season—red line represents long−term average for the respective season, and (e) long-term average across the seasons.
Figure 5. Daily water level regime at PC1 for spring (a), autumn (b), summer (c), and winter (d) season—red line represents long−term average for the respective season, and (e) long-term average across the seasons.
Hydrology 10 00060 g005aHydrology 10 00060 g005b
Hydrology 10 00060 g006 550
Figure 6. Time–series of daily recharge/discharge data.
Figure 6. Time–series of daily recharge/discharge data.
Hydrology 10 00060 g006
Hydrology 10 00060 g007 550
Figure 7. Scatterplot of recharge and discharge data pairs during rainfall events.
Figure 7. Scatterplot of recharge and discharge data pairs during rainfall events.
Hydrology 10 00060 g007
Hydrology 10 00060 g008 550
Figure 8. Scatterplot of recharge against daily rainfall for p > 10 mm/day.
Figure 8. Scatterplot of recharge against daily rainfall for p > 10 mm/day.
Hydrology 10 00060 g008
Hydrology 10 00060 g009 550
Figure 9. Scatterplot of recharge QR and Hmin against daily rainfall for 25 mm/day < p < 50 mm/day.
Figure 9. Scatterplot of recharge QR and Hmin against daily rainfall for 25 mm/day < p < 50 mm/day.
Hydrology 10 00060 g009
Table
Table 1. Summary of the data collected from the HydroStations.
Table 1. Summary of the data collected from the HydroStations.
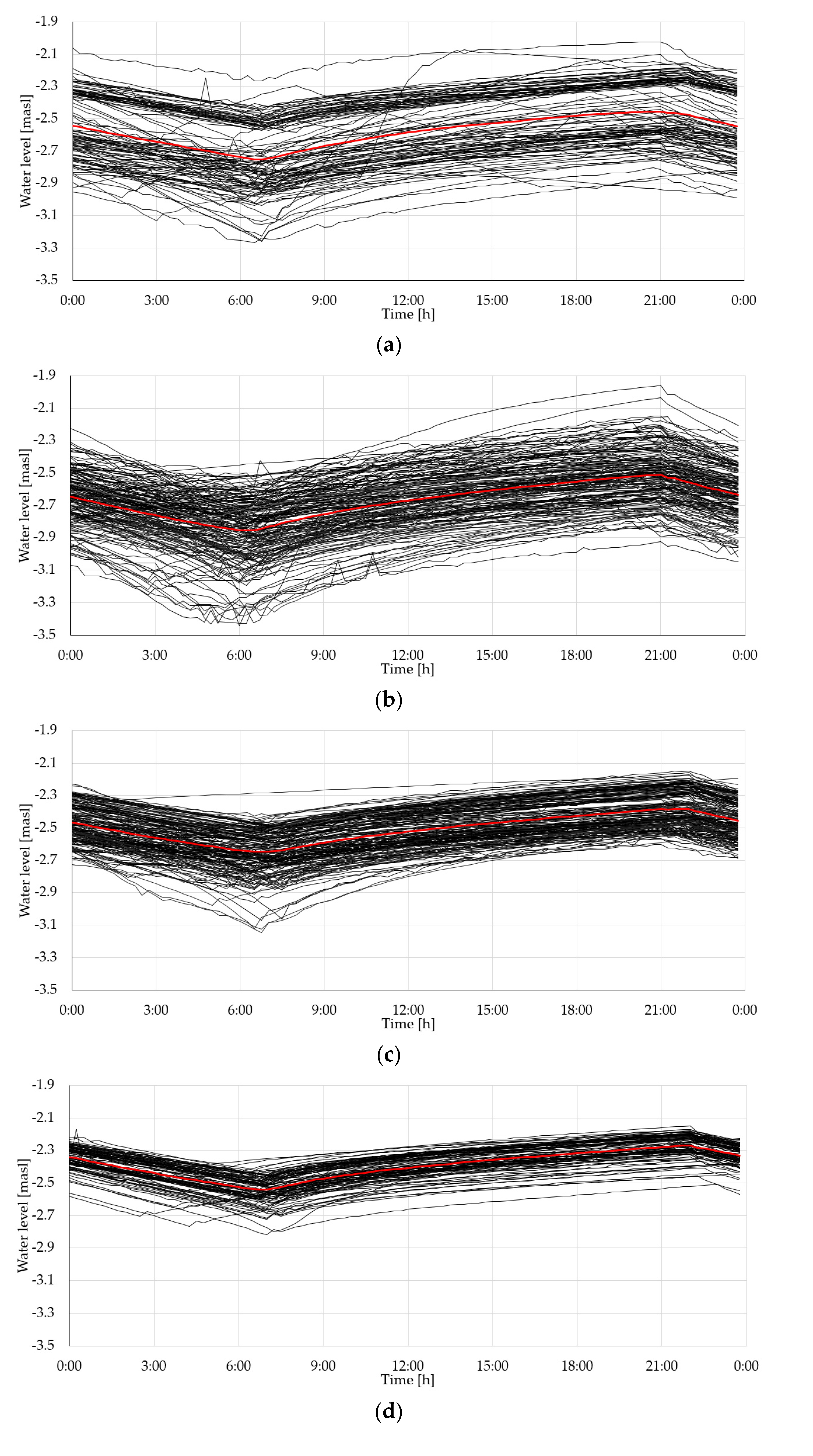
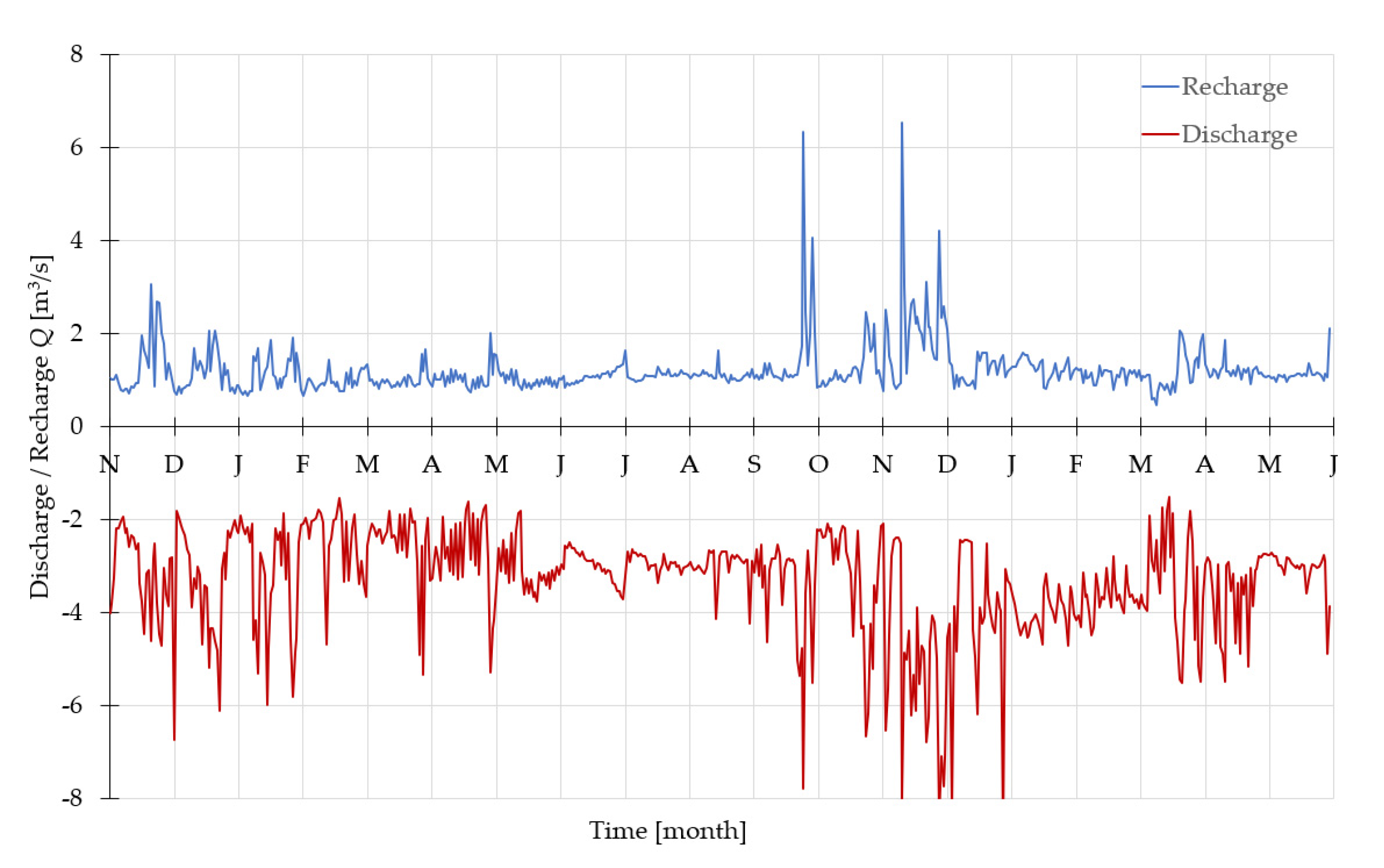
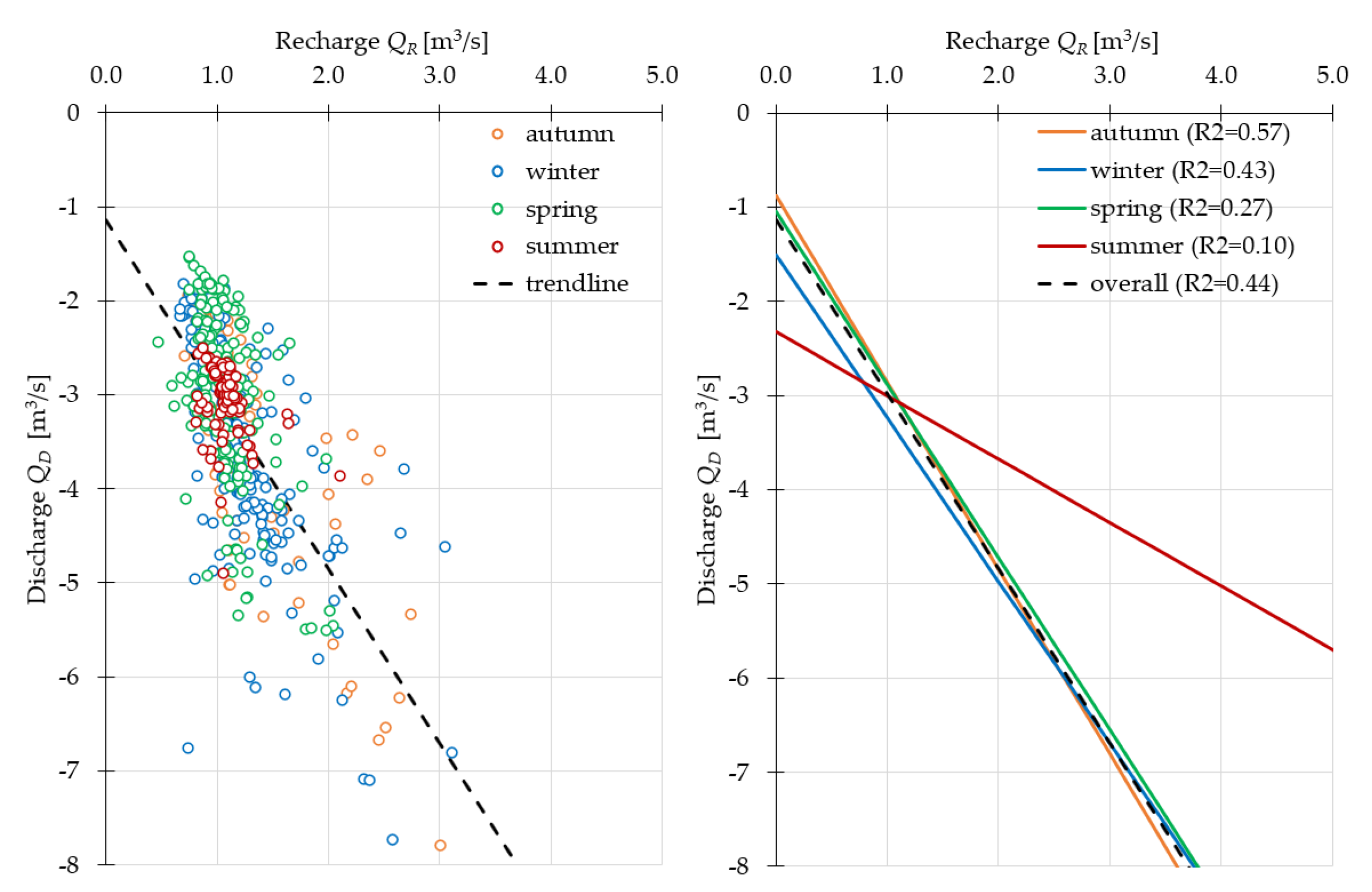
Monitoring
Station		Number of Missing DataNumber of Outliers Removed by FilteringNumber of Data for the Entire Time Span
PC1928254,672
PC28075905
PC38349588
SC4530
Table
Table 2. Summary of the calculated daily water level fluctuation and corresponding recharge data.
Table 2. Summary of the calculated daily water level fluctuation and corresponding recharge data.
SeasonWater Level Fluctuation [cm]Recharge Fluctuation [m3/s]
∆Hmin∆Havg∆HmaxQR,minQR,avgQR,max
all17.234.2140.60.51.26.5
autumn21.237.389.90.81.46.5
winter21.242.7140.60.81.34.2
spring17.230.467.40.51.12.0
summer24.029.857.10.81.12.1
Table
Table 3. Statistical parameters of the seasonal recharge/discharge and rainfall data.
Table 3. Statistical parameters of the seasonal recharge/discharge and rainfall data.
AutumnWinterSpringSummer
P
[mm]		QR
[m3/s]		QD
[m3/s]		P
[mm]		QR
[m3/s]		QD
[m3/s]		P
[mm]		QR
[m3/s]		QD
[m3/s]		P
[mm]		QR
[m3/s]		QD
[m3/s]
Total360//176//425// //
Minimum/0.8−2.1/0.8−1.5/0.5−1.5/0.8−2.5
Average/1.4−3.4/1.3−4.0/1.1−3.0/1.1−3.1
Maximum 6.5−8.0 4.2−8.7 2.0−5.5 2.1−4.9
St. dev/0.941.41/0.491.34/0.250.89/0.170.36
R-Bindex/0.240.34/0.230.32/0.170.35/0.080.10
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Gilja, G.; Kuspilić, N.; Lacko, M.; Romić, D. Reconstruction of Recharge and Discharge Pattern in the Polder Drainage Canal Network. Hydrology 2023, 10, 60. https://doi.org/10.3390/hydrology10030060

AMA Style

Gilja G, Kuspilić N, Lacko M, Romić D. Reconstruction of Recharge and Discharge Pattern in the Polder Drainage Canal Network. Hydrology. 2023; 10(3):60. https://doi.org/10.3390/hydrology10030060

Chicago/Turabian Style

Gilja, Gordon, Neven Kuspilić, Martina Lacko, and Davor Romić. 2023. "Reconstruction of Recharge and Discharge Pattern in the Polder Drainage Canal Network" Hydrology 10, no. 3: 60. https://doi.org/10.3390/hydrology10030060

APA Style

Gilja, G., Kuspilić, N., Lacko, M., & Romić, D. (2023). Reconstruction of Recharge and Discharge Pattern in the Polder Drainage Canal Network. Hydrology, 10(3), 60. https://doi.org/10.3390/hydrology10030060

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop