Suspended Sediments in Environmental Flows: Interpretation of Concentration Profiles Shapes
Abstract
1. Introduction
2. Mathematical Modeling of Suspended Sediment Concentrations
2.1. Classical Advection–Diffusion Equation Based on the Gradient Diffusion Model
2.2. The Kinetic Model
2.3. Improved Advection–Diffusion Equations
3. Sediment Diffusivity
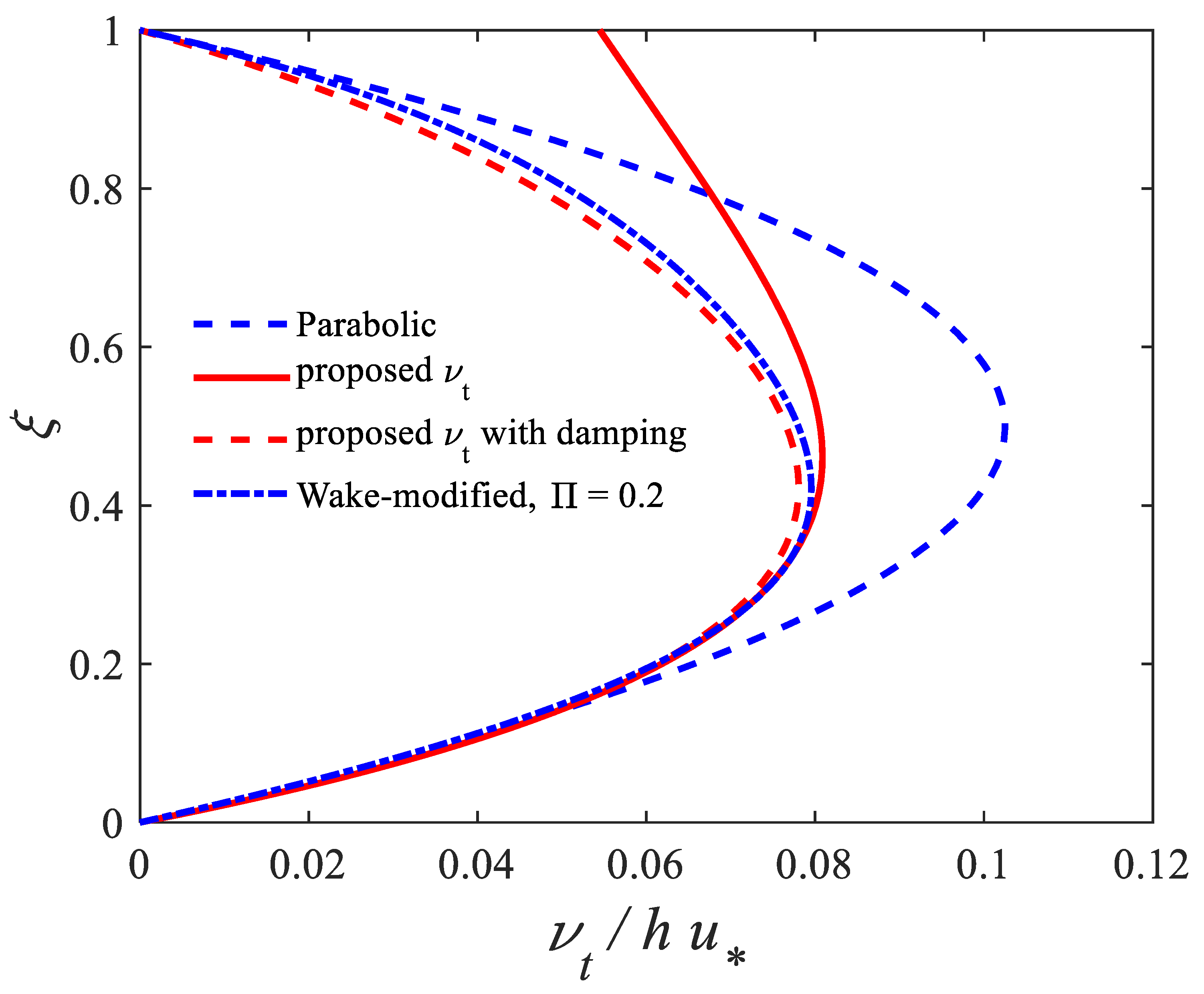
3.1. Eddy Viscosity
3.2. Turbulent Schmidt Number
4. Suspended Sediments in Steady Uniform Open-Channel Flows
4.1. The Kinetic Model and the Classical Advection–Diffusion Equation
4.2. Concentration Profile with the Advection–Diffusion Equation
| Run Number | ||||
|---|---|---|---|---|
| S2 | 12.0 | 1.3 | 12.85 | 2.65 |
| S3 | 11.7 | 1.3 | 13.26 | 2.65 |
| S4 | 11.5 | 1.3 | 14.28 | 2.65 |
4.3. Hindered Settling Velocity
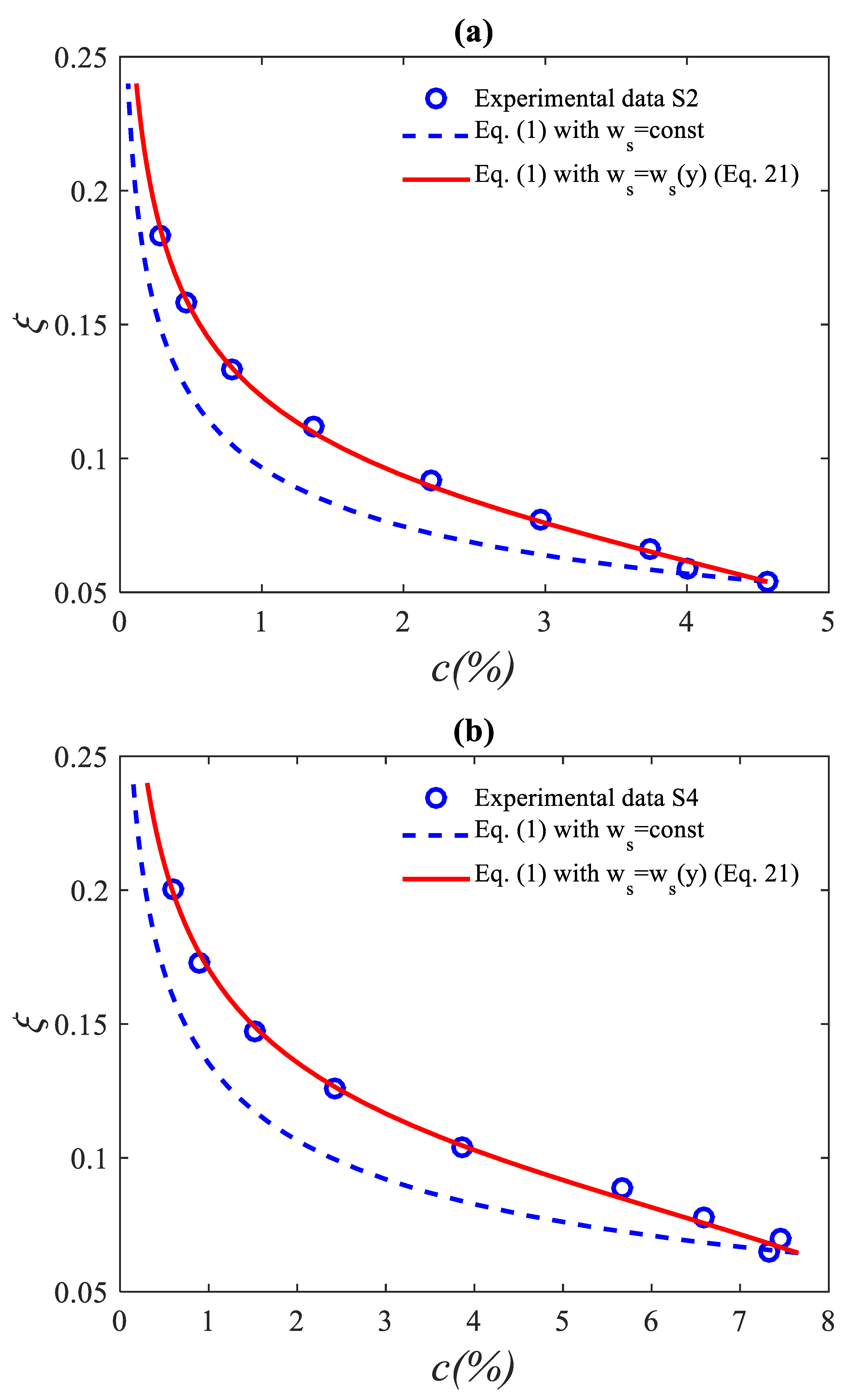
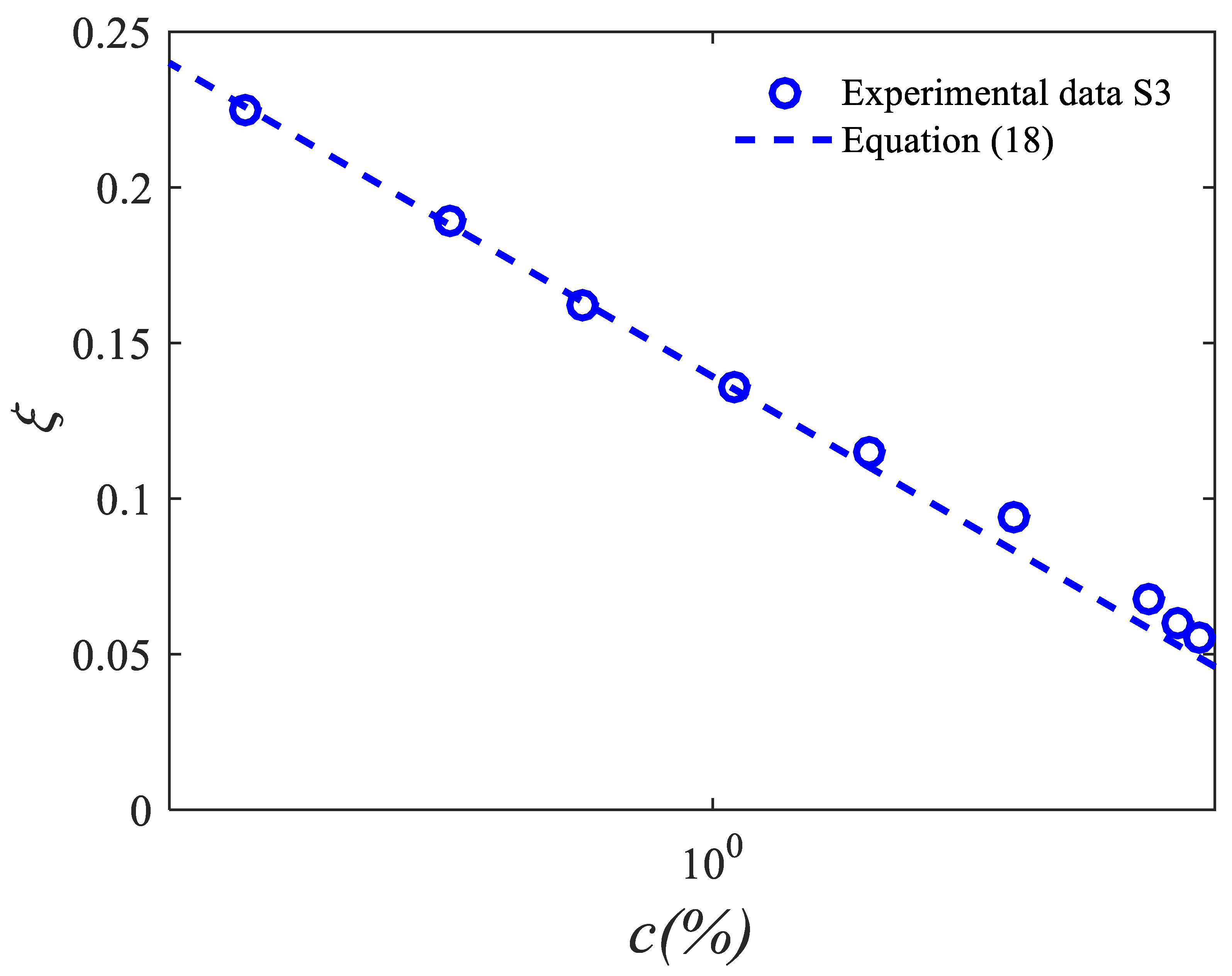
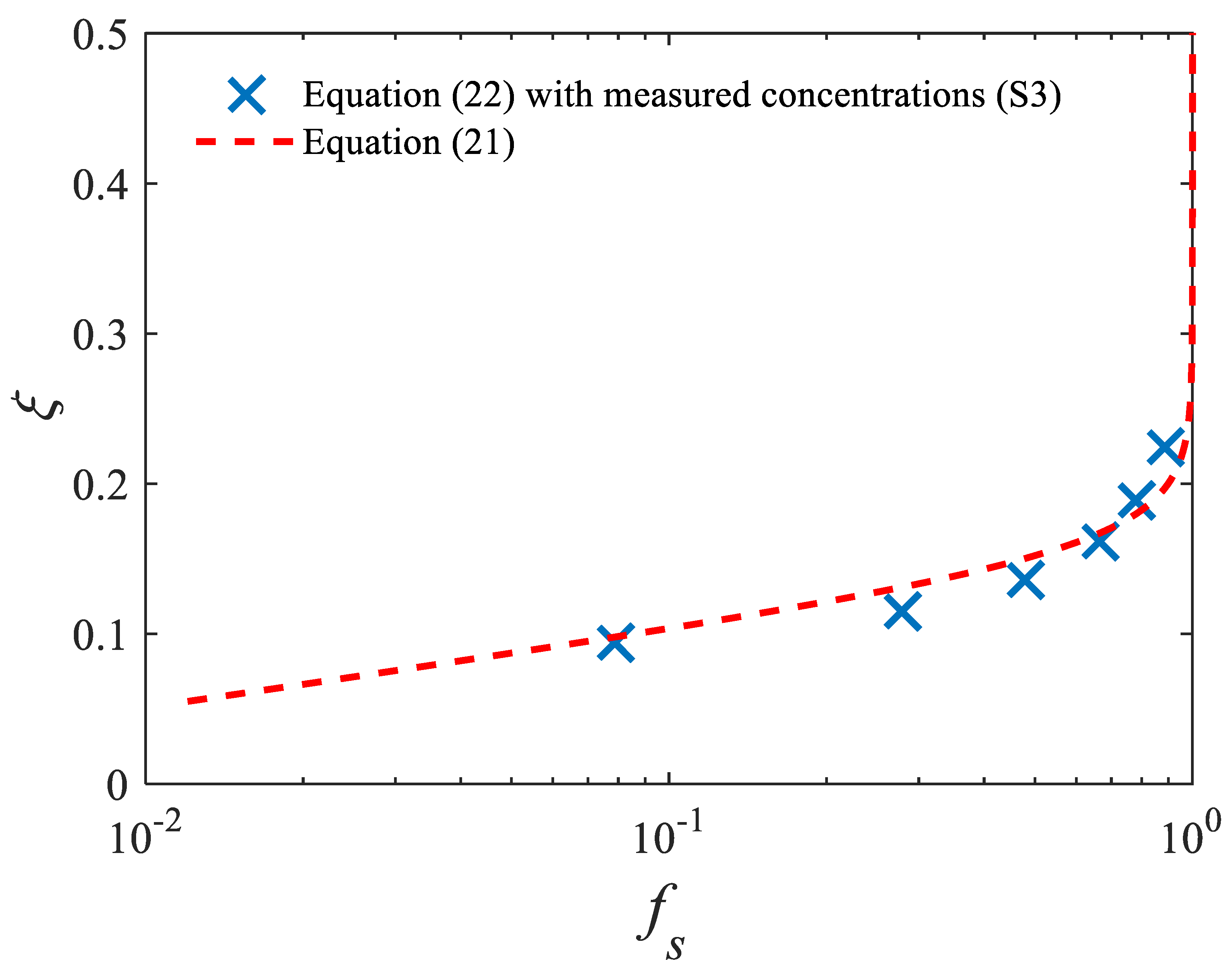
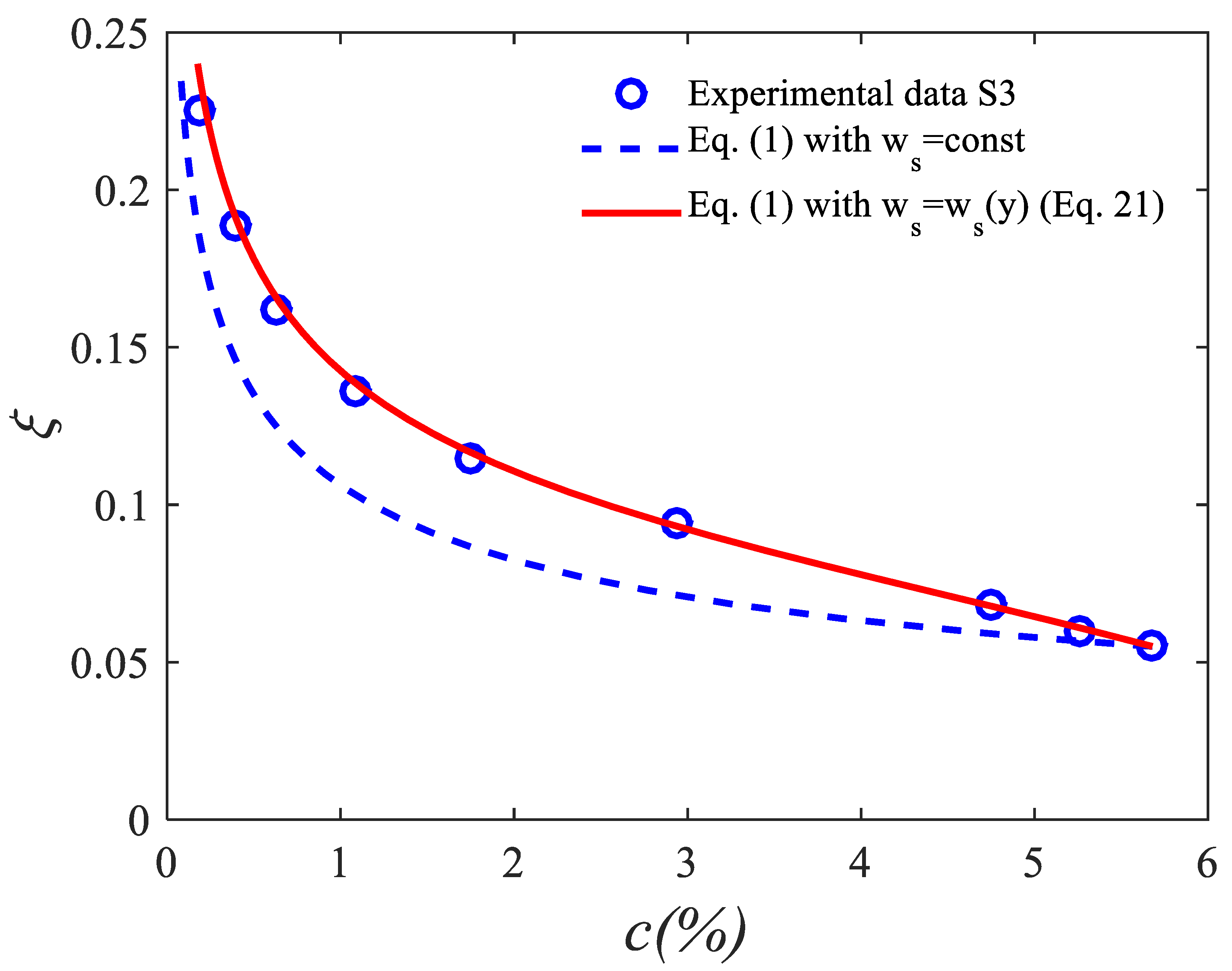
4.4. Results
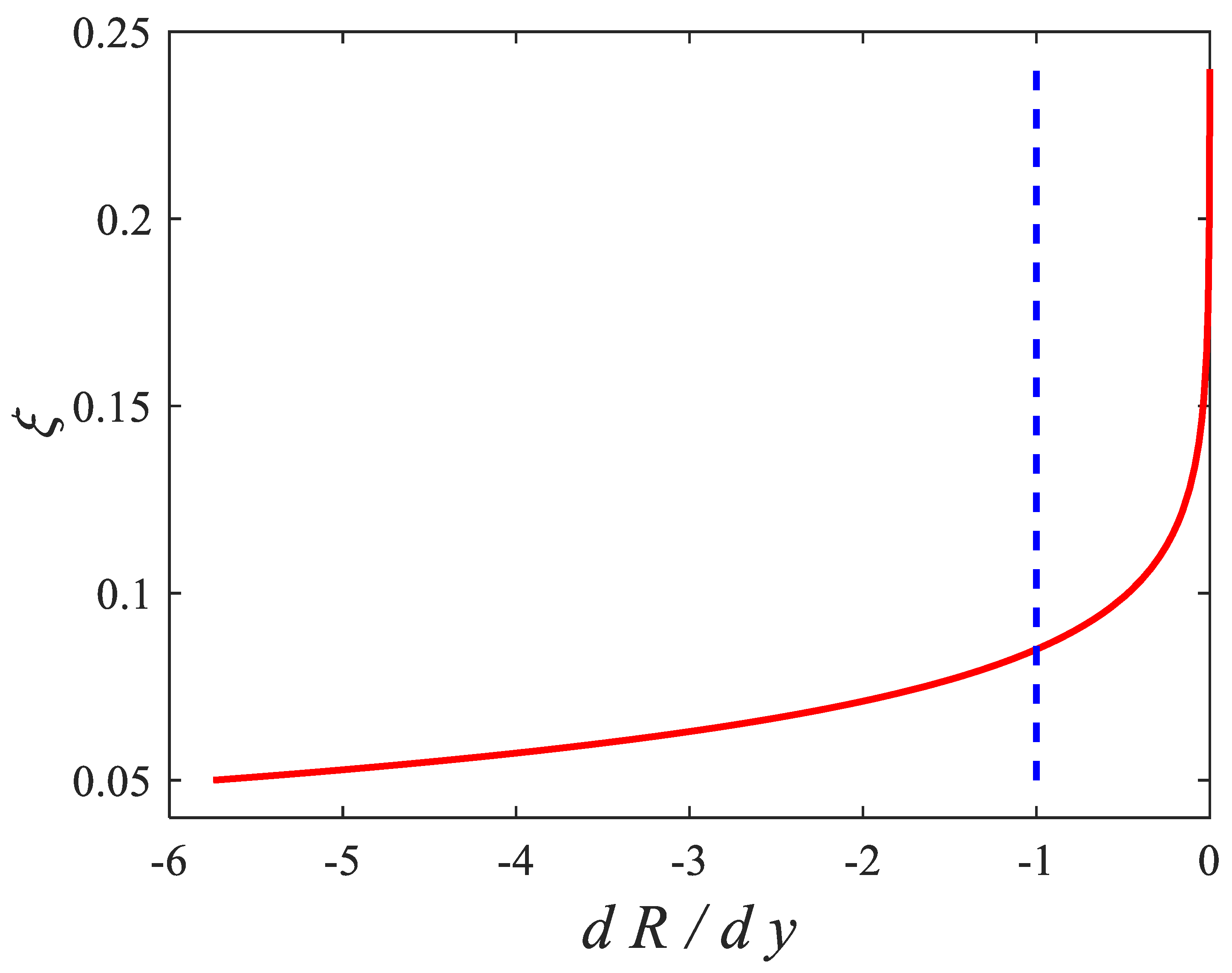
4.5. First Criterion for Concentration Profiles Shape in Cartesain Coordiantes
5. Suspended Sediments in Oscillatory Flows over Sand Ripples
5.1. Convection–Diffusion Equation with Upward Convection Term
5.2. Second Criterion for Concentration Profiles Shape in Semi-Log Plots
6. Conclusions
- -
- In this study, we provided simple and accurate tools for the sediment diffusivity through analytical formulations for both the eddy viscosity and β-factor/function (i.e., the inverse of the turbulent Schmidt number).
- -
- For steady open-channel flows, two models were investigated, namely, the ADE and the kinetic model.
- -
- Our study shows that the kinetic model reverts to the classical ADE with a modified or “apparent” settling velocity.
- -
- Results for the concentration profiles, with a hindered settling function, show good agreement for the open-channel flows.
- -
- An interpretation of the concentration profiles is provided.
- -
- For steady open-channel flows: the concentration profiles shape, in the Cartesian coordinates, depends on the vertical distribution of the derivative of the ratio R between the sediment diffusivity and the settling velocity of the sediments (): for the upward concave concentration profile while for the near-bed upward convex profile.
- -
- For oscillatory flows over sand ripples, the convection–diffusion equation was considered. As for the kinetic model, the convection–diffusion equation reverts to the classical ADE but with an “apparent” sediment diffusivity instead of the “apparent” settling velocity.
- -
- A generalization was proposed for the interpretation of the concentration profiles for fine and coarse sand in oscillatory flows over sand ripples. A relation between the second derivative of the logarithm of the concentration and the derivative of the apparent sediment diffusivity allows interpretation of the concentration profiles in the semi-log plots. This equation provides a link, in the semi-log plots, between the upward concavity/convexity of the concentration profiles and the increasing/decreasing in the apparent sediment diffusivity. Increasing the apparent sediment diffusivity allows an upward concave concentration profile, while decreasing the apparent sediment diffusivity allows an upward convex concentration profile.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vanoni, V.A. Transportation of Suspended Sediment by Water; ASCE: Reston, VA, USA, 1946; Volume 111, pp. 67–133. [Google Scholar]
- Yalin, M.S. Mechanics of Sediment Transport; Pergamon Press: Oxford, UK, 1972. [Google Scholar]
- Fredsoe, J.; Deigaard, R. Mechanics of Coastal Sediment Transport; World Scientific Publishing: Singapore, 1992; 369p. [Google Scholar]
- Nielsen, P. Coastal Bottom Boundary Layers and Sediment Transport; World Scientific Publishing: Singapore, 1992; 324p. [Google Scholar]
- Seminara, G.; Blondeaux, P. River, Coastal and Estuarine Morphodynamics; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Guo, J.; Wood, W.L. Fine Suspended Sediment Transport Rates. J. Hydraul. Eng. ASCE 1995, 121, 919–922. [Google Scholar] [CrossRef]
- Tsai, C.W.; Hung, S.Y. Modeling Suspended Sediment Transport Under Influence of Turbulence Ejection and Sweep Events. Water Resour. Res. 2019, 55, 5379–5393. [Google Scholar] [CrossRef]
- Ghoshal, K.; Jain, P.; Absi, R. Nonlinear Partial Differential Equation for Unsteady Vertical Distribution of Suspended Sediments in Open Channel Flows: Effects of Hindered Settling and Concentration-Dependent Mixing Length. J. Eng. Mech. ASCE 2022, 148, 04021123. [Google Scholar] [CrossRef]
- Gaudio, R. Turbulence and Flow–Sediment Interactions in Open-Channel Flows. Water 2020, 12, 3169. [Google Scholar] [CrossRef]
- Lai, Y.G.; Wu, K.A. Three-Dimensional Flow and Sediment Transport Model for Free-Surface Open Channel Flows on Unstructured Flexible Meshes. Fluids 2019, 4, 18. [Google Scholar] [CrossRef]
- Hu, L.; Dong, Z.; Peng, C.; Wang, L.-P. Direct Numerical Simulation of Sediment Transport in Turbulent Open Channel Flow Using the Lattice Boltzmann Method. Fluids 2021, 6, 217. [Google Scholar] [CrossRef]
- Faraci, C.; Scandura, P.; Petrotta, C.; Foti, E. Wave-Induced Oscillatory Flow over a Sloping Rippled Bed. Water 2019, 11, 1618. [Google Scholar] [CrossRef]
- Gusarov, A.V.; Sharifullin, A.G.; Komissarov, M.A. Contemporary Long-Term Trends in Water Discharge, Suspended Sediment Load, and Erosion Intensity in River Basins of the North Caucasus Region, SW Russia. Hydrology 2021, 8, 28. [Google Scholar] [CrossRef]
- Jain, P.; Kundu, S.; Ghoshal, K.; Absi, R. Direct Derivation of Streamwise Velocity from RANS Equation in an Unsteady Nonuniform Open-Channel Flow. J. Eng. Mech. ASCE 2022, 148, 06022002. [Google Scholar] [CrossRef]
- Sen, S.; Kundu, S.; Absi, R.; Ghoshal, K. A model for coupled fluid velocity and suspended sediment concentration in an unsteady stratified turbulent flow through an open channel. J. Eng. Mech. ASCE 2023, 149, 04022088. [Google Scholar] [CrossRef]
- Einstein, H.A.; Chien, N. Effects of Heavy Sediment Concentration Near the Bed on Velocity and Sediment Distribution; M.R.D. Sediment Series, Rep. No. 8; University of California: Berkeley, CA, USA, 1955. [Google Scholar]
- Fu, X.; Wang, G.; Shao, X. Vertical dispersion of fine and coarse sediments in turbulent open-channel flows. J. Hydraul. Eng. ASCE 2005, 131, 877–888. [Google Scholar] [CrossRef]
- McFetridge, W.F.; Nielsen, P. Sediment Suspension by Non-Breaking Waves over Rippled Beds; Technical Report No. UFL/COEL-85/005; Coast Ocean Eng Dept, University of Florida: Gainesville, FL, USA, 1985. [Google Scholar]
- Nielsen, P.; Teakle, I.A.L. Turbulent diffusion of momentum and suspended particles: A finite-mixing-length-theory. Phys. Fluids 2004, 16, 2342–2348. [Google Scholar] [CrossRef]
- Absi, R. Comment on Turbulent diffusion of momentum and suspended particles: A finite-mixing-length theory. Phys. Fluids 2005, 17, 079101. [Google Scholar] [CrossRef]
- Absi, R. Modeling turbulent mixing and sand distribution in the bottom boundary layer. In Proceedings of the 5th International Conference on Coastal Dynamics 2005—State of the Practice, Barcelona, Spain, 4–8 April 2005; Sanchez-Arcilla, A., Ed.; ASCE: Reston, VA, USA, 2005. [Google Scholar]
- Absi, R. Concentration profiles for fine and coarse sediments suspended by waves over ripples: An analytical study with the 1-DV gradient diffusion model. Adv. Water Resour. 2010, 33, 411–418. [Google Scholar] [CrossRef]
- Rouse, H. Modern conceptions of the mechanics of fluid turbulence. Trans. Am. Soc. Civ. Eng. 1937, 102, 463–543. [Google Scholar] [CrossRef]
- Umeyama, M. Velocity and concentration fields in uniform flow with coarse sands. J. Hydraul. Eng. ASCE 1999, 125, 653–656. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Sediment Transport, Part II: Suspended Load Transport. J. Hydraul. Eng. ASCE 1984, 110, 1613–1641. [Google Scholar] [CrossRef]
- Graf, W.H.; Cellino, M. Suspension flows in open channels: Experimental study. J. Hydraul. Res. 2002, 40, 435–447. [Google Scholar] [CrossRef]
- Kaushal, D.R. Discussion of Vertical dispersion of fine and coarse sediments in turbulent open-channel flows. J. Hydraul. Eng. ASCE 2007, 133, 1292–1294. [Google Scholar] [CrossRef]
- Richardson, J.F.; Zaki, W.N. Sedimentation and fluidisation: Part 1. Trans. Inst. Chem. Eng. 1954, 32, 35–53. [Google Scholar] [CrossRef]
- Absi, R. Time-dependent eddy viscosity models for wave boundary layers. In Proceedings of the 27th International Conference on Coastal Engineering, Sydney, Australia, 16–21 July 2000; Edge, B.L., Ed.; ASCE Press: Reston, VA, USA, 2001; Volume 2, pp. 1268–1281. [Google Scholar]
- Absi, R. Analytical solutions for the modeled k-equation. ASME J. Appl. Mech. 2008, 75, 044501. [Google Scholar] [CrossRef]
- Absi, R. A simple eddy viscosity formulation for turbulent boundary layers near smooth walls. C. R. Mec. 2009, 337, 158–165. [Google Scholar] [CrossRef]
- Absi, R. Eddy viscosity and velocity profiles in fully-developed turbulent channel flows. Fluid Dyn. 2019, 54, 137–147. [Google Scholar] [CrossRef]
- Absi, R. Analytical eddy viscosity model for velocity profiles in the outer part of closed- and open-channel flows. Fluid Dyn. 2021, 56, 577–586. [Google Scholar] [CrossRef]
- Absi, R. Reinvestigating the parabolic-shaped eddy viscosity profile for free surface flows. Hydrology 2021, 8, 126. [Google Scholar] [CrossRef]
- Nezu, I.; Nakagawa, H. Turbulence in Open-Channel Flows; A.A. Balkema: Rotterdam, The Netherlands, 1993. [Google Scholar]
- Absi, R.; Marchandon, S.; Lavarde, M. Turbulent diffusion of suspended particles: Analysis of the turbulent Schmidt number. Defect Diffus. Forum 2011, 312–315, 794–799. [Google Scholar] [CrossRef]
- Jain, P.; Kumbhakar, M.; Ghoshal, K. A mathematical model on depth-averaged β-factor in open-channel turbulent fow. Environ. Earth Sci. 2018, 77, 253. [Google Scholar] [CrossRef]
- Absi, R. Rebuttal on A mathematical model on depth-averaged β-factor in open-channel turbulent flow. Environ. Earth Sci. 2020, 79, 113. [Google Scholar] [CrossRef]
- Gualtieri, C.; Angeloudis, A.; Bombardelli, F.; Jha, S.; Stoesser, T. On the Values for the Turbulent Schmidt Number in Environmental Flows. Fluids 2017, 2, 17. [Google Scholar] [CrossRef]
- Absi, R.; Tanaka, H. Analytical eddy viscosity model for turbulent wave boundary layers: Application to suspended sediment concentrations over wave ripples. J. Mar. Sci. Eng. submitted.
- Absi, R. Calibration of Businger-Arya type of eddy viscosity model’s parameters. J. Waterw. Port Coast. Ocean Eng. ASCE 2000, 126, 108–109. [Google Scholar] [CrossRef]
- Absi, R. Wave boundary layer instability near flow reversal. In Proceedings of the 28th International Conference on Coastal Engineering 2002, Cardiff, UK, 7–12 July 2002; Smith, J.M., Ed.; World Scientific Publishing: Singapore, 2002; Volume 1, pp. 532–544, ISBN 981-238-238-0. [Google Scholar]
- Absi, R. Discussion of One-dimensional wave bottom boundary layer model comparison: Specific eddy viscosity and turbulence closure model. J. Waterw. Port Coast. Ocean Eng. ASCE 2006, 132, 139–141. [Google Scholar] [CrossRef]
- Absi, R. On the effect of sand grain size on turbulent mixing. In Proceedings of the International Conference on Coastal Engineering 2006, San Diego, CA, USA, 3–8 September 2006; Smith, J.M., Ed.; World Scientific Publishing: Singapore, 2006; pp. 3019–3029. [Google Scholar]
- Absi, R.; Tanaka, H.; Kerlidou, L.; André, A. Eddy viscosity profiles for wave boundary layers: Validation and calibration by a k-ω model. In Proceedings of the 33th International Conference on Coastal Engineering, Santander, Spain, 1–6 July 2012. [Google Scholar]
- Sheng, J.; Hay, A.E. Sediment eddy diffusivities in the nearshore zone, from multifrequency acoustic backscatter. Cont. Shelf Res. 1995, 15, 129–147. [Google Scholar] [CrossRef]
- Lee, T.H.; Hanes, D.M. Comparison of field observations of the vertical distribution of suspended sand and its prediction by models. J. Geophys. Res. 1996, 101, 3561–3572. [Google Scholar] [CrossRef]
- Van Rijn, L.C. United view of sediment transport by currents and waves II: Suspended transport. J. Hydraul. Eng. ASCE 2007, 133, 668–689. [Google Scholar] [CrossRef]
- Thorne, P.D.; Williams, J.J.; Davies, A.G. Suspended sediments under waves measured in a large-scale flume facility. J. Geophys. Res. 2002, 107, 3178. [Google Scholar] [CrossRef]
- Thorne, P.D.; Davies, A.G.; Bell, P.S. Observations and analysis of sediment diffusivity profiles over sandy rippled beds under waves. J. Geophys. Res. 2009, 114, C02023. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Absi, R. Suspended Sediments in Environmental Flows: Interpretation of Concentration Profiles Shapes. Hydrology 2023, 10, 5. https://doi.org/10.3390/hydrology10010005
Absi R. Suspended Sediments in Environmental Flows: Interpretation of Concentration Profiles Shapes. Hydrology. 2023; 10(1):5. https://doi.org/10.3390/hydrology10010005
Chicago/Turabian StyleAbsi, Rafik. 2023. "Suspended Sediments in Environmental Flows: Interpretation of Concentration Profiles Shapes" Hydrology 10, no. 1: 5. https://doi.org/10.3390/hydrology10010005
APA StyleAbsi, R. (2023). Suspended Sediments in Environmental Flows: Interpretation of Concentration Profiles Shapes. Hydrology, 10(1), 5. https://doi.org/10.3390/hydrology10010005






