Quantitative Estimation of Rainfall from Remote Sensing Data Using Machine Learning Regression Models
Abstract
1. Introduction
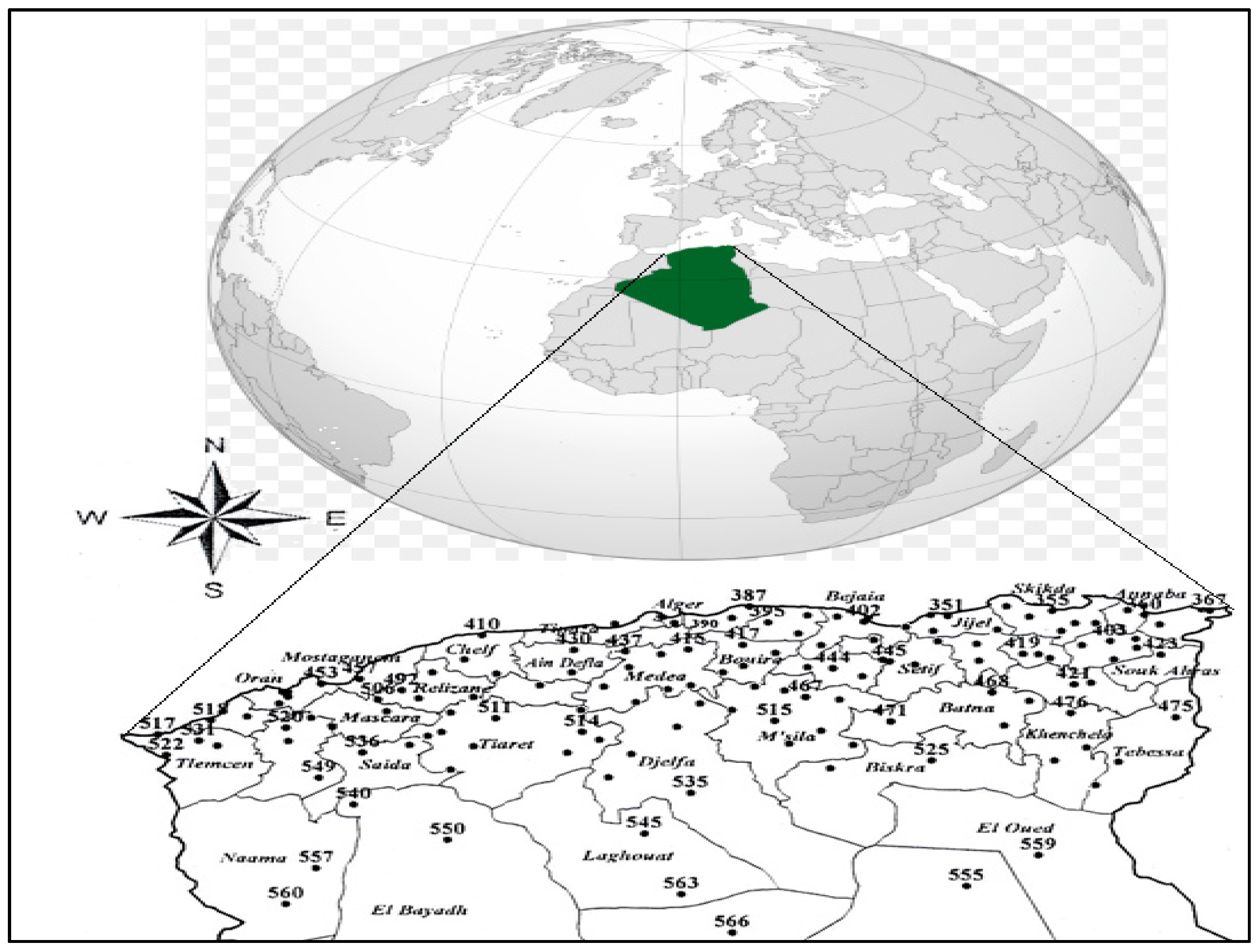
2. Study area and Data
2.1. Rain Gauge Data
2.2. MSG Data
2.3. Coincidence MSG Data/ Rain Gauge Data
3. Methodology
- Mathematical description of the models
- Models learning and tuning
- Combination of three models
3.1. Mathematical Description of the Models
3.1.1. Support Vector Regression
3.1.2. Random Forest Regression
- Creation of the first regression tree from a bootstrap sample taken at random from the database and then returned.
- Creation of the other regression trees in the same way as the first step.
- The final decision is the arithmetic mean of the regression results given by all the decision trees composing the random forest.
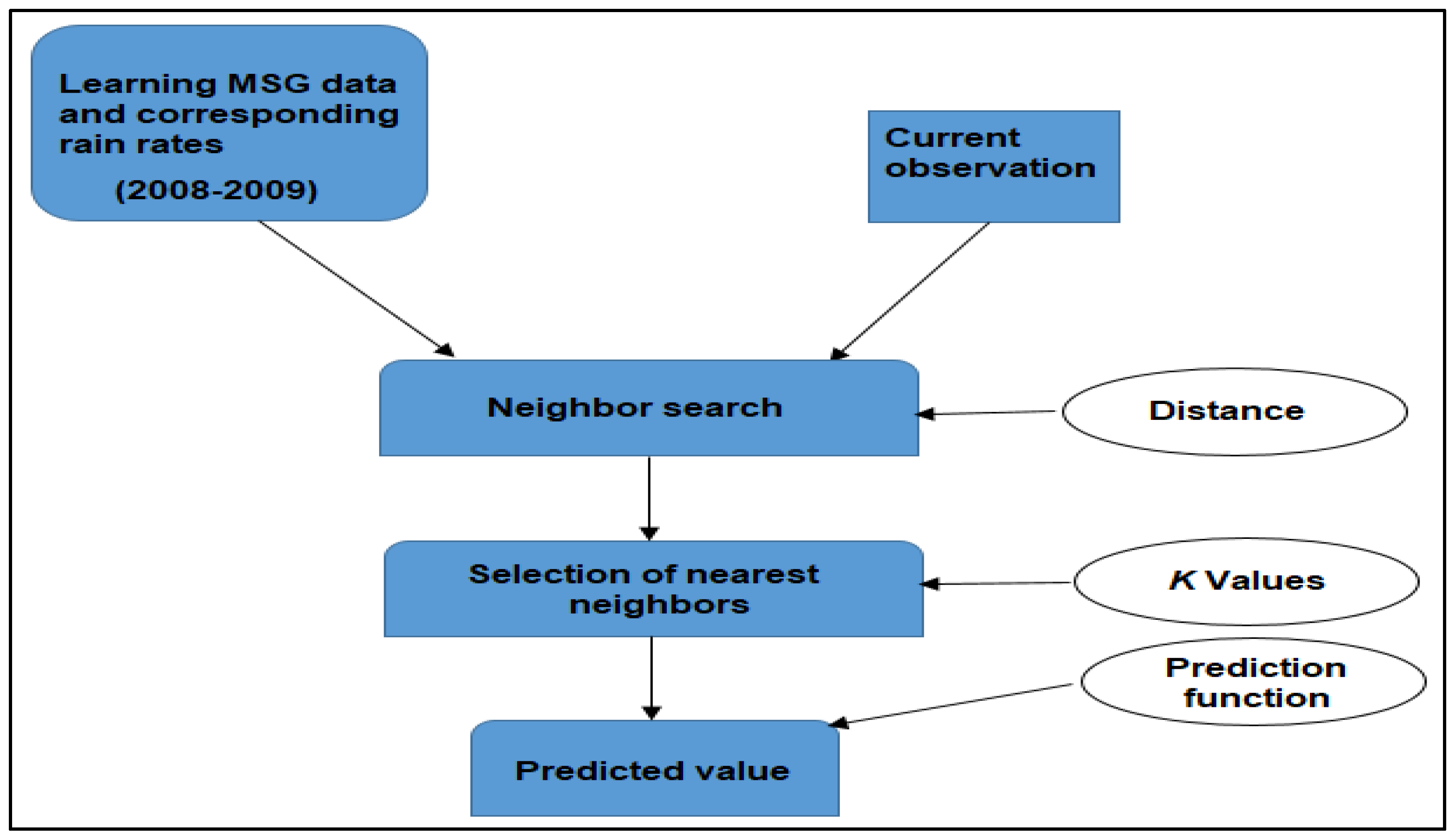
3.1.3. K-Nearest Neighbor Regression
- Construction of a learning database D composed of the inputs and the corresponding outputs.
- Calculate all the distances between this observation X and the other observations of the data set D
- Select the K observations closest to X according to the distance
- Calculate the average of the K observations retained in the case of the regression.
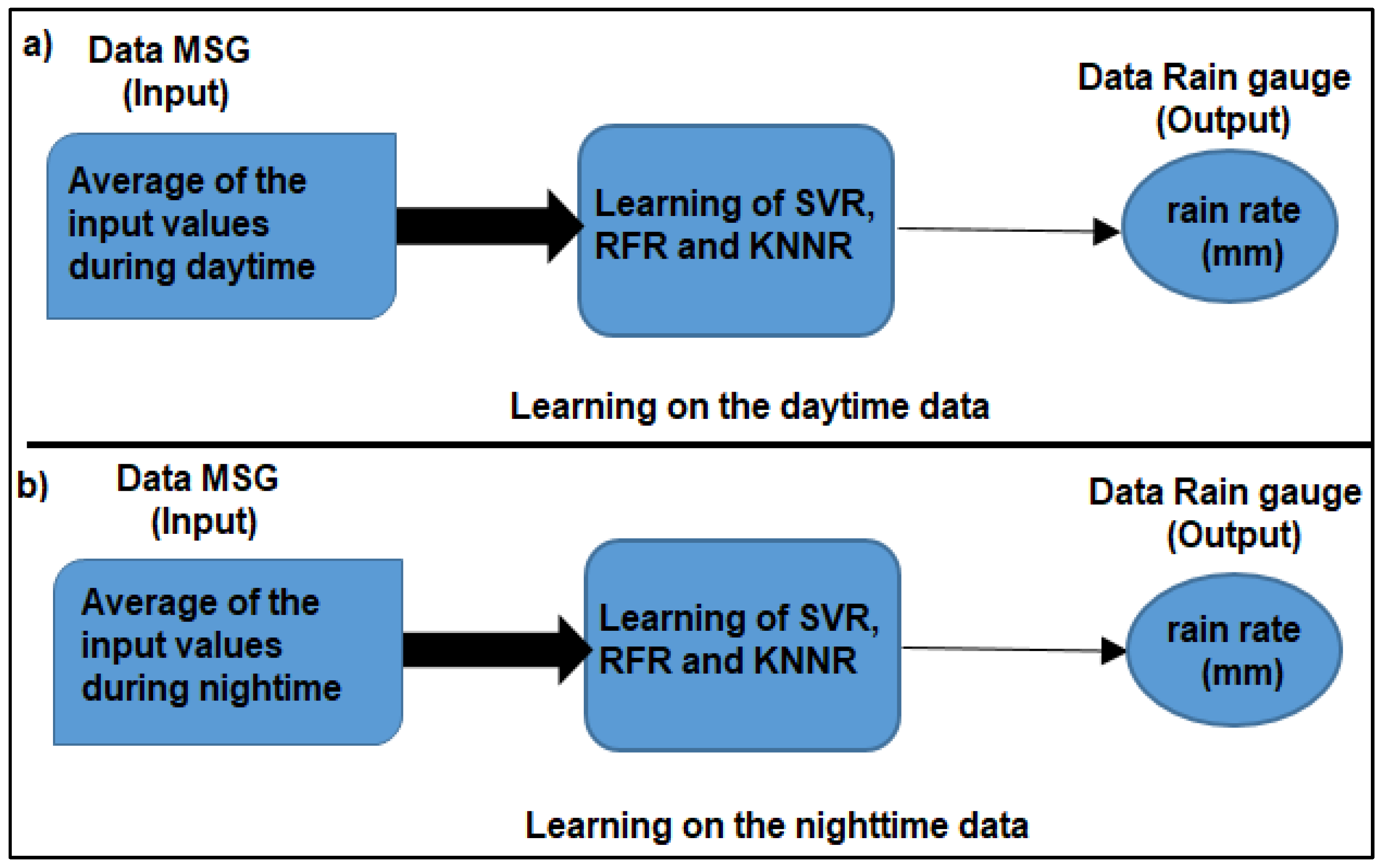
3.2. Learning and Tuning Models
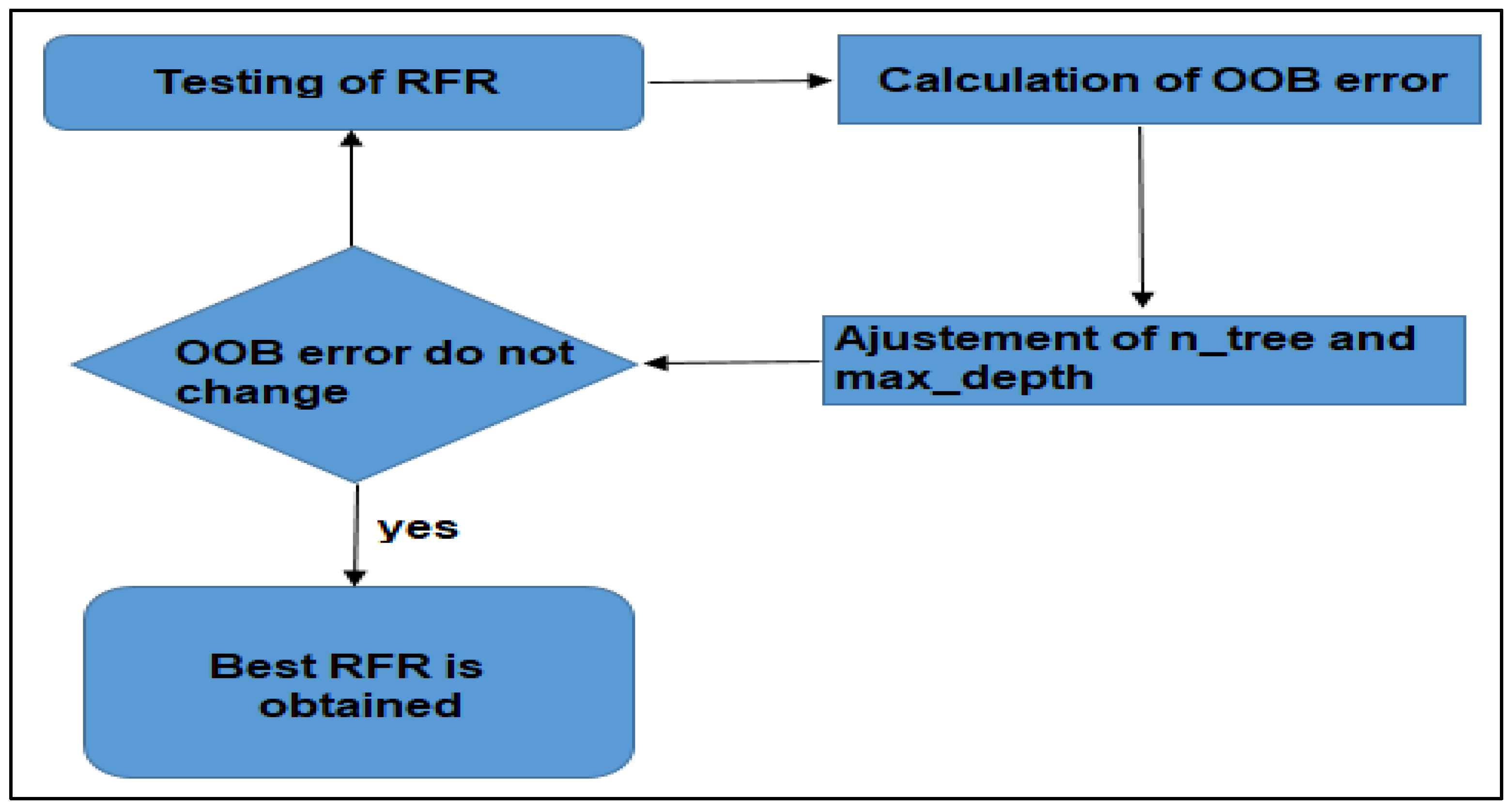
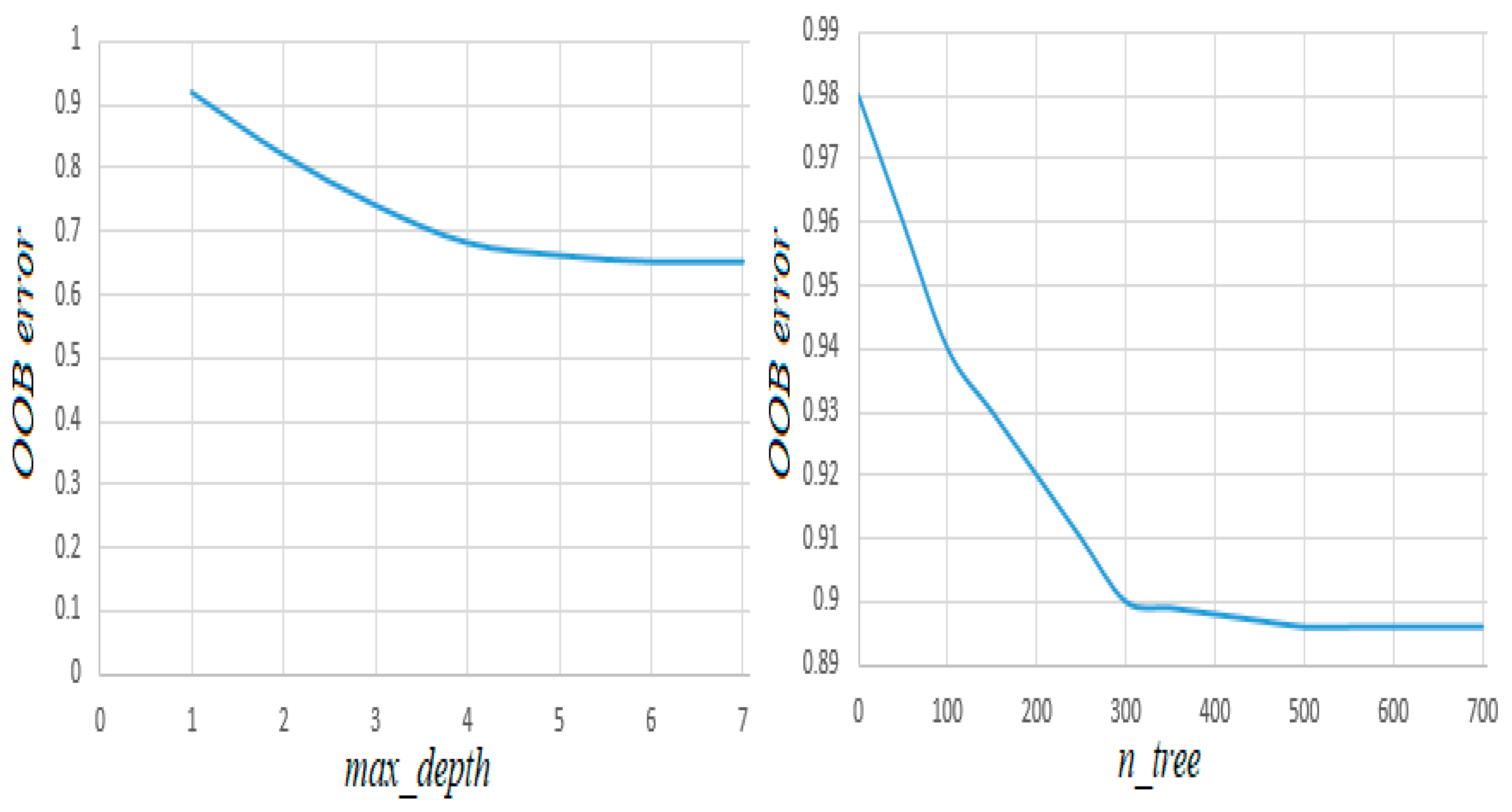
3.2.1. Tuning of RFR
3.2.2. Tuning ofK-NNR
3.2.3. Tuning of SVR
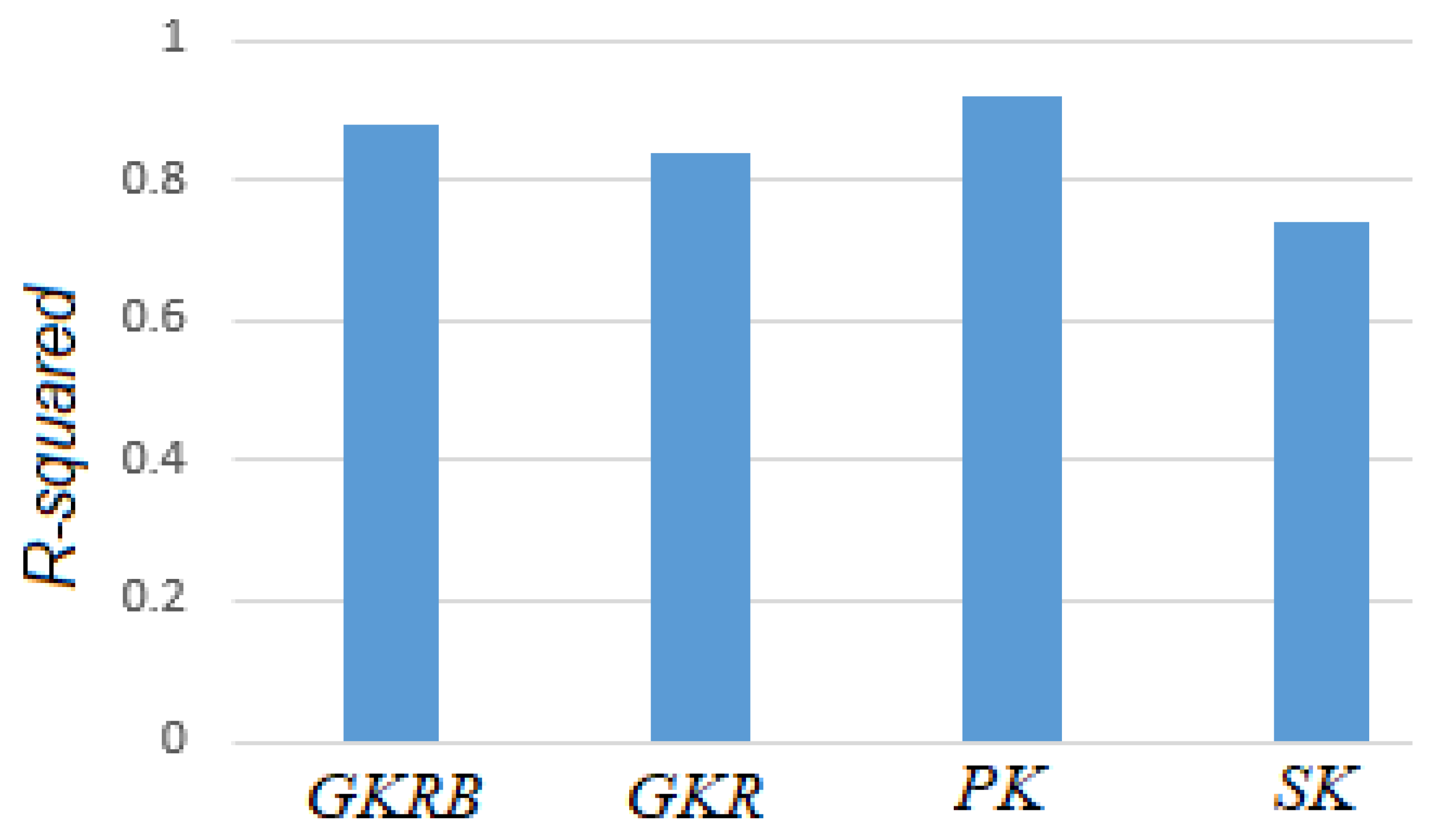
3.2.4. Test of Input Parameters
3.3. Combination of Models
4. Application for Rainfall Estimation
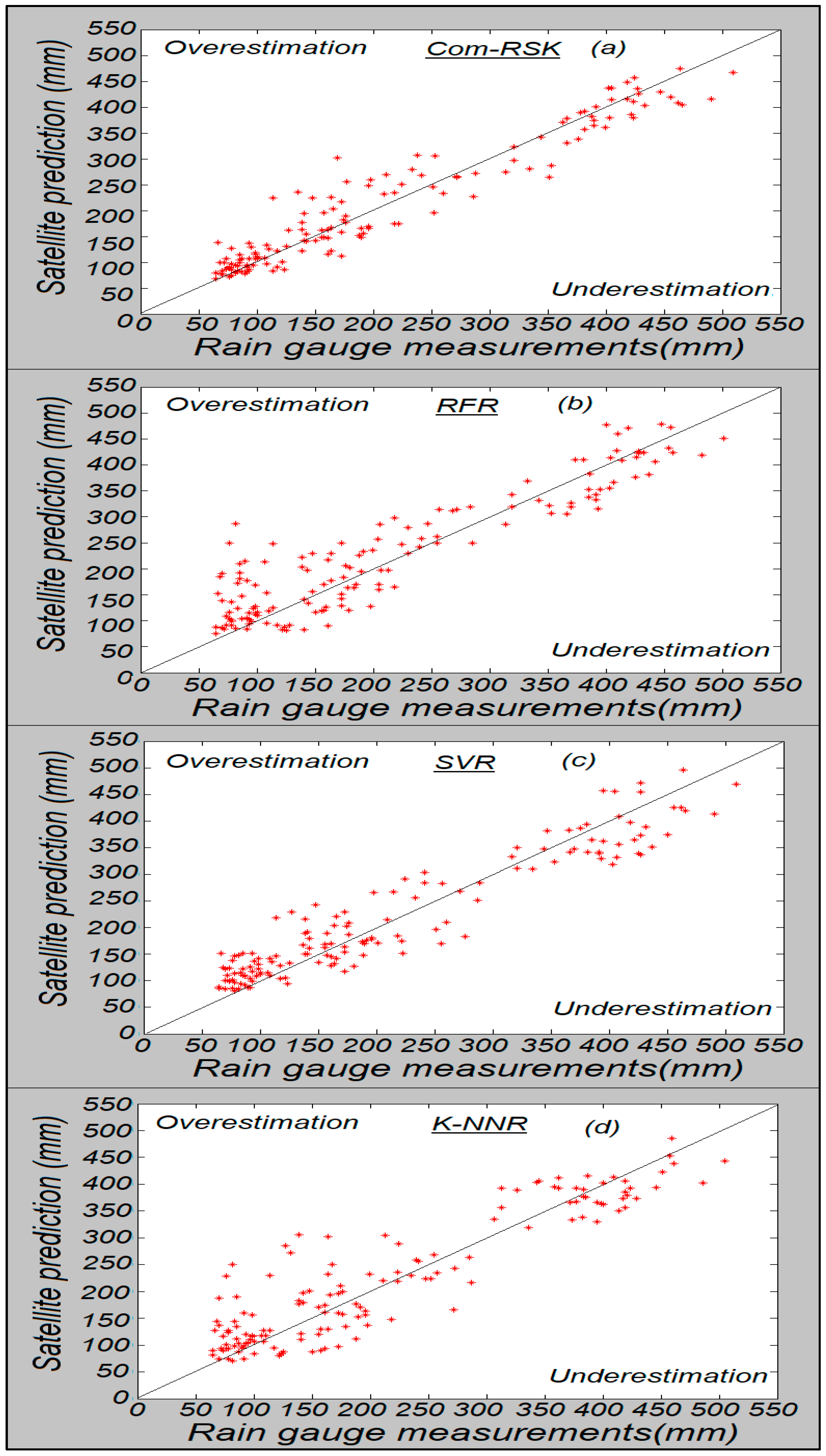
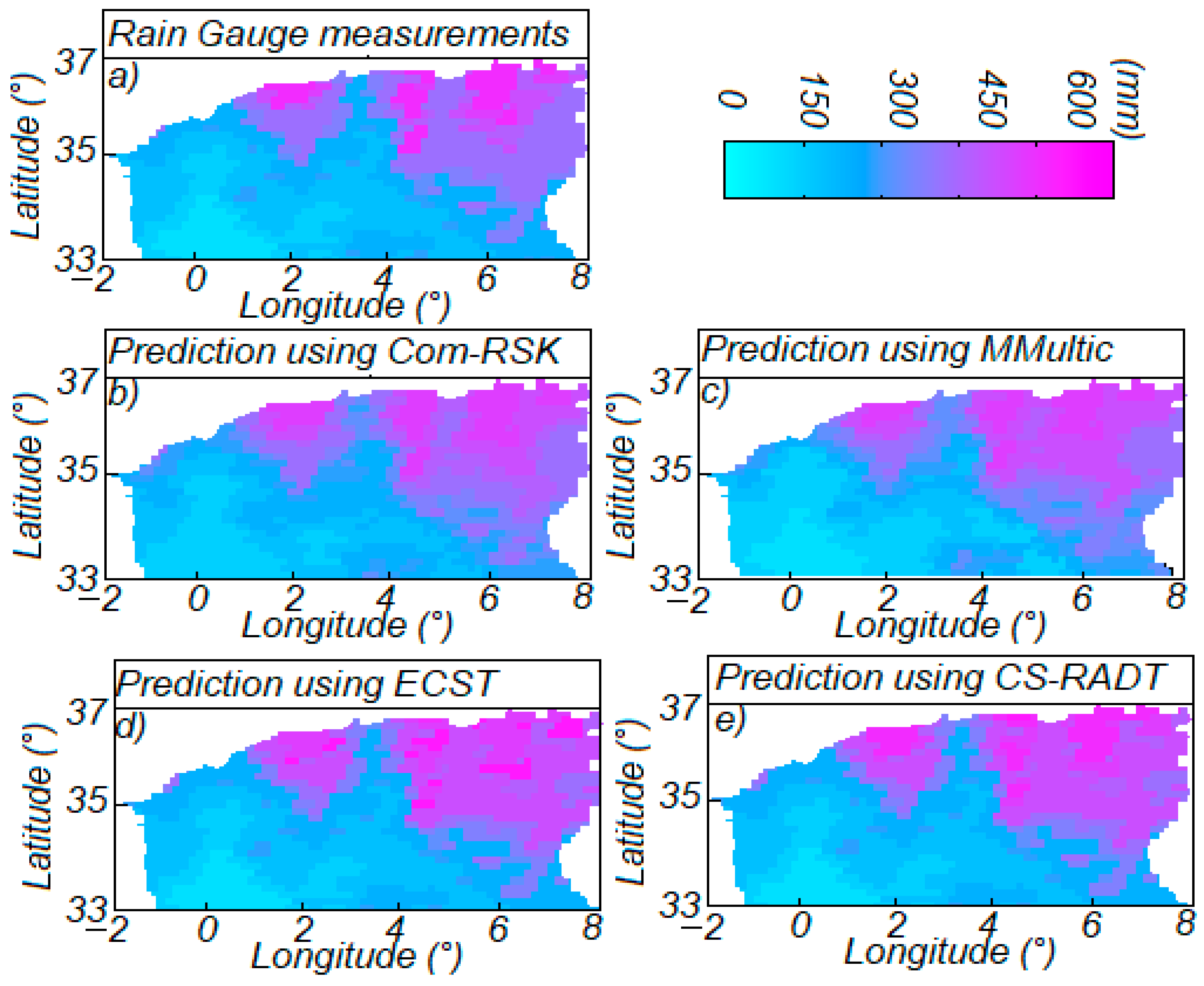
4.1. Prediction Results
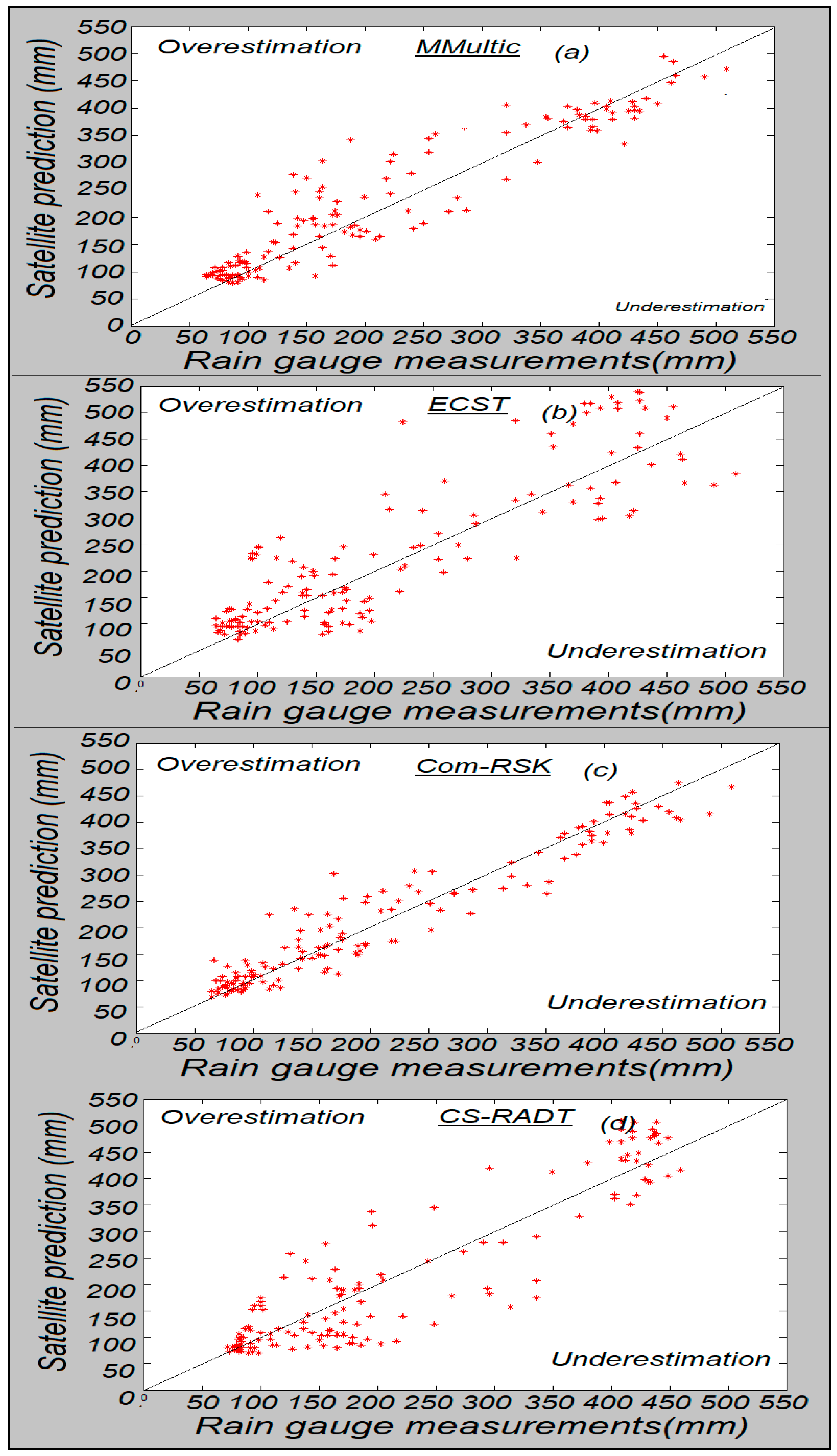
4.2. Inter-Comparison
- The technique “Convective/Stratiform Rain Area Delimitation Technique (CS-RADT)” developed by Lazri et al. [8] uses the thresholds for the classification of precipitation into two types, convective and stratiform, from the spectral parameters of MSG. Then, a rainfall rate is assigned to each precipitation type for the precipitation estimate.
- The ECST technique (Enhanced Convective stratiform technique) is elaborated by Reudenbach et al. [39] from the CST (Convective stratiform technique) originally presented by Adler and Negri [40]. The ECST is applied to extratropical regions and includes water vapor channels to separate cirrus from convective clouds [41].
- The Multi-classifier model (MMultic), developed by Lazri et al. [17], is a technique based on machine learning. The technique combines Support Vector Machine (SVM), Artificial Neural Network (ANN), Weighted k-Nearest Neighbors (WkNN), Naive Bayes (NB), Random Forest (RF), and the Kmeans++ algorithm. The classification responses of the various models are then combined to generate a single optimized decision. To estimate, a rain rate is assigned to each precipitation type.
4.3. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kinouchi, T. Synergetic application of GRACE gravity data, global hydrological model, and in-situ observations to quantify water storage dynamics over Peninsular India during 2002–2017. J. Hydrol. 2021, 596, 126069. [Google Scholar]
- Levizzani, V. Satellite rainfall estimations: New perspectives for meteorology and climate from the EURAINSAT project. Ann. Geophys. 2003, 46, 363–372. [Google Scholar]
- Tebbi, M.A.; Haddad, B. Artificial intelligence systems for rainy areas detection and convective cells’ delineation for the south shore of Mediterranean Sea during day and night time using MSG satellite images. Atmos. Res. 2016, 178, 380–392. [Google Scholar] [CrossRef]
- Hameg, S.; Lazri, M.; Ameur, S. Using naïve Bayes classifer for classification of convective rainfall intensities based on spectral characteristics retrieved from SEVIRI. J. Earth Syst. Sci. 2016, 125, 945–955. [Google Scholar] [CrossRef]
- Kuhnlein, M.; Appelhans, T.; Thies, B.; Nauss, T. Improving the accuracy of rainfall rates from optical satellite sensors with machine learning—A random forests- based approach applied to MSG SEVIRI. Remote Sens. Environ. 2014, 141, 129–143. [Google Scholar] [CrossRef]
- Goshime, D.W.; Absi, R.; Ledésert, B. Evaluation and Bias Correction of CHIRP Rainfall Estimate for Rainfall- Run off Simulation over Lake Ziway Watershed, Ethiopia. Hydrology 2019, 6, 68. [Google Scholar] [CrossRef]
- Goshime, D.W.; Absi, R.; Haile, A.T.; Ledésert, B.; Rientjes, T. Bias-Corrected CHIRP Satellite Rainfall for Water Level Simulation, Lake Ziway, Ethiopia. J. Hydrol. Eng. 2020, 25, 05020024. [Google Scholar] [CrossRef]
- Lazri, M.; Ameur, S.; Brucker, J.M.; Testud, J.; Hamadache, B.; Hameg, S.; Ouallouche, F.; Mohia, Y. Identification of raining clouds using a method based on optical and microphysical cloud properties from Meteosat second generation daytime and nighttime data. Appl. Water Sci. 2013, 3, 1–11. [Google Scholar] [CrossRef]
- Ouallouche, F.; Lazri, M.; Ameur, S. Improvement of rainfall estimation from MSG data using Random Forests classification and regression. Atmos. Res. 2018, 211, 62–72. [Google Scholar] [CrossRef]
- Sehad, M.; Ameur, S. A multilayer perceptron and multiclass support vector machine based high accuracy technique for daily rainfall estimation from MSG SEVIRI data. Adv. Space Res. 2020, 65, 1250–1262. [Google Scholar] [CrossRef]
- Feidas, H.; Giannakos, A. Classifying convective and stratiform rain using multispectral infrared Meteosat Second Generation satellite data. Theor. Appl. Climatol. 2011, 108, 613–630. [Google Scholar] [CrossRef]
- Nauss, T.; Kokhanovsky, A.A. Discriminating raining from non- raining clouds at mid latitudes using multispectral satellite data. Atmos. Chem. Phys. 2006, 6, 5031–5036. [Google Scholar]
- Thies, B.; Turek, A.; Nauss, T.; Bendix, B. Wather type dependent quality assessment of a satellite- based rainfall detection scheme for the mid-latitudes. Meteorol. Atmos. Phys. 2010, 107, 81–89. [Google Scholar] [CrossRef]
- Mohia, Y.; Ameur, S.; Lazri, M.; Brucker, J.M. Combination of spectral and textural features in the MSG satellite remote sensing images for classifying rainy area into Different classes. J. Indian Soc. Remote Sens. 2017, 45, 759–771. [Google Scholar] [CrossRef]
- Sehad, M.; Lazri, M.; Ameur, S. Novel SVM-based technique to improve rainfall estimation over the Mediterranean region (north of Algeria) using the multispectral MSG SEVIRI imagery. Adv. Space Res. 2017, 59, 1381–1394. [Google Scholar] [CrossRef]
- Bensafi, N.; Lazri, M.; Ameur, S. Novel WkNN-based technique to improve instantaneous rainfall estimation over the north of Algeria using the multispectral MSG SEVIRI imagery. J. Atmos. Sol. Terr. Phys. 2019, 183, 110–119. [Google Scholar] [CrossRef]
- Lazri, M.; Labadi, K.; Brucker, J.M.; Ameur, S. Improving satellite rainfall estimation from MSG data in Northern Algeria by using a multi-classifier model based on machine learning. J. Hydrol. 2020, 584, 124705. [Google Scholar] [CrossRef]
- Belmahdi, F.; Lazri, M.; Ouallouche, F.; Labadi, K.; Absi, R.; Ameur, S. Application of Dempster Shafer theory for optimization of precipitation classification and estimation results from remote sensing data using machine learning. Remote Sens. Appl. Soc. Environ. 2023, 29, 100906. [Google Scholar] [CrossRef]
- Oukali, S.; Lazri, M.; Labadi, K.; Brucker, J.M.; Ameur, S. Development of a hybrid classification technique based on deep learning applied to MSG/SEVIRI multispectral data. J. Atmos. Sol. Terr. Phys. 2019, 193, 105062. [Google Scholar] [CrossRef]
- Xue, M.; Hang, R.; Liu, Q.; Yuan, X.T.; L u, X. CNN-based near real time precipitation estimation from Fengyun- 2 satellite over Xinjiang, China. Atmos. Res. 2021, 250, 105337. [Google Scholar] [CrossRef]
- Kavitha, M.; Gayathri, R.; Polat, K.; Alhudhaif, A.; Alenezi, F. Performance evaluation of deep e-CNN with integrated spatial spectral features in hyperspectral image classification. Measurement 2022, 191, 110760. [Google Scholar] [CrossRef]
- Samuel, A.L. Some Studies in Machine Learning Using the Game of Checkers. IBM J. Res. Dev. 1959, 3, 210–229. [Google Scholar] [CrossRef]
- Castillo Botón, C.; Casillas Pérez, D.; Casanova- Mateo, C.; Ghimire, S.; Cerro- Prada, E.; Gutierrez, P.A.; Deo, R.C.; Salcedo Sanz, S. Machine learning regression and classification methods for fog events prediction. Atmos. Res. 2022, 272, 106157. [Google Scholar] [CrossRef]
- Siirtola, P.; Röning, J. Comparison of Regression and Classification Models for User independent and Personal Stress Detection. Sensors 2020, 20, 4402. [Google Scholar] [CrossRef]
- Guo, S.; Jiang, Y.; Long, W. Urban tourism competitiveness evaluation system and its application: Comparison and analysis of regression and classification methods. Procedia Comput. Sci. 2019, 162, 429–437. [Google Scholar] [CrossRef]
- Ouallouche, F.; Labadi, K.; Mohia, Y.; Lazri, M.; Ameur, S. Artificial Intelligence for Satellite Image Processing: Application to Rainfall Estimation. In Intelligent Systems and Application; Springer: Singapore, 2023; Lecture Notes in Electrical Engineering; Chapter 14; Volume 959, ISBN 978-981-19-6580-7. [Google Scholar]
- Belghit, A.; Lazri, M.; Ouallouche, F.; Labadi, K.; Ameur, S. Optimization of One versus All-SVM using Ada Boost algorithm for rainfall classification and estimation from multispectral MSG data. Adv. Space Res. 2023, 71, 946–963. [Google Scholar] [CrossRef]
- EUMETSAT. Applications of Meteosat Second Generation Conversion from Counts to Radiances and from Radiances to Brightness Temperatures and Reflectance. 2004. Available online: http://oiswww.eumetsat.org/WEBOPS/msginterpretation/inex.html (accessed on 20 December 2022).
- EUMETSAT. MSG Level 1.5 Image Data Format Description. Available online: http://www.eumetsat.int/website:home/Data/Products/Formats/index.html (accessed on 20 December 2022).
- Thies, B.; Nauss, T.; Bendix, J. Delineation of raining from non-raining clouds during night time using Meteosat-8 data. Meteorol. Appl. 2008, 15, 219–230. [Google Scholar] [CrossRef]
- Roebeling, R.A.; Feijt, A.J.; Stammes, P. Cloud property retrievals for climate monitoring: Implications of differences between SEVIRI on METEOSAT-8 and AVHRR on NOAA-17. J. Geophys. Res. 2006, 11, D20210. [Google Scholar] [CrossRef]
- Lazri, M.; Ouallouche, F.; Ameur, S.; Brucker, J.M.; Mohia, Y. Identifying Convective and Stratiform Rain by Confronting SEVERI Sensor Multispectral Infrared to Radar Sensor Data Using Neural Network. Sens. Transducers 2012, 145, 19–32. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Guenther, N.; Schonlau, M. Support vector machines. Stata J. 2016, 16, 917. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Puissant, A.; Rougier, S.; Stumpf, A. Object-oriented mapping of urban trees using Random Forest classifiers. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 235–245. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by random Forest. R News 2002, 2, 18–22. [Google Scholar]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Reudenbach, C.; Heinemann, G.; Heuel, E.; Bendix, J.; Winiger, M. Investigation of summertime convective rainfall in Western Europe based on a synergy of remote sensing data and numerical models. Meteorol. Atmos. Phys. 2001, 76, 23–41. [Google Scholar]
- Adler, R.F.; Negri, A.J. A satellite infrared technique to estimate tropical convective and stratiform rainfall. J. Appl. Meteorol. 1988, 27, 30–51. [Google Scholar] [CrossRef]
- Tjemkes, S.A.; Van de berg, L.; Schmetz, J. Warm water vapour pixels over high clouds as observed by Meteosat. Contrib. Atmos. Phys. 1997, 70, 15–21. [Google Scholar]
- Babaousmail, H.; Hou, R.; Ayugi, B.; Tchalim Gnitou, G. Evaluation of satellite-based precipitation estimates over Algeria during 1998–2016. J. Atmos. Sol. Terr. Phys. 2019, 195, 105139. [Google Scholar] [CrossRef]
- Jobard, I.; Chopin, F.; Berges, J.C.; Roca, R. An inter comparison of 10-day satellite precipitation products during West African monsoon Int. J. Remote Sens. 2011, 32, 2353–2376. [Google Scholar] [CrossRef]
- Goshime, D.W.; Absi, R.; Ledésert, B.; Dufour, F.; Haile, A.T. Impact of water abstraction on the water level of Lake Ziway, Ethiopia. WIT Trans. Ecol. Environ. 2019, 239, 67–78. [Google Scholar] [CrossRef]
- Goshime, D.W.; Haile, A.T.; Absi, R.; Ledésert, B. Impact of water resource development plan on water abstraction and water balance of Lake Ziway, Ethiopia. Sustain. Water Resour. Manag. 2021, 7, 36. [Google Scholar] [CrossRef]
- Goshime, D.W.; Haile, A.T.; Rientjes, T.; Absi, R.; Ledésert, B.; Siegfried, T. Implications of water abstraction on the interconnected Central Rift Valley Lakes sub-basin of Ethiopia using WEAP. J. Hydrol. Reg. Stud. 2021, 38, 100969. [Google Scholar] [CrossRef]

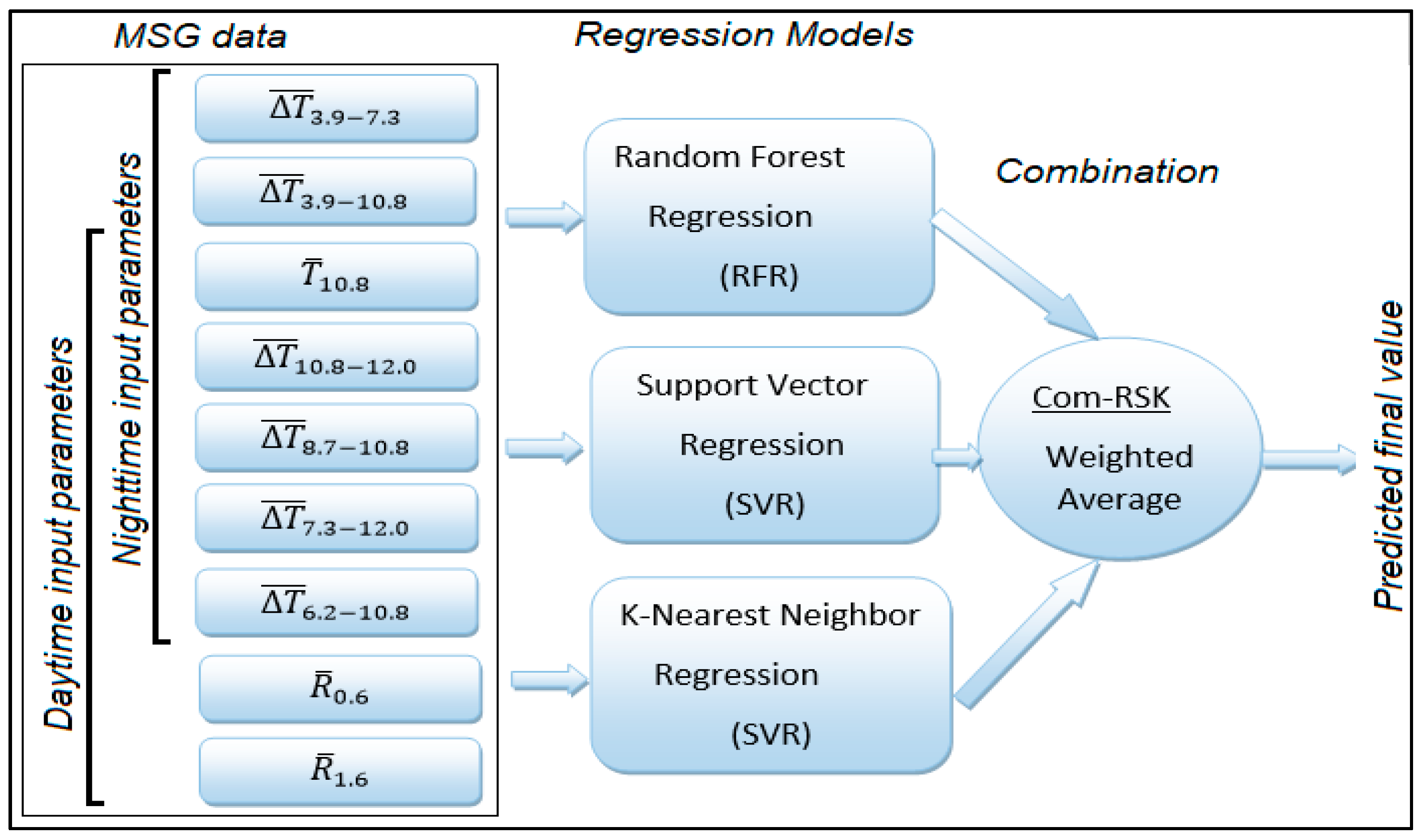


| Channels and Channels Combinations (Kelvin or µm) | Description | Range of Values | Clouds Characteristics | |
|---|---|---|---|---|
| Daytime | Nighttime | |||
| Τ10.8 (K) | Brightness temperature in IR10.8 | 207.2 k to 283.9 k | 205.3 k to 282.4 k | Vertical cloud extent and cloud top temperature [11,30]. |
| ΔΤ10.8–12.0 (K) | Brightness temperature difference between IR10.8 and IR12.0 | −0.3 k to 7.4 k | −0.3 k to 7.1 k | Existence of ice particles in the clouds [30]. |
| ΔT8.7–10.8 (K) | Brightness temperature difference between IR8.7 and IR10.8 | −4.6 k to 1.3 k | −4.8 k to 1.7 k | Existence of ice particles in clouds [31]. |
| ΔT7.3–12.0 (K) | Brightness temperature difference between IR7.3 and IR12.0 | −50.3 k to 6.6 k | −52.0 k to 5.7 k | Cloud top temperature and Vertical cloud extension [11,32]. |
| ΔT6.2–10.8 (K) | Brightness temperature difference between IR6.2 and IR10.8 | −50.1 k to 6.4 k | −51.8 k to 5.1 k | Vertical cloud extension, cloud top temperature [2,11]. |
| R0.6 (µm) | Reflectance in VIS0.6 | 0.02 µm to 1 µm | No used | Cloud Particle Size and Cloud Optical Thickness [5,30]. |
| R1.6 (µm) | Reflectance in NIR1.6 | 0.03 µm to 1 µm | No used | Cloud Particle Size and Cloud Optical Thickness [5,30]. |
| ΔT3.9–7.3 (K) | Brightness temperature difference between IR3.9 and IR7.3 | No used | −4.9 k to 25 k | Cloud Particle Size and Cloud Optical Thickness [5,30]. |
| ΔT3.9–10.8 (K) | Brightness temperature difference between IR3.9 and IR10.8 | No used | −10.3 k to 15.1 k | Cloud Particle Size and Cloud Optical Thickness [5,30]. |
| Rainy Season 2008/2009 | Rainy Season 2009/2010 | |
|---|---|---|
| SVR | Learning (70%) and tuning (30%) | Validation |
| RFR | Learning (70%) and tuning (30%) | Validation |
| K-NNR | Learning (70%) and tuning (30%) | Validation |
| CombinedInput Parameters | Number of Combinations | SVR R-Squared | RFR R-Squared | K-NNR R-Squared |
|---|---|---|---|---|
| 1 | 7 | 0.13 to 0.35 | 0.12 to 0.33 | 0.10 to 0.31 |
| 2 | 21 | 0.17 to 0.38 | 0.14 to 0.38 | 0.14 to 0.35 |
| 3 | 35 | 0.26 to 0.43 | 0.23 to 0.42 | 0.20 to 0.40 |
| 4 | 35 | 0.34 to 0.56 | 0.33 to 0.52 | 0.34 to 0.52 |
| 5 | 21 | 0.48 to 0.69 | 0.47 to 0.70 | 0.47 to 0.67 |
| 6 | 7 | 0.64 to 0.74 | 0.63 to 0.73 | 0.60 to 0.70 |
| 7 | 1 | 0.88 | 0.86 | 0.85 |
| Mean (mm) | MAE (mm) | MBE (mm) | RMSE (mm) | CC | |
|---|---|---|---|---|---|
| SVR | 18.8 | 1.3 | 5.2 | 3.0 | 0.72 |
| K-NNR | 20.3 | 2.5 | 6.7 | 5.3 | 0.62 |
| RFR | 19.7 | 1.9 | 6.1 | 3.6 | 0.69 |
| Com-RSK | 17.7 | 1.0 | 4.1 | 2.1 | 0.78 |
| Optimal | 13.6 | 0 | 0 | 0 | 1 |
| Mean (mm) | MAE (mm) | MBE (mm) | RMSE (mm) | CC | |
|---|---|---|---|---|---|
| SVR | 84.0 | 7.3 | 8.1 | 14.1 | 0.85 |
| K-NNR | 86.1 | 8.7 | 10.2 | 17.3 | 0.72 |
| RFR | 85.1 | 8.2 | 9.2 | 16.9 | 0.74 |
| Com-RSK | 82.5 | 6.1 | 6.6 | 10.8 | 0.88 |
| Optimal | 75.9 | 0 | 0 | 0 | 1 |
| Mean (mm) | MAE (mm) | MBE (mm) | RMSE (mm) | CC | |
|---|---|---|---|---|---|
| SVR | 242.9 | 23.6 | 10.0 | 40.6 | 0.89 |
| K-NNR | 249.2 | 28.3 | 16.3 | 43.5 | 0.87 |
| RFR | 247.1 | 26.1 | 14.2 | 41.6 | 0.88 |
| Com-RSK | 238.4 | 20.7 | 5.5 | 27.4 | 0.94 |
| Optimal | 232.9 | 0 | 0 | 0 | 1 |
| Mean (mm) | MAE (mm) | MBE (mm) | RMSE (mm) | CC | |
|---|---|---|---|---|---|
| CS-RADT | 251.2 | 34.6 | 18.3 | 52.9 | 0.87 |
| ECST | 254.0 | 37.2 | 22.1 | 55.8 | 0.81 |
| MMultic | 239.3 | 21.8 | 6.4 | 41.6 | 0.93 |
| Com-RSK | 238.4 | 20.7 | 5.5 | 27.4 | 0.94 |
| Optimal | 232.9 | 0 | 0 | 0 | 1 |
| Daily Scale | Monthly Scale | Annual Scale | |||||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE (mm) | MBE (mm) | CC(%) | RMSE (mm) | MBE (mm) | CC(%) | RMSE (mm) | MBE (mm) | CC(%) | |
| CMORPH | 0.72/3.76 | −8.37/5.88 | 15/27 | 6.34/21.83 | −0.27/0.19 | 59/83 | 59.29/264.66 | −151.45/102.99 | 82/90 |
| CHIRPS | 0.63/5.15 | −2.51/3.91 | 42/58 | 3.93/21.48 | −0.03/0.18 | 58/87 | 18.62/144.64 | 6/56.48 | 69/99 |
| Com-RSK | 2.1 | 4.1 | 78 | 10.8 | 6.6 | 88 | 37.4 | 5.5 | 94 |
| Optimal | 0 | 0 | 100 | 0 | 0 | 100 | 0 | 0 | 100 |
| RMSE (mm) | MBE (mm) | CC (%) | R-Squared (%) | |
|---|---|---|---|---|
| GSMaP | 24 | −11 | 50 | 25 |
| GPCP-1dd | 23 | 7 | 60 | 36 |
| TRMM-3B42 | 26 | −4 | 46 | 21 |
| EPSAT-SG | 17 | 5 | 71 | 50 |
| TAMSAT | 20 | 3 | 63 | 23 |
| RFE-2.0 | 19 | 0 | 51 | 26 |
| PERSIANN | 63 | 45 | 49 | 24 |
| GPI | 28 | 8 | 58 | 34 |
| Com-RSK | 27.4 | 5.5 | 94 | 88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohia, Y.; Absi, R.; Lazri, M.; Labadi, K.; Ouallouche, F.; Ameur, S. Quantitative Estimation of Rainfall from Remote Sensing Data Using Machine Learning Regression Models. Hydrology 2023, 10, 52. https://doi.org/10.3390/hydrology10020052
Mohia Y, Absi R, Lazri M, Labadi K, Ouallouche F, Ameur S. Quantitative Estimation of Rainfall from Remote Sensing Data Using Machine Learning Regression Models. Hydrology. 2023; 10(2):52. https://doi.org/10.3390/hydrology10020052
Chicago/Turabian StyleMohia, Yacine, Rafik Absi, Mourad Lazri, Karim Labadi, Fethi Ouallouche, and Soltane Ameur. 2023. "Quantitative Estimation of Rainfall from Remote Sensing Data Using Machine Learning Regression Models" Hydrology 10, no. 2: 52. https://doi.org/10.3390/hydrology10020052
APA StyleMohia, Y., Absi, R., Lazri, M., Labadi, K., Ouallouche, F., & Ameur, S. (2023). Quantitative Estimation of Rainfall from Remote Sensing Data Using Machine Learning Regression Models. Hydrology, 10(2), 52. https://doi.org/10.3390/hydrology10020052







