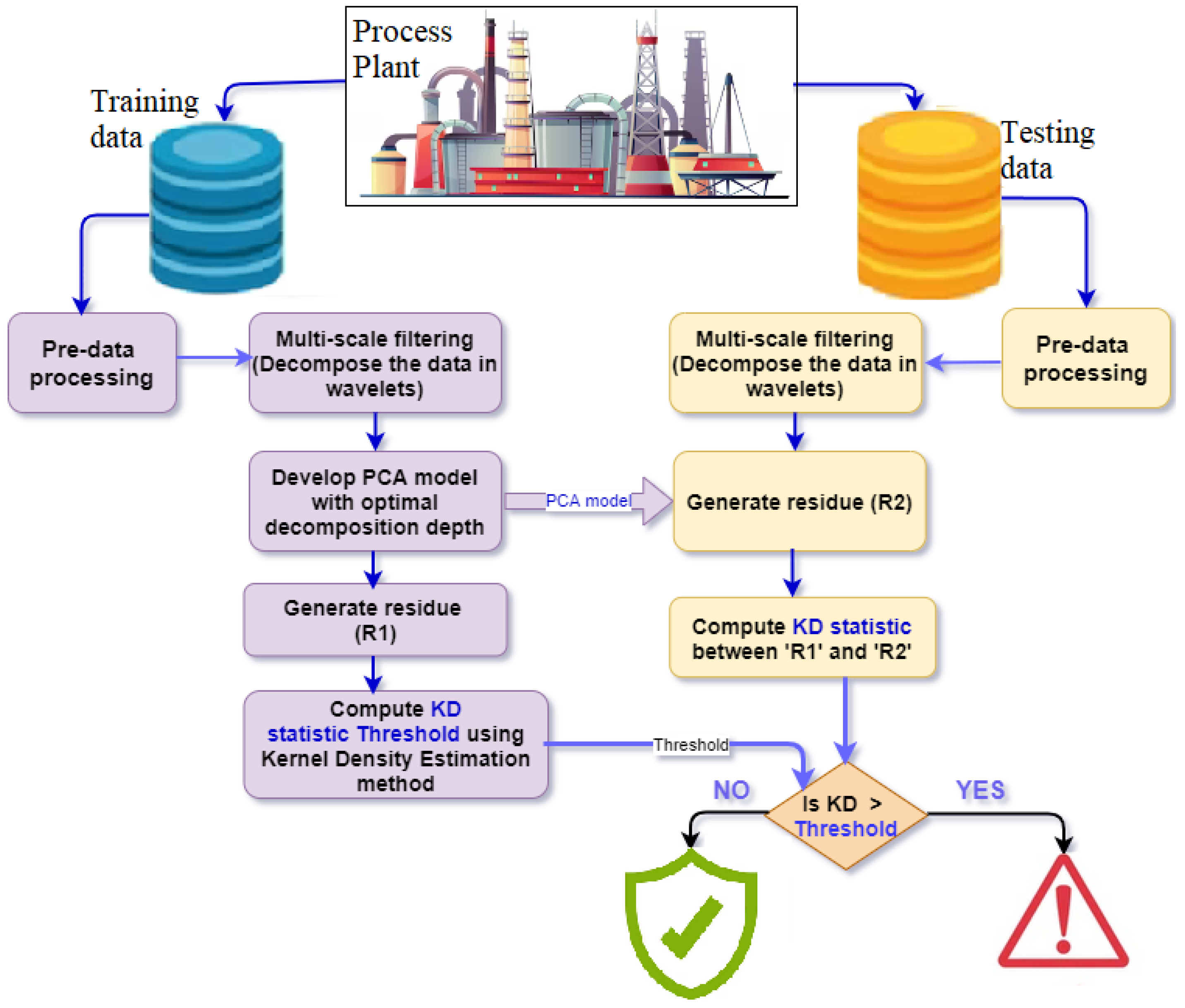
This section involves the validation of the proposed MPCA-KD strategy through two case studies, namely the Distillation Column and Continued Stirred Tank Reactor (CSTR) processes. The performance of the MPCA-KD strategy is analyzed and compared with other fault detection methods such as PCA-
, PCA-Q, PCA-KD, MPCA-
, and MPCA-Q. The evaluation of the different fault detection methods is based on five statistical parameters, which include Fault Detection Rate (FDR), False Alarm Rate (FAR), Precision and F1-score. The details of these various parameters can [
1]. Additionally, an alternate statistic which is based on detection time ratio (DTR) is also computed in this work and is given as follows:
where
N corresponds to the total number of samples in the faulty region,
corresponds to the time instant the fault is introduced and
is the time instant the fault is detected by the proposed FD strategy.
In order to ensure that a complex industrial system runs smoothly, it is vital to closely monitor any faults that may arise. A fault monitoring strategy that is well-designed and effective should prioritize high values for FDR (False Discovery Rate), Precision, and F1-score metrics while also keeping the FAR (False Alarm Rate) value to a minimum. To evaluate the performance of the proposed MPCA-KD strategy, three types of faults are considered: bias faults, intermittent faults, and sensor drift faults. By taking these types of faults into account, it is possible to thoroughly assess the effectiveness of the monitoring strategy in detecting and identifying any potential issues that may arise within the complex system.
3.1. Monitoring Faults in Distillation Column Process
This section comprehensively examines the MSPCA-KD method, focusing on its efficacy in monitoring faults within the distillation column (DC) setup. The DC unit, a critical component in chemical process plants, is pivotal in separating components from a mixture based on their vapor pressure differences [
51,
52].
Figure 3 illustrates a schematic representation of the industrial-scale DC process. The setup consists of 32 plates and is equipped with 10 Resistance Temperature Detector (RTD) sensors strategically placed to monitor temperatures at different locations within the column. The feed stream comprises a binary mixture of propane and isobutene, entering the column at stage 16 as a saturated liquid with a flow rate of 1 kmol/s, a temperature of 322 K, and compositions of 60 mole % isobutene and 40 mole % propane. The process data for the distillation column is generated using the Aspen Tech 7.2 simulator.
The distillation process is a crucial step in chemical process plants, and it is essential to ensure its smooth and efficient operation. In this regard, a study was conducted that involved perturbing the flow rates of the feed and reflux streams from their nominal operating ranges. The perturbations were introduced in a step-wise manner, with the feed flow rate and reflux flow being varied to obtain the necessary data. The data was collected from different locations in the column using 14 sensors located at various points, and each variable was observed for a length of 4096. The wavelet-based multiscale filtering method is used to process the data. The filtered data was then used to develop an MSPCA model by using optimal PCs. The optimal PCs were obtained through cross-validation approach. The KD statistics were employed to detect any faults present in the system. The first step involved introducing step changes of magnitudes 2% in the feed flow rate around its nominal condition. After the system reached a new steady state, a step change of magnitudes 2% in the reflux flow rate was introduced. This process was repeated several times to obtain the necessary data. Overall, this study provides valuable insights into the operation of distillation columns in chemical process plants. By detecting faults early and ensuring the smooth and efficient operation of the process, this study can help improve the plant’s overall performance.
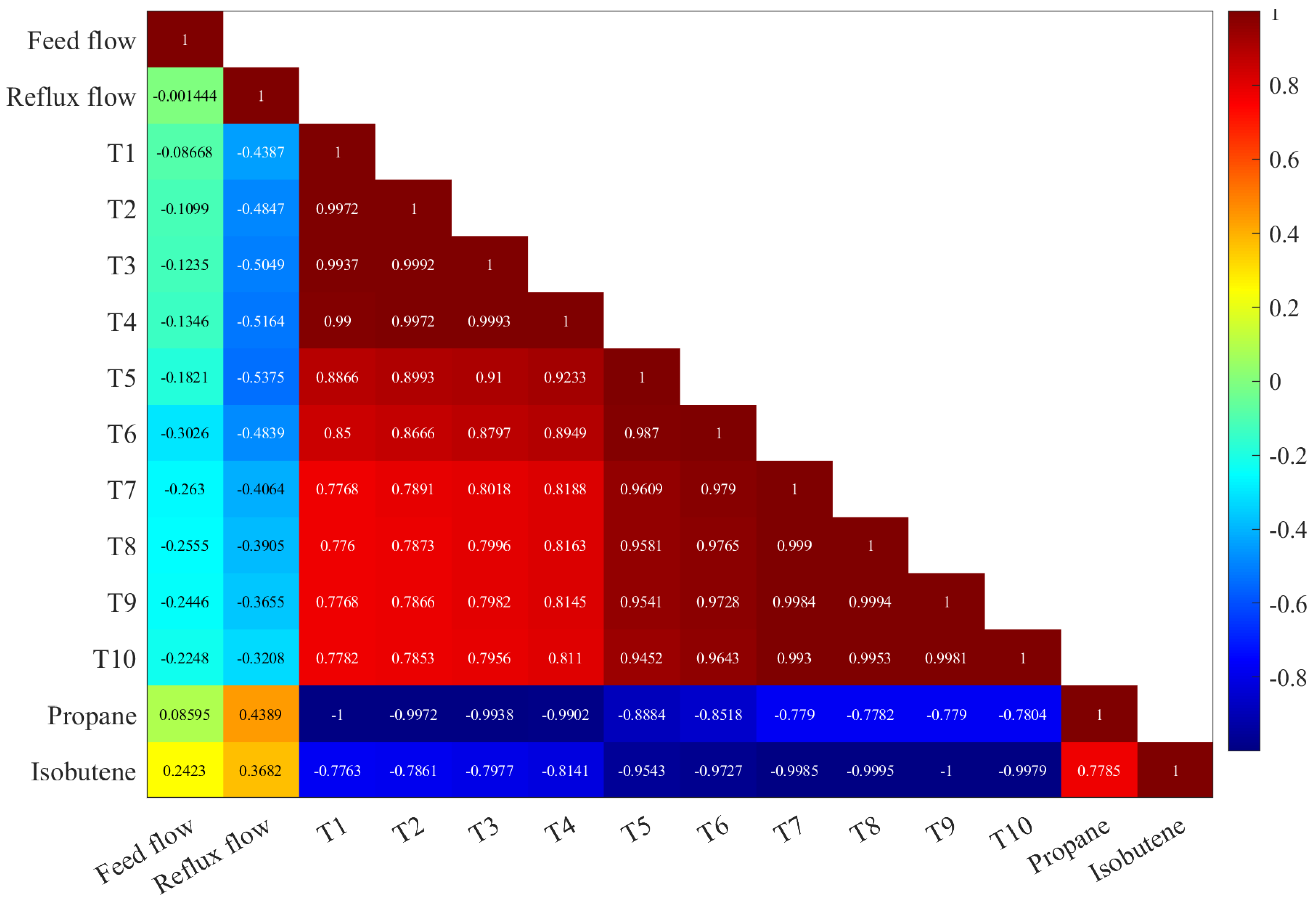
Figure 4 shows the Pearson correlation coefficients among different variables in the fault-free distillation column dataset. Temperature variables (‘T1’ through ‘T10’) exhibit strong positive correlations, indicating a tendency to move together. Such a strong positive correlation among temperature variables is expected in a distillation column because these temperatures are interconnected and influenced by the same underlying thermal processes. For instance, changes in the feed flow rate, reflux flow rate, or heat exchange conditions can impact multiple tray temperatures simultaneously.This coherence suggests redundancy in temperature information, implying that monitoring fewer key temperatures may suffice for effective control without compromising accuracy. This intercorrelation pattern implies a certain degree of redundancy in the temperature information. In practical terms, it might indicate that monitoring fewer key temperature variables could still provide representative information about the thermal conditions within the distillation column, simplifying the monitoring and control strategies without sacrificing accuracy. There is also a high correlation of 0.778 between the component variables ‘Propane’ and ‘Isobutene’. In the context of a distillation column, where the separation of components is based on vapor-liquid equilibrium, a positive correlation between ‘Propane’ and ‘Isobutene’ is reasonable. Changes in operating conditions, such as variations in feed composition or temperature, can influence the vapor-liquid equilibrium, impacting the concentrations of these components simultaneously. Understanding and monitoring these correlations are crucial for effective process control.
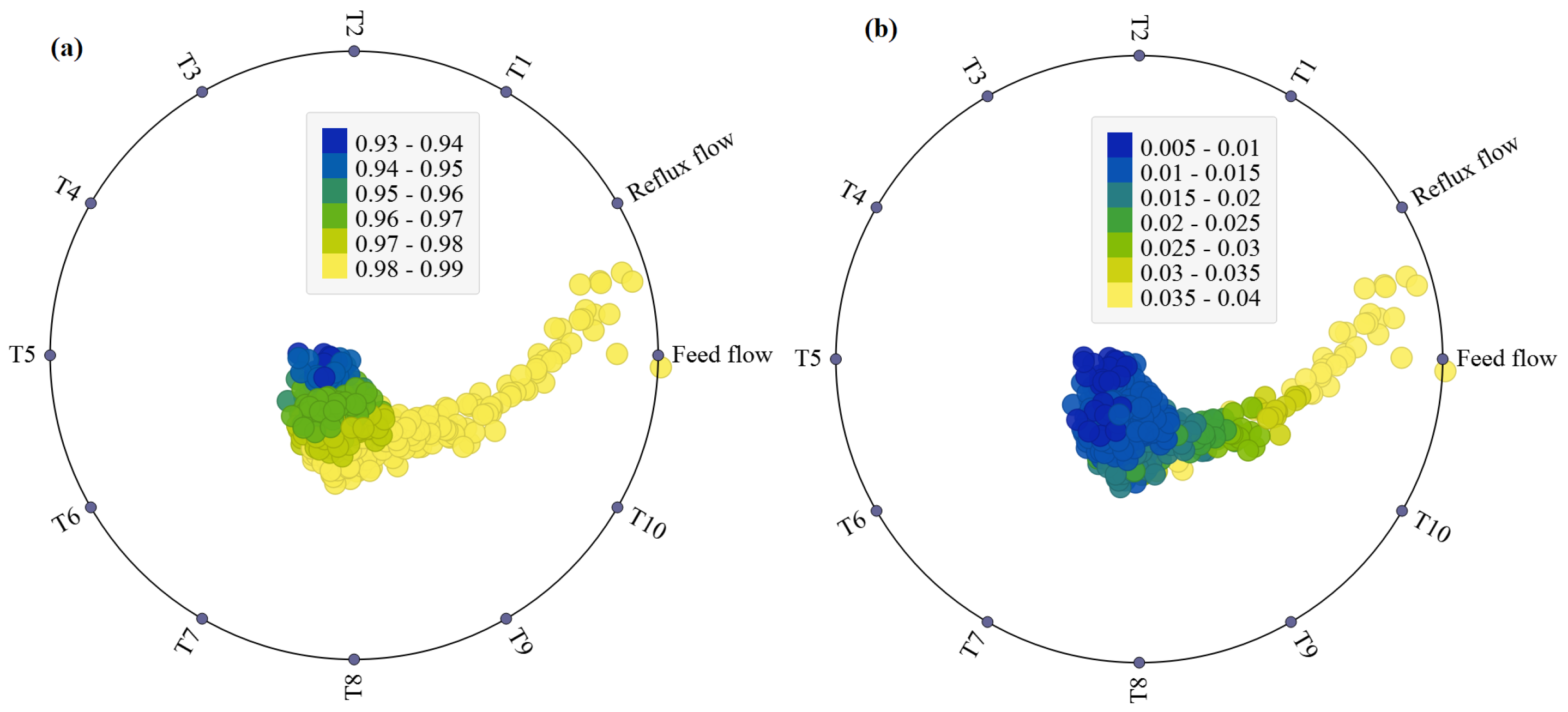
Figure 5a,b, RadViz is utilized to visually represent the relationships between various factors and the concentrations of ‘Propane’ and ‘Isobutene’ in the distillation column (DC). By examining the positioning of points and the density of lines, one can interpret how changes in different factors correspond to variations in the concentrations of these key components. RadViz, short for Radial Visualization, is a data visualization technique designed to understand the influence of multiple variables on a target variable [
53]. The visualization is presented in a circular layout, where each variable is represented as a point on the circle’s circumference. The target variable is placed at the center of the circle. For each data point, the variables’ values determine its position along the circumference. The closer a point is to a particular variable, the higher the variable’s value for that specific data point. From
Figure 5b, the RadViz plot reveals distinctive patterns in the impact of various factors on the concentration of Propane in the distillation column. Notably, Reflux and feed flow exhibit a significant influence, indicating their pivotal roles in determining Propane levels. Additionally, the temperatures T8, T9, and T10 also contribute substantially to the variation in Propane concentrations. The proximity of data points to these factors on the RadViz plot signifies their heightened impact, emphasizing the importance of monitoring and controlling Reflux, feed flow, and specific temperature variables for effectively managing Propane levels in the distillation column. From
Figure 5b, the RadViz plot reveals that Reflux, feed flow, and temperatures T8, T9, and T10 notably influence Isobutene concentration. Efficient control and monitoring of these factors are crucial for managing Isobutene levels in the distillation column.
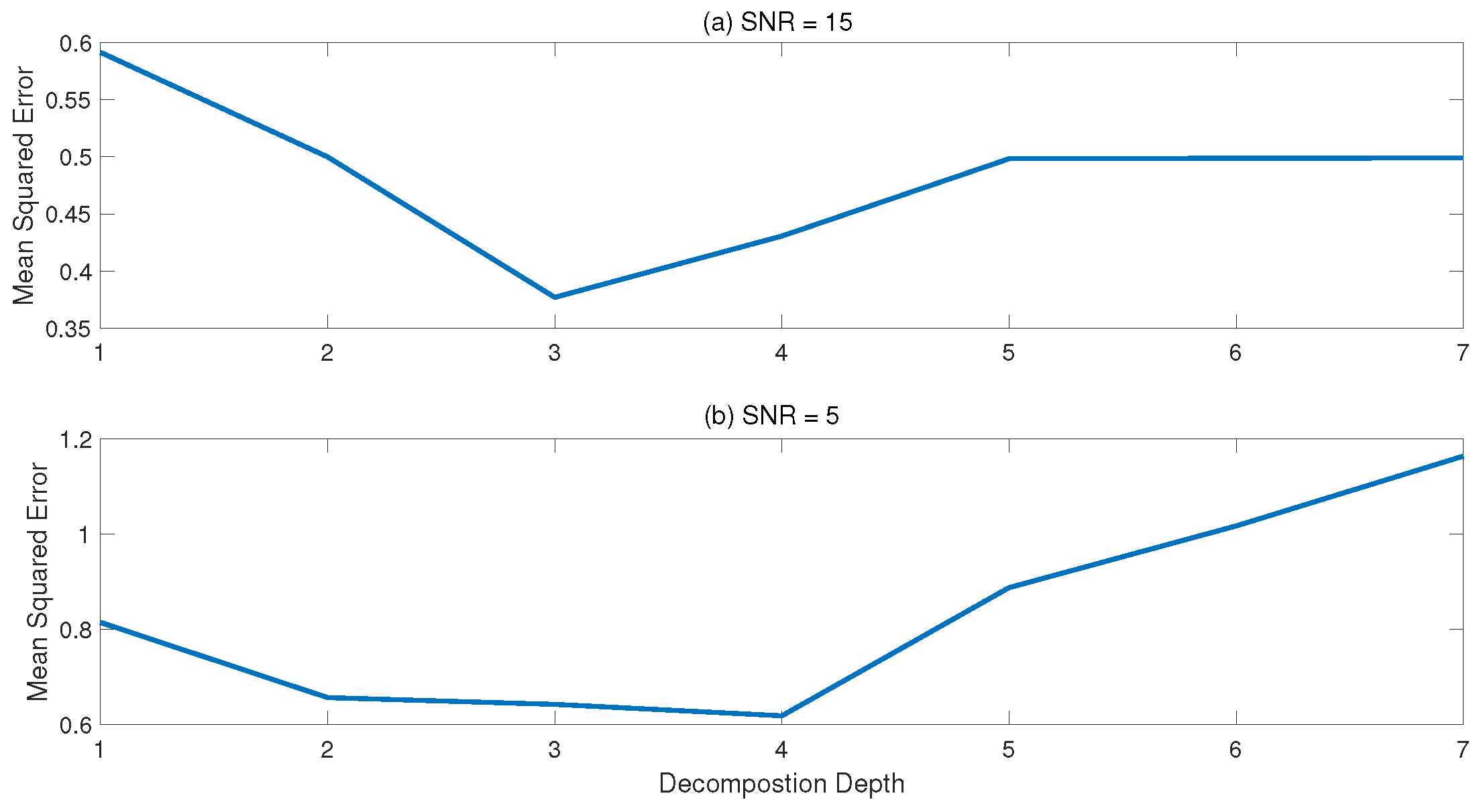
In this analysis, the dataset is divided into two sets: training (fault-free)data and testing data, each comprising 2048 data points. The training data is utilized to build both PCA and MPCA models independently. For a fair comparison, both models are constructed with 8 PCs. The optimal decomposition depths for the data are identified as 3 and 4 for signal-to-noise ratio (SNR) values of 15 and 5, respectively. This is illustrated in
Figure 6.
To evaluate the fault detection performance of the PCA and MPCA models, bias, intermittent, and drift faults are considered in a simulated DC process. These faults in this analysis are assessed under different SNR scenarios (SNR = 15 and SNR = 5), providing insights into the models’ ability to detect and respond to different types of fault in varying noise levels.
Bias fault: A bias fault involves a constant offset in the readings of a particular sensor or variable. In this scenario, a 7% bias fault is introduced into temperature variable 5 from sampling time instant 250 until the end of the testing data. Introducing this fault in temperature variable 5 implies a persistent distortion in the measurements of this specific temperature parameter. This distortion persists throughout the latter part of the testing data, affecting the accuracy of the readings.
Drift fault: A drift fault signifies a gradual change or drift in the sensor readings over time. In this scenario, a drift sensor fault with a slope of 0.01 is introduced into temperature variable 1 during the same time frame. This introduced drift on testing data implies a continuous and gradual shift in the measurements of this temperature parameter. Such a fault can mimic the effect of changing conditions in the distillation column, potentially impacting process control.
Intermittent fault: An intermittent fault involves sporadic variations or disruptions in sensor readings. In this scenario, intermittent faults having a small magnitude with 8% of the total variation are inserted in the concentration variable of the bottom stream between the sampling time instants [100, 200] and [350, 450], respectively. Monitoring intermittent faults is crucial for capturing irregular disturbances in the system.
Understanding and addressing these fault scenarios is vital for maintaining the reliability and efficiency of distillation columns, as faults can impact the accuracy of sensor readings and, consequently, the control and optimization of the distillation process.
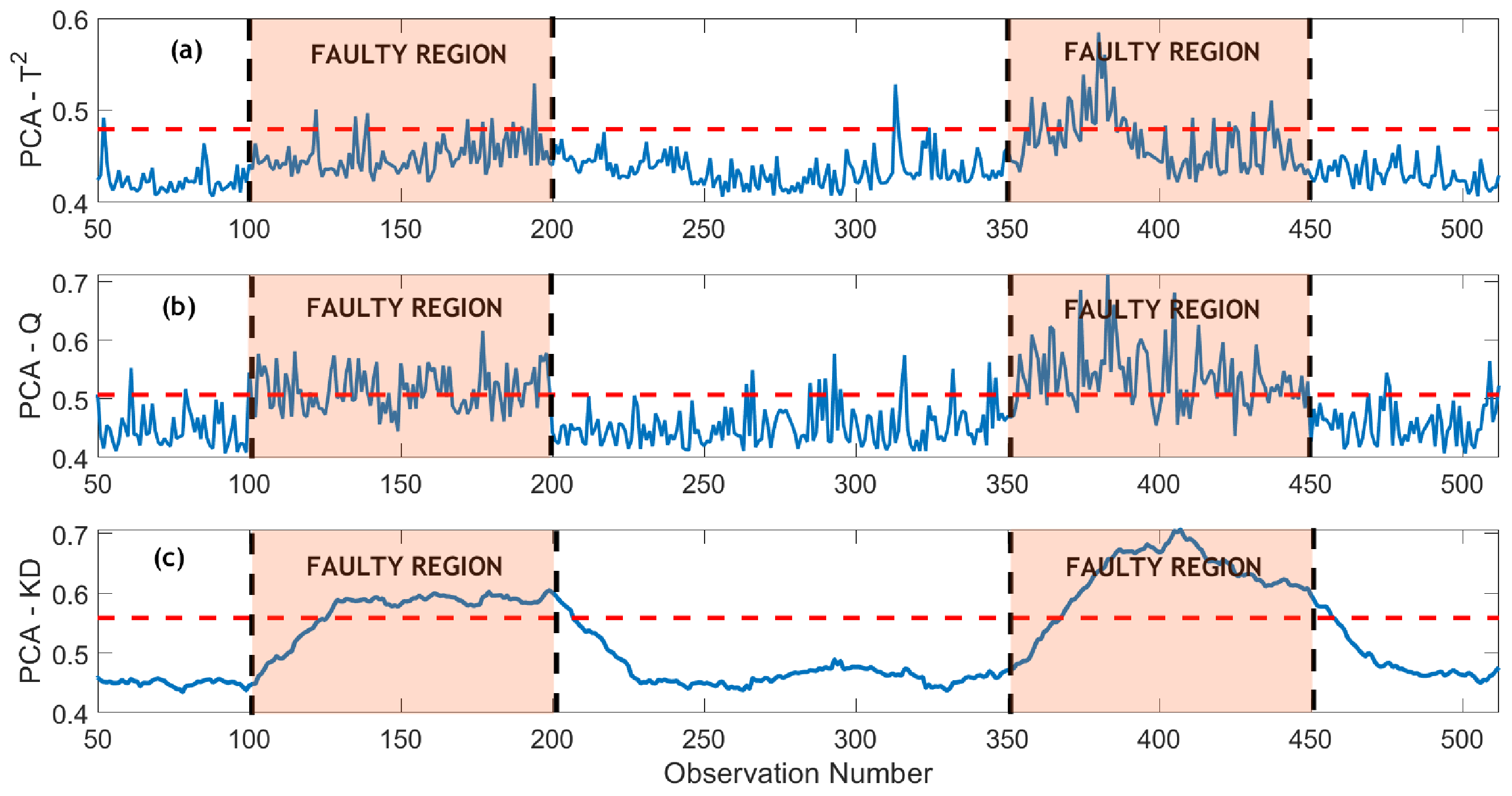
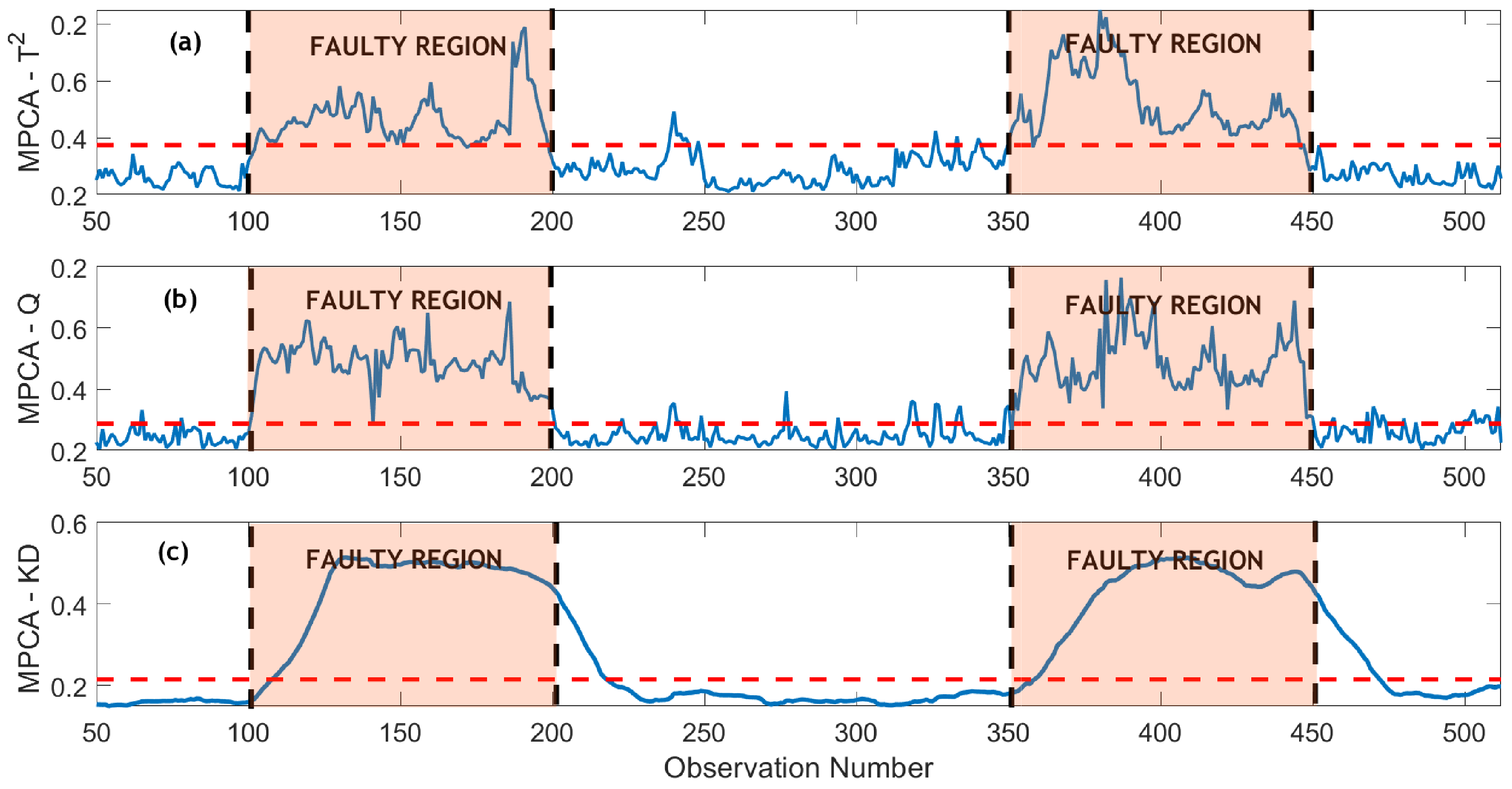
For visual representation,
Figure 7 and
Figure 8 display the monitoring of an intermittent fault using PCA-based and MPCA-based methods under a Signal-to-Noise Ratio (SNR) of 15. In
Figure 7a, the PCA-
method exhibits shortcomings in detecting the intermittent fault, whereas the PCA-SPE method partially captures the fault but demonstrates some missed detections (
Figure 7b). Notably, the PCA-KD scheme, illustrated in
Figure 7c, shows improved fault detection compared to conventional methods but still exhibits some missed detections. In contrast, the wavelet-based methods outperform conventional methods in monitoring capabilities. The MPCA-
and MPCA-SPE schemes show enhanced fault detection compared to PCA-
and PCA-SPE methods, albeit with some missed detections and false alarms (
Figure 8a–c). Remarkably, the proposed MPCA-KD scheme achieves accurate fault detection without missed detections or false alarms, providing a distinct advantage (
Figure 8c). The superior performance of the MPCA-KD approach in fault detection can be attributed to its unique combination of multiscale MPCA with the KD scheme. The MSPCA-KD method excels in capturing critical details in the data by utilizing wavelet-based multiscale representation, which enhances its sensitivity to intermittent faults. The incorporation of KD, a distribution-based monitoring scheme, allows for a more nuanced comparison of data segments, contributing to improved fault detection. This underscores the effectiveness of the MPCA-KD approach in fault detection under conditions of intermittent faults and noise.
The evaluation of PCA and MPCA-based methods for monitoring three types of faults in the DC process has been conducted using several statistical metrics, namely, False Detection Rate (FDR), False Alarm Rate (FAR), Precision, and F1-score.
Table 1 presents a comprehensive summary of the fault detection performance under an SNR of 15. For the bias fault, PCA-KD exhibited a high FDR of 82.06%, indicating a considerable proportion of false detections. On the other hand, MSPCA-KD demonstrated 100% FDR, implying a complete detection of the bias fault without false alarm (FAR = 0). MPCA-KD also achieved a perfect Precision and F1-score, suggesting superior accuracy in detecting the bias fault compared to other methods. In the case of intermittent faults, MSPCA-KD outperformed other methods with a 100% Precision and F1-score. Despite a relatively high FDR of 87.50%, PCA-KD showed moderate fault detection capabilities. MSPCA-Q exhibited higher FDR value with FDR 97%, indicating some trade-off between precision and recall in detecting intermittent faults. For drift faults, all methods demonstrated impressive fault detection performance, achieving 100% Precision and F1-score. MSPCA-Q and MSPCA-KD displayed slightly higher FDR values of 90.85 and 96.12, respectively and without false alarms. In summary, MPCA-KD consistently demonstrated superior fault detection accuracy across all fault types, emphasizing its effectiveness in monitoring complex systems like the distillation column process under an SNR of 15. The multiscale representation helps in efficiently extracting relevant features from the data, and the KD scheme further refines the detection process. This combination proves advantageous, especially in scenarios involving intermittent faults and noise, showcasing the effectiveness of the proposed MPCA-KD approach in enhancing fault detection reliability.
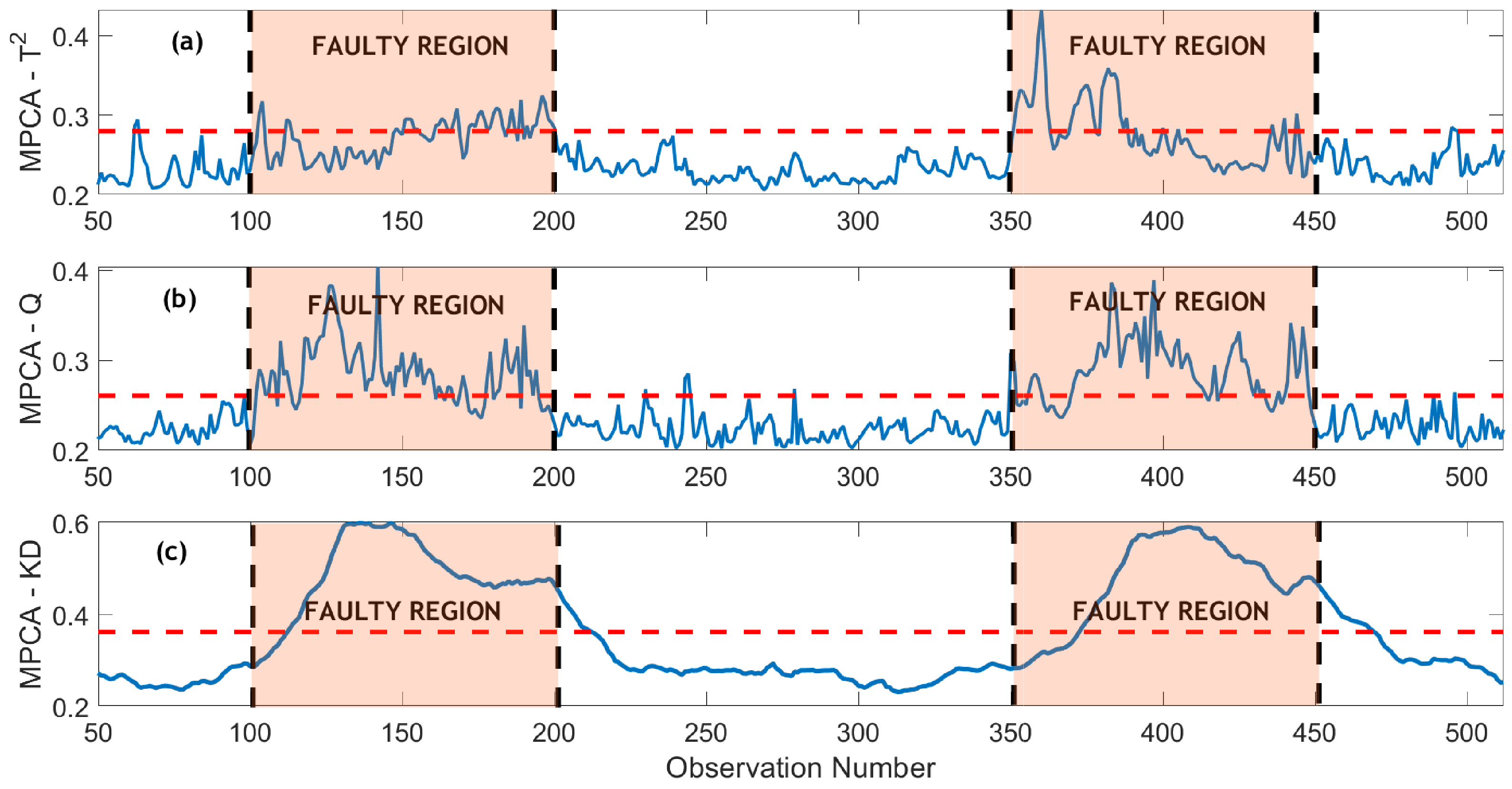
The monitoring of an intermittent fault under a high noise scenario (SNR = 5) is depicted in
Figure 9 and
Figure 10. In such conditions, where the SNR is low, distinguishing relevant signal variations from background noise becomes particularly challenging. The increased noise levels introduce complexities in fault detection, as the higher degree of random variations can obscure fault-related patterns. Conventional PCA-based methods struggle in the presence of substantial noise, failing to accurately identify the fault due to the masking effect of noise on important information. In comparison, the
and MSPCA-SPE schemes exhibit improved performance compared to PCA-based methods, providing partial detection of the fault. However, they still face challenges in achieving precise detection due to the influence of noise. Importantly, the proposed MSPCA-KD approach stands out in this high noise scenario. Despite the considerable noise present in the data, MSPCA-KD demonstrates robust fault detection capabilities. The method is able to discern the fault effectively, showcasing a smooth and accurate detection profile. This resilience to noise and ability to maintain a high level of precision in fault detection underscore the superiority of the MSPCA-KD approach in challenging and noisy environments. Overall, the results highlight the significance of the proposed method, especially in real-world scenarios where noise is inevitable. MSPCA-KD’s capacity to perform through high noise levels and deliver precise fault detection positions it as a valuable tool for monitoring complex systems in practical applications where noisy conditions are prevalent.
Table 2 provides an insightful overview of the fault detection performance of PCA and MPCA-based monitoring methods in the distillation column process under an SNR of 5. For the bias fault, PCA-KD exhibited a high FDR of 71.09%, indicating a significant proportion of false detections. MPCA-KD, while achieving 93.51% FDR, demonstrated superior fault detection capabilities compared to PCA-KD. MPCA-KD also achieved 100% Precision, suggesting precise detection of bias faults with no false alarms. The F1-score of MPCA-KD (87.60%) surpassed other methods, emphasizing its balanced performance in terms of precision and recall. Concerning intermittent faults, MPCA-KD outperformed other methods, achieving 98.75% FDR. Although PCA-KD demonstrated a lower FDR of 57.50%, MPCA-KD showcased superior fault detection accuracy with 100% Precision. This implies that MPCA-KD can accurately detect intermittent faults with minimal false positives. For drift faults, all methods demonstrated commendable fault detection performance, achieving 100% Precision and high F1-scores. PCA-KD and MPCA-KD displayed slightly higher FDR values, indicating a marginally increased rate of false detections compared to other methods. In summary, MPCA-KD consistently demonstrated superior fault detection accuracy across all fault types under an SNR of 5, further highlighting its effectiveness in monitoring the distillation column process in noisy conditions. The balanced performance of MPCA-KD, particularly in terms of Precision and FDR, makes it a robust choice for fault detection in complex systems with lower SNR.
The detection time ratio (DTR) of different methods in monitoring of three faults is highlighted in
Table 3. For bias and intermittent faults, it may be observed that the proposed MSPCA-KD based FD strategy has a slightly higher value of DTR. Since the KD statistic is computed in a moving window, the proposed FD strategy tends to have a higher DTR value. Despite this, the proposed strategy has minimum missed detections and no false alarms. However, in case of drift fault, the proposed FD strategy has a slightly better DTR value. Overall, the superior performance of MPCA-KD, especially in fault detection scenarios with an SNR of 5, can be attributed to the MPCA and the KD scheme. PCA incorporates wavelet-based multiscale filtering, allowing the model to efficiently handle complex datasets with variations at multiple scales. This ensures that relevant features are retained while filtering out noise and irrelevant details, enhancing the model’s robustness. The use of KD as a statistical metric in the monitoring scheme enhances the model’s sensitivity to variations in data distributions. Essentially, MPCA-KD utilizes a distribution-based monitoring scheme, allowing it to compare segments of two distributions. This enables the model to capture critical details in the data, making it particularly effective in identifying anomalies and deviations associated with faults. The MPCA-KD approach employs nonparametric thresholding through kernel density estimation (KDE). This allows for a more flexible and adaptive determination of detection thresholds, accommodating variations in the data distribution without relying on strict assumptions.
3.2. Monitoring Faults in CSTR Process
The experiment employs a nonlinear continuous stirred tank reactor (CSTR) setup to assess the efficacy of the proposed fault detection method. In a CSTR, reactants are introduced into the tank, and a stirrer mixes them to produce the desired product [
54]. Numerous studies have employed different configurations of CSTRs to evaluate the efficacy of fault detection methodologies [
55,
56,
57]. The CSTR process is characterized by a non-isothermal and irreversible first-order reaction [
58]. Analyzing the proposed fault detection scheme’s performance in this particular CSTR setup offers valuable insights into its potential applications and effectiveness in real-world scenarios. The nonlinearity and dynamic nature of CSTR processes make them challenging for fault detection, making this evaluation particularly relevant for assessing the method’s robustness and applicability in complex and dynamic systems.
The discussed process involves a chemical reaction where species
A undergoes a reaction to produce the desired product,
B (i.e.,
).
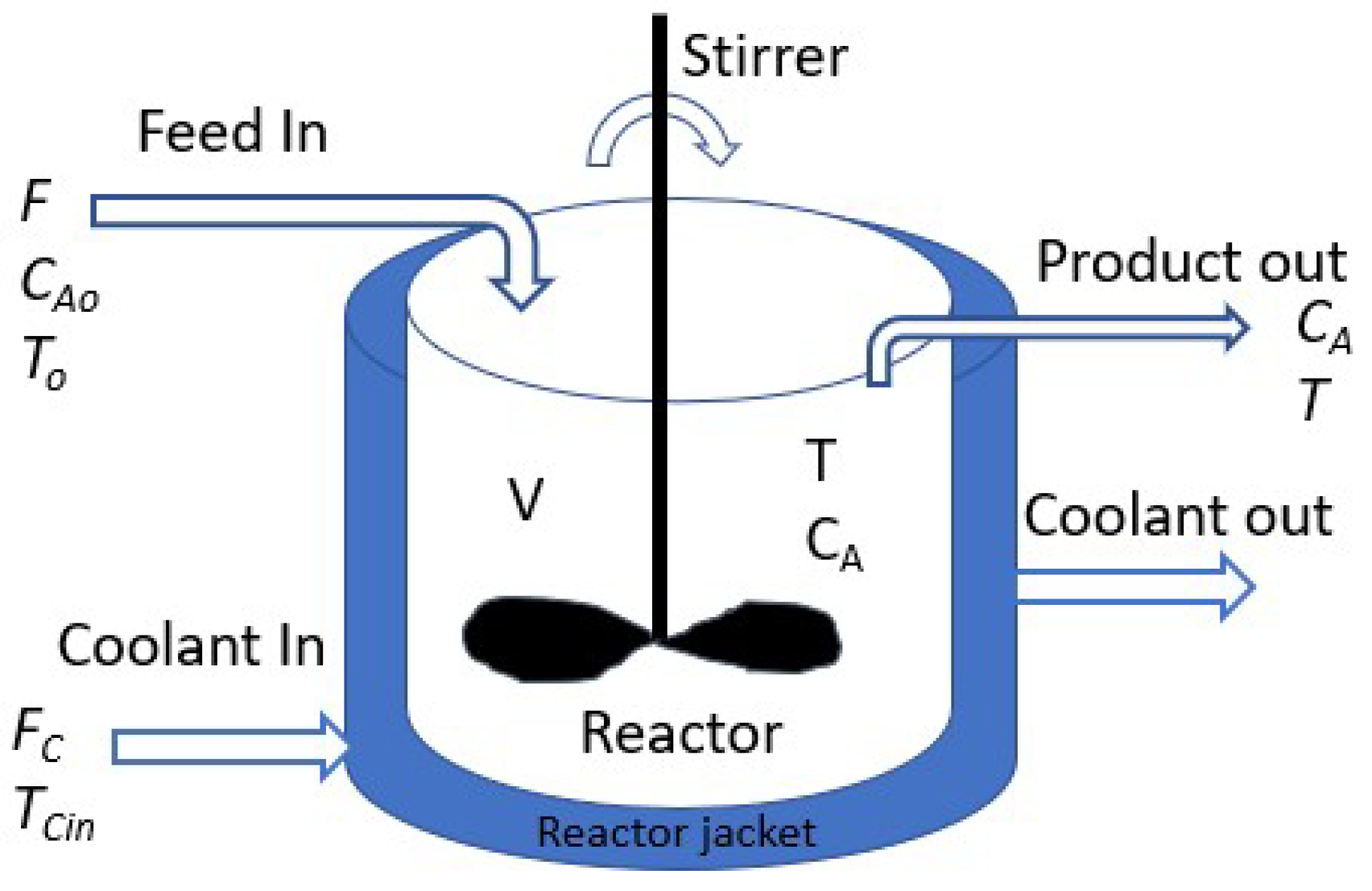
Figure 11 illustrates the configuration of the Continuous Stirred Tank Reactor (CSTR) process. The reaction is highly exothermic, necessitating using the jacket’s fluid to cool the reactor. Precise regulation of the feed and coolant flow rates ensures the attainment of the desired product concentration,
B. The reaction mechanism is described by Equation (
20). By formulating component balance and energy balance equations for the reactor system, a set of Ordinary Differential Equations (ODEs) is derived, as presented in (
21) through (
23).
It is crucial to emphasize that the model relies on various parameters, outlined in
Table 4. These parameters hold a pivotal role in determining the behavior of the reactor system. Consequently, comprehending the significance of each parameter and its influence on the system is essential for process optimization and achieving the target product concentration [
59].
To generate data, the perturbation of feed stream and coolant flow rates around the steady state condition is carried out using a pseudo-random binary signal (PRBS) with frequency of [0 0.05
], where
represents the Nyquist frequency. This allows for the simulation of real-world scenarios where these variables may fluctuate due to external factors. It should also be noted that the variables
,
and
are treated as unmeasured disturbances. This means their dynamics are not directly measured or observed in the experiment. Instead, their behavior is governed by stochastic processes, which are used to model their potential effects on the system.
The , and are white noise sequences that are having standard deviations of 0.5, 1 and 1 respectively.
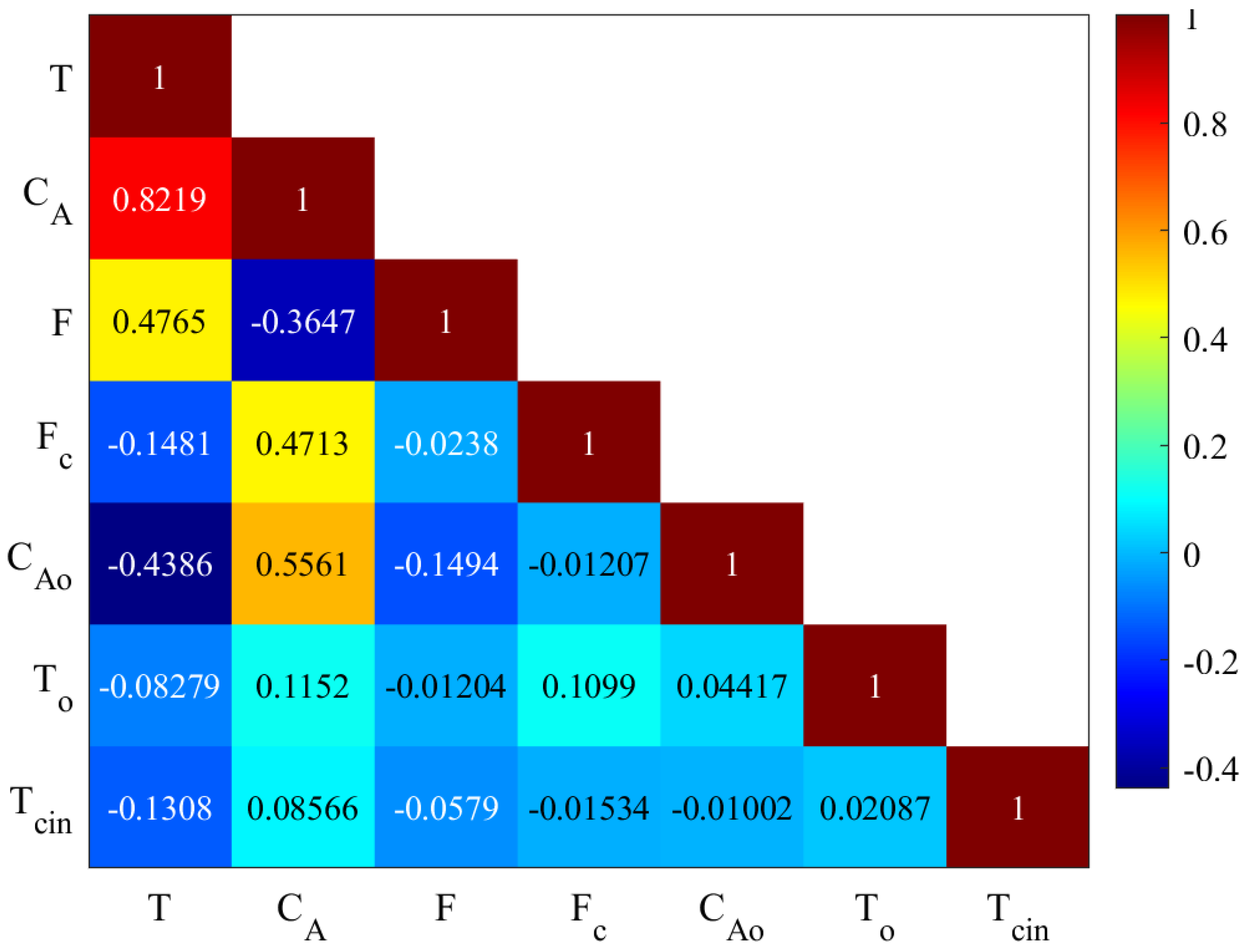
Figure 12 depicts the heat map of the correlation matrix between the CSTR variables. A correlation coefficient of 0.822 between Reactor Temperature (T) and Reactor Concentration (
) indicates a strong positive linear relationship between these two variables. In the context of a chemical reactor like the CSTR, the reactor’s temperature can influence the rate of chemical reactions. The positive correlation observed here might imply that higher temperatures within the reactor are associated with increased reactant concentrations. This relationship could be because many chemical reactions are temperature-dependent, and higher temperatures often lead to higher reaction rates. It’s important to note that correlation does not imply causation. While the correlation coefficient quantifies the strength and direction of a linear relationship, it doesn’t provide information about the underlying mechanisms or causative factors. Further analysis, experimentation, or domain knowledge would be needed to understand the specific reasons behind the observed correlation in the CSTR process.
A dataset of 1390 observations and seven variables is generated (
Table 4). This data is partitioned into 745 samples each for training and testing purposes. PCA and MSPCA models are constructed, retaining five optimal PCs via the CPV method. For PCA-KD and MSPCA-KD strategies, KD computation employs a sliding window of 50. The optimal decomposition depth is determined to be 3 and 4 for SNR = 15 and SNR = 5, respectively. The analysis includes the monitoring of three faults in the CSTR process. In the first scenario, a bias fault, constituting 5% of the total variation, is introduced in the reactor temperature variable between sampling time instant 305 and the end of the testing data. In the second scenario, an intermittent fault with a magnitude of 5% of the total variation is inserted in the reactor concentration variable during two intervals: [200, 300] and [500, 600], respectively. Finally, a drift sensor fault with a slope of 0.001 is injected into the reactor concentration variable from sampling time instant 295 until the end of the testing data.
Detecting the introduced faults in the CSTR process, including a bias fault in the reactor temperature variable, an intermittent fault in the reactor concentration, and a drift sensor fault in the reactor concentration, is crucial for ensuring the robustness and reliability of the chemical reaction. The impact of these faults can influence the overall efficiency, product quality, and safety of the reactor system, making their timely detection and diagnosis essential for optimal process control and performance.
To enhance clarity, a detailed analysis of monitoring a bias fault in both noisy scenarios (SNR = 15 and SNR = 5) is presented through result plots.
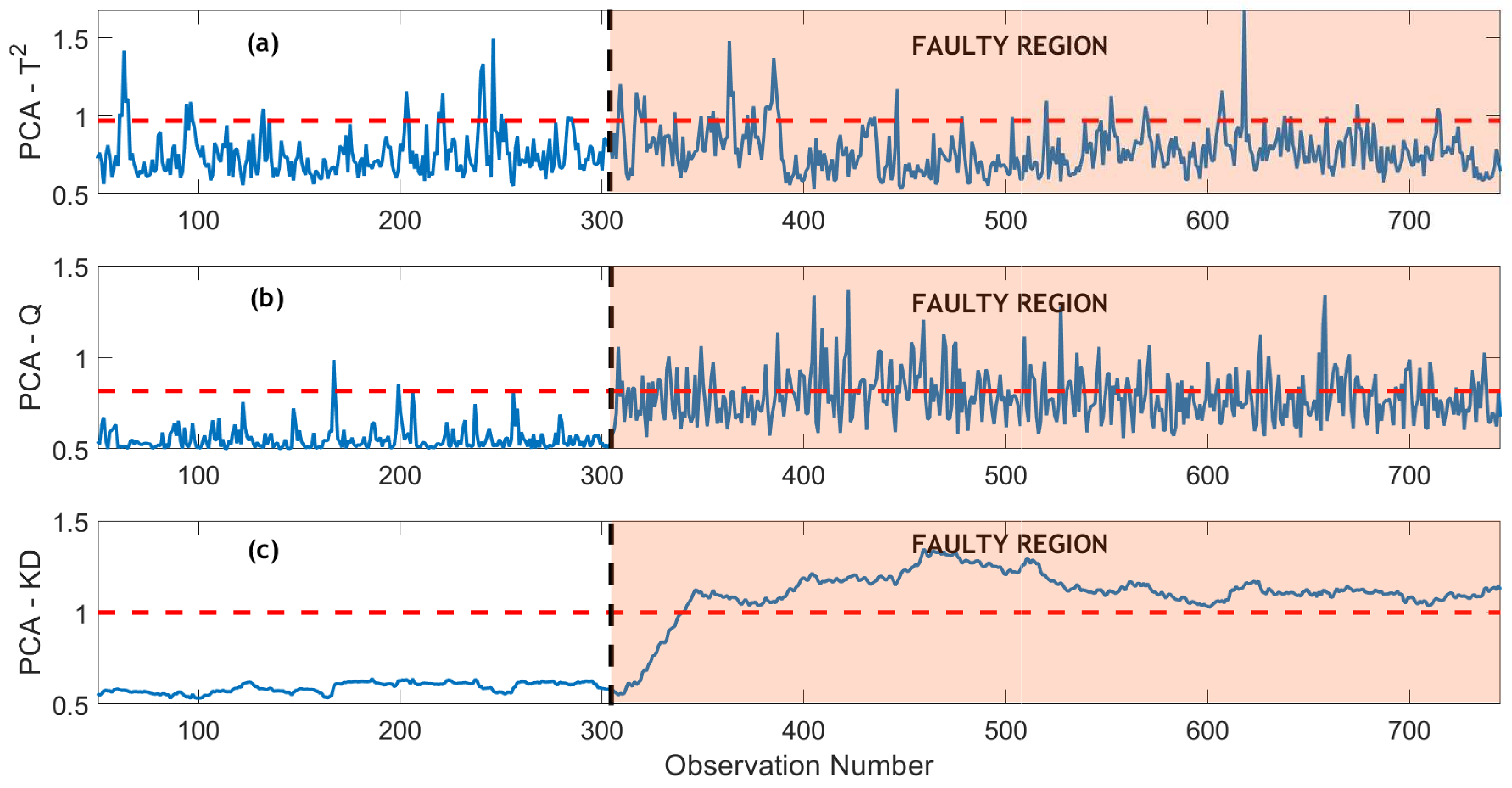
Figure 13 and
Figure 14 illustrate the monitoring of a bias fault by PCA and MPCA-based methods respectively in the SNR = 15 case. In
Figure 13a, the
indicator fails to identify the fault, as its statistical values remain below the reference threshold line within the fault region. Similarly, the PCA-Q strategy in
Figure 13b also lacks effectiveness in detecting the bias fault, displaying multiple missed detections. This insensitivity to relatively small and moderate abnormal changes could stem from the decision statistics of
and Q, which are designed solely based on the current observations without incorporating information from past data.
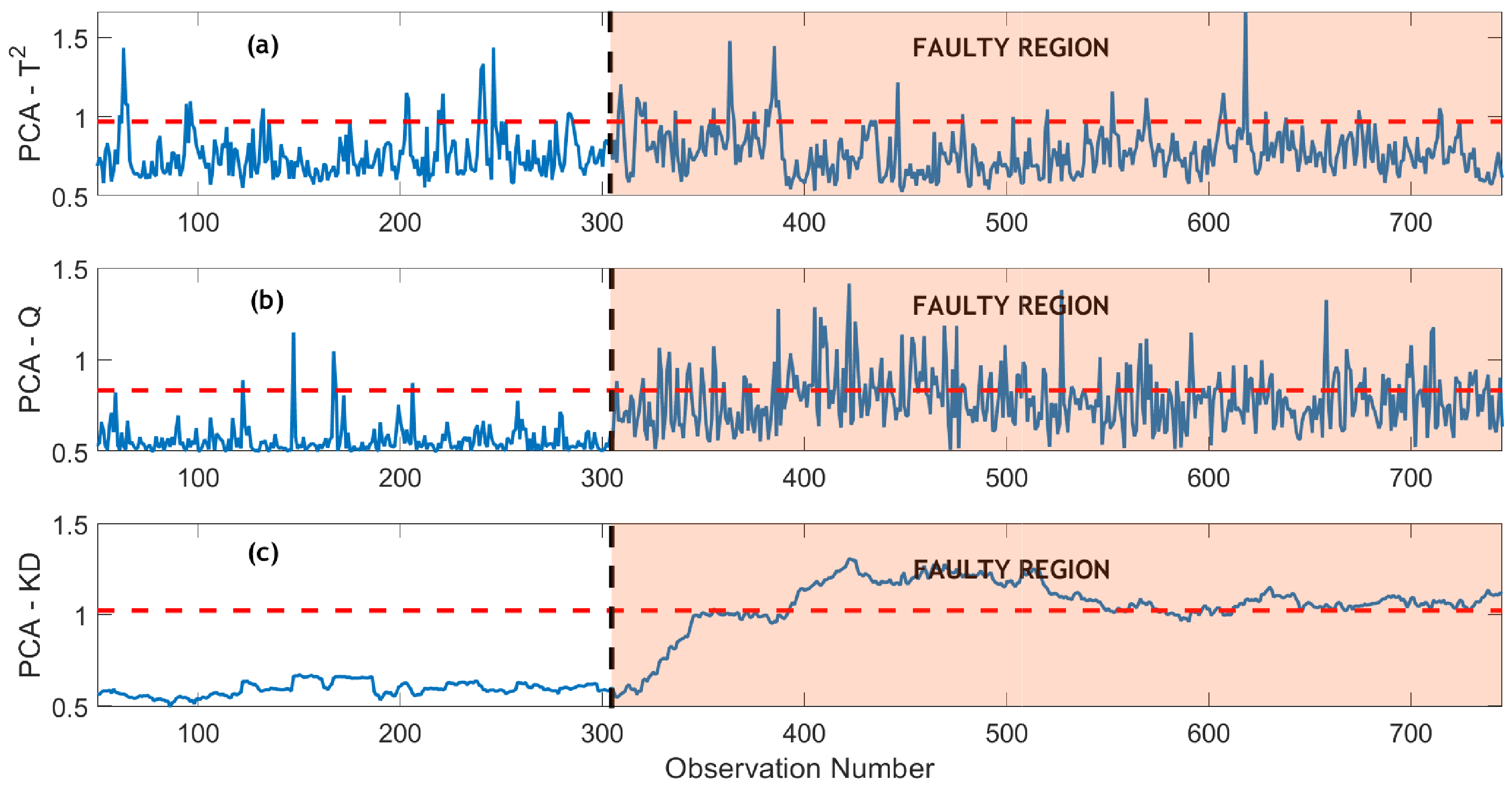
The performance exhibits a slight improvement with the MSPCA-Q strategy, attributed to the wavelet-based filtering (
Figure 14b). Notably, the MSPCA-Q strategy successfully identifies the bias fault with few missed detections in the faulty region. In contrast, both the PCA-KD and MPCA-KD strategies outperform conventional PCA and MPCA-based methods in fault detection (
Figure 13c and
Figure 14c). The KD-based strategies provide smooth detection with minimal missed detections and zero false alarms. Importantly, the proposed MSPCA-KD strategy holds an advantage by detecting the fault with less delay compared to the PCA-KD strategy, showcasing its superiority.
Table 5 presents the performance of monitoring methods in detecting the three simulated faults in the CSTR process under an SNR of 15. In the case of a bias fault, PCA-
shows a low detection rate of 12.45% and a low Precision, indicating frequent false alarms. PCA-Q exhibits a low FDR and a high FAR, making them unsuited in practice. For the Bias Fault, PCA-KD and MSPCA-KD exhibit superior FDR at 94.32% and 97.27%, respectively, indicating their efficacy in accurately identifying the bias fault. Concerning the intermittent fault, MSPCA-KD stands out with the highest FDR (95%) and zero false alarms, showcasing its ability to detect intermittent faults effectively (
Table 5). MPCA-KD achieves perfect precision (100%) and F1-score, making it the most reliable for intermittent fault detection. This is attributed to the robustness provided by the wavelet-based filtering in MSPCA-KD. It is followed by MPCA-Q and PCA-KD, achieving an FDR of 79.5% and 75%, respectively. on the other hand, PCA-
, PCA-Q, and MSPCA-
exhibit high FAR and low FDR, indicating challenges in detecting drift faults accurately (
Table 5). For the drift fault, PCA-
and PCA-Q can recognize this fault but with many missed detections (i.e., FDR of 84.73% and 75.57%, respectively), indicating challenges in detecting drift faults accurately (
Table 5). PCA-KD shows improvement in FDR (85.22 ) but still with several missed detections. MPCA-
and MSPCA-Q offer better performance with improved FDR (88.02% and 90.85%) compared to PCA methods. MSPCA-KD outperforms other methods, achieving high FDR (96.12%), precision (100%), and F1-score (92.52%), making it the most effective in detecting drift faults (
Table 5). MSPCA-KD’s incorporation of wavelet-based filtering contributes to its superior performance in minimizing false alarms while maintaining high precision, which is especially crucial in scenarios with SNR = 15.
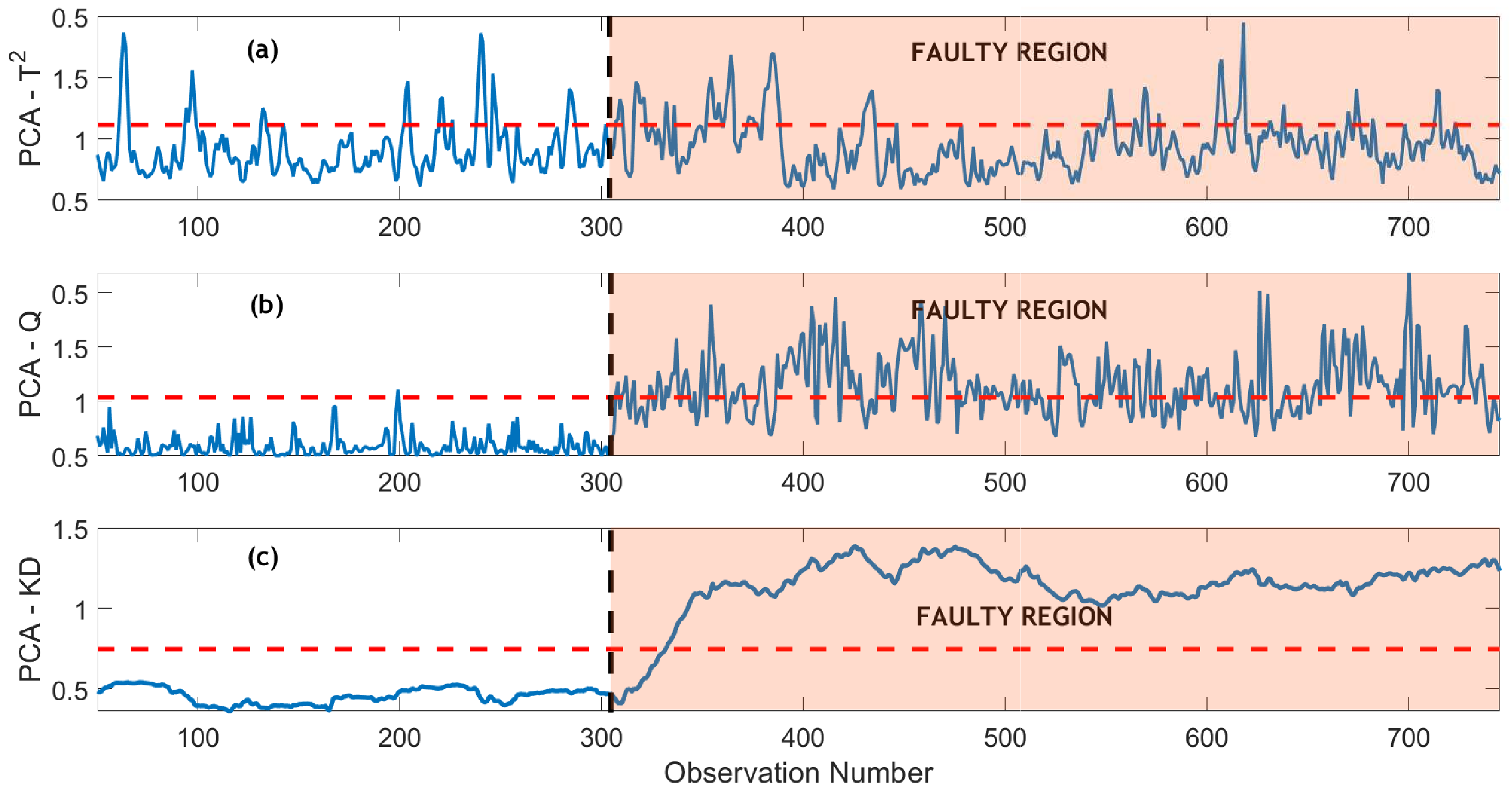
In the subsequent analysis, the monitoring of the bias fault in the presence of heightened noise levels, characterized by an SNR of 5, is depicted in
Figure 15 and
Figure 16 respectively. Due to the significant noise level, the efficacy of PCA-based methods in detecting the bias fault is significantly compromised. Both the PCA-
and PCA-Q schemes fail to identify the fault, underscoring their limitations in noisy conditions (
Figure 15a,b). The PCA-KD strategy, while demonstrating improved detection compared to PCA-
and PCA-Q, still exhibits a few missed detections within the fault region, as discerned in
Figure 15c. In multi-scale-based methods, the MSPCA-
strategy proves inefficient in detecting the bias fault amid the elevated noise environment (
Figure 16a). The MSPCA-Q strategy performs better than PCA-based methods, yet it only achieves partial fault detection (
Figure 16b). In contrast, the proposed MSPCA-KD-based strategy provides notable efficacy with a seamless detection of the bias fault within the fault region (
Figure 16c). The method’s performance in the presence of substantial noise highlights its robustness and potential for reliable fault detection under challenging conditions.
Table 6 provides an insightful evaluation of various monitoring methods in detecting faults within the CSTR process under an SNR of 5. For the case of a bias fault, PCA-based methods exhibit limited effectiveness, particularly with PCA-
displaying an FDR of 11.12%, indicating challenges in accurate fault detection. While PCA-Q demonstrates an improvement with a lower FDR of 32.95%, it still falls short of achieving optimal performance. PCA-KD, however, exhibits significant enhancements with an FDR of 71.73%, demonstrating its capability to identify bias faults more reliably. Multi-scale methods, specifically MPCA-KD, outperform other approaches in this scenario, achieving the highest FDR of 95.15%, indicating its robustness in detecting bias faults even in the presence of elevated noise. In the case of an intermittent fault, PCA-based methods face challenges, with PCA-
and PCA-Q achieving FDRs of 13.25% and 48.00%, respectively. PCA-KD shows improvements with an FDR of 62.00%, but many missed detections remain. Multi-scale methods, especially MSPCA-KD, demonstrate superior fault detection capability with an FDR of 88.50%, showcasing its effectiveness in identifying intermittent faults with reduced missed detections. Considering drift faults, PCA-based methods present limitations, with PCA-
and PCA-Q exhibiting FDRs of 44.11% and 68.67%, respectively. PCA-KD showcases improvement with an FDR of 71.39% but still has considerable missed detections. Multi-scale methods, notably MSPCA-KD, outperform other approaches with an FDR of 84.75%, indicating its ability to detect drift faults, but there is still room for improvement. In summary, under the SNR = 5 scenario, MSPCA-KD is the most effective method across all fault types, demonstrating superior fault detection rates, low false alarms, and high precision. The wavelet-based filtering in MPCA-KD contributes to its robustness, making it a reliable choice for fault detection in noisy environments.
The
Table 7 provides the detection time ratio (DTR) of different methods in monitoring the three sensor faults of CSTR process. It may be noted that the proposed MSPCA-KD based FD strategy takes a small time to detect bias as well as intermittent faults and has a quicker detection for drift fault. It may be noted that the proposed MSPCA-KD strategy involves KD statistic which is computed in a moving window which contributes to small delay in computation. For a slowly varying drift fault, the MSPCA-KD strategy has a small advantage over the traditional methods as it has a better DTR value. The KD statistic excels at capturing subtle changes and patterns in the data, making it well-suited for fault detection, especially in situations where traditional methods may struggle. The utilization of wavelets with PCA model ensures that relevant features of the data are retained while filtering out noise and irrelevant details, enhancing the model’s robustness. This in turn enhanced the detection of different faults in the process.