Prevention and Control of the Spread of Pathogens in a University of Naples Engineering Classroom through CFD Simulations
Abstract
1. Introduction
- The ventilation system is on and operating according to current guidelines; the mask is not worn by the infected student.
- The ventilation system was turned off; the mask was not worn by the infected student.
- The ventilation system is on and functioning according to current guidelines; the mask is worn by infected students.
- The ventilation system is on (flow rate tripled); the mask is not worn by the infected student.
- The ventilation system is on (flow rate tripled); the mask is worn by the infected student.
- 6.
- The exposed students and/or teachers are not wearing PPE.
- 7.
- The exposed students and/or teachers are wearing surgical masks.
- 8.
- The exposed students and/or teachers are wearing FFP2 masks.
2. Methodology
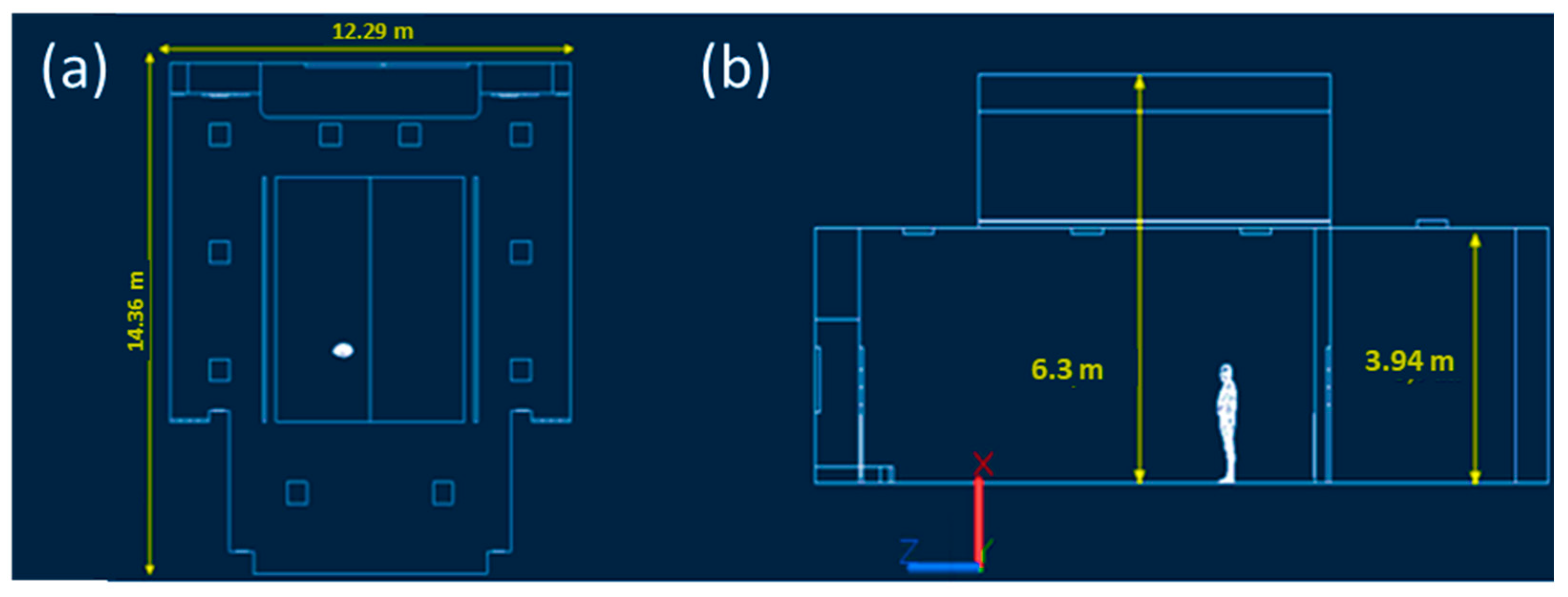
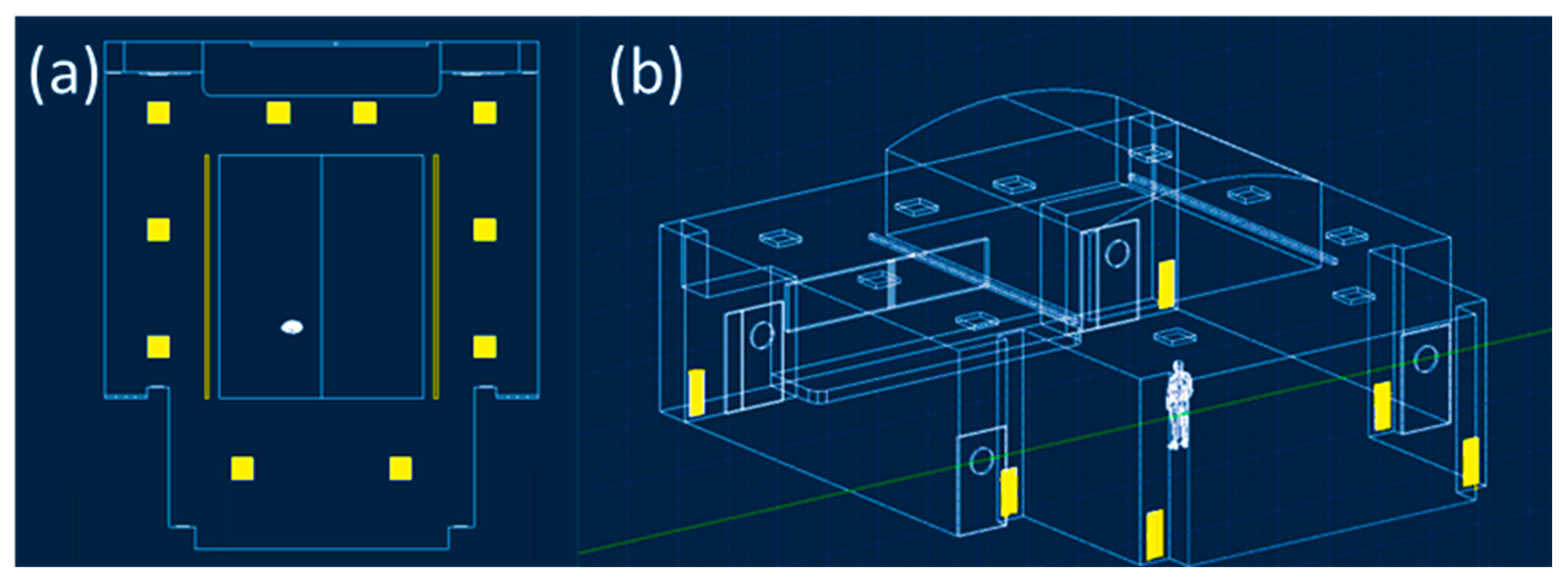
2.1. CFD Model: Geometrical Domain
2.2. CFD Model: Mesh Building
2.3. CFD Model: Equations and Boundary Conditions
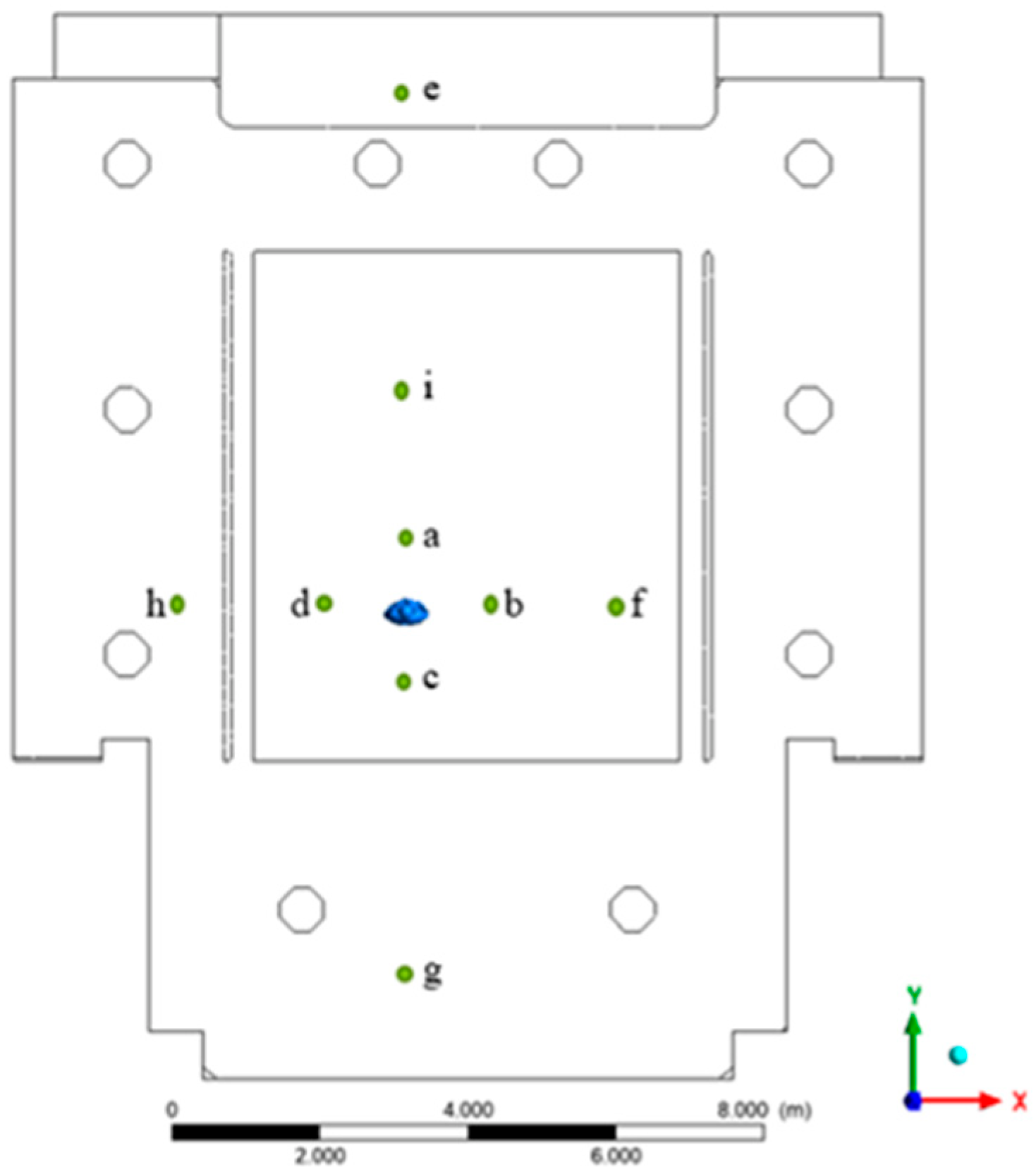
2.4. Calculations of Infection Probability
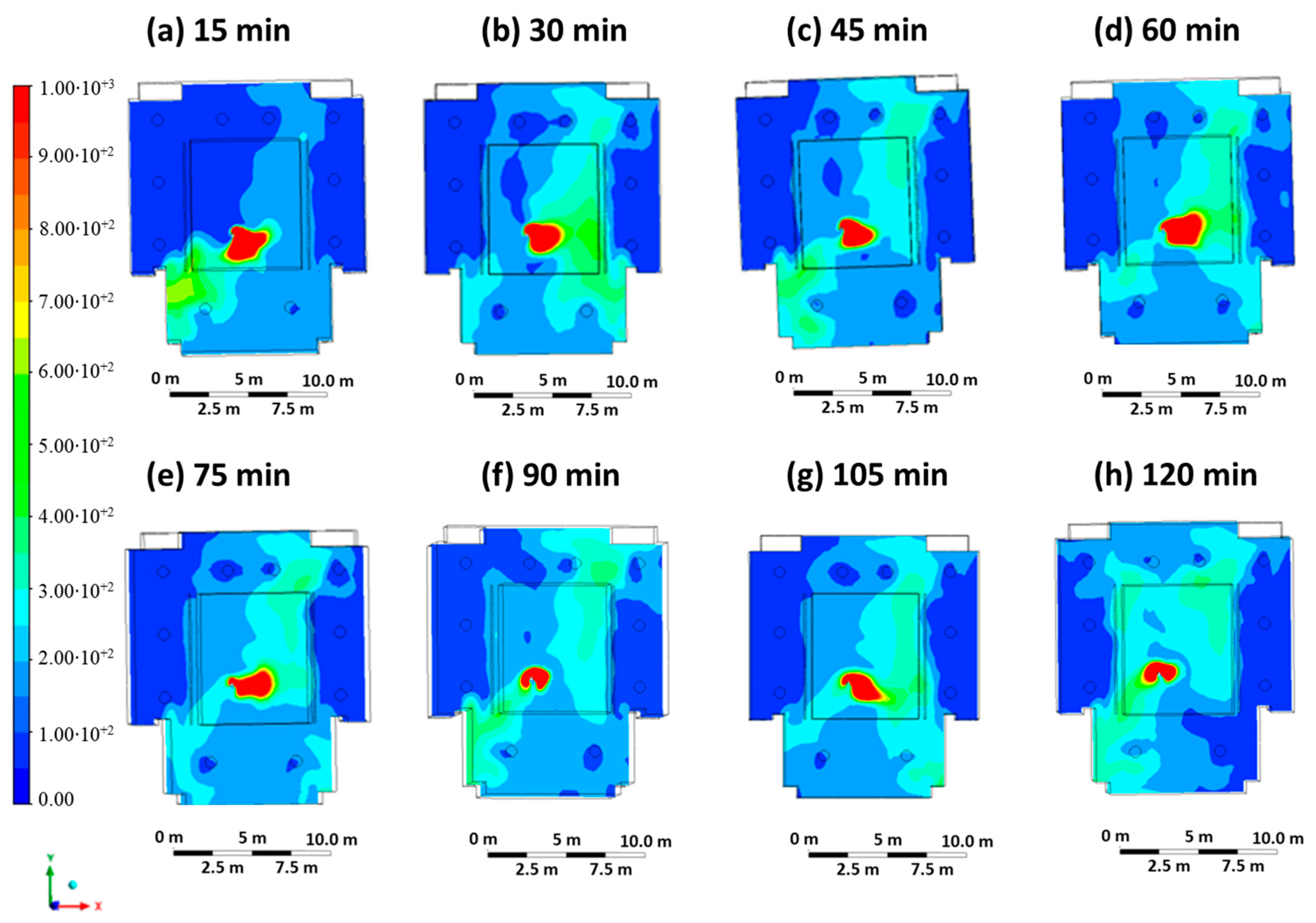
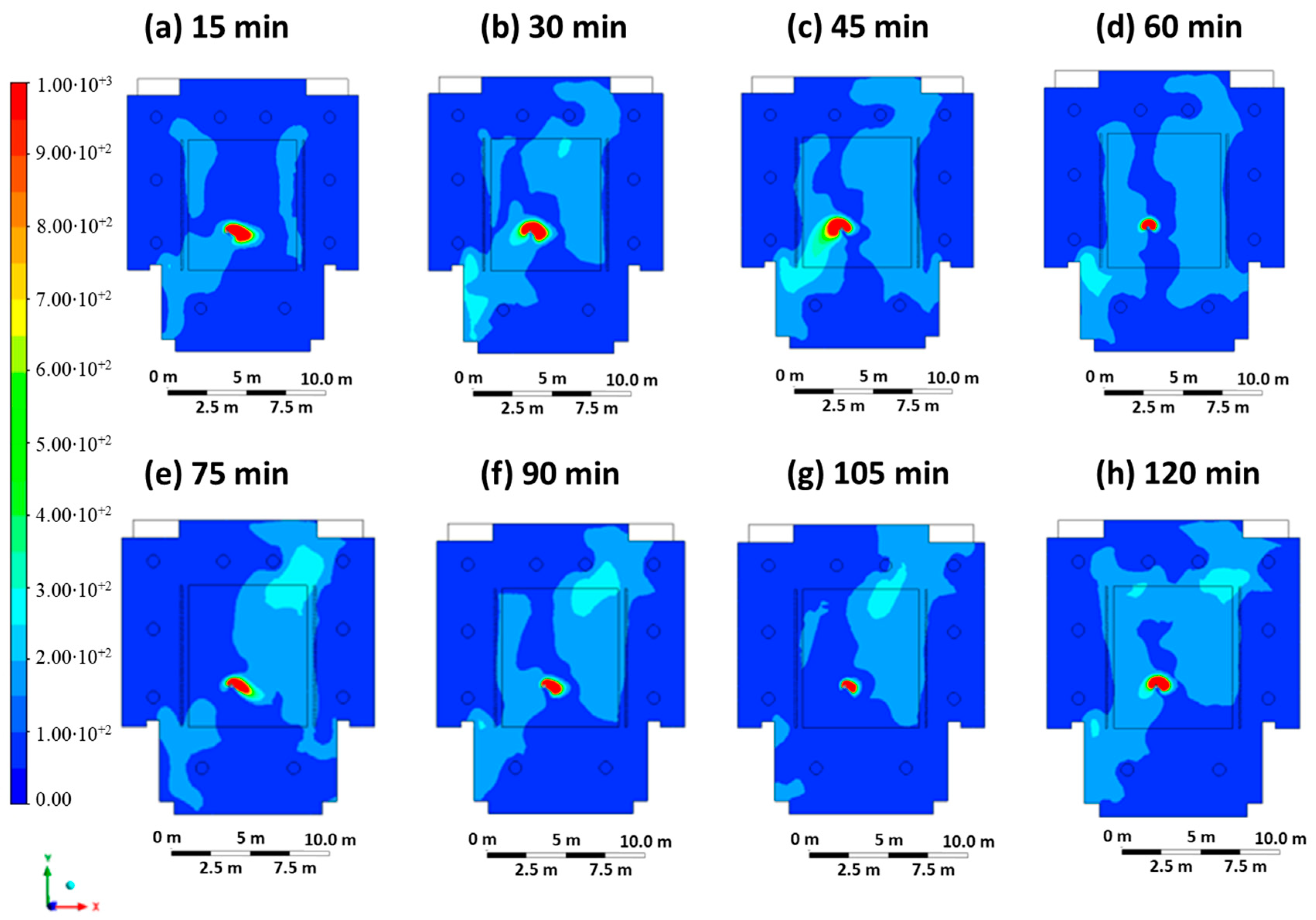
3. Results
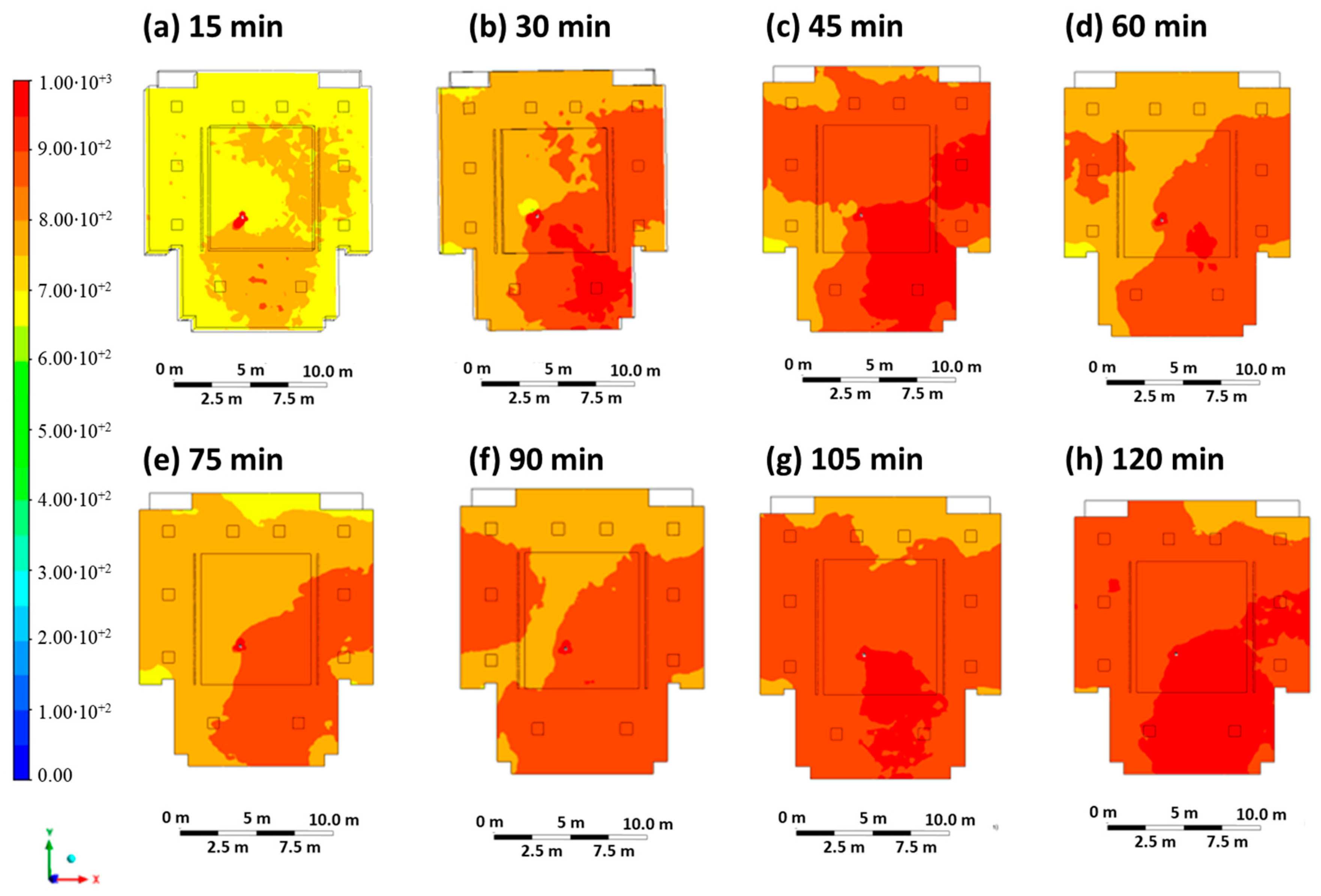
3.1. Results Case 1
3.2. Results Case 2
3.3. Results Case 3
3.4. Results Case 4
3.5. Results Case 5
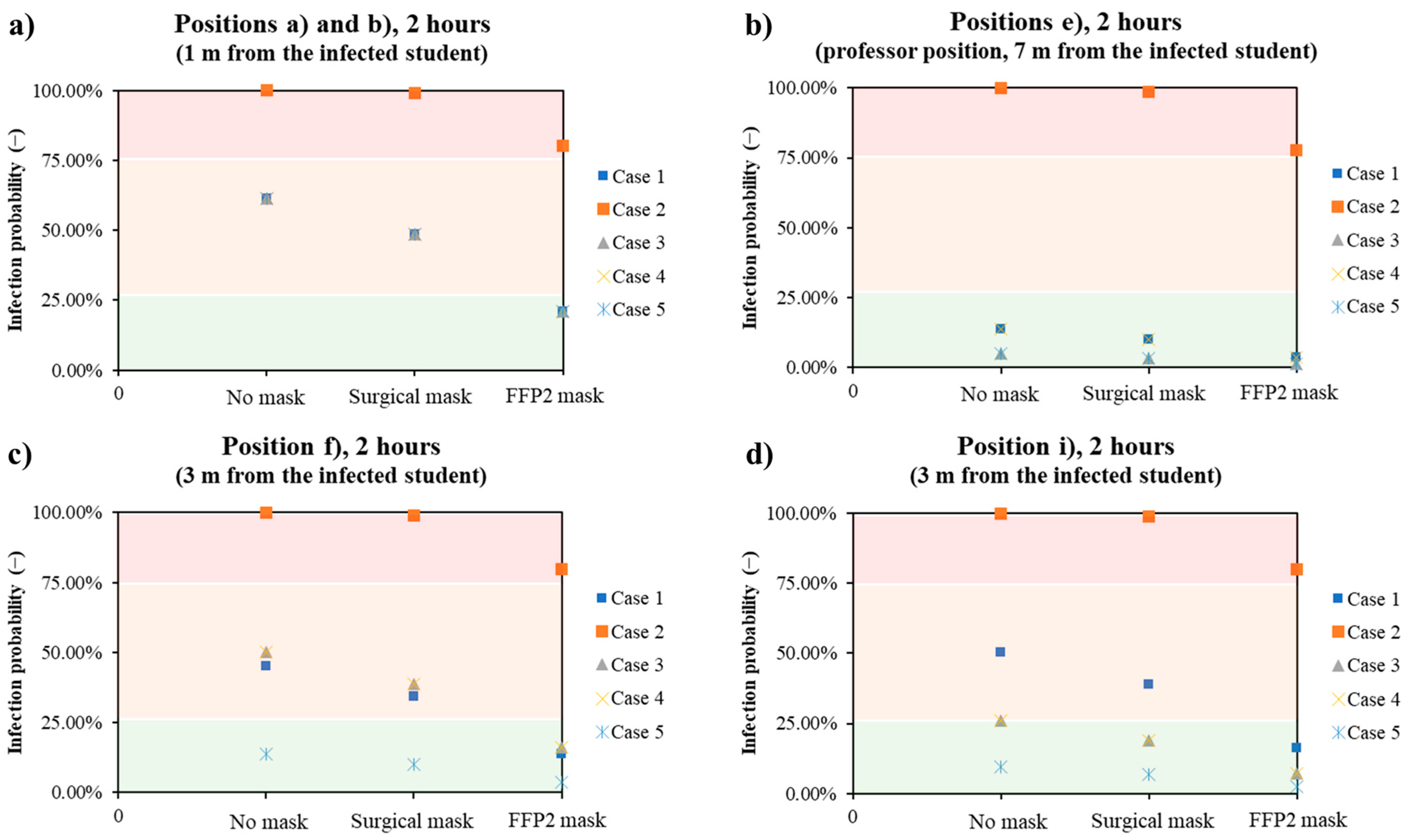
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yin, P.; Brauer, M.; Cohen, A.J.; Wang, H.; Li, J.; Burnett, R.T.; Stanaway, J.D.; Causey, K.; Larson, S.; Godwin, W.; et al. The Effect of Air Pollution on Deaths, Disease Burden, and Life Expectancy across China and Its Provinces, 1990–2017: An Analysis for the Global Burden of Disease Study 2017. Lancet Planet. Health 2020, 4, e386–e398. [Google Scholar] [CrossRef] [PubMed]
- Zheng, W.; Hu, J.; Wang, Z.; Li, J.; Fu, Z.; Li, H.; Jurasz, J.; Chou, S.K.; Yan, J. COVID-19 Impact on Operation and Energy Consumption of Heating, Ventilation and Air-Conditioning (HVAC) Systems. Adv. Appl. Energy 2021, 3, 100040. [Google Scholar] [CrossRef]
- Guo, M.; Xu, P.; Xiao, T.; He, R.; Dai, M.; Miller, S.L. Review and Comparison of HVAC Operation Guidelines in Different Countries during the COVID-19 Pandemic. Build. Environ. 2021, 187, 107368. [Google Scholar] [CrossRef] [PubMed]
- Nazaroff, W.W. Indoor Bioaerosol Dynamics. Indoor Air 2016, 26, 61–78. [Google Scholar] [CrossRef]
- Portarapillo, M.; Di Benedetto, A. Methodology for Risk Assessment of COVID-19 Pandemic Propagation. J. Loss Prev. Process Ind. 2021, 72, 104584. [Google Scholar] [CrossRef] [PubMed]
- Kolmogorov, A. The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds’ Numbers. Dokl. Akad. Nauk SSSR 1941, 30, 301–305. [Google Scholar]
- Bivolarova, M.; Ondráček, J.; Melikov, A.; Ždímal, V. A Comparison between Tracer Gas and Aerosol Particles Distribution Indoors: The Impact of Ventilation Rate, Interaction of Airflows, and Presence of Objects. Indoor Air 2017, 27, 1201–1212. [Google Scholar] [CrossRef]
- Zhang, Z.; Chen, X.; Mazumdar, S.; Zhang, T.; Chen, Q. Experimental and Numerical Investigation of Airflow and Contaminant Transport in an Airliner Cabin Mockup. Build. Environ. 2009, 44, 85–94. [Google Scholar] [CrossRef]
- Noakes, C.; Fletcher, L.; Sleigh, P. Comparison of Tracer Techniques for Evaluating the Behavior of Bioaerosols in Hospital Isolation Rooms. In Proceedings of the Healthy Buildings, Syracuse, NY, USA, 13–17 September 2009. [Google Scholar]
- Gao, N.P.; Niu, J.L.; Perino, M.; Heiselberg, P. The Airborne Transmission of Infection between Flats in High-Rise Residential Buildings: Particle Simulation. Build. Environ. 2009, 44, 402–410. [Google Scholar] [CrossRef]
- Xiaoping, L.; Jianlei, N.; Naiping, G. Spatial Distribution of Human Respiratory Droplet Residuals and Exposure Risk for the Co-Occupant under Different Ventilation Methods. HVAC R Res. 2011, 17, 432–445. [Google Scholar] [CrossRef]
- Beato-Arribas, B.; McDonagh, A.; Noakes, C.; Sleigh, P. Assessing the Near-Patient Infection Risk in Isolation Rooms. In Proceedings of the Healthy Buildings, Eindhoven, The Netherlands, 18–20 May 2015. [Google Scholar]
- Tretiakow, D.; Tesch, K.; Skorek, A. Mitigation Effect of Face Shield to Reduce SARS-CoV-2 Airborne Transmission Risk: Preliminary Simulations Based on Computed Tomography. Environ. Res. 2021, 198, 111229. [Google Scholar] [CrossRef]
- Suen, C.Y.; Kwok, H.H.L.; Tsui, Y.H.; Lui, K.H.; Leung, H.H.; Lam, K.W.; Hung, K.P.S.; Kwan, J.K.C.; Ho, K.F. Experimental and Computational Analysis of Surgical Mask Effectiveness Against COVID-19 in Indoor Environment. Aerosol Air Qual. Res. 2023, 23, 1–15. [Google Scholar] [CrossRef]
- Mirzaie, M.; Lakzian, E.; Khan, A.; Warkiani, M.E.; Mahian, O.; Ahmadi, G. COVID-19 Spread in a Classroom Equipped with Partition—A CFD Approach. J. Hazard. Mater. 2021, 420, 126587. [Google Scholar] [CrossRef] [PubMed]
- Rencken, G.K.; Rutherford, E.K.; Ghanta, N.; Kongoletos, J.; Glicksman, L. Patterns of SARS-CoV-2 Aerosol Spread in Typical Classrooms. Build. Environ. 2021, 204, 108167. [Google Scholar] [CrossRef]
- Burgmann, S.; Janoske, U. Transmission and Reduction of Aerosols in Classrooms Using Air Purifier Systems. Phys. Fluids 2021, 33, 033321. [Google Scholar] [CrossRef] [PubMed]
- He, R.; Liu, W.; Elson, J.; Vogt, R.; Maranville, C.; Hong, J. Airborne Transmission of COVID-19 and Mitigation Using Box Fan Air Cleaners in a Poorly Ventilated Classroom. Phys. Fluids 2021, 33, 033321. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Deng, Z. Transmission and Infection Risk of COVID-19 When People Coughing in an Elevator. Build. Environ. 2023, 238, 110343. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Zhang, T.; You, R.; Chen, Q. Evaluation of Infection Probability of COVID-19 in Different Types of Airliner Cabins. Build. Environ. 2023, 234, 110159. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, S.; Yin, Y.; Zhang, T.; Chen, Q. Airborne Transmission of COVID-19 Virus in Enclosed Spaces: An Overview of Research Methods. Indoor Air 2022, 32, e13056. [Google Scholar] [CrossRef]
- Liu, M.; Liu, J.; Cao, Q.; Li, X.; Liu, S.; Ji, S.; Lin, C.H.; Wei, D.; Shen, X.; Long, Z.; et al. Evaluation of Different Air Distribution Systems in a Commercial Airliner Cabin in Terms of Comfort and COVID-19 Infection Risk. Build. Environ. 2022, 208, 108590. [Google Scholar] [CrossRef]
- Ripartizione Prevenzione e Protezione Attuazione Delle Misure per La Tutela Della Salute e Sicurezza per Lo Svolgimento Di Esami Di Profitto e Sedute Di Laurea in Presenza. Available online: https://www.unina.it/documents/11958/22035952/pg.2020.056683.pdf (accessed on 2 January 2023).
- Shao, X.; Li, X. COVID-19 Transmission in the First Presidential Debate in 2020. Phys. Fluids 2020, 32, 115125. [Google Scholar] [CrossRef] [PubMed]
- Wells, W.F. Airborne Contagion and Air Hygiene. JAMA 1955, 159, 90. [Google Scholar]
- Riley, C.E.; Murphy, G.; Riley, R.L. Airborne Spread of Measles in a Suburban Elementary School. Am. J. Epidemiol. 1978, 107, 421–432. [Google Scholar] [CrossRef] [PubMed]
- Dai, H.; Zhao, B. Association of the Infection Probability of COVID-19 with Ventilation Rates in Confined Spaces. Build. Simul. 2020, 13, 1321–1327. [Google Scholar] [CrossRef] [PubMed]


| Information about Mesh | Sparser Mesh | Sparse Mesh | Dense Mesh | Denser Mesh |
|---|---|---|---|---|
| Nodes number | 180,502 | 461,301 | 660,654 | 774,116 |
| Elements number | 972,754 | 2,467,544 | 3,539,133 | 4,149,493 |
| Average orthogonal quality | 0.751 | 0.753 | 0.754 | 0.747 |
| Case | Description | Inlet Air Velocity | Inlet Mouth Velocity | Outlet Air Gauge Pressure |
|---|---|---|---|---|
| Case 1 | Ventilation on Mask off | 0.3 m/s | 1 m/s | 0 Pa |
| Case 2 | Ventilation off Mask off | 0 m/s | 1 m/s | 0 Pa |
| Case 3 | Ventilation on Mask on | 0.3 m/s | 0.5 m/s | 0 Pa |
| Case 4 | Hyperventilation on Mask off | 0.9 m/s | 1 m/s | 0 Pa |
| Case 5 | Hyperventilation on Mask on | 0.9 m/s | 0.5 m/s | 0 Pa |
| Position | E (ppm) | DR | Probability without DPI | Probability with Surgical Mask | Probability with FFP2 Mask |
|---|---|---|---|---|---|
| a | 600 | 100 | 7.2% | 5.1% | 1.9% |
| b | 750 | 80 | 8.9% | 6.4% | 2.3% |
| c | 950 | 63 | 11.2% | 8.0% | 2.9% |
| d | 300 | 200 | 3.7% | 2.6% | 0.9% |
| e | 50 | 1200 | 0.6% | 0.4% | 0.2% |
| f | 300 | 200 | 3.7% | 2.6% | 0.9% |
| g | 600 | 100 | 7.2% | 5.1% | 1.9% |
| h | 200 | 300 | 2.5% | 1.7% | 0.6% |
| i | 600 | 100 | 7.2% | 5.1% | 1.9% |
| Position | E (ppm) | DR | Probability without DPI | Probability with Surgical Mask | Probability with FFP2 Mask |
|---|---|---|---|---|---|
| a | 1000 | 60 | 11.8% | 8.4% | 3.1% |
| b | 1000 | 60 | 11.8% | 8.4% | 3.1% |
| c | 1000 | 60 | 11.8% | 8.4% | 3.1% |
| d | 800 | 75 | 9.5% | 6.8% | 2.5% |
| e | 800 | 75 | 9.5% | 6.8% | 2.5% |
| f | 800 | 75 | 9.5% | 6.8% | 2.5% |
| g | 850 | 71 | 10.1% | 7.2% | 2.6% |
| h | 800 | 75 | 9.5% | 6.8% | 2.5% |
| i | 850 | 71 | 10.1% | 7.2% | 2.6% |
| Position | E (ppm) | DR | Probability without DPI | Probability with Surgical Mask | Probability with FFP2 Mask |
|---|---|---|---|---|---|
| a | 950 | 63 | 11.2% | 8.0% | 2.9% |
| b | 950 | 63 | 11.2% | 8.0% | 2.9% |
| c | 950 | 63 | 11.2% | 8.0% | 2.9% |
| d | 400 | 150 | 4.9% | 3.4% | 1.2% |
| e | 50 | 1200 | 0.6% | 0.4% | 0.2% |
| f | 600 | 100 | 7.2% | 5.1% | 1.9% |
| g | 400 | 150 | 4.9% | 3.4% | 1.2% |
| h | 50 | 1200 | 0.6% | 0.4% | 0.2% |
| i | 50 | 1200 | 0.6% | 0.4% | 0.2% |
| Position | E (ppm) | DR | Probability without DPI | Probability with Surgical Mask | Probability with FFP2 Mask |
|---|---|---|---|---|---|
| a | 950 | 63 | 11.2% | 8.0% | 2.9% |
| b | 950 | 63 | 11.2% | 8.0% | 2.9% |
| c | 950 | 63 | 11.2% | 8.0% | 2.9% |
| d | 300 | 200 | 3.7% | 2.6% | 0.9% |
| e | 50 | 1200 | 0.6% | 0.4% | 0.2% |
| f | 150 | 400 | 1.9% | 1.3% | 0.5% |
| g | 150 | 400 | 1.9% | 1.3% | 0.5% |
| h | 50 | 1200 | 0.6% | 0.4% | 0.2% |
| i | 50 | 1200 | 0.6% | 0.4% | 0.2% |
| Position | E (ppm) | DR | Probability without DPI | Probability with Surgical Mask | Probability with FFP2 Mask |
|---|---|---|---|---|---|
| a | 950 | 63 | 11.2% | 8.0% | 2.9% |
| b | 950 | 63 | 11.2% | 8.0% | 2.9% |
| c | 350 | 171 | 4.3% | 3.0% | 1.1% |
| d | 50 | 1200 | 0.6% | 0.4% | 0.2% |
| e | 50 | 1200 | 0.6% | 0.4% | 0.2% |
| f | 150 | 400 | 1.9% | 1.3% | 0.5% |
| g | 50 | 1200 | 0.6% | 0.4% | 0.2% |
| h | 50 | 1200 | 0.6% | 0.4% | 0.2% |
| i | 50 | 1200 | 0.6% | 0.4% | 0.2% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Portarapillo, M.; Simioli, S.; Di Benedetto, A. Prevention and Control of the Spread of Pathogens in a University of Naples Engineering Classroom through CFD Simulations. ChemEngineering 2024, 8, 37. https://doi.org/10.3390/chemengineering8020037
Portarapillo M, Simioli S, Di Benedetto A. Prevention and Control of the Spread of Pathogens in a University of Naples Engineering Classroom through CFD Simulations. ChemEngineering. 2024; 8(2):37. https://doi.org/10.3390/chemengineering8020037
Chicago/Turabian StylePortarapillo, Maria, Salvatore Simioli, and Almerinda Di Benedetto. 2024. "Prevention and Control of the Spread of Pathogens in a University of Naples Engineering Classroom through CFD Simulations" ChemEngineering 8, no. 2: 37. https://doi.org/10.3390/chemengineering8020037
APA StylePortarapillo, M., Simioli, S., & Di Benedetto, A. (2024). Prevention and Control of the Spread of Pathogens in a University of Naples Engineering Classroom through CFD Simulations. ChemEngineering, 8(2), 37. https://doi.org/10.3390/chemengineering8020037









