Fe Atom—Mixed Edges Fractal Graphene via DFT Calculation
Abstract
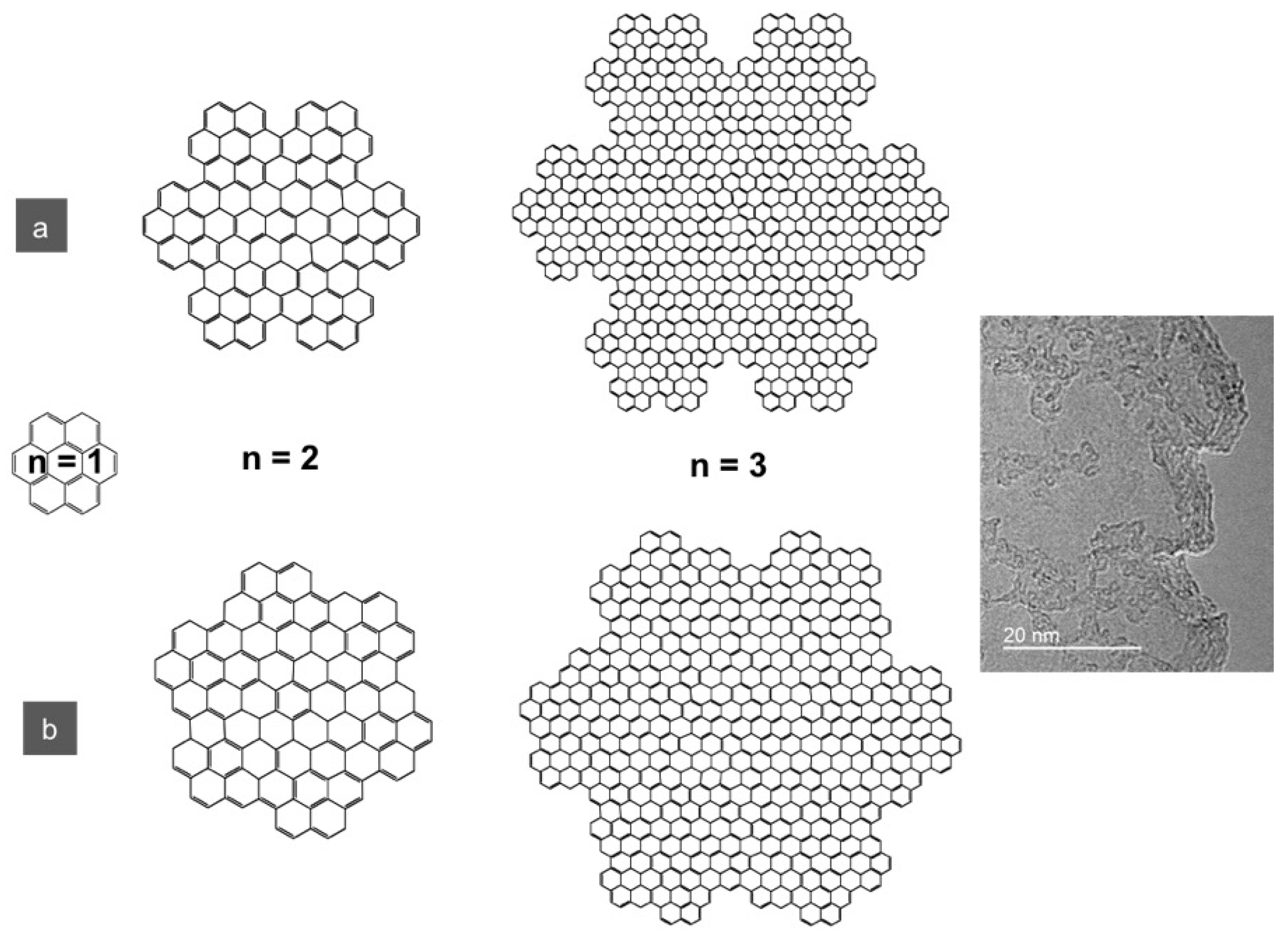
1. Introduction
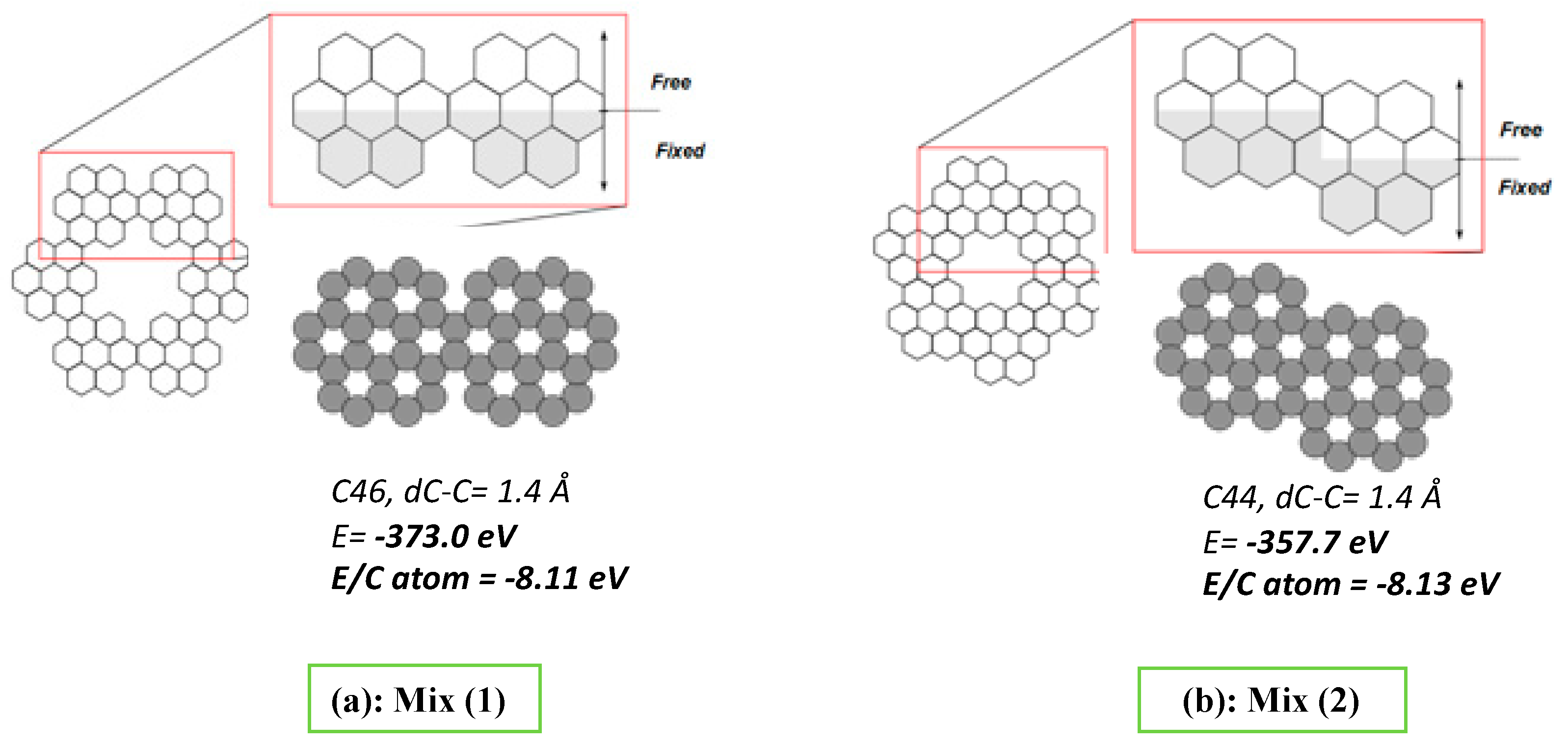
2. Materials and Methods
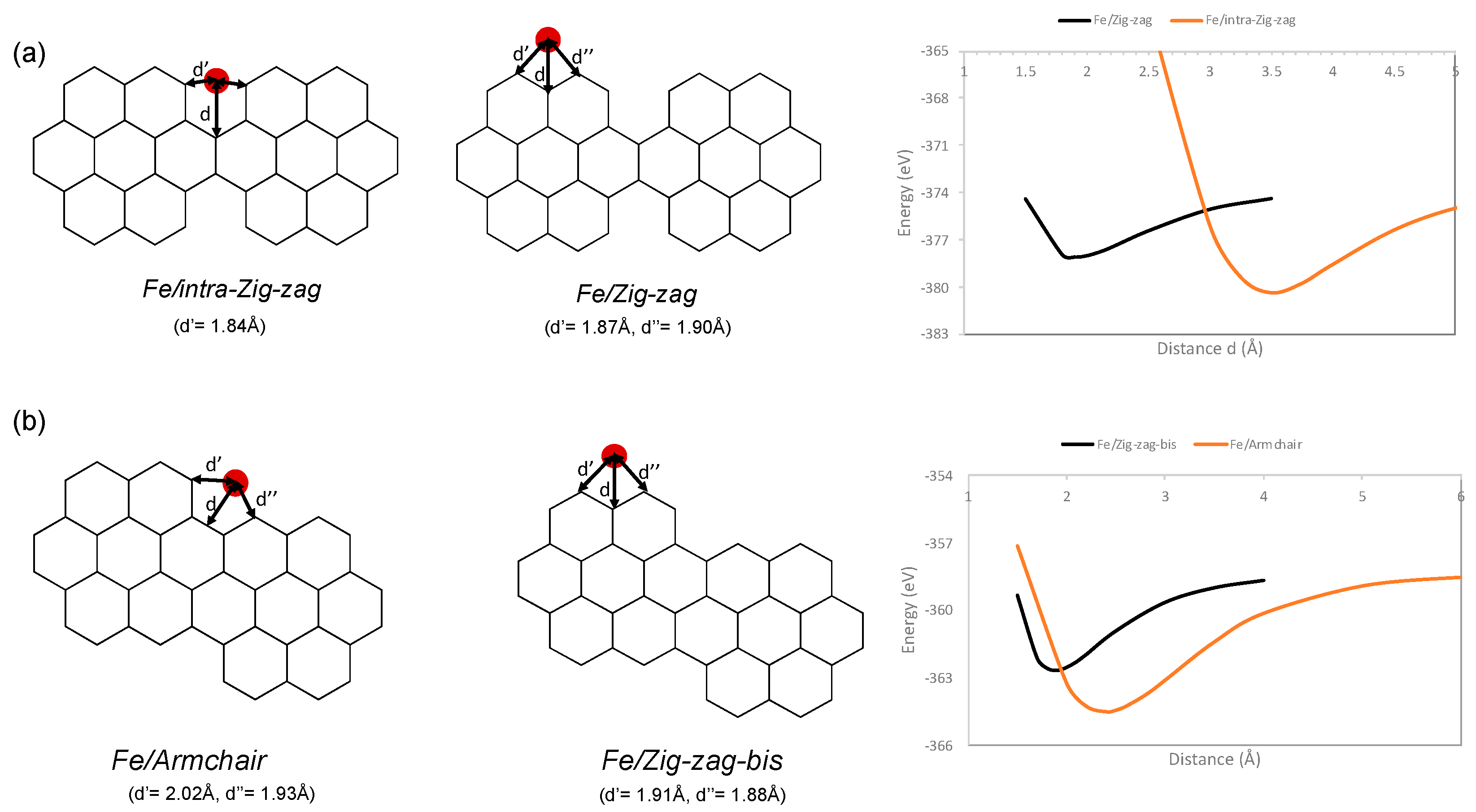
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Delplace, P.; Montambaux, G. WKB analysis of edge states in graphene in a strong magnetic field. Phys. Rev. B 2010, 82, 205412. [Google Scholar] [CrossRef]
- Park, C.; Yang, H.; Mayne, A.J.; Dujardin, G.; Seo, S.; Kuk, Y.; Ihm, J.; Kim, G. Formation of unconventional standing waves at graphene edges by valley mixing and pseudospin rotation. Proc. Natl. Acad. Sci. USA 2011, 108, 18622–18625. [Google Scholar] [CrossRef]
- Yamijala, S.S.R.K.C.; Bandyopadhyay, A.; Pati, S.K. Electronic properties of zigzag, armchair and their hybrid quantum dots of graphene and boron-nitride with and without substitution: A DFT study. Chem. Phys. Lett. 2014, 603, 28–32. [Google Scholar] [CrossRef]
- Sk, M.A.; Huang, L.; Chen, P.; Lim, K.H. Controlling armchair and zigzag edges in oxidative cutting of graphene. J. Mater. Chem. C 2016, 4, 6539–6545. [Google Scholar] [CrossRef]
- Klein, D.J. Graphitic polymer strips with edge states. Chem. Phys. Lett. 1994, 217, 261–265. [Google Scholar] [CrossRef]
- He, K.; Robertson, A.W.; Lee, S.; Yoon, E.; Lee, G.-D.; Warner, J.-H. Extended Klein Edges in Graphene. ACS Nano 2014, 8, 12272–12279. [Google Scholar] [CrossRef]
- Wagner, P.; Ivanovskaya, V.V.; Melle-Franco, M.; Humbert, B.; Adjizian, J.-J.; Briddon, P.R.; Ewels, C.P. Stable hydrogenated graphene edge types: Normal and reconstructed Klein edges. Phys. Rev. B 2013, 88, 094106. [Google Scholar] [CrossRef]
- Zhang, X.; Yazyev, O.V.; Feng, J.; Xie, L.; Tao, C.; Chen, Y.-C.; Jiao, L.; Pedramrazi, Z.; Zettl, A.; Louie, S.G.; et al. Experimentally Engineering the Edge Termination of Graphene Nanoribbons. ACS Nano 2013, 7, 198–202. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Lee, G.D.; Robertson, A.W.; Yoon, E.; Warner, J.H. Hydrogen-free graphene edges. Nat. Commun. 2014, 5, 3040. [Google Scholar] [CrossRef]
- Chełmecka, E.; Pasterny, K.; Kupka, T.; Stobiński, L. DFT studies of COOH tip-functionalized zigzag and armchair single wall carbon nanotubes. J. Mol. Model. 2012, 18, 2241–2246. [Google Scholar] [CrossRef] [PubMed]
- Chełmecka, E.; Pasterny, K.; Kupka, T.; Stobiński, L. OH-functionalized open-ended armchair single-wall carbon nanotubes (SWCNT) studied by density functional theory. J. Mol. Model. 2012, 18, 1463–1472. [Google Scholar] [CrossRef] [PubMed]
- Gusynin, V.P.; Miransky, V.A.; Sharapov, S.G.; Shovkovy, I.A. Edge states, mass and spin gaps, and quantum Hall effect in graphene. Phys. Rev. B 2008, 77, 205409. [Google Scholar] [CrossRef]
- Santana, A.; Popov, A.M.; Bichoutskaia, E. Stability and dynamics of vacancy in graphene flakes: Edge effects. Chem. Phys. Lett. 2013, 557, 80–87. [Google Scholar] [CrossRef][Green Version]
- Terrones, M.; Botello-Méndez, A.R.; Campos-Delgado, J.; López-Urías, F.; Vega-Cantú, Y.I.; Rodríguez-Macías, F.J.; Elías, A.L.; Muñoz-Sandoval, E.; Cano-Márquez, A.G.; Charlier, J.-C.; et al. Graphene and graphite nanoribbons: Morphology, properties, synthesis, defects and applications. Nano Today 2010, 5, 351–372. [Google Scholar] [CrossRef]
- Yang, X.; Dou, X.; Rouhanipour, A.; Zhi, L.; Räder, H.J.; Müllen, K. Two-Dimensional Graphene Nanoribbons. J. Am. Chem. Soc. 2008, 130, 4216–4217. [Google Scholar] [CrossRef]
- Dössel, L.; Gherghel, L.; Feng, X.; Müllen, K. Graphene Nanoribbons by Chemists: Nanometer-Sized, Soluble, and Defect-Free. Angew. Chem. Int. Ed. 2011, 50, 2540–2543. [Google Scholar] [CrossRef]
- Ruffieux, P.; Wang, S.; Yang, B.; Sánchez-Sánchez, C.; Liu, J.; Dienel, T.; Talirz, L.; Shinde, P.; Pognedoli, C.A.; Passerone, D.; et al. On-surface synthesis of graphene nanoribbons with zigzag edge topology. Nature 2016, 531, 489–492. [Google Scholar] [CrossRef]
- Feng, J.; Li, W.; Qian, X.; Qi, J.; Qi, L.; Li, J. Patterning of graphene. Nanoscale 2012, 4, 4883–4899. [Google Scholar] [CrossRef]
- Schäffel, F.; Warner, J.H.; Bachmatiuk, A.; Rellinghaus, B.; Büchner, B.; Schultz, L.; Rümmeli, M.H. Shedding Light on the Crystallographic Etching of Multi-Layer Graphene at the Atomic Scale. Nano Res. 2009, 2, 695–705. [Google Scholar] [CrossRef]
- Baaziz, W.; Melinte, G.; Ersen, O.; Pham-Huu, C.; Janowska, I. Effect of nitriding/nanostructuration of few layer graphene supported iron-based particles; Catalyst in graphene etching and carbon nanofilament growth. PhysChemChemPhys 2014, 16, 15988–15993. [Google Scholar] [CrossRef]
- Geng, D.; Wu, B.; Guo, Y.; Luo, B.; Xue, Y.; Chen, J.; Yu, G.; Liu, Y. Fractal Etching of Graphene. J. Am. Chem. Soc. 2013, 135, 6431–6434. [Google Scholar] [CrossRef]
- Geng, D.; Wang, H.; Wan, Y.; Xu, Z.; Luo, B.; Xu, J.; Yu, G. Direct Top-Down Fabrication of Large-Area Graphene Arrays by an In Situ Etching Method. Adv. Mater. 2015, 27, 4195–4199. [Google Scholar] [CrossRef]
- Janowska, I.; Lafjah, M.; Papaefthymiou, V.; Pronkin, S.; Ulhaq-Bouillet, C. Edges fractal approach in graphene-Defects density gain. Carbon 2017, 123, 395–401. [Google Scholar] [CrossRef]
- Banhart, F.; Kotakoski, J.; Krasheninnikov, A.V. Structural Defects in Graphene. ACS Nano 2010, 5, 26–41. [Google Scholar] [CrossRef]
- Su, D.S.; Perathoner, S.; Centi, G. Nanocarbons for the Development of Advanced Catalysts. Chem. Rev. 2012, 113, 5782–5816. [Google Scholar] [CrossRef] [PubMed]
- Luo, G.; Liu, L.; Zhang, J.; Li, G.; Wang, B.; Zhao, J. Hole Defects and Nitrogen Doping in Graphene: Implication for Supercapacitor Applications. ACS Appl. Mater. Interfaces 2013, 5, 11184–11193. [Google Scholar] [CrossRef] [PubMed]
- Yuan, W.; Zhou, Y.; Li, Y.; Li, C.; Peng, H.; Zhang, J.; Liu, Z.; Dai, L.; Shi, G. The edge- and basal-plane-specific electrochemistry of a single-layer graphene sheet. Sci. Rep. 2013, 3, 2248. [Google Scholar] [CrossRef]
- Shen, A.; Zou, Y.; Wang, Q.; Dryfe, R.A.W.; Huang, X.; Dou, S.; Dai, L.; Wang, S. Oxygen Reduction Reaction in a Droplet on Graphite: Direct Evidence that the Edge Is More Active than the Basal Plane. Angew. Chem. Int. Ed. 2014, 53, 10804–10808. [Google Scholar] [CrossRef]
- Ricciardella, F.; Vollebregt, S.; Polichetti, T.; Miscuglio, M.; Alfano, B.; Miglietta, M.L.; Massera, E.; Di Francia, G.; Sarro, P.M. Effects of Graphene Defects on Gas Sensing Properties Towards NO2 Detection. Nanoscale 2017, 9, 6085–6093. [Google Scholar] [CrossRef]
- Janowska, I.; Moldovan, M.-S.; Ersen, O.; Bulou, H.; Chizari, K.; Ledoux, M.-J.; Pham-Huu, C. High-temperature stability of platinum nanoparticles on few-layer graphene investigated by in-situ HR-TEM. Nano Res. 2011, 4, 511–521. [Google Scholar] [CrossRef]
- Serp, P.; Pham, M.D. Supported Metal Single Atom Catalysis; Wiley-VCH GmbH: Weinheim, Germany, 2022. [Google Scholar]
- Zhao, J.; Deng, Q.; Avdoshenko, S.M.; Fu, L.; Eckert, J.; Rümmeli, M.H. Direct in situ observations of single Fe atom catalytic processes and anomalous diffusion at graphene edges. Proc. Natl. Acad. Sci. USA 2014, 111, 15641–15646. [Google Scholar] [CrossRef] [PubMed]
- Zhang, T.; Ding, K. Hierarchical fractal structure of perfect single-layer graphene. Front. Mech. Eng. 2013, 8, 371–382. [Google Scholar] [CrossRef]
- Dai, Y.-H. A perfect example for the BFGS method. Math. Program. Ser. A 2013, 138, 501–530. [Google Scholar] [CrossRef]
- Dennis, J.E.; Schnabel, R.B. Numerical Methods for Unconstrained Optimization and Nonlinear Equations; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1996. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aloui, L.; Dintzer, T.; Janowska, I. Fe Atom—Mixed Edges Fractal Graphene via DFT Calculation. ChemEngineering 2022, 6, 79. https://doi.org/10.3390/chemengineering6050079
Aloui L, Dintzer T, Janowska I. Fe Atom—Mixed Edges Fractal Graphene via DFT Calculation. ChemEngineering. 2022; 6(5):79. https://doi.org/10.3390/chemengineering6050079
Chicago/Turabian StyleAloui, Lobna, Thierry Dintzer, and Izabela Janowska. 2022. "Fe Atom—Mixed Edges Fractal Graphene via DFT Calculation" ChemEngineering 6, no. 5: 79. https://doi.org/10.3390/chemengineering6050079
APA StyleAloui, L., Dintzer, T., & Janowska, I. (2022). Fe Atom—Mixed Edges Fractal Graphene via DFT Calculation. ChemEngineering, 6(5), 79. https://doi.org/10.3390/chemengineering6050079







