A Hill Equation for Solid Specific Heat Capacity Calculation
Abstract
:1. Introduction
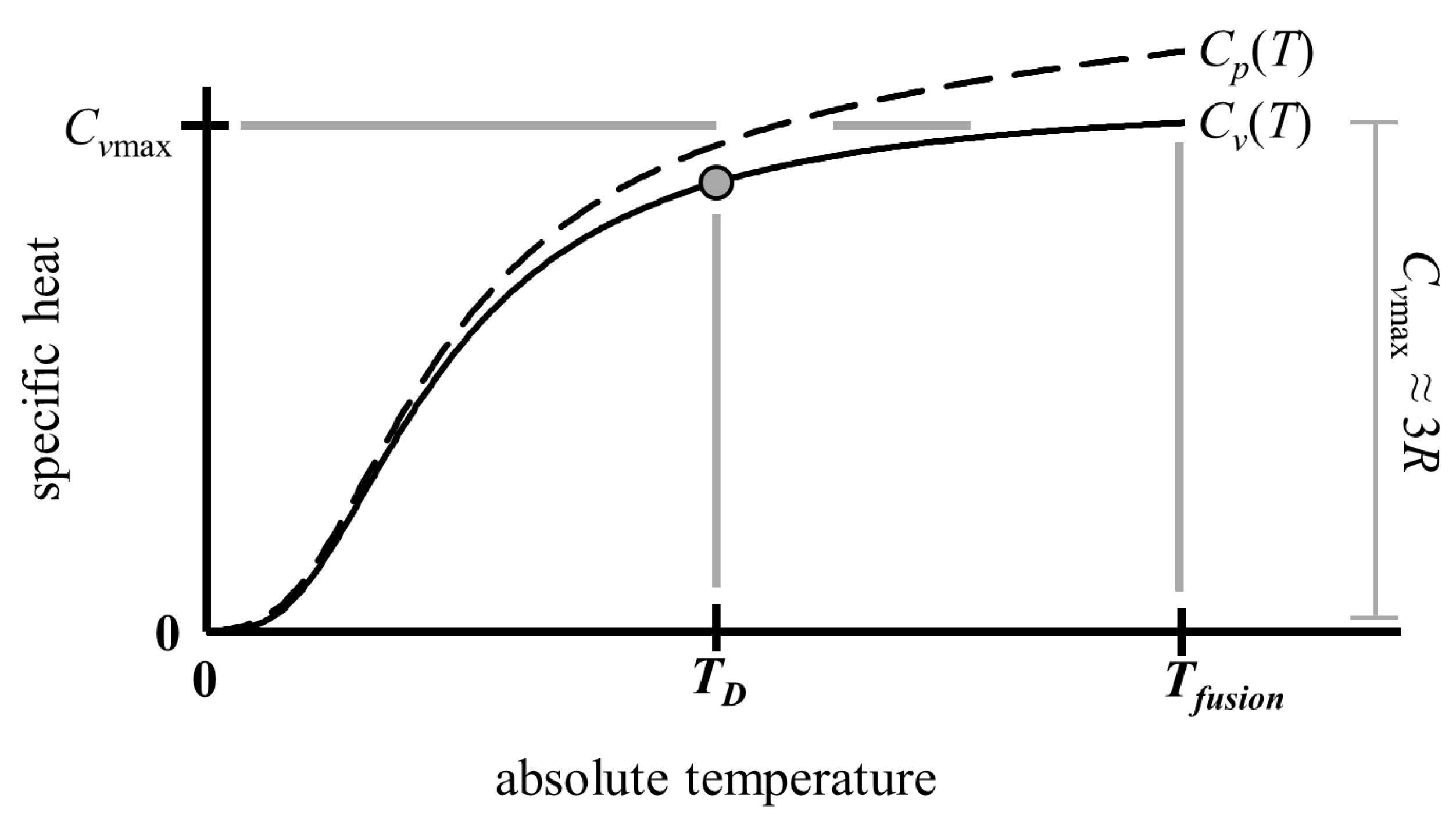
2. Materials and Methods
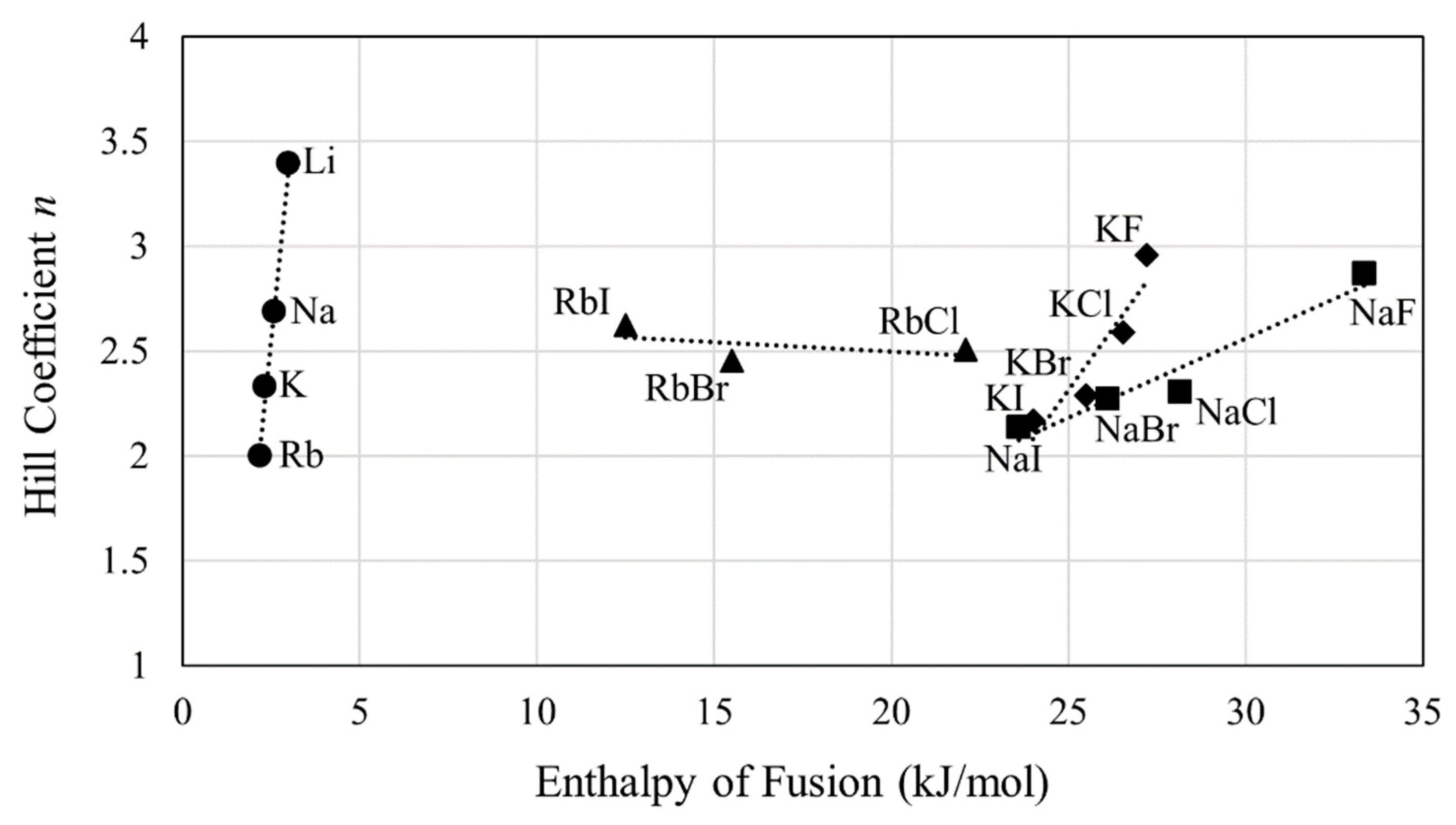
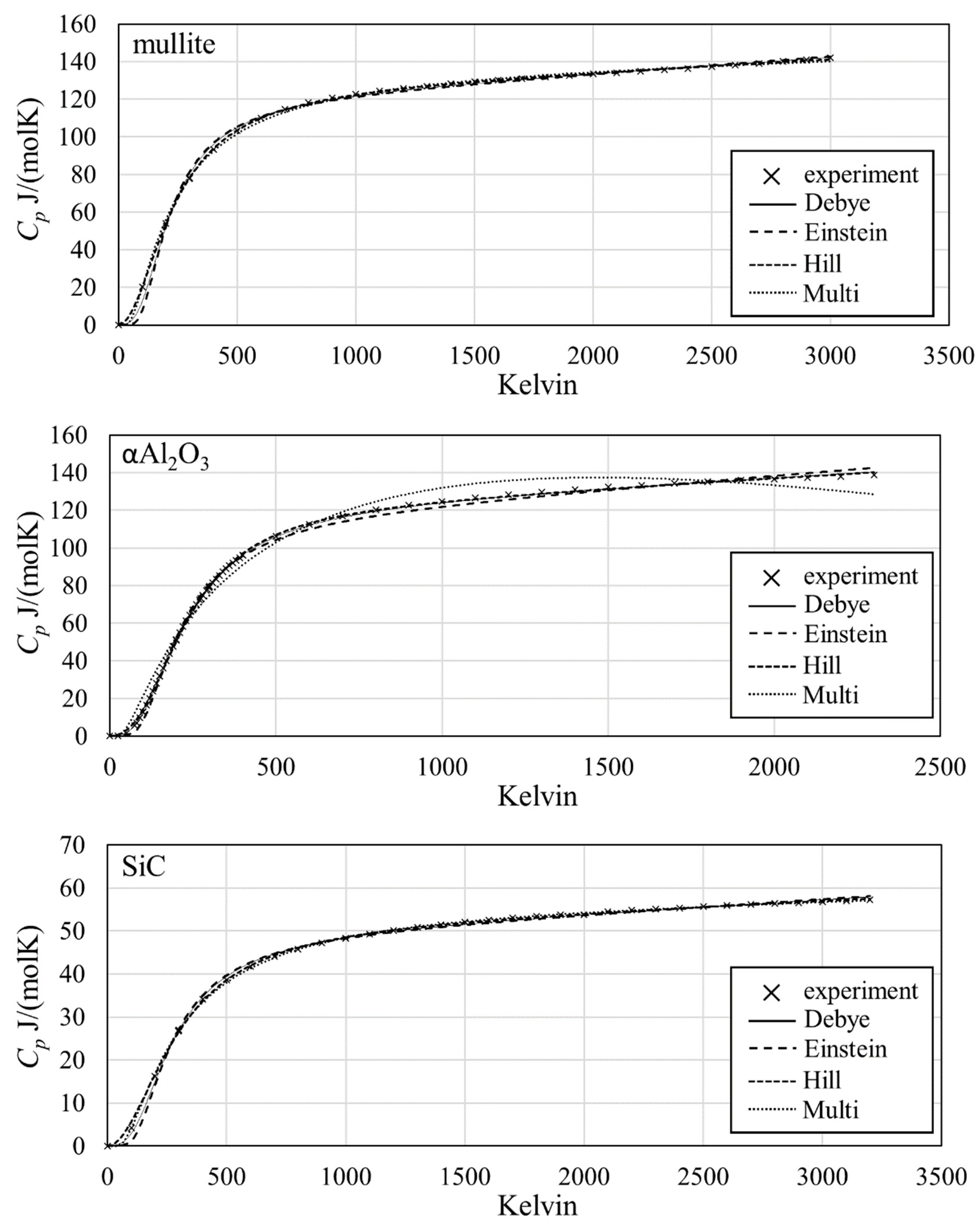
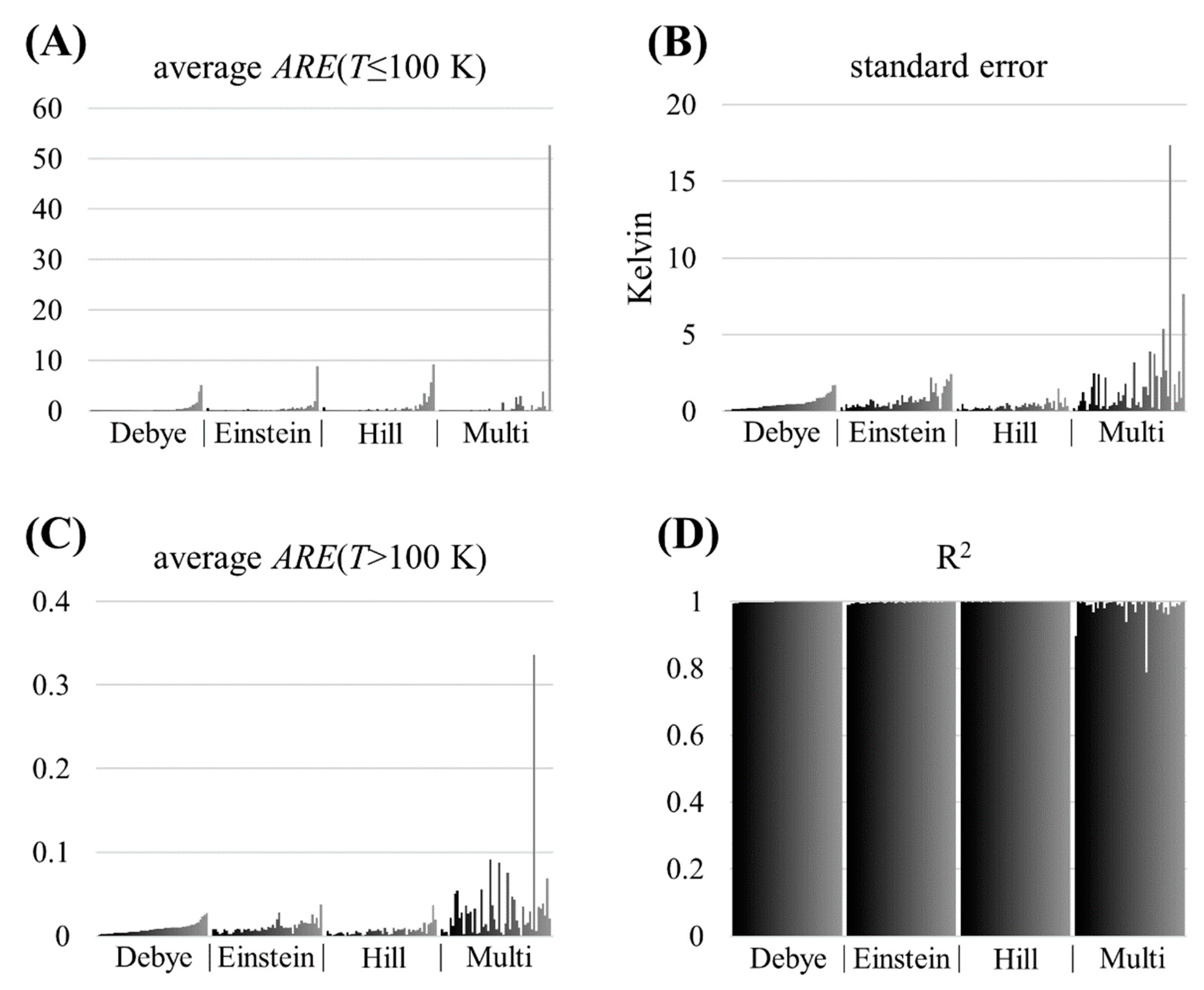
3. Results
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Symbol | Units | Definition |
| α | Kelvin−1 | coefficient of isobaric thermal expansion |
| a | fitted parameter of the empirical multilinear model | |
| ARE | unitless | absolute relative error |
| b | fitted parameter of the empirical multilinear model | |
| c | fitted parameter of the empirical multilinear model | |
| Cp(T) | J/(mole·Kelvin) | constant pressure temperature dependent solid heat capacity |
| Cp,exp(Ti) | J/(mole·Kelvin) | specific heat observed in experiment at temperature Ti |
| Cvmax | J/(mole·Kelvin) | constant-volume solid heat capacity as near melting |
| Cv(T) | J/(mole·Kelvin) | constant-volume temperature-dependent solid heat capacity |
| d | fitted parameter of the empirical multilinear model | |
| D | [Joules]n | deabsorption constant |
| ε | Joules/mole | quantitized energy level within the Einstein Solid |
| k | integer | number of datapoints |
| kB | Joules/Kelvin | Boltzmann constant |
| K | Kelvinn | dissociation constant |
| KT | Pascals | isothermal bulk modulus |
| l | integer | number of fitted parameters in a given heat capacity model |
| m | J/(mole·Kelvin2) | fitted slope |
| n | unitless | Hill Coefficient |
| Q | unitless | partition function |
| R | J/(mole·Kelvin) | gas constant |
| T | Kelvin | absolute temperature |
| TD | Kelvin | Debye temperature |
| Tfusion | Kelvin | Temperature of solid fusion (phase change) |
| Ti | Kelvin | The ith temperature in an experimental dataset |
| U | Joules/mole | internal energy |
| V(T) | m3/mole | temperature-dependent mole volume |
| SE | J/(mole·Kelvin) | standard error of the estimate |
Appendix B
References
- Chen, C.-C.; Mathias, P.M. Applied Thermodynamics for Process Modeling. Am. Inst. Chem. Eng. AIChE J. 2002, 48, 194. [Google Scholar] [CrossRef]
- Corriou, J.-P.; Assaf, J.-C. Special Issue on “Chemical Process Design, Simulation and Optimization”; MDPI: Basel, Switzerland, 2020; Volume 8, p. 1596. [Google Scholar]
- Asprion, N.; Bortz, M. Process Modeling, Simulation and Optimization: From Single Solutions to a Multitude of Solutions to Support Decision Making. Chem. Ing. Tech. 2018, 90, 1727–1738. [Google Scholar] [CrossRef]
- Rhodes, C.L. The Process Simulation Revolution: Thermophysical Property Needs and Concerns. J. Chem. Eng. Data 1996, 41, 947–950. [Google Scholar] [CrossRef]
- Hendriks, E.; Kontogeorgis, G.M.; Dohrn, R.; de Hemptinne, J.-C.; Economou, I.G.; Zilnik, L.F.; Vesovic, V. Industrial Requirements for Thermodynamics and Transport Properties. Ind. Eng. Chem. Res. 2010, 49, 11131–11141. [Google Scholar] [CrossRef]
- Wang, Y.; Shang, S.-L.; Fang, H.; Liu, Z.-K.; Chen, L.-Q. First-Principles Calculations of Lattice Dynamics and Thermal Properties of Polar Solids. NPJ Comput. Mater. 2016, 2, 1–10. [Google Scholar] [CrossRef]
- Nath, P.; Plata, J.J.; Usanmaz, D.; Al Orabi, R.A.R.; Fornari, M.; Nardelli, M.B.; Toher, C.; Curtarolo, S. High-Throughput Prediction of Finite-Temperature Properties Using the Quasi-Harmonic Approximation. Comput. Mater. Sci. 2016, 125, 82–91. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.-F.; Lu, X.-Z.; Tennessen, E.; Rondinelli, J.M. An Efficient Ab-Initio Quasiharmonic Approach for the Thermodynamics of Solids. Comput. Mater. Sci. 2016, 120, 84–93. [Google Scholar] [CrossRef] [Green Version]
- Mathias, P.M. The Gibbs–Helmholtz Equation in Chemical Process Technology. Ind. Eng. Chem. Res. 2016, 55, 1076–1087. [Google Scholar] [CrossRef]
- Kang, J.W.; Diky, V.; Chirico, R.D.; Magee, J.W.; Muzny, C.D.; Abdulagatov, I.; Kazakov, A.F.; Frenkel, M. Quality Assessment Algorithm for Vapor−Liquid Equilibrium Data. J. Chem. Eng. Data 2010, 55, 3631–3640. [Google Scholar] [CrossRef]
- Kontogeorgis, G.M.; Coutsikos, P. Thirty Years with EoS/GE Models What Have We Learned? Ind. Eng. Chem. Res. 2012, 51, 4119–4142. [Google Scholar] [CrossRef] [Green Version]
- Economou, I.G.; de Hemptinne, J.-C.; Dohrn, R.; Hendriks, E.; Keskinen, K.; Baudouin, O. Industrial Use of Thermodynamics Workshop: Round Table Discussion on 8 July 2014. Chem. Eng. Res. Des. 2014, 92, 2795–2796. [Google Scholar] [CrossRef]
- Chase, M.W. National Information Standards Organization (US). NIST-JANAF Thermochemical Tables; American Chemical Society: Washington, DC, USA, 1998; Volume 9. [Google Scholar]
- Thomson, G.H. The DIPPR® Databases. Int. J. Thermophys. 1996, 17, 223–232. [Google Scholar] [CrossRef]
- Debye, P. Zur Theorie Der Spezifischen Wärmen. Ann. Phys. 1912, 344, 789–839. [Google Scholar] [CrossRef] [Green Version]
- Einstein, A. Die Plancksche Theorie Der Strahlung Und Die Theorie Der Spezifischen Wärme. Ann. Phys. 1907, 327, 180–190. [Google Scholar] [CrossRef] [Green Version]
- Abu-Eishah, S.I.; Haddad, Y.; Solieman, A.; Bajbouj, A. A New Correlation for the Specific Heat of Metals, Metal Oxides and Metal Fluorides as a Function of Temperature. Lat. Am. Appl. Res. 2004, 34, 257–265. [Google Scholar]
- Grimvall, G. Thermophysical Properties of Materials; Elsevier: Amsterdam, The Netherlands, 1999; ISBN 0-08-054286-7. [Google Scholar]
- Dulong, P.L.; Petit, A.-T. Recherches sur Quelques Points Importans de la Theorie de la Chaleur; Annales de Chimie et de Physique: Paris, France, 1819. [Google Scholar]
- Smith, J.M.; Van Ness, H.C.; Abbott, M.M. Introduction to Chemical Engineering Thermodynamics; McGraw Hill Chemical Engineering Series 632; McGraw Hill: New York, NY, USA, 1996. [Google Scholar]
- Wyman, J.; Gill, S.J.; Colosimo, A. On Thermal Transitions in Biological Macromolecules. Biophys. Chem. 1979, 10, 363–369. [Google Scholar] [CrossRef]
- Gill, S.J.; Richey, B.; Bishop, G.; Wyman, J. Generalized Binding Phenomena in an Allosteric Macromolecule. Biophys. Chem. 1985, 21, 1–14. [Google Scholar] [CrossRef]
- Cattoni, D.I.; Chara, O.; Kaufman, S.B.; González Flecha, F.L. Cooperativity in Binding Processes: New Insights from Phenomenological Modeling. PLoS ONE 2015, 10, e0146043. [Google Scholar] [CrossRef] [Green Version]
- Gopal, E. Specific Heats at Low Temperatures; Springer: Berlin, Germany, 2012; ISBN 1-4684-9081-8. [Google Scholar]
- Fei, Y.; Saxena, S.K. An Equation for the Heat Capacity of Solids. Geochim. Cosmochim. Acta 1987, 51, 251–254. [Google Scholar] [CrossRef]
- Collocott, S.J.; White, G.K. Thermal Expansion and Heat Capacity of Some Stainless Steels and FeNi Alloys. Cryogenics 1986, 26, 402–405. [Google Scholar] [CrossRef]
- Touloukian, Y.S.; Buyco, E.H. Thermophysical Properties of Matter—The TPRC Data Series, Volume 4. Specific Heat-Metallic Elements and Alloys; Thermophysical and Electronic Properties Information Analysis Center, 1971. Available online: https://onlinelibrary.wiley.com/doi/abs/10.1002/bbpc.19710751034 (accessed on 11 July 2022).
- Clark, J.; Tye, R. Thermophysical Properties Reference Data for Some Key Engineering Alloys. High Temp. High Press. 2003, 35, 1–14. [Google Scholar] [CrossRef]
- Corsan, J.M.; Mitchem, N.I. The Specific Heat of Fifteen Stainless Steels in the Temperature Range 4K-30K. Cryogenics 1979, 19, 11–16. [Google Scholar] [CrossRef]
- Corsan, J.M.; Mitchem, N.I. Specific Heat of Stainless Steels Between 4 and 300 K. In Proceedings of the 6th International Cryogenic Engineering Conference, Grenoble, France, 11–14 May 1976; pp. 342–344. [Google Scholar]
- Lee, S.H.; Kim, S.W.; Kang, K.H. Effect of Heat Treatment on the Specific Heat Capacity of Nickel-Based Alloys. Int. J. Thermophys. 2006, 27, 282–292. [Google Scholar] [CrossRef]
- Douglasr, G.T.F.T.B.; McCoskeYr, R.E.; Ginnings, D.C. Thermal Properties of Aluminum Oxide From 0 to 1200 K. J. Res. Natl. Bur. Stand. 1956, 57, 67–82. [Google Scholar]
- Kelley, K.K.; Moore, G.E. The Specific Heats at Low Temperatures of Anhydrous Chlorides of Calcium, Iron, Magnesium and Manganese1. J. Am. Chem. Soc. 1943, 65, 1264–1267. [Google Scholar] [CrossRef]
- Todd, S.S. Heat Capacities at Low Temperatures and Entropies of Magnesium and Calcium Fluorides. J. Am. Chem. Soc. 1949, 71, 4115–4116. [Google Scholar] [CrossRef]
- Roberts, L.M. The Atomic Heats of Lithium, Sodium and Potassium between 1.5 and 20 K. Proc. Phys. Soc. Sect. B 1957, 70, 744. [Google Scholar] [CrossRef]
- Raman, C.V. The Specific Heats of the Alkali Halides and Their Spectroscopic Behaviour. In Proceedings of the Indian Academy of Sciences-Section A; Springer: Berlin/Heidelberg, Germany, 1962; Volume 56, pp. 60–69. [Google Scholar]
- Berg, W.T.; Morrison, J.A. The Thermal Properties of Alkali Halide Crystals. I. The Heat Capacity of Potassium Chloride, Potassium Bromide, Potassium Iodide and Sodium Iodide between 2.8 and 270 K. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1957, 242, 467–477. [Google Scholar]
- Southard, J.C.; Nelson, R.A. Low Temperature Specific Heats. IV. The Heat Capacities of Potassium Chloride, Potassium Nitrate and Sodium Nitrate1. J. Am. Chem. Soc. 1933, 55, 4865–4869. [Google Scholar] [CrossRef]
- Kirkham, A.J.; Yates, B. The Adiabatic Measurement of the Specific Heats of Potassium Chloride and Rubidium Chloride at Low Temperatures. Cryogenics 1968, 8, 381–385. [Google Scholar] [CrossRef]
- Barron, T.H.K.; Berg, W.T.; Morrison, J.A. On the Heat Capacity of Crystalline Magnesium Oxide. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1959, 250, 70–83. [Google Scholar]
- Robie, R.A.; Hemingway, B.S. Thermodynamic Properties of Minerals and Related Substances at 298.15 K and 1 Bar (105 Pascals) Pressure and at Higher Temperatures; US Government Printing Office: Washington, DC, USA, 1995.
- Archer, D.G. Thermodynamic Properties of the NaCl+ H2O System l. Thermodynamic Properties of NaCl (Cr). J. Phys. Chem. Ref. Data 1992, 21, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Kirkham, A.J.; Yates, B. The Low-Temperature Specific Heats and Related Thermodynamic Properties of Sodium Fluoride and Caesium Bromide. J. Phys. C Solid State Phys. 1968, 1, 1162. [Google Scholar] [CrossRef]
- Munro, R.G. Material Properties of a Sintered α-SiC. J. Phys. Chem. Ref. Data 1997, 26, 1195–1203. [Google Scholar] [CrossRef]
- Smith, S.J.; Stevens, R.; Liu, S.; Li, G.; Navrotsky, A.; Boerio-Goates, J.; Woodfield, B.F. Heat Capacities and Thermodynamic Functions of TiO2 Anatase and Rutile: Analysis of Phase Stability. Am. Mineral. 2009, 94, 236–243. [Google Scholar] [CrossRef]
- Broughton, J. Process Utility Systems: Introduction to Design, Operation, and Maintenance; IChemE: New York, NY, USA, 1994; ISBN 0-85295-483-2. [Google Scholar]
- Charpentier, J.-C. Among the Trends for a Modern Chemical Engineering, the Third Paradigm: The Time and Length Multiscale Approach as an Efficient Tool for Process Intensification and Product Design and Engineering. Chem. Eng. Res. Des. 2010, 88, 248–254. [Google Scholar] [CrossRef]
- Allgöwer, F.; Zheng, A. Nonlinear Model Predictive Control; Birkhäuser: Basel, Switzerland, 2012; Volume 26, ISBN 3-0348-8407-9. [Google Scholar]
- Grossmann, I. Enterprise-wide Optimization: A New Frontier in Process Systems Engineering. AIChE J. 2005, 51, 1846–1857. [Google Scholar] [CrossRef]
- Barlow, R.; Blake, J.F. Hill Coefficients and the Logistic Equation. Trends Pharmacol. Sci. 1989, 10, 440–441. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2004; Volume 85, ISBN 0-8493-0485-7. [Google Scholar]
- Dill, K.A.; Bromberg, S.; Stigter, D. Molecular Driving Forces: Statistical Thermodynamics in Biology, Chemistry, Physics, and Nanoscience; Garland Science: New York, NY, USA, 2010; ISBN 0-203-80907-6. [Google Scholar]
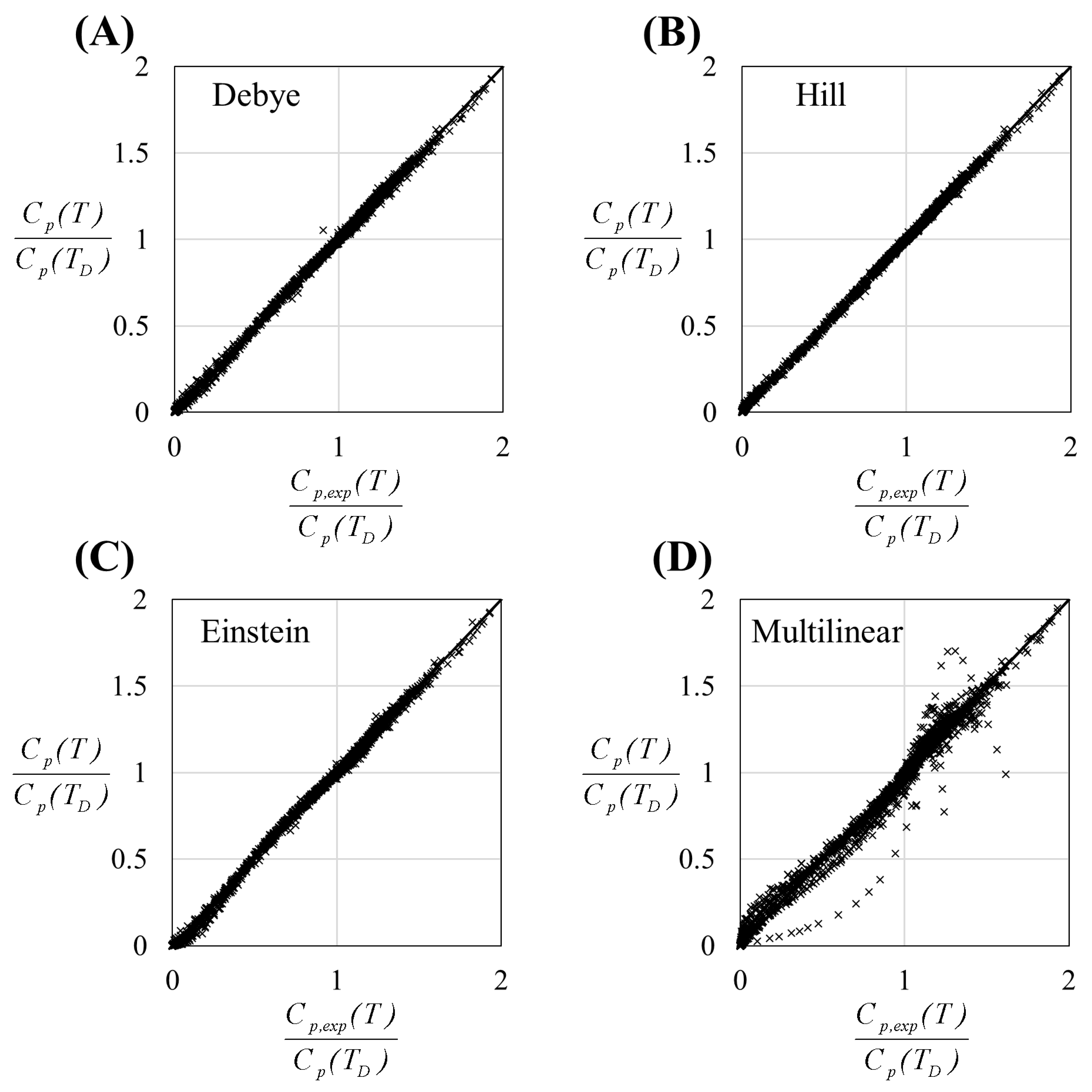

| Debye | 5.06 |
| Einstein | 0.96 |
| Hill | 1 |
| Multi | 0.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rowe, S.C.; Chubukov, B.A.; Telotte, J.C. A Hill Equation for Solid Specific Heat Capacity Calculation. ChemEngineering 2022, 6, 56. https://doi.org/10.3390/chemengineering6040056
Rowe SC, Chubukov BA, Telotte JC. A Hill Equation for Solid Specific Heat Capacity Calculation. ChemEngineering. 2022; 6(4):56. https://doi.org/10.3390/chemengineering6040056
Chicago/Turabian StyleRowe, Scott C., Boris A. Chubukov, and John C. Telotte. 2022. "A Hill Equation for Solid Specific Heat Capacity Calculation" ChemEngineering 6, no. 4: 56. https://doi.org/10.3390/chemengineering6040056
APA StyleRowe, S. C., Chubukov, B. A., & Telotte, J. C. (2022). A Hill Equation for Solid Specific Heat Capacity Calculation. ChemEngineering, 6(4), 56. https://doi.org/10.3390/chemengineering6040056





