A First Approach towards Adsorption-Oriented Physics-Informed Neural Networks: Monoclonal Antibody Adsorption Performance on an Ion-Exchange Column as a Case Study
Abstract
:1. Introduction
2. Materials and Methods
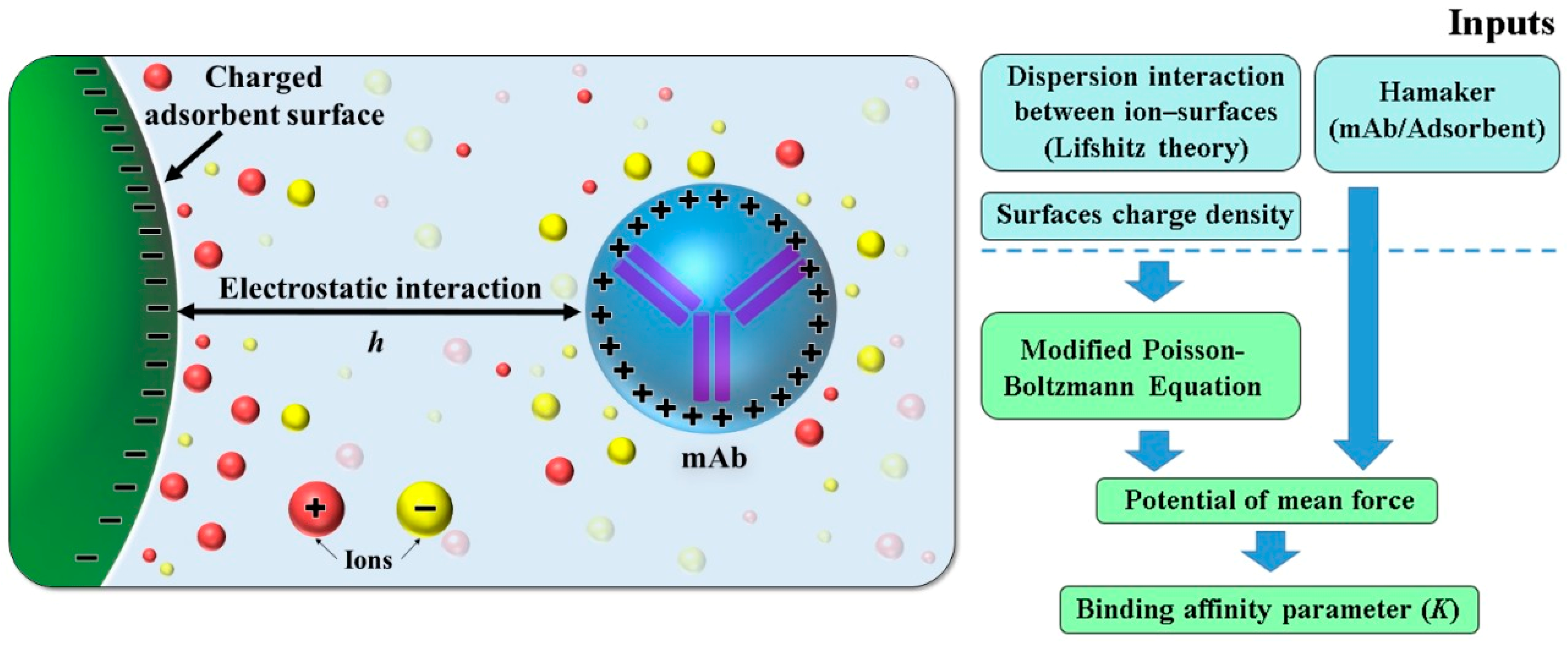
2.1. Mathematical Model for Protein Adsorption in Column Chromatography
2.2. Simulation Scenario
2.3. Physics Informed Neural Networks
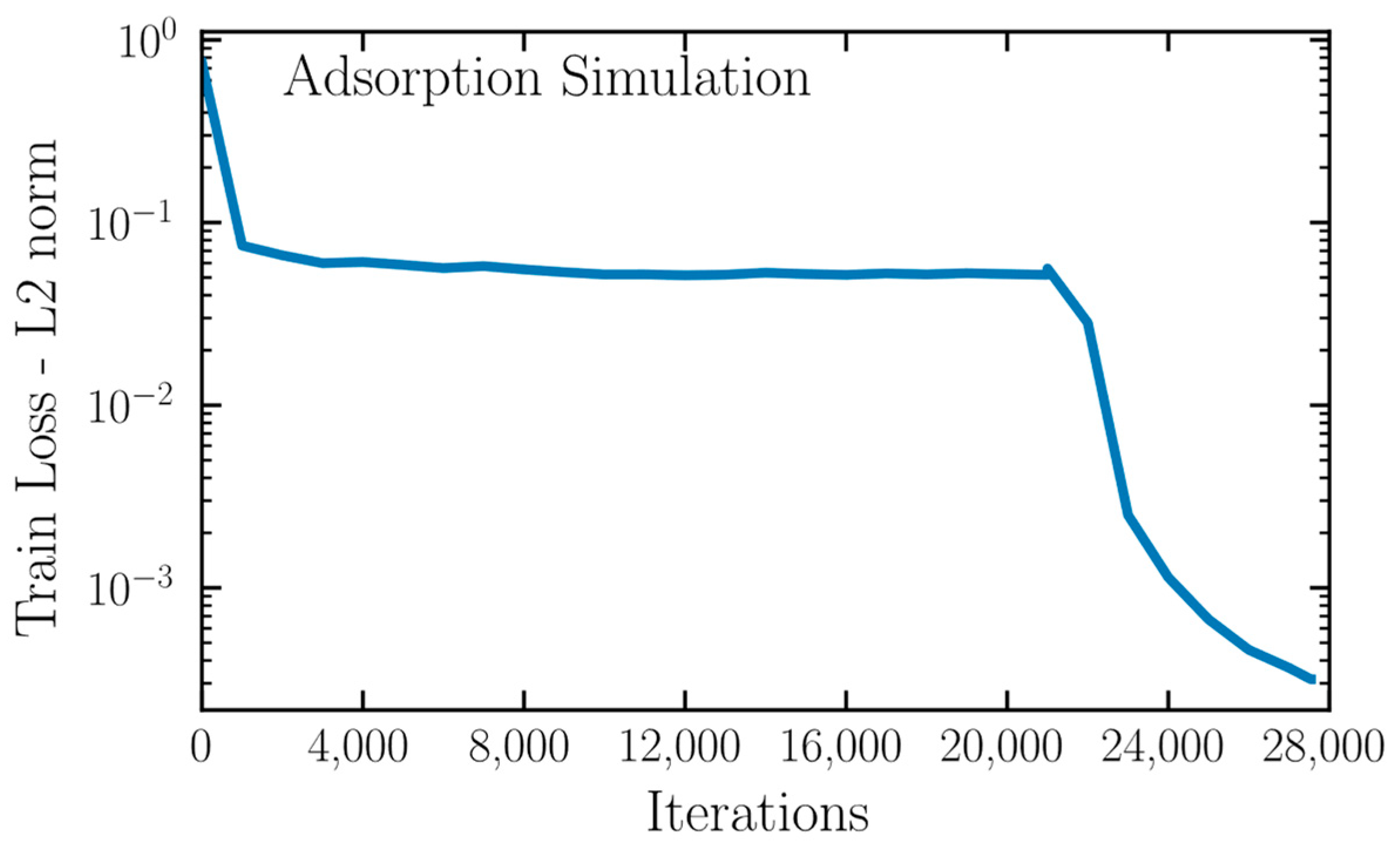
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Lagaris, I.E.; Likas, A.; Fotiadis, D.I. Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans. Neural Netw. 1998, 9, 987–1000. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Zhang, D.; Karniadakis, G.E.M. Physics-informed generative adversarial networks for stochastic differential equations. SIAM J. Sci. Comput. 2020, 42, A292–A317. [Google Scholar] [CrossRef] [Green Version]
- Nicoud, L.; Owczarz, M.; Arosio, P.; Morbidelli, M. A multiscale view of therapeutic protein aggregation: A colloid science perspective. Biotechnol. J. 2015, 10, 367–378. [Google Scholar] [CrossRef] [PubMed]
- Mehta, A.; Tse, M.L.; Fogle, J.; Len, A.; Shrestha, R.; Fontes, N.; Lebreton, B.; Wolk, B.; van Reis, R. Purifying therapeutic monoclonal antibodies. Chem. Eng. Prog. 2008, 104, S14–S20. [Google Scholar]
- Lee, J.; Liu, Z.; Chen, W.H.; Wei, J.; Kundu, R.; Adhikari, R.; Rivera, J.A.; Gillespie, P.M.; Strych, U.; Zhan, B.; et al. Process development and scale-up optimization of the SARS-CoV-2 receptor binding domain–based vaccine candidate, RBD219-N1C1. Appl. Microbiol. Biotechnol. 2021, 105, 4153–4165. [Google Scholar] [CrossRef] [PubMed]
- Guélat, B.; Ströhlein, G.; Lattuada, M.; Delegrange, L.; Valax, P.; Morbidelli, M. Simulation model for overloaded monoclonal antibody variants separations in ion-exchange chromatography. J. Chromatogr. A 2012, 1253, 32–43. [Google Scholar] [CrossRef] [PubMed]
- Gama, M.S.; Simões, M.; Rocha, E.; Lima, D.A.; Wanderley, F.; Gomes, A.; Barreto, B. A modified Poisson-Boltzmann equation applied to protein adsorption. J. Chromatogr. A 2018, 1531, 74–82. [Google Scholar] [CrossRef] [PubMed]
- Gama, M.S.; Barreto, A.G.; Tavares, F.W. The binding interaction of protein on a charged surface using Poisson-Boltzmann equation: Lysozyme adsorption onto SBA-15. Adsorption 2021, 27, 1137–1148. [Google Scholar] [CrossRef]
- Guélat, B.; Ströhlein, G.; Lattuada, M.; Morbidelli, M. Electrostatic model for protein adsorption in ion-exchange chromatography and application to monoclonal antibodies, lysozyme and chymotrypsinogen A. J. Chromatogr. A 2010, 1217, 5610–5621. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Meng, X.; Mao, Z.; Karniadakis, G.E. DeepXDE: A Deep Learning Library for Solving Differential Equations. SIAM Rev. 2021, 63, 208–228. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics Informed Deep Learning (Part I): Data-driven Discovery of Nonlinear Partial Differential Equations. arXiv 2017, arXiv:1711.10561. [Google Scholar]
- Jagtap, A.D.; Kawaguchi, K.; Em Karniadakis, G. Locally adaptive activation functions with slope recovery for deep and physics-informed neural networks. Proc. R. Soc. A Math. Phys. Eng. Sci. 2020, 476, 20200334. [Google Scholar] [CrossRef] [PubMed]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A Limited Memory Algorithm for Bound Constrained Optimization. SIAM J. Sci. Comput. 1994, 16, 1190–1208. [Google Scholar] [CrossRef]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]


| Parameter | Description | Value |
|---|---|---|
| Number of layers | 6 | |
| Number of neurons per layer | 80 | |
| Weights of terms in the loss function | (1.0, 1.0, adaptive,1.0) | |
| Collocation points of PDE, boundary, and initial condition | (2500, 800, 500) | |
| Learning rate of Adam algorithm | 3.0 × 10−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santana, V.V.; Gama, M.S.; Loureiro, J.M.; Rodrigues, A.E.; Ribeiro, A.M.; Tavares, F.W.; Barreto, A.G., Jr.; Nogueira, I.B.R. A First Approach towards Adsorption-Oriented Physics-Informed Neural Networks: Monoclonal Antibody Adsorption Performance on an Ion-Exchange Column as a Case Study. ChemEngineering 2022, 6, 21. https://doi.org/10.3390/chemengineering6020021
Santana VV, Gama MS, Loureiro JM, Rodrigues AE, Ribeiro AM, Tavares FW, Barreto AG Jr., Nogueira IBR. A First Approach towards Adsorption-Oriented Physics-Informed Neural Networks: Monoclonal Antibody Adsorption Performance on an Ion-Exchange Column as a Case Study. ChemEngineering. 2022; 6(2):21. https://doi.org/10.3390/chemengineering6020021
Chicago/Turabian StyleSantana, Vinicius V., Marlon S. Gama, Jose M. Loureiro, Alírio E. Rodrigues, Ana M. Ribeiro, Frederico W. Tavares, Amaro G. Barreto, Jr., and Idelfonso B. R. Nogueira. 2022. "A First Approach towards Adsorption-Oriented Physics-Informed Neural Networks: Monoclonal Antibody Adsorption Performance on an Ion-Exchange Column as a Case Study" ChemEngineering 6, no. 2: 21. https://doi.org/10.3390/chemengineering6020021
APA StyleSantana, V. V., Gama, M. S., Loureiro, J. M., Rodrigues, A. E., Ribeiro, A. M., Tavares, F. W., Barreto, A. G., Jr., & Nogueira, I. B. R. (2022). A First Approach towards Adsorption-Oriented Physics-Informed Neural Networks: Monoclonal Antibody Adsorption Performance on an Ion-Exchange Column as a Case Study. ChemEngineering, 6(2), 21. https://doi.org/10.3390/chemengineering6020021