Simulation-Based Defect Engineering in “α-Spodumene”
Abstract
1. Introduction
2. Computational Methods
3. Results
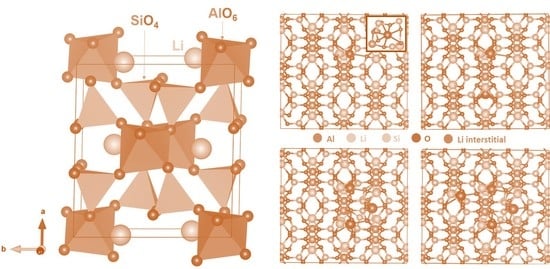
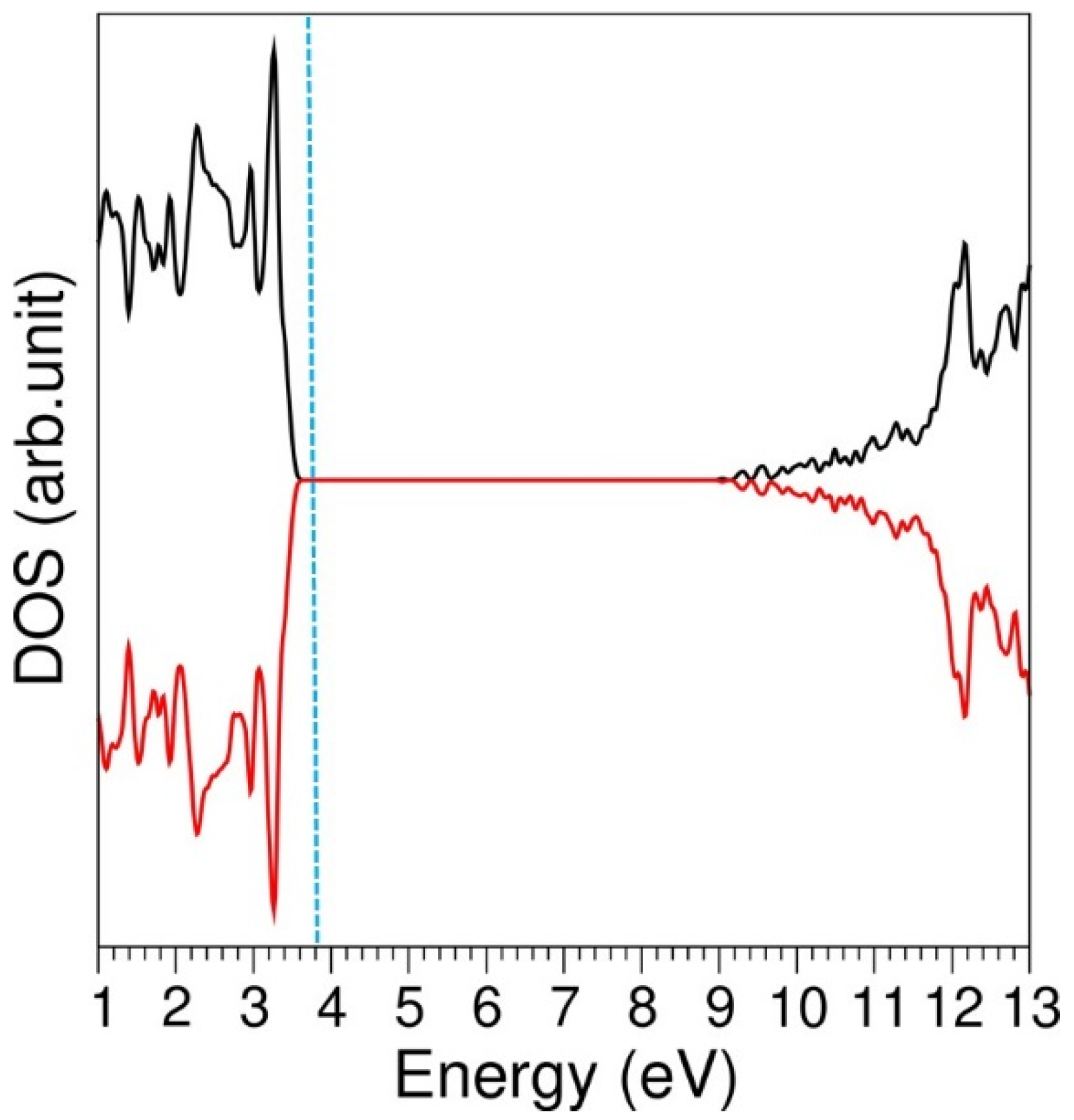
3.1. Computational Modelling of α-LiAlSi2O6
3.2. Intrinsic Defects
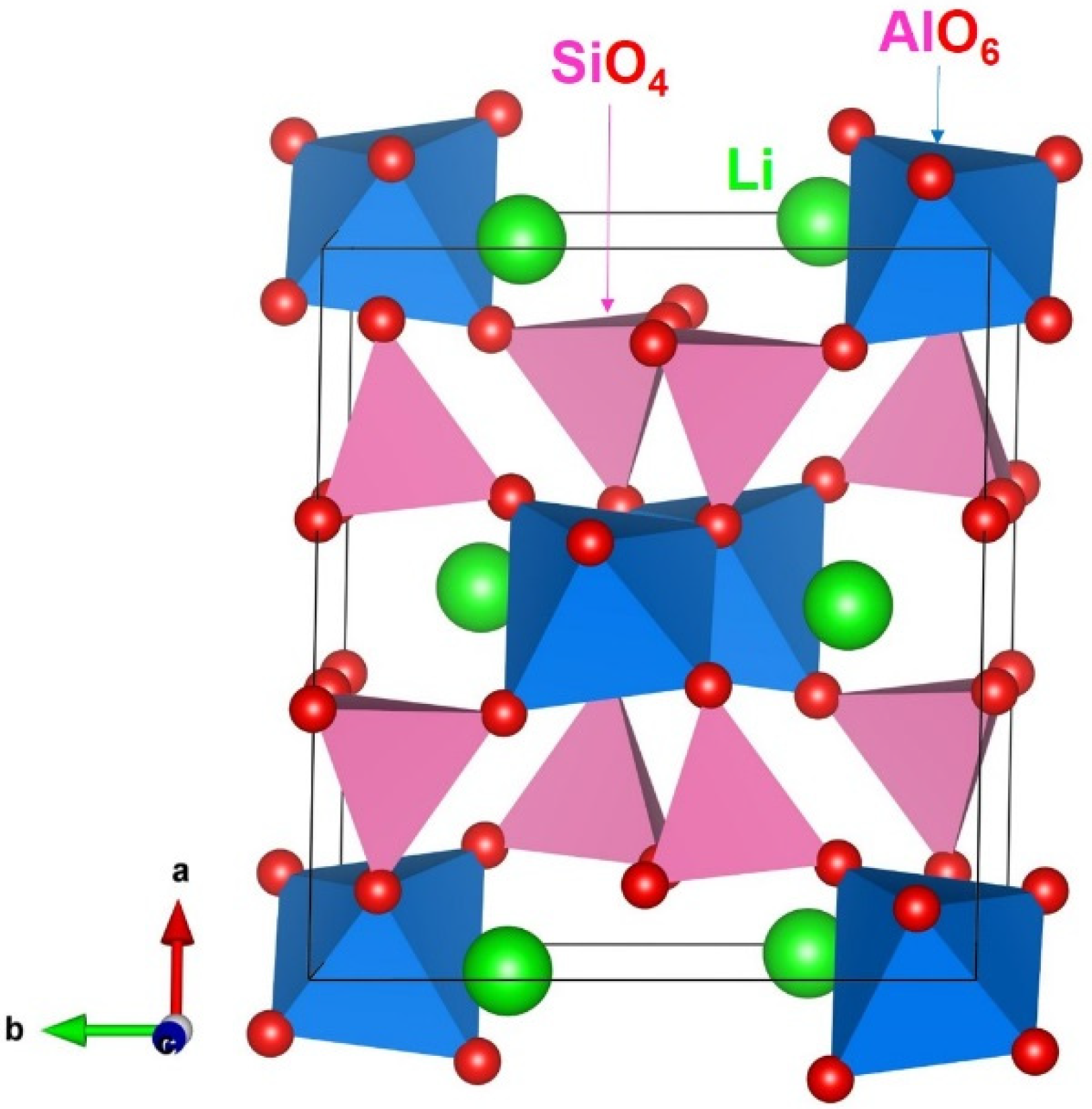
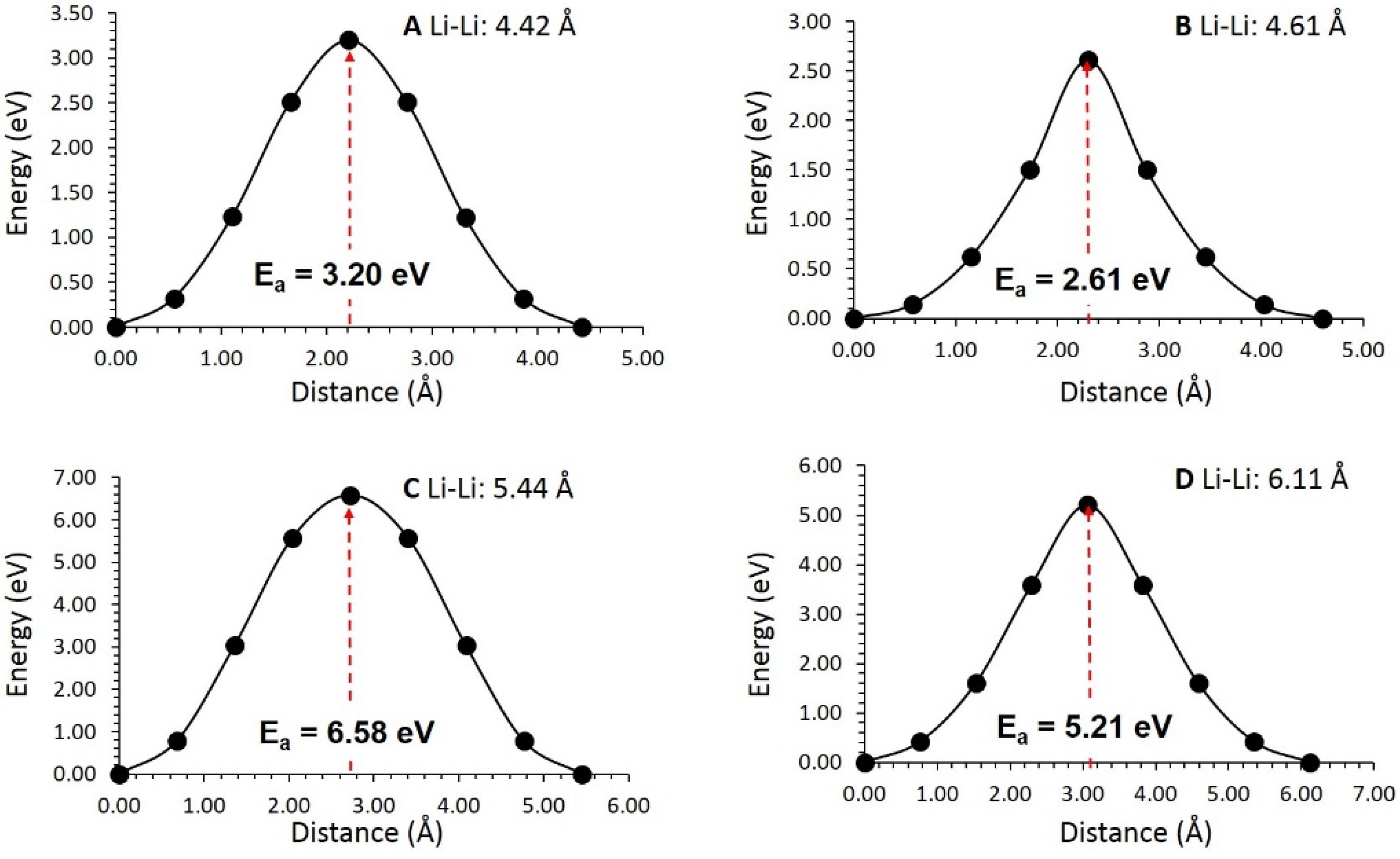
3.3. Li-Ion Diffusion
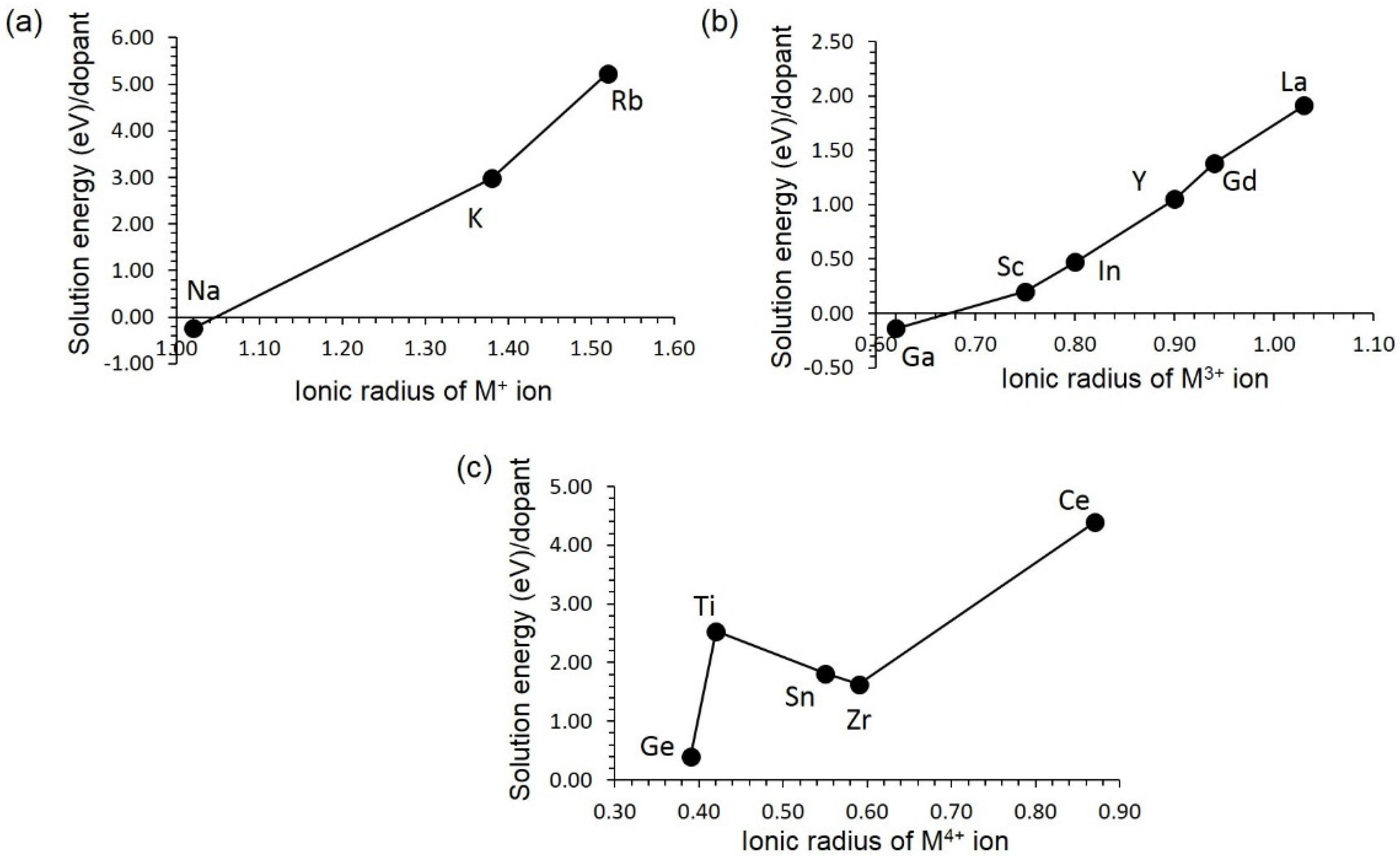
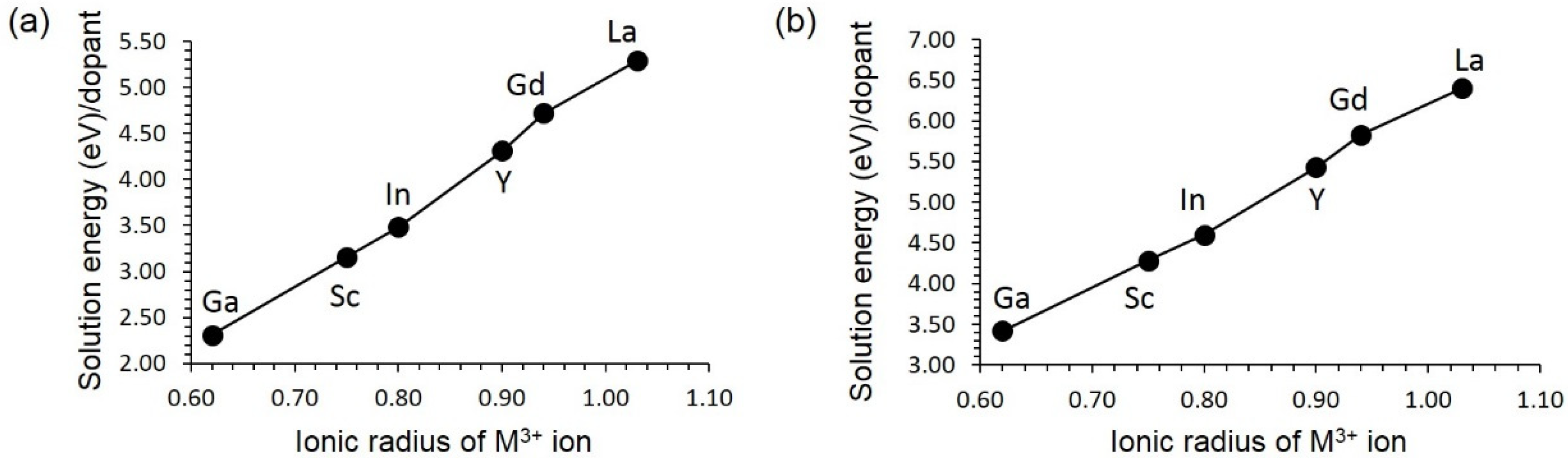
3.4. Solution of Dopants
3.4.1. Isovalent Doping
3.4.2. Aliovalent Doping
3.5. Incorporation of Li into LiAlSi2O6
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dessemond, C.; Lajoie-Leroux, F.; Soucy, G.; Laroche, N.; Magnan, J.-F. Spodumene: The Lithium Market, Resources and Processes. Minerals 2019, 9, 334. [Google Scholar] [CrossRef]
- Benson, T.R.; Coble, M.A.; Rytuba, J.J.; Mahood, G.A. Lithium enrichment in intracontinental rhyolite magmas leads to Li deposits in caldera basins. Nat. Commun. 2017, 8, 270. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Zhou, S.; Tang, C.; Zhai, Q.; Zhang, X.; Wang, R. Li-B Alloy as an Anode Material for Stable and Long Life Lithium Metal Batteries. Energies 2018, 11, 2512. [Google Scholar] [CrossRef]
- Oruch, R.; Elderbi, M.A.; Khattab, H.A.; Pryme, I.F.; Lund, A. Lithium: A review of pharmacology, clinical uses, and toxicity. Eur. J. Pharmacol. 2014, 740, 464–473. [Google Scholar] [CrossRef]
- Beskin, S.M.; Marin, Y.B. Classification of G3ranitic Pegmatites and Pegmatite-Bearing Granitic Systems. Geol. Ore Depos. 2018, 60, 578–586. [Google Scholar] [CrossRef]
- Sundelius, H.W. The Peg Claims spodumene pegmatites, Maine. Econ. Geol. 1963, 58, 84–106. [Google Scholar] [CrossRef]
- Barros, R.; Menuge, J.F. The Origin of Spodumene Pegmatites Associated with the Leinster Granite in Southeast Ireland. Can. Miner. 2016, 54, 847–862. [Google Scholar] [CrossRef]
- Grosjean, C.; Miranda, P.H.; Perrin, M.; Poggi, P. Assessment of world lithium resources and consequences of their geographic distribution on the expected development of the electric vehicle industry. Renew. Sustain. Energy Rev. 2012, 16, 1735–1744. [Google Scholar] [CrossRef]
- Kesler, S.E.; Gruber, P.W.; Medina, P.A.; Keoleian, G.A.; Everson, M.P.; Wallington, T.J. Global lithium resources: Relative importance of pegmatite, brine and other deposits. Ore Geol. Rev. 2012, 48, 55–69. [Google Scholar] [CrossRef]
- Jie, Z.; Weiqing, W.; Jing, L.; Yang, H.; Qiming, F.; Hong, Z. Fe(III) as an activator for the flotation of spodumene, albite, and quartz minerals. Miner. Eng. 2014, 61, 16–22. [Google Scholar] [CrossRef]
- Dessemond, C.; Soucy, G.; Harvey, J.-P.; Ouzilleau, P. Phase Transitions in the α–γ–β Spodumene Thermodynamic System and Impact of γ-Spodumene on the Efficiency of Lithium Extraction by Acid Leaching. Minerals 2020, 10, 519. [Google Scholar] [CrossRef]
- Peltosaari, O.; Tanskanen, P.; Heikkinen, E.-P.; Fabritius, T. α→γ→β-phase transformation of spodumene with hybrid microwave and conventional furnaces. Miner. Eng. 2015, 82, 54–60. [Google Scholar] [CrossRef]
- Song, Y.; Zhao, T.; He, L.; Zhao, Z.; Liu, X. A promising approach for directly extracting lithium from α-spodumene by alkaline digestion and precipitation as phosphate. Hydrometallurgy 2019, 189, 105141. [Google Scholar] [CrossRef]
- Kuganathan, N.; Srikaran, R.; Fossati, C.M.P.; Chroneos, A. Theoretical Modeling of Defects, Dopants, and Diffusion in the Mineral Ilmenite. Minerals 2019, 9, 610. [Google Scholar] [CrossRef]
- Suthaharan, S.; Iyngaran, P.; Kuganathan, N.; Chroneos, A. Defects, diffusion and dopants in the ceramic mineral “Lime- Feldspar”. J. Asian Ceram. Soc. 2021, 9, 570–577. [Google Scholar] [CrossRef]
- Yuan, K.; Lee, S.S.; Cha, W.; Ulvestad, A.; Kim, H.; Abdilla, B.; Sturchio, N.C.; Fenter, P. Oxidation induced strain and defects in magnetite crystals. Nat. Commun. 2019, 10, 703. [Google Scholar] [CrossRef] [PubMed]
- Lowitzer, S.; Wilson, D.J.; Winkler, B.; Milman, V.; Gale, J.D. Defect properties of albite. Phys. Chem. Miner. 2008, 35, 129–135. [Google Scholar] [CrossRef]
- Abdullah, A.A.; Oskierski, H.C.; Altarawneh, M.; Senanayake, G.; Lumpkin, G.; Dlugogorski, B.Z. Phase transformation mechanism of spodumene during its calcination. Miner. Eng. 2019, 140, 105883. [Google Scholar] [CrossRef]
- Salis, M. Lattice defects in natural α-spodumene. Il Nuovo Cim. D 1995, 17, 649–651. [Google Scholar] [CrossRef]
- Gale, J.D. GULP: A computer program for the symmetry-adapted simulation of solids. J. Chem. Soc. Faraday Trans. 1997, 93, 629–637. [Google Scholar] [CrossRef]
- Gale, J.D.; Rohl, A.L. The General Utility Lattice Program (GULP). Mol. Simul. 2003, 29, 291–341. [Google Scholar] [CrossRef]
- Fisher, C.A.J.; Hart Prieto, V.M.; Islam, M.S. Lithium Battery Materials LiMPO4 (M = Mn, Fe, Co, and Ni): Insights into Defect Association, Transport Mechanisms, and Doping Behavior. Chem. Mater. 2008, 20, 5907–5915. [Google Scholar] [CrossRef]
- Sauer, J.; Schroder, K.P.; Termath, V. Comparing the Acidities of Microporous Aluminosilicate and Silico-Aluminophosphate Catalysts: A Combined Quantum Mechanics-Interatomic Potential Function Study. Czech. Chem. Commun. 1998, 63, 1394. [Google Scholar] [CrossRef][Green Version]
- Jones, A.; Slater, P.R.; Islam, M.S. Local Defect Structures and Ion Transport Mechanisms in the Oxygen-Excess Apatite La9.67(SiO4)6O2.5. Chem. Mater. 2008, 20, 5055–5060. [Google Scholar] [CrossRef]
- Olson, C.L.; Nelson, J.; Islam, M.S. Defect Chemistry, Surface Structures, and Lithium Insertion in Anatase TiO2. J. Phys. Chem. B 2006, 110, 9995–10001. [Google Scholar] [CrossRef] [PubMed]
- Mott, N.F.; Littleton, M.J. Conduction in polar crystals. I. Electrolytic conduction in solid salts. Trans. Faraday Soc. 1938, 34, 485–499. [Google Scholar] [CrossRef]
- Grimes, R.W.; Busker, G.; McCoy, M.A.; Chroneos, A.; Kilner, J.A.; Chen, S.-P. The Effect of Ion Size on Solution Mechanism and Defect Cluster Geometry. Ber. Der Bunsenges. Für Phys. Chem. 1997, 101, 1204–1210. [Google Scholar] [CrossRef]
- Varotsos, P. Point defect parameters in β-PbF2 revisited. Solid State Ion. 2008, 179, 438–441. [Google Scholar] [CrossRef]
- Varotsos, P. Comparison of models that interconnect point defect parameters in solids with bulk properties. J. Appl. Phys. 2007, 101, 123503. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C, 2nd ed.; The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Sasaki, S.; Fujino, K.; Takeuchi, Y.; Sadanaga, R. On the estimation of atomic charges by the X-ray method for some oxides and silicates. Acta Crystallogr. Sect. A 1980, 36, 904–915. [Google Scholar] [CrossRef]
- Kröger, F.A.; Vink, H.J. Relations between the Concentrations of Imperfections in Crystalline Solids. In Solid State Physics; Seitz, F., Turnbull, D., Eds.; Academic Press: Cambridge, MA, USA, 1956; Volume 3, pp. 307–435. [Google Scholar]
- Armstrong, A.R.; Kuganathan, N.; Islam, M.S.; Bruce, P.G. Structure and Lithium Transport Pathways in Li2FeSiO4 Cathodes for Lithium Batteries. J. Am. Chem. Soc. 2011, 133, 13031–13035. [Google Scholar] [CrossRef]
- Liu, H.; Choe, M.-J.; Enrique, R.A.; Orvañanos, B.; Zhou, L.; Liu, T.; Thornton, K.; Grey, C.P. Effects of Antisite Defects on Li Diffusion in LiFePO4 Revealed by Li Isotope Exchange. J. Phys. Chem. C 2017, 121, 12025–12036. [Google Scholar] [CrossRef]
- Politaev, V.V.; Petrenko, A.A.; Nalbandyan, V.B.; Medvedev, B.S.; Shvetsova, E.S. Crystal structure, phase relations and electrochemical properties of monoclinic Li2MnSiO4. J. Solid State Chem. 2007, 180, 1045–1050. [Google Scholar] [CrossRef]
- Kuganathan, N.; Kordatos, A.; Kelaidis, N.; Chroneos, A. Defects, Lithium Mobility and Tetravalent Dopants in the Li3NbO4 Cathode Material. Sci. Rep. 2019, 9, 2192. [Google Scholar] [CrossRef]
- Islam, M.S.; Driscoll, D.J.; Fisher, C.A.J.; Slater, P.R. Atomic-Scale Investigation of Defects, Dopants, and Lithium Transport in the LiFePO4 Olivine-Type Battery Material. Chem. Mater. 2005, 17, 5085–5092. [Google Scholar] [CrossRef]
- Kuganathan, N.; Ganeshalingam, S.; Chroneos, A. Defects, Dopants and Lithium Mobility in Li9V3(P2O7)3(PO4)2. Sci. Rep. 2018, 8, 8140. [Google Scholar] [CrossRef]
- Kuganathan, N.; Kordatos, A.; Anurakavan, S.; Iyngaran, P.; Chroneos, A. Li3SbO4 lithium-ion battery material: Defects, lithium ion diffusion and tetravalent dopants. Mater. Chem. Phys. 2019, 225, 34–41. [Google Scholar] [CrossRef]
- Tealdi, C.; Saiful Islam, M.; Malavasi, L.; Flor, G. Defect and dopant properties of MgTa2O6. J. Solid State Chem. 2004, 177, 4359–4367. [Google Scholar] [CrossRef]
- Shannon, R. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- He, G.-C.; Xiang, H.-M.; Jiang, W.; Kang, Q.; Chen, J.-H. First-principles theory on electronic structure and floatability of spodumene. Rare Met. 2014, 33, 742–748. [Google Scholar] [CrossRef]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]


| Two-Body [Φij (rij) = Aij exp (−rij/ρij) − Cij/rij6] | |||||
|---|---|---|---|---|---|
| Interaction | A/eV | ρ/Å | C/eV∙Å6 | Y/e | K/eV∙Å−2 |
| Li+–O2− | 632.1018 | 0.29060 | 0.00 | 1.00 | 99,999 |
| Al3+–O2− | 1109.92381 | 0.31540 | 0.00 | 3.00 | 99,999 |
| Si4+‒O2− | 1283.91 | 0.32052 | 10.66 | 4.00 | 99,999 |
| O2−–O2− | 12,420.5 | 0.22150 | 29.07 | –2.96 | 65.0 |
| Parameter | Calculated | Experiment [36] | |Δ|(%) | ||
|---|---|---|---|---|---|
| Classical | DFT | Force Field | DFT | ||
| a (Å) | 9.373 | 9.557 | 9.461 | 0.93 | 1.01 |
| b (Å) | 8.323 | 8.417 | 8.395 | 0.86 | 0.26 |
| c (Å) | 5.271 | 5.249 | 5.217 | 1.03 | 0.61 |
| α = γ (°) | 90.00 | 90.00 | 90.00 | 0.00 | 0.00 |
| β (°) | 109.03 | 110.42 | 110.09 | 0.96 | 0.30 |
| V (Å3) | 388.73 | 395.73 | 389.15 | 0.10 | 1.69 |
| Site | Point Defect Energy (eV) | |
|---|---|---|
| Vacancy | Interstitial | |
| Li | 7.77 | –4.95 |
| Al | 53.63 | –42.69 |
| Si | 96.44 | –79.27 |
| O | 23.53 | –15.14 |
| Defect Process | Equation Number | Defect Energy (eV)/Defect |
|---|---|---|
| Li Frenkel | 1 | 1.41 |
| Al Frenkel | 2 | 5.47 |
| Si Frenkel | 3 | 8.59 |
| O Frenkel | 4 | 4.31 |
| Full Schottky | 5 | 4.16 |
| Li2O partial Schottky | 6 | 2.62 |
| Al2O3 partial Schottky | 7 | 4.03 |
| SiO2 partial Schottky | 8 | 4.97 |
| Li-Al anti-site (isolated) | 9 | 2.26 |
| Li-Al anti-site (cluster) | 10 | 1.17 |
| Li-Si anti-site (isolated) | 11 | 6.37 |
| Li-Si anti-site (cluster) | 12 | 2.70 |
| Al-Si anti-site (isolated) | 13 | 1.39 |
| Al-Si anti-site (cluster) | 14 | 1.08 |
| Migration Path | Li-Li Separation (Å) | Activation Energy (eV) |
|---|---|---|
| A | 4.42 | 3.20 |
| B | 4.61 | 2.61 |
| C | 5.44 | 6.58 |
| D | 6.11 | 5.21 |
| Reaction | Incorporation Energy (eV)/Li | Bader Charge (|e|) | ΔV (%) |
|---|---|---|---|
| Li + LiAlSi2O6 → Li.LiAlSi2O6 | 0.10 eV (1.77 eV) | +1.00 | 0.34 |
| 2 Li + LiAlSi2O6 → 2 Li.LiAlSi2O6 | 0.59 eV (2.26 eV) | +1.00 (2) | 2.16 |
| 3 Li + Li.LiAlSi2O6 → 3 Li.LiAlSi2O6 | –0.71 eV (1.04 eV) | +1.00 (3) | 2.37 |
| 4 Li + Li.LiAlSi2O6 → 4 Li.LiAlSi2O6 | –0.85 eV (0.82 eV) | +1.00 (4) | 2.73 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suthaharan, S.; Iyngaran, P.; Kuganathan, N. Simulation-Based Defect Engineering in “α-Spodumene”. ChemEngineering 2021, 5, 57. https://doi.org/10.3390/chemengineering5030057
Suthaharan S, Iyngaran P, Kuganathan N. Simulation-Based Defect Engineering in “α-Spodumene”. ChemEngineering. 2021; 5(3):57. https://doi.org/10.3390/chemengineering5030057
Chicago/Turabian StyleSuthaharan, Sivanujan, Poobalasuntharam Iyngaran, and Navaratnarajah Kuganathan. 2021. "Simulation-Based Defect Engineering in “α-Spodumene”" ChemEngineering 5, no. 3: 57. https://doi.org/10.3390/chemengineering5030057
APA StyleSuthaharan, S., Iyngaran, P., & Kuganathan, N. (2021). Simulation-Based Defect Engineering in “α-Spodumene”. ChemEngineering, 5(3), 57. https://doi.org/10.3390/chemengineering5030057