Simplified Approach to Predict Food Safety through the Maximum Specific Bacterial Growth Rate as Function of Extrinsic and Intrinsic Parameters
Abstract
1. Introduction
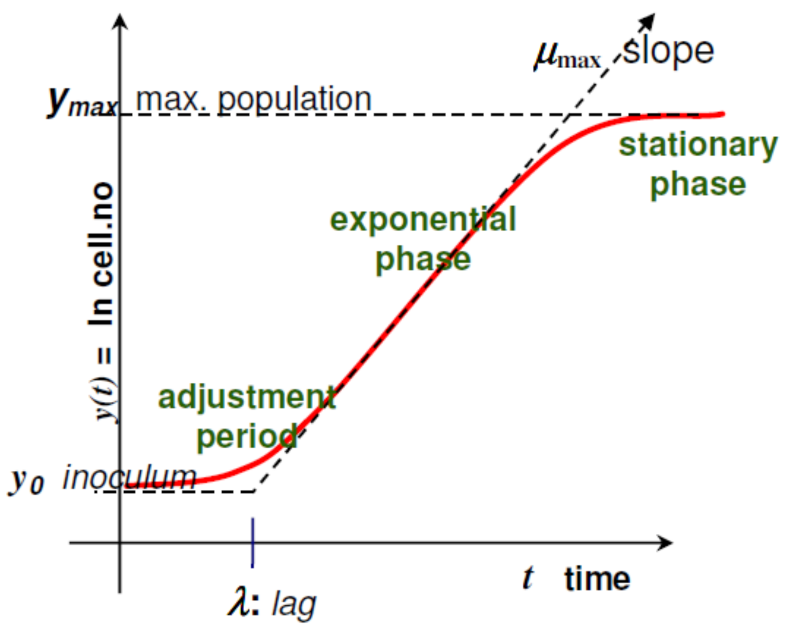
- is the same as where is the number of colony-forming unit (CFU)/g;
- is the initial value of CFU/g (scaled logarithmically) and its value derived from Tables 1–6 is shown as result in Table 7;
- is the maximum value of CFU/g (scaled logarithmically) and its value is also defined in Table 7;
- µmax is the maximum specific growth rate and its value is affected by intrinsic and extrinsic factors;
- is a constant defined by , where is the physiological state; It is also related with (lag phase), where ;
- is the parameter that define the curvature between the exponential and stationary phase;
- is the parameter that define the curvature between the initial and exponential phase through the equation ;
- is the time since the beginning of the bacteria growth.
2. Materials and Methods
- Aeromonas hydrophila;
- Bacillus cereus;
- Bacillus licheniformis;
- Bacillus subtilis;
- Clostridium botulinum;
- Clostridium perfringens;
- Escherichia coli;
- Listeria monocytogenes;
- Salmonella;
- Shigella flexneri;
- Staphylococcus aureus;
- Yersinia enterocolitica;
- Brochothrix thermosphacta;
- Pseudomonas.
2.1. Determination of the Maximum Specific Growth Rate
2.2. Calculation of Coefficients
- Relative error below 5%, er < 5%;
- Relative error between 5% and 10%, 5% < er < 10%;
- Relative error between 10% and 15%, 10% < er < 15%;
- Relative error above 15%, er > 15%.
2.3. Graphic Generating
3. Results
3.1. Aeromonas hydrophila
3.2. Bacillus cereus
3.3. Bacillus licheniformis
3.4. Bacillus subtilis
3.5. Clostridium botulinum
3.6. Clostridium perfringens
3.7. Escherichia coli
3.8. Listeria monocytogenes
3.9. Salmonella
3.10. Shigella flexneri
3.11. Staphylococcus aureus
3.12. Yersinia enterocolitica
3.13. Brochothrix thermosphacta
3.14. Pseudomonas
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| ai | Coefficients that define the maximum specific growth rate; |
| aw | Water activity; |
| bw | Constant (bw = ); |
| e | Euler’s number (e = 0.5772); |
| er | Relative error [%]; |
| h0 | Logarithmic value of a bacteria physiological state (h0 = -ln α0); |
| m | Parameter that define the curvature between the exponential and stationary phase; |
| nc | Parameter that define the curvature between the initial and exponential phase; |
| pH | Potential of hydrogen; |
| t | Time [h]; |
| T | Temperature [°C]; |
| X%opt | Percentage of the value range in which bacteria grow, for which bacterial growth is optimal (with X = Temperature or X = pH); |
| Xopt | Value for which bacterial growth is optimal (with X = Temperature or X = pH); |
| Xmin | Minimum value for which a bacteria grows (with X = Temperature or X = pH); |
| Xmax | Maximum value for which a bacteria grows (with X = Temperature or X = pH); |
| y | Logarithmic value of the number of colony forming unit by gram; |
| y0 | Initial number of colony forming unit by gram; |
| ymax | Maximum number of colony forming unit by gram; |
| α0 | Bacteria physiological state; |
| λ | Lag [h]; |
| µmax | Maximum specific growth rate [log(CFU/g)/h]. |
References
- Gao, T.; Tian, Y.; Zhu, Z.; Sun, D.W. Modelling, responses and applications of time-temperature indicators (TTIs) in monitoring fresh food quality. Trends Food Sci. Technol. 2020, 99, 311–322. [Google Scholar] [CrossRef]
- Zhang, X.; Sun, G.; Xiao, X.; Liu, Y.; Zheng, X. Application of microbial TTIs as smart label for food quality: Response mechanism, application and research trends. Trends Food Sci. Technol. 2016, 51, 12–23. [Google Scholar] [CrossRef]
- Villalobos, J.R.; Soto-Silva, W.E.; González-Araya, M.C.; González-Ramirez, R.G. Research directions in technology development to support real-time decisions of fresh produce logistics: A review and research agenda. Comput. Electron. Agric. 2019, 167, 105092. [Google Scholar] [CrossRef]
- Barska, A.; Wyrwa, J. Innovations in the food packaging market—Intelligent packaging—A review. Czech J. Food Sci. 2017, 35, 1–6. [Google Scholar] [CrossRef]
- Realini, C.E.; Marcos, B. Active and intelligent packaging systems for a modern society. Meat Sci. 2014, 98, 404–419. [Google Scholar] [CrossRef] [PubMed]
- Jang, N.Y.; Won, K. New pressure-activated compartmented oxygen indicator for intelligent food packaging. Int. J. Food Sci. Technol. 2014, 49, 650–654. [Google Scholar] [CrossRef]
- Martin, N.H.; Torres-Frenzel, P.; Wiedmann, M. Invited review: Controlling dairy product spoilage to reduce food loss and waste. J. Dairy Sci. 2021, 104, 1251–1261. [Google Scholar] [CrossRef]
- Kalpana, S.; Priyadarshini, S.R.; Maria Leena, M.; Moses, J.A.; Anandharamakrishnan, C. Intelligent packaging: Trends and applications in food systems. Trends Food Sci. Technol. 2019, 93, 145–157. [Google Scholar] [CrossRef]
- Müller, P.; Schmid, M. Intelligent packaging in the food sector: A brief overview. Foods 2019, 8, 16. [Google Scholar] [CrossRef] [PubMed]
- Gaspar, P.D.; Silva, P.D.; Andrade, L.P.; Nunes, J.; Santo, C.E. Technologies for monitoring the safety of perishable food products. In Research Anthology on Food Waste Reduction and Alternative Diets for Food and Nutrition Security; Information Resources Management Association, Ed.; IGI Global: Hershey, PA, USA, 2021; pp. 63–98. [Google Scholar] [CrossRef]
- Kuswandi, B. Freshness Sensors for Food Packaging. In Reference Module in Food Science; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar] [CrossRef]
- Dalmoro, V.; Santos, J.H.Z.; Pires, M.; Simanke, A.; Baldino, G.B.; Oliveira, L. Encapsulation of sensors for intelligent packaging. In Food Packaging; Grumezescu, A.M., Ed.; Academic Press: Cambridge, MA, USA, 2017; pp. 111–145. [Google Scholar] [CrossRef]
- Vilela, C.; Kurek, M.; Hayouka, Z.; Röcker, B.; Yildirim, S.; Antunes, M.D.C.; Nilsen-Nygaard, J.; Pettersen, M.K.; Freire, C.S.R. A concise guide to active agents for active food packaging. Trends Food Sci. Technol. 2018, 80, 212–222. [Google Scholar] [CrossRef]
- FDA. Bad Bug Book, 2nd ed.; Center for Food Safety and Applied Nutrition (CFSAN) of the Food and Drug Administration (FDA); U.S. Department of Health and Human Services: Silver Springs, FL, USA, 2012. [Google Scholar]
- Willey, J.M.; Sherwood, L.; Woolverton, C.J.; Prescott, L.M. Prescott’s Principles of Microbiology, 1st ed.; McGraw-Hill Higher Education: Boston, MA, USA, 2009. [Google Scholar]
- Baranyi, J.; Roberts, T.A.; McClure, P.J. A non-autonomous differential equation to model bacterial growth. Food Microbiol. 1993, 10, 43–59. [Google Scholar] [CrossRef]
- Baranyi, J.; Roberts, T.A. A dynamic approach to predicting bacterial growth in food. Int. J. Food Microbiol. 1994, 23, 277–294. [Google Scholar] [CrossRef]
- Grijspeerdt, K.; Vanrolleghem, P. Estimating the parameters of the Baranyi model for bacterial growth. Food Microbiol. 1999, 16, 593–605. [Google Scholar] [CrossRef]
- Baranyi, J. Modelling and Parameter Estimation of Bacterial Growth with Distributed Lag Time. Ph.D.Thesis, Doctoral School of Informatics, University of Szeged, Szeged, Hungary, 2010. [Google Scholar]
- Masana, N.O.; Baranyi, J. Adding new factors to predictive models: The effect on the risk of extrapolation. Food Microbiol. 2000, 17, 367–374. [Google Scholar] [CrossRef]
- Gibson, A.M.; Baranyi, J.; Pitt, J.I.; Eyles, M.J.; Roberts, T.A. Predicting fungal growth: The effect of water activity on Aspergillus flavus and related species. Int. J. Food Microbiol. 1994, 23, 419–431. [Google Scholar] [CrossRef]
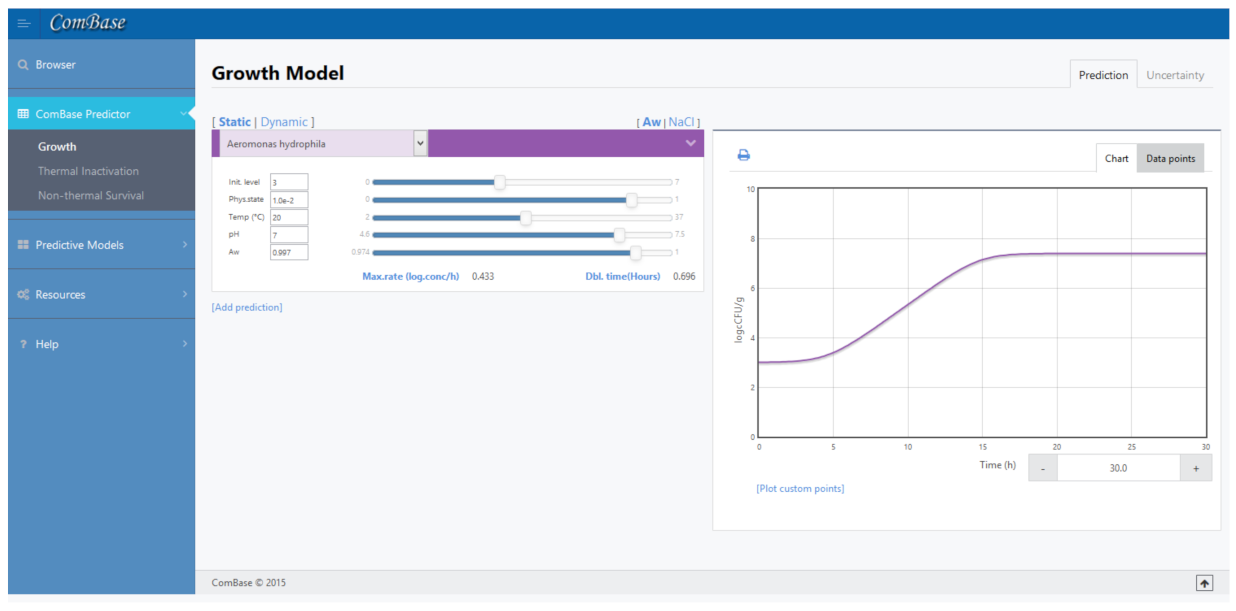
- ComBase Predictor: Growth Model. Available online: https://browser.combase.cc/ComBase_Predictor.aspx?model=1 (accessed on 3 May 2021).
- Dang, Y.T.H.; Gangadoo, S.; Rajapaksha, P.; Truong, V.K.; Cozzolino, D.; Chapman, J. Biosensors in Food Traceability and Quality. In Comprehensive Foodomics; Cifuentes, A., Ed.; Elsevier: Amsterdam, The Netherlands, 2020; pp. 308–321. [Google Scholar] [CrossRef]
- Gaspar, P.D.; Domingues, C.; Gonçalves, L.C.C.; Andrade, L.P. Avaliação da qualidade e segurança alimentar pela previsão do crescimento microbiano em diferentes condições de conservação. In Proceedings of the V Congreso Ibérico y III Congreso Iberoamericano de Ciencias y Técnicas del Frío (CYTEF-2009), Castelló, Spain, 23–25 September 2009. [Google Scholar]

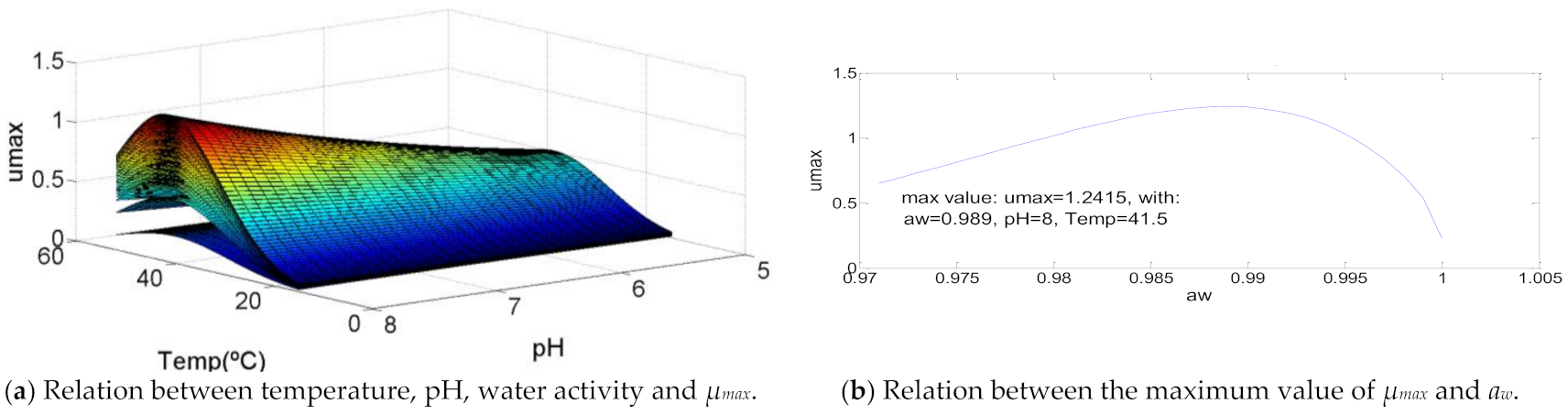
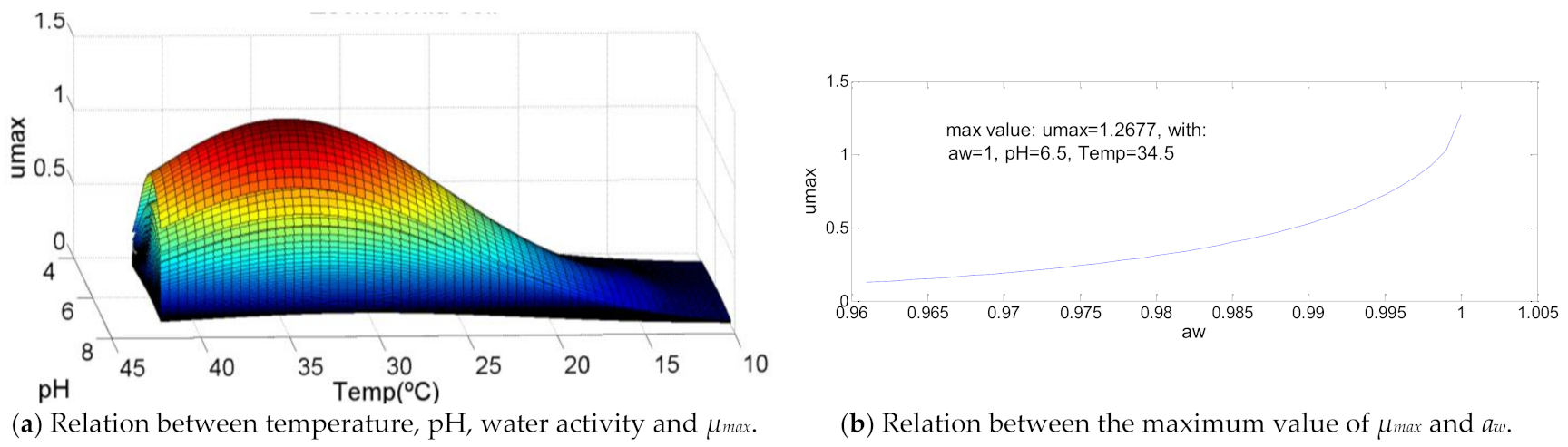
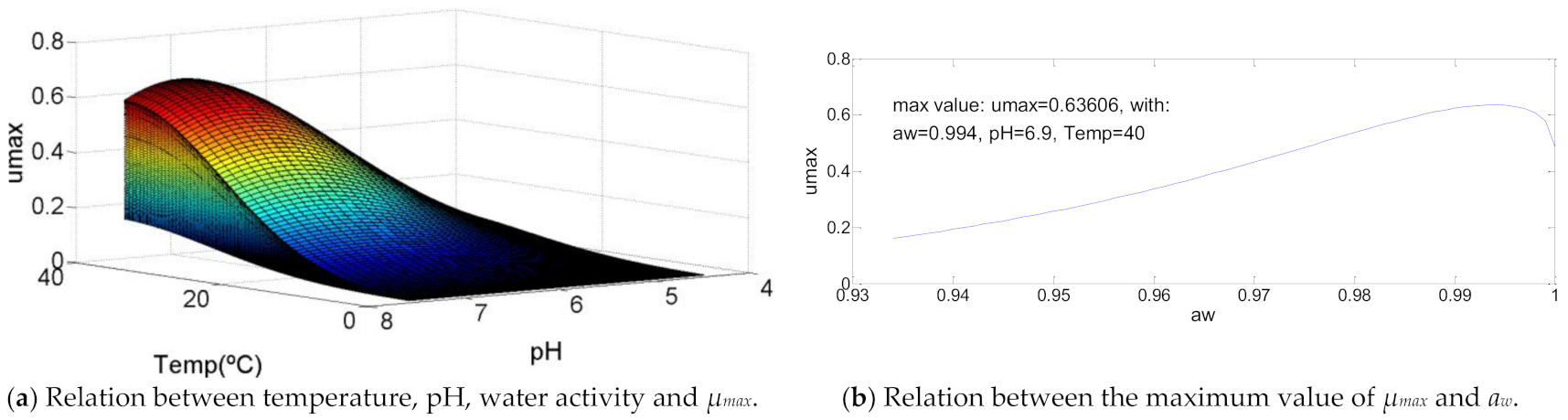

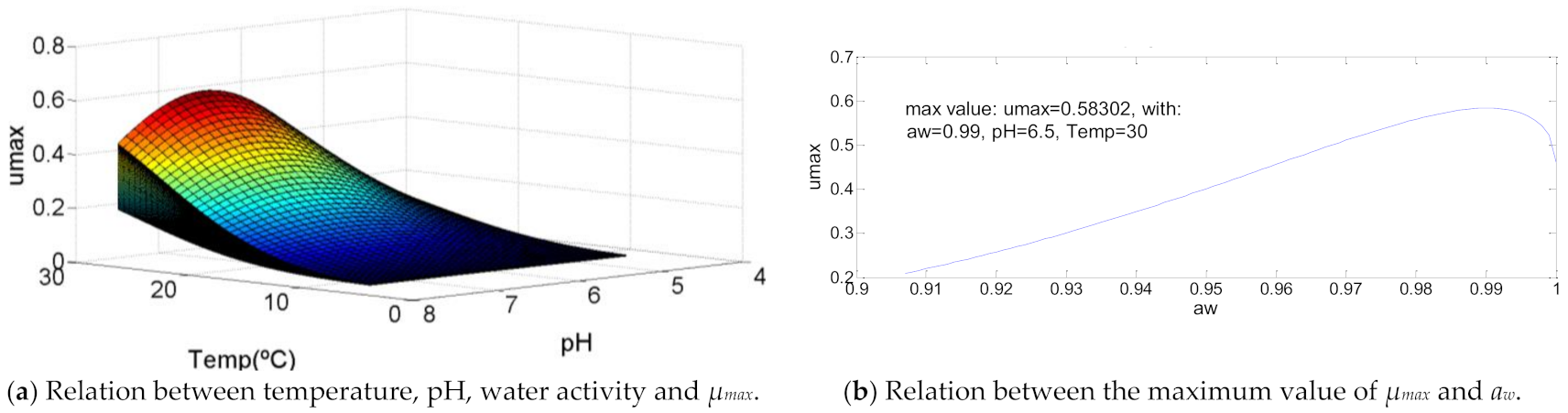
| Input | |||
|---|---|---|---|
| T [°C] | pH | aw | µmax |
| 1 | 5.50 | 0.950 | 0.012 |
| 1 | 6.25 | 0.975 | 0.027 |
| 1 | 7.00 | 0.95 | 0.011 |
| 15 | 5.50 | 1.000 | 0.132 |
| 15 | 6.25 | 1.000 | 0.247 |
| 30 | 5.50 | 0.950 | 0.028 |
| 30 | 6.25 | 0.950 | 0.061 |
| 30 | 7.00 | 0.950 | 0.066 |
| 30 | 7.00 | 0.975 | 0.145 |
| 30 | 7.00 | 1.000 | 0.313 |
| Matrix A | Matrix B | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| T | pH | bw | T·pH | T·bw | pH.bw | T2 | pH2 | bw2 | ln(µmax) | |
| 1 | 1 | 5.50 | 0.223607 | 5.50 | 0.2236068 | 1.229837388 | 1 | 30.2500 | 0.050 | −4.42285 |
| 1 | 1 | 6.25 | 0.158114 | 6.25 | 0.1581139 | 0.988211769 | 1 | 39.0625 | 0.025 | −3.61192 |
| 1 | 1 | 7.00 | 0.223607 | 7.00 | 0.2236068 | 1.565247584 | 1 | 49.0000 | 0.050 | −4.50986 |
| 1 | 15 | 5.50 | 0 | 82.5 | 0 | 0 | 225 | 30.2500 | 0 | −2.02495 |
| 1 | 15 | 6.25 | 0 | 93.75 | 0 | 0 | 225 | 39.0625 | 0 | −1.39837 |
| 1 | 30 | 5.50 | 0.223607 | 165.00 | 6.7082039 | 1.229837388 | 900 | 30.2500 | 0.050 | −3.57555 |
| 1 | 30 | 6.25 | 0.223607 | 187.5 | 6.7082039 | 1.397542486 | 900 | 39.0625 | 0.050 | −2.79688 |
| 1 | 30 | 7.00 | 0.223607 | 210.00 | 6.7082039 | 1.565247584 | 900 | 49.0000 | 0.050 | −2.71810 |
| 1 | 30 | 7.00 | 0.158114 | 210.00 | 4.7434165 | 1.106797181 | 900 | 49.0000 | 0.025 | −1.93102 |
| 1 | 30 | 7.00 | 0 | 210.00 | 0 | 0 | 900 | 49.0000 | 0 | −1.16155 |
| ai | Value |
|---|---|
| a0 | −28.3244 |
| a1 | 0.0976 |
| a2 | 7.8197 |
| a3 | 8.0746 |
| a4 | 0.0217 |
| a5 | −0.1346 |
| a6 | −0.5496 |
| a7 | −0.0051 |
| a8 | −0.6221 |
| a9 | −31.9812 |
| Input | µmax | |||||
|---|---|---|---|---|---|---|
| T [°C] | pH | aw | µmax | µmax (estimated) | Absolute Error | Relative Error |
| 4.65 | 5.7 | 0.960 | 0.031 | 0.0313837 | 3.837 × 10−4 | 1.2% |
| 17.00 | 6.8 | 0.962 | 0.129 | 0.1302418 | 12.418 × 10−4 | 1.0% |
| 28.00 | 6.5 | 0.990 | 0.257 | 0.2611274 | 41.274 × 10−4 | 1.6% |
| 1.50 | 6.5 | 0.990 | 0.036 | 0.0360317 | 0.317 × 10−4 | 0.1% |
| 1.50 | 5.8 | 0.960 | 0.020 | 0.0199184 | 0.816 × 10−4 | 0.4% |
| 3.50 | 6.0 | 0.990 | 0.051 | 0.0520164 | 10.164 × 10−4 | 2.0% |
| 5.40 | 6.0 | 0.997 | 0.074 | 0.0746830 | 6.83 × 10−4 | 0.9% |
| 20.00 | 7.0 | 0.997 | 0.323 | 0.3226309 | 3.691 × 10−4 | 0.1% |
| 3.00 | 5.9 | 0.960 | 0.027 | 0.0271576 | 1.576 × 10−4 | 0.6% |
| 10.00 | 6.8 | 0.960 | 0.070 | 0.0702477 | 2.477 × 10−4 | 0.4% |
| 23.00 | 6.0 | 0.962 | 0.114 | 0.1167338 | 27.338 × 10−4 | 2.4% |
| Microorganism | ai | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| a0 | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | |
| Aeromonas hydrophila | −28.0530 | 0.2469 | 7.2505 | 3.1783 | 0.0067 | −0.0561 | 1.3009 | −0.0054 | −0.5609 | −125.5860 |
| Bacillus cereus | −2.7330 | 0.1622 | −0.8614 | 1.5969 | 0.0122 | −0.1831 | 1.2199 | −0.0025 | 0.0720 | −59.3343 |
| Bacillus licheniformis | −29.1238 | 0.4592 | 6.4417 | −12.1128 | −0.0053 | 0.0649 | 2.7058 | −0.0055 | −0.4889 | −54.4646 |
| Bacillus subtilis | −20.5091 | 0.2066 | 4.7178 | 2.1808 | 0.0075 | 0.0456 | −1.1555 | −0.0025 | −0.3835 | 19.8195 |
| Clostridium botulinum | −32.7539 | 0.4803 | 7.6414 | 26.4667 | 0 | −0.0939 | −1.0452 | −0.0096 | −0.5609 | −163.932 |
| Clostridium perfringens | −7.4775 | 0.2831 | 0.0580 | 8.6498 | 0.0068 | 0.1154 | 2.3642 | −0.0042 | −0.0195 | −153.4672 |
| Escherichia coli | −20.3231 | 0.4115 | 4.1261 | 2.2349 | 0.0002 | −0.2249 | −0.0415 | −0.0060 | −0.3162 | −31.9882 |
| Listeria monocytogenes | −18.2070 | 0.2029 | 3.9028 | 6.0167 | 0.0024 | 0.0408 | −0.1241 | −0.0028 | −0.2886 | −43.1797 |
| Salmonella | −12.9739 | 0.3529 | 1.8967 | 6.4026 | −0.0048 | 0.0224 | −0.0118 | −0.0043 | −0.1336 | −62.1296 |
| Shigella flexneri | −17.2012 | 0.4993 | 1.7936 | 21.6882 | −0.0044 | 0.3454 | −0.5534 | −0.0065 | −0.1091 | −182.8641 |
| Staphylococcus aureus | −18.4275 | 0.3267 | 3.8293 | −4.5893 | 0.0029 | 0.1031 | 0.9995 | −0.0050 | −0.3105 | −25.0405 |
| Yersinia enterocolitica | −15.3130 | 0.2159 | 3.2613 | 4.7524 | −0.0118 | 0.1356 | 0.4380 | −0.0016 | −0.2312 | −93.5564 |
| Brochothrix thermosphacta | −28.3244 | 0.0976 | 7.8197 | 8.0746 | 0.0217 | −0.1346 | −0.5496 | −0.0051 | −0.6221 | −31.9812 |
| Pseudomonas | −14.0267 | 0.1571 | 3.2135 | 0.4892 | 0.0005 | −0.0371 | 2.9697 | −0.0021 | −0.2671 | −117.0019 |
| Microorganism | Relative Error, er | Total Number of Tests | |||
|---|---|---|---|---|---|
| er < 5% | 5% < er < 10% | 10% < er < 15% | er > 15% | ||
| Aeromonas hydrophila | 45% | 23% | 7% | 25% | 60 |
| Bacillus cereus | 64% | 19% | 14% | 3% | 36 |
| Bacillus licheniformis | 62% | 24% | 10% | 5% | 21 |
| Bacillus subtilis | 100% | 0% | 0% | 0% | 21 |
| Clostridium botulinum | 86% | 10% | 5% | 0% | 21 |
| Clostridium perfringens | 95% | 5% | 0% | 0% | 20 |
| Escherichia coli | 80% | 10% | 10% | 0% | 20 |
| Listeria monocytogenes | 64% | 27% | 9% | 0% | 22 |
| Salmonella | 83% | 4% | 8% | 4% | 24 |
| Shigella flexneri | 86% | 5% | 10% | 0% | 21 |
| Staphylococcus aureus | 62% | 14% | 24% | 0% | 21 |
| Yersinia enterocolitica | 76% | 14% | 5% | 5% | 21 |
| Brochothrix thermosphacta | 100% | 0% | 0% | 0% | 21 |
| Pseudomonas | 95% | 5% | 0% | 0% | 20 |
| Microorganism | Tmin [°C] | Topt [°C] | Tmax [°C] | pHmin | pHopt | pHmax | aw,min | aw,opt | aw,max | µmax,opt | Initial Colony [UFC/g] | Infective Colony [UFC/g] | Final Colony [UFC/g] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
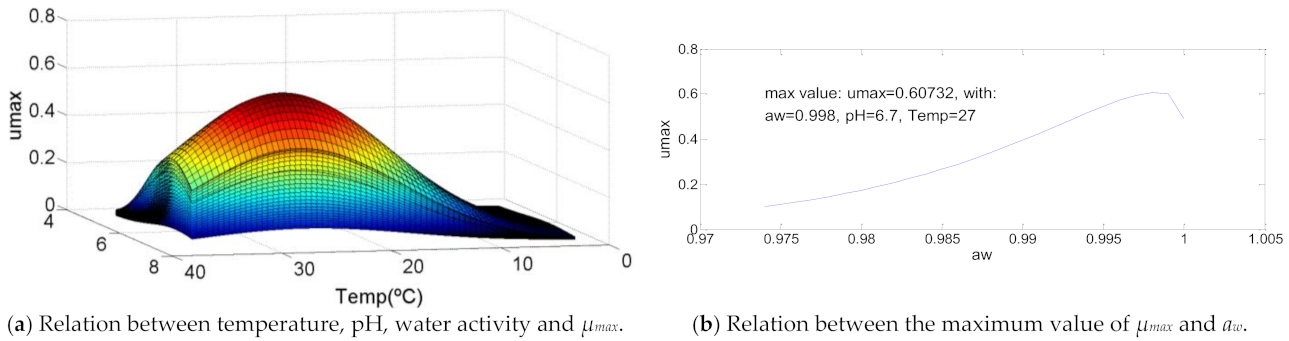
| Aeromonas hydrophila | 2.0 | 27-0 | 37.0 | 4.6 | 6.7 | 7.5 | 0.974 | 0.998 | 1 | 0.60732 | 103 | >105 | 107.39 |
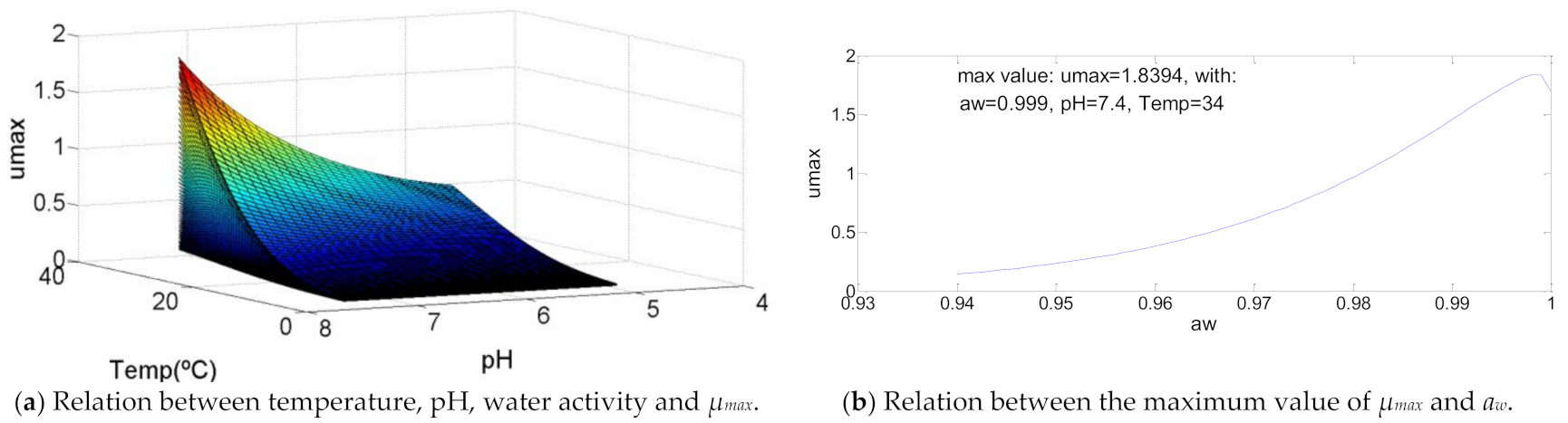
| Bacillus cereus | 5.0 | 34-0 | 34.0 | 4.9 | 7.4 | 7.4 | 0.94 | 0.999 | 1 | 1.83940 | 101 | >105 | 107.61 |
| Bacillus licheniformis | 13.0 | 34.0 | 34.0 | 4 | 6.6 | 7.6 | 0.907 | 0.995 | 1 | 1.56890 | 103 | >105 | 107.83 |
| Bacillus subtilis | 10.0 | 34.0 | 34.0 | 4.3 | 6.1 | 7.8 | 0.933 | 0.933 | 1 | 1.17800 | 101 | >105 | 107.83 |
| Clostridium botulinum | 4.0 | 24.5 | 30.0 | 5.1 | 6.8 | 7.5 | 0.974 | 0.997 | 1 | 0.75511 | 100 | >104 | 107.04 |
| Clostridium perfringens | 15.0 | 41.5 | 52.0 | 5.0 | 8.0 | 8.0 | 0.971 | 0.989 | 1 | 1.24150 | 101 | >106 | 107.61 |
| Escherichia coli | 10.0 | 34.5 | 42.0 | 4.5 | 6.5 | 7.5 | 0.961 | 1 | 1 | 1.26770 | 102 | >106 | 108.7 |
| Listeria monocytogenes | 1.0 | 40.0 | 40.0 | 4.4 | 6.9 | 7.5 | 0.934 | 0.994 | 1 | 0.63606 | 101 | >102 | 108.52 |
| Salmonella | 7.0 | 37.5 | 40.0 | 3.9 | 6.4 | 7.4 | 0.973 | 0.997 | 1 | 0.93591 | 102 | >105 | 108.52 |
| Shigella flexneri | 15.0 | 37.0 | 37.0 | 5.5 | 7.3 | 7.5 | 0.971 | 0.993 | 1 | 0.76419 | 100 | >102 | 108.78 |
| Staphylococcus aureus | 7.5 | 30.0 | 30.0 | 4.4 | 6.5 | 7.5 | 0.907 | 0.99 | 1 | 0.58302 | 101 | >105 | 108.09 |
| Yersinia enterocolitica | −1.0 | 37.0 | 37.0 | 4.4 | 6.2 | 7.2 | 0.957 | 0.996 | 1 | 0.66226 | 102 | >107 | 108.3 |
| Brochothrix thermosphacta | 0.0 | 23.5 | 30.0 | 5.5 | 6.7 | 7.0 | 0.950 | 0.999 | 1 | 0.38374 | 102 | >107 | 107.83 |
| Pseudomonas | 0.0 | 20.0 | 20.0 | 5.0 | 6.5 | 7.4 | 0.961 | 0.993 | 1 | 0.27746 | 102 | >107 | 108.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaspar, P.D.; Alves, J.; Pinto, P. Simplified Approach to Predict Food Safety through the Maximum Specific Bacterial Growth Rate as Function of Extrinsic and Intrinsic Parameters. ChemEngineering 2021, 5, 22. https://doi.org/10.3390/chemengineering5020022
Gaspar PD, Alves J, Pinto P. Simplified Approach to Predict Food Safety through the Maximum Specific Bacterial Growth Rate as Function of Extrinsic and Intrinsic Parameters. ChemEngineering. 2021; 5(2):22. https://doi.org/10.3390/chemengineering5020022
Chicago/Turabian StyleGaspar, Pedro D., Joel Alves, and Pedro Pinto. 2021. "Simplified Approach to Predict Food Safety through the Maximum Specific Bacterial Growth Rate as Function of Extrinsic and Intrinsic Parameters" ChemEngineering 5, no. 2: 22. https://doi.org/10.3390/chemengineering5020022
APA StyleGaspar, P. D., Alves, J., & Pinto, P. (2021). Simplified Approach to Predict Food Safety through the Maximum Specific Bacterial Growth Rate as Function of Extrinsic and Intrinsic Parameters. ChemEngineering, 5(2), 22. https://doi.org/10.3390/chemengineering5020022








