Next Article in Journal
Correction: Ränger, L.-M., et al. Robust Initialization of Rigorous Process Simulations of Multiple Dividing Wall Columns via Vmin Diagrams. ChemEngineering 2018, 2, 25
Next Article in Special Issue
Coagulated Mineral Adsorbents for Dye Removal, and Their Process Intensification Using an Agitated Tubular Reactor (ATR)
Previous Article in Journal
Prediction of Excess Enthalpy Using Volume-Translated Peng–Robinson Equation of State
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
ChemEngineering
Volume 5
Issue 1
10.3390/chemengineering5010009
ChemEngineering-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Kinetic Studies of Cs+ and Sr2+ Ion Exchange Using Clinoptilolite in Static Columns and an Agitated Tubular Reactor (ATR)

by
Muhammad Yusuf Prajitno
1,*,
Mohamad Taufiqurrakhman
2,
David Harbottle
1 and
Timothy N. Hunter
1,*
1
School of Chemical and Process Engineering, University of Leeds, Leeds LS2 9JT, UK
2
School of Mechanical Engineering, University of Leeds, Leeds LS2 9JT, UK
*
Authors to whom correspondence should be addressed.
ChemEngineering 2021, 5(1), 9; https://doi.org/10.3390/chemengineering5010009
Submission received: 14 December 2020 / Revised: 7 January 2021 / Accepted: 4 February 2021 / Published: 11 February 2021
(This article belongs to the Special Issue Role of Colloid and Surface Science in Decontaminating Ground and Groundwater Systems)
Browse Figures
Review Reports Versions Notes

Abstract

:
Natural clinoptilolite was studied to assess its performance in removing caesium and strontium ions, using both static columns and an agitated tube reactor (ATR) for process intensification. Kinetic breakthrough curves were fitted using the Thomas and Modified Dose Response (MDR) models. In the static columns, the clinoptilolite adsorption capacity (qe) for 200 ppm ion concentrations was found to be ~171 and 16 mg/g for caesium and strontium, respectively, highlighting the poor material ability to exchange strontium. Reducing the concentration of strontium to 100 ppm, however, led to a higher strontium qe of ~48 mg/g (close to the maximum adsorption capacity). Conversely, halving the column residence time to 15 min decreased the qe for 100 ppm strontium solutions to 13–14 mg/g. All the kinetic breakthrough data correlated well with the maximum adsorption capacities found in previous batch studies, where, in particular, the influence of concentration on the slow uptake kinetics of strontium was evidenced. For the ATR studies, two column lengths were investigated (of 25 and 34 cm) with the clinoptilolite embedded directly into the agitator bar. The 34 cm-length system significantly outperformed the static vertical columns, where the adsorption capacity and breakthrough time were enhanced by ~30%, which was assumed to be due to the heightened kinetics from shear mixing. Critically, the increase in performance was achieved with a relative process flow rate over twice that of the static columns.

Graphical Abstract

1. Introduction

Caesium-137 and strontium-90 have some of the highest yield ratios of medium-lived fission products from nuclear power production (at approximately 6.3% and 4.5%, respectively), both with half-lives of around 30 years [1]. These radioisotopes are also extremely hazardous in nature, and are present as species that readily solubilise in water [2,3,4], potentially leading to rapid environmental contamination. Therefore, they are considered to be two of the primary heavy metals that must be removed from wastewaters resulting from ongoing nuclear generation as well as radiation clean-up activities. For example, several processes were employed to remove these ions from the cooling waters used at Fukushima [5].
In order to separate radioactive heavy metal ions from aqueous waste streams, there are a number of techniques that can be used, including ion exchange, co-precipitation, and coagulation methods; selective membranes; as well as the use of nano-adsorbents or organic conjugate materials [6,7,8,9,10,11,12,13,14,15,16,17,18,19]. The use of ion exchange media is perhaps the commonly used technique in the nuclear industry, due to the high specific decontamination factors, low production of secondary wastes, reliability, and cost effectiveness [8,9,16,20]. For caesium and strontium removal in particular, zeolite materials such as clinoptilolite are widely employed in nuclear effluent remediation [6,21,22,23,24]. Clinoptilolite naturally occurs with low impurities in a wide range of deposits around the world, and it can be relatively easily pre-treated to improve its efficacy, while it has good resistance to radiation exposure [6,9,25,26,27,28,29,30].
It is possible to utilise zeolite ion exchange material either in batch or continuous processes [25,29,30,31,32]. While batch systems offer a greater process flexibility [8,31], they are much less operationally efficient overall and require large mixing units. Therefore, most nuclear treatment systems operate static ion exchange columns [30,31], where the effluent is continuously injected through a fixed bed depth of adsorbent; such as with the Site Ion Exchange Plant (SIXEP) at Sellafield in the UK (one of Europe’s largest legacy nuclear sites) [9,25,28,29,30]. However, there are several critical limitations to ion exchange column operation which result in a low throughput. In particular, large particle sizes (>250 µm) are required to reduce frictional pressure drop issues. Therefore, as ion exchange in zeolites primarily occurs through surface sites, resins are not materially efficient, due to their low surface area to volume ratio. Indeed, previous work by the current authors has shown clear enhancements to caesium and strontium uptake as clinoptilolite is milled to increase the relative surface area [26]. Columns must also be run at relatively low liquid velocities to further limit the frictional pressure drop in addition to mitigating the slow adsorption kinetics associated with diffusive ion exchange interactions [7,9,26]. Overall, these process limitations significantly increase the footprint of industrial ion exchange operations, as a number of units have to be run in parallel to achieve the required output rates.
Thus, there is industrial interest in enhancing ion exchange operational efficiencies, where, importantly for this study, methods of process intensification (PI) offer particular advantages [33]. In general, PI is focused on novel operational unit designs that can provide step-changes in the process efficiency while considerably decreasing the equipment foot-prints, energy consumption, and/or waste formation [34], often achieved through unit modularisation and process combination. While originally focused on fine chemical production, there is increasing research into the PI of multiphase solids handling operations, driven largely by successes in the pharmaceuticals industry [35]. The use of PI in effluent treatment specifically is comparatively less developed, although it is an area with a lot of potential to drive solutions through technology transfer [33]. In many respects, flotation can be considered one of the original PI techniques for effluent treatment. While primarily adapted for mineral separation [36,37], it has gained increasing use as a rapid solid–liquid separation technique for wastewater sludges and mineral wastes, reducing unit footprints and enhancing throughput rates when compared to traditional gravity separators. Indeed, there has been a number of studies published on its use to separate nuclear wastes and adsorbents used for effluent treatment [14,37,38,39,40,41,42,43]. PI methods are also being used in conjunction with the development of related nanotechnologies for effluent treatment [44], such as with rapid magnetic separation methods to capture and recycle magnetic nano-adsorbents [45,46].
For adsorption or ion exchange processes, there is increasing research into using intensified flow reactors to overcome constraints associated with diffusion limited adsorption kinetics [34,47,48,49,50]. One of the most prevalent examples in the literature is rotating bed reactors (RBRs), which were originally designed for gas–liquid separation operations, where high centrifugal gravity fields lead to enhanced mass transfer characteristics [33]. More recently, they have also been utilised for the removal of contaminants from liquids, including dyes, fertilisers, and heavy metals [47,48,49,50,51]. However, the disadvantage of RBRs is that they have relatively small residence times which are dependent on the rotation speed, and thus, for the high percentage removal of species, effluent requires multiple passes. Therefore, flow reactors which can generate additional shear (to improve mixing) independently of process throughput or residence time would be highly beneficial. One approach is to generate shear through vortex flows formed from pulsed pump cycles, as with oscillatory baffle reactors and pulse columns, which have been utilised as intensified liquid–liquid and solid–liquid contactors [33,52,53]. However, the internal plate and baffle arrangements of these designs would not easily accommodate large granular ion exchange media.
An alternative design for independently controlling mixing and throughput rates are agitated tubular reactors (ATRs), which are intensified plug-flow reactors where high-rate lateral shear is generated with an inner, hollow, agitator bar, decoupling mixing dynamics from the bulk flow [49,54]. While they have been previously utilised for chemical synthesis, they also present a flexible design to enhance mass transfer rates in solid–liquid adsorption operations, owing to their relatively simple agitator arrangement. A number of authors have characterised the mixing dynamics and performance of ATRs [44,54,55], such as in simulations by He et al. [56,57], who found volumetric mass transfer more efficient with enhanced energy dissipation in comparison to batch processes. However, while these initial characterisation studies highlight the advantages of ATR mixing, the potential to use ATRs as novel intensified exchange units has not previously been investigated by any authors.
Therefore, in this study the performance of a zeolite ion exchange resin is assessed in both static vertical columns, as well an intensified ATR, to remove strontium and caesium ions. Here, clinoptilolite is selected as the ion exchange media, owing to its common use in nuclear effluent treatment [9,25,26,28,29,30]. In vertical elution column tests, kinetic breakthrough is measured for various ion concentrations, residence times, and column diameters in order to compare the adsorption data to previous batch studies of the same systems [26], allowing the optimisation of column operation. An industrially relevant pilot-scale ATR device was then selected for comparison, where the influence of different column lengths was investigated by embedding the zeolite directly into the agitator bar. Critically, the kinetic breakthrough performance matched the static column results, both through enhancements in the equilibrium adsorption of the clinoptilolite as well as the relative process flowrates achieved from either system.

2. Materials and Methods

2.1. Materials

Natural clinoptilolite was supplied from Holistic Valley, UK as a ~300 µm powder [26]. Caesium chloride (CsCl) and strontium chloride (SrCl2) were of analytical grade with a purity ≥99.0%, supplied by Sigma Aldrich, UK and Fisher Scientific, UK, respectively.
Prior to column studies, treatment was required to gain a homogeneous particle size with a low level of polydispersity and remove any naturally present ions, which have previously been shown to impact on its performance [26]. Firstly, the clinoptilolite was rinsed several times with distilled water at a neutral pH, where the supernatant on every rinse was removed and measured using a conductivity meter until the values reached an equilibrium low level. The rinsed clinoptilolite was then dried at 100 °C [6] and sieved using an AS 200 shaker (Retsch GmbH, Haan, Germany) with a 250 µm mesh for 30 min. Once the process was completed, the clinoptilolite was separated using a course brush in order to observe its uniformity. These processes were repeated three times in order to ensure a low level of fines. The sieved clinoptilolite was analysed using a Mastersizer 2000E laser diffractometer (Malvern Panalytical Ltd., Malvern, UK). The particle size distribution is shown within the Electronic Supplementary Materials (ESM), Figure S1, with a mean particle size of ~312 µm.

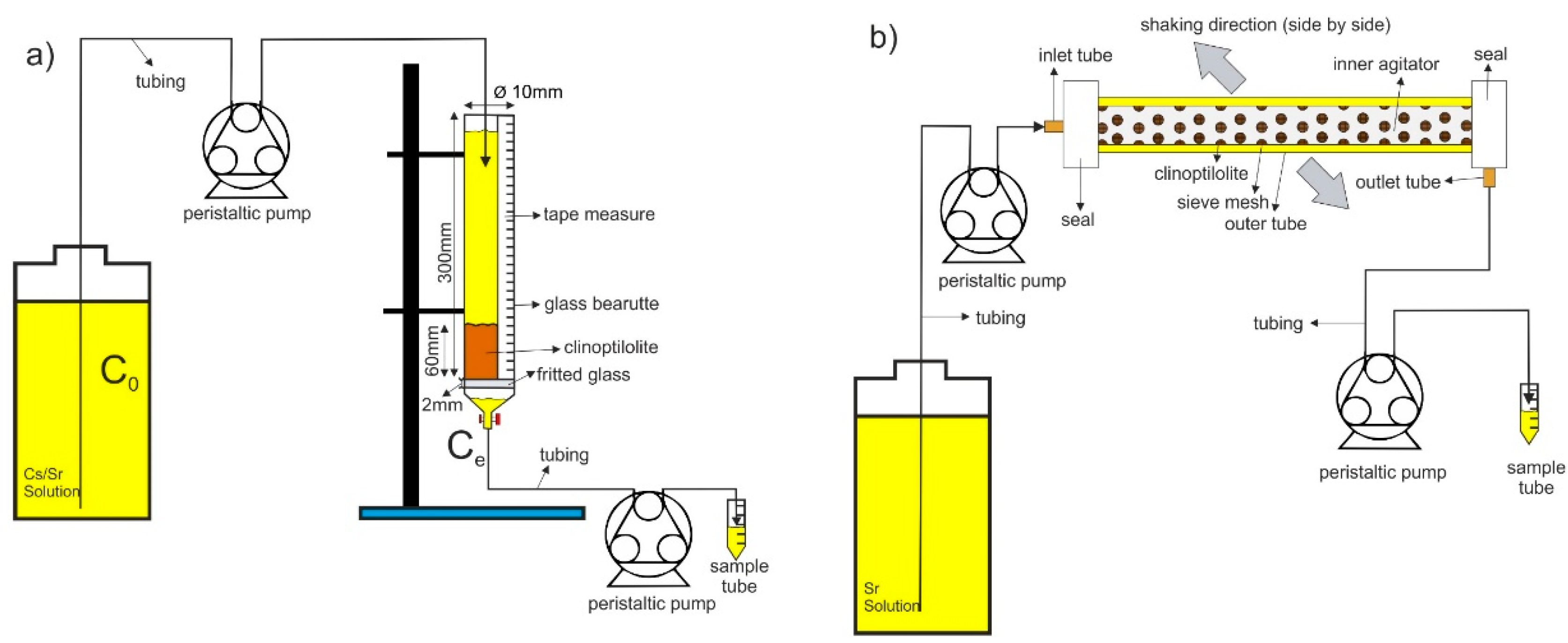
2.2. Static Column Ion Exchange Experiments

Column ion exchange studies were carried out in a fritted chromatography glass column with a 10 mm inner diameter and 300 mm height [29], as illustrated in Figure 1a. The clinoptilolite was fixed at a 6 cm bed depth, which has been shown in previous research by El-Kamash [29] to be sufficient for good performance. Additionally, liquid flowrates through the column were adjusted to initially give a residence time of 30 min (2 bed volumes [BV] per hour), which was initially assumed to be a reasonable residence time for high performance from the previously determined adsorption kinetics of strontium [26]. Industrially, similar ion exchange systems for nuclear effluent treatments may operate at much reduced residence times to better balance the throughput capacity and material performance (e.g., [9]). However, for this study the initial conditions were chosen to maximise the ion exchange adsorption capacity. Nevertheless, further studies were also completed with a faster flowrate to give a residence time of 15 min (4 BV per hour) and thus an expected lower overall performance. Additionally, scale-up experiments were conducted in a similar fritted glass column with a 2 cm diameter and a residence time of 15 min. Scale-up tests were conducted with two different bed heights, one where the volume of clinoptilolite was conserved (using a 1.5 cm bed height) and a second with the same 6 cm bed height as the smaller column.
The caesium and strontium were prepared by dissolving stock solutions of CsCl and SrCl2 (1 M) with Milli-Q water at neutral pH (which tends to ~6.5 [9]) for nominal initial concentrations of 5–200 ppm, which is similar to the concentration range used in previous research by the current authors [25,29]. The caesium and strontium solutions were pumped through the column for a minimum of 24 h using two peristaltic pumps (Watson Marlow, Falmouth, UK, 323 series) to ensure that both the inlet to the top of the column and the outlet were set at identical rates. Aliquots from the outlet were sampled every hour regularly within working hours, until the outlet concentration equalled the initial ion concentration. All the samples were filtered through 0.3 µm filters (to ensure no fine particles were present) and analysed using an Atomic Absorption Spectrophotometer (AAS) 240 fs (Varian/Agilent Technologies, Oxfordshire, UK). For the initial caesium studies, a caesium lamp with a wavelength and optimum working range of 459.3 nm and 5–4000 ppm was used, while for the main strontium studies a strontium lamp was used with a wavelength of 460.7 nm and an optimum working range of 0.02–10 ppm [26].
It is noted that all column exchange experiments were completed in triplicate. Breakthrough data from all individual runs are shown within the Electronic Supplementary material (Dataset S1, Table S1a–e), showing the outlet ion concentration (Ce) against the processed liquid volume (in BVs). Good reproducibility was evidenced, with percentage differences between average sample standard deviations < 5%.

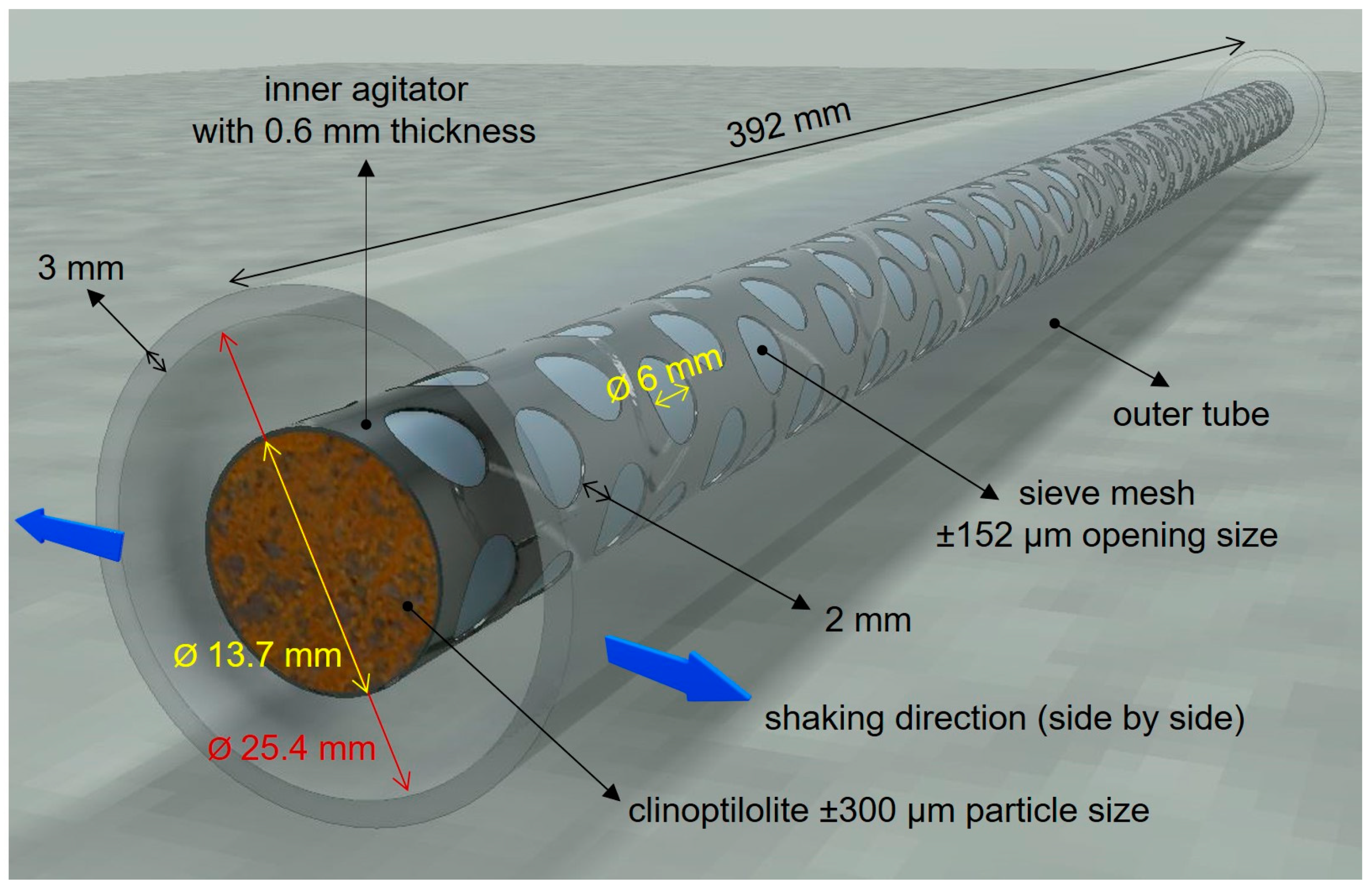
2.3. Agitated Tubular Reactor (ATR) Studies

To understand whether static ion exchange processes could be intensified using shear enhancement, a pilot-scale agitated tubular reactor (ATR) was modified utilising a Coflore ATR (AM Technology, Runcorn, UK), and a schematic of the process is illustrated in Figure 1b.
The ATR consists of an inner perforated agitator that sits within an outer reactor tube which is subject to fast lateral movement (1–6 Hz), causing significant radial shear for low plug flows. The design is similar to that described by other authors in recent publications [55,56]. For testing purposes, a separated outer Perspex reactor tube of 25.4 mm inner diameter, 3 mm thickness, and 392 mm length was utilised, with an inner perforated stainless-steel agitator tube of 13.7 mm inner diameter and 0.6 mm thickness. For ion exchange studies, the inner agitator was covered with a ±152 µm sieve mesh and pre-sieved clinoptilolite was filled into the agitator to various lengths (25 and 34 cm). The sieve mesh cover was small enough so that all the ion exchange resin was retained in the agitator as a plug, while the mesh perforations allowed liquid diffusion into the resin, with the aim of enhancing efficiency through the high lateral shear from agitation. For the flow experiments, the agitation frequency was set to 5 Hz (with a corresponding amplitude of 12.5 mm). A detailed schematic of the agitator arrangement is shown in Figure 2.
For the reactor studies, strontium solutions of 100 ppm concentration were pumped for a minimum of 24 h through the ATR, again using identical peristaltic pumps (Watson Marlow 323 series) at the reactor inlet and outlet. The flow rates were set to give an equivalent residence time of 15 min for liquid contacting the ion exchange plug (based on the calculated average streamwise velocity of fluid in the liquid annulus around the plug). Therefore, the actual bulk flow rate varied depending on the length of the ion exchange plug and the ratio between the plug volume and the total reactor volume. The supernatant was then collected at regular intervals, where samples were filtered by a 0.3 µm filter and analysed using AAS to determine the strontium uptake and breakthrough curves, with the same parameters as previously described. Again, trials were conducted in triplicate, with similar levels of reproducibility to the column studies (see Electronic Supplementary Materials, Dataset S2, Table S2).

2.4. Kinetics Breakthrough Model Analysis

To determine the breakthrough behaviour during static column ion exchange and ATR experiments, the Thomas and Modified Dose Response (MDR) models were fitted to the kinetic adsorption data [58,59,60]. The Thomas model is determined by the specific adsorption rate during ion exchange (KTH) and the flowrate of the effluent injected through the column (Q) [58,59]. Meanwhile, the MDR model has been shown in some studies to improve breakthrough correlations by altering the rate fitting parameter (a) to be a simpler (but non-physical) defined constant, dependent on the linear regression gradient function [60]. In both cases, breakthrough models help determine the kinetics and critically give an estimate of the final equilibrium adsorption amount (qe).
The Thomas model is defined in Equation (1):
C e C 0 = 1 1 + e x p [ K T H Q ( q e m − C 0 V e f f ) ] ,
where Ce and C0 (in ppm or mg/L) are the column outlet and initial influent concentration, respectively; KTH (mL/mg·min) is the Thomas rate constant; Q (mL/min) is the liquid effluent flowrate; m (g) is the adsorbent mass; Veff (L) is the effluent volume; and qe (mg/g) is the adsorption capacity. In order to determine KTH and qe, the model can linearised as follows in Equation (2), where plotting ln(C0/Ce − 1) versus Veff gives a gradient of ( k T H Q C 0 ) and an intercept of k T H Q ( q e m ) :
ln ( C 0 C e − 1 ) = K T H Q ( q e m ) − ( k T H Q C 0 ) V e f f .
Meanwhile, the Modified Dose Response (MDR) model is given in Equation (3).
C e C 0 = 1 − 1 1 + ( V e f f b ) a .
Here, a, the power law exponent and b (L) are constant values. The linearised model is shown in Equation (4), where plotting ln(C0/Ce − 1) versus ln(Veff) gives a gradient of a, while b can be determined from the intercept. Importantly, the adsorption capacity (qe) can be calculated from b, where qe = (b.C0/)m.
ln ( C 0 C e − 1 ) = a ln ( b ) − a ln ( V e f f ) .

3. Results and Discussion

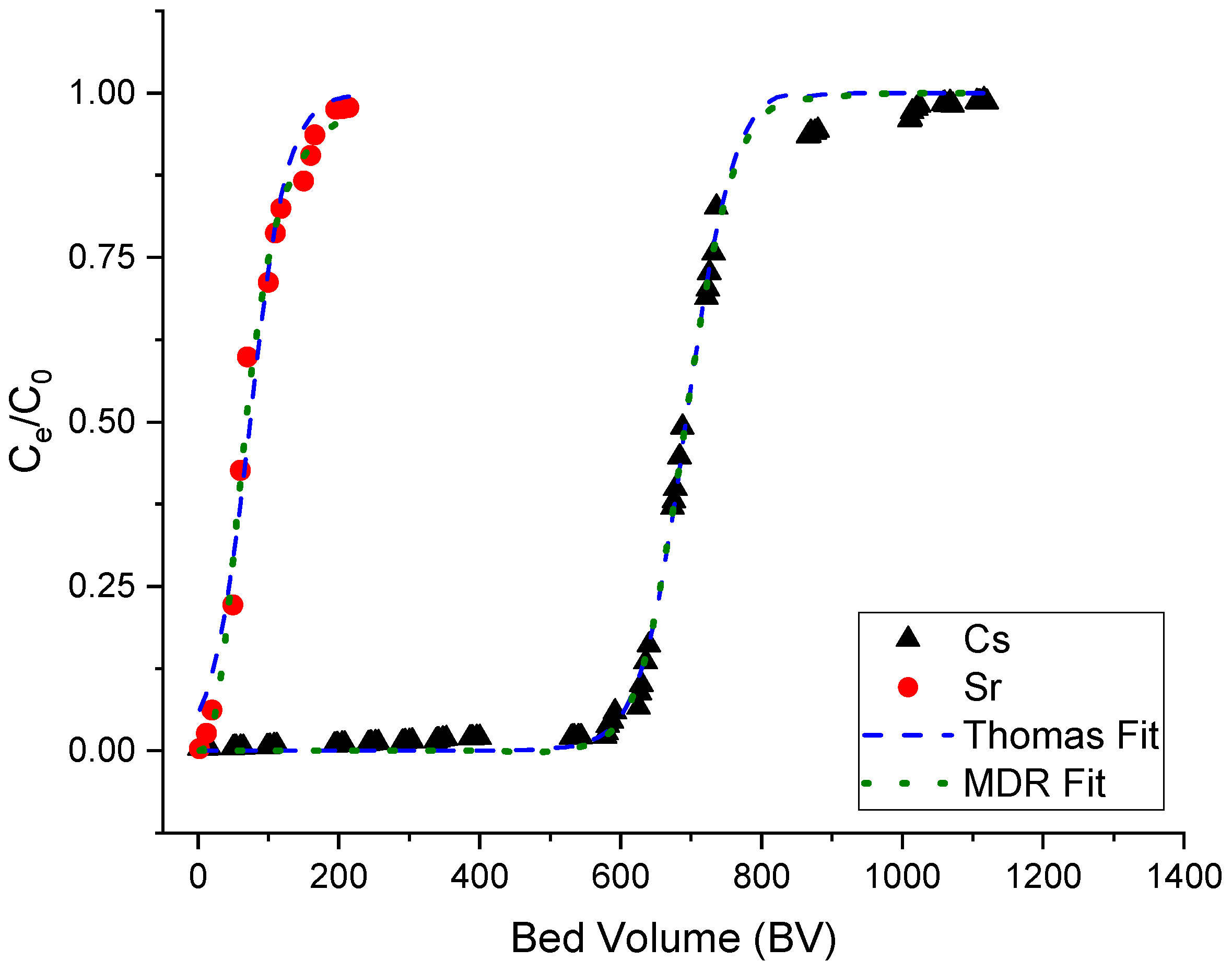
3.1. Static Column Studies

Initially, the clinoptilolite’s performance in removing caesium and strontium was compared, with the assumption from previous studies that the zeolite would be considerably more effective at removing caesium [2,6,7,9,23,32,61,62,63,64,65,66]. A high concentration of 200 ppm solution of the metal ions was chosen to reflect a worst-case scenario in terms of potential effluent concentrations, although most nuclear treatment operations generally consider much lower levels [2,9,66,67]. Very low ion concentration effluents were also not considered in detail, owing to the long time periods required to reach breakthrough (which was not experimentally feasible). Indeed, an initial trial with 5 ppm caesium was completed and is shown within the Electronic Supplementary Material (Figure S2). Due to the time constraints, the breakthrough was still not achieved after 4500 bed volumes (BV). This trend follows from other results for low concentrations of caesium removal by nuclear grade clinoptilolite, as shown by Dyer et al. [9], where a breakthrough started to occur after 10,000 bed volumes.
The static column comparison for 200 ppm Cs+ and Sr2+ at a 30 min residence time is presented in Figure 3, in terms of the ratio of the column outlet to inlet concentrations (Ce/C0) versus the number of effective bed volumes (BV) of liquid effluent processed. Also given are the MDR and Thomas model correlations, with the linearised fits used to determine the optimised parameters shown in the Electronic Supplementary Material (Figure S3). The fitted model parameters are given in Table 1.
It is clear based on Figure 3 that clinoptilolite is able to remove significantly more caesium than strontium, with approximately a factor of 8–10 more bed volumes being processed until the exhaustion of the ion exchange media (Ce/C0 = 1). However, both species show the expected breakthrough behaviour kinetics. In general, the breakthrough criterion is considered the condition where the equilibrium concentration at a specific time (Ce) starts elevating exponentially over time [30], and it is caused by the rapid reduction in adsorption once the ion exchange sites of the adsorbent are close to becoming fully occupied [30,68]. Once the ion exchange media are fully occupied, no more adsorption can occur, which is considered as the exhaustion point [30]. In this study, a breakthrough level of 50% (Ce/C0 = 0.5) was taken as a comparative point to help understand the breakthrough kinetics.
Using the estimated breakthrough level of 50% as a comparison, the clinoptilolite was able to process around 700 bed volumes with caesium and only 70 bed volumes with strontium, which is broadly consistent with a previous batch testing of the same clinoptilolite [26]. The difference in performance from caesium and strontium is considered because of the general low-energy state of adsorption for large monovalent ions in clinoptilolite ion exchange sites, where the ion valency effect is significant [26,32,69,70]. Additionally, as discussed by Woods and Gunter [71], the affinity of adsorbent toward the ions is dependent on their hydrated ionic radii, where the hydrated radii for caesium and strontium are 3.29 and 4.12 Å, respectively [71,72]. Generally, the hydrated ion radius is inversely proportional to the dehydrated ion size due to the better distribution of the charges [73,74]. Smaller hydrated ions may diffuse more freely in or out of adsorbent channels during the adsorption process [6,65,71,75], where additionally in zeolite-cation exchange the process happens in association with the bound water molecules. The dehydration of the bound water occurs prior to adsorption, which is more energetically favourable for smaller hydrated ions [71,73].
It is also evident from Figure 3 that both the MDR and Thomas models were similar in their goodness-of-fit for the breakthrough data, although the MDR model gave slightly higher R2 values (see Table 1). The fitted equilibrium adsorption capacity (qe) values were also correspondingly similar between both models, where, importantly, the qe values for caesium are considerably higher than for strontium (at 171.90 or 170.44 mg/g for caesium against 15.31 or 16.67 mg/g for strontium using the Thomas and MDR models, respectively). There is also a direct correlation between the qe values and the number of bed volumes processed to breakthrough, which is expected to follow a linear trend following previous research [9,25,29,76,77].
It is interesting to compare the fitted qe values from this kinetic data with the adsorption capacity values from equilibrium batch experiments for clinoptilolite, which have been previously published by the current authors [26]. In fact, the qe values estimated in the column tests are actually slightly greater than those found directly for the same clinoptilolite pre-activated with NaCl in batch tests (which gave a maximum adsorption capacity value, Qc = 140.53 mg/g, [26]). The slight discrepancy between the column and batch capacities is most likely due to the additional uncertainties with qe estimates from the column breakthrough model fits, although the good correlation between the Thomas and MDR models gives confidence in the determined values. Additionally, as it is also known that the clinoptilolite contains some ionic impurities [26], this suggests that the long elution times in the column experiments may have self-activated the zeolite as the fluid is exchanged, exposing additional ion exchange sites. Nevertheless, the fact that the column adsorption capacity is close to, or, indeed, above the maximum adsorption capacity estimates indicates that the experimental conditions (specifically the 30 min residence time) lead to a high adsorption efficiency in the column.
It is also evident that the strontium exchange performs very differently. Here, previous batch tests with NaCl pre-activated clinoptilolite (of the same type) gave a maximum adsorption capacity of Qc = 47.5 mg/g, almost three times the qe value found from the breakthrough data fitted to the MDR model (and even more than from the Thomas model). The reason for the large difference in the case of strontium is mostly likely due to its adsorption kinetics, where it has previously been found that the Pseudo Second Order (PSO) rate constant for strontium adsorption on activated clinoptilolite was less than half that for caesium. Thus, in these concentration conditions it appears that the 30 min column residence time is not sufficient for a high material uptake efficiency.
Given the significant difference between caesium and strontium uptake, investigations were focused on modifying column conditions to better understand the system limitations for strontium removal. The static column breakthrough data for strontium contamination are presented in Figure 4, highlighting the effect of concentration, residence time, and column scale-up. Here, the concentration of strontium was reduced to 100 ppm for column residence times of 30 min and 15 min. Additionally, a trial using a residence time of 15 min was repeated in the larger 2 cm-diameter column (increasing the liquid flow rate, Q, from 0.314 to 1.257 mL/min for the same contact time). The resulting Thomas and MDR breakthrough model fits are also shown in Figure 4, with the linear forms used for parameter estimation shown in the Electronic Supplementary Material, Figure S4. The resulting model parameters and R2 fit values are also given in Table 1.
It would be expected from previous research that reducing the strontium concentration would expand the breakthrough curve [25,29]. Indeed, it is evident from Figure 4 that reducing strontium concentration from 200 ppm to 100 ppm led to a considerably enhanced column performance, where the 50% breakthrough occurred around 400 bed volumes for the 100 ppm solution (as opposed to 70 bed volumes for 200 ppm in Figure 3). An increase in breakthrough time occurs due to the lower number of ions per unit volume at 100 ppm, leading to a greater number of bed volumes being processed until the material becomes exhausted. However, the performance difference is greater than would be equated simply from the lower number of ions. In fact, the material efficiency of the clinoptilolite is also much improved at the lower 100 ppm concentration, with qe = 48.1 mg/g (from the MDR model, Table 1) which is around three times higher than qe of 200 ppm and consistent with maximum expected adsorption capacities from batch studies [26].
The greater material efficiency for the lower 100 ppm strontium solution is assumed to be due to the faster adsorption kinetics. Previous kinetic studies on strontium uptake using clinoptilolite in batch systems have suggested the pseudo second-order rate constant reduced by almost two orders of magnitude as the concentration increased from 5 to 300 ppm [26]. The reason for the faster adsorption kinetics at lower concentrations is the reduced statistical competition between ions for exchange sites. The faster kinetics coupled with the lower total amount of ions that must be removed in the 100 ppm system results in large differences to overall column performance.
Figure 4 also shows the change in column performance for a residence time of 15 min in comparison to 30 min, for the same 100 ppm of strontium concentration. By reducing the residence time, the breakthrough curve is shifted to lower bed volumes, where the 50% breakthrough point (Ce/C0 = 0.5) is decreased to around 100 bed volumes. Testing column residence time limits is industrially important, as obviously, reducing residence times will also increase the effluent flowrate of solution (and increase process capacity) while at the same time it will lower the contact time between the adsorbent and contaminants [29,30,77]. In this case, the contact time is far too small at 15 min for efficient material performance. In fact, it is observed from Table 1 that the qe for 15 min residence time is only around 13–14 mg/g (taking an average between Thomas and MDR models) and thus critically smaller than the value for 30 min at 100 ppm.
The effect of scale-up is also examined in Figure 4, with data for 100 ppm strontium and a 15 min residence time for a double, 2 cm-diameter column (with the adsorbent depth kept at 6 cm). The performance for the larger column was similar, although the 50% breakthrough level and fitted qe values did increase slightly to around 128 bed volumes and ~17 mg/g (average of Thomas and MDR values, see Table 1), respectively, for the 2 cm column. This result is similar to McCabe et al. [78], who used specific resins to remove caesium and technetium from radioactive effluent waste in column ion exchange of different sizes, where the results showed that the breakthrough kinetics were not changed significantly. The slight reduction in performance from the smaller 1 cm diameter column may be attributed to enhanced wall effects, most likely influencing local flow tortuosity near the wall surface in relation to the bulk porous flow. It is noted also that similar performance was evidenced for 2 cm column tests, where the volume of ion exchange was conserved rather than the height (given in the Electronic Supplementary Materials, Figure S5), highlighting a good consistency in the scale-up parameterisation. In general, for the scale-up tests the MDR model was found to give a better fit to the collected breakthrough data compared to the Thomas model (from R2 values in Table 1), which is a similar finding to that of other works [77,79,80], although differences between the models were minor.

3.2. Ion Exchange Performance Using an Agitated Tubular Reactor (ATR)

Breakthrough kinetic curves for the clinoptilolite incorporated within the agitator bar of the agitated tube reactor (ATR) are presented in Figure 5. The results are given for two comparative column lengths, 25 and 34 cm (noting the full reactor length is 35 cm) along with resultant Thomas and MDR model fits, for 100 ppm strontium and a 15 min active column residence time. In these conditions, it is reemphasised that the residence time is that of the active ion exchange column and not the total reactor tube. Some data points for the 25 cm trial at intermediate times were omitted due to some sampling issues that occurred (however, data up to a breakthrough level of 70% and >90% were gained). Linearised data for model fitting are presented within the Electronic Supplementary Materials (Figure S6), where determined fit parameters are given in Table 2.
From Figure 5, it is clear that the 34 cm-length column outperforms the 25 cm column significantly (again noting that the residence time was 15 min through both lengths). The 25 cm adsorbent gives a 50% breakthrough level (Ce/C0 = 0.5) of ~90 bed volumes, which is around half that of the 34 cm length at 180 bed volumes. Correspondingly, the qe of the 25 cm column was determined as ~10.2 mg/g, which is also around half that of the 34 cm column at ~21.5 mg/g (average of Thomas and MDR model values from Table 2). The greater performance of the longer column is largely attributed to the larger column to reactor ratio. Unlike in the static ion exchange columns, the ATR operates with the active ion exchange (held within the agitator) completely submerged in the larger reactor tube, which was initially filled with the strontium solution at the beginning of the extraction. Therefore, for relatively small column lengths (low column to tube ratio) there is a large number of solution metal ions initially held within the tube, which are washed out in the initial start-up phase of the reactor. We believe the initial strontium ions in solution begin to adsorb onto the clinoptilolite in this initial start-up, reducing the efficacy of the column. To highlight this effect by changing the column to tube ratio, additional experiments were conducted with a 12 cm column length (see Electronic Supplementary Materials, Figure S7) which performed very poorly, where the 50% breakthrough level occurred after less than 25 bed volumes.
The performance of the ATR is compared to the static columns in Figure 6 for 100 ppm strontium at a residence time of 15 min. Presented are the determined qe values from the MDR model, for both 1 and 2 cm diameter (Ø) columns, in addition to the 25 and 34 cm active column length ATR in (a), as well as the 50% breakthrough level in (b). The figures also give the liquid flowrate (Q) through each system. It is noted that for the ATR experiments, the bulk flow rate is actually slightly lower for the longer 34 cm column in comparison to the 25 cm length (despite the same 15 min active residence time) due to the reduction in overall tube volume with the longer active column.
It is evident from Figure 6 that the 34 cm ATR column system considerably outperforms both static column systems. The qe value is around 30% greater than the 2 cm static column (and around 35% greater than the 1 cm diameter column), while the 50% breakthrough level is increased to around 40% greater than the 2 cm column. This increase in performance is assumed to be due to the lateral shear of the reactor causing enhanced mixing between the fluid and the resin, increasing the adsorption kinetics from the purely diffusion limited rate attainable in the static columns. Similar enhancements in mass transfer have been evidenced in high centrifuge rotating bed reactors [50,51]; however, the ATR has the advantage that the column residence times can be easily independently controlled, giving additional operational flexibility and control for this type of intensified system.
The increase in performance is even more considerable when the differences in the process flowrate (Q) are analysed. As the 1 cm-diameter column has a much smaller volume, the flowrate (at 0.314 mL/min) cannot be correlated directly to the ATR. Nevertheless, the larger 2 cm column is of the same order of size, where the mass of the static column is around half that of the 34 cm length ATR, while the process flow rate is only ~1/6 that of the ATR (1.257 mL/min against 6.217 mL/min, respectively). Therefore, for a comparative column volume, the ATR would achieve almost three times the volume of treated liquid for a given time (because of its lower tube to column ratio). When this increase in process liquid capacity is considered along with the enhanced material performance from the lateral mixing, an industrial-scale ATR system would require a significantly smaller footprint than traditional static columns, a key focus of process intensification [35].

4. Conclusions

This study compared the performance of static column ion exchange with a process intensified agitated tube reactor (ATR) for the separation of caesium and strontium ions from nuclear effluents using natural-grade clinoptilolite. In column ion exchange studies, it was found that caesium had a ~10× greater removal efficiency than strontium with 200 ppm solutions. Column performance envelopes were further evaluated using strontium systems, where there was a significant improvement in the strontium removal when the concentration was reduced to 100 ppm, with the 50% breakthrough level occurring after 400 bed volumes. In comparison, minimising the residence time from 30 to 15 min reduced the 50% breakthrough level to ~100 bed volumes. Scale-up parameterisation was also considered, where doubling the column diameter to 2 cm resulted in a marginal relative increase in performance. The breakthrough kinetic data of all systems were fitted with the Thomas and Modified Dose Response (MDR) models, with adsorption capacities (qe) directly correlated to previous batch adsorption experiments using the same systems [26]. It was highlighted that for 30 min residence time conditions, 100 ppm strontium and 200 ppm caesium systems were operating at close to the maximum adsorption capacity of the material, indicating optimum column operation. For the intensified ATR comparison, two effective column lengths were considered (25 and 34 cm), where the 34 cm length system was found to materially outperform the static columns by ~30% (in terms of both qe and breakthrough values) due to the enhanced mixing and adsorption kinetics from the lateral shear imparted in the ATR. Critically, the ATR was able to operate at much greater relative flow rates of 2–3× those possible in static columns due to the smaller column to tube volume ratio. Such performance increases would result in a significant reduction in the overall industrial footprint of ion exchange columns, where the ATR could be incorporated into mobile, modular units for nuclear effluent treatment with flexible operating capacity.

Supplementary Materials

The following are available online at https://www.mdpi.com/2305-7084/5/1/9/s1: Figure S1: Particle size distribution of clinoptilolite after sieving; Figure S2: The breakthrough of caesium at 5 ppm initial concentration; Figure S3: Linearised column breakthrough fits for caesium and strontium solutions at 200 ppm; Figure S4: Linearised column breakthrough fitting for strontium at 100 ppm; Figure S5: Experimental breakthrough data as well as Thomas and MDR fitting models for strontium at 100 ppm concentration for two systems with identical residence times (15 min) and the same adsorbent volume; Figure S6: Linearised breakthrough fitting data from the agitated tubular reactor ATR; Figure S7: Preliminary breakthrough data from the agitated tubular reactor (ATR) with a 12 cm column length (for 100 ppm strontium). Table S1a–e—raw dataset for column breakthrough experiments. Table S2a,b raw dataset for ATR breakthrough experiments.

Author Contributions

M.Y.P.: Conceptualization, Methodology, Validation, Formal analysis, Investigation, Resources, Writing—original draft, Funding acquisition. M.T.: Conceptualization, Validation, Visualization. D.H.: Supervision, Funding acquisition, Writing—review and editing. T.N.H.: Conceptualization, Supervision, Resources, Funding acquisition, Writing—review and editing. All authors have read and agreed to the published version of the manuscript.

Funding

M.Y.P. and M.T. were fully funded by the Indonesia Endowment Fund for Education (LPDP). T.N.H. and D.H. received additional funding from the Engineering and Physical Sciences Research Council (EPSRC), UK, and the University of Leeds, through an Impact Acceleration Account (EP/R511717/1).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The authors thank the listed funding agencies (LPDP, EPSRC, University of Leeds) for financial support. We would also like to gratefully acknowledge Robert Ash and AM Technology for the use of the pilot-scale CofloreTM ATR.

Conflicts of Interest

We wish to confirm that there is no known conflict of interest associated with this publication, and there has been no significant financial support for this work that could have influenced its outcome, apart from the grant funding listed in the funding and acknowledgements.

References

  1. Budnitz, R.J. Strontium-90 and Strontium-89: A Review of Measurement Techniques in Environmental Media. In Proceedings of the 3rd InterAmerican Meeting on Radiochemistry, Sao Paulo, Brazil, 2–6 December 1974; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 1974; p. 15. [Google Scholar]
  2. Ojovan, M.I.; Lee, W.E. An Introduction to Nuclear Waste Immobilisation, 2nd ed.; Elsevier: Oxford, UK, 2014; pp. 75–97. [Google Scholar]
  3. Nagasaki, S.; Nakayama, S. Radioactive Waste Engineering and Management; Springer: Tokyo, Japan, 2015; pp. 17–46. [Google Scholar]
  4. De Haro-Del Rio, D.A.; Al-Jubouri, S.; Kontogiannis, O.; Papadatos-Gigantes, D.; Ajayi, O.; Li, C.; Holmes, S.M. The removal of caesium ions using supported clinoptilolite. J. Hazard. Mater. 2015, 289, 1–8. [Google Scholar] [CrossRef]
  5. Lehto, J.; Koivula, R.; Leinonen, H.; Tusa, E.; Harjula, R. Removal of Radionuclides from Fukushima Daiichi Waste Effluents. Sep. Purif. Rev. 2019, 48, 122–142. [Google Scholar] [CrossRef]
  6. Smičiklas, I.; Dimović, S.; Plećaš, I. Removal of Cs1+, Sr2+ and Co2+ from aqueous solutions by adsorption on natural clinoptilolite. Appl. Clay Sci. 2007, 35, 139–144. [Google Scholar] [CrossRef]
  7. Abusafa, A.; Yücel, H. Removal of 137 Cs from aqueous solutions using different cationic forms of a natural zeolite: Clinoptilolite. Sep. Purif. Technol. 2002, 28, 103–116. [Google Scholar] [CrossRef]
  8. Olatunji, M.A.; Khandaker, M.U.; Mahmud, H.N.M.E.; Amin, Y.M. Influence of adsorption parameters on cesium uptake from aqueous solutions—A brief review. RSC Adv. 2015, 5, 71658–71683. [Google Scholar] [CrossRef]
  9. Dyer, A.; Hriljac, J.; Evans, N.; Stokes, I.; Rand, P.; Kellet, S.; Harjula, R.; Moller, T.; Maher, Z.; Heatlie-Branson, R. The use of columns of the zeolite clinoptilolite in the remediation of aqueous nuclear waste streams. J. Radioanal. Nucl. Chem. 2018, 318, 2473–2491. [Google Scholar] [CrossRef] [Green Version]
  10. Fu, F.; Wang, Q. Removal of heavy metal ions from wastewaters: A review. J. Environ. Manag. 2011, 92, 407–418. [Google Scholar] [CrossRef] [PubMed]
  11. Xu, Y.; Gu, P.; Zhang, G.; Wang, X. Investigation of coagulation as a pretreatment for microfiltration in cesium removal by copper ferrocyanide adsorption. J. Radioanal. Nucl. Chem. 2017, 313, 435–444. [Google Scholar] [CrossRef]
  12. Ortiz-Oliveros, H.B.; Flores-Espinosa, R.M.; Jiménez-Domínguez, H.; Jiménez-Moleón, M.C.; Cruz-González, D. Dissolved air flotation for treating wastewater of the nuclear industry: Preliminary results. J. Radioanal. Nucl. Chem. 2012, 292, 957–965. [Google Scholar] [CrossRef]
  13. Ding, D.; Zhang, Z.; Chen, R.; Cai, T. Selective removal of cesium by ammonium molybdophosphate—Polyacrylonitrile bead and membrane. J. Hazard. Mater. 2017, 324, 753–761. [Google Scholar] [CrossRef]
  14. Aziz, M.; Beheir, S.G. Removal of 60Co and 134Cs from radioactive process waste water by flotation. J. Radioanal. Nucl. Chem. 1995, 191, 53–66. [Google Scholar] [CrossRef]
  15. Boglaienko, D.; Emerson, H.P.; Katsenovich, Y.P.; Levitskaia, T.G. Comparative analysis of ZVI materials for reductive separation of 99Tc(VII) from aqueous waste streams. J. Hazard. Mater. 2019, 380, 120836. [Google Scholar] [CrossRef]
  16. James, A.M.; Harding, S.; Robshaw, T.; Bramall, N.; Ogden, M.D.; Dawson, R. Selective Environmental Remediation of Strontium and Cesium Using Sulfonated Hyper-Cross-Linked Polymers (SHCPs). ACS Appl. Mater. Interfaces 2019, 11, 22464–22473. [Google Scholar] [CrossRef] [Green Version]
  17. Zhang, H.; Hodges, C.S.; Mishra, P.K.; Yoon, J.Y.; Hunter, T.N.; Lee, J.W.; Harbottle, D. Bio-Inspired Preparation of Clay–Hexacyanoferrate Composite Hydrogels as Super Adsorbents for Cs+. ACS Appl. Mater. Interfaces 2020, 12, 33173–33185. [Google Scholar] [CrossRef] [PubMed]
  18. Shiels, J.; Harbottle, D.; Hunter, T.N. Synthesis and physical property characterisation of spheroidal and cuboidal nuclear waste simulant dispersions. Materials 2018, 11, 1235. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  19. Awual, M.R.; Yaita, T.; Kobayashi, T.; Shiwaku, H.; Suzuki, S. Improving cesium removal to clean-up the contaminated water using modified conjugate material. J. Environ. Chem. Eng. 2020, 8, 103684. [Google Scholar] [CrossRef]
  20. Zhang, H.; Kim, Y.K.; Hunter, T.N.; Brown, A.P.; Lee, J.W.; Harbottle, D. Organically modified clay with potassium copper hexacyanoferrate for enhanced Cs+ adsorption capacity and selective recovery by flotation. J. Mater. Chem. A 2017, 5, 15130–15143. [Google Scholar] [CrossRef] [Green Version]
  21. Valcke, E.; Engels, B.; Cremers, A. The use of zeolites as amendments in radiocaesium-and radiostrontium-contaminated soils: A soil-chemical approach. Part I: Cs-K exchange in clinoptilolite and mordenite. Zeolites 1997, 18, 205–211. [Google Scholar] [CrossRef]
  22. Valcke, E.; Engels, B.; Cremers, A. The use of zeolites as amendments in radiocaesium-and radiostrontium-contaminated soils: A soil-chemical approach. Part II: Sr-Ca exchange in clinoptilolite, mordenite, and zeolite A. Zeolites 1997, 18, 212–217. [Google Scholar] [CrossRef]
  23. Faghihian, H.; Marageh, M.G.; Kazemian, H. The use of clinoptilolite and its sodium form for removal of radioactive cesium, and strontium from nuclear wastewater and Pb2+, Ni2+, Cd2+, Ba2+ from municipal wastewater. Appl. Radiat. Isot. 1999, 50, 655–660. [Google Scholar] [CrossRef]
  24. Figueiredo, B.R.; Cardoso, S.P.; Portugal, I.; Rocha, J.; Silva, C.M. Inorganic Ion Exchangers for Cesium Removal from Radioactive Wastewater. Sep. Purif. Rev. 2018, 47, 306–336. [Google Scholar] [CrossRef]
  25. Ararem, A.; Bouras, O.; Bouzidi, A. Batch and continuous fixed-bed column adsorption of Cs+ and Sr2+ onto montmorillonite–iron oxide composite: Comparative and competitive study. J. Radioanal. Nucl. Chem. 2013, 298, 537–545. [Google Scholar] [CrossRef]
  26. Prajitno, M.Y.; Harbottle, D.; Hondow, N.; Zhang, H.; Hunter, T.N. The effect of pre-activation and milling on improving natural clinoptilolite for ion exchange of cesium and strontium. J. Environ. Chem. Eng. 2020, 8, 102991. [Google Scholar] [CrossRef]
  27. Moraetis, D.; Christidis, G.E.; Perdikatsis, V. Ion exchange equilibrium and structural changes in clinoptilolite irradiated with β-and γ-radiation: Monovalent cations. Am. Mineral. 2007, 92, 1714–1730. [Google Scholar] [CrossRef]
  28. Brooks, K.P. Cesium Ion Exchange Using Actual Waste: Column Size Considerations; Pacific Northwest National Laboratory: Richland, WA, USA, 1996; p. 40. [Google Scholar]
  29. El-Kamash, A. Evaluation of zeolite A for the sorptive removal of Cs+ and Sr 2+ ions from aqueous solutions using batch and fixed bed column operations. J. Hazard. Mater. 2008, 151, 432–445. [Google Scholar] [CrossRef]
  30. Patel, H. Fixed-bed column adsorption study: A comprehensive review. Appl. Water Sci. 2019, 9, 45. [Google Scholar] [CrossRef] [Green Version]
  31. Cortés-Martínez, R.; Olguín, M.; Solache-Ríos, M. Cesium sorption by clinoptilolite-rich tuffs in batch and fixed-bed systems. Desalination 2010, 258, 164–170. [Google Scholar] [CrossRef]
  32. Borai, E.H.; Harjula, R.; Malinen, L.; Paajanen, A. Efficient removal of cesium from low-level radioactive liquid waste using natural and impregnated zeolite minerals. J. Hazard. Mater. 2009, 172, 416–422. [Google Scholar] [CrossRef] [PubMed]
  33. Coward, T.; Tribe, H.; Harvey, A.P. Opportunities for process intensification in the UK water industry: A review. J. Water Process Eng. 2018, 21, 116–126. [Google Scholar] [CrossRef] [Green Version]
  34. Stankiewicz, A.I.; Moulijn, J.A. Process intensification: Transforming chemical engineering. Chem. Eng. Prog. 2000, 96, 22–34. [Google Scholar]
  35. Wang, H.; Mustaffar, A.; Phan, A.N.; Zivkovic, V.; Reay, D.; Law, R.; Boodhoo, K. A review of process intensification applied to solids handling. Chem. Eng. Process. Process Intensif. 2017, 118, 78–107. [Google Scholar] [CrossRef]
  36. Hunter, T.N.; Pugh, R.J.; Franks, G.V.; Jameson, G.J. The role of particles in stabilising foams and emulsions. Adv. Colloid Interface Sci. 2008, 137, 57–81. [Google Scholar] [CrossRef] [PubMed]
  37. Prajitno, M.Y.; Tangparitkul, S.; Zhang, H.; Harbottle, D.; Hunter, T.N. The effect of cationic surfactants on improving natural clinoptilolite for the flotation of cesium. J. Hazard. Mater. 2021, 402, 123567. [Google Scholar] [CrossRef]
  38. Zhang, H.; Tangparitkul, S.; Hendry, B.; Harper, J.; Kim, Y.K.; Hunter, T.N.; Lee, J.W.; Harbottle, D. Selective separation of cesium contaminated clays from pristine clays by flotation. Chem. Eng. J. 2019, 355, 797–804. [Google Scholar] [CrossRef]
  39. Maciejewski, P.; Walkowiak, W.; Robak, W. Selective removal of Cs-137, Sr-90, Ba-133, Co-60 and Pb-210 radioisotopes with proton-ionizable lariat ethers in the ion flotation process. Radioisotopes 2005, 2, R1. [Google Scholar]
  40. Shakir, K.; Ghoneimy, H.F.; Beheir, S.G.; Refaat, M. Flotation of Cesium Coprecipitated with Nickel Hexacyanoferrate(II) from Aqueous Solutions and Radioactive Waste Simulants. Sep. Sci. Technol. 2007, 42, 1341–1365. [Google Scholar] [CrossRef]
  41. Shakir, K.; Sohsah, M.; Soliman, M. Removal of cesium from aqueous solutions and radioactive waste simulants by coprecipitate flotation. Sep. Purif. Technol. 2007, 54, 373–381. [Google Scholar] [CrossRef]
  42. Zouboulis, A.; Peleka, E.; Zamboulis, D.; Matis, K. Application of Flotation for the Separation of Metal-Loaded Resins. Sep. Sci. Technol. 2005, 40, 861–876. [Google Scholar] [CrossRef]
  43. Ortiz-Oliveros, H.B.; Flores-Espinosa, R.M. Design of a mobile dissolved air flotation system with high rate for the treatment of liquid radioactive waste. Process Saf. Environ. Prot. 2020, 144, 23–31. [Google Scholar] [CrossRef]
  44. Nagar, A.; Pradeep, T. Clean Water through Nanotechnology: Needs, Gaps, and Fulfillment. ACS Nano 2020, 14, 6420–6435. [Google Scholar] [CrossRef]
  45. Kheshti, Z.; Ghajar, K.A.; Moreno-Atanasio, R.; Neville, F.; Ghasemi, S. Investigating the high gradient magnetic separator function for highly efficient adsorption of lead salt onto magnetic mesoporous silica microspheres and adsorbent recycling. Chem. Eng. Process. Process Intensif. 2020, 148, 107770. [Google Scholar] [CrossRef]
  46. Kim, J.-H.; Kim, S.-M.; Yoon, I.-H.; Kim, I. Application of polyethylenimine-coated magnetic nanocomposites for the selective separation of Cs-enriched clay particles from radioactive soil. RSC Adv. 2020, 10, 21822–21829. [Google Scholar] [CrossRef]
  47. Lodha, H.; Jachuck, R.; Singaram, S.S. Intensified Biodiesel Production Using a Rotating Tube Reactor. Energy Fuels 2012, 26, 7037–7040. [Google Scholar] [CrossRef]
  48. Modak, J.B.; Bhowal, A.; Datta, S. Experimental study and mathematical modeling of breakthrough curve in rotating packed bed. Chem. Eng. Process. Process Intensif. 2016, 99, 19–24. [Google Scholar] [CrossRef]
  49. Visscher, F.; van der Schaaf, J.; Nijhuis, T.A.; Schouten, J.C. Rotating reactors—A review. Chem. Eng. Res. Des. 2013, 91, 1923–1940. [Google Scholar] [CrossRef]
  50. Wu, Y.; Chang, C.-C.; Guan, C.-Y.; Chang, C.-C.; Li, J.-W.; Chang, C.-Y.; Yu, C.-P. Enhanced removal of ammonium from the aqueous solution using a high-gravity rotating packed bed loaded with clinoptilolite. Sep. Purif. Technol. 2019, 221, 378–384. [Google Scholar] [CrossRef]
  51. Ng, Y.-S.; Tan, Y.-T.; Chua, A.S.M.; Hashim, M.A.; Sen Gupta, B. Removal of nickel from water using rotating packed bed contactor: Parametric studies and mode of operations. J. Water Process Eng. 2020, 36, 101286. [Google Scholar] [CrossRef]
  52. Brunet, L.; Prat, L.; Casamatta, G.; Carvin, P. An Innovative Pulsed Column Applied to Solid-Liquid Contacting the BPC Column. Chem. Eng. Technol. 2006, 29, 729–735. [Google Scholar] [CrossRef]
  53. Charton, S.; Duhamet, J.; Borda, G.; Ode, D. Axial dispersion in pulsed disk and doughnut columns: A unified law. Chem. Eng. Sci. 2012, 75, 468–477. [Google Scholar] [CrossRef]
  54. Jones, E.; McClean, K.; Housden, S.; Gasparini, G.; Archer, I. Biocatalytic oxidase: Batch to continuous. Chem. Eng. Res. Des. 2012, 90, 726–731. [Google Scholar] [CrossRef]
  55. Derksen, J.J. Mixing in an agitated tubular reactor. Can. J. Chem. Eng. 2019, 97, 523–527. [Google Scholar] [CrossRef] [Green Version]
  56. He, Y.; Bayly, A.E.; Hassanpour, A.; Fairweather, M.; Muller, F. Flow behaviour of an agitated tubular reactor using a novel dynamic mesh based CFD model. Chem. Eng. Sci. 2020, 212, 115333. [Google Scholar] [CrossRef]
  57. He, Y.; Bayly, A.E.; Hassanpour, A.; Muller, F.; Wu, K.; Yang, D. A GPU-based coupled SPH-DEM method for particle-fluid flow with free surfaces. Powder Technol. 2018, 338, 548–562. [Google Scholar] [CrossRef]
  58. Thomas, H.C. Chromatography: A Problem in Kinetics. Ann. N. Y. Acad. Sci. 1948, 49, 161–182. [Google Scholar] [CrossRef] [PubMed]
  59. Thomas, H.C. Heterogeneous Ion Exchange in a Flowing System. J. Am. Chem. Soc. 1944, 66, 1664–1666. [Google Scholar] [CrossRef]
  60. Yan, G.; Viraraghavan, T.; Chen, M. A New Model for Heavy Metal Removal in a Biosorption Column. Adsorpt. Sci. Technol. 2001, 19, 25–43. [Google Scholar] [CrossRef]
  61. Endo, M.; Yoshikawa, E.; Muramatsu, N.; Takizawa, N.; Kawai, T.; Unuma, H.; Sasaki, A.; Masano, A.; Takeyama, Y.; Kahara, T. The removal of cesium ion with natural Itaya zeolite and the ion exchange characteristics. J. Chem. Technol. Biotechnol. 2013, 88, 1597–1602. [Google Scholar] [CrossRef]
  62. Rajec, P.; Domianová, K. Cesium exchange reaction on natural and modified clinoptilolite zeolites. J. Radioanal. Nucl. Chem. 2007, 275, 503–508. [Google Scholar] [CrossRef]
  63. Rajec, P.; Macášek, F.; Feder, M.; Misaelides, P.; Šamajová, E. Sorption of caesium and strontium on clinoptilolite-and mordenite-containing sedimentary rocks. J. Radioanal. Nucl. Chem. 1998, 229, 49–55. [Google Scholar] [CrossRef]
  64. Amanipour, S.; Faghihian, H. Potassium hexacyanoferrate–clinoptilolite adsorbent for removal of Cs+ and Sr2+ from aqueous solutions. Int. J. Environ. Stud. 2017, 74, 86–104. [Google Scholar] [CrossRef]
  65. Ames, L.L., Jr. Effect of base cation on the cesium kinetics of clinoptilolite. Am. Mineral. 1962, 47, 1310–1316. [Google Scholar]
  66. Dyer, A. Use of zeolites in the treatment of nuclear waste. Anal. Proc. 1993, 30, 190–191. [Google Scholar] [CrossRef] [Green Version]
  67. NDA. Ion Exchange Material (Clinoptilolite) and Sand; Nuclear Decommissioning Authority: Cumbria, UK, 2013. [Google Scholar]
  68. Xu, Z.; Cai, J.-G.; Pan, B.-C. Mathematically modeling fixed-bed adsorption in aqueous systems. J. Zheijang Univ. Sci. A 2013, 14, 155–176. [Google Scholar] [CrossRef] [Green Version]
  69. Valisko, M.; Boda, D.; Gillespie, D. Selective adsorption of ions with different diameter and valence at highly charged interfaces. J. Phys. Chem. C 2007, 111, 15575–15585. [Google Scholar] [CrossRef]
  70. Ersoy, B.; Çelik, M.S. Electrokinetic properties of clinoptilolite with mono-and multivalent electrolytes. Microporous Mesoporous Mater. 2002, 55, 305–312. [Google Scholar] [CrossRef]
  71. Woods, R.-M.; Gunter, M.E. Na-and Cs-exchange in a clinoptilolite-rich rock: Analysis of the outgoing cations in solution. Am. Mineral. 2001, 86, 424–430. [Google Scholar] [CrossRef]
  72. Nightingale, E., Jr. Phenomenological theory of ion solvation. Effective radii of hydrated ions. J. Phys. Chem. 1959, 63, 1381–1387. [Google Scholar] [CrossRef]
  73. Mihaly-Cozmuta, L.; Mihaly-Cozmuta, A.; Peter, A.; Nicula, C.; Tutu, H.; Silipas, D.; Indrea, E. Adsorption of heavy metal cations by Na-clinoptilolite: Equilibrium and selectivity studies. J. Environ. Manag. 2014, 137, 69–80. [Google Scholar] [CrossRef]
  74. Tansel, B.; Sager, J.; Rector, T.; Garland, J.; Strayer, R.F.; Levine, L.; Roberts, M.; Hummerick, M.; Bauer, J. Significance of hydrated radius and hydration shells on ionic permeability during nanofiltration in dead end and cross flow modes. Sep. Purif. Technol. 2006, 51, 40–47. [Google Scholar] [CrossRef]
  75. Ames, L.L., Jr. Characterization of a strontium-selective zeolite. Am. Mineral. 1962, 47, 1317–1326. [Google Scholar]
  76. Ararem, A.; Bouzidi, A.; Mohamedi, B.; Bouras, O. Modeling of fixed-bed adsorption of Cs+ and Sr2+ onto clay–iron oxide composite using artificial neural network and constant–pattern wave approach. J. Radioanal. Nucl. Chem. 2014, 301, 881–887. [Google Scholar] [CrossRef]
  77. Foster, R.I.; Amphlett, J.T.M.; Kim, K.-W.; Kerry, T.; Lee, K.; Sharrad, C.A. SOHIO process legacy waste treatment: Uranium recovery using ion exchange. J. Ind. Eng. Chem. 2020, 81, 144–152. [Google Scholar] [CrossRef]
  78. McCabe, D.J. Comprehensive Scale Testing of the Ion Exchange Removal of Cesium and Technetium from Hanford Tank Wastes. In Proceedings of the Waste Management 01, Tucson, AZ, USA, 25 February–1 March 2001. [Google Scholar]
  79. Sana, D.; Jalila, S. A comparative study of adsorption and regeneration with different agricultural wastes as adsorbents for the removal of methylene blue from aqueous solution. Chin. J. Chem. Eng. 2017, 25, 1282–1287. [Google Scholar] [CrossRef]
  80. Lee, C.-G.; Kim, J.-H.; Kang, J.-K.; Kim, S.-B.; Park, S.-J.; Lee, S.-H.; Choi, J.-W. Comparative analysis of fixed-bed sorption models using phosphate breakthrough curves in slag filter media. Desalination Water Treat. 2015, 55, 1795–1805. [Google Scholar] [CrossRef]
Chemengineering 05 00009 g001 550
Figure 1. Schematic diagrams showing (a) static vertical ion exchange column and (b) agitated tubular reactor (ATR) with a horizontal ion exchange column.
Figure 1. Schematic diagrams showing (a) static vertical ion exchange column and (b) agitated tubular reactor (ATR) with a horizontal ion exchange column.
Chemengineering 05 00009 g001
Chemengineering 05 00009 g002 550
Figure 2. Rendered image highlighting the motion of the inner agitator and outer tube of the ATR.
Figure 2. Rendered image highlighting the motion of the inner agitator and outer tube of the ATR.
Chemengineering 05 00009 g002
Chemengineering 05 00009 g003 550
Figure 3. Static column breakthrough curve data for caesium and strontium at 200 ppm concentration and 30 min residence time, along with the Thomas and Modified Dose Response (MDR) model fits.
Figure 3. Static column breakthrough curve data for caesium and strontium at 200 ppm concentration and 30 min residence time, along with the Thomas and Modified Dose Response (MDR) model fits.
Chemengineering 05 00009 g003
Chemengineering 05 00009 g004 550
Figure 4. Static column breakthrough data for strontium contamination at 100 ppm concentration, highlighting the effect of concentration, residence time, and column scale-up, along with Thomas and Modified Dose Response (MDR) model fits.
Figure 4. Static column breakthrough data for strontium contamination at 100 ppm concentration, highlighting the effect of concentration, residence time, and column scale-up, along with Thomas and Modified Dose Response (MDR) model fits.
Chemengineering 05 00009 g004
Chemengineering 05 00009 g005 550
Figure 5. Agitated Tubular Reactor (ATR) breakthrough data, along with Thomas and Modified Dose Response (MDR) model fits, for strontium at a 100 ppm concentration and residence times of 15 min for two different bed lengths (25 cm and 34 cm).
Figure 5. Agitated Tubular Reactor (ATR) breakthrough data, along with Thomas and Modified Dose Response (MDR) model fits, for strontium at a 100 ppm concentration and residence times of 15 min for two different bed lengths (25 cm and 34 cm).
Chemengineering 05 00009 g005
Chemengineering 05 00009 g006 550
Figure 6. (a) The maximum adsorption capacity (qe) and (b) number of bed volumes (BVs) for a 50% breakthrough (Ce/C0 = 0.5) for both 1 cm- and 2 cm-diameter (Ø) static columns and the agitated tube reactor (ATR) for two different column lengths. All the data for strontium are at a 100 ppm concentration and a 15 min residence time.
Figure 6. (a) The maximum adsorption capacity (qe) and (b) number of bed volumes (BVs) for a 50% breakthrough (Ce/C0 = 0.5) for both 1 cm- and 2 cm-diameter (Ø) static columns and the agitated tube reactor (ATR) for two different column lengths. All the data for strontium are at a 100 ppm concentration and a 15 min residence time.
Chemengineering 05 00009 g006
Table
Table 1. Fitted Thomas and Modified Dose Response (MDR) model parameters for 6 cm-depth static column breakthrough tests with Cs+ and Sr2+.
Table 1. Fitted Thomas and Modified Dose Response (MDR) model parameters for 6 cm-depth static column breakthrough tests with Cs+ and Sr2+.
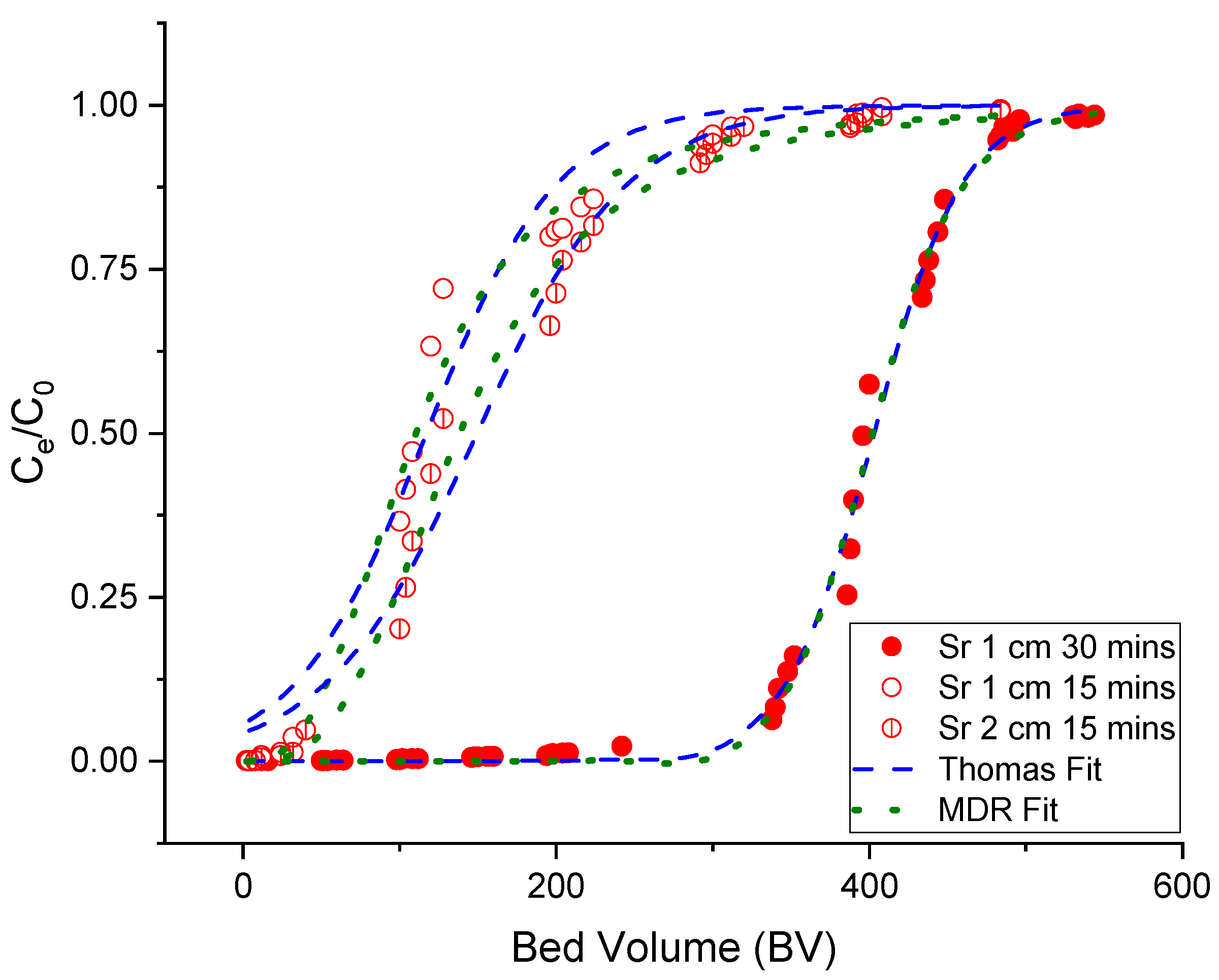
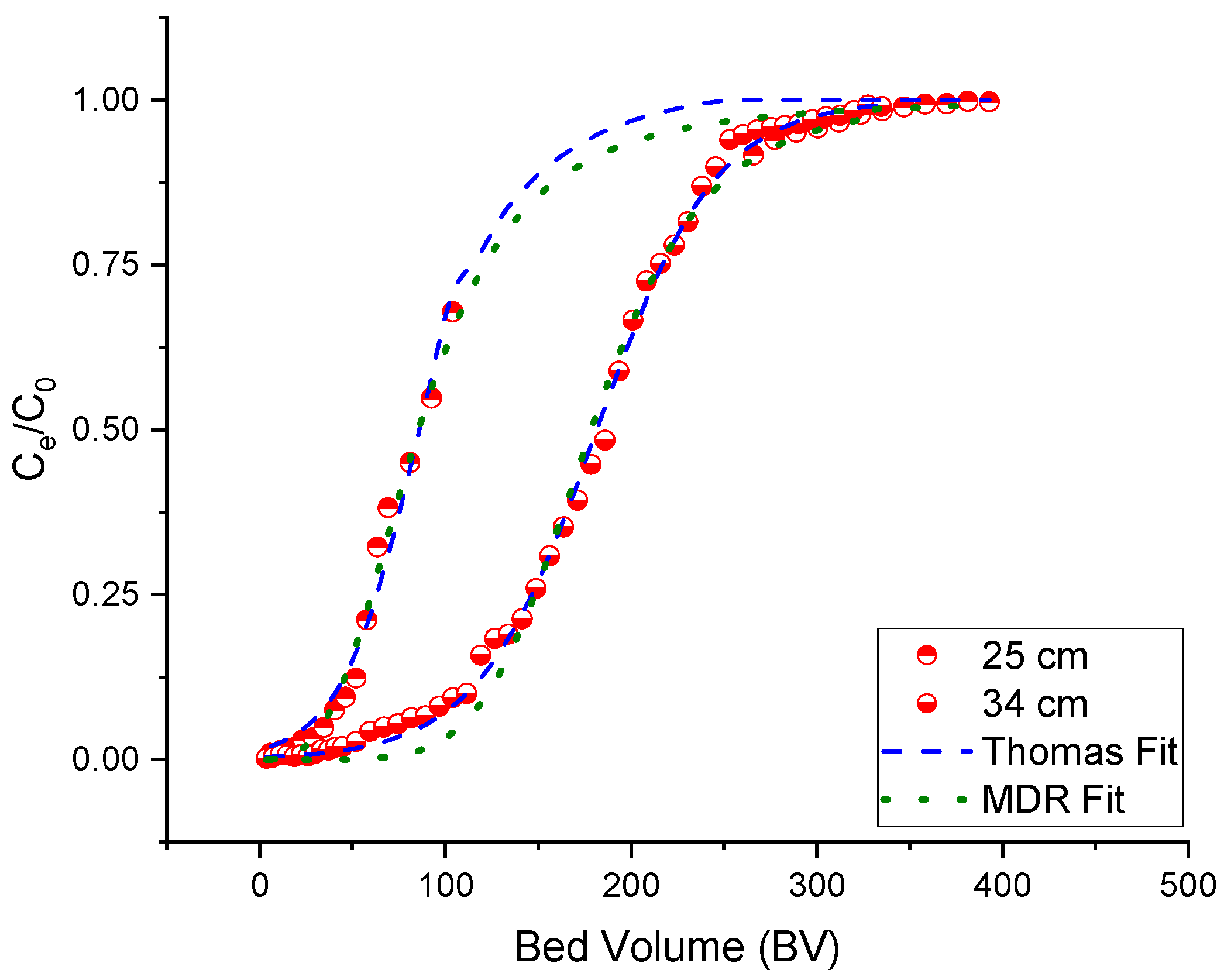
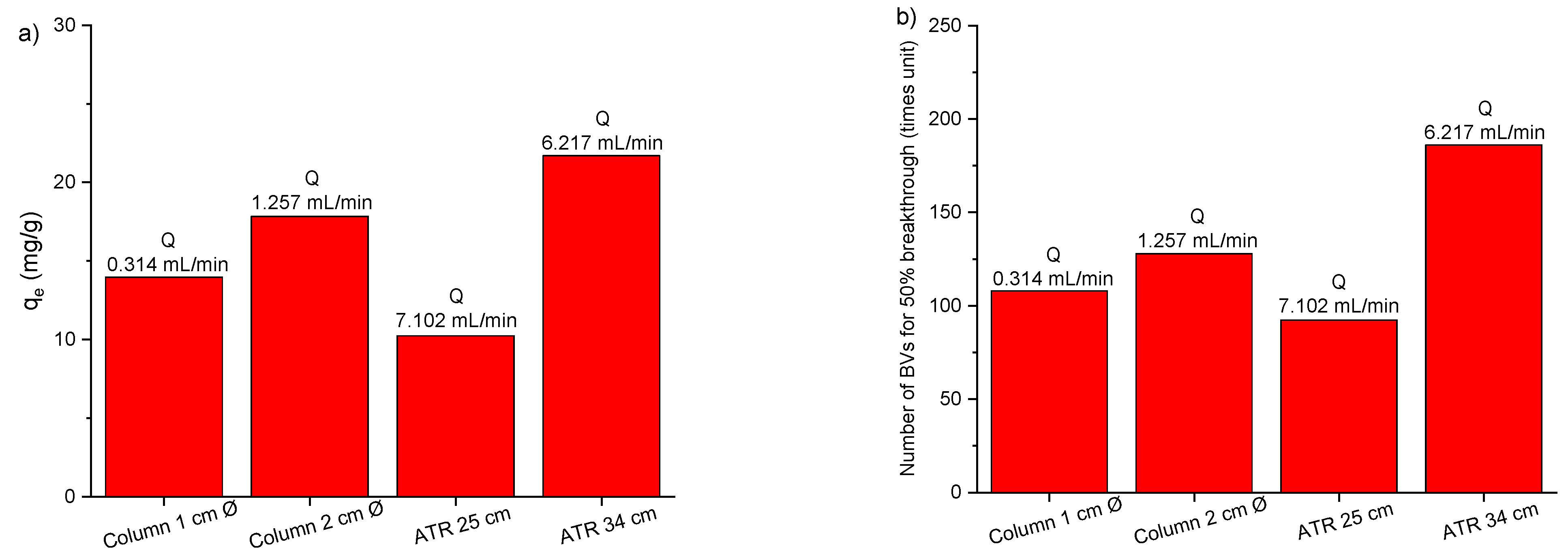
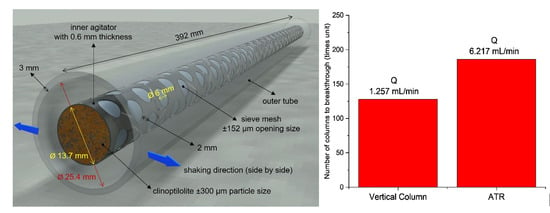
Experimental ParametersThomas ModelMDR Model
Diameter (cm)C0 (ppm)Q (mL/min)KTH (mL/mg·min)qe (mg/g)R2qe (mg/g)R2
Cs+ (30 min residence time)
12000.1570.002171.900.912170.440.941
Sr2+ (30 min residence time)
12000.1570.00415.310.98116.670.948
11000.1570.01248.100.97847.960.985
Sr2+ (15 min residence time)
11000.3140.01613.970.92513.150.962
21001.2570.01417.830.95416.510.968
Table
Table 2. Fitted Thomas and Modified Dose Response (MDR) model parameters for agitated tubular reactor (ATR) breakthrough tests. Sr2+ concentration was set at a 100 ppm concentration and trials maintained a 15 min residence time along the active column length.
Table 2. Fitted Thomas and Modified Dose Response (MDR) model parameters for agitated tubular reactor (ATR) breakthrough tests. Sr2+ concentration was set at a 100 ppm concentration and trials maintained a 15 min residence time along the active column length.
Experimental ParametersThomas ModelMDR Model
Bed Depth (cm)Q (mL/min)KTH (mL/mg·min)qe (mg/g)R2qe (mg/g)R2
257.1020.09410.240.99310.200.957
346.2170.03921.680.98721.320.939
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Prajitno, M.Y.; Taufiqurrakhman, M.; Harbottle, D.; Hunter, T.N. Kinetic Studies of Cs+ and Sr2+ Ion Exchange Using Clinoptilolite in Static Columns and an Agitated Tubular Reactor (ATR). ChemEngineering 2021, 5, 9. https://doi.org/10.3390/chemengineering5010009

AMA Style

Prajitno MY, Taufiqurrakhman M, Harbottle D, Hunter TN. Kinetic Studies of Cs+ and Sr2+ Ion Exchange Using Clinoptilolite in Static Columns and an Agitated Tubular Reactor (ATR). ChemEngineering. 2021; 5(1):9. https://doi.org/10.3390/chemengineering5010009

Chicago/Turabian Style

Prajitno, Muhammad Yusuf, Mohamad Taufiqurrakhman, David Harbottle, and Timothy N. Hunter. 2021. "Kinetic Studies of Cs+ and Sr2+ Ion Exchange Using Clinoptilolite in Static Columns and an Agitated Tubular Reactor (ATR)" ChemEngineering 5, no. 1: 9. https://doi.org/10.3390/chemengineering5010009

APA Style

Prajitno, M. Y., Taufiqurrakhman, M., Harbottle, D., & Hunter, T. N. (2021). Kinetic Studies of Cs+ and Sr2+ Ion Exchange Using Clinoptilolite in Static Columns and an Agitated Tubular Reactor (ATR). ChemEngineering, 5(1), 9. https://doi.org/10.3390/chemengineering5010009

Article Metrics

Back to TopTop