Abstract
In this work volume-translated Peng–Robinson group contribution equation of state was used to calculate excess enthalpies. Four model systems were selected with the purpose to compare experimental and predicted enthalpy values at different temperatures. After the calculations were performed in Matlab software, results were verified with free software tool of Dortmunder Datenbank (DDB). In a next step, the mixing process and interaction forces were described on the basis of the sign and course of enthalpy values. The endothermic behavior of three systems could be well predicted, while for the most polar system, predictions were less precise. Furthermore, the discrepancy between experimental data from the literature and predicted values was discussed to evaluate the accuracy of the selected model. Lowest mean deviations (<75 J/mol and <15% at all temperatures) could be stated for alkane/benzene mixtures, while highest deviations could be again observed for the most polar mixture. Although the magnitude of deviations was in agreement with the literature, it could be shown that the selected temperature is of major importance for the quality of predictions. Furthermore, a review of different literature values for the n-hexane/benzene system could reveal that the reliability of experimental data has to be carefully checked.
1. Introduction
In order to design thermal separation processes, the knowledge of fundamental thermodynamic properties as well as equilibria conditions is necessary. Even if only binary mixtures are regarded, it is laborious to collect experimental data for every possible combination [1]. Therefore, predictive models are required that allow the description of binary and multiple component systems based on few adjustable parameters. One of the most used concepts is the so-called group contribution concept, which assumes that every mixture can be sufficiently described if the interaction between functional groups of the molecules inside the mixture are considered [2].
Originally, the group contribution concept was introduced for activity coefficient models in 1969 [3]. Shortly after the ASOG GC model, the UNIFAC model was presented and in the next years developed further by the University of Dortmund [3,4]. While in the first years a focus was set on a good description of vapor liquid equilibria, the model was continuously improved in order to describe excess enthalpies and activity coefficients with a satisfying accuracy as well [3]. However, the treatment of supercritical compounds and the prediction of other thermodynamic properties (gas solubilities, enthalpies, densities, heat capacities) is not possible with activity coefficient models [2,3,5]. For this purpose, the group contribution concept was extended to equations of state, and in 1991 the predictive Soave–Redlich–Kwong group contribution equation of state was presented [6]. Ten years later the volume-translated Peng–Robinson GC EOS was introduced by [7], mainly to address the weaknesses of PSRK EOS [5].
- One weakness of SRK EOS is that often inaccurate results are obtained for liquid densities. Therefore, the same phenomenon can be stated for PSRK EOS, too.
- Unsatisfactory results can be observed in many cases for activity coefficients at infinite dilution, heats of mixing, and for strongly asymmetric systems. This can be explained by the fact that the UNIFAC model, used in the mixing rule, is not able to predict those properties accurately.
In this article a focus will be set on the prediction of excess enthalpies. In general, excess properties are important tools to describe deviations from ideal behavior. In the case of liquid mixtures, they are defined as the difference between real and ideal solutions. Those differences can be directly attributed to the fact that interactions between the molecules in a mixture differ from those observed for the pure components. Excess enthalpies, also known as heats of mixing, are particularly suited to illustrate those interactions. A positive sign of excess enthalpy means that the mixing process is an endothermic event. The interactions between molecules in the mixture are therefore weaker compared with those which can be stated for pure components. In contrast, a negative value of excess enthalpy indicates an exothermic mixing process and stronger interactions. For some mixtures even both phenomena can be observed. The discriminating factor in those cases is the molar ratio of the components in the mixture [8,9].
Beside the fact that excess enthalpies give important hints for the caloric behavior of the mixing process, it is important to note that those values describe the temperature dependence of activity coefficients. Both properties are connected via the Gibbs–Helmholtz equation. Experimental data of excess enthalpies at different temperatures are important information used during the fitting procedure of parameters for group contribution models [3]. Nevertheless, investigations on how well group contribution models can predict excess enthalpies at different temperatures can rarely be found. A short overview about results reported in the literature for VTPR EOS is given in Table 1. On the basis of four selected model systems, the present paper gives a more detailed quantitative insight on how good predictions with VTPR EOS are.

Table 1.
Literature results for predictions of excess enthalpy at different temperatures using VTPR EOS.
2. Calculation of Excess Enthalpy Using VTPR EOS
Before the results will be presented, the equations that were used to calculate excess enthalpies are given within this section. The formula of VTPR EOS first mentioned by [7] can be seen in Equation (1). It is a so-called cubic equation of state, which connects the state variables temperature (T), pressure (P), and (molar) volume (v). The symbol R stands for the ideal gas constant.
The modifications in comparison with PSRK EOS can be seen if the three coefficients a, b, and c are regarded.
- For the calculation of parameter a, which accounts for attractive forces, a modified function (so-called Twu- function) is used (pure component i; see Equations (2) and (3). A proper description of the sub- and supercritical range is possible with the help of adjustable parameters L, M, N, and the usage of critical temperature () and pressure (). Compared with Mathias–Copeman- function, used in PSRK EOS, results are more reliable at high reduced temperatures [2,3]. The good applicability is also shown in recent publications; the authors of [15] could successfully model catalytic hydrogenation processes by modification of original Peng–Robinson EOS with Twu- function. For binary mixtures a new mixing rule leads to improved prediction accuracies (Formula (4)) [1,5,10]. The parameter z stands for the mole ratio of component i.
- In order to get a better description for asymmetric systems parameter b, which accounts for repulsive forces, is not calculated by a linear mixing rule (binary mixture). Instead, a quadratic mixing rule as shown in Equation (5) is used. For pure components the equation is similar to original PR EOS (Formula (6)) [5,10].
- With the introduction of parameter c a volume translation is implemented. Together with the usage of PR instead of SRK EOS, this leads to improved results for liquid densities. The volume translation parameter c for pure component i can be calculated on the basis of the difference between experimental density and the density calculated with PR EOS () at the reference temperature as shown in Equation (7) (temperature-independent volume translation) [1,7]. For all the compounds mentioned in this article, c values published by [1] were used. If binary mixtures are regarded, a simple linear mixing rule can be used (Equation (8)) [10].
For the application of the mixing rule (parameter a) the Gibbs energy () has to be derived. The residual part of UNIFAC model was proposed as suitable GC model [10]. Formulas (9)–(11) show the calculation based on the residual part of the activity coefficient of component i () and group activity coefficients for each individual subgroup k in the mixture () or for the pure component i () [4,5]. The number of the subgroup k in the compound i is considered with the parameter .
To achieve better results over a large temperature and pressure range similar to the modified UNIFAC model (Dortmund), three energy parameters , , and are adjusted to account for temperature-dependent interactions (often described as difference ) between different functional groups m and n (Formula (12)) [1,4]. Parameter is finally obtained.
Furthermore, the calculation of surface area fraction and group mole fraction X is given in Equations (13) and (14). The relative van der Waals group surface areas Q for the individual subgroups were either adopted from the PSRK model or adjusted for the VTPR model [5,16].
Excess enthalpies () can then be calculated with equations of state using the so-called residual enthalpies of mixture and pure components (Formula (15)) [5,17].
The residual enthalpy itself can be derived on the basis of mixing parameters for pure components (a, b, c) and the mixture as shown in Equation (16) [5]. In this formula z describes the compressibility factor .
Furthermore, the temperature derivative of parameter a must be calculated. This was done in agreement with the descriptions of [5,18]. First of all, on the basis of the mixing rule Equation (17) can be derived [5].
3. Results
To obtain the results for excess enthalpy, a program code was written in Matlab analysis software, which is built of four important parts:
- The main m-file that executes the program contains the basic information needed for the calculations (name of compounds, temperature, pressure) as well as experimental data of the system. The first mentioned information is passed to the excess enthalpy function.
- Calculations of excess enthalpy are performed in a function stored as separate file. It interacts not only with the main m-file but also with other functions described in the next point.
- In order to improve the clarity of the Matlab program, additional functions were written to read necessary data out of an Excel file, to calculate mixing parameters for pure components and the mixture, to carry out calculations of the part, and to differentiate the part with respect to temperature.
- The required pure component properties and the parameter for VTPR EOS were saved in an Excel file, which allows to use an extension of the program for other components in future. The data were retrieved from [1,12,13,16,19].
An illustration of the deviations between predicted results and experimental data is given in Figure 1. First of all, it is remarkable that three of four mixtures showed positive values of excess enthalpy, which means respective mixing processes are endothermic [8]. In all cases this behavior was predicted by VTPR EOS, too. Only for the mixture acetone/water heat was released during the mixing process (exothermic behavior) if the molar ratio of acetone was low (<0.3–0.5) [8]. Again, this course of enthalpy values was predicted by VTPR EOS. However, the molar ratio at which the excess enthalpy changed the sign was shifted.
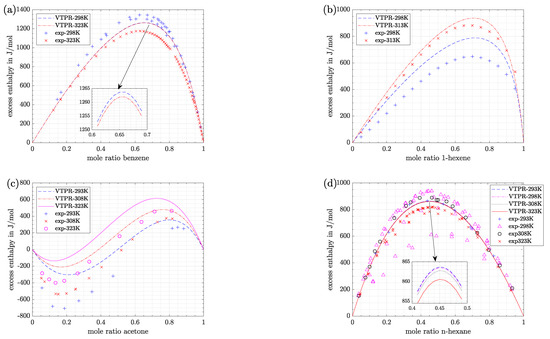
Figure 1.
Experimental and predicted values of selected model systems. (a) n-hexadecane/benzene (T = 298.15/323.15 K); experimental data: [20,21,22] (b) 1-hexene/n-BuOH (T = 298.15/313.15 K); experimental data: [23] (c) acetone/water (T = 293.15/308.15/323.15 K); experimental data: [24] (d) n-hexane/benzene (T = 293.15/298.15/308.15/323.15 K); experimental data: [21,25,26,27,28,29].
In addition, it can be seen that the system n-hexadecane/benzene showed the biggest values of excess enthalpy, which indicates that only weak interaction forces between the molecules can be found in the mixture (compared with pure components). Furthermore, the asymmetric curvature of the system 1-hexene/n-BuOH indicates that interaction forces between 1-hexene molecules clearly differ from those of n-BuOH molecules [8]. The opposite can be stated for the system n-hexane/benzene which gives an almost symmetric curvature course.
Finally, from this figure it is visible that the accuracy of predicted results depends on the temperature, which is regarded as follows:
- For the model system n-hexadecane/benzene (Figure 1a) predictions with VTPR EOS are nearly independent of temperature, although experimental data clearly differ at the selected temperatures. At low molar ratios of benzene a good fit can be stated when experimental data at 323.15 K are regarded, while at higher molar ratios the fit is better for a temperature of 298.15 K.
- For the model system 1-hexene/n-BuOH (Figure 1b) predictions are better for a temperature of 313.15 K. Although this time the predicted results show a temperature dependence at 298.15 K, a large gap between predicted and experimental data has to be stated.
- For the model system acetone/water (Figure 1c) deviations between experimental data and predicted values are rather big at all temperatures. Again, a temperature dependence can be stated for experimental as well as predicted values.
- For the model system n-hexane/benzene (Figure 1d) predicted results are nearly independent of temperature. Predictions are best for a temperature of 293.15 K. However, it is visible that experimental data itself show big fluctuations, especially at 298.15 K. This circumstance will be further discussed in the next section.
4. Discussion
Before entering a more profound discussion it seems worth to mention that the results obtained with Matlab software were compared with the predictions of DDB software tool. The values for absolute deviations of the selected model systems at different temperatures are given in Figure 2. Arithmetic mean average deviations (AMADs) were calculated as shown in Equation (26) using the values calculated with Matlab (), those given by DDB software tool (), and the total number of datapoints N. From Figure 2 the conclusion can be drawn that in all cases deviations were negligibly small (<0.05 J/mol in all cases), and therefore the Matlab code was accurate enough to return valid results.
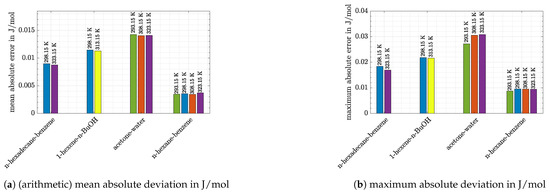
Figure 2.
Absolute deviations between results obtained with Matlab program and DDB software tool.
In a next step relative and absolute errors were calculated on the basis of experimental data and predicted values. Mean absolute values were calculated as shown in Formula (26), and arithmetic mean relative deviations (AMRD) were computed according to Equation (27) using results from Matlab (), experimental data (), and the total number of datapoints N.
In the last section it was already mentioned that the system n-hexane/benzene showed the biggest fluctuations in experimental data. Therefore, this system will be discussed at first. In Figure 3 experimental data from different sources measured at 25 °C are shown.
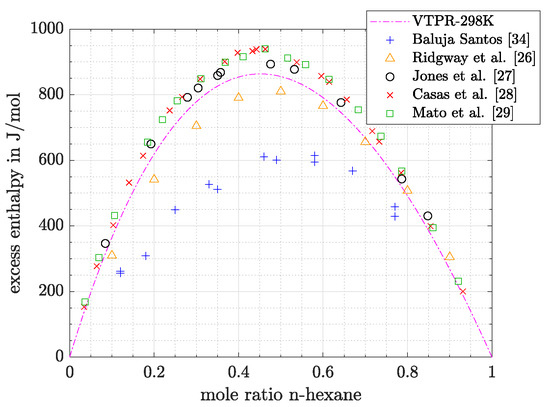
Figure 3.
Comparison between experimental data and predicted values of excess enthalpy (system n-hexane/benzene; T = 298.15 K).
On the basis of those data the following conclusions can be drawn:
- Highest values for heats of mixing are measured by the newest publications [28,29]. The authors used the same method (Calvet microcalorimeter) for their measurements and state an inaccuracy of excess enthalpy measurements below 1%.
- Slightly lower values for excess enthalpy are measured by Jones et al. [27]. A Brass calorimeter was used. Errors of this apparature were estimated to be below 2% for aqueous/alcohol solutions [30]. Jones et al. [27] compared their results graphically with those obtained by Prigogine et al. [31] and Schnaible et al. [32]. Good agreement between the three publications could be stated at molar ratios of benzene above 0.5, while at lower molar ratios results of Schnaible et al. [32] and Progogine et al. [31] were higher. Finally, excess enthalpies measured by Romani et al. [33] were in the same range as the results of Jones et al. [27], following descriptions of Mato et al. [29].
- Significantly lower values were measured by Ridgway et al. [26] and Baluja Santos [34]. The authors of the first mentioned publication measured their data in a Dewar vessel and state an accuracy around 1% [26]. According to the graphical presentation of Mato et al. [29], Andrade et al. [35] also obtained maximum values for excess enthalpy, which are comparable to those of Ridgway et al. [26].
The predictions of VTPR EOS show low deviations to most of the experimental data. This can be quantitatively confirmed with the help of mean absolute and relative errors, which are given in the following Figure 4.
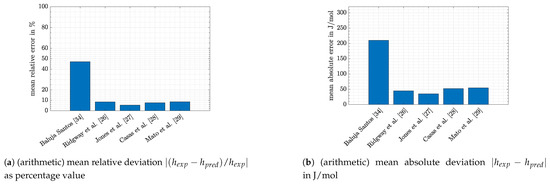
Figure 4.
Deviations between experimental and predicted values.
Except for the data of Baluja Santos [34], absolute mean deviations were below 55 J/mol and relative mean errors were below 10%. Together with the other literature data mentioned in the bullet points above, the results of Baluja Santos [34] seem to be questionable. However, for a final evaluation, a reliability check would be necessary. A proper description how this can be done mathematically is seldom described in the literature. Schmid [1] briefly stated that a polynomial function might be a useful tool, but no details are given. Another possibility might be an evaluation of the measurement aperture and its error sources, which lies beyond the scope of this article. Nevertheless, the big differences illustrate the importance of verifying that reliable experimental data are chosen in order to obtain accurate model predictions.
At this point the absolute and relative deviations of the three other systems should be introduced. Those are shown, together with deviations of n-hexane/benzene system at other temperatures, in the two bar charts in Figure 5.
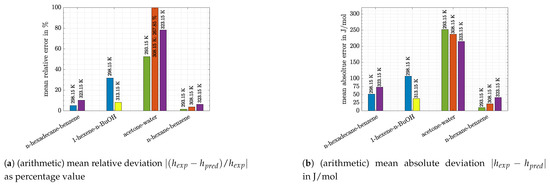
Figure 5.
Deviations between experimental and predicted values.
From these charts the following observations can be made:
- Again, it can be seen that the accuracy of predictions was temperature-dependent. Especially for the system 1-hexene/n-BuOH (absolute error 2.5 times higher at 298.15 K compared with the value at 313.15 K) the difference was pronounced for the temperatures which were investigated. However, it has to be noted that the deviations at 313.15 K were low (8.2% or 38 J/mol).
- For the system n-hexane/benzene the same temperature dependence can be stated, although differences were low at all temperatures shown in Figure 5 (<10% or <25 J/mol). For measurements at 298.15 K literature data were already discussed with the help of Figure 4. If the dataset of Baluja Santos [34] is not regarded, relative as well as absolute mean errors are close to those obtained at 323.15 K or slightly higher.
- The other alkane/benzene system (n-hexadecane/benzene) shows slightly higher error values (12–20% or 52–73 J/mol). For both systems it is striking that predictions of VTPR EOS were nearly temperature-independent (Figure 1a,d). An explanation can be given when the main group interaction parameters are regarded (see Table 2; main group 1-CH2 and 3-ACH are relevant). For those mixtures no energy parameter c was determined, which causes the temperature dependence of the derivative of to be missing (see also derivation of temperature derivation described in Section 2 and especially Formulas (24) and (25)).
 Table 2. Energy interaction parameters for the relevant main groups.
Table 2. Energy interaction parameters for the relevant main groups.
- Predictions exhibit the greatest deviations for the most polar system acetone/water, which is in agreement with the conclusion drawn based on Figure 1. The high relative and absolute errors (>50% and >200 J/mol) confirm that care must be taken if such a system is regarded. However, it can be said that with VTPR EOS still a tremendous improvement could be achieved compared to previous models. To underline this statement, the results for excess enthalpy of acetone/water system are shown for PSRK EOS in Figure 6.
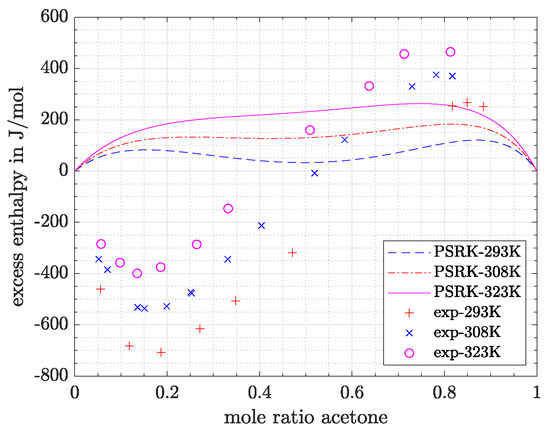 Figure 6. Prediction of excess enthalpy for the acetone/water system using PSRK EOS.
Figure 6. Prediction of excess enthalpy for the acetone/water system using PSRK EOS.
The above-mentioned error values raise the question whether the observed deviations are in agreement with the literature. To answer this question some sources should be named which deal with accuracy of predictions with GC models:
- Schmid [1] gives relative deviations for different group combinations using VTPR, PSRK, and the modified UNIFAC (Dortmund) model. For the combination HO/CHCO a value of ∼20% is given for the modified UNIFAC (Dortmund) and a value of ∼25% is given for VTPR EOS. However, no information on how these deviations were calculated or what data were used is described.
- Hayashi et al. [36] evaluated predictions of excess enthalpy data using the ASOG GC model. For 51% of 871 binary data sets the maximum absolute deviation is below 100 J/mol, but also for 21.8% a maximum deviation >300 J/mol was stated. For the predictions presented in this article, maximum absolute deviations were for 5 of 11 datasets (system at one temperature taken as dataset) below 100 J/mol, for 3 datasets deviations were between 100 and 150 J/mol, and 3 datasets showed even higher deviations.
- Gmehling et al. [37] gives a mean deviation of 30% or 103.8 J/mol from investigations of 6000 datasets using the modified UNIFAC model. Several authors describe that accuracy of predictions with VTPR EOS is comparable with the modified UNIFAC (Dortmund) model [1,2,3,12]. In the present work only mean deviations of acetone/water system were higher than 30%.
- Vigh et al. [38] gives deviations for excess enthalpy data predicted with the modified UNIFAC models (Lungby and Dortmund). For the system n-hexane/benzene a value 7.6% is given for a temperature range between 25 and 45 C, which is close to the predictions presented in this article if the results of Baluja Santos [34] are neglected. For the system acetone/water a relative deviation of 30.6% (25–35 C) was observed, but maximum experimental excess enthalpy was taken as reference value for all datapoints used for the calculation of relative errors. If this modification is applied to the datasets that were presented beforehand, a good agreement with the literature can be confirmed.
- Chen et al. [39] investigated deviations for the modified UNIFAC (Dortmund) model and PSRK model. For alkane/benzene systems a mean deviation of 66 J/mol or 6.6% is given for the modified UNIFAC (Dortmund) model, while for PSRK EOS clearly higher errors are mentioned (454 J/mol or 43%). If an accuracy close to modified UNIFAC (Dortmund) model is expected, a good agreement can be stated with regard to the results presented in this article (results of Baluja Santos [34] neglected).
Overall, it seems reasonable to conclude that the results are in an expected range. Finally, it has to be stressed that investigations with additional binary systems will give a clearer picture on how well experimental data can be predicted by VTPR EOS.
5. Conclusions
Excess enthalpy values of four selected model systems could be predicted using the volume-translated Peng–Robinson equation of state. The necessary calculations were performed with Matlab analysis software.
In a first step the results allowed to draw conclusions about the kind and strength of interaction forces in the mixture compared with pure components. In addition, the caloric behavior of the mixing process could be assessed. In three of four cases an endothermic mixing process, which corresponds with weaker interaction forces in the mixture (compared with pure components), could be stated. Only for the acetone/water system was an exothermic behavior (and therefore stronger interaction forces in the mixture) found for low molar ratios of acetone.
From the deviations between experimental and predicted data of the selected model systems, it could be shown that predictions of strongly polar systems is challenging: mean deviations for the system acetone/water were above 50% or 200 J/mol at all temperatures. In contrast, deviations were lowest for alkane/benzene systems reaching a minimum mean value of 1.6% or 10 J/mol for the system n-hexane/benzene at 20 C. Furthermore, especially for the systems n-hexane/benzene and 1-hexene/n-BuOH, the accuracy of predictions was strongly dependent on the temperature that was regarded. For the system 1-hexene/n-BuOH deviations at 25 C were 2.5 times (absolute values) or almost 4 times higher (relative values) than at 40 C.
Finally, a literature review of excess enthalpy measurements of n-hexane/benzene system at 25 C could underline the importance of carefully checking experimental data: while eight sources showed maximum values between 800 and 950 J/mol, one source presented maximum values of 650 J/mol.
6. Software
Matlab analysis software (version 2020b, Update 1, 64-bit) was used for all calculations.
To verify results Dortmund Data Bank Explorer Version 2015 (2.6.1.16) was used. The software can be downloaded from the following website: http://www.ddbst.com/free-software.html#New (accessed on 8 November 2020).
Evaluation of data was carried out in Microsoft Excel® (part of Microsoft 365 MsO package; 64-bit).
Author Contributions
Conceptualization, C.K.; data curation, C.K.; writing—original draft preparation, C.K.; writing—review and editing, B.C.S., U.K.; supervision, B.C.S., C.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data were retrieved from sources listed under references. A large database of freely accessible thermodynamic properties of pure compounds and mixtures can be found on the website of Dortmunder Datenbank: http://www.ddbst.com/free-data.html (accessed on 5 February 2021).
Conflicts of Interest
The authors declare no conflict of interest.
| List of Symbols | |
| a | parameter volume-translated Peng–Robinson equation of state, dm bar· mol |
| interaction parameter UNIFAC model, K | |
| b | parameter volume-translated Peng–Robinson equation of state, dm mol |
| interaction parameter UNIFAC model, - | |
| C | constant used for calculation of temperature derivative of parameter a, - |
| c | parameter volume-translated Peng–Robinson equation of state, dm mol |
| interaction parameter UNIFAC model, K | |
| D | constant used for calculation of temperature derivative of parameter a, - |
| g | molar Gibbs energy, J · mol |
| h | molar enthalpy, J · mol |
| L | parameter Twu--function, - |
| M | parameter Twu--function, - |
| N | parameter Twu--function, - |
| P | pressure, bar |
| Q | group surface area UNIFAC model, - |
| R | universal gas constant, J · mol K |
| T | absolute temperature, K |
| / | interaction parameter UNIFAC model, J · mol |
| v | molar volume, dm mol |
| number main group k in component i, - | |
| X | group mole fraction UNIFAC model, - |
| z | compressibility factor, - |
| , | molar ratio of component i/j, - |
| Greek Symbols | |
| temperature-dependent function to calculate parameter a of volume-translated | |
| Peng–Robinson equation of state | |
| activity coefficient | |
| group activity coefficient | |
| surface area fraction UNIFAC model | |
| temperature-dependent interaction parameter UNIFAC model | |
| Abbreviations | |
| AMAD | arithmetic mean absolute deviation |
| AMRD | arithmetic mean relative deviation |
| ASOG | Analytical Solutions of Groups |
| BuOH | butanol |
| EOS | equation of state |
| GC | group contribution |
| mod | modified |
| p | primary |
| PR | Peng–Robinson |
| PSRK | predictive Soave–Redlich–Kwong |
| SRK | Soave–Redlich–Kwong |
| UNIFAC | universial quasichemical theory functional group activity coefficients |
| VTPR | volume-translated Peng–Robinson |
| Superscripts | |
| E | excess |
| id | ideal |
| i | component i |
| Subscripts | |
| crit | critical |
| exp | experimental |
| i,j,k,m,n | component or functional group i/j/k/m/n |
| mix | mixture |
| P | constant pressure |
| PR | Peng–Robinson |
| pred | predicted |
| red | reduced |
| ref | reference |
| res | residual |
| T | constant temperature |
| constant molar ratio of component i |
References
- Schmid, B. Einsatz Einer Modernen Gruppenbeitragszustandsgleichung für die Synthese Thermischer Trennprozesse. Ph.D. Thesis, Carl von Ossietzky University, Oldenburg, Germany, 2011. [Google Scholar]
- Gmehling, J.; Constantinescu, D.; Schmid, B. Group Contribution Methods for Phase Equilibrium Calculations. Annu. Rev. Chem. Biomol. Eng. 2015, 6, 267–292. [Google Scholar] [CrossRef]
- Gmehling, J. Present status and potential of group contribution methods for process development. J. Chem. Thermodyn. 2009, 41, 731–747. [Google Scholar] [CrossRef]
- Fredenslund, A.; Jones, R.L.; Prausnitz, J.M. Group-contribution estimation of activity coefficients in nonideal liquid mixtures. Am. Inst. Chem. Eng. J. 1975, 21, 1086–1099. [Google Scholar] [CrossRef]
- Gmehling, J.; Kleiber, M.; Kolbe, B.; Rarey, J. Chemical Thermodynamics for Process Simulation, 2nd ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2019. [Google Scholar]
- Holderbaum, T.; Gmehling, J. PSRK: A Group Contribution Equation of State Based on UNIFAC. Fluid Phase Equilibria 1991, 70, 251–265. [Google Scholar] [CrossRef]
- Ahlers, J.; Gmehling, J. Development of an universal group contribution equation of state: I. Prediction of liquid densities for pure compounds with a volume translated Peng—Robinson equation of state. Fluid Phase Equilibria 2001, 191, 177–188. [Google Scholar] [CrossRef]
- Atkins, P.W.; de Paula, J. Physikalische Chemie, 5th ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2013; pp. 175–177. [Google Scholar]
- Stephan, P.; Schaber, K.; Stephan, K.; Mayinger, F. Thermodynamik- Grundlagen und Technische Anwendungen Band 2: Mehrstoffsysteme und Chemische Reaktionen, 15th ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 137–147. [Google Scholar]
- Ahlers, J.; Gmehling, J. Development of a Universal Group Contribution Equation of State. 2. Prediction of Vapor-Liquid Equilibria for Asymmetric Systems. Ind. Eng. Chem. Res. 2002, 41, 3489–3498. [Google Scholar] [CrossRef]
- Gmehling, J. Potential of group contribution methods for the prediction of phase equilibria and excess properties of complex mixtures. Pure Appl. Chem. 2003, 75, 875–888. [Google Scholar] [CrossRef]
- Schmid, B.; Schedemann, A.; Gmehling, J. Extension of the VTPR Group Contribution Equation of State: Group Interaction Parameters for Additional 192 Group Combinations and Typical Results. Ind. Eng. Chem. Res. 2014, 53, 3393–3405. [Google Scholar] [CrossRef]
- Schmid, B.; Gmehling, J. Present status of the group contribution equation of state VTPR and typical applications for process development. Fluid Phase Equilibria 2016, 425, 443–450. [Google Scholar] [CrossRef]
- Ahlers, J.; Gmehling, J. Development of a Universal Group Contribution Equation of State III. Prediction of Vapor-Liquid Equilibria, Excess Enthalpies, and Activity Coefficients at Infinite Dilution with the VTPR Model. Ind. Eng. Chem. Res. 2002, 41, 5890–5899. [Google Scholar] [CrossRef]
- Nikolaos, C.K. Modeling and simulation of biphasic catalytic hydrogenation of a hydroformylated fuel. Int. J. Hydrogen Energy 2020. [Google Scholar] [CrossRef]
- Schmid, B.; Gmehling, J. Revised parameters and typical results of the VTPR group contribution equation of state. Fluid Phase Equilibria 2012, 317, 110–126. [Google Scholar] [CrossRef]
- Fermeglia, M.; Kikic, I. Excess enthalpy calculations by means of equations of state. J. Therm. Anal. 1984, 29, 687–695. [Google Scholar] [CrossRef]
- Weidlich, U.; Gmehling, J. A modified UNIFAC model. 1. Prediction of VLE, hE, and γ∞. Ind. Eng. Chem. Res. 1987, 26, 1372–1381. [Google Scholar] [CrossRef]
- Horstmann, S.; Jabłoniec, A.; Krafczyk, J.; Fischer, K.; Gmehling, J. PSRK group contribution equation of state: Comprehensive revision and extension IV, including critical constants. Fluid Phase Equilibria 2005, 227, 157–164. [Google Scholar] [CrossRef]
- Peña, M.D.; Menduiña, C. Excess enthalpies at 298.15 K of binary mixtures of benzene with n-alkanes. J. Chem. Thermodyn. 1974, 6, 387–393. [Google Scholar]
- Peña, M.D.; Menduiña, C. Excess enthalpies at 323.15 K of binary mixtures of benzene with n-alkanes. J. Chem. Thermodyn. 1974, 6, 1097–1102. [Google Scholar]
- Lundberg, G.W. Thermodynamics of Solutions XI. Heats of Mixing of Hydrocarbons. J. Chem. Eng. Data 1964, 9, 193–198. [Google Scholar] [CrossRef]
- Aguilar, F.; Alaoui, F.E.M.; Segovia, J.J.; Villamañán, M.A.; Montero, E.A. Ether + alcohol + hydrocarbon mixtures in fuels and bio-fuels: Excess enthalpies of binary mixtures containing dibutyl ether (DBE) or 1-butanol and 1-hexene or methylcyclohexane or toluene or cyclohexane or 2,2,4-trimethylpentane at 298.15 K and 313.15 K. Fluid Phase Equilibria 2012, 315, 1–8. [Google Scholar] [CrossRef]
- Excess Enthalpy Data-Enthalpy of Mixing Data Set 1407. Available online: http://www.ddbst.com/en/EED/HE/HE%20Acetone%3BWater.php (accessed on 8 December 2020).
- Excess Enthalpy Data-Enthalpy of Mixing Data Set 2761. Available online: ttp://www.ddbst.com/en/EED/HE/HE%20Benzene%3BHexane.php (accessed on 8 December 2020).
- Ridgway, K.; Butler, P.A. Some Physical Properties of the Ternary System Benzene-Cyclohexane-n-Hexane. J. Chem. Eng. Data 1967, 12, 509–515. [Google Scholar] [CrossRef]
- Jones, H.K.; De, Q.; Lu, B.C.Y. Heats of Mixing of Liquids for the System Ethanol-Benzene-n-Hexane. J. Chem. Eng. Data 1966, 11, 488–492. [Google Scholar] [CrossRef]
- Casas, H.; Segade, L.; Franjo, C.; Jiménez, E.; Paz Andrade, M.I. Excess Molar Enthalpies of Propyl Propanoate + Hexane + Benzene at 298.15 K and 308.15 K. J. Chem. Eng. Data 2000, 45, 445–449. [Google Scholar] [CrossRef]
- Mato, M.M.; Balseiro, J.; Jiménez, E.; Legido, J.L.; Galiñanes, A.V.; Paz Andrade, M.I. Excess Molar Enthalpies and Excess Molar Volumes of the Ternary System 1,2-Dichlorobenzene + Benzene + Hexane at 298.15 K. J. Chem. Eng. Data 2002, 47, 1436–1441. [Google Scholar] [CrossRef]
- Lama, R.F.; Lu, B.C.-Y. Excess Thermodynamic Properties of Aqueous Alcohol Solutions. J. Chem. Eng. Data 1965, 10, 216–219. [Google Scholar] [CrossRef]
- Prigogine, I.; Mathot, V. Application of the Cell Method to the Statistical Thermodynamics of Solutions. J. Chem. Phys. 1952, 20, 49–57. [Google Scholar] [CrossRef]
- Schnaible, H.W.; Van Ness, H.C.; Smith, J.M. Heats of mixing of liquids. AIChE J. 1957, 3, 147–152. [Google Scholar] [CrossRef]
- Romani, L.; Paz-Andrade, M.I. Funciones termodinamicas de exceso a 25. C. III. Benceno + isoomeros del hexano. An. Quim. 1974, 70, 422–425. [Google Scholar]
- Baluja Santos, M.D.C. Aplicacion al estudio de sistemas binarios y ternarios. Acta Cient. Compostel. 1970, 70, 3–15. [Google Scholar]
- Paz-Andrade, M.I.; Regueiro, M. Entalpias de mezcla a temperaturas mediassistema hexanobenceno. Acta Cient. Compostel. 1970, 3–4, 147–152. [Google Scholar]
- Hayashi, H.; Tochigi, K.; Kojima, K. Prediction of excess enthalpy by using thirty-one ASOG groups. Ind. Eng. Chem. Res. 1992, 31, 2795–2804. [Google Scholar] [CrossRef]
- Gmehling, J. From UNIFAC to modified UNIFAC to PSRK with the help of DDB. Fluid Phase Equilibria 1995, 107, 1–29. [Google Scholar] [CrossRef]
- Vigh, L.; Kojima, K. Prediction of Excess Enthalpy and Excess Entropy Using Modified UNIFAC Group Contribution Methods. J. Chem. Eng. Jpn. 1996, 29, 881–884. [Google Scholar] [CrossRef][Green Version]
- Chen, J.; Fischer, K.; Gmehling, J. Modification of PSRK mixing rules and results for vapor–liquid equilibria, enthalpy of mixing and activity coefficients at infinite dilution. Fluid Phase Equilibria 2002, 200, 411–429. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).