Abstract
One of the hallmarks of ionic liquids (ILs) and a critical part of their sustainable implementation is their low volatility, although statements in this regard are frequently made in the absence of a critical evaluation. Although it is generally accepted that conventional ILs exhibit significantly reduced vapor pressures relative to common organic solvents, glib statements about ILs having zero volatility can no longer be abided, even if a concrete temperature-dependent vapor pressure, Pvap(T), framework for placement of IL performance has not yet been established. In this communication, Pvap(T) values of 30 illustrative low-volatility fluids—including representative imidazolium-, ammonium-, and pyrrolidinium-based aprotic ILs; examples of protic, polymeric, and di-cationic ILs; as well as deep eutectic solvents (DESs) and glycols—were determined using a simple, convenient, and reproducible isothermal thermogravimetric method. Guided by this “vapor pressure map”, observed trends can be discussed in terms of anion basicity, cation geometry, alkane chain length, hydrogen bonding strength, and van der Waals forces, providing a context for the placement of theoretical and experimental vapor pressures gleaned in future IL and DES studies.
1. Introduction
Ionic liquids (ILs) are a class of molten salts that possess unusually low melting points (generally less than 373.15 K) and a reputation for exhibiting essentially no vapor pressure (Pvap), properties that distinguish them from conventional solvents [1,2]. In addition, ILs are considered to be designer solvents because their physicochemical properties can be tuned by selective combination of cation and anion chemical identities. Perhaps more than a million binary mixtures and over 1012 ternary mixtures are possible, generating a need to analyze the physicochemical properties of ILs and elucidate trends to predict these properties for other ion pair combinations [3]. One of the more attractive features of ILs is their negligible Pvap, a property which has provoked their application in catalysis, extraction, absorption, and chromatography [4,5]. While this property was once thought to be so low as to be inconsequential, it can actually be measured under reduced pressure and/or high temperatures [6,7,8,9]. In 2005, Rebelo et al. [6] were the first to estimate the Pvap and normal boiling temperature of ILs based on experimental surface tension and density. Later, Earle et al. [7] reported the vacuum distillation of ILs using a Kugelrohr and sublimation apparatus at 473.15–573.15 K, with no signs of decomposition either in the distillate or residue. Both works showed that the Pvap of ILs can indeed be measured, which encouraged the study of their thermodynamic behavior (Pvap, enthalpy of vaporization (ΔvapH), distillation temperature, and boiling temperature) for a wide range of ILs using both experimental [10,11,12,13,14] and theoretical [15,16,17,18] methods. Rigorous determination of these properties could prove invaluable for gas-phase synthesis and purification of ILs, potentially allowing for IL distillation and alleviating long-standing issues regarding IL impurity.
Deep eutectic solvents (DESs) are an emerging class of liquids that are generally considered to be attractive alternatives to ILs due to similarities in their physicochemical properties [19,20] while being easier to prepare and purify, less expensive, less toxic, and more biodegradable and environmentally friendly. DESs should be more volatile at a given temperature because they contain molecular (non-ionic) components and rely instead on hydrogen bonding for component association, but to what extent is not well-known. Reports of efforts to measure Pvap and ΔvapH for DESs are extremely rare [21,22], but of particular note and related to this study, Shahbaz et al. [23] measured the volatile nature of DES mixtures using a thermogravimetric analysis method between 343.15 and 393.15 K.
Numerous techniques, including the Knudsen method [10,11], temperature-programmed desorption line of sight mass spectrometry (LOMS) [17,24], high-temperature absorbance (UV) spectroscopy [25], quartz crystal microbalance (QCM) analysis [14,26], calorimetry [16,27], transpiration [16,28], and thermogravimetric analysis (TGA) [13,29,30], have been utilized to measure the free evaporation process of ILs as a function of temperature. Notably, the use of TGA is straightforward, reliable, and reproducible, requiring minimal sample size and time allocation while allowing for a wide temperature range analysis under controlled conditions. Luo et al. [13] were the first to use an isothermal gravimetric method to determine the ΔvapH of 1-alkyl-3-methylimidazolium ([CnmIm+]) ILs (paired with [Tf2N−] or [beti−] anions, where n is the number of carbons in the alkyl chain; see structures in Figure S1) for an accuracy of ±3 kJ·mol−1. They observed two interesting outcomes: ΔvapH values for [CnmIm][Tf2N] were consistently ~5% higher than their [beti−] counterparts, and a methyl group at the C2 position in [CnmIm+] possesses a distinctly higher ΔvapH value relative to an analog with the same side chain length and no methylated C2.
A great deal of effort has been devoted to determining and understanding structure-property (ΔvapH) relationships for several series of ILs, although discrepancies still exist within these data. Recently, Deyko et al. [31] and Zaitsau et al. [32] analyzed the ΔvapH for a series of pyrrolidinium- and pyridinium-based ILs using LOMS and QCM-TGA, respectively. However, as ILs become more extensively applied in evolving technologies (e.g., Li-ion batteries, solar energy conversion, waste recycling, cellulose processing), the glaring issue is that they cannot be designed based on their Pvap and ΔvapH values. Therefore, a need exists to develop a simple method to measure or estimate the Pvap values of all classes of ILs at various temperatures.
We present a simple, straightforward, and reproducible TGA method to measure the Pvap of various ILs, DESs, and molecular solvents at various temperatures below their respective decomposition temperatures (Tdcp). A total of 30 low-volatility liquids were investigated, and their determined Pvap values were compared against those found in the literature. Structure-volatility trends are discussed in association with physiochemical properties, such as polarity scales (hydrogen-bond acidity (α), hydrogen-bond basicity (β), polarizability (π*), ET(30)), structural geometry, and distillation temperatures. These data will allow for the understanding and design of ILs and DESs with reduced vapor pressure in a host of applications.
2. Materials and Methods
2.1. Materials
All fluids investigated herein were either obtained commercially or were synthesized and purified in-house, as summarized in Table S1 of the Supplementary data. Purification was performed as specified in the supplied references for each liquid, with an example 1H-NMR spectrum for [C4mIm][Tf2N] provided in Figure S2. All fluids were dried under vacuum for at least 12 h at a temperature well below Tdcp prior to analysis. For instance, conventional ILs were dried at 343.15 K for 24 h.
2.2. Vapor Pressure Measurements
Thermogravimetric analysis was performed using either a TGA-Q50 V20.13 Build 39 (designated as TGA-1) or a Perkin Elmer TGA, Model 4000 (TGA-2). Sample weights were in the 10–80 mg range. A heating ramp of 10 °C·min−1 was used to bring samples from room temperature to their respective hold temperature. The isothermal gravimetric analysis was performed similarly to earlier work utilizing a 300 min hold period [13]. Samples were analyzed within a dry nitrogen stream at a flow rate of 60 mL·min−1 (TGA-1) or 20 mL·min−1 (TGA-2) to prevent sample oxidation. Uniform sample cross-sectional areas were maintained using platinum (TGA-1) or ceramic (TGA-2) crucibles. Four distinct analysis temperatures were selected for each sample based on the thermal stability shown in a scanning TGA experiment. Experimental isothermal temperatures were typically in the 100–160 (373.15–433.15 K) or 190–250 °C (463.15–523.15) range for ILs and in the 60–140 °C (333.15–413.15 K) regime for polyols and DESs. A fresh sample on a clean TGA pan (i.e., previously heated in air to 800 °C (1073.15 K) for 30 min in a Thermo Scientific™ Thermolyne™ benchtop muffle furnace, then allowed to cool to room temperature) was used for each temperature. Sigma Plot 11.0 software was used for statistical analysis and plotting.
2.3. Fluid Water Contents
As we demonstrated previously [13], disregarding the first 120 min of isothermal TGA data collection ensured that evaporation of minor traces of water did not contribute to the observed mass loss profiles. Indeed, the resulting thermograms were rigorously zero-order in mass loss and highly linear (r2 ≥ 0.99), consistent with clean evaporative loss of the fluid in question, with no discernible interference from water. The initial water contents (i.e., prior to the 120 min of in situ drying on the TGA instrument) for conventional hydrophobic, water-immiscible ILs (fluids #2, 6, 8–18, 21, and 30 in the Supplementary data) were in the range of 30–100 ppm, values that should be considered scrupulously dry [33]. The initial water contents for hydrophilic, water-miscible ILs (fluid #1, 3–5, 7, 19, and 20) fell in the 100–600 ppm range, and 500–2000 ppm for the protic IL propylammonium nitrate (PAN, #28) and the DESs, glycols, and polyols (fluid #22–27, 29, and 31). When considering the possible contribution from traces of water, it should be noted that water’s vapor pressure at the temperatures analyzed (313.15–623.15 K) falls in the 103–107 Pa range, which is orders of magnitude higher than that of the tested liquids, in some cases being as much as four or five orders of magnitude higher at a particular temperature.
3. Results and Discussion
In this work, 30 liquids were either acquired commercially or synthesized in-house. Detailed information, including solvent names, structures, abbreviations, Tdcp, densities, viscosities, and thermal stabilities, are compiled in Figures S1 and S3, and Table S1. Gückel et al. [34,35] have extensively studied the Pvap of pesticides using an isothermal gravimetric method at ambient pressure and suggested that the logarithm of the evaporation rate (k) of a substance at a given temperature is linearly proportional to the logarithm of vapor pressure at this temperature:
where Pvap is the vapor pressure of a substance (bar) at a given temperature and k is the corresponding evaporation rate (%·min−1). The coefficients (a and b) are dependent on the instrument, operational conditions (e.g., gas purge rate), and sample containment procedures [36]. This proportionality is reported to be independent of the sample and the temperature range [13,23,37,38]. Glycerol was used as a reference compound to attain the instrument constants for our TGA instrument (TGA-1) because the Pvap data are well-established. Figure 1 illustrates the typical isothermal mass loss of glycerol under nitrogen purge, yielding linear curves (pseudo-zeroth-order) with r2 ≥ 0.99 (note that temperatures greater than 353.15 K produced more linear mass losses with r2 ≥ 0.9998). This linear relationship provides evidence that vaporization is the sole cause of mass loss in the absence of sample degradation or evolution of impurities. A range of holding temperatures was chosen to acquire instrument coefficients. Further, the evaporation rates of glycerol are comparable with repetitive measurements (Figure 1B) and consistent with those found in the literature [37]. Hereafter, mean evaporation rate values measured on TGA-1 were used to estimate Pvap data. Experiments were repeated on a different TGA instrument (denoted TGA-2), under similar conditions (see experimental section for details).
ln(Pvap) = a ln(k) + b
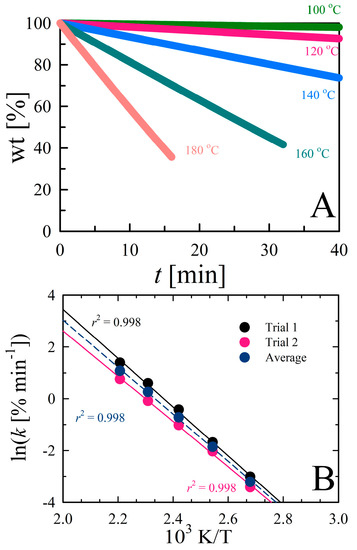
Figure 1.
(A) Normalized mass loss curves for glycerol determined at various temperatures under nitrogen purge. (B) Comparison of temperature-dependent glycerol evaporation rates measured using isothermal gravimetry for two different trials. The average response for this particular apparatus (TGA-1) is denoted by the dashed profile.
Figure S4 and Table S2 provide the determined evaporation rates, suggesting that isothermal vaporization of glycerol is comparable between instruments. Figure S5 shows the Pvap data of glycerol obtained from the literature and the results correlate with each other, suggesting the reproducibility and consistency of the data. The standard glycerol Pvap data from the literature [37,39] and the evaporation rates measured in this work were plotted according to Equation (1). Figure 2 shows a linear correlation between the Pvap and rates of glycerol evaporation estimated using TGA-1 and -2, with r2 = 0.995.
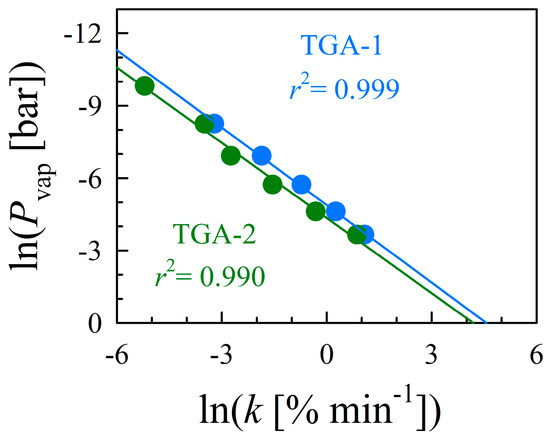
Figure 2.
The linear relationship between the natural logs of both the evaporation rates of glycerol and their corresponding Pvap as reported in the literature [37,39]. The theoretical line is obtained by fitting the data to Equation (1) with r2 = 0.995. Coefficients a and b represent the constants of Equation (1), which are dependent on the instrument and operational parameters.
The instrument coefficients of Equation (1) for TGA-1 and TGA-2 are: a = 1.14 ± 0.03 and 0.98 ± 0.02, and b = −5.04 ± 0.07 and −4.47 ± 0.06, respectively. The a and b coefficients of the two instruments exhibit high precision and produced values within 8% of each other. Thus, we conservatively estimate that any calculated Pvap values will be reliable to within 10% if the instrument conditions remain constant (e.g., crucible area, gas purge rate). By substituting the measured coefficients into Equation (1), the Pvap of any substance can be calculated on a per-instrument basis.
3.1. Vapor Pressure Determination for [C4mIm][Tf2N]
Figure 3 illustrates the thermal stability and normalized time-dependent isothermal gravimetric analysis of [C4mIm][Tf2N]. The Tdcp (Table S1, entry 8) was determined by finding the temperature at which 10% mass loss was observed after initial solvent evaporation. Four distinct temperatures (463.15, 483.15, 503.15, and 523.15 K) below Tdcp were chosen for isothermal measurements. The first 120 min of the isotherm were discarded to eliminate solvent evaporation from our analysis, after which the remaining data were normalized with respect to mass to obtain a rigorously linear correlation (r2 = 0.9999), with a slope that represents the evaporation rate for [C4mIm][Tf2N] at the respective temperature. Since TGA-1 was used for these experiments, Equation (2) was used to predict each corresponding Pvap (i.e., 0.1497, 0.2523, 0.9834, and 2.0647 Pa at 463.15, 483.15, 503.15, and 523.15 K, respectively). The thermal stabilities of 29 other liquids were measured in an analogous manner (Figure S3), isothermal gravimetric analysis temperatures were chosen accordingly, and their respective Pvap values were calculated and are tabulated in Table S3.
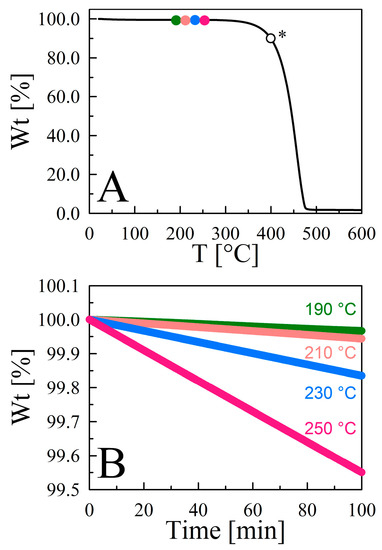
Figure 3.
(A) Thermal stability of [C4mIm][Tf2N] under nitrogen purge at a constant flow rate of 60 mL·min−1 from room temperature to 600 °C (873.15 K) at a heating rate of 10 °C·min−1. The color of the symbols on the thermograms in panel A corresponds to the isothermal gravimetric weight loss curves in the lower panel. The open symbol marked * denotes the Tdcp (672.65 K) for this sample. (B) A normalized magnification showing the rigorously linear (r2 ≥ 0.9999) evaporation curves of [C4mIm][Tf2N] at different temperatures.
As seen in Table S3 and Figure 4, the Pvap values for ILs are in the range of 1.4 × 10−3 to 26.80 Pa at 373.15–523.15 K. The Pvap for [C4mIm][Tf2N] and [C6mIm][Tf2N] (Table S3, entries 8 and 9, respectively) have been studied using a variety of techniques and reported [10,11,26,40]. Several of these literature values are plotted with the Pvap values determined here to facilitate a more thorough assessment of our data (Figure S6A). The plot suggests that our vapor pressure results are in reasonably good agreement with the literature data, in particular with Brunetti et al. [40] and Rocha et al. [26]. However, the Pvap value obtained by Aschenbrenner et al. [29] for [C4mIm][Tf2N] at 393.15 K (1.2 Pa) is several orders of magnitude greater than our Pvap under similar conditions (2.029 × 10−3 Pa), despite using a similar TGA instrument. As our data closely matches literature data, we suggest that this discrepancy may be attributed to either the presence of impurities or solvent in their IL or the significantly brief evaporation period that they examined (10 min). In general, the evaporation rates (and therefore Pvap) for ILs decrease as the alkyl chain lengthens. This is due to the non-electrostatic interactions (i.e., van der Waals force) outweighing the electrostatic interactions (Coulombic force) because of efficient packing of alkyl chains and increased molecular weight, which results in greater electron density for polarization [12]. However, the volatility of [C6mIm][Tf2N] is indistinguishable from [C4mIm][Tf2N] (a finding that is consistent with those of Zaitsau et al. [11], Rocha et al. [26], and Rebelo et al. [6]), see Figure S6B, so this effect appears to be insignificant within the experimental temperature range for a two hydrocarbon difference.
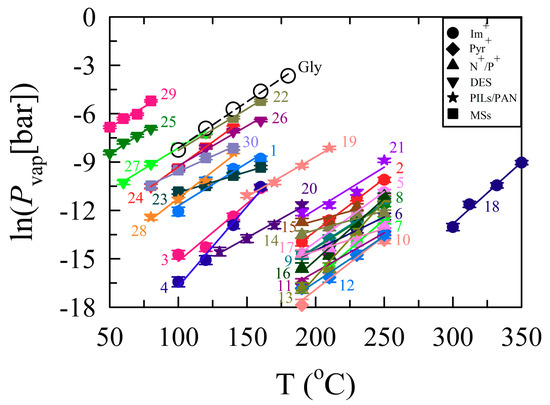
Figure 4.
A map illustrating isothermal-gravimetry-determined temperature-dependent vapor pressure for representative ionic liquids (ILs), deep eutectic solvents (DESs), and miscellaneous low-volatility fluids. The individual solvents are identified numerically corresponding to the entries of Table S3 in the Supplementary Information. The solid lines connecting experimental values for a given liquid denote linear regression fits for vapor pressure data and are shown primarily to guide the eye. Legend abbreviations: Im+: imidazolium; Pyr+: pyrrolidinium; N+/P+: ammonium/phosphonium; PILs/PAN: polyionic liquids/propylammonium nitrate; MSs: molecular solvents. 1: [C2mIm][EtSO4]; 2: [C2mIm][beti]; 3: [C4mIm][Br]; 4: [C4mIm][dca]; 5: [C4mIm][BF4]; 6: [C4mIm][PF6]; 7: [C4mIm][TfO]; 8: [C4mIm][Tf2N]; 9: [C6mIm][Tf2N]; 10: [C3mPy][Tf2N]; 11: [C4mPy][Tf2N]; 12: [C6mPy][Tf2N]; 13: [Nip311][Tf2N]; 14: [N6111][Tf2N]; 15: [N8111][Tf2N]; 16: [N8881][Tf2N]; 17: [P14,666][Tf2N]; 18: [C3(C1Im)2] [Tf2N]2; 19: p([VBBIm][Cl]); 20: p([VBIm][Br]); 21: p([VBIm][Tf2N]); 22: PEG 200; 23: PEG 600; 24: Reline; 25: Ethaline; 26: Glyceline; 27: Bu4NBr:Im; 28: PAN; 29: Triglyme; 30:[Li(trigly)][Tf2N]; Gly: Glycerol.
3.2. Effect of the Anion on IL Vapor Pressure
The size, shape, and nucleophilicity of the anions in ILs play a crucial role in determining the intermolecular forces that exist between the ions in the liquid phase, including ion–ion interactions, hydrogen bonding, polarizability, and van der Waals forces. However, very recently, Tokuda et al. [41,42] reported that the ab initio molecular orbital calculations of cation–anion interaction energies in [C2mIm]-based ILs were −85.2, −82.6, −78.8, and −78.4 kcal·mol−1 for [BF4−], [TfO−], [Tf2N−], and [PF6−], respectively. These interaction energies clearly indicate that [C4mIm+] is more interactive with [BF4−] than [PF6−], therefore exhibiting a higher Pvap. In contrast, ILs involving [Tf2N−] vaporize more readily than those with [TfO−] at all temperatures even though the interactive energy and basicity values of [Tf2N−] are lower than those of the [TfO−] anion. This is likely caused by the slow diffusion of triflate salts due to high solution viscosity [43]. Additionally, this trend coincides with distillation work reported by Earle et al. [7] and Widegren et al. [12]. As a result, the observed vaporization trend for ILs with a similar cation and different anions is as follows: Br− > [dca−] > [BF4−] > [Tf2N−] > [PF6−] > [TfO−]. Figure S7 displays a comparison between the present results and literature data [16,44] for [C4mIm][PF6] and [C4mIm][dca].
3.3. Effect of the Cation on IL Vapor Pressure
Interestingly, the Pvap values of pyrrolidinium- and ammonium-based [Tf2N−] ILs (Table S3, entries 10–17) are less than those of the [CnmIm][Tf2N] IL series [12]. We attribute this to the planar geometry of [Im+], which bistriflamide can effectively approach and form a stable ion pair reinforced through hydrogen bonding. The tetrahedral geometries of [Py+] and [R4N+] complicate this interaction [12]. Therefore, the structure-volatility series determined in this study for different cation classes at 523.15 K is [C6mIm+] > [N6111+] > [C4mPy+]. Our results are in agreement with the solvatochromic polarity parameters of ILs and the experiments conducted in other groups, signifying that the aromatic compounds are more volatile than the non-aromatic compounds due to geometry [12,41,42,45].
In the case of [Nip311][Tf2N], the low-temperature Pvap is much lower than those of other long-chain alkyl groups, likely because the branched alkyl group influences the charge on the center and isolates the anion. Further, [P14,666][Tf2N] exhibits a lower Pvap at higher temperatures when compared to [N8881][Tf2N] and [C3(C1Im)2][Tf2N]2 (Table S3, entries 17, 16, and 18, respectively). This decrease in volatility with increased alkyl chain length is attributed to the potential for longer-chain alkyl groups to pack more efficiently, resulting in increasing van der Waals interactions that ultimately outweigh the decreasing Coulombic interactions to decrease volatility [12]. Further, the di-cationic [C3(C1Im)2][Tf2N]2 has a much lower Pvap result when compared to similar mono-cationic [Cnmim][Tf2N] ILs, likely because the di-cationic species requires more energy to vaporize one mole of the neutral ion pair than an equivalent one mole of mono-cationic IL [44].
3.4. Vapor Pressure of Polyols
PEG 200 and triglyme (and the other polyol derivatives to a lesser extent) exhibited the highest Pvap values of any liquid tested in Figure 4 and Table S3. This finding is attributed to their lower molecular weights. The Pvap value found on a chemical database [46] for triglyme at 293.15 K is 0.12 kPa compared to the extrapolated Pvap (~0.02 kPa) in this study. As the database did not provide any explicit experimental details, we believe that our measurements are within the range of uncertainties. In addition, when comparing the Pvap of triglyme to its IL analog [Li(trigly)][Tf2N] (Table S3, entry 30), we noted that the addition of Li+ and [Tf2N−] provides strong Coulombic interactions, increasing the ionic character and density of the solvent while simultaneously decreasing the observed Pvap by over 2 orders of magnitude at 353.15 K [47]. Notably, this striking change in Pvap provides fundamental insight into the consequences with regard to solvent physicochemical properties of turning glymes into complex ions, a finding that may not be possible to correlate with other similar systems (e.g., crown ethers). PEG 600 (Table S3, entry 23) exhibits a similar decrease in Pvap when compared to PEG 200 due to an increase in molecular weight through the extension of the PEG chain [47]. Similar to what was observed previously, the Pvap values measured by Aschenbrenner et al. [29] for PEG 200 and PEG 600 at 368.15 K are 9.9 and 0.2 Pa, respectively, which are 2–8 times lower than our estimated values (19.86, and 1.77 Pa, respectively).
3.5. Vapor Pressure of DESs
We note that, strictly speaking, it is not currently possible to satisfactorily determine the vapor pressure for a deep eutectic solvent, given the lack of knowledge about the relative vapor pressures of the components when mixed and the possible evolution of component volatility during extensive evaporation. That is to say, estimating Pvap values for a DES system is complicated by the fact that DESs comprise two or more components (most typically, this means a salt pair plus a neutral hydrogen bond donor species) interacting via dynamic hydrogen bonding and it is not possible, by evaporation alone, to assert the nature of the volatile fraction. Whereas ion pairs are often assumed to be predominantly lost during ionic liquid evaporation a priori (and computational evidence exists to support this) [48], the neutral species is likely to display relatively higher volatility in the DES, complicating matters. Thus, any pronounced mass loss for a DES system likely corresponds to a change in the composition of the components over time. Having stated these caveats, we include representative DES vapor pressure data alongside our other studies for reasons of operational utility, as they still guide useful temperature regimes of application. That is, despite not representing rigorous vapor pressures for the reasons just outlined, we include DES vapor pressure values derived from thermogravimetric analysis to place them in useful context with values displayed by ionic liquids and other molecular solvents, with the understanding that they represent “apparent” Pvap values. Moreover, despite these stated limitations, Pvap values have in fact already been reported for typical DESs.
Table S3 and Figure 4 display the Pvap of four DES mixtures (entries 24–27), which fall in the range of 2.12–161.95 Pa at 313.15–433.15 K. These values are lower than their individual components due to strong intermolecular hydrogen bonding interactions between the hydrogen bond donator and a quaternary ammonium salt (choline chloride) in the mixtures. For instance, glyceline (Table S3, entry 26) possesses vapor pressures of 6.97 Pa at 373.15 K and 161.9 Pa at 433.15 K, which makes it 3.7–6.0 times less volatile than glycerol (Pvap = 26 and 980 Pa) [39] at the respective temperatures. The structure-volatility series for the DES mixtures containing choline chloride but with different hydrogen bond donors is ethaline > reline > glyceline (most to least volatile), emphasizing that ethaline is one of the most volatile DESs. This trend agrees with solvent polarity (ET(30) and α) values reported in the literature and TGA experiments conducted by Shahbaz et al. [23,49]. Figure S8 shows the temperature dependence of measured values against the Shahbaz data for reline and glyceline. The glyceline Pvap determined here coincides with their data, while we observe higher values for reline in our study.
3.6. Vapor Pressures of Protic ILs
Protic ILs are a subset of ILs that possess properties similar to those of typical ILs [50]. Of particular note, ethylammonium nitrate (EAN) and to a lesser extent propylammonium nitrate (PAN) have been widely studied, as EAN is regarded as the first truly room temperature ionic liquid to have been discovered [50,51]. Figure S9 presents the Pvap values of PAN (this work) and EAN (as measured by Emel’yanenko et al. [52]) as a function of temperature, indicating the slightly more volatile nature of PAN when compared to EAN. This difference in volatility is attributed to the intermolecular hydrogen bonding interactions between the ions (+NH•••O–). As the alkyl chain lengthens, the average distance between ions increases, making weaker hydrogen bonds that result in increased Pvap [53]. In addition, the exponential rise in vaporization at 413 K indicates acid-base proton transfer to form neutral molecules. Nevertheless, reasonable agreement was observed between these two data sets. Moreover, the vapor values of PAN and EAN are much lower than those of DESs, PEG 200, and molecular solvents, promoting the use of protic ILs as electrolytes for batteries and fuel cells.
4. Conclusions
In summary, we have presented a simple and efficient isothermal TGA method for rapid screening of the Pvap values for liquid compounds possessing extremely low volatilities. The measured evaporation rates of a reference sample (glycerol) were repeatable and reproducible, allowing for the determination of instrument constants for use in our study. The Pvap was estimated for 30 liquids, and when possible, validated against literature values. We found that triglyme and PEG 200 are more volatile than longer-chain analogs, followed (in general) by DESs, protic ILs, polymeric ILs, imidazolium-, ammonium-, and pyrrolidinium-based Tf2N ILs, and finally di-cationic ILs. However, solvent volatility was found to be dependent on the specific IL cation–anion combination. Our results show that the Pvap of related fluids can be estimated within 10% uncertainty. Our method can easily be applied to calculate instrument constants for the determination of Pvap values in other laboratories. Overall, this method was successfully used to analyze the vaporization of substances once thought and claimed to have zero vapor pressure and provides valuable information towards the design of future ILs and other low-volatility solvents.
Supplementary Materials
The following are available online at https://www.mdpi.com/2305-7084/3/2/42/s1, Table S1: Names, abbreviations, sources, molecular weights, decomposition temperatures, densities, viscosities, and typical water contents of scrupulously dry ionic liquids and other solvents studied; Table S2: The experimental evaporation rates of glycerol measured on two different commercial TGA instruments and the vapor pressures values taken from the literature; Table S3: Vapor pressure summary of ILs, DESs, and miscellaneous low-volatility conventional solvents at various temperatures; Figure S1: Summary of cations, anions, DESs, and other solvents studied and their abbreviations (R = alkyl group); Figure S2: Representative 1H-NMR spectrum for [C4mIm][Tf2N] using deuterated acetone as the solvent. Peaks are assigned numerically beside the molecule; Figure S3: Thermal stabilities of 30 liquids. (A) [C4mIm]-based ILs with different anionic structures (5: [C4mIm][BF4]; 6: [C4mIm][PF6]; 7: [C4mIm][TfO]; 8: [C4mIm][Tf2N]; 9: [C6mIm][Tf2N]); (B) ammonium-, and pyrrolidinium-based Tf2N ILs; (C) PEGs, dicationic ILs, [P14,6,6,6][Tf2N], and polymeric ILs; (D) protic IL, triglyme, and DESs; Figure S4: Comparison of experimental evaporation rates of glycerol measured on two commercial instruments (TGA-1 and TGA-2) at various temperatures. The evaporation rate of glycerol from both instruments are comparable with each other and are used to estimate the instrument coefficients (a and b); Figure S5: Pvap values of pure glycerol obtained from the literature (blue: ref [24], dark green: ref. [25], and black: ref. [26]. All Pvap data obtained from different studies at different temperatures correlate with each other, suggesting the Pvap values are consistent and reliable. Pvap values used in this study originate from ref. [24]; Figure S6: Correlation between present and literature Pvap values with respect to temperature. (Upper) [C4mim][Tf2N] (Zaitsau et al. [27], Rocha et al. [28], Aschenbrenner et al. [29], and Brunetti et al. [30]). (Lower) [C6mim][Tf2N] (Zaitsau et al. [27] and Rocha et al. [28]); Figure S7: Comparison of Pvap results with literature data as function of temperature. (A) [C4mim][PF6] (Zaitsau et al. [31]), (B) [C4mim][dca] (Emel’yanenko et al. [32]); Figure S8: Pvap results of glyceline (circles) and reline (rhombus) DESs mixtures in comparison with Shahbaz et al. [34]. This study (blue) and Shahbaz et al. (green) were measured using TGA. Inset shows the values of reline measured by Shahbaz et al.; Figure S9: Pvap plot of PAN (as measured in this study) and EAN (as measured by Emel’yanenko et al. [35]) as a function of temperature.
Author Contributions
Conceptualization, G.A.B.; Data curation, S.R., N.E.L. and M.A.M.; Formal analysis, S.R., N.E.L. and M.A.M.; Funding acquisition, G.A.B.; Project administration, M.P.H. and G.A.B.; Supervision, G.A.B.; Validation, S.R., M.P.H. and G.A.B.; Writing—original draft, S.R.; Writing—review & editing, N.E.L., M.P.H. and G.A.B.
Funding
The current research was partially supported by a Research Council grant from the University of Missouri (G.A.B.) and by the Research Corporation for Science Advancement (G.A.B.).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Baker, G.A.; Baker, S.N.; Pandey, S.; Bright, F.V. An Analytical View of Ionic Liquids. Analyst 2005, 130, 800–808. [Google Scholar] [CrossRef] [PubMed]
- Castner, E.W., Jr.; Margulis, C.J.; Maroncelli, M.; Wishart, J.F. Ionic Liquids: Structure and Photochemical Reactions. Annu. Rev. Phys. Chem. 2011, 62, 85–105. [Google Scholar] [CrossRef] [PubMed]
- Rogers, R.D.; Seddon, K.R. Ionic Liquids–Solvents of the Future? Science 2003, 302, 792–793. [Google Scholar] [CrossRef] [PubMed]
- Wishart, J.F. Energy Applications of Ionic Liquids. Energy Environ. Sci. 2009, 2, 956–961. [Google Scholar] [CrossRef]
- Tang, S.; Baker, G.A.; Zhao, H. Ether- and Alcohol-Functionalized Task-Specific Ionic Liquids: Attractive Properties and Applications. Chem. Soc. Rev. 2012, 41, 4030–4066. [Google Scholar] [PubMed]
- Rebelo, L.P.N.; Canongia Lopes, J.N.; Esperança, J.M.S.S.; Filipe, E. On the Critical Temperature, Normal Boiling Point, and Vapor Pressure of Ionic Liquids. J. Phys. Chem. B 2005, 109, 6040–6043. [Google Scholar] [CrossRef]
- Earle, M.J.; Esperanca, J.M.S.S.; Gilea, M.A.; Canongia Lopes, J.N.; Rebelo, L.P.N.; Magee, J.W.; Seddon, K.R.; Widegren, J.A. The Distillation and Volatility of Ionic Liquids. Nature 2006, 439, 831–834. [Google Scholar] [CrossRef]
- Esperança, J.M.S.S.; Canongia Lopes, J.N.; Tariq, M.; Santos, L.M.N.B.F.; Magee, J.W.; Rebelo, L.P.N. Volatility of Aprotic Ionic Liquids—A Review. J. Chem. Eng. Data 2010, 55, 3–12. [Google Scholar] [CrossRef]
- Ludwig, R.; Kragl, U. Do We Understand the Volatility of Ionic Liquids? Angew. Chem. Int. Ed. 2007, 46, 6582–6584. [Google Scholar] [CrossRef]
- Paulechka, Y.U.; Zaitsau, D.H.; Kabo, G.J.; Strechan, A.A. Vapor Pressure and Thermal Stability of Ionic Liquid 1-Butyl-3-methylimidazolium Bis(trifluoromethylsulfonyl)amide. Thermochim. Acta 2005, 439, 158–160. [Google Scholar] [CrossRef]
- Zaitsau, D.H.; Kabo, G.J.; Strechan, A.A.; Paulechka, Y.U.; Tschersich, A.; Verevkin, S.P.; Heintz, A. Experimental Vapor Pressures of 1-Alkyl-3-methylimidazolium Bis(trifluoromethylsulfonyl)imides and a Correlation Scheme for Estimation of Vaporization Enthalpies of Ionic Liquids. J. Phys. Chem. A 2006, 110, 7303–7306. [Google Scholar] [CrossRef]
- Widegren, J.A.; Wang, Y.-M.; Henderson, W.A.; Magee, J.W. Relative Volatilities of Ionic Liquids by Vacuum Distillation of Mixtures. J. Phys. Chem. B 2007, 111, 8959–8964. [Google Scholar] [CrossRef]
- Luo, H.; Baker, G.A.; Dai, S. Isothermogravimetric Determination of the Enthalpies of Vaporization of 1-Alkyl-3-methylimidazolium Ionic Liquids. J. Phys. Chem. B 2008, 112, 10077–10081. [Google Scholar] [CrossRef] [PubMed]
- Verevkin, S.P.; Zaitsau, D.H.; Emelyanenko, V.N.; Heintz, A. A New Method for the Determination of Vaporization Enthalpies of Ionic Liquids at Low Temperatures. J. Phys. Chem. B 2011, 115, 12889–12895. [Google Scholar] [CrossRef]
- Ludwig, R. Thermodynamic Properties of Ionic Liquids-A Cluster Approach. Phys. Chem. Chem. Phys. 2008, 10, 4333–4339. [Google Scholar] [CrossRef] [PubMed]
- Emel’yanenko, V.N.; Verevkin, S.P.; Heintz, A. The Gaseous Enthalpy of Formation of the Ionic Liquid 1-Butyl-3-methylimidazolium Dicyanamide from Combustion Calorimetry, Vapor Pressure Measurements, and Ab Initio Calculations. J. Am. Chem. Soc. 2007, 129, 3930–3937. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, J.P.; Hurst, C.; Jones, R.G.; Licence, P.; Lovelock, K.R.J.; Satterley, C.J.; Villar-Garcia, I.J. Vapourisation of Ionic Liquids. Phys. Chem. Chem. Phys. 2007, 9, 982–990. [Google Scholar] [CrossRef] [PubMed]
- Dong, K.; Zhao, L.; Wang, Q.; Song, Y.; Zhang, S. Are Ionic Liquids Pairwise in Gas Phase? A Cluster Approach and In situ IR Study. Phys. Chem. Chem. Phys. 2013, 15, 6034–6040. [Google Scholar] [CrossRef]
- Sze, L.L.; Pandey, S.; Ravula, S.; Pandey, S.; Zhao, H.; Baker, G.A.; Baker, S.N. Ternary Deep Eutectic Solvents Tasked for Carbon Dioxide Capture. ACS Sustain. Chem. Eng. 2014, 2, 2117–2123. [Google Scholar] [CrossRef]
- Wagle, D.V.; Zhao, H.; Baker, G.A. Deep Eutectic Solvents: Sustainable Media for Nanoscale and Functional Materials. Acc. Chem. Res. 2014, 47, 2299–2308. [Google Scholar] [CrossRef]
- Wu, S.-H.; Caparanga, A.R.; Leron, R.B.; Li, M.-H. Vapor Pressure of Aqueous Choline Chloride-Based Deep Eutectic Solvents (ethaline, glyceline, maline and reline) at 30–70 °C. Thermochim. Acta 2012, 544, 1–5. [Google Scholar] [CrossRef]
- Boisset, A.; Jacquemin, J.; Anouti, M. Physical Properties of a New Deep Eutectic Solvent Based on Lithium Bis[(trifluoromethyl)sulfonyl]imide and N-methylacetamide as Superionic Suitable Electrolyte for Lithium Ion Batteries and Electric Double Layer Capacitors. Electrochim. Acta 2013, 102, 120–126. [Google Scholar] [CrossRef]
- Shahbaz, K.; Mjalli, F.S.; Vakili-Nezhaad, G.; AlNashef, I.M.; Asadov, A.; Farid, M.M. Thermogravimetric Measurement of Deep Eutectic Solvents Vapor Pressure. J. Mol. Liq. 2016, 222, 61–66. [Google Scholar] [CrossRef]
- Deyko, A.; Hessey, S.G.; Licence, P.; Chernikova, E.A.; Krasovskiy, V.G.; Kustov, L.M.; Jones, R.G. The Enthalpies of Vaporisation of Ionic Liquids: New Measurements and Predictions. Phys. Chem. Chem. Phys. 2012, 14, 3181–3193. [Google Scholar] [CrossRef]
- Wang, C.; Luo, H.; Li, H.; Dai, S. Direct UV-Spectroscopic Measurement of Selected Ionic-Liquid Vapors. Phys. Chem. Chem. Phys. 2010, 12, 7246–7250. [Google Scholar] [CrossRef]
- Rocha, M.A.A.; Lima, C.F.R.A.C.; Gomes, L.R.; Schröder, B.; Coutinho, J.A.P.; Marrucho, I.M.; Esperança, J.M.S.S.; Rebelo, L.P.N.; Shimizu, K.; Lopes, J.N.C.; et al. High-Accuracy Vapor Pressure Data of the Extended [CnC1im][NTf2] Ionic Liquid Series: Trend Changes and Structural Shifts. J. Phys. Chem. B 2011, 115, 10919–10926. [Google Scholar] [CrossRef]
- Santos, L.M.N.B.F.; Canongia Lopes, J.N.; Coutinho, J.A.P.; Esperança, J.M.S.S.; Gomes, L.R.; Marrucho, I.M.; Rebelo, L.P.N. Ionic Liquids: First Direct Determination of their Cohesive Energy. J. Am. Chem. Soc. 2007, 129, 284–285. [Google Scholar] [CrossRef] [PubMed]
- Verevkin, S.P.; Zaitseva, K.V.; Stanton, A.D.; Hindman, M.S.; Irvin, A.C.; Bara, J.E. Building Blocks for Ionic Liquids: Vapor Pressures and Vaporization Enthalpies of N-Functionalized Imidazoles with Branched and Cycloalkyl Substituents. Ind. Eng. Chem. Res. 2015, 54, 9850–9856. [Google Scholar] [CrossRef]
- Aschenbrenner, O.; Supasitmongkol, S.; Taylor, M.; Styring, P. Measurement of Vapour Pressures of Ionic Liquids and Other Low Vapour Pressure Solvents. Green Chem. 2009, 11, 1217–1221. [Google Scholar] [CrossRef]
- Verevkin, S.P.; Ralys, R.V.; Zaitsau, D.H.; Emel’yanenko, V.N.; Schick, C. Express Thermo-Gravimetric Method for the Vaporization Enthalpies Appraisal for Very Low Volatile Molecular and Ionic Compounds. Thermochim. Acta 2012, 538, 55–62. [Google Scholar] [CrossRef]
- Deyko, A.; Lovelock, K.R.J.; Corfield, J.-A.; Taylor, A.W.; Gooden, P.N.; Villar-Garcia, I.J.; Licence, P.; Jones, R.G.; Krasovskiy, V.G.; Chernikova, E.A.; et al. Measuring and Predicting ΔvapH298 Values of Ionic Liquids. Phys. Chem. Chem. Phys. 2009, 11, 8544–8555. [Google Scholar] [CrossRef]
- Zaitsau, D.H.; Yermalayeu, A.V.; Emel’yanenko, V.N.; Heintz, A.; Verevkin, S.P.; Schick, C.; Berdzinski, S.; Strehmel, V. Structure–property Relationships in ILs: Vaporization Enthalpies of Pyrrolidinium Based Ionic Liquids. J. Mol. Liq. 2014, 192, 171–176. [Google Scholar] [CrossRef]
- Jin, H.; O’Hare, B.; Dong, J.; Arzhantsev, S.; Baker, G.A.; Wishart, J.F.; Benesi, A.J.; Maroncelli, M. Physical Properties of Ionic Liquids Consisting of the 1-Butyl-3-Methylimidazolium Cation with Various Anions and the Bis(trifluoromethylsulfonyl)imide Anion with Various Cations. J. Phys. Chem. B 2008, 112, 81–92. [Google Scholar] [CrossRef]
- Gückel, W.; Kästel, R.; Kröhl, T.; Parg, A. Methods for Determining the Vapour Pressure of Active Ingredients Used in Crop Protection. Part IV. An Improved Thermogravimetric Determination Based on Evaporation Rate. Pestic. Sci. 1995, 45, 27–31. [Google Scholar] [CrossRef]
- Gückel, W.; Kästel, R.; Lewerenz, J.; Synnatschke, G. A Method for Determining the Volatility of Active Ingredients used in Plant Protection. Part III: The Temperature Relationship Between Vapour Pressure and Evaporation Rate. Pestic. Sci. 1982, 13, 161–168. [Google Scholar] [CrossRef]
- Elder, J.P. Sublimation Measurements of Pharmaceutical Compounds by Isothermal Thermogravivletry. J. Therm. Anal. 1997, 49, 897–905. [Google Scholar] [CrossRef]
- Yan, W.; Suppes, G.J. Vapor Pressures and Evaporation Studies of Sugars and Sugar Alcohols. J. Chem. Eng. Data 2008, 53, 2033–2040. [Google Scholar] [CrossRef]
- Wright, S.F.; Dollimore, D.; Dunn, J.G.; Alexander, K. Determination of the Vapor Pressure Curves of Adipic Acid and Triethanolamine using Thermogravimetric Analysis. Thermochim. Acta 2004, 421, 25–30. [Google Scholar] [CrossRef]
- Association, G.P. Physical Properties of Glycerine and Its Solutions; Glycerine Producers’ Association: New York, NY, USA, 1963. [Google Scholar]
- Brunetti, B.; Ciccioli, A.; Gigli, G.; Lapi, A.; Misceo, N.; Tanzi, L.; Vecchio Ciprioti, S. Vaporization of the Prototypical Ionic Liquid BMImNTf2 under Equilibrium Conditions: A Multitechnique Study. Phys. Chem. Chem. Phys. 2014, 16, 15653–15661. [Google Scholar] [CrossRef] [PubMed]
- Tokuda, H.; Ishii, K.; Susan, M.A.B.H.; Tsuzuki, S.; Hayamizu, K.; Watanabe, M. Physicochemical Properties and Structures of Room-Temperature Ionic Liquids. 3. Variation of Cationic Structures. J. Phys. Chem. B 2006, 110, 2833–2839. [Google Scholar] [CrossRef]
- Tokuda, H.; Tsuzuki, S.; Susan, M.A.B.H.; Hayamizu, K.; Watanabe, M. How Ionic Are Room-Temperature Ionic Liquids? An Indicator of the Physicochemical Properties. J. Phys. Chem. B 2006, 110, 19593–19600. [Google Scholar] [CrossRef] [PubMed]
- Tokuda, H.; Hayamizu, K.; Ishii, K.; Susan, M.A.B.H.; Watanabe, M. Physicochemical Properties and Structures of Room Temperature Ionic Liquids. 1. Variation of Anionic Species. J. Phys. Chem. B 2004, 108, 16593–16600. [Google Scholar] [CrossRef]
- Lovelock, K.R.J.; Deyko, A.; Corfield, J.-A.; Gooden, P.N.; Licence, P.; Jones, R.G. Vaporisation of a Dicationic Ionic Liquid. ChemPhysChem 2009, 10, 337–340. [Google Scholar] [CrossRef]
- Jessop, P.G.; Jessop, D.A.; Fu, D.; Phan, L. Solvatochromic Parameters for Solvents of Interest in Green Chemistry. Green Chem. 2012, 14, 1245–1259. [Google Scholar] [CrossRef]
- Organization, I.L. The International Chemical Safety Cards Database. Available online: https://www.ilo.org/dyn/icsc/showcard.listCards3?p_lang=en (accessed on 3 January 2017).
- Ueno, K.; Yoshida, K.; Tsuchiya, M.; Tachikawa, N.; Dokko, K.; Watanabe, M. Glyme–Lithium Salt Equimolar Molten Mixtures: Concentrated Solutions or Solvate Ionic Liquids? J. Phys. Chem. B 2012, 116, 11323–11331. [Google Scholar] [CrossRef]
- Kelkar, M.S.; Maginn, E.J. Calculating the Enthalpy of Vaporization for Ionic Liquid Clusters. J. Phys. Chem. B 2007, 111, 9424–9427. [Google Scholar] [CrossRef]
- Pandey, A.; Pandey, S. Solvatochromic Probe Behavior within Choline Chloride-Based Deep Eutectic Solvents: Effect of Temperature and Water. J. Phys. Chem. B 2014, 118, 14652–14661. [Google Scholar] [CrossRef]
- Greaves, T.L.; Drummond, C.J. Protic Ionic Liquids: Properties and Applications. Chem. Rev. 2008, 108, 206–237. [Google Scholar] [CrossRef]
- MacFarlane, D.R.; Tachikawa, N.; Forsyth, M.; Pringle, J.M.; Howlett, P.C.; Elliott, G.D.; Davis, J.H.; Watanabe, M.; Simon, P.; Angell, C.A. Energy Applications of Ionic Liquids. Energy Environ. Sci. 2014, 7, 232–250. [Google Scholar] [CrossRef]
- Emel’yanenko, V.N.; Boeck, G.; Verevkin, S.P.; Ludwig, R. Volatile Times for the Very First Ionic Liquid: Understanding the Vapor Pressures and Enthalpies of Vaporization of Ethylammonium Nitrate. Chem. Eur. J. 2014, 20, 11594. [Google Scholar] [CrossRef]
- Capelo, S.B.; Méndez-Morales, T.; Carrete, J.; López Lago, E.; Vila, J.; Cabeza, O.; Rodríguez, J.R.; Turmine, M.; Varela, L.M. Effect of Temperature and Cationic Chain Length on the Physical Properties of Ammonium Nitrate-Based Protic Ionic Liquids. J. Phys. Chem. B 2012, 116, 11302–11312. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).