Abstract
Background: The soybean market is representative of the world. Brazil is the largest producer and exporter of this crop and has low production costs but high logistical costs, which are influenced mainly by transport costs. Added to these characteristics, the disputed grain supply, the possibility of crop failure, and the randomness of some parameters that influence the soybean supply chain make decisions even more challenging. Methods: To mathematically model this problem, we carried out an analysis of the scientific production related to grain supply chain and the models used to address the problem, as well as a document analysis and a case study. Results: This paper proposes a new two-stage stochastic linear programming model with fixed recourse for tactical planning in the soybean supply chain from the perspective of the shipper under take or pay contracts over a one-year time horizon. The first-stage variables are the grain purchasing decisions and the volumes of rail and road transportation hired in advance. The model addresses 243 scenarios derived from four uncertainty sources: the purchase and sale prices of raw agricultural products on the spot market, the probability of crop failure, and the external demand. Conclusions: The model is successfully applied to a soybean trade firm in Brazil with expected gain of US$4,299,720 when using the stochastic model instead of the deterministic model. The stochastic model protected the firm from take or pay fines and crop failures, contracting a smaller volume of rail transport than what the company does.
Keywords:
soybean supply chain; grain; agriculture; transport; stochastic; uncertainty; optimization; linear programming 1. Introduction
Soybeans hold a prominent position as one of the primary agricultural commodities in the global market [1]. Last year, the world’s soybean production reached approximately 359 million metric tons, with 155 million metric tons traded on the international market. In the lead, Brazil stands out as the largest producer and exporter of this commodity, contributing 36% of world soy production and 51% of the exported volume [2].
Brazil has favorable conditions for planting crops and low production costs. According to [3], the country has a soybean production cost 9.2% lower than that of the USA, which is the second largest producer and exporter of soybeans, and 18% lower than the production cost of Argentina, which is the third largest exporter and producer. The land values in the USA and Argentina are two and a half to three times those in Brazil.
Although production cost is an important indicator, the logistical cost in the soybean supply chain, as with other agricultural commodities, is quite representative [4], at about 30% of the final value of soybeans, with transport costs averaging 80% of the logistics total cost [5].
Transport is also an important factor in export competitiveness. In the United States, more grain is transported to ports through barges and rail transport, which have lower costs. In contrast, transportation by truck at higher cost is more common in South America, including Brazil, due to the limitations of the network and the low supply of rail transport [3].
The low supply of rail transport in Brazil and the high price of road transport during the harvest period force shippers to secure transportation in advance through take or pay contracts, in which the shipper either takes the transport volume or pays the transporter a penalty if not used.
Crop failure represents a disadvantage for transport contracts, as it can prevent the delivery of agreed soybean volumes. Consequently, the shipper may carry less than the contracted amount, incurring fines. These additional costs further contribute to the representation of transport costs in the final result. The grain supply chain is susceptible to several factors that can cause crop failures and have negative impacts [6] on it.
Many deterministic mathematical models have been published for agricultural commodities supply chains, as can be seen in [7]. Notwithstanding the advantages of applying these models to support decision making, deterministic models use estimated values and averages for the values of the random variables and do not result in better long-term decision strategies, even when they apply intervals for the analysis of sensitivity [8].
Given that some of the parameters present in agricultural commodities supply chains are uncertain in nature [9], the research addressed in this paper extends the deterministic mathematical model presented by [10] and accounts for the stochastic nature of relevant parameters of this supply chain.
Here, we present some research questions that guided the development of the model: 1. how to represent the logistic network with its sets of nodes representing the elements that interact in the system; 2. how to represent the flows of raw materials and products in the soybean market; 3. how to represent contract and spot market modes of transport; 4. how to represent take or pay fines and crop failure; 5. how to depict the scenarios considered in the problem; 6. how to relate the periods of the problem; and 7. what kind of stochastic model to build.
The scientific contribution of this research is in offering a modeling for take or pay transportation contracts with payback mechanisms for non-compliance due to crop failure, considering four sources of uncertainty for the grain: demand, purchase price, selling price, and crop failure. It is a two-stage stochastic linear programming model for the tactical plan of the grain supply chain that is multiproduct, multiperiod, and multimodal.
To the best of the authors’ knowledge, there are no published models incorporating such characteristics for grain in the agri-food supply chain, such as take or pay contracts, crop failure, and their consequences, as well as no published works on tactical planning of the grain supply chain from the shipper’s point of view, considering sources of uncertainty.
The model of this paper responds to the following questions of the decision makers:
- The volume of soybeans and rail and road transport to buy in advance as a first stage variable.
Further, it considers as the second-stage variables:
- The volume of grains to be purchased at their points of origin in the market spot;
- The volumes of road transport to be purchased in the spot market for each origin-destination pair;
- The volumes to be processed (e.g., for the production of soybean meal and oil) in each factory;
- The volumes of processed products and grains to be sold; and
- The flow routes.
The great academic motivation for this research was to fill the gap in decision support models for the grain market, especially the soybean market. This gap includes characteristics that cannot be found in other works, such as take or pay contracts, crop failure, and the randomness of important chain parameters. The contribution to the business environment lies in its addressing of the agricultural commodities market, which is very competitive and important for Brazil.
The remainder of this paper is as follows. Section 2 reviews the literature. Section 3 states the problem. Section 4 presents the logistical network and details the proposed model. Section 5 describes the uncertainty scenarios of stochastic programming. Section 6 is an application of the model to Brazil’s soybean supply chain. The conclusion closes the study in Section 7.
2. Related Works
In this section we present a literature review with the most important works related to our research. At the end of the review-based section, we summarize the main contributions of this article.
Mathematical programming models are important tools to support decision making, as they allow processes to be modeled considering limitations aimed at final optimization. According to [11], models force decision-makers to make their objectives explicit, help identify relationships between decisions, force the identification of variables to be included and in what terms they will be quantifiable, clarify limitations, and allow for the communication of ideas and their understanding, facilitating group work.
Among the various processes that can be modeled, supply chain management planning stands out here. According to [12], this process covers the planning and management of all activities that are involved in supply and acquisition, conversion, and all logistics management activities.
When supply chain management is optimized, we understand that less polluting resources will be used, as in [13]. Since transport freight is directly linked to the traveled distance, optimal routes will reduce distances. The potential for changing the transportation mode depends on the size of the shipment and the distance [14], and this goal can be achieved through a mathematical model.
Furthermore, it is possible to include parameters related to sustainability in a model, such as the reduction in food waste, either during consumption or during transport; prioritizing transport with lower pollutant emissions; and taking advantage of routes for other products, suppliers, and returns. In this sense, ref. [15] proposed a mathematical model to minimize costs that determines suppliers, factory locations, and the number of transported parts and products with costs, free trade agreements, and carbon taxes.
The agri-food supply chain encompasses the process of production and delivery of agricultural products from production to consumption, involving several interconnected steps. Each participant in this chain faces challenges in carrying out its respective activities, making it necessary to make complex decisions at all levels of planning [6].
According to [9], decisions under uncertainty are among the main issues of the agricultural sector. The inclusion of uncertain elements has increasingly become significant in managerial decision-making in the agricultural supply chain, covering operational, tactical, and strategic planning levels.
This increase can be observed in literature reviews in the area: in [9] 68% of the contemplated articles published between 2009 and 2015, over a six-year horizon; and 32% between 1984 and 2008, over a 24-year horizon. The review by [7] agreed with this statistic, with only 30% of the reviewed works classified as stochastic.
A literature review was performed to identify the characteristics of existing stochastic decision support models for the grain supply chain. The protocol proposed by [16] was used, covering “research articles” published in the Science Direct database from 2008 to 2022. Four searches were performed with the following keywords in all parts of the document (excluding references): “stochastic” and “agricultural” and “supply chain” and “planning models” and “grain”, with agri-food being replaced by agricultural and mathematical model in the place of planning models, for a result of 155 articles for reading.
Among the 155 articles reviewed, only 11 were selected for detailed analysis, as they fit the objective of the research, that is, that they concerned grains and considered stochasticity in the mathematical model. Noteworthy here is the exclusion of 30% of articles focused on the area of biomass and/or biofuel. The selected articles can be viewed in Table 1 and Table 2.

Table 1.
Selected articles.

Table 2.
Selected articles.
Table 1 presents the authors, year, journal titles, and article titles of the reviewed articles. Although the review covers the period between 2009 and 2022, 36% are 2021, which indicates a significant increase in mathematical models considering stochasticity. Table 2 presents the characteristics researched in the works, among them the type of grain, the point of view from which the model is applied, the type of model used, the uncertain parameters contemplated, and the level of planning of the model.
The articles contemplated in this review, presented in Table 2, were grouped by similarities and are described below.
Regarding the articles studied that contemplated dynamic processes, [17] presented a cost minimization model of the “chance constrained” type of tactical planning from the point of view of the wheat farmer (producer) for the multifaceted problem of the period of wheat quality control during the harvest under the uncertainty of the climate, mainly rainfall. The model performs dynamic stochastic programming with probabilistic constraints. It can be used for products that must be harvested before or after an established ripeness.
Additionally for this area [18], proposed a multi-objective mixed integer linear programming model for a dynamic food supply chain, considering the uncertainties of demand and solar radiation and proposing a more sustainable supply chain. The sustainable synthesis of a company’s network was designed with regard to the integration of renewable sources, such as biomass, other residues, and solar energy. The solutions obtained were for maximum profit, reflecting ever-changing dynamic market conditions and protecting the environment.
For two-stage stochastic programming models, [19] proposed a revenue maximization model of the two-stage stochastic mixed integer programming type for the supply chain of industries that use agricultural raw materials as production inputs. Uncertain parameters were the selling price of the product and the quality and quantity of inputs. The work used Cplex as a solver. The first stage decisions were the planting area to be contracted and the additional amount of raw material to be contracted in advance. The model was run with 180 scenarios.
Ref. [20] presented a two-stage mixed integer programming stochastic model for the corn supply chain that maximizes return on sales minus costs by considering environmental effects, such as greenhouse gas emissions, carbon sequestration, soil erosion, and nitrogen leakage into water. The stochastic parameters are prices and harvest yields. The first stage variables are binary and determine land allocation for specific crops, while the second stage variables are for operational decisions. Benders’ cutting algorithm was used to solve this problem.
For soybean, [21] analyzed via discrete simulation the flow of soy from the state of Mato Grosso. Four scenarios were built, diversifying the transport flow alternatives, port capacities, and volume received in foreign destinations. The port of Vitória proved to be the most apt to receive soy when there was no adequate capacity restriction placed on it, indicating that investments in infrastructure could be made for this flow at a lower cost. Verification was provided of the best route and port for transporting soy from a region of Brazil.
Regarding multi-objective functions, in addition to [18], as already mentioned, [22] allocated limited water, energy, and land resources to different crops in different regions to obtain optimal comprehensive benefits, using multi objective function, random-boundary interval, and fuzziness. [23] proposed a multi-objective model for the design of the wheat supply chain network, comprising multiple suppliers, existing silos, candidate sites to establish silos, flour mills, and demand zones, including social impact and resilience using hybrid fuzzy stochastic robust programming.
Ref. [24] built a model to maximize return on harvest minus costs, considering migrant seasonal labor planning for sugarcane harvesting and yield uncertainty. The objective of this research was to determine the optimal flows of migrant workers from multiple sources to multiple fronts to maximize the expected total contribution subject to worker availability at each origin through a stochastic logistic model.
For small farmers, [25] proposed a robust optimization model for an optimal network for delivering agricultural products from farms to regional hubs to the central hub using robust optimization minimizing the ton-miles traveled, considering uncertainty in agricultural production. The solver used was GAMS/CPLEX. [26] built a heuristic to verify the economic viability of farmers’ participation in cooperatives, and among the decision variables were to join a closed-membership agricultural cooperative and the number of initial shares, as well as the production capacity, production planning, equity investment, and production capacity.
Using robust optimization, [27] also developed a decision support tool that could help decision makers to formulate robust economic development plans within stringent pollution control programs.
With regard to the models developed for the soybean supply chain, in addition to the deterministic mathematical model from [10], as already mentioned, ref. [4] created an equilibrium model to optimally allocate soy from origin to destination, considering Brazilian supply and export demand using a constrained gravity model. It is important to highlight that the model of [4] contemplates a general point of view of Brazil and not of a stakeholder in the chain, such as the shipper, and it does not consider stochastic parameters.
Similarly, also for the level of strategic planning, [21] found the lowest cost routes for shipping soybeans. However, they considered a region of Brazil as the origin, depicting the model from the perspective of the shipper and using simulation as a decision support tool.
Regarding similarities and opportunities raised in the literature review, only two articles contemplated two-stage stochastic programming models. Both used integer programming, which increases the complexity of solving problems [28], making it difficult to increase the number of scenarios, that is, more possibilities for variation in stochastic variables. The model presented in this work, in addition to being a type of two-stage stochastic programming, is linear and is solved in a matter of seconds, facilitating its operation and use and filling a research gap.
Regarding the uncertain parameters most contemplated in the models, weather, price, and yield appeared the most, aligned with review of [9]. Despite advancements in technology and other fronts, weather and climate influence agricultural systems. Changing climate variables can substantially affect crop yields [29].
In this research, we consider as sources of uncertainty the following: the purchase and sale prices of agricultural raw materials on the spot market, the probability of crop failure, and external demand, with the weather indirectly contemplated for the forecast of crop failure.
Briefly, to the best of our knowledge, we did not find in the literature decision support models for the grain chain that contemplated the possibilities of crop failure and contracts in advance with the take or pay railway model, which are typical problems faced in Brazil’s grain harvests. In addition, unlike many models that were researched for other grains, such as those reported in Table 1, the proposed model is of the linear programming type, allowing for a quick solution with a large number of variables.
In addition, specifically for the soybean or corn production chain of important agricultural commodities, we did not find any research optimizing the process by considering uncertain parameters.
3. Problem Description and Methods
3.1. Problem Description
The supply of soybeans in Brazil falls short of the demand in the international market [1]. As a farmer’s strategy, soybeans are offered for pre-sale approximately one year before harvest. During this period, shippers try to guarantee most of the desired quantities of soybeans, given the risk of possible unavailability in the spot market throughout the year.
The decision process begins with purchasing soybeans from producers. The shipper can buy in advance via contracts, with fixed prices, or on the spot market with stochastic prices. In this sense, the problems that the shipper has is to solve are whether a purchase is anticipated, the purchase place, and the volume to be purchased.
One dilemma the shipper faces is related to crop failure. Crop failure is when a farmer’s expected volume of soybeans is not achieved. Such an outcome is usually unexpected and may occur for various reasons, such as pest activity or excess or rain shortage. According to [6], climate significantly affects farmer productivity and harvests, including due to rainfall variability, drought, pests, and environmental problems.
In the case of crop failure, as in other fortuitous cases, neither the shipper nor the supplier is responsible. The volume contracted in advance is not actually provided to the shipper, making its true product volume differ from its estimates, and it must bear the consequences. This phenomenon is typically stochastic and is included in the mathematical model that we present here. In this context, [30] analyzed the grain market in a post-disaster situation and developed a structural equation model to simulate the behavior of two echelons (distributor and retailers) of the grain supply chain to promote supply recovery and maximize profits.
Regarding transport, the contracts between shippers and carriers are established over a minimum one-year horizon because of the low supply of transport available during the soybean harvest season. Failure to use the contracted transport volume results in fines for shippers. The annual contracts established by shippers, rail, and road companies are of the “take or pay” type.
Such contracts are subdivided into volumes for each monthly period and for each route that must be satisfied by both parties. Some percentage of failure of service is permitted for both parties. For any volume that has not been met, a fine is applied that is equal to the accorded fare for that period and for that route multiplied by a percentage. The shipper can also purchase transport on the spot market in the case of road transport only. In the case of rail transport, there is no supply available for sale on the spot market during the harvest period.
Concerning silos and warehouses, the following constraints are relevant: the input and output storage capacities for soybeans and processed products; the storage costs, including the costs of handling into and out of the warehouse; the opportunity cost; the rent of the leased warehouse; and the safety stock. In Brazil, there is a lack of storage capacity for grain [31], negatively influencing the flow in the soybean chain. Grain storage facilities in this country face great pressure to keep up with increased production [32].
Soybeans can be sold as grain, with a stochastic price on the spot market, or they can be processed to produce meal and soybean oil. Factories, warehouses, silos, transshipment points, and ports are each subject to capacity constraints for storage and for the inputs and outputs of grains, meal, and soybean oil. For factories, we consider the processing capacity, and for ports, we consider the export capacity.
Thus, a shipper in a chain of an agricultural commodity with the demand being greater than the supply and a shortage of low-cost transport must decide in advance the volumes of grain and road and rail transportation that need to be contracted before the harvest. This need should be aligned with the tactical planning of the supply chain of the grain, which also provides the following information: the amount that should be purchased during the harvest; the grain volume to be transformed into oil and bran; the quantity to be sold; and the places of purchase, sale, processing, and flow routes.
3.2. Method
This research can be classified as applied, exploratory, and quantitative. We used a literature review, a document analysis, and a case study as technical procedures. Regarding data collection instruments, we used semi-structured interviews, direct observation, and document analysis. The acquired input was used to construct a mathematical model to help solve the aforementioned problem.
The systematic and narrative literature reviews aimed to identify the types of models and uncertain parameters that have been used in the state-of-the-art literature to solve this type of problem. More details about the systematic review can be obtained in Section 2 of this article.
According to [33], the stages of a mathematical programming study consist of definition of the problem; construction, solution, and validation of the model; implementation of the solution; and final evaluation.
The proposed model considers that some decisions must be made without complete information about random events that influence the model. These decisions are made during the first stage. Later, using information received regarding the realization of random vectors, such as crop failure, purchase and sale prices, and foreign market demand, suitable corrective actions are determined in the second stage. Therefore, this model is characterized as a two-stage stochastic programming problem with recourse.
The classical problem of two-stage stochastic programming with recourse, which was introduced by [34], can be formulated as follows [35]:
In this model, is the vector of the decision variables from the first stage, which must be fixed before the random values become known; and is the vector of the second-stage variables, which can be called recourse actions, corrective actions, or control decisions and are determined after the realization of the random variables. The optimal value for depends on the decisions made in the first stage and the realization of the random variables.
Moreover, is the cost vector for the first stage, is the coefficient matrix for the first stage, and represents the number of resources available when the model represents a resource allocation problem. These parameters apply to the first stage and are therefore deterministic.
In the second stage, is the random vector that influences the vectors of variables . For each realization of a random-event data point in the second stage of the problem, become known. Each component of is then a possible random variable with a known probability distribution. In this model, is the cost vector for the second stage, and is the coefficient matrix for the second stage (called the recourse matrix).
It is assumed that the random vector has a finite number of possible realizations , with the corresponding probabilities . Thus, the expected value can be written as the following sum:
Under the assumption of a discrete model, the problem can be described as follows:
where is the optimal value of the second-stage problem for each realization, is the transposition of the vector , and In the first stage, the decisions regarding the vector should be made before the uncertainties are realized. The vector x will thus be the same for all possible events that may occur in the second stage of the problem [35].
In the second stage, in which the information regarding the random vector is already available, the decisions regarding the values of vector are made. According to [36], recourse models can be classified as fixed, relatively complete, or simple recourse models depending on the type of recourse matrix used. The model developed in this paper is a fixed recourse model, meaning that the matrix of the second-stage coefficients is deterministic.
In an applied way, this research’s model responds to the decision maker, the volume of soybeans, and the rail and road transport to buy in advance as the first stage variables and the volume of grains to be purchased at their points of origin in the market spot, the volumes of road transport to be purchased in the spot market for each origin–destination pair, the volumes to be processed (e.g., for the production of soybean meal and oil) in each factory, the volumes of processed products and grains to be sold, and the flow routes as the second stage variables.
The proposed model compares favorably with the other models described in Table 1 and offers several unique features. First, it is the only model in the extant literature that simultaneously addresses the following four sources of uncertainty: the purchase and sale prices of commodities, the probability of crop failure, and international demand. Second, in addition to being a multi-product model, it is also a multimodal and multi-period model. Third, it considers the specific characteristics of take or pay transport contracts. Fourth, it incorporates payback mechanisms for contractual non-compliance due to crop failure.
4. Mathematical Model
This section presents the logistic network and the stochastic model based on the logistic network.
4.1. The Logistics Network
The soybean logistics network is made up of the origin set, with the soybean supply (O), the warehouse (X), the port (D), the internal market (H), the soybean meal and oil processing plant (F), and the transshipment point (B).
Figure 1 shows the logistics network that was used to build the mathematical model.
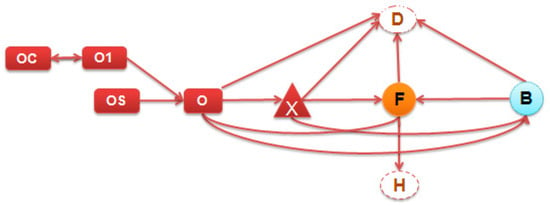
Figure 1.
Logistic network of the model.
The network components described below, which correspond to those shown in Figure 1, were used to develop the mathematical model proposed in this paper. Consider the network G = (N,A), which consists of sets of nodes N and directed arcs A. The set of nodes is subdivided into eight subsets as follows.
O is the set of nodes representing the origins; X is the set of nodes representing the warehouses; B is the set of nodes representing the points of transshipment; F is the set of nodes representing the factories; H is the set of nodes representing the internal market; D is the set of nodes representing the destination ports for exporting to the foreign market; V is the set of nodes representing the points of sales, i.e., the union of sets H and D; S is the total set of nodes that have local inventory for products; and Z is the union of sets B, F, X, and D.
The origins’ nodes O Ɛ N represent the grain growers. Three virtual nodes, NVj (set of virtual nodes of node j), were created for each node j of set O. The sets of virtual nodes were defined as follows: OC(), O1(), and OS() j. The set OC() represents, for each node j O, a possible region of grain purchase under contract. The set O1() represents for each node j a virtual place of destination to return the money spent by the shipper with the volume of grain that was not delivered due to crop failure, and OS() represents the grain purchase region in the spot market associated with node j .
4.2. Stochastic Model
The proposed model is a linear stochastic programming model with two stages and a fixed recourse structure. It is also multi-period, multi-modal, and multi-product in nature.
The purpose of the model is to support the decision-making process for a shipper while maximizing its profit, which is defined in this study as the difference between the revenue gained from the sales of all products and subproducts and the costs incurred for purchase, storage, transport, and processing, as well as contractual penalties.
Table 3 summarizes the sets and subsets considered in the model, Table 4 summarizes the variables, Table 5 presents the model parameters, Table 6 presents the objective function, and Table 7 presents the constraints of the proposed model.

Table 3.
Table of sets.

Table 4.
Table of variables.

Table 5.
Table of parameters.

Table 6.
Objective function.

Table 7.
Table of Constraints.
The constraints in Table 7 can be detailed as follows. Constraint (7) shows that the total virtual flow between node and is equal to the total volume of grain purchased in advance during the first stage of decision-making. Constraint (8) indicates the minimum and maximum grain purchase allowed. Constraint (9) defines the value that the shipper will receive back, corresponding to the volume of grain that is not delivered due to crop failure. Constraint (10) represents the mass balance returning to node , that is, the flow that was not sent to due to capacity constraintd related to crop failure. Constraint (11) ensures that the volume originally purchased in advance by annual contract that will continue in the process will be discounted from the volume corresponding to crop failure.
Constraint (12) indicates that the flow volume from origin during period t is equal to the amount that already exists plus the volume purchased on the spot market. Constraint (13) shows that the volume of p purchased on the spot market in each period t from each origin is less than or equal to the maximum volume offered in that period. Constraint (14) shows that the flow of grain that remains in the system originating from node is less than or equal to the estimated restricted capacity in arc (, j). The arc capacity indicates the volume of the crop that did not fail and was actually produced. The parameter indicates the expected volume of grain, already discounting the expected volume of crop failure.
Furthermore, Equation (15) establishes the flow balance in node for grain. Constraint (16) shows the flow balance for processed products. Constraints (17) and (18) represent the contractual fines for the rail and road modes, respectively. Expression (19) defines the allowed passage volume by road or rail via annual contract, which is the largest volume contracted for that mode of transport, defined in the first stage by the variable.
Constraint (20) states that the volume used for each section of route in each period (e.g., volume contracted with railway in advance) must be within a given range. In the case of soybeans, it must be lower than 140% (Vmax) and higher than 60% (Vmin) of the monthly average volume transported. Equations (21) and (22) establish flow balances in silos and at transshipment points, respectively.
The following expressions provide for entry input (23), output (24), and storage capacities in warehouses (25). Equation (26) shows that the existing volume in each warehouse during the first period is equal to the initial stock. Constraint (27) states that the volume stored in each period in each warehouse must be greater than the safety stock volume, as defined by the shipper.
Everything that comes to the internal processed market must be equal to the volume sold in advance over what was sold over the model. This model constraint is represented by Equation (28). Constraint (29) shows that the total volume sold on the domestic market of processed products must be between a minimum and maximum value, as defined by the shipper.
For each grain and processed product, Equations (30) and (31), respectively, show that every volume that arrives at the port plus what was stored should be equal to the pre-existing sale (sold before the beginning of the planning period) plus both what was sold during the period and what will be stored for the subsequent month. The quantities destined to each port must be less than the flow capacity of this port, which can be seen in Constraint (32) for grain and in Constraint (33) for processed products.
The amount of grain or processed products sold monthly should be between the minimum and maximum demand values, which can be viewed in Constraints (34) and (35), respectively. Constraint (36) indicates that the total quantity sold throughout the year plus the pre-existing sale must be less than or equal to the annual stochastic demand. Equation (37) shows the grain flow balance in the factory. The volume arriving over what was in stock is equal to the volume stored for the subsequent period plus the volume processed.
Equation (38) shows that the volume of grain processed in each factory is converted into processed products, according to a constant yield . Soybean is assumed to have a of 0.73 to meal and 0.19 to oil. Constraint (39) indicates the constraint for each plant’s processing capacity, and finally, Expression (40) restricts the variables to being non-negative.
5. Scenarios Tree
The stochastic parameters considered in the model were selected considering the importance of these parameters in the management of the soybean supply chain, obtained through the responses to interviews conducted with specialists, the existence of reliable historical data, and the computational restrictions.
The semi-structured interviews were conducted with the directors of the logistics and commercial areas of a large soybean trading company, constituting the case study of this work, with the director of the grain area of the largest railway transport company in Brazil and with two suppliers of soybean, corn, and sorghum.
The selected stochastic parameters were the following: demand for the grain (soybean), purchase price of the grain (soybean) in the spot market, selling price of the grain (soybean), and crop failure (soybean crop). Some other parameters, such as the possibility of breach of contract by road companies and the price of road transport in the spot market, although considered deterministic in this work, are highly unpredictable’ however, due to the lack of reliable data, they were not considered as stochastic.
In this study, historical series were used to obtain the probability of random events. The historical series were obtained through the Brazilian Association of Vegetable Oil Industries [37] and the Brazilian Institute of Geography and Statistics [38].
For scenario generation, this work follows [39] using time series, statistical distributions, and expert opinions. There are many methods for building scenario sets and scenario trees with respect to the probability of the occurrence of each event.
Researchers in this area have made considerable efforts to capture important subjective aspects for decision-makers and to ensure the quality of information and the cross-impact thereof. Details can be seen in the works of [40,41,42,43,44,45,46,47].
In this sense, [48] compared the quality of solutions provided by different scenario-generation methods and different scenario trees. With regard to discretization of continuous random variables, many methods have been developed; [48,49,50] tested approximation methods using three points to represent a function of a univariate random variable with a continuous distribution.
In Keefer’s first work in 1983, among the methods that were tested, an extension of the method of [51] proved to be the best. In this method, a continuous distribution curve is divided into three points representing three regions: the two extreme regions, each with an 18.5% chance of occurring; and the remaining middle region, with a 63% chance of occurring.
Although the tests performed by [49,50] were based on a triangular distribution, the same author stated that similar results were obtained for normal curves [50]. According to [52], the discretization of a normal curve into either three or five points is well accepted.
For each stochastic parameter, in this research, a set of values was predicted for the horizon of one year. The techniques of regression, moving averages, and exponential smoothing were tested, and those with the least forecast error were selected.
For exponential smoothing, each value predicted for horizon “n” follows a normal distribution, with the mean (μ), standard deviation (σ), upper limit (+1.96 σ), and lower limit (−1.96 σ), with 95% significance. For each normally distributed random variable, the normal curve was discretized into three values following [51,52] with probabilities of 18.5% for the worst-case scenario, 63% for the conservative scenario, and 18.5% for the optimistic scenario.
As defended by [49], it is common for scenarios to be formed from the opinions of experts, and these parameters are generally distributed by a triangular distribution. The three-point selection method from [51] is valid for triangular distribution. Thus, the pessimistic, conservative, and optimistic scenarios, derived from the regression method and expert opinion, had respective probabilities of 18.5%, 63%, and 18.5%.
5.1. Purchase Price
For the purchase price of soybeans, a historical series from [37] was used, divided by Brazilian state. A dispersion chart was constructed for each series. For each graph, regression was used with the trend curve that best fit the series and with the least forecast error. According to the opinion of experts in the area, the average variation in the predicted purchase price of soybeans is 10% higher for a pessimistic scenario and 10% lower for an optimistic scenario.
According to [43], within the country, the price of soybeans is strongly correlated. That is, when in one state the price presents an optimistic scenario, this same scenario will happen in the other states.
5.2. Selling Prices
According to [53], the sales prices of soy are directly related to international values and are practiced in line with the Chicago Exchange. Based on the monthly historical series of soybean price on the Chicago-CBTO|Exchange, obtained through [37], the conservative sales price values for soybeans in grain for the subsequent year were forecast, with downward variations of 10% in the price for the pessimistic scenario and 10% in the price for the optimistic scenario, according to experts.
5.3. External Grain Demand
Regarding the external grain demand parameter, the forecast for soybean production in Brazil was initially calculated, and then the forecasted volume was multiplied by the percentage that the company aims to buy, that is, the company’s market share, already computing the target of increasing representativeness in this segment for the subsequent year.
From this volume, the quantity foreseen for processing was withdrawn in accordance with the company’s sales growth targets in this segment, and the remaining volume was considered the possible export demand. Assuming the premise that every volume that the company manages to buy and has the capacity to buy it can also sell, everything that is not transformed into bran and oil can be sold on the foreign market.
The calculation of external demand was performed through the forecasted volume of production because, according to experts, the existing demand for this company is greater than the supply, and what limits the soybean trade are the supply of the product, the lack of capacity to storage, and port flow capacity.
5.4. Crop Failure
To determine the crop failure scenarios in the micro-regions, production regression curves were calculated for each micro-region based on soybean production data obtained from the Brazilian Institute of Geography and Statistics [38] for a period of 15 years.
The peak and valley points in each data series were adjusted before estimating the regression curve such that the curve would reflect the forecast for a series without extreme crop failure or overproduction. Using the resulting regression curve, the expected value of production was calculated for each year from the 15 years.
From these newly estimated values, the differences between the estimated volumes and the volumes that were actually produced in each year were calculated. Thus, the differences between the planned production volumes () (calculated from the regression curve) and the outputs actually obtained (), divided by the planner, yielded a number of prediction errors (), where t denotes the year.
For each origin cluster, a series of crop failure predictions was generated. These values, denoted by were used to represent the probability of annual crop failure for each cluster. From the series obtained using this equation, future values were estimated using an exponential smoothing method.
Through the analysis of the time series of production data in all regions of Brazil, two areas suffered severely from crop failure problems independently of each other, namely the midwest and the south. Accordingly, these two regions were chosen as those with significant likelihoods of crop failure.
The stochastic parameters considered in this work were considered univariate. An in-depth statistical study was not carried out with respect to the correlation between stochastic parameters and the interference of external factors in the series of each parameter because it is not the focus of this work.
In this sense, ref. [54] concluded that it is not possible to define a direct or inverse relationship between the price and the quantity demanded or offered for the soybeans. According to [53], for producers, soybean prices are always subject to fluctuations, the cause of which is difficult to predict, causing some difficulty in decision-making. Thus, it was decided to consider the series as univariate since the consideration of factors that could influence the series would collide in the absence of reliable data for many of them.
Some works try to describe relationships between prices and other factors. Ref. [55] showed the mutual impact of soybean market in the USA and Brazil considering seasonalities. Ref. [56] analyzed the impacts of the Brazilian logistical and transportation sectors on soybean prices. Ref. [57] used system analysis to model supply and demand dynamics considering price mechanisms applied to commodities markets, including soybeans.
Thus, since the stochastic parameters considered in this work are univariate, to construct the scenario tree, combinations of all three scenarios of different probabilities for the four stochastic parameters were used. Because the “crop failure” parameter has three possible occurrences for each of the two distinct areas, it generates a total of 35 (demand-3 x purchase price-3 x selling price-3 x crop failureA-3 x crop failureB-3) = 243 scenarios.
6. Case Study
We developed the proposed mathematical model based on a partnership between the university and one of the leading trading companies of Brazil’s soybean supply chain, to which this model was applied, without involving financial resources on either side. The company contributed to the interviews, provided information about the company, and validated the model after its application.
The studied network consisted of 21 source nodes representing producers providing a soybean supply, which are called clusters in this research; 11 nodes representing silos; 6 nodes representing soybean processing plants; 6 nodes representing transfer points; 5 nodes representing the domestic market; and 6 nodes representing ports, for a total of 55 nodes.
All possible source-destination combinations were analyzed. Subsequently, all combinations that were identified as improbable based on distance or shipping price were removed from the network. The final feasible network included 19 rail segments and 82 road segments that could be reserved via annual contracts and 124 alternative road routes that could be reserved on the spot market.
6.1. Computational Performance
The proposed model was implemented in the Advanced Integrated Multidimensional Modeling Software (AIMMS) modeling system, version 4.82, using the academic version (free academic license) and was solved with the CPLEX 20.1 solver through the following algorithms: Simplex, Logarithmic Barrier, and Dual Simplex. The computational performance of the solver is reported for a computer with a 2.70-GHz Intel(R) Core(TM) I7-7500 CPU and 8 GB of RAM, and it is shown in Table 8. The analysis of the stochastic model required the consideration of 2,288,220 constraints and 1,987,225 variables.

Table 8.
Computational results.
The results presented in Table 8 indicate that the solution time was low for all algorithms. The stochastic tactical model, with approximately 2,000,000 restrictions and 2,000,000 variables, ran in 1 min and 24 s with the Logarithmic Barrier Algorithm, followed by the Simplex Dual Algorithm and Simplex Primal Algorithm, for approximately 4 and 5 min, respectively.
The Logarithmic Barrier method was developed by Fiacco and McCormic in [58] for nonlinear programming. However, it was after the work by [59], which presented an efficient polynomial complexity algorithm for solving linear programming problems, that the interior point methods have been intensively studied. A derivation of Karkamar’s projective method allows for classifying it among the logarithmic barrier methods [60]. For a reference to barrier algorithms, see [61].
6.2. Analysis of Results
An optimal value of US$3,885,045,160 was achieved for the objective function of the stochastic model. The value of the objective function, which we call profit in this study, is the difference between the revenues from the sale of soybeans, meal, and oil and the costs of purchase, storage, transport, and processing.
Considering the volumes of soybeans that had already been bought and sold, as well as the volume of processed products that were stocked, the profit per ton of soy was about US$132.00/t. Considering US$300.00/t as the average value used for soybeans, the return on investment is around 44%.
According to the obtained solution, 8.6 million tons of soybeans were acquired during the first stage, out of the 11.9 million tons of soybeans that were offered. At the beginning of the planning period, 4.0 million tons of soybeans had already been purchased; therefore, 12.6 million tons of soybeans were purchased at least one year in advance.
Regarding the values provided by the model for each second-stage variable in each scenario, the minimum, average, and maximum volumes of soybeans to be purchased on the spot market during the second stage were 3.9, 5.6, and 7.1 million tons, respectively.
The model indicates that, before the soybean harvest begins, a shipper must contract between 65% and 76% of the soybeans that it expects to use throughout the year. The current practice of the studied company is to contract 70% of this total volume in advance.
According to the model, the maximum volume of soybeans sold to the export market was 11.8 million tons, the average volume was 10.5 million tons, and the minimum volume was 9.6 million tons. The maximum processed volume was 6.9 million tons of soybeans, and the variation between the maximum and minimum values was approximately 10%.
Considering that approximately 1.2 million tons of oil and meal were stored during the initial period, the percentage of soybean crops converted into meal and oil amounted to between 41% and 49%. In comparison, the current practices of the studied company involved processing 50% of the acquired soybeans.
Moreover, the results of the first-stage decision problem corresponded to contracted transport volumes of 6.6 million tons for transport by rail and 20.2 million tons for transport by road, plus 2.0 tons on the road spot market.
Thus, the model suggests that 23% of the volume should be transported via railway. In practice, the studied company transports 30% of its volume by rail and 70% via highway; of the latter, 60% is reserved via annual contracts, and 40% is acquired via the spot market.
Such result highlights the importance of using this mathematical model to support decision making. Contrary to what we expected, due to the lower freight value, as proposed by [3], the model did not “contract” the railway transport as much as it could and still hired 7% less than the company usually contracts, resulting in about 2 million fewer tons for rail transport due to the fines generated in the take or pay contracts, crop failure, and Brazil’s high value of rail freight.
Any changes in logistical operations, especially in transport, generate major impacts due to high logistical costs in the supply chain, the product of which has low added value. The mathematical model helps the shipper to make tactical decisions and generate higher profits.
The model structure was validated with hypothetical data, with samples having result that were known, before being applied to the case study, as suggested by [28]. After applying the company data, the model was validated by the company, which verified consistency in the results obtained.
6.2.1. Solutions Obtained
The wait-and-see (WS) solution is the optimal value of the problem when the realization of ξ is known. According [35], the expected value of the WS solution is given as follows:
where is the optimal solution, and is the value of the objective function for a given scenario.
The WS solution for each scenario was calculated using a deterministic model proposed by [10].
Figure 2 illustrates the WS solutions obtained for each scenario.
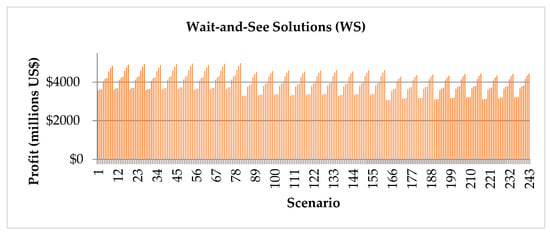
Figure 2.
Wait-and-see solutions for each scenario.
According to Figure 2, scenarios 1 to 81, in which the purchase prices are low, correspond to a region in which profits appear to be higher on average. In scenarios 82 to 163, the purchase prices are conservative, and in scenarios 163 to 243, in which the purchase prices are high, the profits appear to be lower on average. The peaks representing the highest profits correspond to scenarios in which the purchase and sale prices are favorable to the shipper.
The expected value of the WS solution for the studied problem was US$3,926,527,070. This value is the predicted optimal value were the decision-maker to have perfect information regarding what will happen in the future.
The stochastic model proposed in this paper was used to calculate the optimal solution, that is, the here-and-now solution, for the proposed fixed recourse problem.
Ref. [35] defined the here-and-now (RP) solution as follows:
This solution is obtained by totaling the product of the probability of each scenario with the stochastic solution obtained for each scenario. The RP solution is related to decision-making without knowledge of the uncertainty of ξ. The RP solution of US$3,885,045,160 was achieved for the objective function of the stochastic model when all scenarios were considered concurrently, weighted by their probabilities of occurrence.
6.2.2. Expected Value of Perfect Information (EVPI) and the Value of the Stochastic Solution (VSS)
The expected value of perfect information (EVPI) is the maximum value that the decision-maker could gain from obtaining perfect information. According to [35], the EVPI is calculated as the difference between the expected values of the WS solution and the stochastic RP solution.
Thus, for the problem considered in this work, the EVPI is US$41,481,910, which means that a shipper should be willing to pay up to this value for perfect information, about 1% of the value of the objective function. The lower that the EVPI is, the closer that the value from objective function of the stochastic model is to the expected value of the perfect information.
The value of the stochastic solution (VSS) is a measure used to determine the importance of considering the randomness in a system, and it is obtained by the module difference between the RP and EEV solutions. The expected value of the solution (the EEV) is obtained when the first stage solution of the deterministic model is fixed and used. The random variables assume their values for each scenario, and the optimal value obtained is then multiplied by the respective probabilities of each scenario. For the problem considered in this work, the calculated EEV is US$3,880,745,440.
As the RP solution is US$3,885,045,160, the difference between the two is the VSS. Therefore, the value of the VSS for this problem is US$4,299,720, i.e., the expected benefit that the decision-maker (shipper) can gain by considering uncertainty. This value is the decision maker’s gain in using the stochastic model instead of the deterministic one.
6.2.3. Analysis of First-Stage Decisions
Although the results for the second-stage variables of the model also serve as a basis for decision-making, the primary gain achieved through the application of the stochastic model is in the first stage of decision-making, which consists of the decisions to be made at the beginning of the planning period without any real knowledge of the future.
The first-stage decisions include the purchase volume of soybeans to be contracted in advance (VCA), the volume of rail transport to be contracted in advance (VToPV-Rail), and the volume of road transport to be contracted in advance (VToPV-Road).
The results of these first-stage decisions are summarized in Table 9.

Table 9.
Variable values determined during the first stage.
The results shown in Table 9 were obtained using the stochastic model and by applying the deterministic model proposed by [10], in which only one scenario is considered, using the average stochastic parameters (expected values of ξ) as input data.
In the stochastic model, 12 (63%) of the 19 available rail segments and 41 (51%) of the 80 available road segments were selected for advance purchase, and 8.639 million tons of soybeans (73%) of the 11.891 million tons of available soybeans were contracted from the 21 clusters.
From the Table 9, it is evident that the contracted rail and road volumes in the deterministic model are larger than those in the stochastic model. This difference arose because, in certain scenarios, the cost of a fine multiplied by its probability was greater than the cost of acquiring transport on the spot market.
The proposed model is degenerate, and the optimal solution with m restrictions has fewer than m positive variables [62], a characteristic present in many transport models. Then, the sensitivity indicators, such as those resulting from the dual, exported by software reports are no longer reliable [28].
As illustrated in [63,64], sensitivity analyzes in large degenerate models are possible but not feasible, given the complexity of the operations that need to be performed to obtain a single value. It is more efficient to run the model with the new parameters and intervals that one wants to test.
6.2.4. Summary of the Results
In tactical planning for a logistics chain, certain differences arise concerning the optimal value of the objective function and the values of the variables when we consider the uncertainties inherent to the process of interest.
The case of a large trading company participating in Brazil’s soybean market was analyzed while considering the uncertainties in four parameters: the purchase and sale prices of soybeans, the foreign market demand for soybeans, and the probability of crop failure. In addition, take or pay contracts were considered in an unprecedented way.
The model provides decision makers with how many soybeans and how much rail and road transport should be contracted one year in advance before unforeseen events occur, such as crop failure; the purchase and sale prices; and the foreign market demand at the harvest time.
Additionally, the model provides monthly tactical planning, which is a the second-stage variable regarding how many soybeans should be purchased for grain and road transport in the spot market and how much should be stored, transformed into oil and bran, and sold, in addition to informing which paths, ports, warehouses, and factories should be used and for which volume.
We investigated the model’s computational performance and its adherence to reality, and we performed a comparative analysis among the stochastic, WS, and deterministic solutions. Furthermore, we calculated the indicators of the gains that were achieved through the stochastic model compared with the deterministic model proposed by [10].
The expected gain that was achieved through the stochastic model was found to be US$4,299,720. The model achieved this expected gain by “protecting” the shipper against pessimistic scenarios, thereby minimizing losses. Contrary to expectations, due to the lower freight value, as proposed by [3], the model contracted the railway transport less than the company usually contracted it for due to the fines generated in the take or pay contracts, crop failure, and Brazil’s high value of rail freight.
It is essential for a company to have strategic, tactical, and operational planning models as a basis. Strategic models will provide information, such as location, structure, and facilities sizes and modes of transport to be used. Tactical models use the networks discovered through strategic planning and provide inputs to prepare the company for the next period, in this case, one year. Operational models use the tactical model’s results to prepare and adapt day to day.
According to [65], competition occurs between supply chains, and when it is well managed, it generates better financial gains for the chains’ members and the availability of products with better service levels. Good management requires, among other factors, the use of management models, planning, agreements, data sharing, and well-made forecasts [66].
In general, the decision-making manager is not the person who coordinates the model. The model operator needs intermediate knowledge of mathematical programming and creates reports using the model responses for the manager. The manager is needed for some data inputs. However, most of the data come from the company’s databases or open sources, as mentioned in this article. Normally, the software pulls data directly from the company’s databases, facilitating the process, even though many data are needed to execute the model.
The planning model rationalizes decisions and makes companies less dependent on people’s know-how. Without using a model, a correct decision in a period does not imply that subsequent decisions not using an optimization model will also be close to the optimal point. In addition to the model’s optimal quantitative responses, it reduces the negative impacts of personal relationships within a company, as it does not depend on them.
Furthermore, given the speed of execution and explanation of the model, few extra resources will be necessary to manage one’s application. Other programming languages, such as Python and Julia; free platforms, such as Google Colab and Spyder; and free solvers, such as GLPK and HiGHS, can also be used to run this model.
The lack of a tactical stochastic planning model for the soybean supply chain in the literature and that this model exhibits good computational performance highlight the importance of the proposed model for this type of logistics chain at this level of planning. With no loss of generality, this model applies to other non-perishable agricultural commodities; in stochastic scenarios for multiproduct, multiperiod, and multimodal production-distribution problems; and with transportation take or pay contracts and payback mechanisms due to harvest uncertainties.
The primary gain achieved by applying a stochastic model of two stages is in the first stage of decision-making. In this case, the volume of grains and transportation should be contracted in advance. From the results in Section 6.2, we noted that the model contracted rail transportation less than the offer and what the company usually hires. In an agricultural commodity market, in which transport cost represents 80% of the logistical cost, which is about 30% of soybean’s final value [5], this result showed the importance of using this decision support model.
The model also includes multiple phases of the soybean logistics chain and indicates what should be undertaken in each scenario to achieve the best return: when and where to purchase soybeans and how much; the best way to transport soybeans; when and where to process and store soybeans and their derivative products; and when and where to sell processed and whole soybeans and how much.
Furthermore, another major advantage of the proposed stochastic model is the diversity of analyses that can be performed based on its results. The shipper can understand the factors that most strongly impact the process by analyzing the results for each scenario or some subset of scenarios, making it possible to reduce the effort wasted in addressing less important concerns.
Thus, considering uncertainties in a tactical planning model for a complex and integrated soybean logistic chain can affect a shipper’s initial decisions regarding the establishment of advance contracts for soybean purchases and transport by rail and road. In the studied case, it resulted in smaller losses in many pessimistic scenarios and greater returns in some optimistic scenarios, as reflected by an expected increase in profits of US$4,299,720.
7. Conclusions
This paper presented a two-stage stochastic programming model with a fixed recourse structure for tactical planning in the soybean supply chain from the shipper’s perspective, considering the uncertainties associated with the purchase and sale prices of soybeans, the external demand for soybeans, and the probability of crop failure.
The uncertainties present in the soybean supply chain and the need to make decisions before uncertain events motivated the construction of a stochastic programming model with two stages and a fixed recourse structure. The need to model various intrinsic factors in the process, such as the characteristics of take or pay contracts and the possibility of crop failure, led to the construction of a model with features not previously seen in the scientific literature.
In accordance with an analysis of the parameters that influence the complex soybean trade, scenarios were generated with appropriate probabilities. The model considered a complex case study with 243 possible scenarios and achieved good computational performance. The results confirmed that the model produces consistent results. Thus, the model can be incorporated into the tactical planning process to be used as a decision support tool.
The results obtained from the model were validated and applied for a large trader of the soybeans produced in Brazil, thus enabling a thorough evaluation of the proposed model. The model’s first stage variables indicated the volume of grains and transportation that should be contracted in advance. The cost of transportation constituted a large share of the total logistics cost, which is very representative in the soybean supply chain. As a result, the model hired less from rail transport than the case study’s company usually does. The expected gain from using the stochastic model was US$4,299,720.
The developed stochastic model supports a shipper’s decision-making concerning the initial decisions that must be made before uncertain events occur by assessing the impact of each potential scenario in supply chain projections, and it reveals the optimal decisions to be made were each scenario to occur.
Furthermore, the model can also be applied to agricultural commodities with characteristics that are similar to those of soybean logistics or even to analyze two or more logistic chains for agricultural commodities that operate in parallel, sharing the same structure of shipper logistics. Parts of the model can also be adopted for other purposes, such as modeling soybean crop failure and take or pay contracts.
Finally, as future research, we suggest analyzing the trade-off between the cost of installing and using this model versus its benefits, measured by the profit margin, as well as by the time that operators and model managers spend throughout the process. We suggest the development of stochastic models for the strategic and operational levels of the soybean supply chain and the inclusion of parameters related to the sustainability of that production chain. We also suggest applying the model in a free solver to make it available to farmers who have to make decisions similar to those of a shipper.
Author Contributions
Conceptualization, S.A.d.R.; Methodology, S.A.d.R., J.E.L. and A.M.T.T.; Software, S.A.d.R.; Validation, S.A.d.R.; Formal analysis, S.A.d.R. and J.E.L.; Resources, S.A.d.R. and J.E.L.; Data curation, S.A.d.R.; Writing—original draft, S.A.d.R.; Writing—review & editing, S.A.d.R., J.E.L. and A.M.T.T.; Visualization, S.A.d.R.; Funding acquisition, S.A.d.R., J.E.L. and A.M.T.T. All authors have read and agreed to the published version of the manuscript.
Funding
The authors Silvia Araújo dos Reis and José Eugenio Leal thank the National Council for Scientific and Technological Development (CNPq) for the financial support that allowed this research. The author Antônio Márcio Tavares Thomé acknowledge the support of the National Council for Scientific and Technological Development (CNPq) [311862/2019-5]; Coordination for the Improvement of Higher Education Personnel (CAPES) [Finance Code 001]; and the Foundation for Support of Research in the State of Rio de Janeiro (FAPERJ) [E26-203.252/2017; E26-201.251/12021].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jia, F.; Peng, S.; Green, J.; Koh, L.; Chen, X. Soybean Supply Chain Management and Sustainability: A Systematic Literature Review. J. Clean. Prod. 2020, 255, 120254. [Google Scholar] [CrossRef]
- USDA. Available online: https://www.usda.gov/oce/commodity/wasde (accessed on 30 April 2023).
- Meade, B.; Puricelli, E.; Mcbride, W.; Valdes, C.; Hoffman, L.; Foreman, L.; Dohlman, E. Corn and Soybean Production Costs and Export Competitiveness in Argentina, Brazil, and the United States. Available online: www.ers.usda.gov/publications/eib-economic-information-bulletin/eib-154 (accessed on 19 July 2023).
- Da Silva, M.A.V.; De Almeida D’Agosto, M. A Model to Estimate the Origin-Destination Matrix for Soybean Exportation in Brazil. J. Transp. Geogr. 2013, 26, 97–107. [Google Scholar] [CrossRef]
- Kussano, M.R.; Batalha, M.O. Custos Logísticos Agroindustriais: Avaliação Do Escoamento Da Soja Em Grão Do Mato Grosso Para o Mercado Externo. Gestão Produção 2012, 19, 619–632. [Google Scholar] [CrossRef][Green Version]
- Yadav, V.S.; Singh, A.R.; Gunasekaran, A.; Raut, R.D.; Narkhede, B.E. A Systematic Literature Review of the Agro-Food Supply Chain: Challenges, Network Design, and Performance Measurement Perspectives. Sustain. Prod. Consum. 2022, 29, 685–704. [Google Scholar]
- Ahumada, O.; Villalobos, J.R. Application of Planning Models in the Agri-Food Supply Chain: A Review. Eur. J. Oper. Res. 2009, 196, 1–20. [Google Scholar] [CrossRef]
- Maiyar, L.M.; Thakkar, J.J. A Combined Tactical and Operational Deterministic Food Grain Transportation Model: Particle Swarm Based Optimization Approach. Comput. Ind. Eng. 2017, 110, 30–42. [Google Scholar] [CrossRef]
- Borodin, V.; Bourtembourg, J.; Hnaien, F.; Labadie, N. Handling Uncertainty in Agricultural Supply Chain Management: A State of the Art. Eur. J. Oper. Res. 2016, 254, 348–359. [Google Scholar] [CrossRef]
- Reis, S.A.; Leal, J.E. A Deterministic Mathematical Model to Support Temporal and Spatial Decisions of the Soybean Supply Chain. J. Transp. Geogr. 2015, 43, 48–58. [Google Scholar] [CrossRef]
- Lachtermacher, G. Pesquisa Operacional Na Tomada de Decisões, 3rd ed.; Campus, Ed.; Rio de Janeiro, Brazil, 2007. [Google Scholar]
- Council of Supply Chain Management Professionals. Available online: https://cscmp.org/CSCMP/Academia_and_Awards/SCM_Definitions_and_Glossary_of_Terms/CSCMP/Educate/SCM_Definitions_and_Glossary_of_Terms.aspx?hkey=60879588-f65f-4ab5-8c4b-6878815ef921 (accessed on 8 July 2023).
- Mostafa, N.A.; Eldebaiky, O. A Sustainable Two-Echelon Logistics Model with Shipment Consolidation. Logistics 2023, 7, 18. [Google Scholar] [CrossRef]
- Yousefi, J.; Ashtab, S.; Yasaei, A.; George, A.; Mukarram, A.; Sandhu, S.S. Multiple Linear Regression Analysis of Canada’s Freight Transportation Framework. Logistics 2023, 7, 29. [Google Scholar] [CrossRef]
- Kinoshita, Y.; Nagao, T.; Ijuin, H.; Nagasawa, K.; Yamada, T.; Gupta, S.M. Utilization of Free Trade Agreements to Minimize Costs and Carbon Emissions in the Global Supply Chain for Sustainable Logistics. Logistics 2023, 7, 32. [Google Scholar] [CrossRef]
- Cronin, P.; Ryan, F.; Coughlan, M. Undertaking a Literature Review: A Step-by-Step Approach. Br. J. Nurs. 2008, 17, 38–43. [Google Scholar] [CrossRef] [PubMed]
- Borodin, V.; Bourtembourg, J.; Hnaien, F.; Labadie, N. A Multi-Step Rolled Forward Chance-Constrained Model and a Proactive Dynamic Approach for the Wheat Crop Quality Control Problem. Eur. J. Oper. Res. 2015, 246, 631–640. [Google Scholar] [CrossRef]
- Vujanović, A.; Čuček, L.; Novak Pintarič, Z.; Pahor, B.; Kravanja, Z. Synthesis of Environmentally-Benign Energy Self-Sufficient Processes under Uncertainty. J. Clean. Prod. 2015, 88, 90–104. [Google Scholar] [CrossRef]
- Wiedenmann, S.; Geldermann, J. Supply Planning for Processors of Agricultural Raw Materials. Eur. J. Oper. Res. 2015, 242, 606–619. [Google Scholar] [CrossRef]
- Cobuloglu, H.I.; Büyüktahtakın, E. A Two-Stage Stochastic Mixed-Integer Programming Approach to the Competition of Biofuel and Food Production. Comput. Ind. Eng. 2017, 107, 251–263. [Google Scholar] [CrossRef]
- Lopes, H.d.S.; da Lima, R.S.; Leal, F.; de Nelson, A.C. Scenario Analysis of Brazilian Soybean Exports via Discrete Event Simulation Applied to Soybean Transportation: The Case of Mato Grosso State. Res. Transp. Bus. Manag. 2017, 25, 66–75. [Google Scholar] [CrossRef]
- Li, M.; Fu, Q.; Singh, V.P.; Liu, D.; Li, T. Stochastic Multi-Objective Modeling for Optimization of Water-Food-Energy Nexus of Irrigated Agriculture. Adv. Water Resour. 2019, 127, 209–224. [Google Scholar] [CrossRef]
- Hosseini-Motlagh, S.M.; Samani, M.R.G.; Saadi, F.A. A Novel Hybrid Approach for Synchronized Development of Sustainability and Resiliency in the Wheat Network. Comput. Electron. Agric. 2020, 168, 105095. [Google Scholar] [CrossRef]
- Amaruchkul, K. Planning Migrant Labor for Green Sugarcane Harvest: A Stochastic Logistics Model with Dynamic Yield Prediction. Comput. Ind. Eng. 2021, 154, 107016. [Google Scholar] [CrossRef]
- Kambli, A.; McGarvey, R.G. Network Design for Local Agriculture Using Robust Optimization. Inf. Process. Agric. 2021, 8, 469–483. [Google Scholar] [CrossRef]
- Qian, X. Production Planning and Equity Investment Decisions in Agriculture with Closed Membership Cooperatives. Eur. J. Oper. Res. 2021, 294, 684–699. [Google Scholar] [CrossRef]
- Zhou, Y.; Han, J.; Li, J.; Zhou, Y.; Wang, K.; Huang, Y. Building Resilient Cities with Stringent Pollution Controls: A Case Study of Robust Planning of Shenzhen City’s Urban Agriculture System. J. Clean. Prod. 2021, 311, 127452. [Google Scholar] [CrossRef]
- Hillier, F.S.; Lieberman, G.J. Introduction to Operations Research, 8th ed.; McGraw Hill: New York, NY, USA, 2005. [Google Scholar]
- Kim S., M.; Mendelsohn, R. Climate change to increase crop failure in US. Environ. Res. Lett. 2023, 18, 014014. [Google Scholar] [CrossRef]
- Sheu, J.-B. Supplier Hoarding, Government Intervention, and Timing for Post-Disaster Crop Supply Chain Recovery. Transp. Res. E Logist. Transp. Rev. 2016, 90, 134–160. [Google Scholar] [CrossRef]
- Filippi, A.C.G.; Guarnieri, P.; Carvalho, J.M.; Reis, S.A.; da Cunha, C.A. New Configurations in Brazilian Agribusiness: Rural Warehouse Condominiums. J. Agribus. Dev. Emerg. Econ. 2020, 10, 41–63. [Google Scholar] [CrossRef]
- An, K.; Ouyang, Y. Robust Grain Supply Chain Design Considering Post-Harvest Loss and Harvest Timing Equilibrium. Transp. Res. Logist. Transp. Rev. 2016, 88, 110–128. [Google Scholar] [CrossRef]
- Eduardo Leopoldino de Andrade Introdução à Pesquisa Operacional. Métodos e Modelos Para Análise de Decisões, 5th ed.; LTC: Rio de Janeiro, Brazil, 2015. [Google Scholar]
- Dantzig, G.B. Linear Programming under Uncertainty Dantzig. Manag. Sci. Suppl. 1955, 50, 1764–1769. [Google Scholar]
- Birge, J.R.; Louveaux, F. Introduction to Stochastic Programming, 2nd ed.; Mikosch, T., Resnick, S., Robinson, S., Eds.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Hoppe, R.H.W. Stochastic Linear and Nonlinear Programming. In Optimization Theory II; Springer: New York, NY, USA, 2007; pp. 1–47. Available online: https://www.math.uh.edu/~rohop/Spring_12/Chapter1.pdf (accessed on 30 April 2023).
- Abiove. Available online: https://abiove.org.br/estatisticas/ (accessed on 22 May 2023).
- IBGE–Instituto Brasileiro de Geografia e Estatística. Available online: https://www.ibge.gov.br/en/statistics/economic/agriculture-forestry-and-fishing/21929-2017-2017-censo-agropecuario-en.html?=&t=o-que-e (accessed on 22 July 2023).
- Michal Kaut Scenario Generation for Stochastic Programming: A Practical Introduction. Available online: https://work.michalkaut.net/papers_etc/scen-gen_intro.pdf (accessed on 22 May 2023).
- Mitchell, R.B.; Tydeman, J.; Curnow, R. Scenario Generation: Limitations and Developments in Cross-Impact Analysis. Futures 1977, 9, 205–215. [Google Scholar] [CrossRef]
- Turoff, M. An Alternative Approach to Cross Impact Analysis. Technol. Forecast. Soc. Chang. 1972, 3, 309–339. [Google Scholar] [CrossRef]
- Høyland, K.; Wallace, S.W. Generating Scenario Trees for Multistage Decision Problems. Manag. Sci. 2001, 47, 295–307. [Google Scholar] [CrossRef]
- Pflug, G.C. Scenario Tree Generation for Multiperiod Financial Optimization by Optimal Discretization. Math. Program. 2001, 89, 251–271. [Google Scholar] [CrossRef]
- Kouwenberg, R. Scenario Generation and Stochastic Programming Models for Asset Liability Management q. Eur. J. Oper. Res. 2001, 134, 279–292. [Google Scholar] [CrossRef]
- Høyland, K.; Wallace, S.W. A Heuristic for Moment-Matching Scenario Generation. Comput. Optim. Appl. 2003, 24, 169–185. [Google Scholar] [CrossRef]
- King, A.J. Modeling with Stochastic Programming; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Michal Kaut Forecast-Based Scenario-Tree Generation Method. Available online: https://optimization-online.org/wp-content/uploads/2017/03/5898.pdf (accessed on 22 May 2023).
- Rios, I.; Weintraub, A.; Wets, R.J.-B. Building a Stochastic Programming Model from Scratch: A Harvesting Management Example. Quant. Financ. 2016, 16, 189–199. [Google Scholar] [CrossRef]
- Keefer, D.L.; Bodily, S.E. Three-Point Approximations for Continuous Random Variables. Manag. Sci. 1983, 29, 595–609. [Google Scholar] [CrossRef]
- Keefer, D.L. Certainty Equivalents for Three-Point Discrete-Distribution Approximations. Manag. Sci. 1994, 40, 760–773. [Google Scholar] [CrossRef]
- Pearson, E.S.; Tukey, J.W. Approximate Means and Standard Deviations Based on Distances between Percentage Points of Frequency Curves. Biometrika 1965, 52, 533. [Google Scholar] [CrossRef]
- Hirschfeld, H. Engenharia Econômica e Análise de Custos: Aplicações Práticas Para Economistas, Engenheiros, Analistas de Investimentos e Administradores; Atlas: São Paulo, Brasil, 2000. [Google Scholar]
- dos Santos, A.M.D. A Evolução Dos Preços Agrícolas e as Bolsas de Mercadorias e Futuros: Um Estudo Para o Mercado Da Soja Em Grão, Farelo e Óleo No Brasil (1995–2002). Master’s Thesis, Federal University of Rio Grande do Sul, Porto Alegre, Brazil, 2003. [Google Scholar]
- Fernardo, L.T.; Queiroz, A.M.D. A Elasticidade-Preço Da Demanda e a Elasticidade-Preço Da Oferta Nas Commodities Agrícolas Milho e Soja No Brasil. Rev. Econ. 2011, 7, 48–65. [Google Scholar] [CrossRef]
- Soon, B.M.; Whistance, J. Seasonal Soybean Price Transmission between the U.S. and Brazil Using the Seasonal Regime-Dependent Vector Error Correction Model. Sustainability 2019, 11, 5315. [Google Scholar] [CrossRef]
- Fliehr, O.; Zimmer, Y.; Smith, L.H. Impacts of Transportation and Logistics on Brazilian Soybean Prices and Exports. Transp. J. 2019, 58, 65–77. [Google Scholar] [CrossRef]
- Olafsdottir, A.H.; Sverdrup, H.U. Defining a Conceptual Model for Market Mechanisms in Food Supply Chains, and Parameterizing Price Functions for Coffee, Wheat, Corn, Soybeans and Beef. Int. J. Food Syst. Dyn. 2019, 10, 224–247. [Google Scholar] [CrossRef]
- Powell, M.J.D. Nonlinear Programming--Sequential Unconstrained Minimization Techniques. Comput. J. 1969, 12, 207. [Google Scholar] [CrossRef]
- Karmarkar, N. A New Polynomial-Time Algorithm for Linear Programming. Combinatorica 1984, 4, 373–395. [Google Scholar] [CrossRef]
- Lustig, I.J.; Marsten, R.E.; Shanno, D.F. Feature Article—Interior Point Methods for Linear Programming: Computational State of the Art. ORSA J. Comput. 1994, 6, 1–105. [Google Scholar] [CrossRef]
- Wright, S.J. Primal-Dual Interior-Point Methods, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1997. [Google Scholar]
- Moore, J.H.; Weatherford, L.R. Tomada de Decisão Em Administração Com Planilhas Eletrônicas, 6th ed.; Bookman: Porto Alegre, Brazil, 2005. [Google Scholar]
- Koltai, T.; Tatay, V. A Practical Approach to Sensitivity Analysis in Linear Programming under Degeneracy for Management Decision Making. Int. J. Prod. Econ. 2011, 131, 392–398. [Google Scholar] [CrossRef]
- Ferreira Lopes, T.; Araújo dos Reis, S.; Rezende Celestino, V.R. ANAC’S Degenerate Mathematical Model: A Sensitivity Analysis. Indep. J. Manag. Prod. 2022, 13, 1278–1299. [Google Scholar] [CrossRef]
- Mentzer, J.T.; Dewitt, W.; Keebler, J.S.; Min, S.; Nix, N.W.; Smith, C.D.; Zacharia, Z.G. Defining Supply Chain Management. J. Bus. Logist. 2001, 22, 1–25. [Google Scholar] [CrossRef]
- Ballou, R.H. Gerenciamento Da Cadeia de Suprimentos: Logística Empresarial, 5th ed.; Bookman: Porto Alegre, Brazil, 2006. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).