Nonlinear Model-Based Inferential Control of Moisture Content of Spray Dried Coconut Milk
Abstract
:1. Introduction
2. Materials and Methods
2.1. Dynamic Model of the Spray Drying Process
2.1.1. Drying Kinetic Study
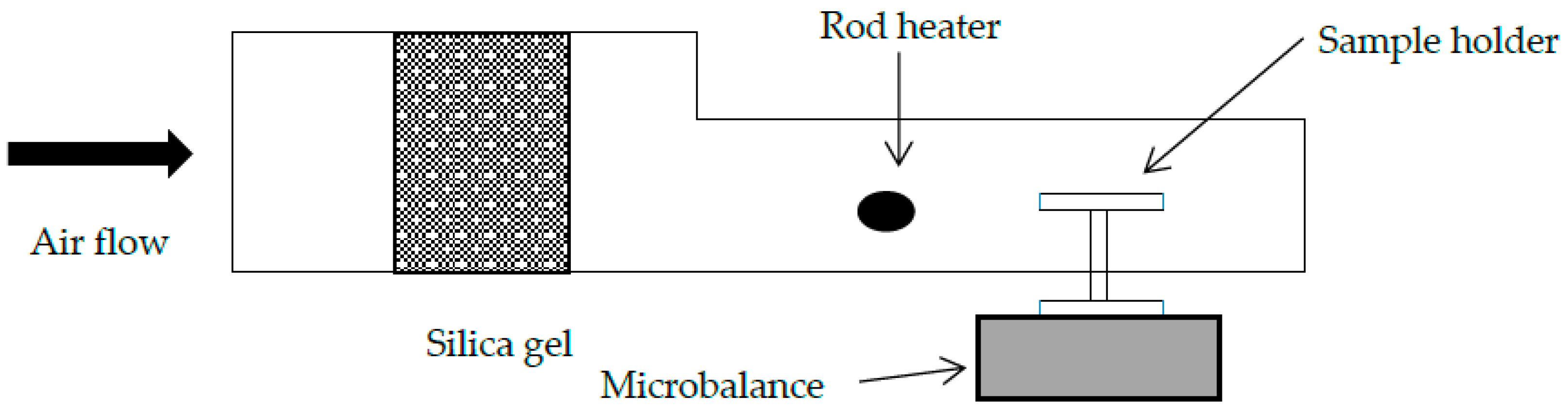
2.1.2. Experimental Setup of Drying Tunnel
2.1.3. Sessile Droplet Drying
2.1.4. Development of Drying Kinetic Model
2.1.5. Mathematical Formulation of Reaction Engineering Approach Model
2.2. Mathematical Formulation of One-Dimensional Spray Dryer Model
- The air behavior is close to that of an ideal gas, therefore the properties of air can be determined based on ideal gas law
- Hold-ups of dry air and solid powder are constant; therefore, the flowrate of dry powder is equal for stream entering and leaving the chamber
- The pressure in the dryer remained at atmospheric pressure
2.3. Formulation of Empirical Models
2.3.1. NARX Model Development
2.3.2. Neural Network (NN) Estimator Development
2.4. Inferential Controller Design
2.5. Controller Performance
3. Results
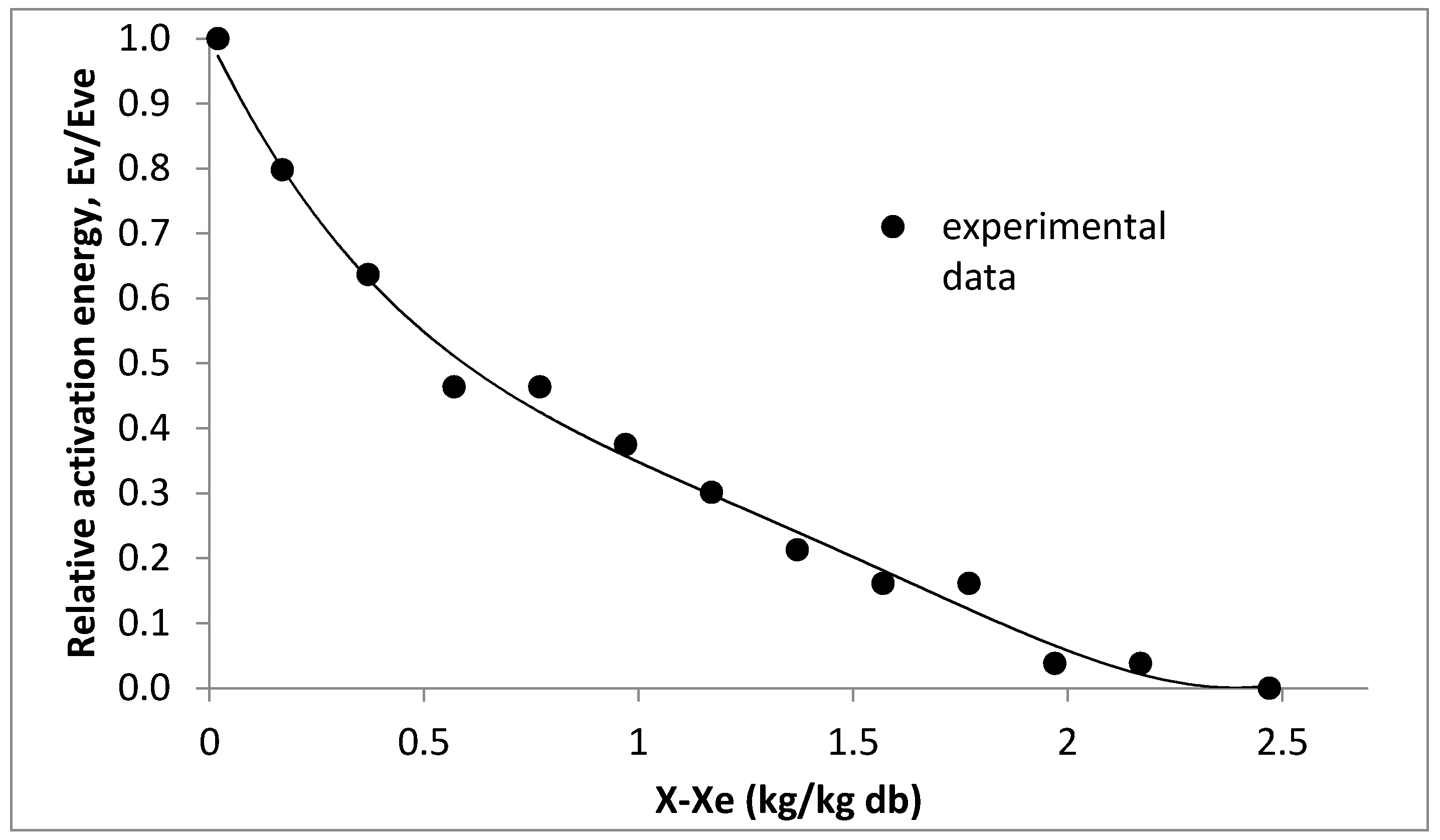
3.1. Drying Kinetic Model of Coconut Milk Droplet
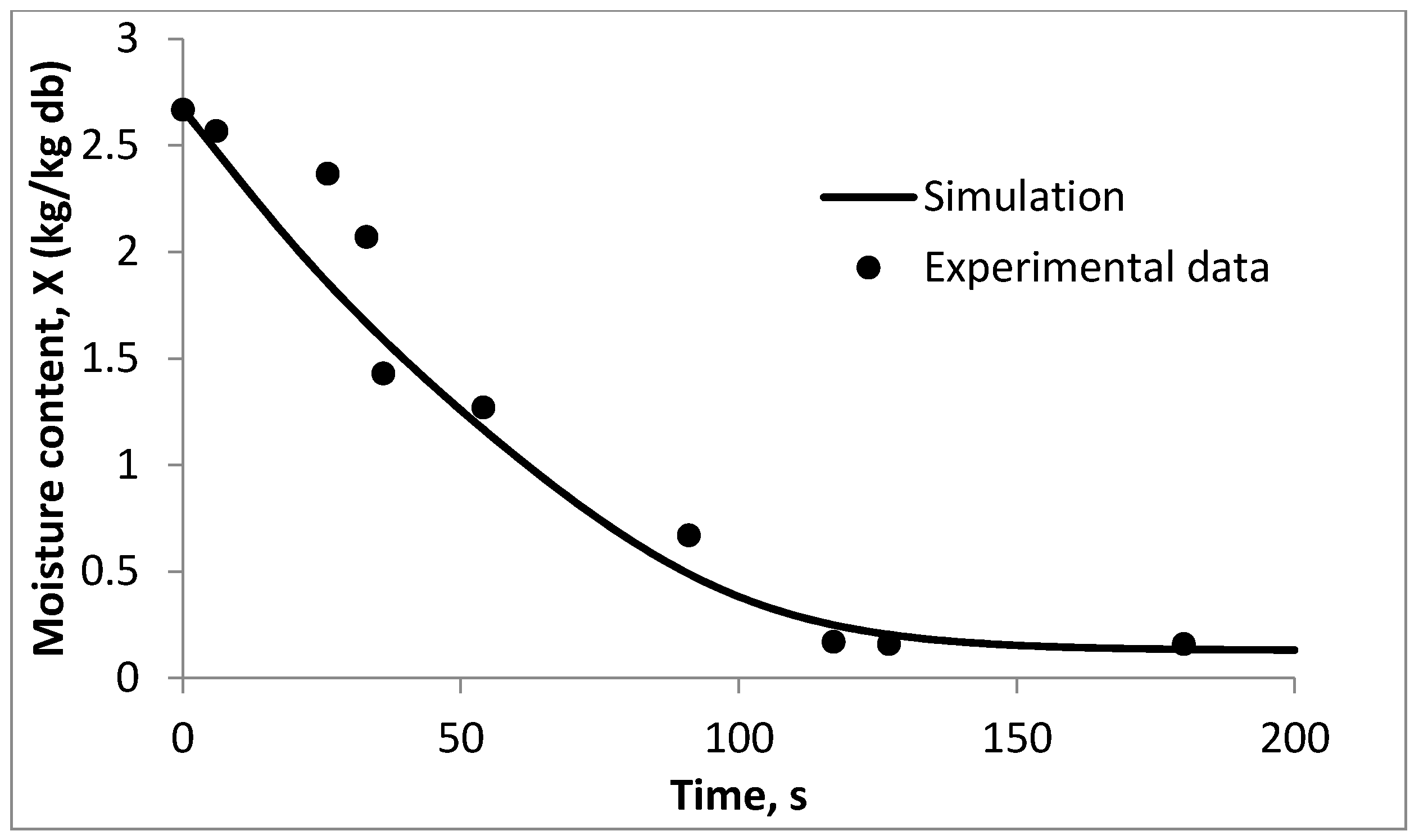
3.2. One-Dimensional Model
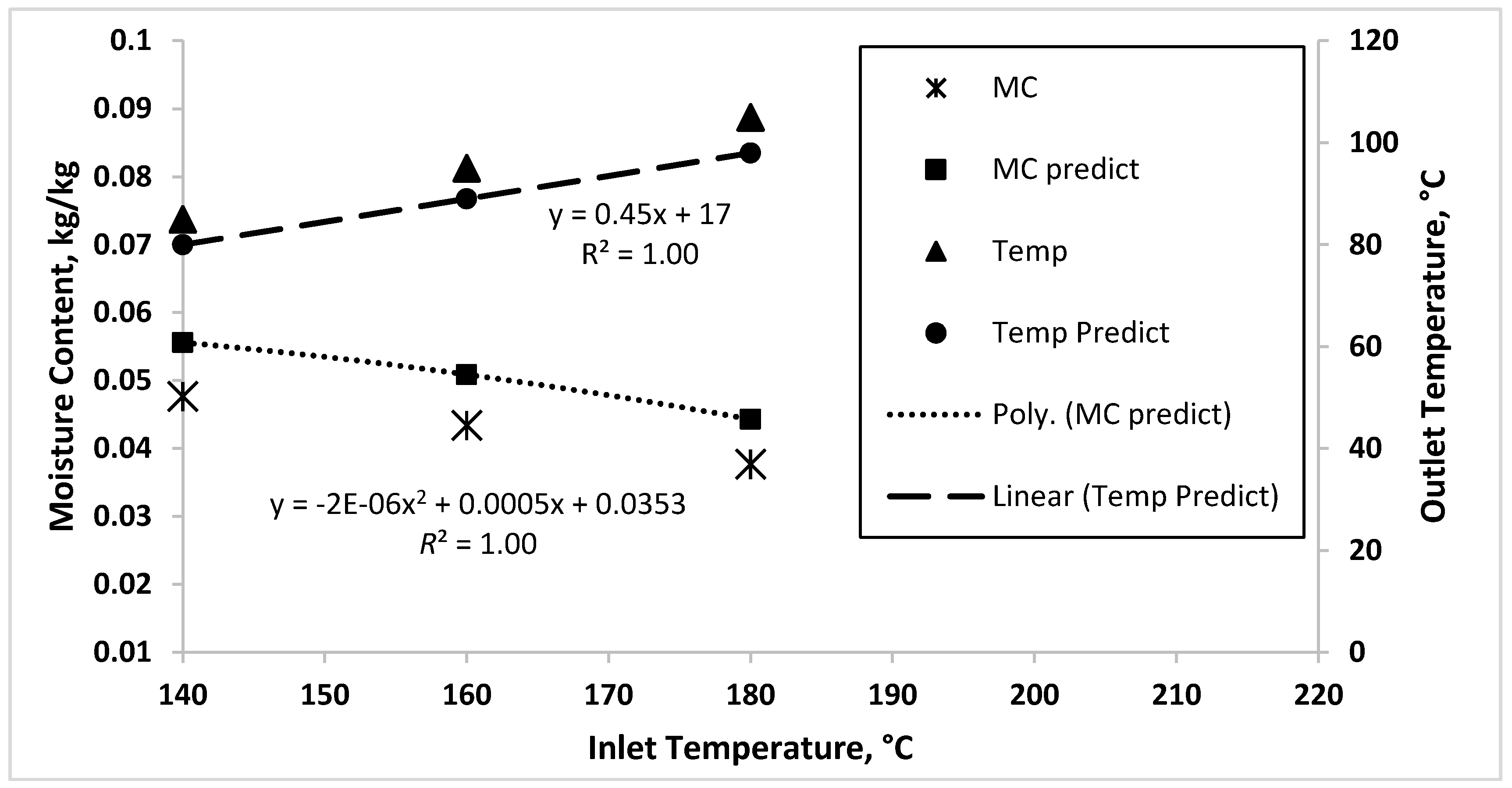
3.3. NARX Model
3.4. Neural Network Estimator
3.5. Inferential Control of Moisture Content
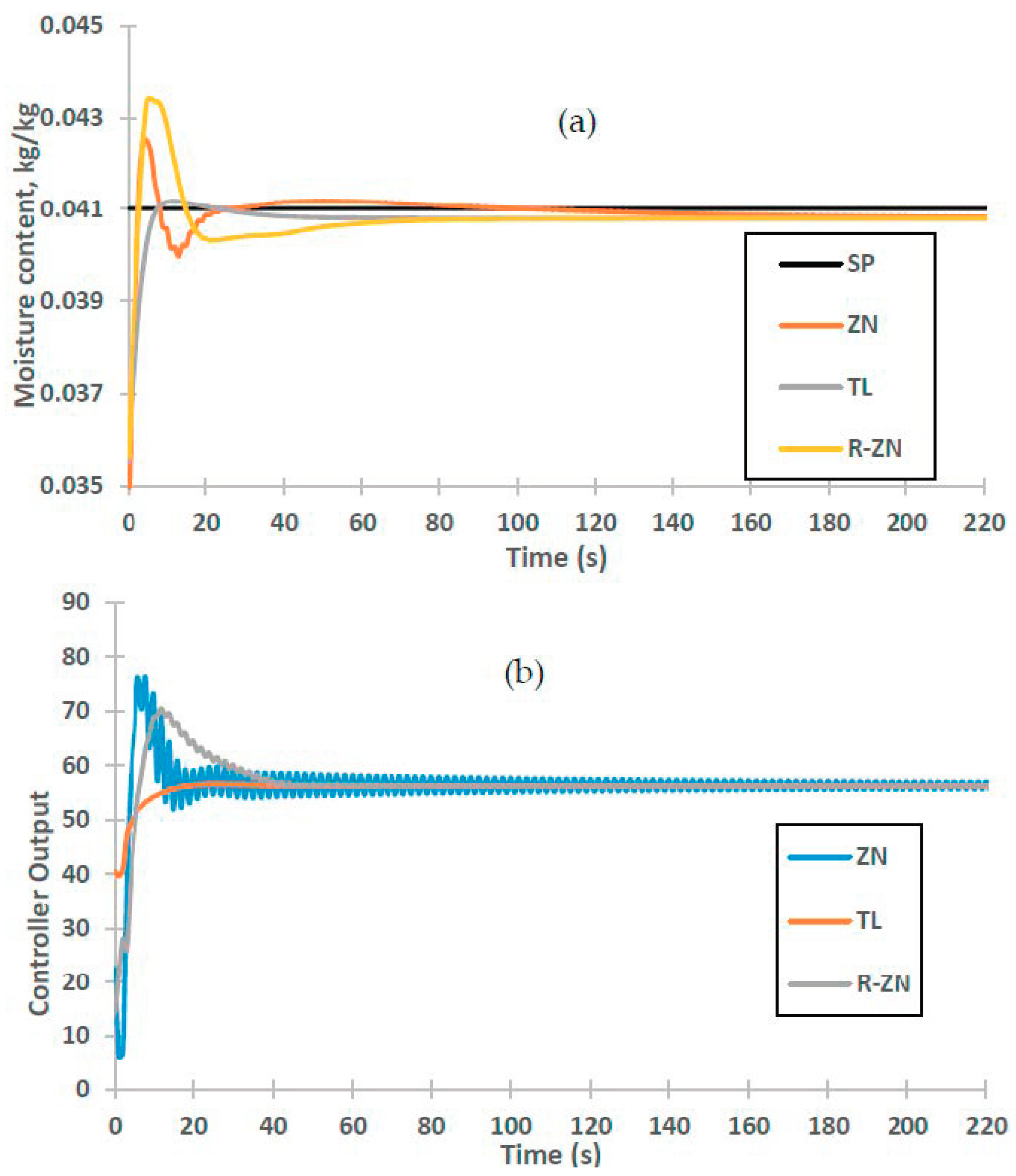
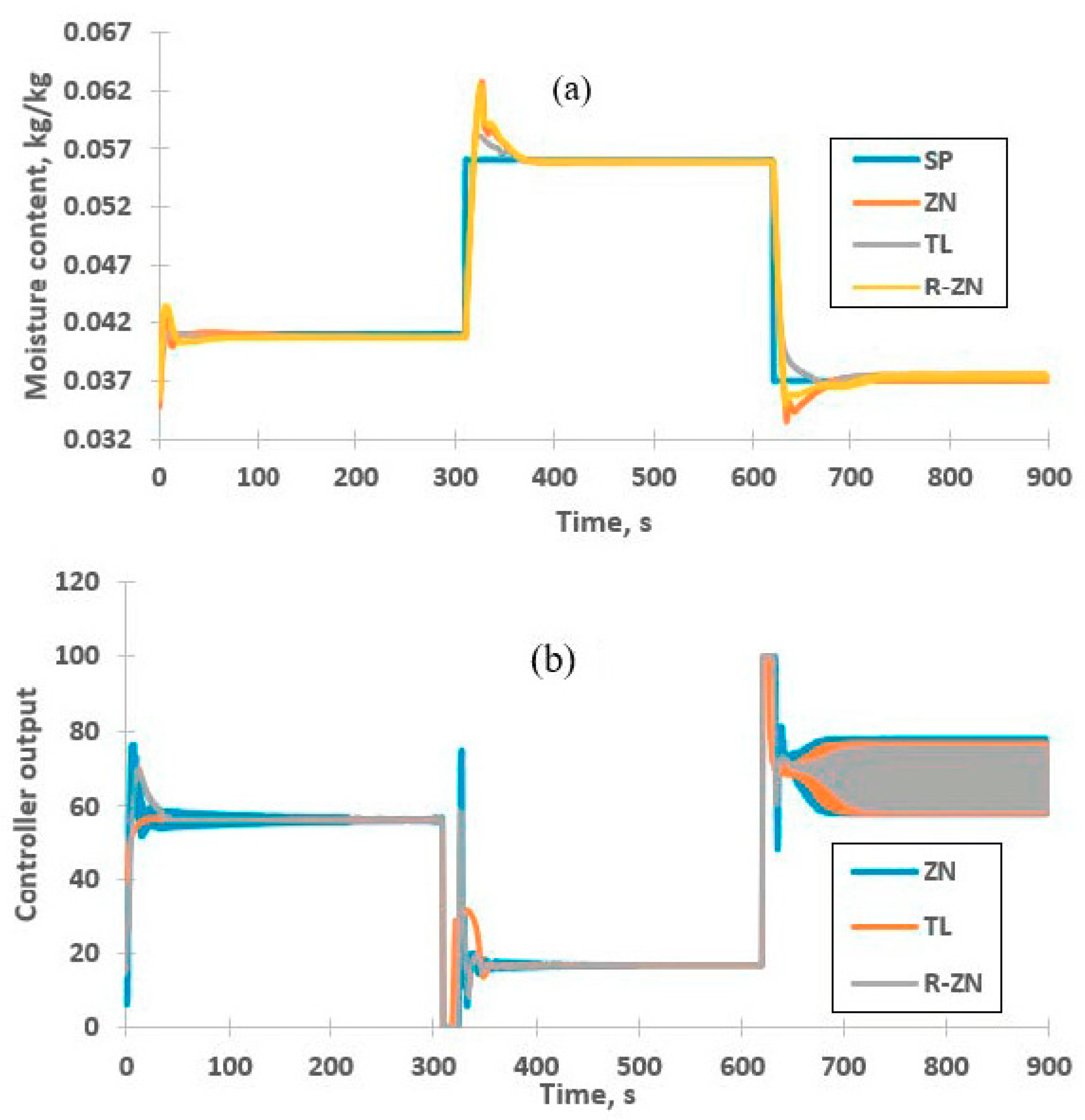
3.6. Set Point Tracking
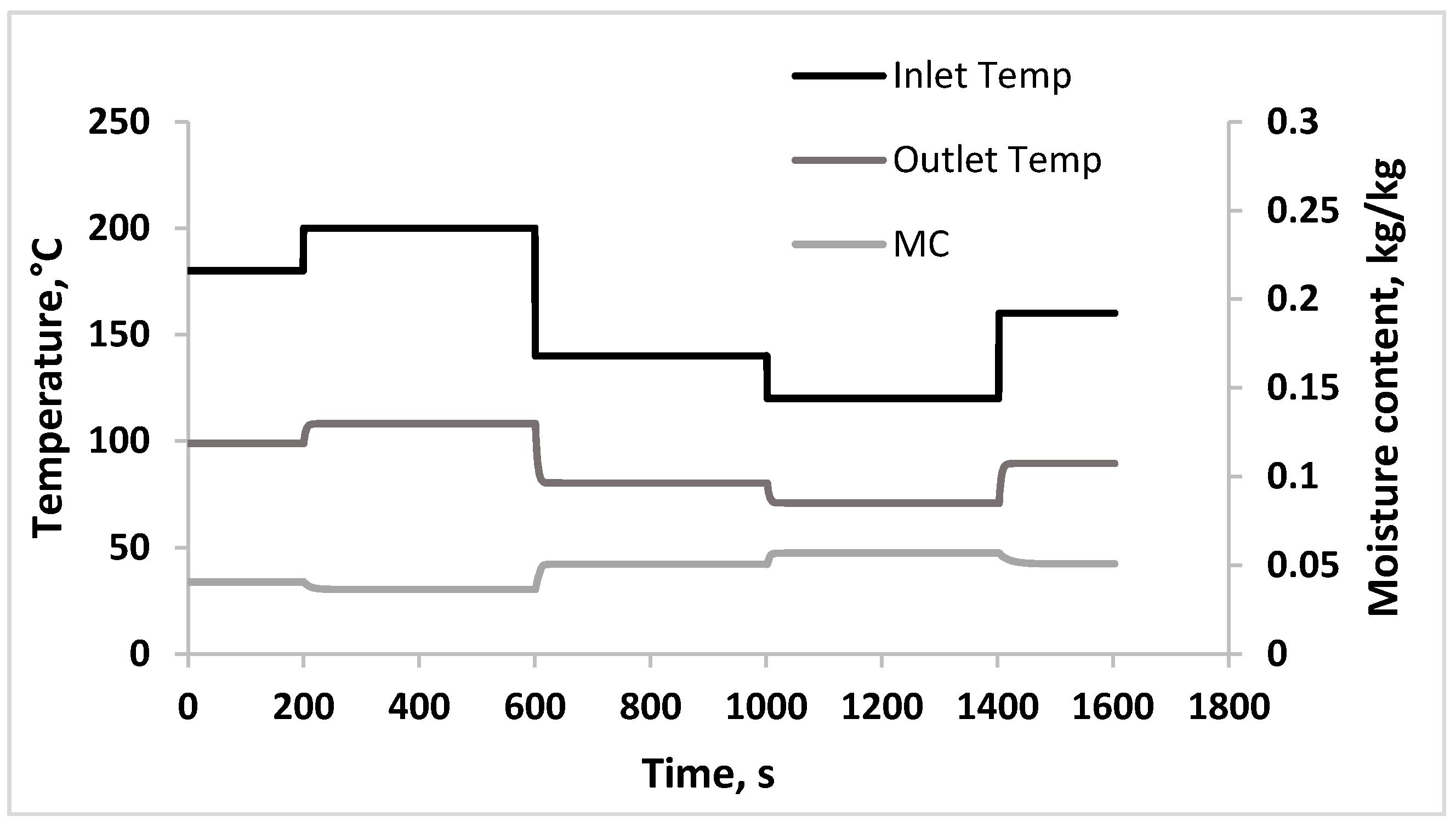
3.7. Disturbance Rejection
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Correlations Used in REA Model and One-Dimensional Model Development
References
- Nikolova, Y.; Petit, J.; Gianfrancesco, A.; Sanders, C.F.W.; Scher, J.; Gaiani, C. Impact of Spray-Drying Process Parameters on Dairy Powder Surface Composition and Properties. Dry. Technol. 2015, 33, 1654–1661. [Google Scholar] [CrossRef] [Green Version]
- Schuck, P.; Jeantet, R.; Bhandari, B.; Chen, X.D.; Perrone, I.T.; de Carvalho, A.F.; Mark Fenelon, M.; Kelly, P. Recent advances in spray drying relevant to the dairy industry: A comprehensive critical review. Dry. Technol. 2016, 34, 1773–1790. [Google Scholar] [CrossRef]
- Kim, E.H.J.; Xiao, D.C.; Pearce, D. Effect of surface composition on the flowability of industrial spray-dried dairy powders. Colloids Surf. B Biointerfaces 2005, 46, 182–187. [Google Scholar] [CrossRef] [PubMed]
- Verma, A.; Singh, S.V. Spray Drying of Fruit and Vegetable Juices—A Review. Crit. Rev. Food Sci. Nutr. 2015, 55, 701–719. [Google Scholar] [CrossRef] [PubMed]
- Shishir, M.R.I.; Chen, W. Trends of spray drying: A critical review on drying of fruit and vegetable juices. Trends Food Sci. Technol. 2017, 65, 49–67. [Google Scholar] [CrossRef]
- Castro-Muñoz, R.; Barragán-Huerta, B.E.; Yáñez-Fernández, J. Use of gelatin-maltodextrin composite as an encapsulation support for clarified juice from purple cactus pear (Opuntia stricta). Lwt Food Sci. Technol. 2015, 62, 242–248. [Google Scholar] [CrossRef]
- Reineccius, G.A. The spray drying of food flavors. Dry. Technol. 2004, 22, 1289–1324. [Google Scholar] [CrossRef]
- Soottitantawat, A.; Partanen, R.; Neoh, T.L.; Yoshii, H. Encapsulation of hydrophilic and hydrophobic flavors by spray drying. Jpn. J. Food Eng. 2015, 16, 37–52. [Google Scholar] [CrossRef] [Green Version]
- Bhandari, B.R.; Dumoulin, E.D.; Richard, H.M.J.; Noleau, I.; Lebert, A.M. Flavor encapsulation by spray drying: Application and linalyl acetate. Food Rev. Int. 1992, 57, 217–221. [Google Scholar] [CrossRef]
- Re, M.I. Microencapsulation by Spray Drying. Dry. Technol. Int. J. 1998, 16, 37–41. [Google Scholar]
- Phisut, N. Spray drying technique of fruit juice powder: Some factors influencing the properties of product. Int. Food Res. J. 2012, 19, 1297–1306. [Google Scholar]
- Jung, H.; Lee, Y.J.; Yoon, W.B. Effect of moisture content on the grinding process and powder properties in food: A review. Processes 2018, 6, 69. [Google Scholar] [CrossRef] [Green Version]
- Michalska, A.; Lech, K. The Effect of Carrier Quantity and Drying Method on the Physical Properties of Apple Juice Powders. Beverages 2018, 4, 2. [Google Scholar] [CrossRef] [Green Version]
- Cheng, H.; Erichsen, H.; Soerensen, J.; Petersen, M.A.; Skibsted, L.H. Optimising water activity for storage of high lipid and high protein infant formula milk powder using multivariate analysis. Int. Dairy J. 2019, 93, 92–98. [Google Scholar] [CrossRef]
- Aguirre-Loredo, R.Y.; Rodriguez-Hernandez, A.I.; Velazquez, G. Modelling the effect of temperature on the water sorption isotherms of chitosan films. Food Sci. Technol. 2017, 37, 112–118. [Google Scholar] [CrossRef] [Green Version]
- Maas, S.G.; Schaldach, G.; Littringer, E.M.; Mescher, A.; Griesser, U.J.; Braun, D.E.; Walzel, P.E.; Urbanetz, N.A. The impact of spray drying outlet temperature on the particle morphology of mannitol. Powder Technol. 2011, 213, 27–35. [Google Scholar] [CrossRef]
- Dufour, P. Control engineering in drying technology: Review and trends. Dry. Technol. 2006, 24, 889–904. [Google Scholar] [CrossRef] [Green Version]
- Schuck, P.; Dolivet, A.; Serge, M.; Jeantet, R. Relative humidity of outlet air: The key parameter to optimize moisture content and water activity of dairy powders. Dairy Sci. Technol. 2008, 88, 313–325. [Google Scholar] [CrossRef] [Green Version]
- Zaror, C.A.; Pérez-Correa, J.R. Model based control of centrifugal atomizer spray drying. Food Control 1991, 2, 170–175. [Google Scholar] [CrossRef]
- Langrish, T.A.G. Multi-scale mathematical modelling of spray dryers. J. Food Eng. 2009, 93, 218–228. [Google Scholar] [CrossRef]
- Truong, V.; Bhandari, B.R.; Howes, T. Optimization of co-current spray drying process of sugar-rich foods. Part I-Moisture and glass transition temperature profile during drying. J. Food Eng. 2005, 71, 55–65. [Google Scholar] [CrossRef]
- Patel, K.; Chen, X.D.; Jeantet, R.; Schuck, P. One-dimensional simulation of co-current, dairy spray drying systems—Pros and cons. Dairy Sci. Technol. 2010, 90, 181–210. [Google Scholar] [CrossRef]
- Patel, K.C.; Chen, X.D. Prediction of spray-dried product quality using two simple drying kinetics models. J. Food Process Eng. 2005, 28, 567–594. [Google Scholar] [CrossRef]
- George, O.A.; Chen, X.D.; Xiao, J.; Woo, M.; Che, L. An Effective Rate Approach to Modeling Single-Stage Spray Drying. Aiche J. 2015, 61, 857–866. [Google Scholar] [CrossRef]
- Pérez-Correa, J.R.; Farías, F. Modelling and control of a spray dryer: A simulation study. Food Control 1995, 6, 219–227. [Google Scholar] [CrossRef]
- Govaerts, R.; Johnson, A.; Crezee, R.; Reyman, G.; Swinkels, P.L.S. Control of an industrial spray drying unit. Control Eng. Pr. 1994, 2, 69–85. [Google Scholar] [CrossRef]
- Petersen, L.N.; Poulsen, N.K.; Niemann, H.H.; Utzen, C.; Jorgensen, J.B. Application of constrained linear MPC to a spray dryer. In Proceedings of the 2014 IEEE Conference on Control Applications (CCA), Juan Les Antibes, France, 8–10 October 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 2120–2126. [Google Scholar] [CrossRef] [Green Version]
- Petersen, L.N.; Poulsen, N.K.; Niemann, H.H.; Utzen, C.; Jorgensen, J.B. Comparison of three control strategies for optimization of spray dryer operation. J. Process Control 2017, 57, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Abdullah, Z.; Taip, F.S.; Siti Mazlina, M.K.; Abdul Rahman, R.Z. Fundamental and empirical modelling of co-current spray drying process—A review. Acta Hortic. 2017, 1152, 219–228. [Google Scholar] [CrossRef]
- O’Callaghan, D.; Cunningham, P. Modern process control techniques in the production of dried milk products—A review. Le Lait 2005, 85, 335–342. [Google Scholar] [CrossRef] [Green Version]
- Plant Services. Advanced Process Control: When Does APC Make Sense? Available online: https://www.plantservices.com/blogs/the-feedback-loop/advanced-process-control-when-does-apc-make-sense/ (accessed on 2 February 2020).
- Perdana, J.; Fox, M.B.; Schutyser, M.A.I.; Boom, R.M. Single-droplet experimentation on spray drying: Evaporation of a sessile droplet. Chem. Eng. Technol. 2011, 34, 1151–1158. [Google Scholar] [CrossRef]
- Fu, N.; Woo, M.W.; Chen, X.D. Single Droplet Drying Technique to Study Drying Kinetics Measurement and Particle Functionality: A Review. Dry. Technol. 2012, 30, 1771–1785. [Google Scholar] [CrossRef]
- Chen, X.D.; Xie, G.Z. Fingerprints of the Drying Behaviour of Particulate or Thin Layer Food Materials Established Using a Reaction Engineering Model. Food Bioprod. Process. 1997, 75, 213–222. [Google Scholar] [CrossRef]
- Schmitz-schug, I. Improving the Nutritional Quality of Dairy Powders—Analyzing and Modeling Lysine Loss during Spray Drying as in Influenced by Drying Kinetics, Thermal Stress, Physical State and Molecular Mobility. Ph.D. Thesis, Technische Universität München, München, German, 2013. [Google Scholar]
- Chandramohan, V.P.; Talukdar, P. Estimation of Equilibrium Moisture Content and Drying Time of Potato Through Hot Air Drying. In Fluid Mechanics and Fluid Power—Contemporary Research; Springer: New Delhi, India, 2017; pp. 205–213. [Google Scholar]
- Douglas, P.L.; Kwade, A.; Lee, P.L.; Mallick, S.K. Simulation of a rotary dryer for sugar crystalline. Dry. Technol. 1993, 11, 129–155. [Google Scholar] [CrossRef]
- AOAC. Official Methods of Analysis, 17th ed.; The Association of Official Analytical Chemists: Gaithersburg, MD, USA, 2000. [Google Scholar]
- García, M.A.; Ragazzo, A. Mathematical modeling of continuous dryers using the heat and mass transfer properties and product-air equilibrium relation. Dry. Technol. 2000, 18, 67–80. [Google Scholar] [CrossRef]
- Kemp, I.C.; Wadley, R.; Hartwig, T.; Cocchini, U.; See-Toh, Y.; Gorringe, L.; Fordham, K.; Ricard, F. Experimental Study of Spray Drying and Atomization with a Two-Fluid Nozzle to Produce Inhalable Particles. Dry. Technol. 2013, 31, 930–941. [Google Scholar] [CrossRef]
- Lin, S.X.Q.; Chen, X.D.; Pearce, D.L. Desorption isotherm of milk powders at elevated temperatures and over a wide range of relative humidity. J. Food Eng. 2005, 68, 257–264. [Google Scholar] [CrossRef]
- Vieira, G.N.A.; Freire, F.B.; Freire, J.T. Control of the moisture content of milk powder produced in a spouted bed dryer using a grey-box inferential controller. Dry. Technol. 2015, 33, 1920–1928. [Google Scholar] [CrossRef]
- Kano, M.; Miyazaki, K.; Hasebe, S.; Hashimoto, I. Inferential control system of distillation compositions using dynamic Partial Least Squares regression. J. Process Control 2000, 10, 157–166. [Google Scholar] [CrossRef]
- Haugen, F.; Lie, B.; Haugen, F.; Bakke, R.; Lie, B. Relaxed Ziegler-Nichols Closed Loop Tuning of PI Controllers. Model. Identif. Control A Nor. Res. Bull. 2013, 34, 83–97. [Google Scholar] [CrossRef] [Green Version]
- Shamaei, S.; Kharaghani, A.; Seiiedlou, S.S.; Aghbashlo, M.; Sondej, F.; Tsotsas, E. Drying behavior and locking point of single droplets containing functional oil. Adv. Powder Technol. 2016, 27, 1750–1760. [Google Scholar] [CrossRef]
- Fu, N.; Huang, S.; Xiao, J.; Chen, X.D. Producing Powders Containing Active Dry Probiotics with the Aid of Spray Drying, 1st ed.; Academic Press: London, UK, 2018; Volume 85. [Google Scholar]
- Larose, D. Data Mining Methods and Models; Wiley-Interscience: Hoboken, NJ, USA, 2006; Volume 2, p. 43. [Google Scholar]
- Putranto, A.; Chen, X.D. The relative activation energy of food materials: Important parameters to describe drying kinetics. Int. J. Food Prop. 2016, 19, 1726–1737. [Google Scholar] [CrossRef]
- Palencia, C.; Nava, J.; Herman, E.; Rodiıguez-Jimenes, G.C.; Garcia-Alvarado, M.A. Spray drying dynamic modeling with a mechanistic model. Dry. Tachnol. 2002, 20, 569–586. [Google Scholar] [CrossRef]
- Chen, R.J.C.; Bloomfield, P.; Fu, J.S. An evaluation of alternative forecasting methods to recreation visitation. J. Leis. Res. 2003, 35, 441–454. [Google Scholar] [CrossRef]
- Ramesh, K.; Aziz, N.; Abd Shukor, S.R. Development of NARX model for distillation column and studies on effect of regressors. J. Appl. Sci. 2008, 8, 1214–1220. [Google Scholar]
- Al Kalbani, F.K.; Zhang, J. Inferential active disturbance rejection control of a heat integrated distillation column. In Proceedings of the 2016 14th International Conference on Control, Automation, Robotics and Vision, Miedzyzdroje, Poland, 29 August–1 September 2016; pp. 403–408. [Google Scholar] [CrossRef]
- Osman, M.; Ramasamy, M. Neural network based soft sensor for inferential control of a binary distillation column. J. Appl. Sci. 2010, 10, 2558–2564. [Google Scholar] [CrossRef]
- Singh, G.; Chandel, A.; Chauhan, D.S. Neural Nework-Based Time Series Methods for Load Forecasting. Int. J. Recent Technol. Eng. 2020, 9, 2441–2444. [Google Scholar]
- Seborg, D.E.; Mellichamp, D.A.; Edgar, T.F.; Doyle, F.J., III. Process Dynamic and Control; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]





| Variable/Property | Value | Reference |
|---|---|---|
| 4185 J/kg·K | [39] | |
| 1389 J/kg·K | Measured | |
| 1800 J/kg·K | [39] | |
| 1000 J/kg·K | [39] | |
| 200 μm | [24] | |
| 5 m/s | [40] | |
| 100 m/s | [40] | |
| 8.314 J/mol·K | [39] | |
| 2501 103 J kg−1 | [39] | |
| 300 K | Measured | |
| 22.8 W/m2·K | Calculated | |
| 0.5 m | Measured | |
| 0.22 m | Measured |
| Variable | Value |
|---|---|
| Droplet: | |
| Moisture content | 2.67 kg/kg |
| Temperature | 27 °C |
| Flowrate | 9.8 10−4 kg/s |
| Hot air: | |
| Humidity | 0.021 kg/kg |
| Temperature | 160 °C |
| Flowrate | 0.011 kg/s |
| Tuning Rules | ||
|---|---|---|
| Zigler-Nichols (ZN) | 0.45 Kcu | Pu /1.2 |
| Tyreus-Luyben (TL) | 0.32 Kcu | Pu |
| Relaxed-Ziegler Nichols (R-ZN) | 0.31 Kcu | 2.2 Pu |
| Model | Number of Delay, d | MSE | |
|---|---|---|---|
| Training | Validation | ||
| NN-NARX | 1 | 3.960 × 10−9 | 8.678 × 10−10 |
| 2 | 1.482 × 10−9 | 1.583 × 10−9 | |
| NN-N | 1 | 7.589 × 10−8 | 1.327 × 10−7 |
| 2 | 1.251 × 10−7 | 7.987 × 10−7 | |
| Tuning Rules | Controller Gain, Kc | Integral Time (s), τI |
|---|---|---|
| Ziegler Nichols (ZN) | −12.75 | 1.67 |
| Tyreus-Luyben (TL) | −8.79 | 4.40 |
| Relaxed-Ziegler Nichols (R-ZN) | −9.072 | 2.00 |
| Tuning Rules | Overshoot (%) | Settling Time (s) | Rise Time (s) | Static Control Offset ×10−4 (kg/kg) |
|---|---|---|---|---|
| ZN | 3.8 | 208 | 2 | 2.04 |
| TL | 0.4 | 126 | 11 | 2.18 |
| R-ZN | 5.9 | 100 | 2.9 | 2.18 |
| Set Point (kg/kg) | Tuning Rules | ITAE | IAE | Static Control Offset ×10−4 (kg/kg) |
|---|---|---|---|---|
| 0.041 | ZN | 2.0683 | 0.0461 | 2.04 |
| TL | 0.1917 | 0.0205 | 2.18 | |
| R-ZN | 0.7400 | 0.0426 | 2.18 | |
| 0.056 | ZN | 5.7465 | 0.3226 | 0.85 |
| TL | 3.4722 | 0.2625 | 0.85 | |
| R-ZN | 5.7180 | 0.3260 | 0.85 | |
| 0.037 | ZN | 7.8142 | 0.2081 | 0.48 |
| TL | 6.0877 | 0.1531 | 2.00 | |
| R-ZN | 8.2237 | 0.2001 | 2.80 |
| Tuning Rules | Positive Deviation | Negative Deviation | ||
|---|---|---|---|---|
| ITAE | IAE | ITAE | IAE | |
| ZN | 0.237 | 0.008 | 0.761 | 0.023 |
| TL | 0.370 | 0.018 | 6.277 | 0.112 |
| R-ZN | 0.210 | 0.010 | 1.622 | 0.044 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdullah, Z.; Taip, F.S.; Kamal, S.M.M.; Rahman, R.Z.A. Nonlinear Model-Based Inferential Control of Moisture Content of Spray Dried Coconut Milk. Foods 2020, 9, 1177. https://doi.org/10.3390/foods9091177
Abdullah Z, Taip FS, Kamal SMM, Rahman RZA. Nonlinear Model-Based Inferential Control of Moisture Content of Spray Dried Coconut Milk. Foods. 2020; 9(9):1177. https://doi.org/10.3390/foods9091177
Chicago/Turabian StyleAbdullah, Zalizawati, Farah Saleena Taip, Siti Mazlina Mustapa Kamal, and Ribhan Zafira Abdul Rahman. 2020. "Nonlinear Model-Based Inferential Control of Moisture Content of Spray Dried Coconut Milk" Foods 9, no. 9: 1177. https://doi.org/10.3390/foods9091177
APA StyleAbdullah, Z., Taip, F. S., Kamal, S. M. M., & Rahman, R. Z. A. (2020). Nonlinear Model-Based Inferential Control of Moisture Content of Spray Dried Coconut Milk. Foods, 9(9), 1177. https://doi.org/10.3390/foods9091177





