Combined Experimental and CFD Approach of Two-Phase Flow Driven by Low Thermal Gradients in Wine Tanks: Application to Light Lees Resuspension
Abstract
1. Introduction
2. Experimental Procedure: Highlighting the Thermal Resuspension Process of Light Lees
2.1. Flow Dynamics Within the Wine Bulk
2.2. Settling Dynamics of the Light Lees
2.3. Resuspension of Light Lees
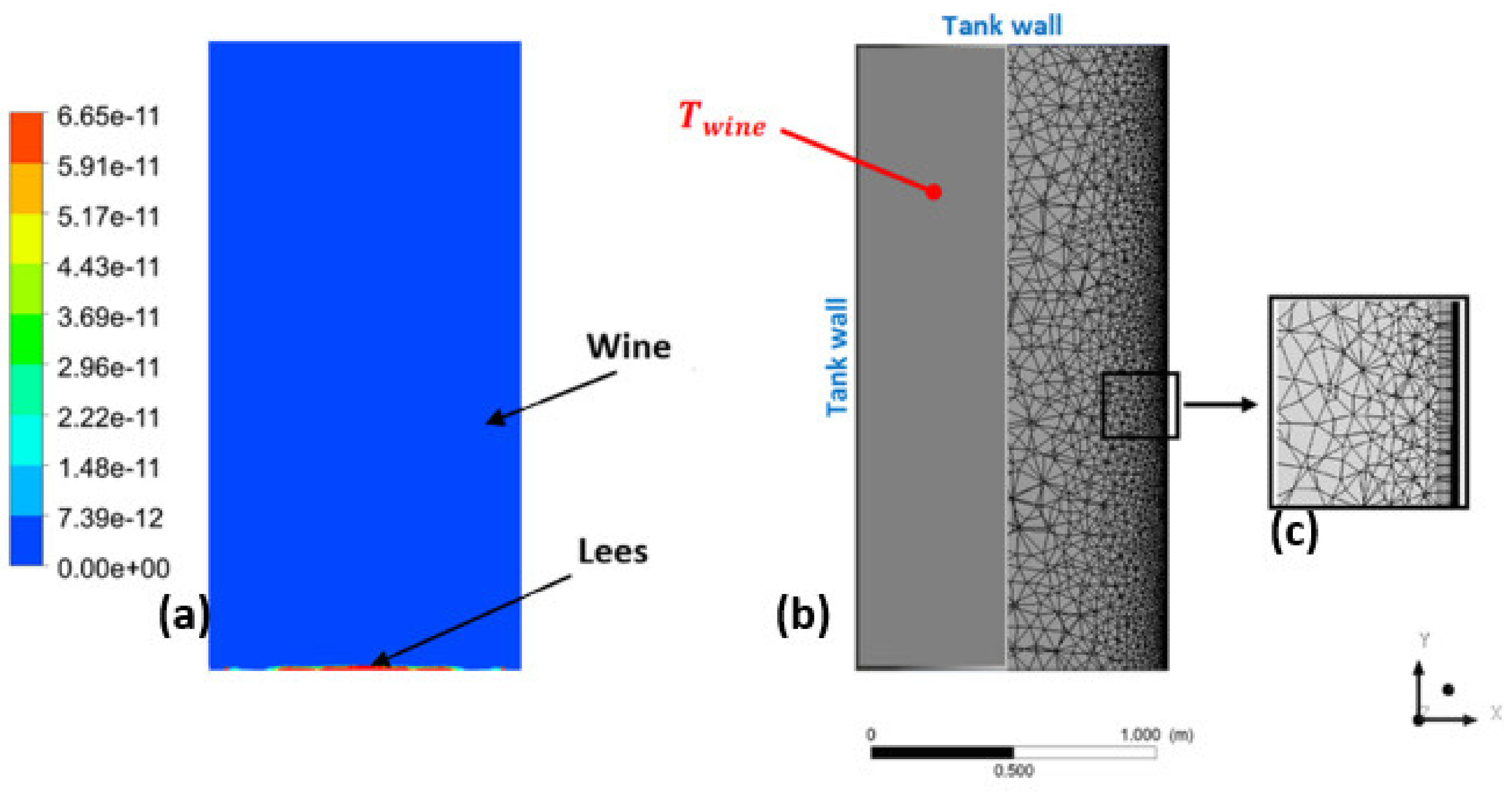
3. Numerical Procedure: Application of CFD to a Full-Scale Wine Tank
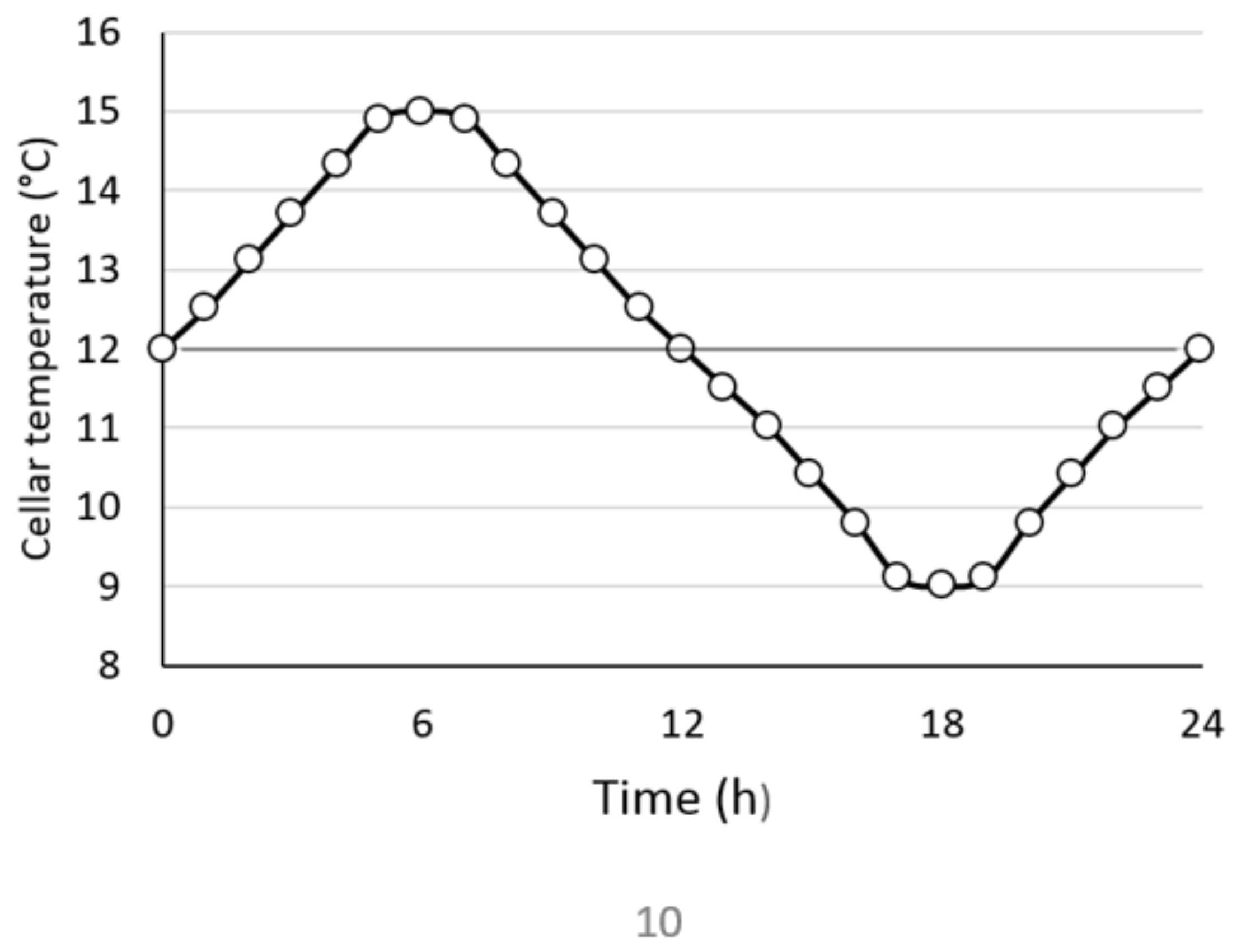
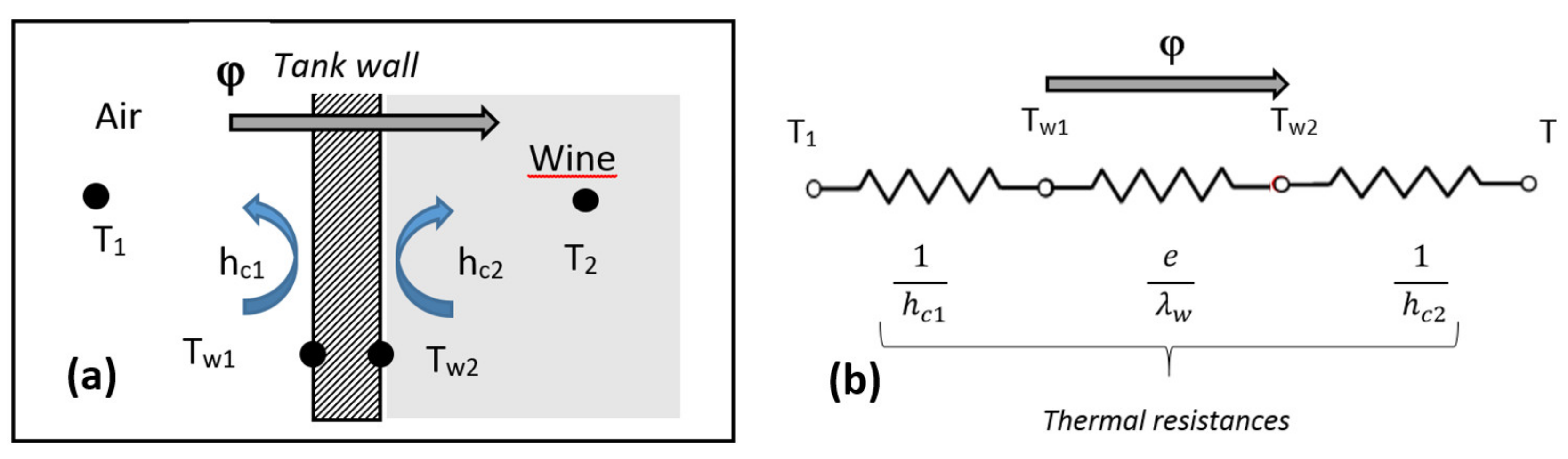
3.1. Heat Transfer and Numerical Methods
3.2. Equations and Numerical Scheme
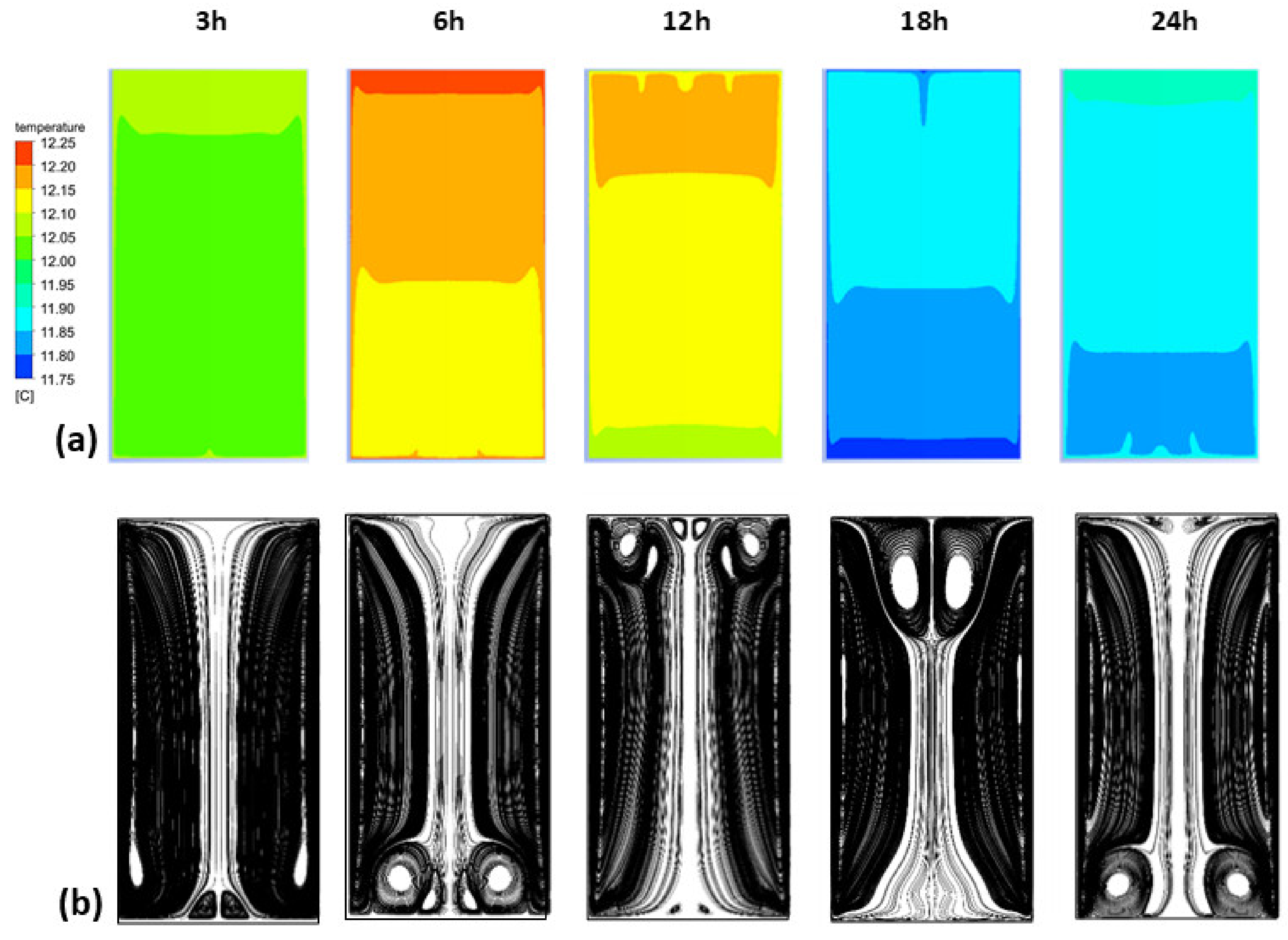
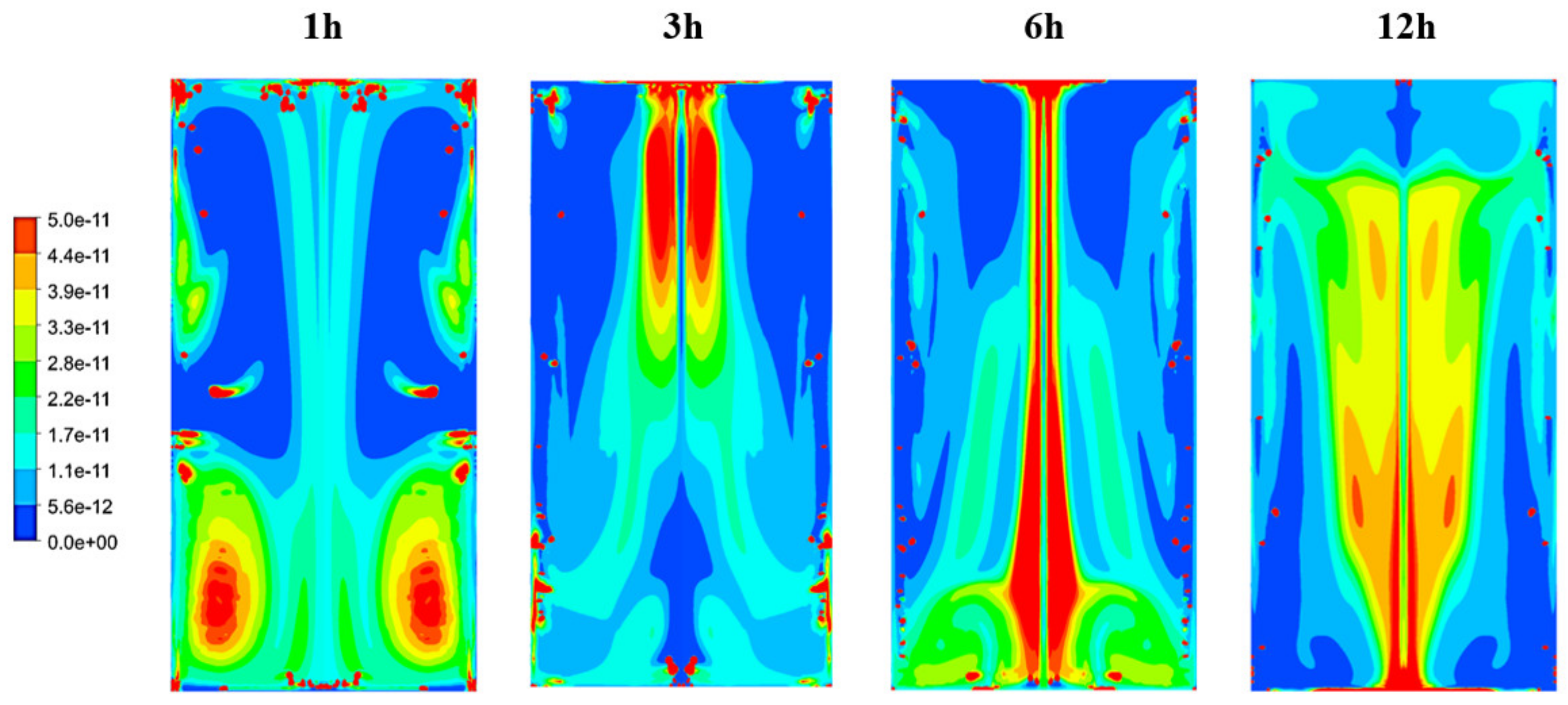
3.3. Numerical Results
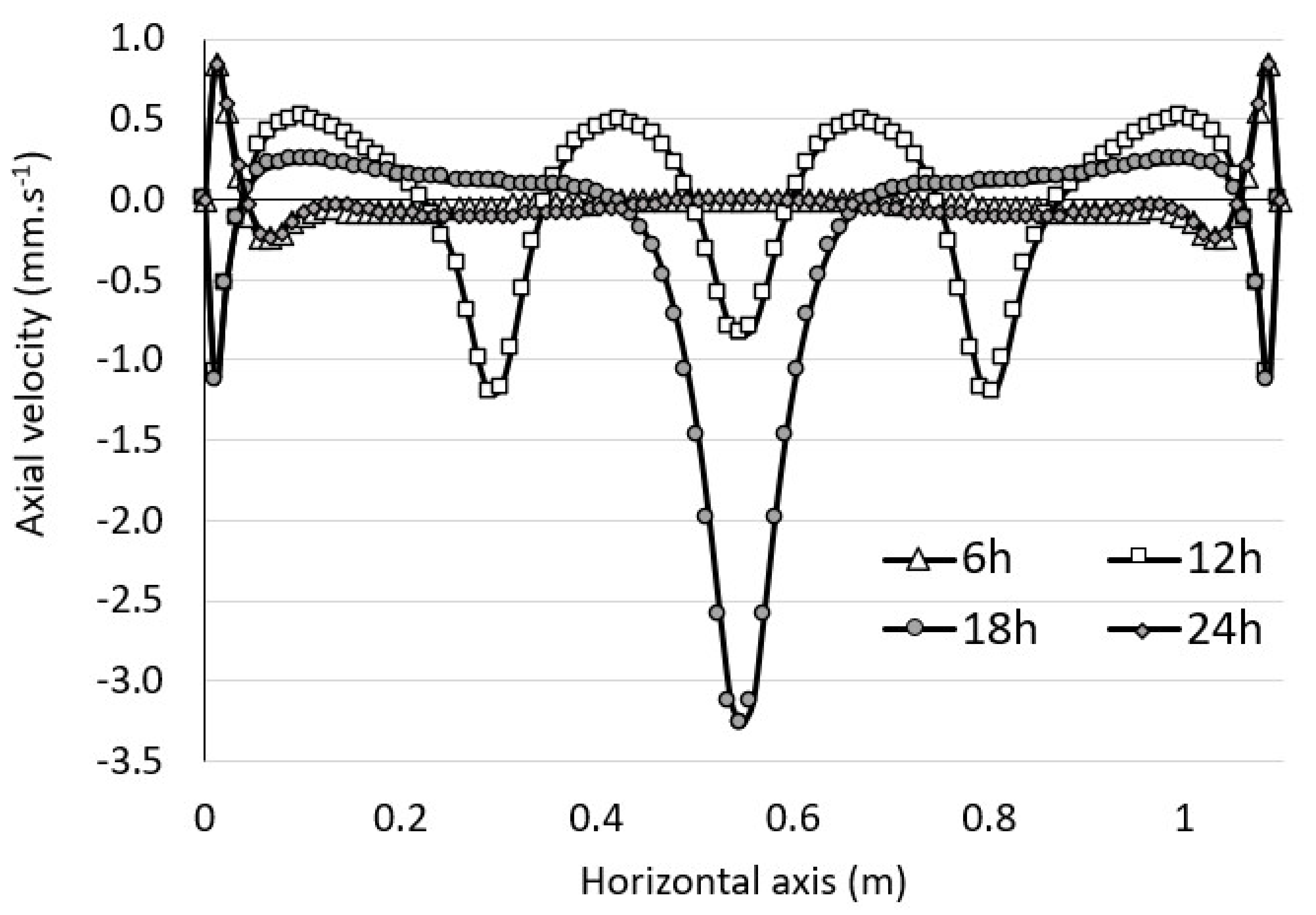
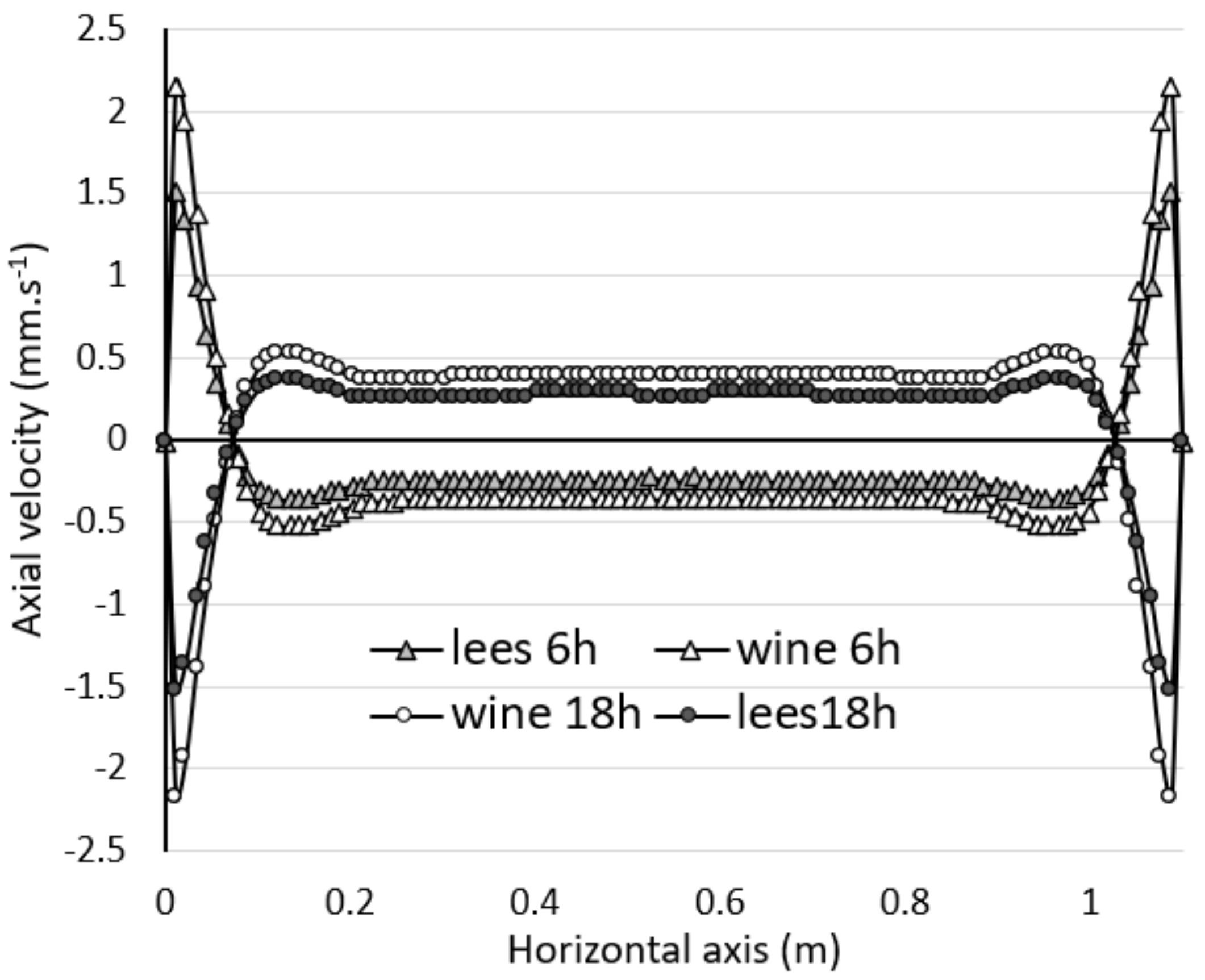
3.4. Contribution of the Wine Mixing Dynamics on the Resuspension of Light Lees
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| D | Diameter of the tank, m |
| Average lees diameter, m | |
| e | Wall tank thickness, m |
| External body forces, N | |
| Grashof number | |
| H | Height of the tank, m |
| Convective heat transfer coefficient of air, W·m−2·K−1 | |
| Convective heat transfer coefficient of wine, W·m−2·K−1 | |
| Nu | Nusselt number |
| Static pressure, Pa | |
| Prandtl number | |
| Radial coordinate | |
| Raleigh number | |
| Mass added to the continuous phase from the dispersed second phase | |
| Tw1 | Temperature of the outer surface of the tank, K |
| Tw2 | Temperature of the inner surface of the tank, K |
| T1 | Air temperature, K |
| T2 | Wine temperature, K |
| Axial velocity, m·s−1 | |
| Radial velocity, m·s−1 | |
| Axial coordinate | |
| Thermal conductivity of air, W·m−1·K−1 | |
| Thermal conductivity of wine, W·m−1·K−1 | |
| Dynamic viscosity of wine, kg·m−1·s−1 | |
| Density of lees, kg·m−3 | |
| Density of wine, kg·m−3 | |
| ϕ | Heat flux, W·m−2 |
| Density, kg·m−3 | |
| Gravitational acceleration, m·s−2 | |
| ν | Kinematic viscosity, m2·s−1 |
| β | Thermal expansion coefficient, K−1 |
References
- Galanakis, C.M. Handbook of Grape Processing by-Products; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Versari, A.; Castellari, M.; Spinabelli, U.; Galassi, S. Recovery of tartaric acid from industrial enological wastes. J. Chem. Technol. Biotechnol. 2001, 76, 485–488. [Google Scholar] [CrossRef]
- Pérez-Serradilla, J.A.; Luque de Castro, M.D. Role of lees in wine production: A review. Food Chem. 2008, 111, 447–456. [Google Scholar] [CrossRef] [PubMed]
- Sancho-Galán, P.; Amores-Arrocha, A.; Jiménez-Cantazino, A.; Ferreiro-González, M.; Palacios, V.; Barbero, G.F. Ultrasound-assisted extraction of anthocyanins and total phenolic compounds in Vitis vinifera L. Tempranillo winemaking lees. VITIS 2019, 58, 39–47. [Google Scholar] [CrossRef]
- Fornairon-Bonnefond, C.; Camarasa, C.; Moutounet, M.; Salmon, J.-M. New trends on yeast autolysis and wine ageing on lees: A bibliographic review. J. Int. Sci. Vigne Vin 2002, 36, 49–69. [Google Scholar] [CrossRef]
- Fia, G.; Zanoni, B.; Gori, C. A new technique for exploitation of wine lees. Agric. Agric. Sci. Procedia 2016, 8, 748–754. [Google Scholar] [CrossRef][Green Version]
- Liger-Belair, G. Uncorked: The Science of Champagne; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Colombié, S.; Malherbe, S.; Sablayrolles, J.M. Modeling of heat transfer in tanks during wine-making fermentation. Food Control 2016, 18, 953–960. [Google Scholar] [CrossRef]
- Kakaç, S.; Yener, Y.; Pramuanjaroenkij, A. Convective Heat Transfer; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Lachman, J.; Rutkowski, K.; Travnicek, P.; Vitez, T.; Burg, P.; Turan, J.; Junga, P.; Visacki, V. Determination of rheological behaviour of wine lees. Int. Agrophys. 2015, 29, 307–311. [Google Scholar] [CrossRef]
- Liger-Belair, G.; Religieux, J.-B.; Fohanno, S.; Vialatte, M.-A.; Jeandet, P.; Polidori, G. Visualization of mixing flow phenomena in champagne glasses under various glass shape and engravement conditions. J. Agric. Food Chem. 2007, 55, 882–888. [Google Scholar] [CrossRef] [PubMed]
- Liger-Belair, G.; Beaumont, F.; Jeandet, P.; Polidori, G. Flow patterns of bubble nucleation sites (called fliers) freely floating in champagne glasses. Langmuir 2007, 23, 10976–10983. [Google Scholar] [CrossRef] [PubMed]
- Polidori, G.; Beaumont, F.; Jeandet, P.; Liger-Belair, G. Ring vortex scenario in engraved champagne glasses. J. Vis. 2009, 12, 275–282. [Google Scholar] [CrossRef]
- Beaumont, F.; Liger-Belair, G.; Polidori, G. Unveiling self-organized two-dimensional (2D) convective cells in champagne glasses. J. Food Eng. 2016, 188, 58–65. [Google Scholar] [CrossRef]
- Hlavac, P.; Bozikova, M.; Hlavacova, Z.; Kardjilova, K. Changes in selected wine physical properties during the short-time storage. Res. Agric. Eng. 2016, 62, 147–153. [Google Scholar] [CrossRef]
- Correia, J.; Mourão, A.; Cavique, M. Energy evaluation at a winery: A case study at a Portuguese producer. MATEC Web Conf. 2017, 112, 10001. [Google Scholar] [CrossRef]
- Rodrigues, A.; Ricardo-da-Silva, J.-M.; Lucas, C.; Laureano, O. Characterization of mannoproteins during white wine (Vitis vinifera L. cv. Encruzado) ageing on lees with stirring in oak wood barrels and in a stainless-steel tank with oak staves. J. Int. Sci. Vigne Vin 2012, 46, 321–329. [Google Scholar] [CrossRef]
- Liger-Belair, G.; Parmentier, M.; Jeandet, P. Modeling the kinetics of bubble nucleation in champagne and carbonated beverages. J. Phys. Chem. B 2006, 110, 21145–21151. [Google Scholar] [CrossRef] [PubMed]
- Beaumont, F.; Liger-Belair, G.; Polidori, G. Flow analysis from PIV in engraved champagne tasting glasses: Flute versus coupe. Exp. Fluids 2015, 56, 170. [Google Scholar] [CrossRef]
- Bogard, F.; Beaumont, F.; Vasserot, Y.; Murer, S.; Simescu-Lazar, F.; Polidori, G. Passive wine macromixing from 3D natural convection for different winery tank shapes: Application to lees resuspension. Mech. Ind. 2020, 21, 207. [Google Scholar] [CrossRef]
- Barbaresi, L.; Torreggiani, D.; Benni, S.; Tassinari, P. Indoor air temperature monitoring: A method lending support to management and design tested on a wine-aging room. Build. Environ. 2015, 86, 203–210. [Google Scholar] [CrossRef]
- Park, H.W.; Yoon, W.B. Computational fluid dynamics (CFD) modelling and application for sterilization of foods: A review. Processes 2018, 6, 62. [Google Scholar] [CrossRef]


| Kinematic Viscosity, ν (m2·s−1) | Thermal Conductivity, λ (W·m−1·K−1) | Thermal Expansion Coefficient, β (K−1) | Prandtl Number, Pr | |
|---|---|---|---|---|
| Stainless steel | — | 16 | — | — |
| Air | 1.57·10−5 | 0.0262 | — | 0.7 |
| Wine | 1.25·10−6 | 0.46 | 8·10−4 | 9.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bogard, F.; Beaumont, F.; Vasserot, Y.; Simescu-Lazar, F.; Nsom, B.; Liger-Belair, G.; Polidori, G. Combined Experimental and CFD Approach of Two-Phase Flow Driven by Low Thermal Gradients in Wine Tanks: Application to Light Lees Resuspension. Foods 2020, 9, 865. https://doi.org/10.3390/foods9070865
Bogard F, Beaumont F, Vasserot Y, Simescu-Lazar F, Nsom B, Liger-Belair G, Polidori G. Combined Experimental and CFD Approach of Two-Phase Flow Driven by Low Thermal Gradients in Wine Tanks: Application to Light Lees Resuspension. Foods. 2020; 9(7):865. https://doi.org/10.3390/foods9070865
Chicago/Turabian StyleBogard, Fabien, Fabien Beaumont, Yann Vasserot, Florica Simescu-Lazar, Blaise Nsom, Gérard Liger-Belair, and Guillaume Polidori. 2020. "Combined Experimental and CFD Approach of Two-Phase Flow Driven by Low Thermal Gradients in Wine Tanks: Application to Light Lees Resuspension" Foods 9, no. 7: 865. https://doi.org/10.3390/foods9070865
APA StyleBogard, F., Beaumont, F., Vasserot, Y., Simescu-Lazar, F., Nsom, B., Liger-Belair, G., & Polidori, G. (2020). Combined Experimental and CFD Approach of Two-Phase Flow Driven by Low Thermal Gradients in Wine Tanks: Application to Light Lees Resuspension. Foods, 9(7), 865. https://doi.org/10.3390/foods9070865





