The Optimization of the Dehydration Temperature of Peels from Prickly Pears
Abstract
1. Introduction
2. Materials and Methods
2.1. Prickly Pear Peel Dehydration Process
2.2. Prickly Pear Peel Water Concentration
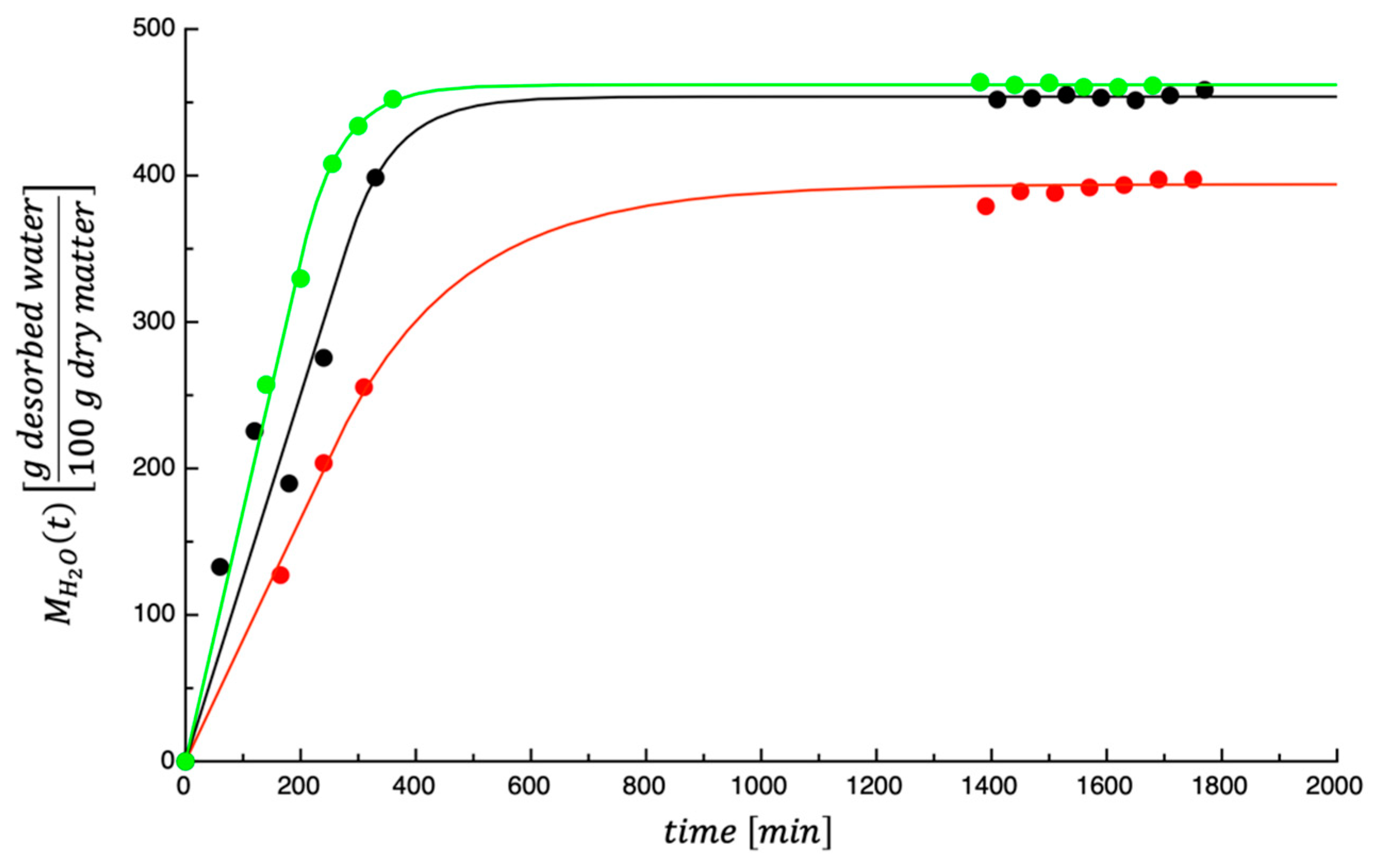
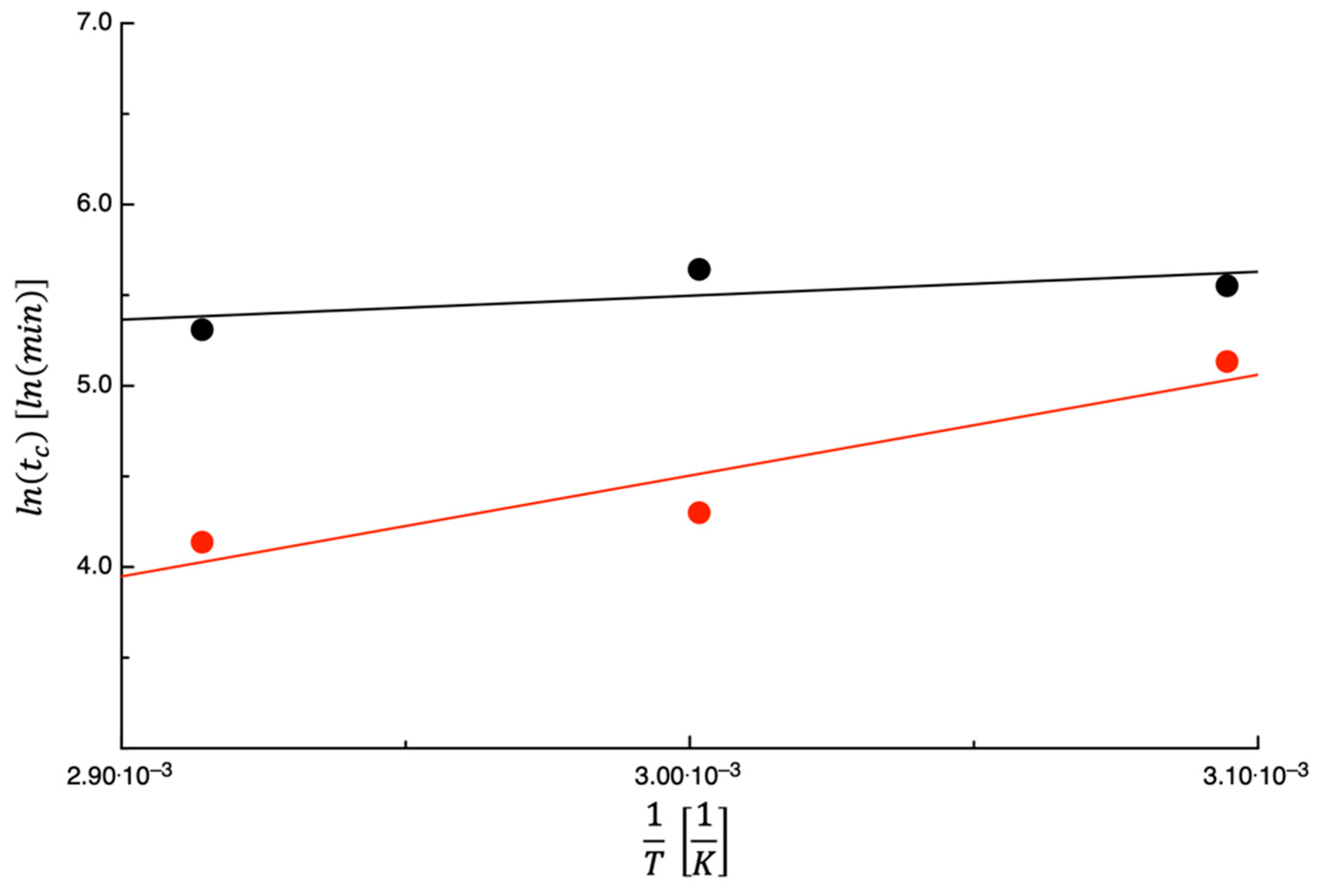
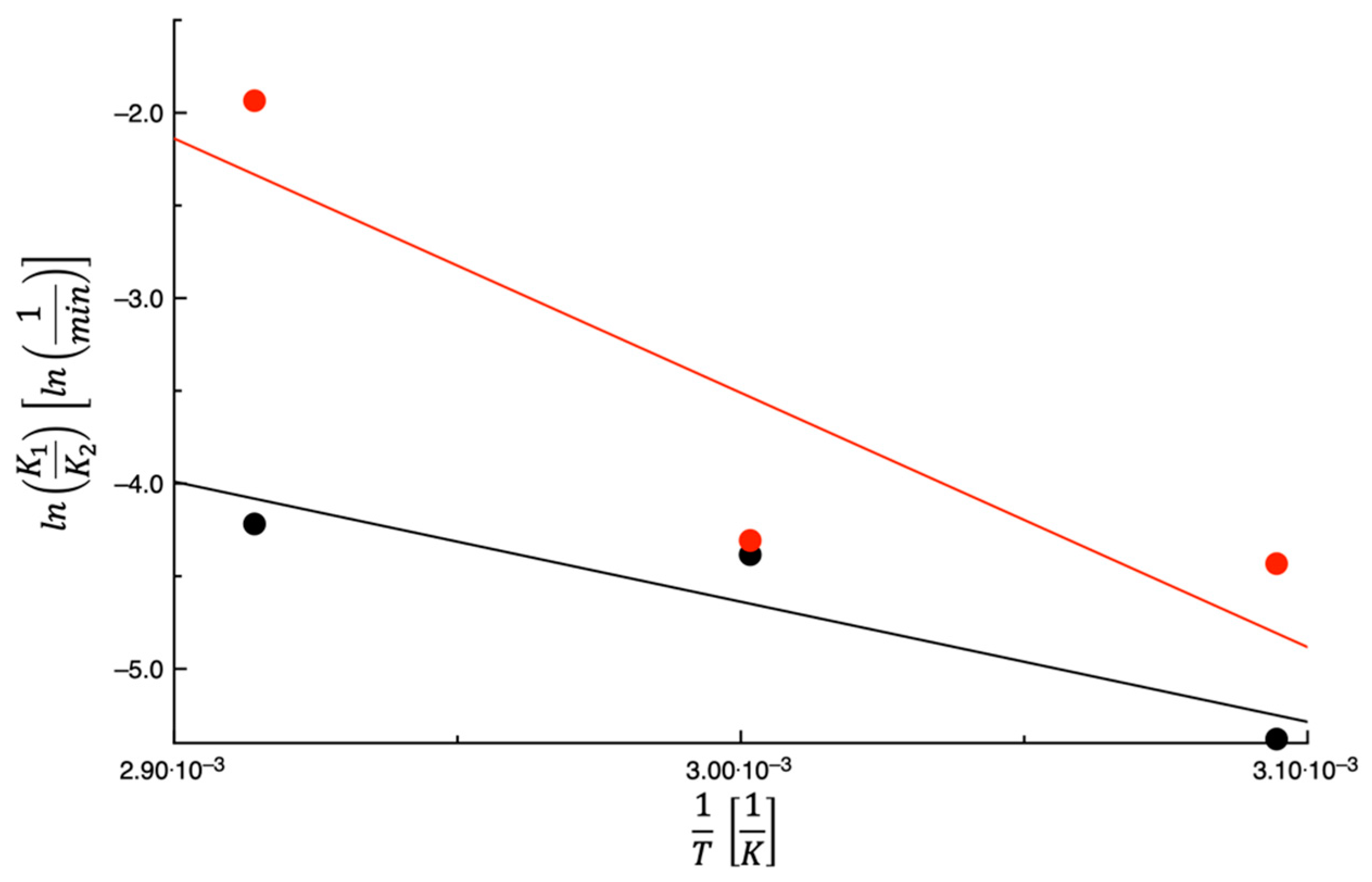
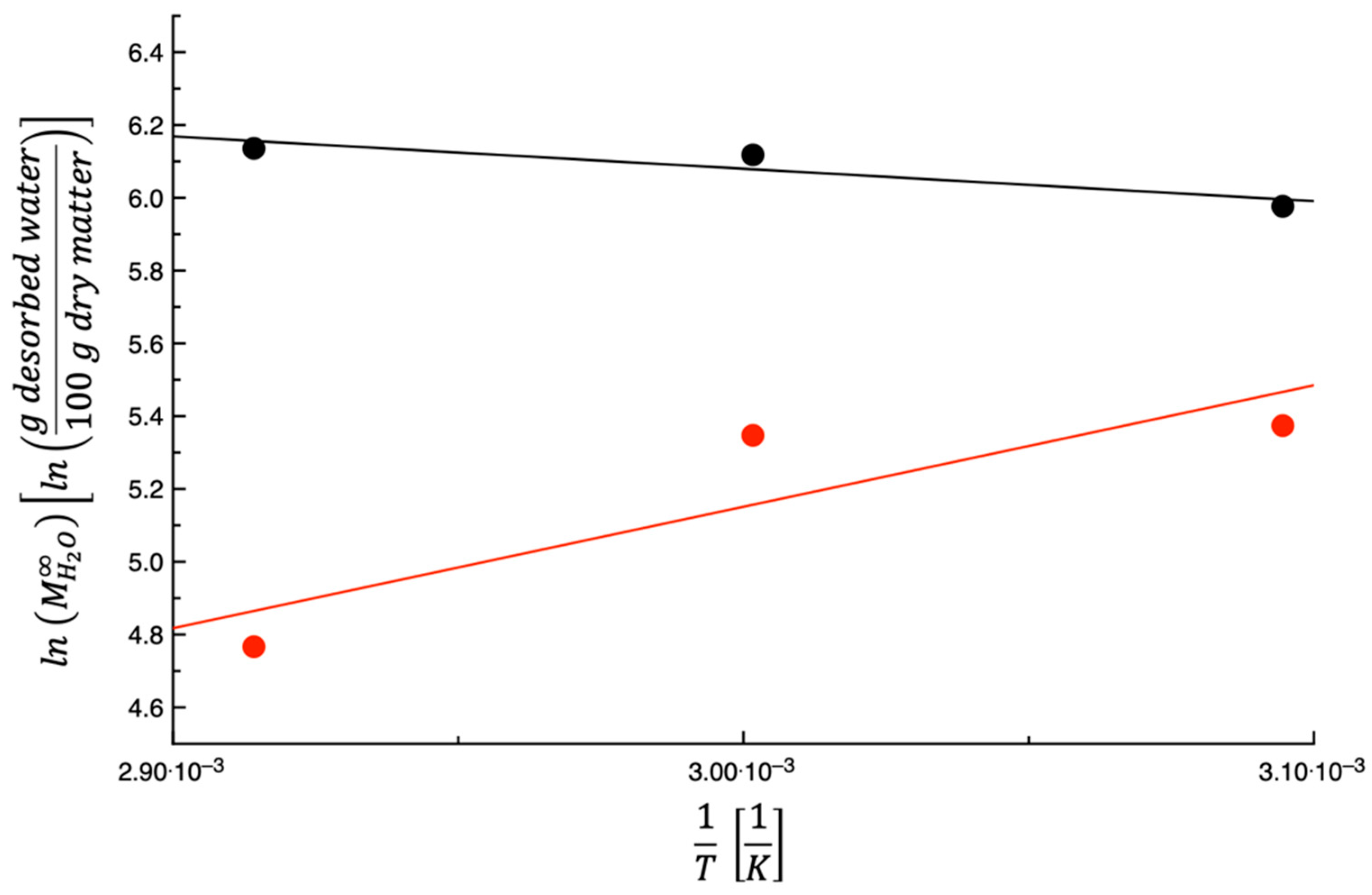
2.3. Dehydration Kinetic
2.4. Dehydration Process Productivity
2.5. Energy Consumption of the Dehydration Process
3. Results and Discussion
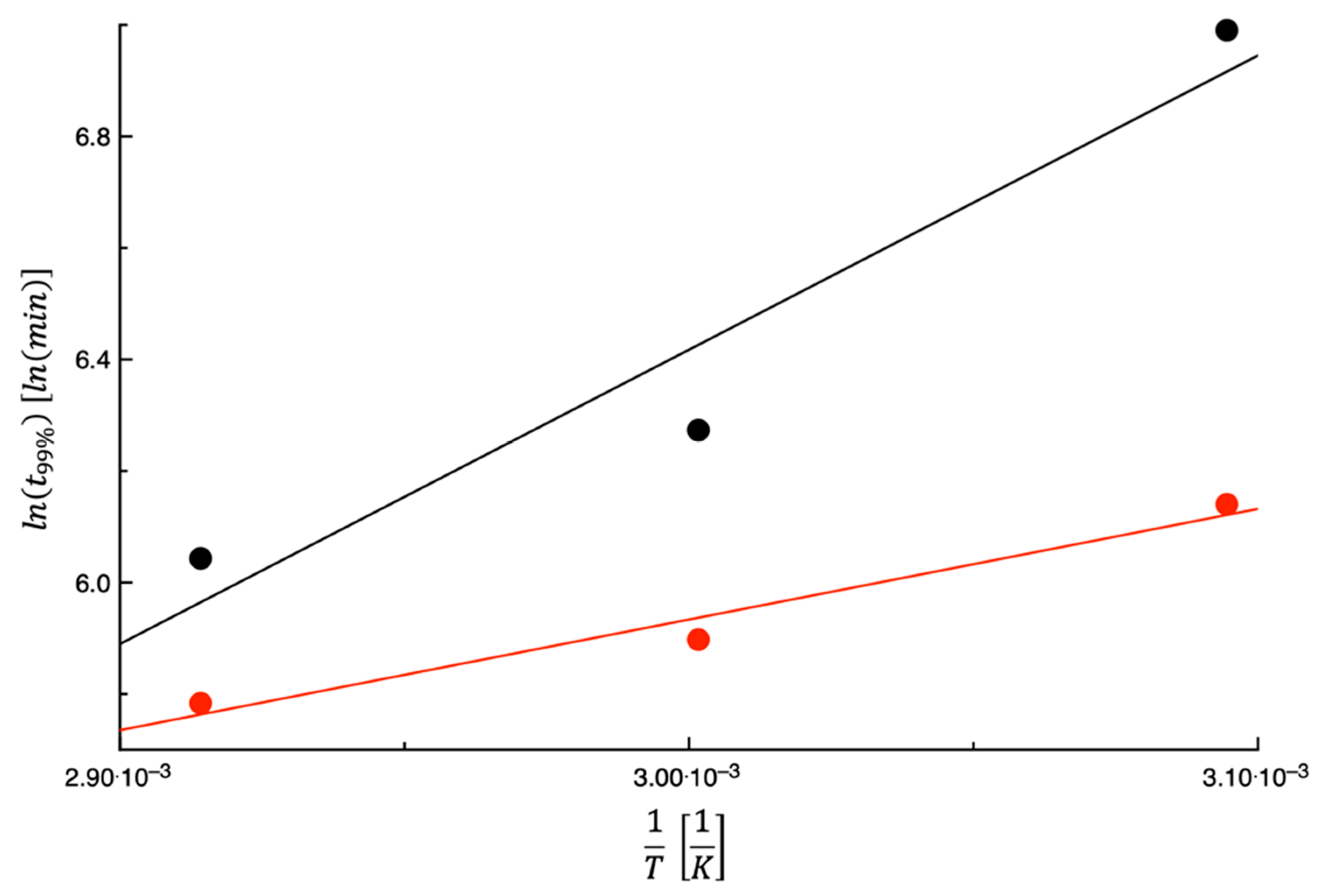
3.1. Dehydration Kinetics
3.2. Dehydration Process Productivity
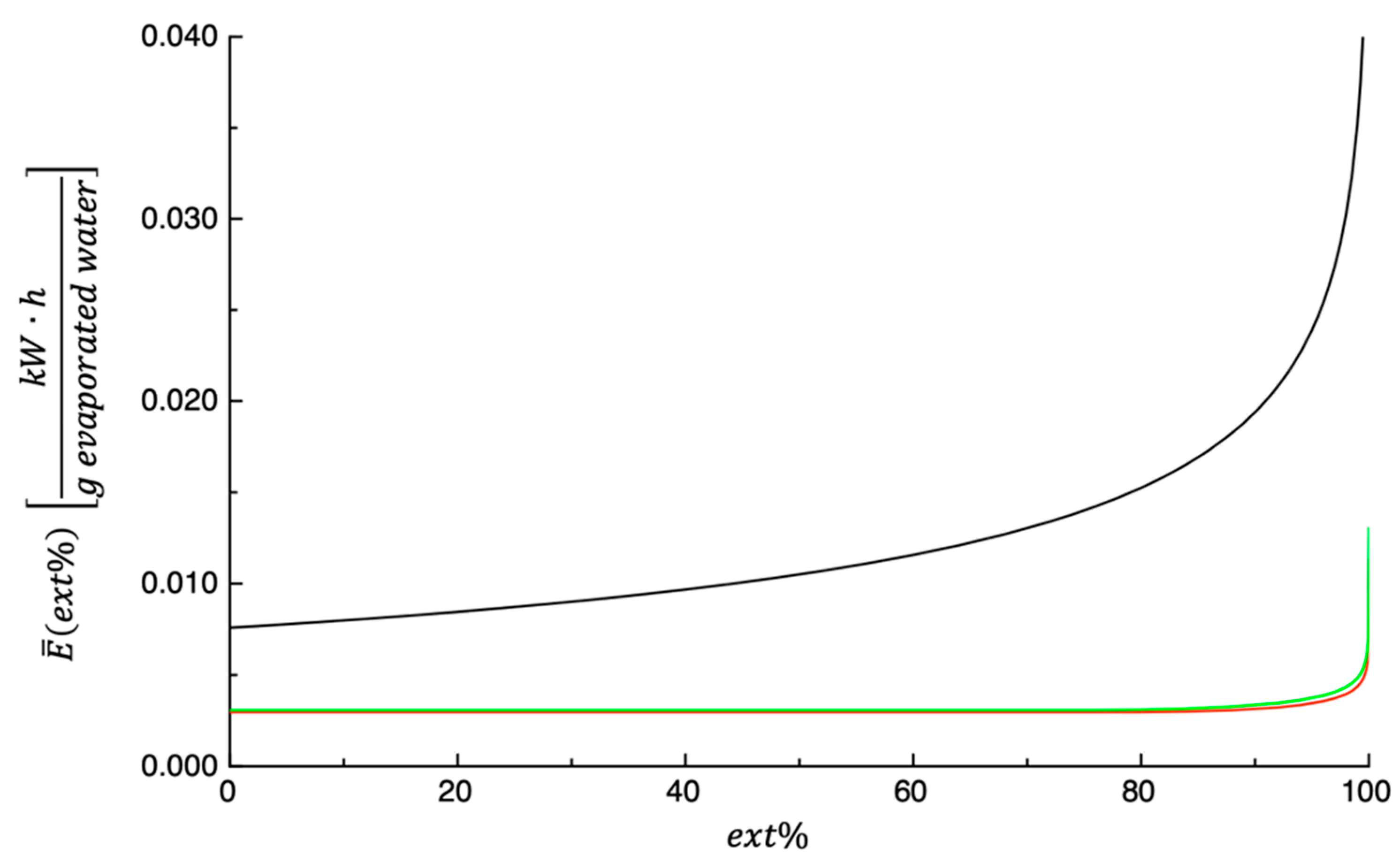
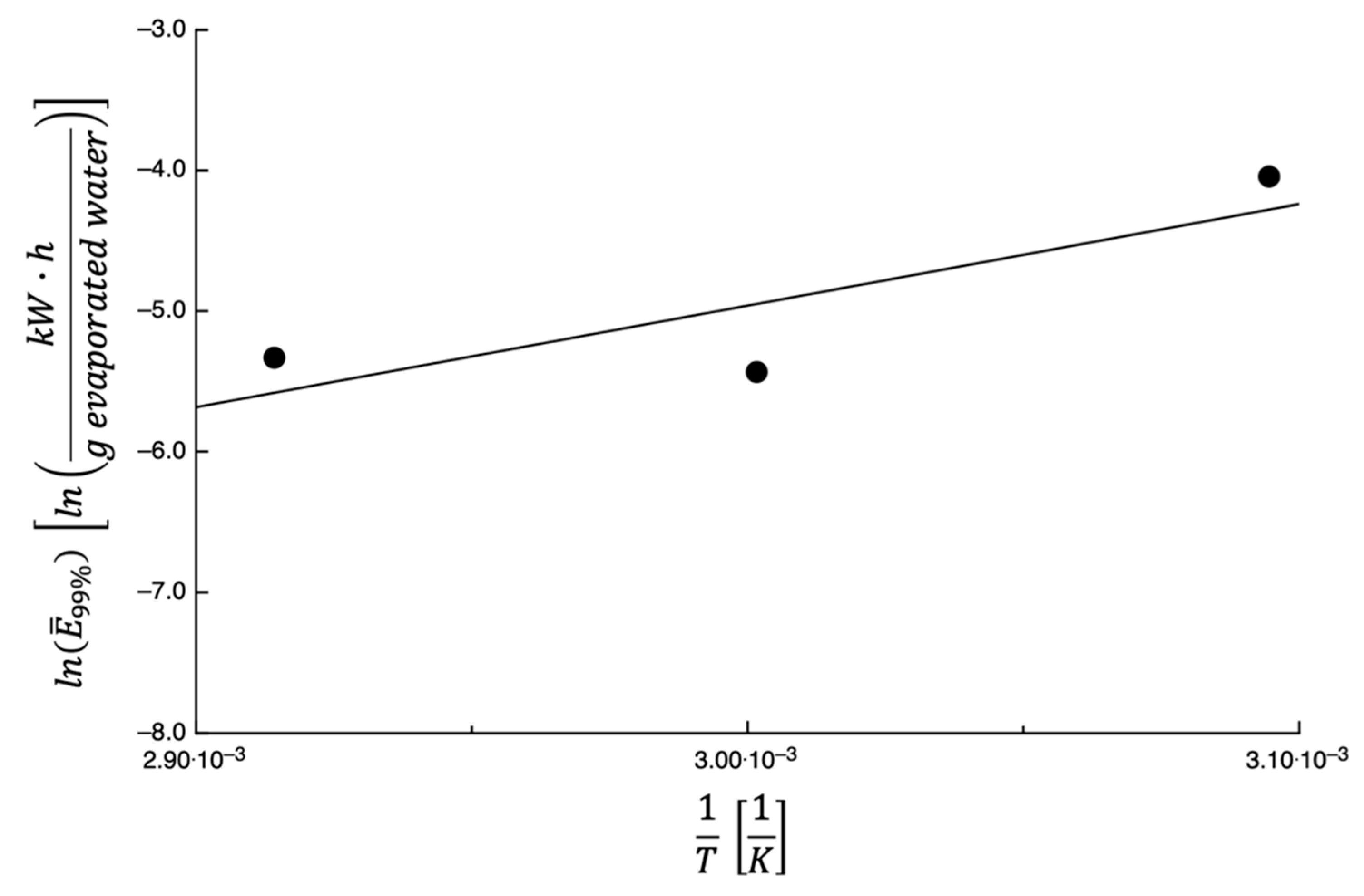
3.3. Energy Consumption Calculation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lipsa, F.D.; Ulea, E.; Gafencu, A.-M.; Florea, A.-M.; Rat, R.N.; Stoica, F.; Motrescu, I.; Râpeanu, G. Pumpkin Pomace Powder as a Bioactive Powder Ingredient for Whey Cheese Production. Appl. Sci. 2024, 14, 9624. [Google Scholar] [CrossRef]
- Chowdhary, P.; Gupta, A.; Gnansounou, E.; Pandey, A.; Chaturvedi, P. Current trends and possibilities for exploitation of grape pomace as a potential source for value addition. Environ. Pollut. 2021, 278, 116796. [Google Scholar] [CrossRef]
- Grassino, A.N.; Ostojic, J.; Miletic, V.; Djakovic, S.; Bosiljkov, T.; Zoric, Z.; Ježek, D.; Brncic, S.R.; Brncic, M. Application of high hydrostatic pressure and ultrasound-assisted extractions as a novel approach for pectin and polyphenols recovery from tomato peel waste. Innov. Food Sci. Emerg. Technol. 2020, 64, 102424. [Google Scholar] [CrossRef]
- Constantin, O.E.; Stoica, F.; Ratu, R.N.; Stanciuc, N.; Bahrim, G.E.; Râpeanu, G. Bioactive Components, Applications, Extractions, and Health Benefits of Winery By-Products from a Circular Bioeconomy Perspective: A Review. Antioxidants 2024, 13, 100. [Google Scholar] [CrossRef]
- Timpanaro, G.; Cosentino, S.; Danzì, C.; Foti, V.T.; Testa, G. Cactus pear for biogas production: Technical-economic validation of a biogas power installation in an area with a high prevalence of cacti in Italy. Biofu. Bioprod. Bioref. 2021, 15, 615–636. [Google Scholar] [CrossRef]
- Kowalska, H.; Czajkowska, K.; Cichowska, J.; Lenart, A. What’s new in biopotential of fruit and vegetable by-products applied in the food processing industry. Trends Food Sci. Technol. 2017, 67, 150–159. [Google Scholar] [CrossRef]
- Danzì, C.; Testa, G.; Stella, G.; Foti, V.T.; Timpanaro, G. Potential and location of an anaerobic digestion plant using cactus pear biomass in semi-arid Mediterranean environment. J. Clean. Prod. 2020, 249, 119396. [Google Scholar] [CrossRef]
- Manzur-Valdespino, S.; Arias-Rico, J.; Ramírez-Moreno, E.; Sánchez-Mata, M.D.C.; Jaramillo-Morales, O.A.; Angel-García, J.; Zafra-Rojas, Q.Y.; Barrera Gálvez, R.; Cruz-Cansino, N.D.S. Applications and pharmacological properties of cactus pear (Opuntia spp.) peel: A review. Life 2022, 12, 1903. [Google Scholar] [CrossRef]
- Pérez-Jiménez, J.; Saura-Calixto, F. Fruit peels as sources of non-extractable polyphenols or macromolecular antioxidants: Analysis and nutritional implications. Food Res. Int. 2018, 111, 148–152. [Google Scholar] [CrossRef]
- Amaya-Cruz, D.M.; Pérez-Ramírez, I.F.; Delgado-García, J.; Mondragón-Jacobo, C.; Dector-Espinoza, A.; Reynoso-Camacho, R. An integral profile of bioactive compounds and functional properties of prickly pear (Opuntia ficus-indica L.) peel with different tonalities. Food Chem. 2019, 278, 568–578. [Google Scholar] [CrossRef]
- Bouazizi, S.; Montevecchi, G.; Antonelli, A.; Hamdi, M. Effects of prickly pear (Opuntia ficus-indica L.) peel flour as an innovative ingredient in biscuits formulation. LWT-Food Sci Technol. 2020, 124, 109155. [Google Scholar] [CrossRef]
- Chafai, Y.; Raffak, A.; El-Aalaoui, M.; Sbaghi, M.; Djerrari, A.; Zahar, M. Valorization of prickly pear peels & seed press-cake in traditional sourdoughs and evaluation of their bread-making capacities. J. Microbiol. Biotechnol. Food Sci. 2023, 13, e9744. [Google Scholar]
- Kallel, F.; Chaieb, Z.; Belghith Fendri, L.; Ellouz Chaabouni, S.; Neifar, M. By-product of prickly pear juice industry: A novel ingredient to improve the physicochemical, texture and sensory properties of cake. J. Food Measur. Charact. 2024, 18, 7656–7668. [Google Scholar] [CrossRef]
- Gómez-López, I.; Eseberri, I.; Cano, M.P.; Portillo, M.P. Anti-obesity effect of different Opuntia stricta var. dillenii’s prickly pear tissues and industrial by-product extracts in 3T3-L1 mature adipocytes. Nutrients 2024, 16, 499. [Google Scholar]
- Panza, O.; Lacivita, V.; Conte, A.; Del Nobile, M.A. Quality preservation of ready-to-eat prickly pears by peels recycling. Foods 2022, 11, 2016. [Google Scholar] [CrossRef] [PubMed]
- Gannuscio, R.; Vastolo, A.; Maniaci, G.; Lucia, C.; Calabrò, S.; Todaro, M.; Cutrignelli, M.I. Improve nutritive value of silage based on prickly pear peel by-products. Ital. J. Animal Sci. 2024, 23, 492–503. [Google Scholar] [CrossRef]
- Noor Mohammed, A.; Chauhan, O.P.; Semwal, A.D. Emerging technologies for fruits and vegetables dehydration. Food Human. 2024, 2, 100303. [Google Scholar] [CrossRef]
- Gouws, C.A.; D’Cunha, N.M.; Georgousopoulou, E.N.; Mellor, D.D.; Naumovski, N. The effect of different drying techniques on phytochemical content and in vitro antioxidant properties of Australian-grown prickly pears (Opuntia ficus-indica). J. Food Process. Preserv. 2019, 43, e13900. [Google Scholar] [CrossRef]
- Ferreira, R.M.; Wessel, D.F.; Silva, A.M.S.; Saraiva, J.A.; Cardoso, S.M. Infusion from Opuntia ficus-indica Peels: The Effects of Drying and Steeping Conditions. Beverages 2023, 9, 97. [Google Scholar] [CrossRef]
- Lahsasni, S.; Kouhila, M.; Mahrouz, M.; Jaouhari, J.T. Drying kinetics of prickly pear fruit (Opuntia ficus-indica). J. Food Eng. 2004, 61, 173–179. [Google Scholar] [CrossRef]
- Abraham-Juárez, D.M.A.; Olalde-Portugal, V.; Cerón-García, A.; Sosa-Morales, M.E. Hot airdrying kinetics of thin layers of prickly pear fruit paste. Sains Malays. 2019, 48, 361–367. [Google Scholar] [CrossRef]
- Garcia-Amezquita, L.E.; Tejada-Ortigoza, V.; Campanella, O.H.; Welti-Chanes, J. Influence of drying method on the composition, physicochemical properties, and prebiotic potential of dietary fibre concentrates from fruit peels. J. Food Qual. 2018, 2018, 9105237. [Google Scholar] [CrossRef]
- Noshad, M.; Taki, M.; Ghasemi, P.; Gandomani, M.P. Greenhouse solar drying of tarragon: Mathematical modeling and quality features. J. Agric. Food Res. 2025, 19, 101626. [Google Scholar] [CrossRef]
- Sridhar, K.; Charles, A.L. Mathematical Modeling to Describe Drying Behavior of Kyoho (Vitis labruscana) Skin Waste: Drying Kinetics and Quality Attributes. Processes 2022, 10, 2092. [Google Scholar] [CrossRef]
- Conte, A.; Panza, O.; Del Nobile, M.A. Modeling the dehydration kinetic of grape pomace. LWT-Food Sci Technol. 2024, 198, 116021. [Google Scholar] [CrossRef]
- Conte, A.; Lordi, A.; Del Nobile, M.A. Dehydration of tomato peels and seeds as affected by the temperature. Int. J. Food Sci. Technol. 2024, 59, 7325–7333. [Google Scholar] [CrossRef]
- Lordi, A.; Conte, A.; Del Nobile, M.A. Nutritional and antimicrobial properties of tomato by-products as affected by dehydration temperature. Food Biosci. 2025, 63, 105797. [Google Scholar] [CrossRef]
- Buonocore, G.G.; Del Nobile, M.A.; Di Martino, C.; Gambacorta, G.; La Notte, E.; Nicolais, L. Modeling the water transport properties of casein-based edible coating. J. Food Eng. 2003, 60, 99–106. [Google Scholar] [CrossRef]
- Kabore, K.; Konate, K.; Dakuyo, R.; Sanou, A.; Sama, H.; Santara, B.; Dicko, H.M. Evaluation of phytonutrients composition and nutraceutical potential of tomato by-products. CyTA—J. Food 2022, 20, 404–411. [Google Scholar] [CrossRef]
- Aruwa, C.E.; Amoo, S.; Kudanga, T. Phenolic compound profile and biological activities of Southern African Opuntia ficus-indica fruit pulp and peels. LWT 2019, 111, 337–344. [Google Scholar] [CrossRef]

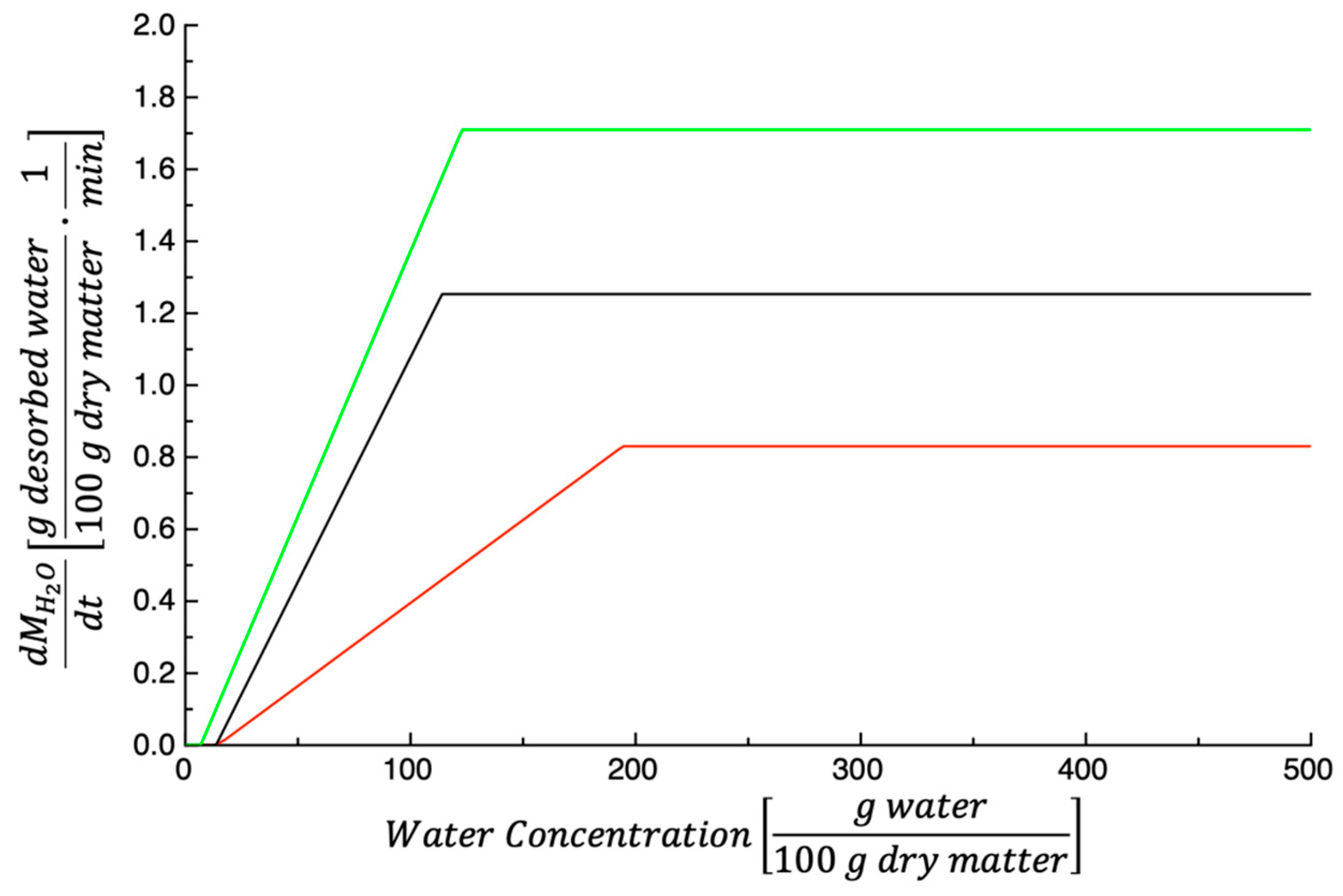
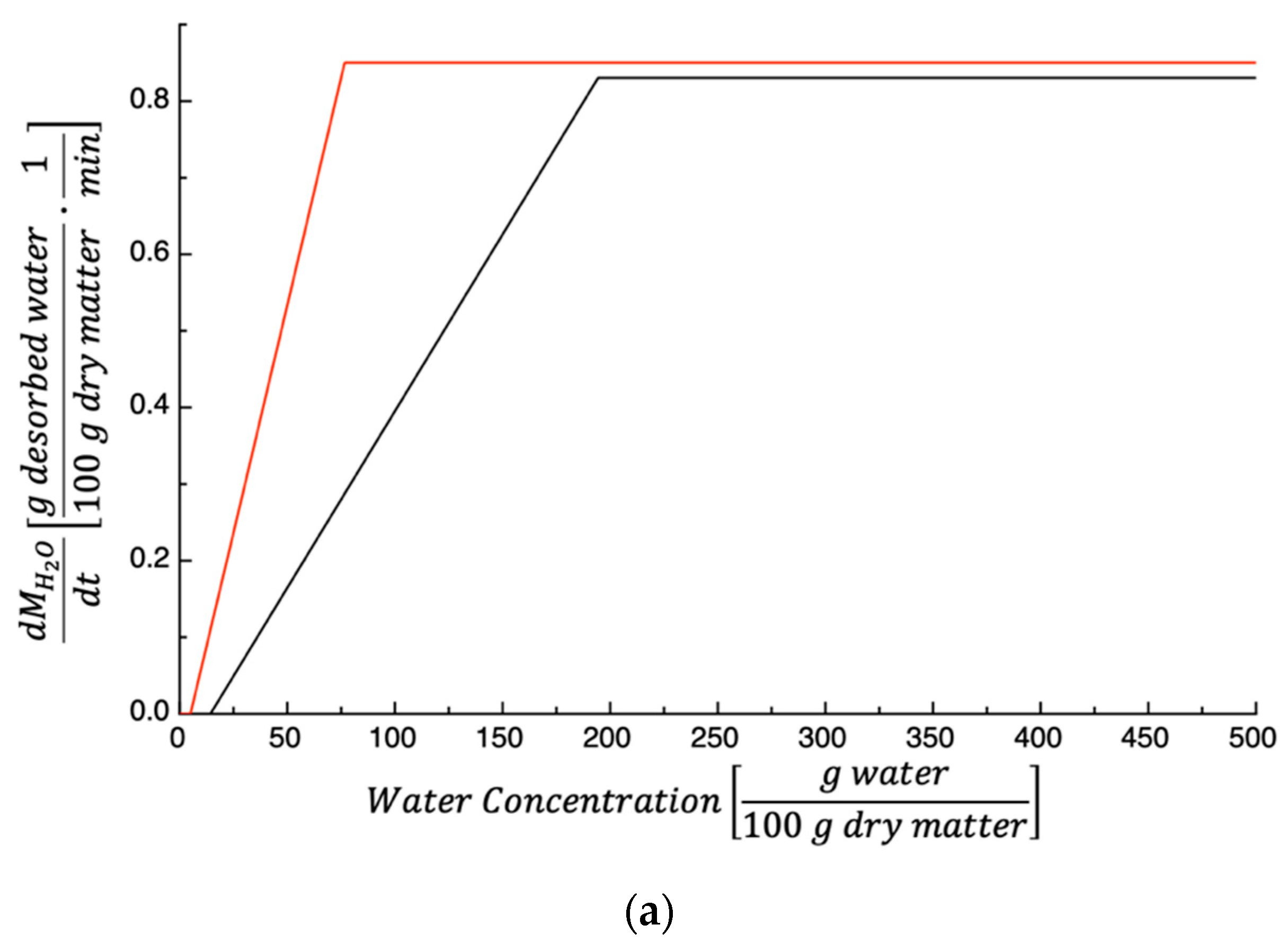
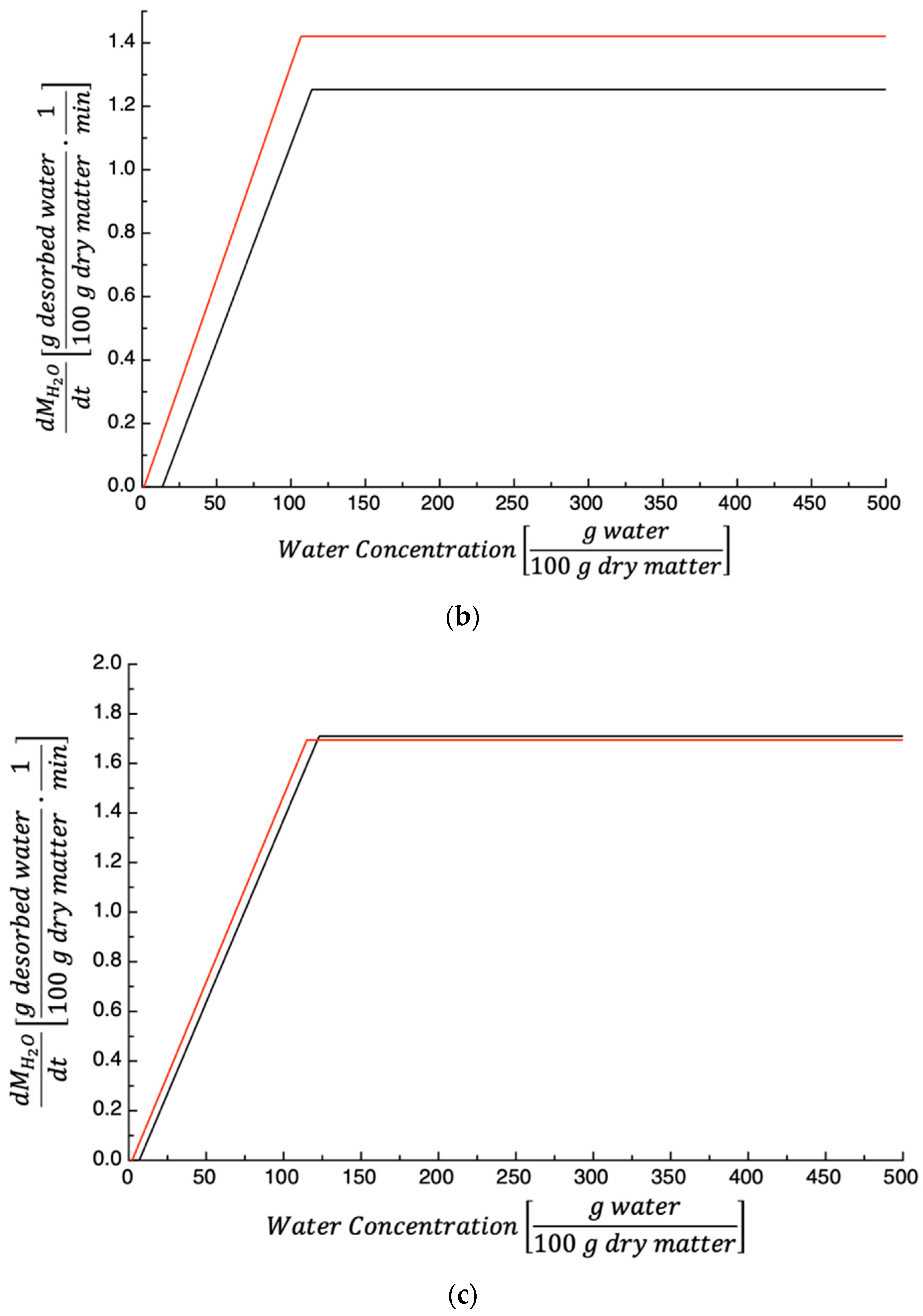

| Parameters | 50 °C | 60 °C | 70 °C |
|---|---|---|---|
| 258 | 282 | 202 | |
| 0.830 | 1.25 | 1.71 | |
| 180 | 100 | 116 |
| Parameter | |||
|---|---|---|---|
| 2.44 | |||
| 3.89 | |||
| 0.434 | |||
| 1.60 | |||
| 6.47 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Panza, O.; Del Nobile, M.A.; Conte, A. The Optimization of the Dehydration Temperature of Peels from Prickly Pears. Foods 2025, 14, 811. https://doi.org/10.3390/foods14050811
Panza O, Del Nobile MA, Conte A. The Optimization of the Dehydration Temperature of Peels from Prickly Pears. Foods. 2025; 14(5):811. https://doi.org/10.3390/foods14050811
Chicago/Turabian StylePanza, Olimpia, Matteo Alessandro Del Nobile, and Amalia Conte. 2025. "The Optimization of the Dehydration Temperature of Peels from Prickly Pears" Foods 14, no. 5: 811. https://doi.org/10.3390/foods14050811
APA StylePanza, O., Del Nobile, M. A., & Conte, A. (2025). The Optimization of the Dehydration Temperature of Peels from Prickly Pears. Foods, 14(5), 811. https://doi.org/10.3390/foods14050811










